72

7. Rozwiązywanie zadań opisanych równaniami nieliniowymi

Pierwiastki rzeczywiste równania nieliniowego o ogólnej postaci f(x)=0 można
wyznaczyć za pomocą funkcji fzero.
Tekst

funkcji

fzero można wyświetlić na ekranie – podobnie jak wiele innych

funkcji - pisząc polecenie

type

fzero

Opis wywołania funkcji fzero jest dostępny za pomocą polecenia

help

fzero

Wywołanie funkcji z 2 argumentami wejściowymi

p = fzero(‘nazwafunkcji’,x0)

daje w wyniku pierwiastek równania znajdujący się w otoczeniu punktu x0.

Przykładowo

polecenie

p = fzero(‘sin’,3)

daje w wyniku wartość pierwiastka p = pi, co odpowiada przejściu funkcji sinus przez
zero w punkcie 180

O

.

Wyliczone pierwiastki równania nieliniowego f(x)=0 można pokazać na wykresie

za pomocą funkcji fplot.

Jeśli wykładniki potęg zmiennej x w równaniu nieliniowym f(x)=0 są liczbami
naturalnymi, to do rozwiązania zaleca się stosowanie funkcji roots wyznaczającej
miejsca zerowe wielomianu.

Polecenie

p = roots(c)

pozwala wyznaczyć pierwiastki wielomianu o następującej postaci

1

n

n

2

1

n

1

n

2

n

1

c

x

c

x

c

...

x

c

x

c

)

x

(

y

+

−

−

+

+

+

+

+

=

(7.1)

Należy zwrócić uwagę, że postać wielomianu podana wzorem (7.1) różni się od
postaci stosowanej w podręcznikach matematyki, w których zwykle wyraz wolny ma
indeks 0.

73

Przykład

rozwiązania równania nieliniowego za pomocą fzero oraz roots

Należy wyznaczyć wszystkie rozwiązania równania nieliniowego

0

3

x

3

x

x

2

3

=

−

−

+

(7.2)

za pomocą funkcji fzero oraz roots, a następnie zilustrować na wykresie funkcji
położenie tych rozwiązań.

function y=wielom(x)
% wielomian, w ktorym zmienna x moze byc wektorem
y=x.^3 + x.^2 -3.*x -3; return

function yzero=osx(x)
% zerowa os odcietych
yzero=0; return

function [xroots,xfzero] = oblicz
% funkcja znajduje pierwiastki za pomoca roots oraz fzero
% wielomian: y = x^3+x^2-3*x-3
format long; % zwiekszenie ilosci wyswietlanych cyfr
disp('pierwiastki wyznaczone za pomoca roots :');
xroots = roots([1 1 -3 -3]);
disp(xroots);
disp(' sprawdzenie dokladnosci za pomoca funkcji polyval');
epsxroots = polyval([1 1 -3 -3], xroots); disp(epsxroots);
disp('pierwiastki wyznaczone za pomoca fzero :');
disp('pierwiastek 1-szy w otoczeniu x0=2 :');
x1=fzero('wielom',2); disp(x1);
disp('pierwiastek 2-gi w otoczeniu x0=-2 :');
x2=fzero('wielom',-2); disp(x2);
disp('pierwiastek 3-ci w otoczeniu x0=0 :');
x3=fzero('wielom',0); disp(x3);
xfzero=[x1; x2; x3];
disp('roznica rozwiazan xroots oraz xfzero');
roznica=xroots-xfzero; disp(roznica);
% Wykres wielomianu y=x^3+x^2-3*x-3
fplot('[wielom(x),osx(x)]',[-2,2]);
hold on;
plot(x1,0,'kO',x2,0,'bO',x3,0,'rO');
text(x1,0.5,'x1'); text(x2,0.5,'x2'); text(x3,0.5,'x3');
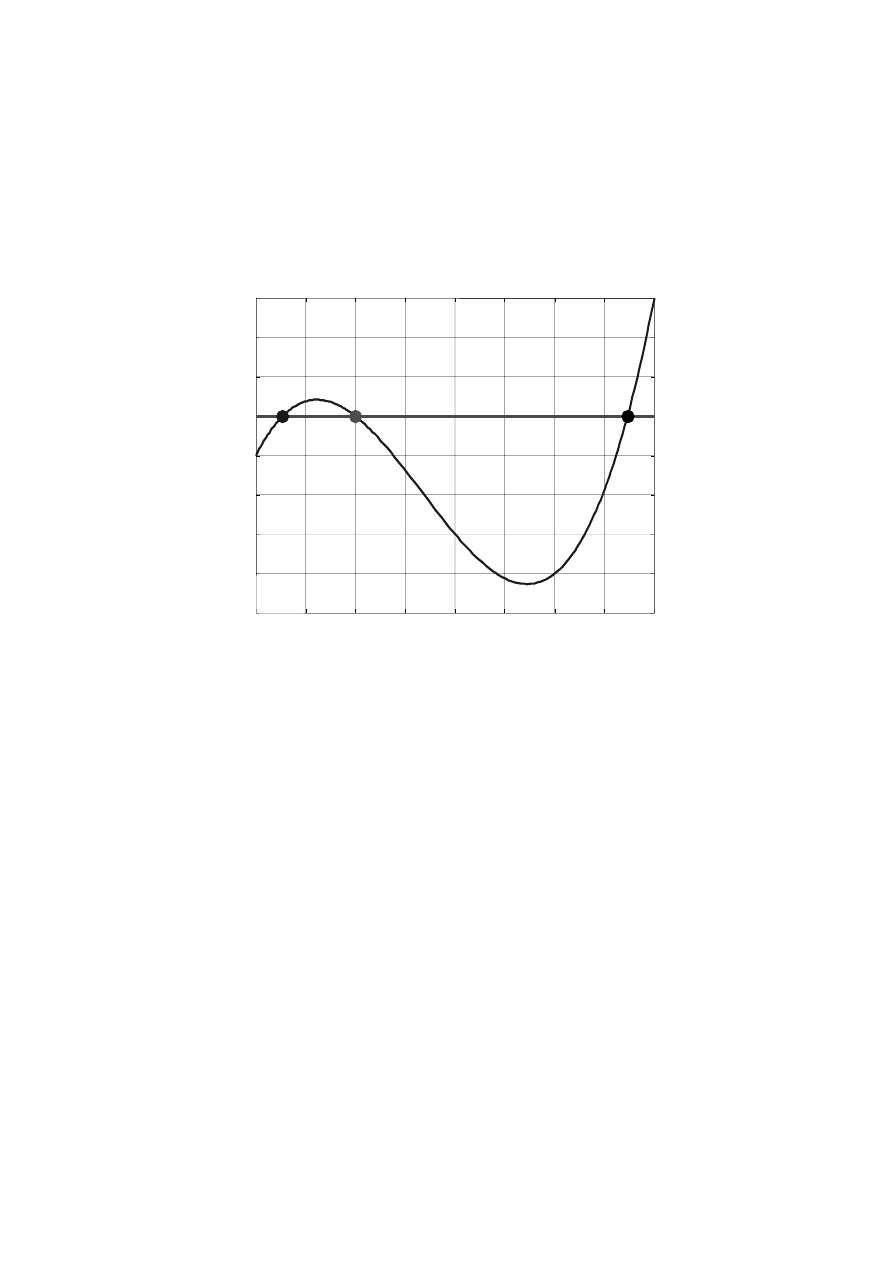
title(' Wielomian y = x^3 +x^2 - 3*x -3 ');
xlabel(' x'); ylabel(' y'); grid on;
return

74

Po wywołaniu funkcji oblicz otrzymuje się wykres pokazany na rys. 7.2. oraz
wyniki obliczeń w oknie poleceń Matlaba.

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

-4

-3

-2

-1

0

1

2

3

x1

x2

x3

Wielomian y = x

3

+ x

2

- 3x - 3

x

y

Rys. 7.1. Wykres wielomianu z naniesionymi wartościami pierwiastków

>> [w,z]=oblicz

pierwiastki wyznaczone za pomoca roots :
1.73205080756888
-1.73205080756888
-1.00000000000000
sprawdzenie dokladnosci za pomoca funkcji polyval
1.0e-014 *
0.22204460492503
-0.39968028886506
0

pierwiastki wyznaczone za pomoca fzero :
pierwiastek 1-szy w otoczeniu x0=2 :
1.73205080756888
pierwiastek 2-gi w otoczeniu x0=-2 :
-1.73205080756888
pierwiastek 3-ci w otoczeniu x0=0 :

75

-1.00000000000000
roznica rozwiazan xroots oraz xfzero
1.0e-014 *
0
-0.11102230246252
0

w =
1.73205080756888
-1.73205080756888
-1.00000000000000

z =
1.73205080756888
-1.73205080756888

W nowszych wersjach Matlaba funkcję fzero można stosować do rozwiązywania

równania nieliniowego zdefiniowanego w postaci funkcji z parametrami
wejściowymi.

Zadania elektrotechniczne są często opisane układami równań nieliniowych. Do
ich rozwiązania można wykorzystać funkcję fsolve.
Układ

równań nieliniowych ma następującą ogólną postać

0

f(x)

=

(7.3)

gdzie

(x)]

f

...

(x),

f

(x),

[f

f(x)

n

2

1

=

(7.4)

]

[

x

n

2

1

x

...,

,

x

,

x

=

(7.5)

Funkcja

fsolve rozwiązuje układ równań nieliniowych metodą najmniejszych

kwadratów. Należy zwrócić uwagę, że funkcja fsolve w nowszych wersjach Matlaba
korzysta z tablic strukturalnych, w których dostęp do danych odbywa się przez
podanie nazwy pola. Tablice strukturalne mogą zawierać różne typy danych, np. jedno
pole zawiera liczbę, inne łańcuch.

Tablicę strukturalną można utworzyć za pomocą instrukcji przypisania albo za
pomocą funkcji struct:

•

za pomocą instrukcji przypisania, np.

tabstrukt.nazwa=’pomiar 1’;
tabstrukt.srednia=37.31;
tabstrukt.pomiar=[1 2 3 4 5 6 7 8 9];

76

•

za pomocą funkcji tabstruct=struct(‘pole1’,wartosc1,’pole2’,wartosc2,..)

tabstrukt=...
struct('nazwa','pomiar 1','srednia',57,'pomiar',[1 2 3 4 5])
tabstrukt =
nazwa: 'pomiar 1'
srednia: 57
pomiar: [1 2 3 4 5]

Aby

powiększyć tablicę strukturalną, dodaje się indeks za nazwą tablicy przed

polem

tabstrukt(2).nazwa=’pomiar 2’;
tabstrukt(2).srednia=17.31;
tabstrukt(2).pomiar=[11 12 13 14 15 16 17 18 19];

Podczas rozszerzania struktury Matlab wypełnia niewyspecyfikowane pola
macierzami pustymi. Dostęp do danego pola jest możliwy po podaniu nazwy struktury
i nazwy pola

tabstrukt(1).pomiar
ans =
1 2 3 4 5

Dostęp do danego elementu wewnątrz pola jest możliwy po przez podanie
indeksów

tabstrukt(1).pomiar(1,3)
ans =
3

Inny sposób dostępu wykorzystuje funkcję getfield

f=getfield(nazwa_tablicy,{ineks_tablicy},’nazwa_pola’,{indeks_pola} )

Pola

są usuwane za pomocą funkcji rmfiled

rmfiled(nazwa_tablicy,’nazwa_pola’)

Nazwy pól tablicy strukturalnej można odczytać za pomocą funkcji fieldnames.

Przykładowo

tabstrukt.nazwa='pomiar 1';
tabstrukt.srednia=3.7;
tabstrukt.pomiar=[1 2 3 4 5 6 7 8 9];
fieldnames(tabstrukt)
ans =

77

'nazwa'
'srednia'
'pomiar'

Warianty

wywołań funkcji fsolve

1. x = fsolve(fun,x0)
gdzie fun – funkcja akceptująca parametr wejściowy x, zwracająca wartość f(x).

2. x = fsolve(fun,x0,options)
gdzie options – opcje poszukiwania rozwiązania ustalane poprzez wywołanie funkcji
foptions lub w nowszych wersjach Matlaba przez optimset.

3. x = fsolve(fun,x0,[])
gdzie [] – pusta macierz zamiast wektora options powoduje przyjęcie standardowych
wartości opcji.

4. x = fsolve(fun,x0,options,p1,p2,...)
lub

x = fsolve(fun,x0,[],p1,p2,...)

gdzie p1,p2,... – parametry funkcji fun od których zależy rozwiązanie.

5. [x,fval] = fsolve(fun,x0,options,p1,p2,...)
gdzie fval – wartość funkcji celu, czyli sumy kwadratów błędów rozwiązań.

6. [x,fval,exitflag] = fsolve(fun,x0,options,p1,p2,...)
gdzie

exitflag >0 – rozwiązanie zbieżne,

exitflag = 0 – osiągnięto maksymalną liczbę iteracji,

exitflag < 0 – brak zbieżności procesu iteracyjnego.

7. [x,fval,exitflag,output] = fsolve(fun,x0,options,p1,p2,...)
gdzie

output.iterations – liczba iteracji,

output.funcCount – liczba szacowania funkcji celu,

output.algorithm – wykorzystany algorithm,

output.cgiterations – liczba iteracji CG,

output.firstorderopt – optymalizacja rzędu pierwszego.

8. [x,fval,exitflag,output,jacob] = fsolve(fun,x0,options,p1,p2,...)
gdzie jacob – macierz Jacobiego funkcji f(x) w punkcie x.

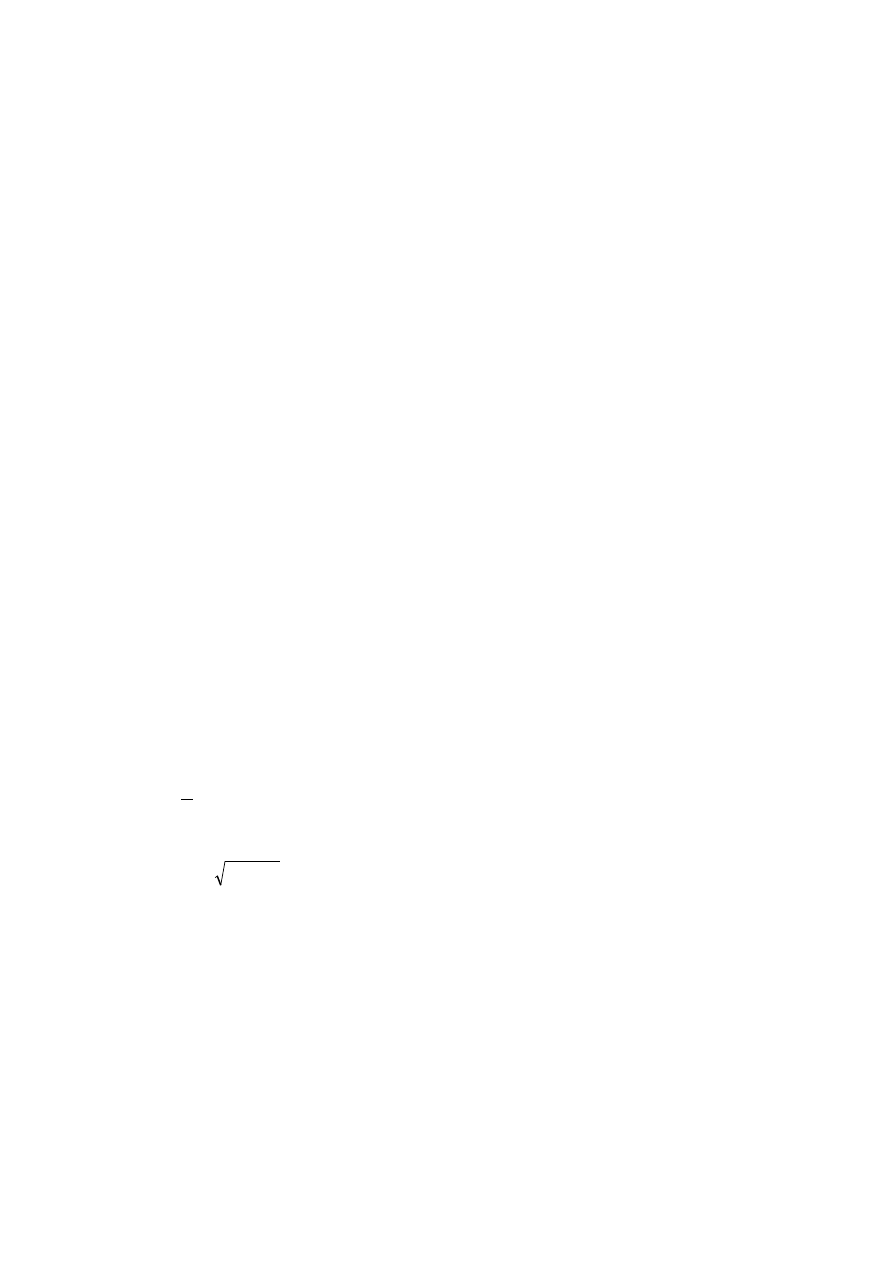
78

W Matlabie 4.2 funkcję fsolve wywołuje się z podaniem gradientu stosując
następującą postać polecenia

options=foptions;

x=fsolve(fun,x0,options,grad,p1,p2,..);

gdzie

grad – m-plik zawierający gradient funkcji y=f(x).

Należy zwrócić uwagę na fakt, że macierze w Matlabie zapamiętywane są
kolejnymi kolumnami, a nie wierszami jakby się wydawało. Z tego powodu gradient
jest równy transponowanej macierzy Jacobiego danego układu równań nieliniowych.

Wykorzystanie

funkcji

fsolve do rozwiązywania układu równań nieliniowych

zilustrowano na przykładzie równań węzłowych napięciowo-mocowych.

Przykład zastosowania funkcji fsolve do analizy układu przesyłowego: system-

linia-odbiór

Duży zakład przemysłowy jest zasilany linią wysokiego napięcia 220 kV, rys. 7.2.
Moc czynna i bierna dopływająca do odbioru wyrażona jest układem 2 równań
węzłowych kwadratowych, zapisanych w jednostkach względnych odniesionych do
mocy bazowej 484 MV

⋅

A oraz napięcia znamionowego 220 kV

Bf

Ge

GU

P

2

−

−

=

−

(7.6)

Gf

Be

BU

Q

2

−

+

−

=

−

(7.7)

gdzie

P, Q – moc czynna i bierna odbioru,

G, B – konduktancja i susceptancja podłużna linii,

U = e + jf – napięcie zespolone odbioru zapisane w postaci algebraicznej,

e – składowa prostokątna rzeczywista napięcia odbioru,

f – składowa prostokątna urojona napięcia odbioru,

U

2

= e

2

+ f

2

- kwadrat modułu napięcia odbioru,

U =

2

2

f

e

+

– wartość skuteczna napięcia odbioru.

Należy wyznaczyć napięcie odbioru odpowiadające poborowi mocy czynnej i
biernej. Dodatkowo należy wyznaczyć zależność napięcia odbioru od zmieniającego
się poboru mocy biernej, przy stałym poborze mocy czynnej.

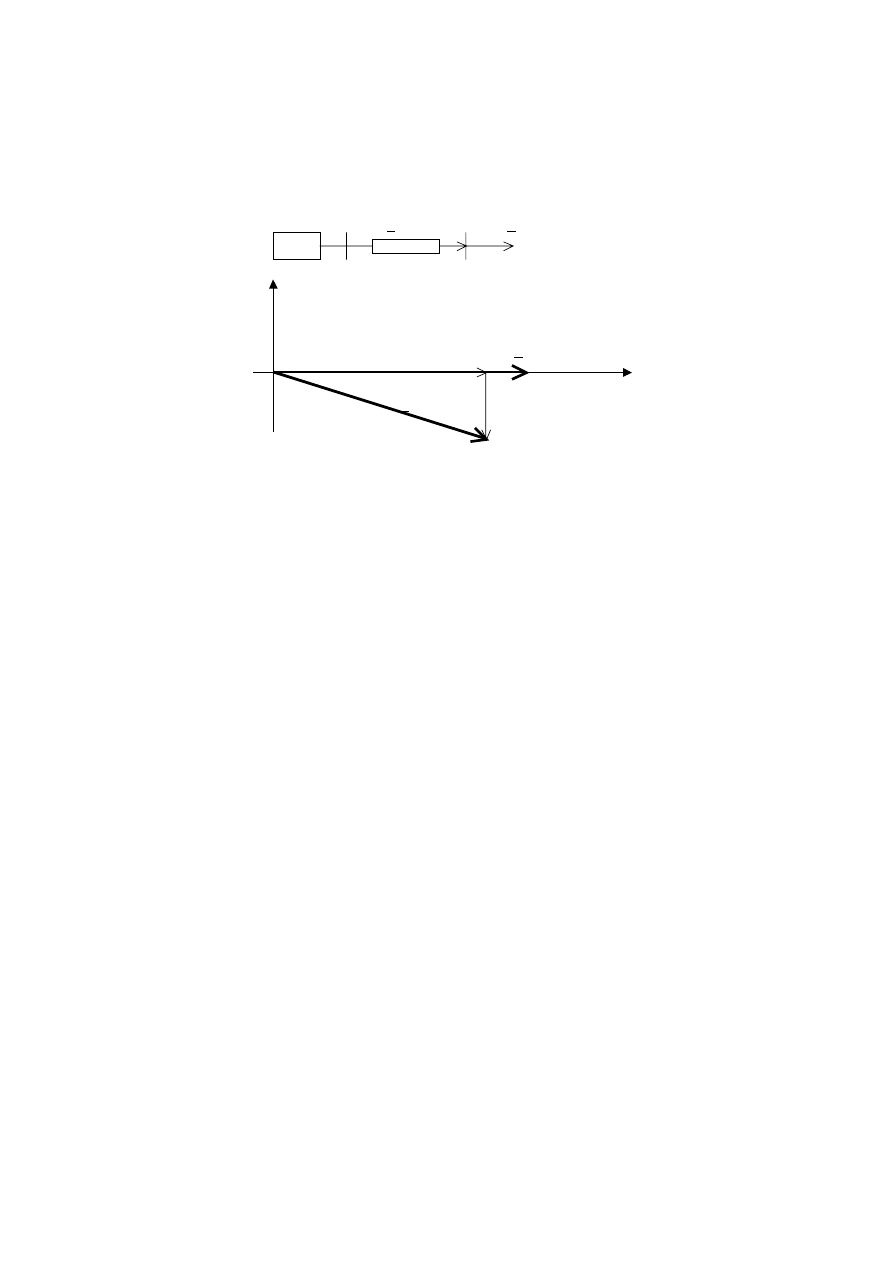
79

SEE

U

s

U

Z=R+jX S=P+jQ

U

s

=U

s

+j0

U=e+jf

Re

Im

e

f

Rys. 7.2. Schemat układu zasilającego duży zakład przemysłowy oraz wykres napięć w

układzie.

Równania

węzłowe opisujące układ przesyłowy pokazany na rys. 7.2 mają postać

0

P

Bf

Ge

Gf

Ge

2

2

=

+

−

−

+

(7.8)

0

Q

Gf

Be

Bf

Be

2

2

=

+

−

+

−

−

(7.9)

Układ

równań napięciowo-mocowych można rozwiązać za pomocą fsolve. Przy

pisaniu programu wygodnie jest dokonać podstawień pozwalających wykorzystać
standardowe sposoby wywołania funkcji fsolve .

W naszym przypadku będą to następujące podstawienia

x(1)=e, x(2)=f, p1= G, p2= B, p3=P, p4=Q

W celu rozwiązania zadania za pomocą funkcji fsolve utworzono 3 następujące
funkcje:

•

rmf() – funkcja definiująca układ równań nieliniowych,

•

rmg() – funkcja obliczająca gradient równań węzłowych,

•

rmobl() – funkcja sterująca obliczeniami.

function f = rmf(x,G,B,P,Q)
% rownania wezlowe mocy
f(1)= G*x(1)^2 + G*x(2)^2 - G*x(1) - B*x(2) + P;
f(2)=-B*x(1)^2 - B*x(2)^2 + B*x(1) - G*x(2) + Q;
return

80

function df = rmg(x,G,B,P,Q)
% gradient rownan wezlowych mocy odbioru
% f(1)= G*x(1)^2 + G*x(2)^2 - G*x(1) - B*x(2) + P;
% f(2)=-B*x(1)^2 - B*x(2)^2 + B*x(1) - G*x(2) + Q;
macJac=[ 2*G*x(1)-G

2*G*x(2)-B

-2*B*x(1)+B

-2*B*x(2)-G];

df = macJac'; %gradient rowny transponowanej m. Jacobiego
return


function [Q,U] = rmobl(R,X,Podb,Qodb,Sb,Un)
% function [Q,U] = rmroz(P,Q,Sb,Un)
% wyznacza charakterystyke Q-U mocy biernej
% dostarczanej linia wysokiego napiecia
% R, X - rezystancja i reaktancja linii w omach,
% P - moc czynna odbioru, MW
% Q - moc bierna odbioru, Mvar
% Sb - moc bazowa, MVA
% Un - napiecie znamionowe linii, kV
% Q - wektor mocy biernej zmienianej od 0 do Qmax, Mvar
% U - wartosc skuteczna napiecia odbioru, kV
if nargin < 6 Un=220; end
if nargin < 5 Sb=484; end
if nargin < 4 Podb=242; end
if nargin < 3 Qodb=121; end
if nargin < 2 R=10; end
if nargin < 1 X=20; end
j=sqrt(-1);
Zb=Un^2/Sb; % impedancja bazowa
Z=(R+j*X)/Zb; Y=1/Z;
G=real(Y); B=imag(Y); % parametry linii w jedn. wzglednych
P=Podb/Sb; Q=Qodb/Sb; % przeliczenie mocy na jednostki wzgledne
x0=[1 0]; x=x0; % punkt startowy obliczen
options=foptions; % opcje standardowe
% Wyznaczenie napiecia odbioru
x=fsolve('rmf',x0,options,'rmg',G,B,P,Q);
u=sqrt(x(1).^2 + x(2)^2); % wyznaczone napiecie odbioru
Urm = u*Un; % napiecie odbioru w kV
Qrm=Q*Sb; % moc bierna odbioru w Mvar
disp('Napiecie odbioru w kV wynosi:');
disp(Urm);
% Wyznaczanie charakterystyki napieciowej Q-U
i=0; Q=0;
U=[]; u0=1; U(1)=u0; u=1;
Qodb=[]; Qodb(1)=Q;
Ulawina=0.65*u0; % przyblizony punkt lawiny napiecia

81

while u > Ulawina % obliczenia az do lawiny napiecia
i=i+1; % kolejny krok charakterystyki Q-U

Q=Q+0.01; % przyrost mocy biernej

x=fsolve('rmf',x0,options,'rmg',G,B,P,Q);
u=sqrt(x(1).^2 + x(2)^2); % napiecie
Qodb(i)=Q*Sb; % moc bierna w Mvar
Uodb(i)=u*Un; % napiecie w kV
Urmi(i)=Urm; % napiecie odbioru
end
nroz=i; Qlawina=Q*Sb; Ulawina=Ulawina*Un;
disp(' Liczba wyznaczonych punktow charakterystyki
napieciowej');
disp(nroz);
plot(Qodb,Uodb,'b-',Qodb,Urmi,'r--');
title('Charakterystyka Q-U mocy biernej dostarczanej linia 220
kV');
xlabel('Q, Mvar'); ylabel('U, kV');
legend('Krzywa Q-U','Napiecie odbioru');
hold on;
plot(Qrm,Urm,'O');
text(Qrm,Urm+2,'Punkt pracy ukladu przesylowego');
plot(Qlawina,Ulawina,'O');
text(Qlawina-150,Ulawina+1,'Punkt lawiny napiecia');
grid on;
disp('KONIEC');
return

Przebieg

obliczeń numerycznych po wywołaniu funkcji rmobl jest następujący

Napiecie odbioru w kV wynosi:
194.2949
Liczba wyznaczonych punktow charakterystyki napieciowej
89
KONIEC

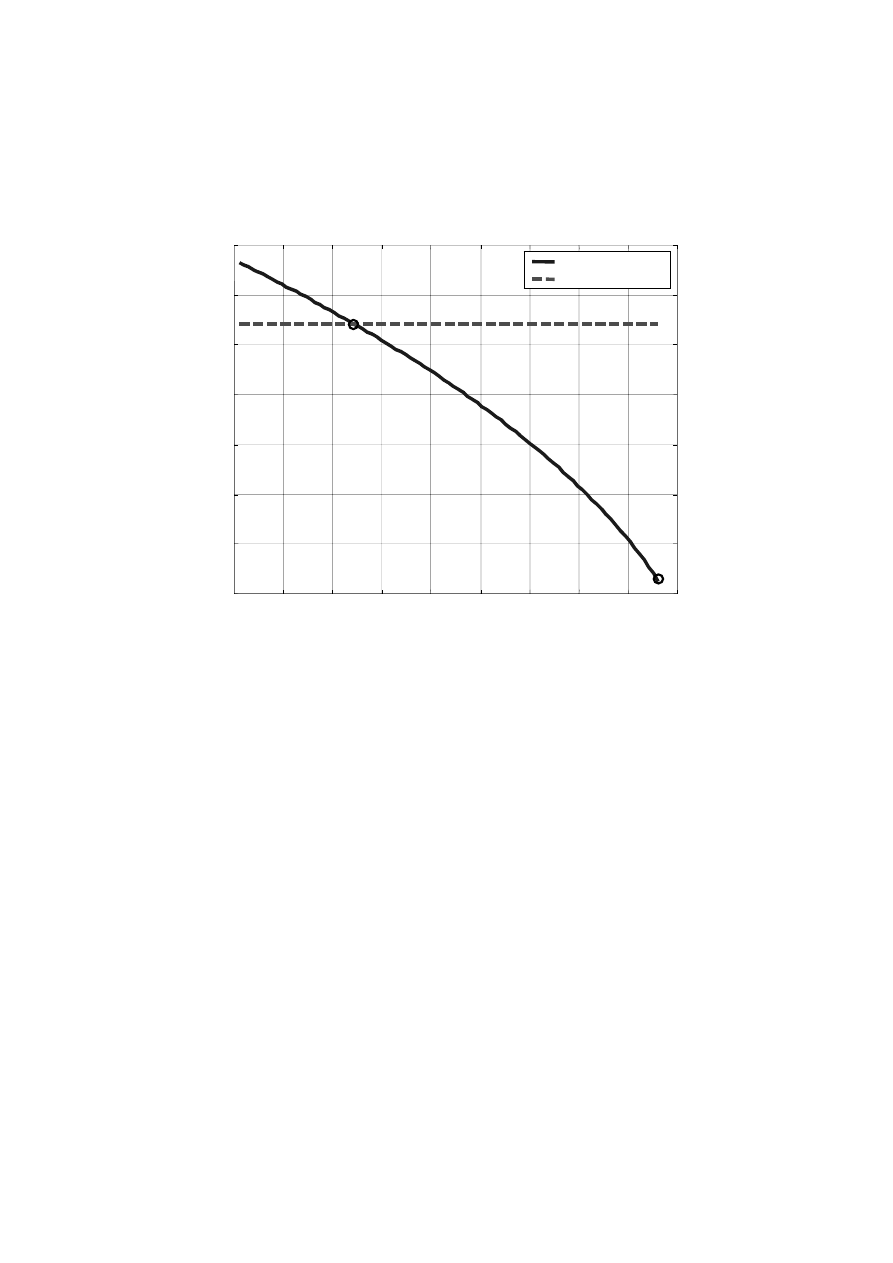
Funkcja

rmobl() po wyznaczeniu kolejnych rozwiązań za pomocą funkcji fsolve

tworzy wykres zmian napięcia odbioru od poboru mocy biernej pokazany na rys. 7.3.

82

0

50

100

150

200

250

300

350

400

450

140

150

160

170

180

190

200

210

Charakterystyka Q-U mocy biernej dostarczanej linia 220 kV

Q, Mvar

U,
kV

Punkt pracy ukladu przesylowego

Punkt lawiny napiecia

Krzywa Q-U

Napiecie odbioru

Rys. 7.3. Wyniki analizy układu przesyłowego: system-linia-odbiór otrzymane za pomocą funkcji solve

Zadania do samodzielnego rozwiązania

Zadanie

1

Zmodyfikować funkcje rmf(), rmg(), rmobl() tak, aby uzyskać charakterystykę
zmian napięcia od zmian przesyłanej mocy czynnej zamiast zmian mocy biernej.

Zadanie

2

Wzorując się na funkcjach rmf(), rmg(), rmobl() opracować program
rozwiązujący następujący układ równań nieliniowych

0

b

bx

bx

x

x

2

2

1

2

1

=

−

−

+

(7.10)

0

b

2

bx

2

bx

x

x

2

2

1

2

1

=

−

−

+

(7.11)

Parametr b może przyjmować dowolną wartość z przedziału

8

.

0

b

2

.

0

≤

≤

(7.12)

Przyjąć punkt startowy

x0=[2*b+0.1 b+0.1];