Z. Kąkol-Notatki do Wykładu z Fizyki

19-1

Wykład 19

19. Elektrostatyka I

19.1 Wstęp

Większość ciał stałych można podzielić na

przewodniki

i

izolatory

. W izolatorze

nadmiarowy ładunek może być rozmieszczony w całej objętości natomiast w przewod-
nikach swobodne elektrony będą się zbierały na powierzchni dopóty, dopóki nie wytwo-
rzy się pole równoważące pole zewnętrzne.
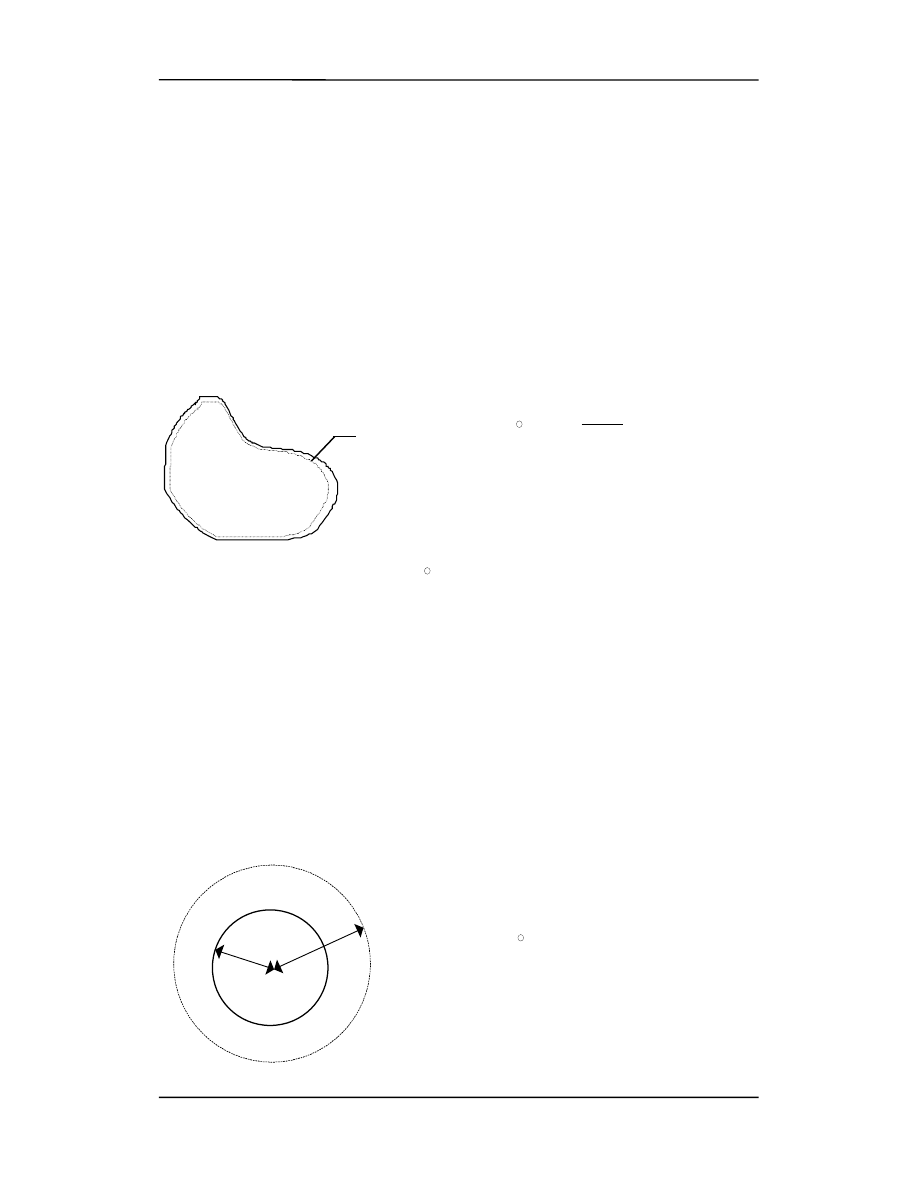
Rozpatrzmy dowolny w kształcie przewodnik. Wybierzmy powierzchnię zamkniętą tuż
poniżej powierzchni przewodnika. Zastosujmy prawo Gaussa do tej powierzchni

0

.

d

ε

wewn

Q

=

∫

S

E

Wewnątrz przewodnika w dowolnym punkcie po-
wierzchni S pole musi być równe zeru, bo inaczej elek-
trony poruszałyby się czyli

0

d

=

∫

S

E

Zatem

0 = Q

wewn.

/

ε

0

Stąd

Q

wewn.

= 0

Tak więc ładunek wewnątrz dowolnej zamkniętej powierzchni (przewodnika) musi być
równy zeru; cały ładunek gromadzi się na powierzchni.

19.2 Kuliste rozkłady ładunków

19.2.1 Jednorodnie naładowana sfera

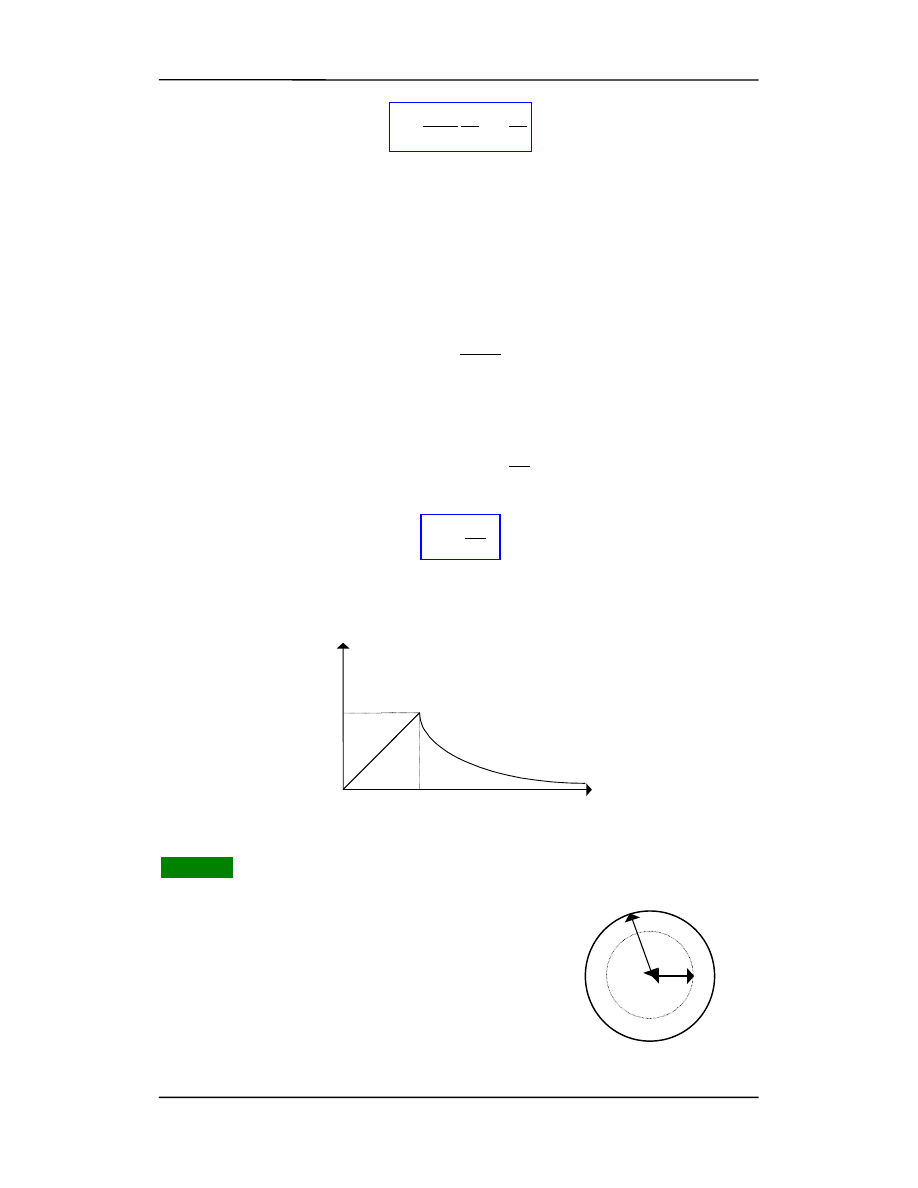
Rozpatrzmy jednorodnie naładowaną po-

wierzchnię kulistą. W dowolnym punkcie sfery E



S więc

∫

=

)

4

(

d

2

r

E

π

S

E

Zgodnie z prawem Gaussa:

E(4

π

r

2

) = Q/

ε

0

czyli

S

r

R

+Q

Z. Kąkol-Notatki do Wykładu z Fizyki

19-2

2

2

0

4

1

r

Q

k

r

Q

E

=

=

πε

(19.1)

dla r > R (tak jakby cały ładunek skupiony był w środku sfery).
Dla r < R, E = 0.

19.2.2 Jednorodnie naładowana kula

Przewodniki - równoważne sferze bo ładunek na powierzchni.

Izolator - równoważny szeregowi współśrodkowych sfer.

2

.

r

Q

k

E

wewn

=

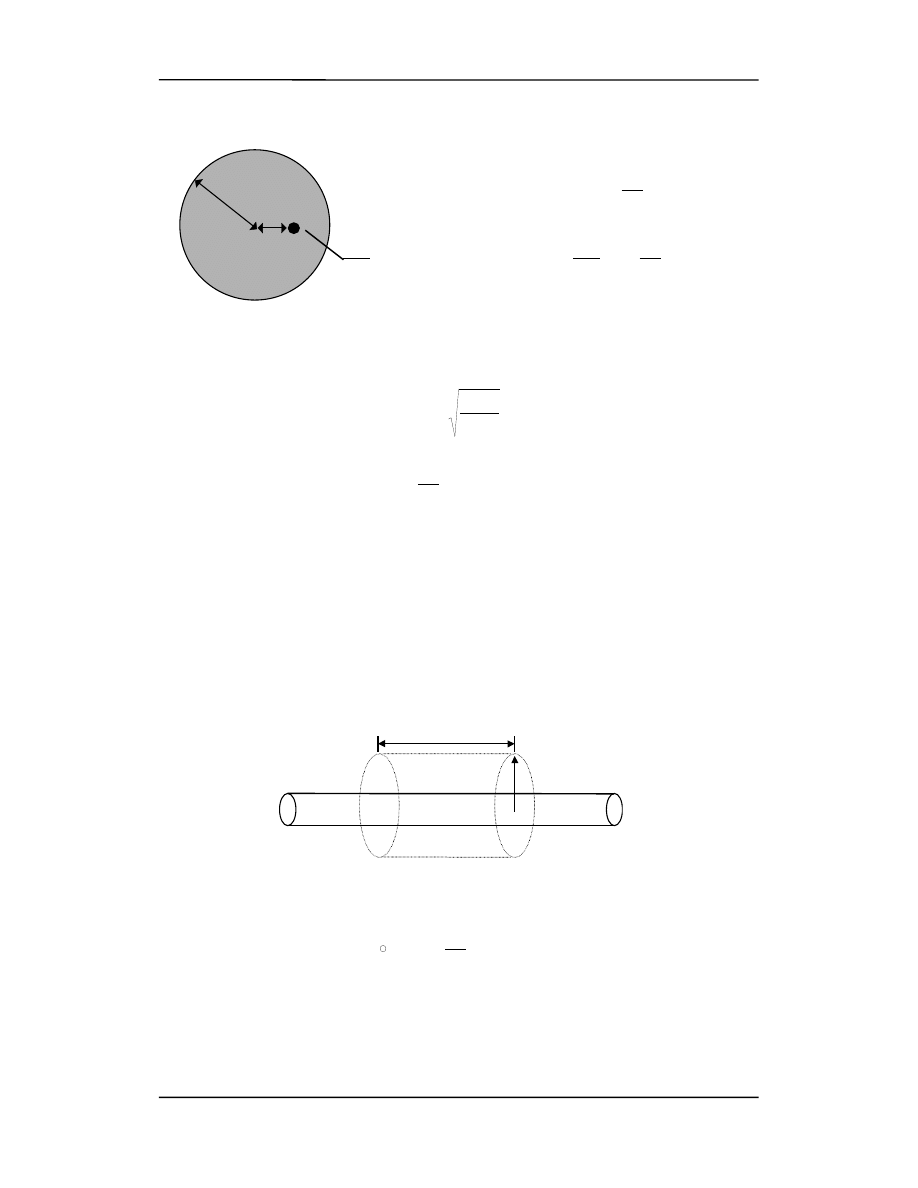
gdzie Q

wewn.

= Q(r

3

/R

3

) (stosunek objętości kuli o promieniu r do objętości kuli o pro-

mieniu R, rysunek obok).









=

3

3

2

4

)

4

(

R

r

Q

k

r

E

π

π

Czyli

r

R

Q

k

E

3

=

(19.2)

Wykres E w funkcji odległości od środka jednorodnie naładowanej kuli jest pokazany
poniżej.

Przykład 1

Atom wodoru traktujemy jako sztywną jednorodnie

naładowaną kulę o promieniu R = 10

-10

m, całkowitym

ładunku Q = e = -1.6·10

-19

C i masie m

e

= 9.1·10

-31

kg.

Proton znajdujący się w środku chmury elektronowej
(stan podstawowy) zostaje przemieszczony o małą odle-
głość x

0

i puszczony swobodnie. Jaka będzie częstotli-

wość drgań jakie elektron i proton będą wykonywały wo-
kół ich położeń równowagi?

R

r

Q

Q

wewn

.

kQ

2

/R

2

R

E

r

Z. Kąkol-Notatki do Wykładu z Fizyki

19-3

Siła przywracająca proton do położenia
równowagi F = eE czyli

x

R

e

k

F

3

2

−

=

lub

x

R

e

k

t

x

m

e

3

2

2

2

d

d

−

=

Powinniśmy się posługiwać raczej masą

zredukowaną

µ =M

p

m

e

/(M

P

+ m

e

) ale m

e

<< M

p

więc

µ

≈

m

e

.

Zgodnie z równaniem dla ruchu harmonicznego

3

2

R

m

ke

e

=

ω

π

ω

2

=

f

= 2.5·10

15

Hz

Ta częstotliwość jest bliska promieniowaniu wysyłanemu przez atom wodoru w pierw-
szym stanie wzbudzonym czyli, że taki model jest uzasadniony.

19.2.3 Liniowe rozkłady ładunków

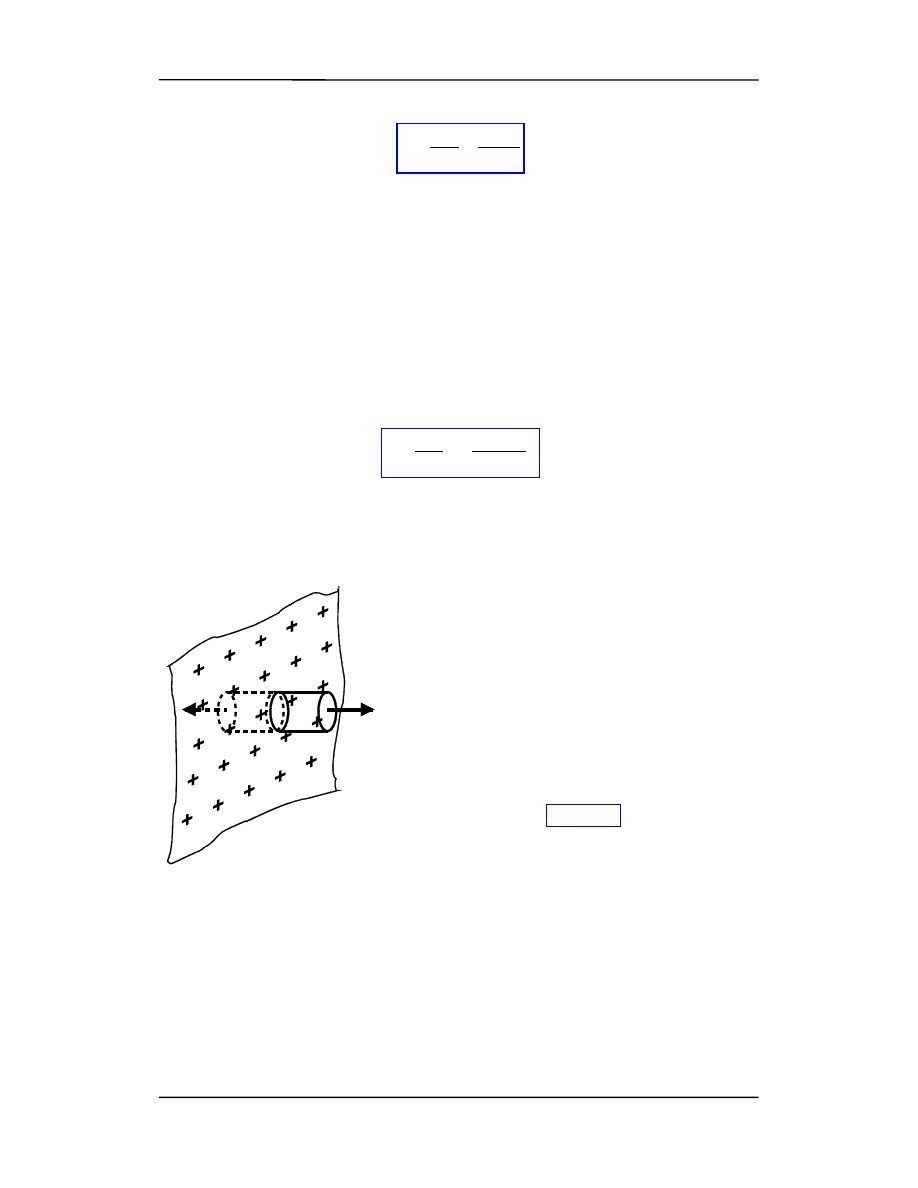
Liczymy pole E w odległości r od jednorodnie naładowanego pręta (drutu) o długo-

ści l >> r.
Wprowadzamy liniową gęstość ładunku

λ (ładunek na jednostkę długości).

Jako powierzchnię Gaussa wybieramy walec (możemy wybierać dowolnie).

Z prawa Gaussa

∫

=

=

)

(

4

d

0

L

k

L

λ

π

ε

λ

S

E

E jest równoległe do wektora S i ma taką samą wartość w każdym punkcie powierzchni
więc

2

πrLE = 4πkLλ

R

x

0

chmura
elektronowa

proton

L

r

+

+

+

Z. Kąkol-Notatki do Wykładu z Fizyki

19-4

r

r

k

E

0

2

2

πε

λ

λ

=

=

(19.3)

Teraz pole wewnątrz. Wybieramy powierzchnię Gaussa o promieniu r < R.
Ładunek wewnątrz powierzchni Gaussa Q

wewn.

=

ρπr

2

L, gdzie

ρ - gęstość objętościowa

ładunku. Z prawa Gaussa otrzymujemy

E(2

πrL) = 4πk(ρπr

2

L)

E = 2k

ρπr

ponieważ

λ = ρπR

2

więc

r

R

r

R

k

E

2

0

2

2

2

πε

λ

λ

=

=

(19.4)

19.2.4 Płaskie rozkłady ładunków

Obliczamy pole od nieskończonej jednorodnie naładowanej płaszczyzny.

Ładunek otoczony przez powierzchnię Gaus-

sa jest równy Q

wewn.

=

σS, gdzie σ jest gęstością po-

wierzchniową, a S powierzchnią podstawy walca. Z
prawa Gaussa

2ES =

σS/ε

0

gdzie czynnik 2 odpowiada dwóm podstawom wal-
ca.
Ostatecznie otrzymujemy

E =

σ/2ε

0

(19.5)

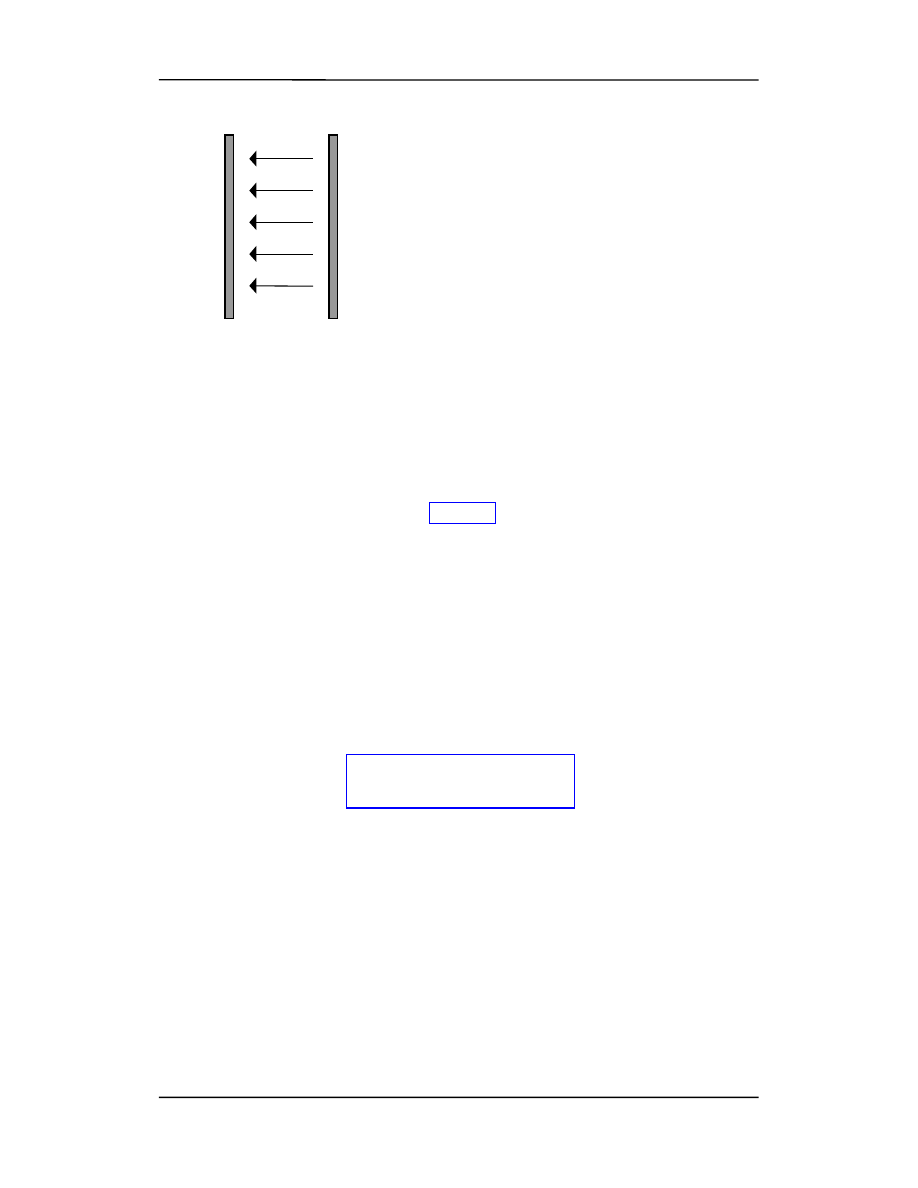
Wiele zastosowań dotyczy układu dwóch, płaskich

równoległych płyt (kondensator płaski).

Pole wytwarzane przez płytę "po lewej stronie" (rysunek poniżej) jest równe

E

minus

=

σ/2ε

0

i skierowane ku płycie. Pole wytwarzane przez płytę po prawej

E

plus

=

σ/ε

0

i skierowane jest od płyty.

Zatem w obszarze I

E

I

=

σ/2ε

0

+ (–

σ/2ε

0

) = 0

E

E

Z. Kąkol-Notatki do Wykładu z Fizyki

19-5

w obszarze II

E

II

= –

σ/2ε

0

+ (–

σ/2ε

0

) = –

σ/ε

0

w obszarze III

E

III

= (–

σ/2ε

0

) +

σ/2ε

0

= 0

19.2.5 Powierzchnia przewodnika

Jeżeli przedstawiona na rysunku naładowana

powierzchnia stanowi część powierzchni przewodnika to ponieważ cały ładunek groma-
dzi się na zewnętrznej powierzchni to wewnątrz E = 0. Co więcej E musi być prostopa-
dłe do powierzchni (równoległe do S) bo gdyby istniała składowa styczna to elektrony
poruszałyby się. Z prawa Gaussa

ES = (

σS)/ε

0

więc

E =

σ/ε

0

(19.6)

na powierzchni przewodnika.

19.3 Potencjał elektryczny

Zgodnie z naszymi rozważaniami różnica energii potencjalnych jest dana przez

∫

−

=

−

B

A

pA

pB

E

E

r

F d

co dla pola elektrycznego daje

∫

∫

−

=

−

=

−

B

A

B

A

pA

pB

q

E

E

r

E

r

F

d

d

(19.7)

Podobnie jak dla grawitacyjnej energii potencjalnej możemy zdefiniować punkt zerowej
energii potencjalnej dla ciała znajdującego się w nieskończoności. Wtedy

∫

∞

−

=

r

p

q

r

E

r

E d

)

(

Jeżeli przenosimy ładunek q z nieskończoności do punktu odległego o r od innego ła-
dunku punktowego Q, to

energia potencjalna jest równa pracy wykonanej przeciw sile

elektrycznej

, czyli

+
+
+
+
+
+
+
+

-
-
-
-
-
-
-
-

I

II

III

Z. Kąkol-Notatki do Wykładu z Fizyki

19-6

∫

∞

∞

∞







−

−

=

−

=

=

r

r

r

p

r

qQk

r

r

Q

k

q

W

r

E

1

d

)

(

2

r

qQ

k

r

E

p

=

)

(

(19.8)

jest

energią potencjalną

ładunków q i Q.

Potencjał elektryczny

jest definiowany jako

energia potencjalna na jednostkowy ładu-

nek

q

W

q

r

E

r

V

r

p

∞

=

=

)

(

)

(

(19.9)

Dla ładunku punktowego

r

Q

k

V

=

(19.10)

Potencjał

= praca potrzebna do przeniesienia jednostkowego ładunku z nieskończoności

do r od ładunku punktowego Q.

Różnica potencjałów

czyli

napięcie U

pomiędzy dwoma punktami = praca na przenie-

sienie ładunku jednostkowego między tymi punktami

∫

−

=

=

=

−

B

A

AB

A

B

W

U

V

V

r

E d

(19.11)