Ostatnia aktualizacja: 04-11-08
M. Tomera
1
Akademia Morska w Gdyni
Katedra Automatyki Okrętowej
Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Mirosław Tomera
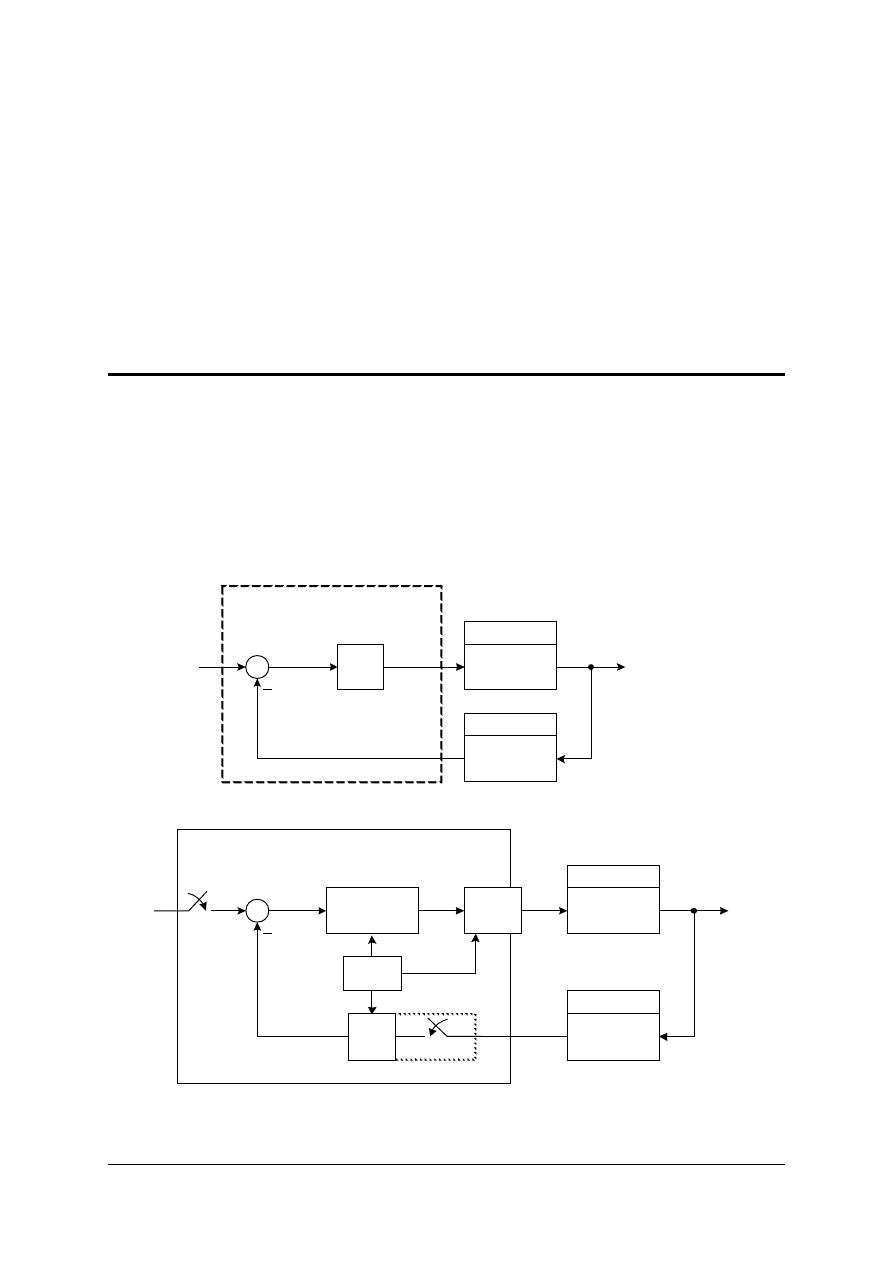
Można zaprojektować układ sterowania ciągłego i zaimplementować go w układach sterowania
cyfrowego stosując metody aproksymacji równań różniczkowych. Układ taki będzie mógł spełniać
zadane wymagania jakościowe jeśli częstotliwość próbkowania będzie przynajmniej 30 razy większa
od szerokości pasma układu. Na rysunku 1(a) pokazany jest typowy układ ciągły. Obliczenie sygnału
uchybu e i kompensacja dynamiczna C(s) może zostać zrealizowana w komputerze tak jak pokazano
to na rysunku 1(b). Podstawowe różnice pomiędzy tymi dwoma implementacjami są takie, że układ
cyfrowy przetwarza próbki pomierzonego sygnału wyjściowego, a nie sygnał ciągły i dynamika
opisana przez C(s) jest implementowana przez równania algebraiczne, które nazywają się
równaniami różnicowymi.
C(s)
u(t)
G(s)
H(s)
y(t)
e(t)
y(t)
r(t)
Regulator ciągły
Obiekt
Czujnik
(a)
Zegar
C/A
i hold
u(kT)
u(t)
Równania
różnicowe
C/A
y(t)
e(kT)
y(kT)
r(t)
T
r(kT)
H(s)
Czujnik
G(s)
Obiekt
T
Regulator cyfrowy
Impulsator
y(t)
(b)
Rys. 1. Podstawowy schemat blokowy układu sterowania, (a) układ ciągły, (b) z systemem mikropcesorowym.

Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
2
Pewnym szczególnym sposobem zrealizowania aproksymaty dla komputera cyfrowego w celu
rozwiązania równania różniczkowego jest metoda Eulera. Metoda ta wyprowadzona została
z następującej definicji różniczki
t
x
x
t
δ
δ
δ
0
.
lim
→
=
(1)
gdzie x
δ
jest zmianą zmiennej x w czasie t
δ
, nawet jeśli t
δ
nie jest całkiem równe zero to ta
zależność może być prawdziwa po zastosowaniu poniższych aproksymat. W metodzie Eulera
wyróżnia się dwie metody:
•
aproksymację prostokątną w przód (forward rectangular rule)
( )
T
k
x
k
x
k
x
)
(
)
1
(
.
−
+
≅
(2)
gdzie:
k
k
t
t
T
−
=
+
1
(przedział próbkowania w sekundach)
kT
t
k
=
(dla stałego przedziału próbkowania)
k liczba całkowita
x(k) wartość x w chwili t
k
x(k+1) wartość x w chwili t
k+1
•
aproksymację prostokątną wstecz (backward rectangular rule)
( )
T
k
x
k
x
k
x
)
1
(
)
(
.
−
−
≅
(3)
gdzie:
1
−
−
=
k
k
t
t
T
(przedział próbkowania w sekundach)
kT
t
k
=
(dla stałego przedziału próbkowania)
k liczba całkowita
x(k) wartość x w chwili t
k
x(k
−
1) wartość x w chwili t
k
−
1
Aproksymacje te mogą być używane w miejsce wszystkich różniczek, które pojawiają się
w równaniach różniczkowych regulatora po to aby uzyskać zbiór równań, które mogą być rozwiązane
przez komputer cyfrowy. Równania te nazywane są równaniami różnicowymi i są rozwiązywane
cyklicznie z krokiem czasu o długości T. Przykład pierwszy ilustruje sposób uzyskiwania równań
różnicowych na podstawie równań różniczkowych metodą dyskretyzacji Eulera aproksymacją wprzód.
Przykład 1
Korzystając z metody Eulera w przód, dokonaj dyskretyzacji z okresem próbkowania T = 0.1 [s]
następującego równania różniczkowego
2
2
)
(
dt
t
y
d
+ 2
dt
t
dy )
(
+ 5
)
(
t
y
= 10
)
(
1
t
⋅
(1.1)
z warunkami początkowymi
)
0
(
y
=
−
4
(1.2)
)
0
(
)
1
(
y
=
−
10
(1.3)
a) Na podstawie uzyskanego równania różnicowego wygeneruj w Matlabie kolejne próbki
sygnału dyskretnego.
b) Zaimplementuj w
Simulinku powyższe równanie różniczkowe wraz z warunkami
początkowymi.
c) Dokonaj porównania na wykresie wyników uzyskanych w punkcie (a) i (b).
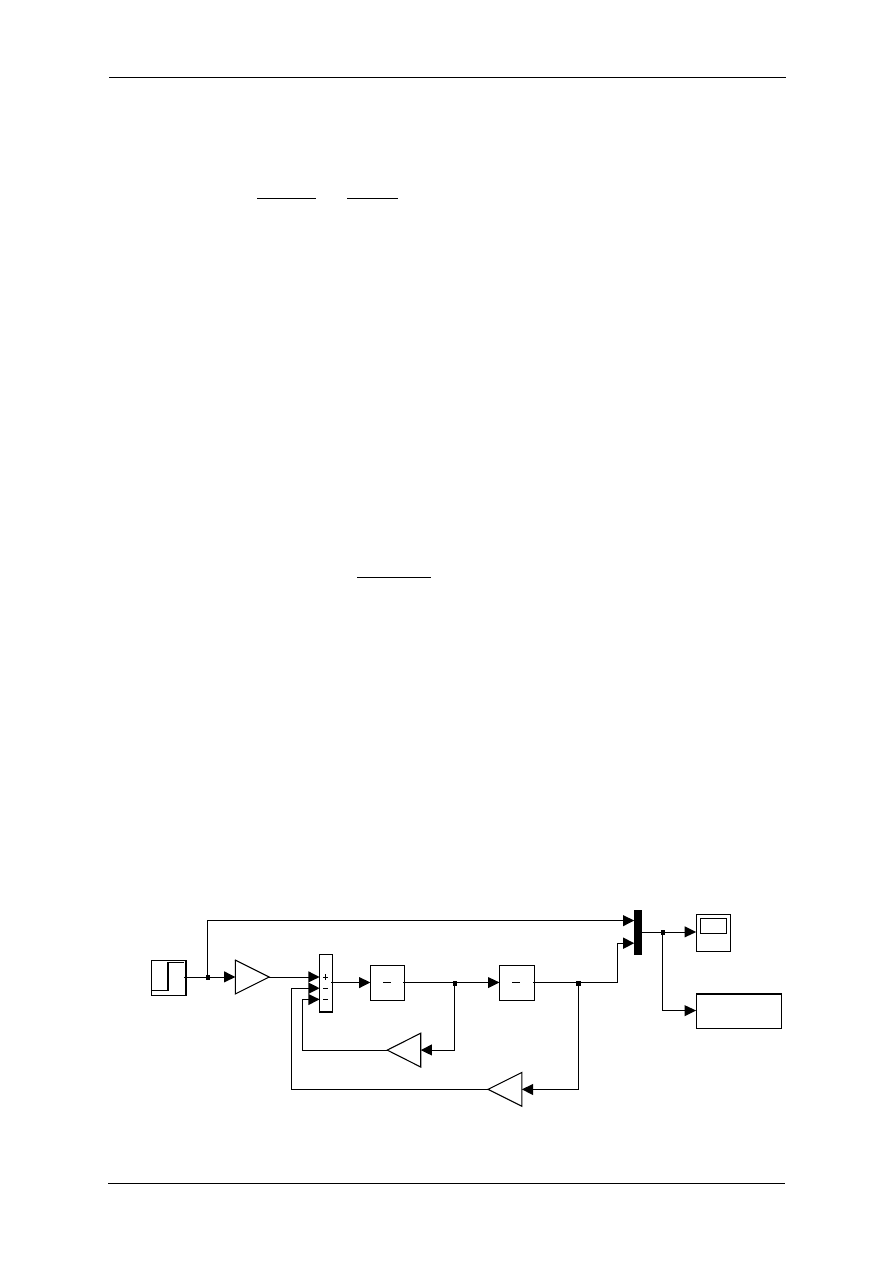
Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
3
Rozwiązanie: Chcąc uzyskać postać dyskretną równania różniczkowego (1.1) w pierwszej
kolejności należy zastąpić pochodne odpowiednimi różnicami czyli równanie różniczkowe
przechodzi w następujące równanie różnicowe
2
2
)
(
T
kT
y
∆
+ 2
T
kT
y
)
(
∆
+ 5
)
(
kT
y
= 10
)
(
1
kT
⋅
(1.4)
Przy użyciu metody prostokątnej Eulera w przód pierwsza różnica zapisywana jest następująco:
)
(
kT
y
∆
=
[
]
T
k
y
)
1
(
+
−
( )
kT
y
(1.5)
natomiast druga różnica
)
(
2
kT
y
∆
=
[
]
( )
kT
y
T
k
y
∆
−
+
∆
)
1
(
=
[
]
T
k
y
)
2
(
+
−
[
]
T
k
y
)
1
(
2
+
⋅
+
( )
kT
y
(1.6)
Podstawiając różnice opisane wzorami (1.5) oraz (1.6) do równania różnicowego (1.4)
i przekształcając je uzyskuje się następującą postać nadającą się do implementacji
komputerowej
[
]
T
k
y
)
2
(
+
=
(
) (
)
[
]
T
k
y
T
1
2
2
+
−
+
(
)
( )
kT
y
T
T
⋅
⋅
−
⋅
+
−
2
5
2
1
+
)
(
1
10
2
kT
T
⋅
⋅
(1.7)
Po podstawieniu do wzoru (1.7) okresu próbkowania T = 0.1 [s] uzyskuję się następujące
równanie różnicowe
)
2
(
+
k
y
−
)
1
(
8
.
1
+
⋅
k
y
+
)
(
85
.
0
k
y
⋅
=
)
(
1
1
.
0
k
⋅
(1.8)
Pozostaje do przeliczenia jeszcze drugi warunek początkowy
)
0
(
)
1
(
y
=
T
y
y
)
0
(
)
1
(
−
(1.9)
Stąd wyznaczona zostanie wartość dla k = 1.
)
1
(
y
= y(0) +
)
0
(
)
1
(
y
T
⋅
(1.10)
Równanie różnicowe (1.7) wraz z warunkami początkowymi (1.8) oraz (1.9) można rozwiązać
bezpośrednio w Matlabie przy użyciu odpowiednio zapisanego programu.
Aby zaimplementować w Simulinku równanie różniczkowe (1.1) wraz z warunkami
początkowymi to najpierw należy to równanie zapisać w postaci zmiennych dynamicznych
2
1
.
x
x
=
4
)
0
(
1
−
=
x
)
(
1
10
2
5
2
1
2
.
t
x
x
x
⋅
+
−
−
=
10
)
0
(
2
−
=
x
(1.11)
1
x
y
=
Równania (1.10) można zamodelować w postaci następującego modelu Simulinka (Rys. 1.1),
który zachowany został pod nazwą
ex_1_sim.mdl
.
x2
x1
10
b1
5
a2
2
a1
wyniki_sym
To Workspace
Step
Scope
1
s
Integrator1
1
s
Integrator
Rys. 1.1. Schemat pozwalający na rozwiązanie w Simulinku równań dynamicznych (1.4).
Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
4
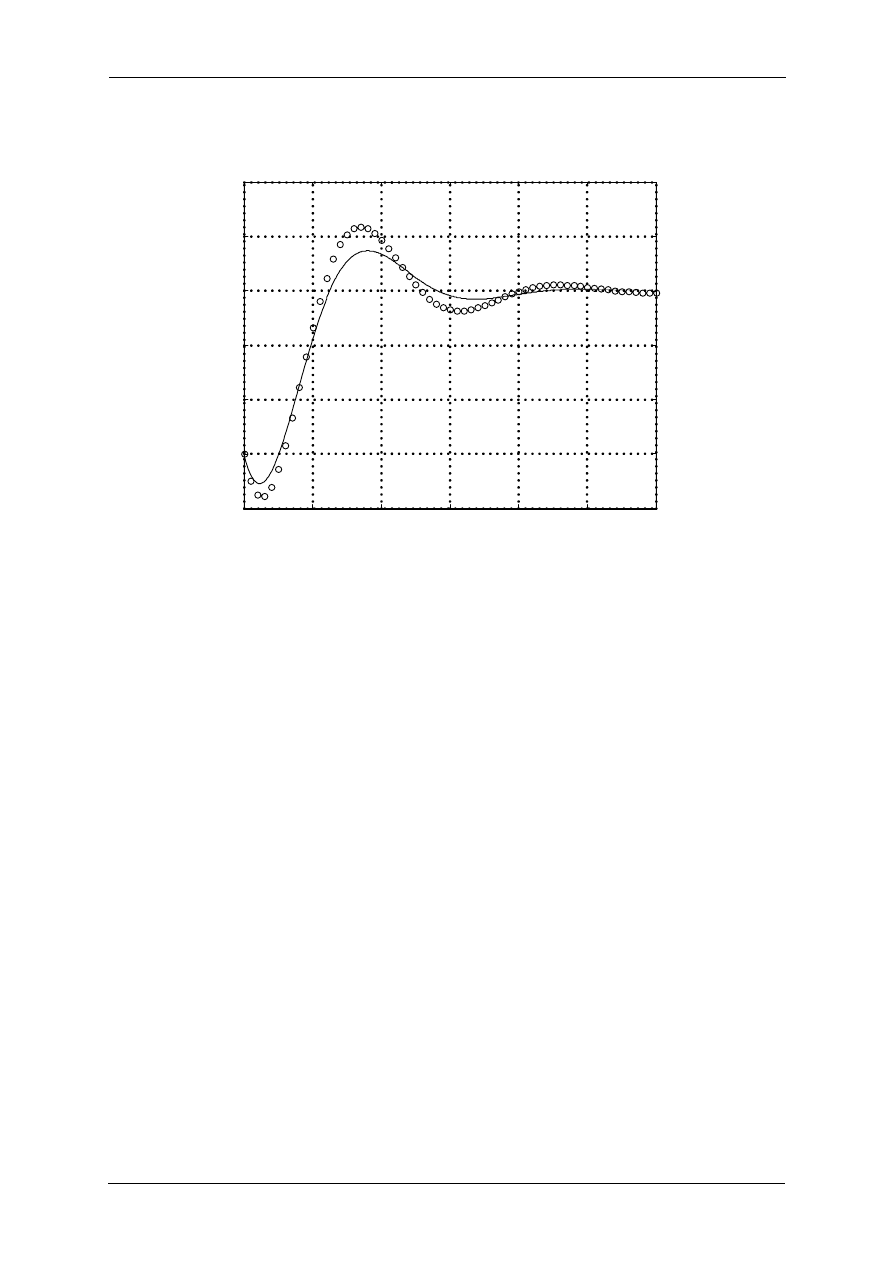
Na rysunku 1.2 znajdują się wyniki rozwiązania równania różniczkowego i uzyskanego
równania różnicowego dla T = 0.1 [s].
0
1
2
3
4
5
6
-6
-4
-2
0
2
4
6
Przybliżone rozwiązanie równania różniczkowego
t [s]
y(
k)
Rys. 1.2. Uzyskane wyniki rozwiązania równania różniczkowego (linia ciągłą) i równania różnicowego
(próbki) uzyskanego z dyskretyzacji dla okresu próbkowania T = 0.1 [s].
Wyniki przedstawione na rysunku 1.2. uzyskane zostały przy użyciu następującego kodu
programu zapisanego w Matlabie.
close all
% Zamkni
ę
cie wszystkich okien graficznych
clear
% Wyczyszczenie pami
ę
ci roboczej Matlaba
tmax = 6;
% Odcinek czasu
open_system('ex_1_sim')
% Otwarcie przygotowanego modelu Simulinka
sim('ex_1_sim',tmax)
% Wykonanie symulacji w zadanym odcinku
% czasu
close_system
% Zamkni
ę
cie modelu Simulinka
tC = tout;
% Podstawienie wektora czasu
yC = wyniki_sym(:,2);
% Pobranie z przestrzeni roboczej Matlaba
% uzyskanego rozwi
ą
zania
% Rozwi
ą
zanie dyskretne
Tp = 0.1;
% Okres próbkowania
y0 = -4;
% Warunki pocz
ą
tkowe
Dy0 = -10;
y1 = y0 + Dy0*Tp;
% Przeliczenie warto
ś
ci pocz
ą
tkowych
% na warto
ść
drugiej próbki
tk(1) = 0*Tp;
% Współrz
ę
dne pierwszych dwóch próbek
yk(1) = y0;
tk(2) = 1*Tp;
yk(2) = y1;
for k = 1:(tmax/Tp)-1;
tk(k+2) = (k+1)*Tp;
yk(k+2) = (2-2*Tp)*yk(k+1) - (1-2*Tp+5*Tp^2)*yk(k) + 10*Tp^2;
end;
% Wykre
ś
lenie uzyskanych wyników w Matlabie
figure(1)
Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
5
plot( tC, yC, 'k-', tk, yk, 'ko')
title('Rozwi
ą
zanie równania ró
ż
nicowego')
xlabel('t [s]')
ylabel('y(k)')
grid on
Przykład 2
Korzystając z metody prostokątów Eulera z reguły wstecznej, dokonaj dyskretyzacji równania
różniczkowego (1.1) wraz z warunkami początkowymi (1.2) i (1.3) znajdującego się
w przykładzie 1. Okres próbkowania T =
−
0.1 [s]. Na wykresie dokonaj porównania wyników
uzyskanych obydwoma metodami.
Rozwiązanie: Chcąc uzyskać postać dyskretną równania różniczkowego (1.1) metodą
prostokątów Eulera wstecz postępuje się w podobny sposób jak w przykładzie 1. Do równania
(1.5) dokonuje się następujących podstawień: pierwsza różnica zapisywana jest następująco:
)
(kT
y
∆
=
( )
kT
y
−
[
]
T
k
y
)
1
(
−
(2.1)
natomiast druga różnica
)
(
2
kT
y
∆
=
( )
[
]
T
k
y
kT
y
)
1
(
−
∆
−
∆
=
( )
kT
y
−
[
]
T
k
y
)
1
(
2
−
⋅
+
[
]
T
k
y
)
2
(
−
(2.2)
Podstawiając różnice opisane wzorami (2.1) oraz (2.2) do równania różnicowego (1.4)
i przekształcając je uzyskuje się w ten sposób kolejną postać równania nadającą się do
implementacji komputerowej
)
(kT
y
=
(
)
[
]
T
k
y
T
T
T
1
5
2
1
2
2
2
−
+
+
+
−
(
)
[
]
T
k
y
T
T
2
5
2
1
1
2
−
+
+
+
)
(
1
5
2
1
10
2
2
kT
T
T
T
⋅
+
+
(2.3)
Po podstawieniu do wzoru (2.3) okresu próbkowania T = 0.1 [s] uzyskuje się następujące
równanie różnicowe
0
1
2
3
4
5
6
-6
-4
-2
0
2
4
6
t [s]
y(
k)
m. Eulera w przód
m. Eulera wstecz
Przybliżone rozwiązania równania różniczkowego
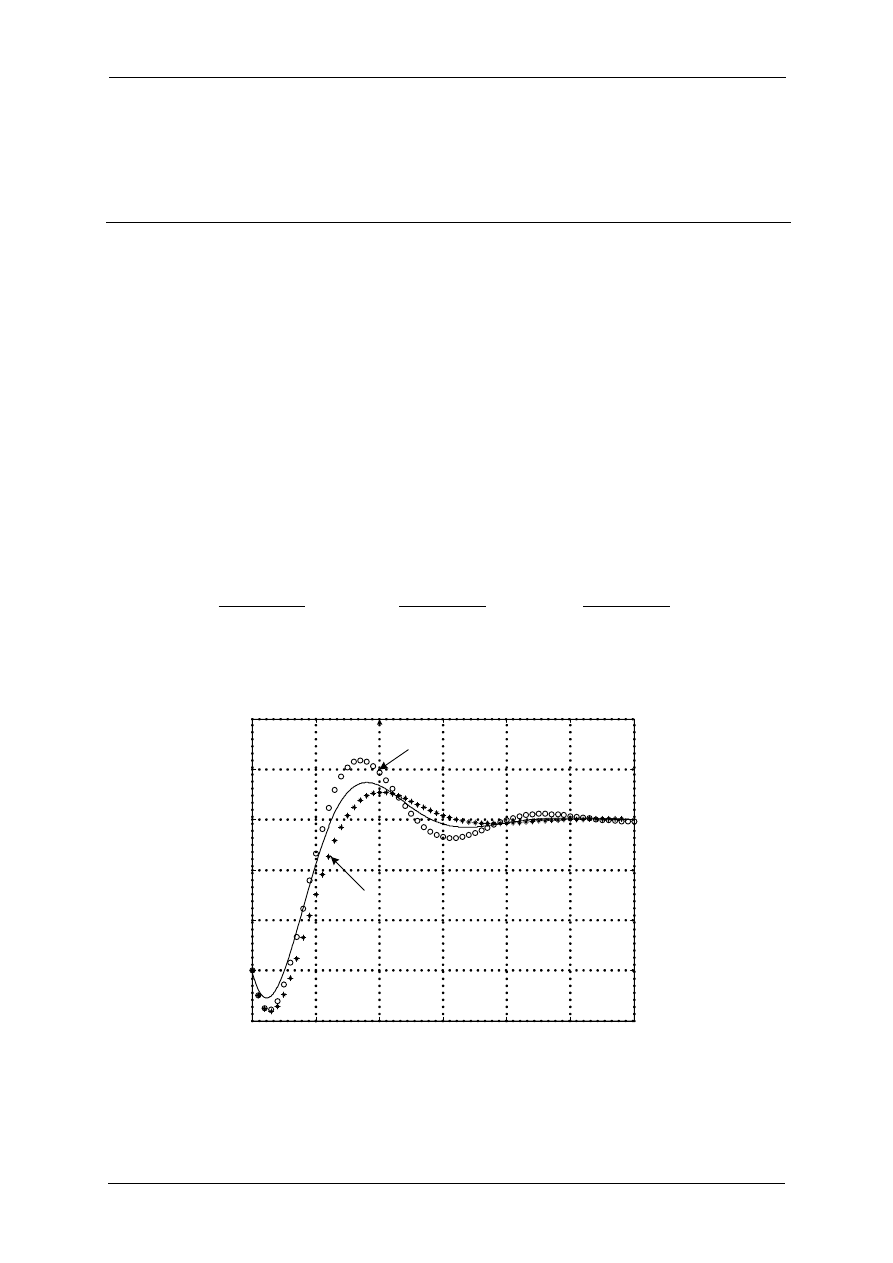
Rys. 2.1. Porównanie rozwiązań równań różnicowych uzyskanych z aproksymacji równania
różniczkowego (linia ciągłą) metodą prostokątów Eulera przy użyciu reguł w przód i wstecz
dla okresu próbkowania T = 0.1 [s].

Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
6
)
(k
y
−
)
1
(
76
.
1
−
⋅
k
y
+
)
2
(
8
.
0
−
⋅
k
y
=
)
(
1
08
.
0
k
⋅
(2.4)
Warunki początkowe przelicza się w identyczny sposób jak w metodzie Eulera w przód.
Z porównania uzyskanych równań (1.8) oraz (2.4) widać, że różnią się między sobą
wartościami współczynników. Na rysunku 2.1 dokonane zostało porównanie uzyskanych
wyników.
W przykładzie 2 przedstawione zostało porównanie aproksymacji rozwiązań równania różniczkowego
przy użyciu metody prostokątnej Eulera. Z rysunku 2.1 wynika, że jeśli do aproksymacji zastosuje się
regułę Eulera w przód wówczas uzyskuje się rozwiązania z nadmiarem, natomiast przy zastosowaniu
reguły Eulara wstecz rozwiązania z niedomiarem.
ĆWICZENIA W MATLABIE
M.1. Poniższe równania różniczkowe
zaimplementuj w postaci schematów
Simulinka, następnie korzystając
z
metody prostokątów Eulera w
przód
(forward rectangular rule) wyznacz
aproksymujące równania różnicowe. Okres
próbkowania T = 0.1 [s]. Sekwencyjnie
przy użyciu Matlaba wykreśl rozwiązania
równań różnicowych i porównaj je
z rozwiązaniami uzyskanymi w Simulinku.
a)
3
3
)
(
dt
t
y
d
+ 5
2
2
)
(
dt
t
y
d
+ 4
dt
t
dy )
(
= 2
)
(t
δ
)
0
(
y
= 1
)
0
(
)
1
(
y
=
−
1
)
0
(
)
2
(
y
= 1
b)
2
2
)
(
dt
t
y
d
+ 5
dt
t
dy )
(
+ 6
)
(t
y
= 2
t
e
−
)
0
(
y
= 0
)
0
(
)
1
(
y
=
−
2
c)
dt
t
dy )
(
+ 2
)
(t
y
= 6
t
2
cos
)
0
(
y
=
−
2
d)
3
3
)
(
dt
t
y
d
+ 4
2
2
)
(
dt
t
y
d
+ 3
dt
t
dy )
(
= 3
)
(
t
δ
)
0
(
y
= 1
)
0
(
)
1
(
y
=
−
1
)
0
(
)
2
(
y
= 1
e)
dt
t
dy )
(
+ 2
)
(
t
y
=
2
2
1
t
)
0
(
y
=
−
1
f)
dt
t
dy )
(
+ 3
)
(
t
y
= 4
t
4
sin
)
0
(
y
= 1
g)
2
2
)
(
dt
t
y
d
+ 4
dt
t
dy )
(
+ 5
)
(
t
y
=
)
(
1
t
)
0
(
y
=
−
3
)
0
(
)
1
(
y
= 2
h)
2
2
)
(
dt
t
y
d
+ 3
dt
t
dy )
(
+ 2
)
(
t
y
= 3
t
e
3
−
)
0
(
y
= 0
)
0
(
)
1
(
y
= 1
i)
2
2
)
(
dt
t
y
d
+ 2
dt
t
dy )
(
+ 2
)
(
t
y
= sin2t
( )
0
y
= 2
( )
0
)
1
(
y
=
−
3
j)
2
2
)
(
dt
t
y
d
+ 2
dt
t
dy )
(
+
)
(
t
y
=
)
(
1
5
t
⋅
( )
0
y
= 1
( )
0
)
1
(
y
=
−
2
k)
2
2
)
(
dt
t
y
d
+
dt
t
dy )
(
+ 4
)
(
t
y
= cos3t
( )
0
y
= 1
( )
0
)
1
(
y
= 2
l)
2
2
)
(
dt
t
y
d
+ 3
dt
t
dy )
(
+ 6
)
(
t
y
=
t
e
t
3
sin
2
−
( )
0
y
= 0
( )
0
)
1
(
y
= 3

Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
7
M.2. P
rzy użyciu metody prostokątów Eulera
wstecz (backward rectangular rule)
wyznacz aproksymujące równania
różnicowe dla równań różniczkowych
znajdujących się w zadaniu M.1. Okres
próbkowania T = 0.1 [s]. Sekwencyjnie
przy użyciu Matlaba wykreśl rozwiązania
i porównaj je z rozwiązaniami uzyskanymi
w zadaniu M.1.
ODPOWIEDZI DO WYBRANYCH ĆWICZEŃ
M1.
a)
)
(
02
.
0
)
(
54
.
0
)
1
(
04
.
2
)
2
(
5
.
2
)
3
(
k
k
y
k
y
k
y
k
y
δ
⋅
=
−
+
+
+
−
+
1
)
0
(
=
y
9
.
0
)
1
(
=
y
81
.
0
)
2
(
=
y
b)
(
)
k
k
y
k
y
k
y
9048
.
0
02
.
0
)
(
56
.
0
)
1
(
54
.
1
)
2
(
⋅
=
+
+
−
+
0
)
0
(
=
y
2
.
0
)
1
(
−
=
y
c)
(
)
k
k
y
k
y
⋅
⋅
=
−
+
2
.
0
cos
6
.
0
)
(
8
.
0
)
1
(
2
)
0
(
−
=
y
d)
)
(
03
.
0
)
(
63
.
0
)
1
(
23
.
2
)
2
(
6
.
2
)
3
(
k
k
y
k
y
k
y
k
y
δ
⋅
=
−
+
+
+
−
+
1
)
0
(
−
=
y
1
.
1
)
1
(
−
=
y
18
.
1
)
2
(
−
=
y
e)
2
0005
.
0
)
(
8
.
0
)
1
(
k
k
y
k
y
⋅
=
−
+
1
)
0
(
−
=
y
f)
(
)
k
k
y
k
y
⋅
⋅
=
−
+
4
.
0
sin
4
.
0
)
(
7
.
0
)
1
(
1
)
0
(
=
y
g)
)
(
1
01
.
0
)
(
65
.
0
)
1
(
6
.
1
)
2
(
k
k
y
k
y
k
y
⋅
=
+
+
−
+
3
)
0
(
−
=
y
8
.
2
)
1
(
−
=
y
h)
(
)
k
k
y
k
y
k
y
7408
.
0
03
.
0
)
(
72
.
0
)
1
(
7
.
1
)
2
(
⋅
=
+
+
−
+
0
)
0
(
=
y
1
.
0
)
1
(
=
y
i)
(
)
k
k
y
k
y
k
y
⋅
⋅
=
+
+
−
+
2
.
0
sin
01
.
0
)
(
82
.
0
)
1
(
8
.
1
)
2
(
2
)
0
(
=
y
7
.
1
)
1
(
=
y
j)
)
(
1
05
.
0
)
(
81
.
0
)
1
(
8
.
1
)
2
(
k
k
y
k
y
k
y
⋅
=
+
+
−
+
1
)
0
(
=
y
8
.
0
)
1
(
=
y
k)
(
)
k
k
y
k
y
k
y
⋅
⋅
=
+
+
−
+
3
.
0
cos
01
.
0
)
(
94
.
0
)
1
(
9
.
1
)
2
(
1
)
0
(
=
y
2
.
1
)
1
(
=
y
l)
(
)
(
)
k
k
y
k
y
k
y
k
⋅
⋅
=
+
+
−
+
3
.
0
cos
8187
.
0
01
.
0
)
(
76
.
0
)
1
(
7
.
1
)
2
(
0
)
0
(
=
y

Teoria sterowania
Dyskretyzacja równań różniczkowych
−
Matlab
Ostatnia aktualizacja: 04-11-08
M. Tomera
8
3
.
0
)
1
(
=
y
M2.
a)
)
(
013
.
0
)
3
(
6494
.
0
)
2
(
2727
.
2
)
1
(
6234
.
2
)
(
k
k
y
k
y
k
y
k
y
δ
⋅
=
−
−
−
+
−
−
1
)
0
(
=
y
9
.
0
)
1
(
=
y
81
.
0
)
2
(
=
y
b)
(
)
k
k
y
k
y
k
y
9048
.
0
0128
.
0
)
2
(
6410
.
0
)
1
(
6026
.
1
)
(
⋅
=
−
+
−
−
0
)
0
(
=
y
2
.
0
)
1
(
−
=
y
c)
(
)
k
k
y
k
y
⋅
⋅
=
−
−
2
.
0
cos
5
.
0
)
1
(
8333
.
0
)
(
2
)
0
(
−
=
y
d)
)
(
021
.
0
)
3
(
6993
.
0
)
2
(
3776
.
2
)
1
(
6283
.
2
)
(
k
k
y
k
y
k
y
k
y
δ
⋅
=
−
−
−
+
−
−
1
)
0
(
−
=
y
1
.
1
)
1
(
−
=
y
18
.
1
)
2
(
−
=
y
e)
2
00042
.
0
)
1
(
8333
0
)
(
k
k
y
.
k
y
⋅
=
−
−
1
)
0
(
−
=
y
f)
(
)
k
k
y
k
y
⋅
⋅
=
−
4
.
0
sin
3077
.
0
)
(
7692
.
0
)
(
1
)
0
(
=
y
g)
)
(
1
0069
.
0
)
2
(
6897
.
0
)
1
(
6552
.
1
)
(
k
k
y
k
y
k
y
⋅
=
−
+
−
−
1
)
0
(
=
y
9
.
0
)
1
(
=
y
81
.
0
)
2
(
=
y
h)
(
)
k
k
y
k
y
k
y
7408
.
0
0227
.
0
)
2
(
7576
.
0
)
1
(
7424
.
1
)
(
⋅
=
−
+
−
−
0
)
0
(
=
y
1
.
0
)
1
(
=
y
i)
(
)
k
k
y
k
y
k
y
⋅
⋅
=
+
−
−
2
.
0
sin
0082
.
0
)
(
8197
.
0
)
1
(
8033
.
1
)
(
2
)
0
(
=
y
7
.
1
)
1
(
=
y
j)
)
(
1
0413
.
0
)
2
(
8264
.
0
)
1
(
8182
.
1
)
(
k
k
y
k
y
k
y
⋅
=
−
+
−
−
1
)
0
(
=
y
8
.
0
)
1
(
=
y
k)
(
)
k
k
y
k
y
k
y
⋅
⋅
=
−
+
−
−
3
.
0
cos
0088
.
0
)
2
(
8772
.
0
)
1
(
8421
.
1
)
(
1
)
0
(
=
y
2
.
1
)
1
(
=
y
l)
(
)
(
)
k
k
y
k
y
k
y
k
⋅
⋅
=
−
+
−
−
3
.
0
cos
8187
.
0
0074
.
0
)
2
(
7353
.
0
)
1
(
6912
.
1
)
(
0
)
0
(
=
y
3
.
0
)
1
(
=
y
LITERATURA
1. Amborski K., Teoria sterowania. Podręcznik programowany, PWN, Warszawa, 1985.
2. Franklin G.F, Powell J.D., Emami-Naeini A. Digital Control of Dynamic Systems, 3rd ed.
Addison-Wesley Publishing Company, 1998.
Wyszukiwarka
Podobne podstrony:
Własności dynamiczne układów dyskretnych − Matlab
dyskretyzacja matlab
Dyskretyzacja równań różniczkowych − Matlab
Matlab cw1 2 zaoczni
5 Algorytmy wyznaczania dyskretnej transformaty Fouriera (CPS)
cz 1, Matlab moj
Image Processing with Matlab 33
01Zmienne losowe dyskretneid 3335 ppt
w 5 ciagle a dyskretne
MATLAB graf(1)
kod matlab
dyskretna lista5
Cw08 Matlab2
Dyskretne przeksztaĹ'cenie Fouriera
matematyka dyskretna w 2 id 283 Nieznany
Matlab wiadomości wstępne
Denisjuk A Matematyka Dyskretna
Matlab Class Chapter 1
więcej podobnych podstron