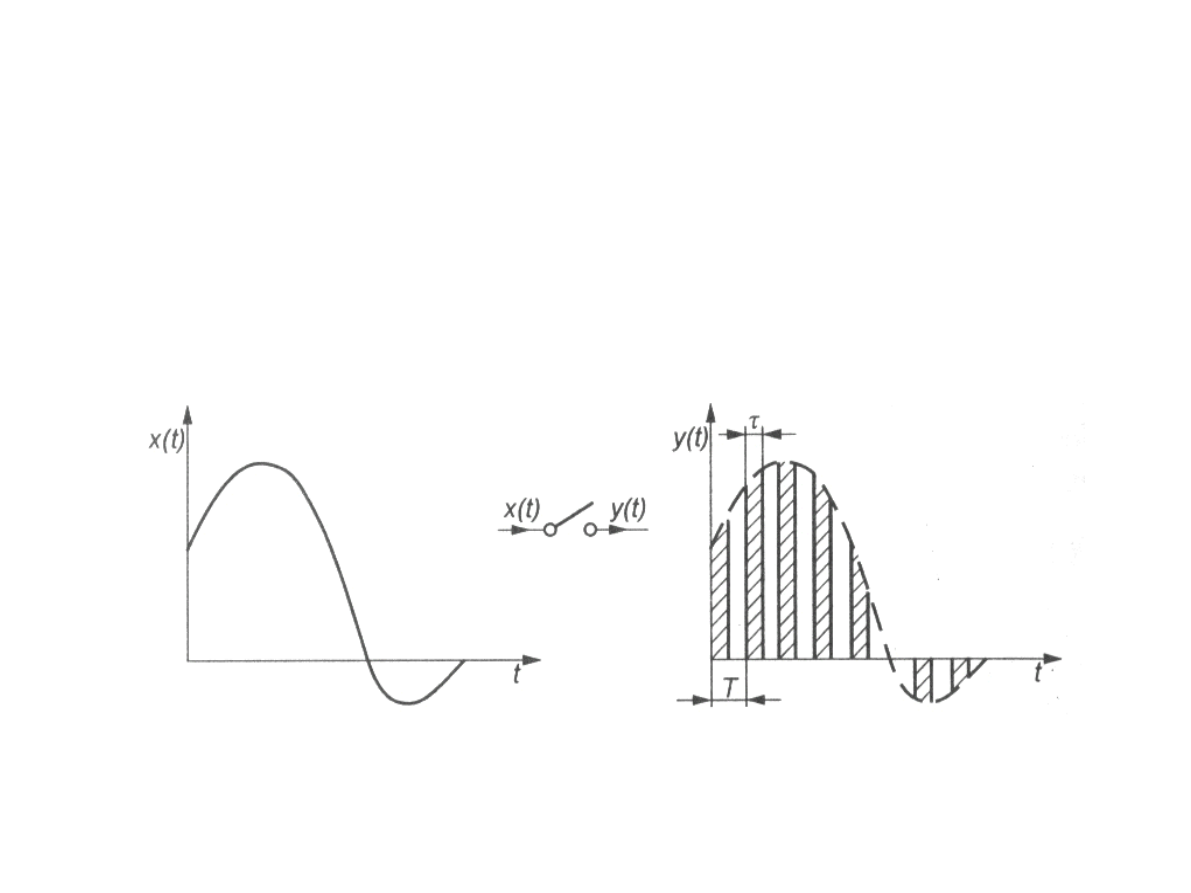
Próbkowanie sygnału

Przetwarzanie sygnału ciągłego w sygnał

impulsowy, przyjmujący niezerowe wartości

tylko w określonych przedziałach czasu.

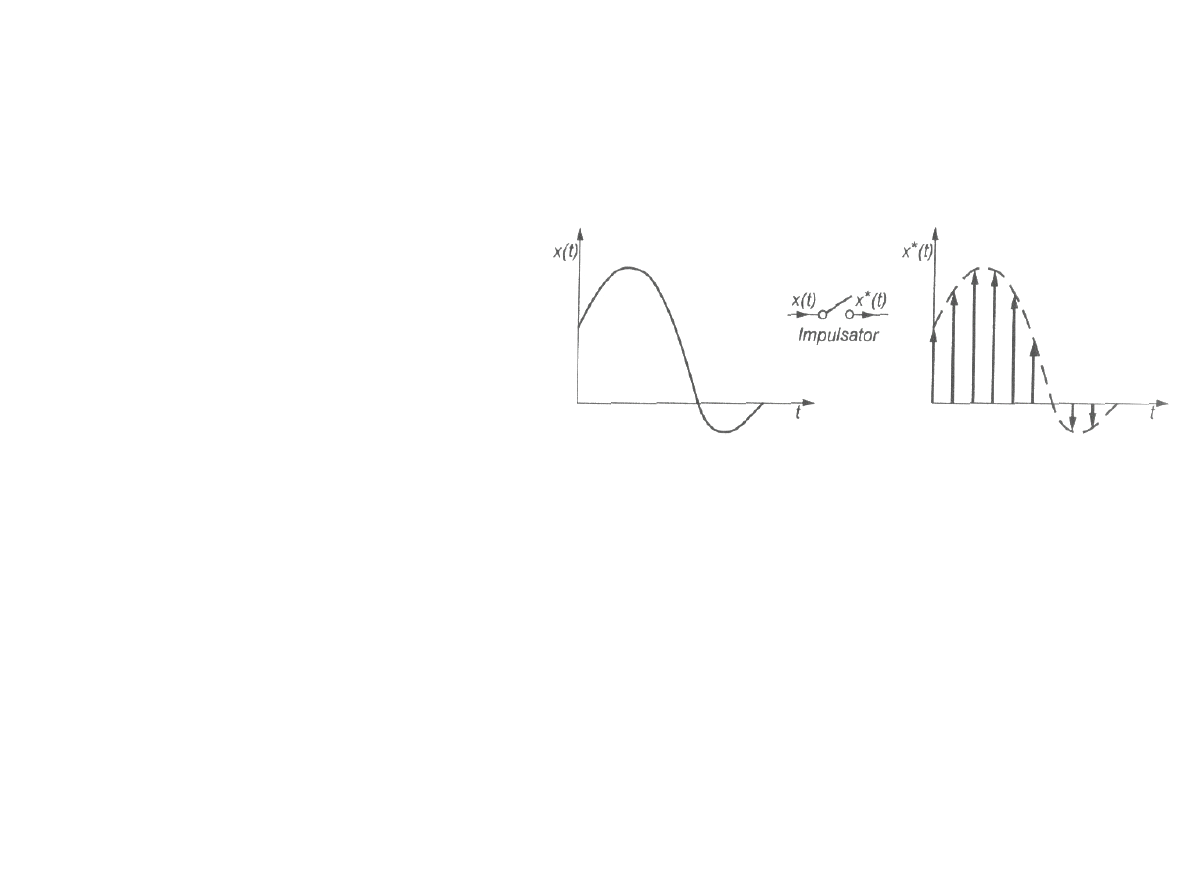
Próbkowanie idealne

x t= xt

T

t

*



T

t= 

n=−∞

n=∞

t−nT

x t=xt 

n=−∞

n=∞

t−nT

x t=xt 

n=0

n=∞

 t−nT = 

n=0

n=∞

xnTt−nT

*

*

X s=L[ x t]= 

n=0

n=∞

xnT L[t−nT]

X s= 

n=0

n=∞

xnTe

−nTs

X s=Z[ xt]

z=e

Ts

*

*

*

*

Widmo sygnałów impulsatora idealnego



T

t=

1
T



n=−∞

n=∞

e

jn

s

t

gdzie

s

=

2

T

− pulsacja impulsowaniaw[rad/ sek]

Rozwijając 

T

t wszereg Fourieraotrzymujemy:

x t=xt

T

t=

1
T



n=−∞

n=∞

xte

jn

s

t

*

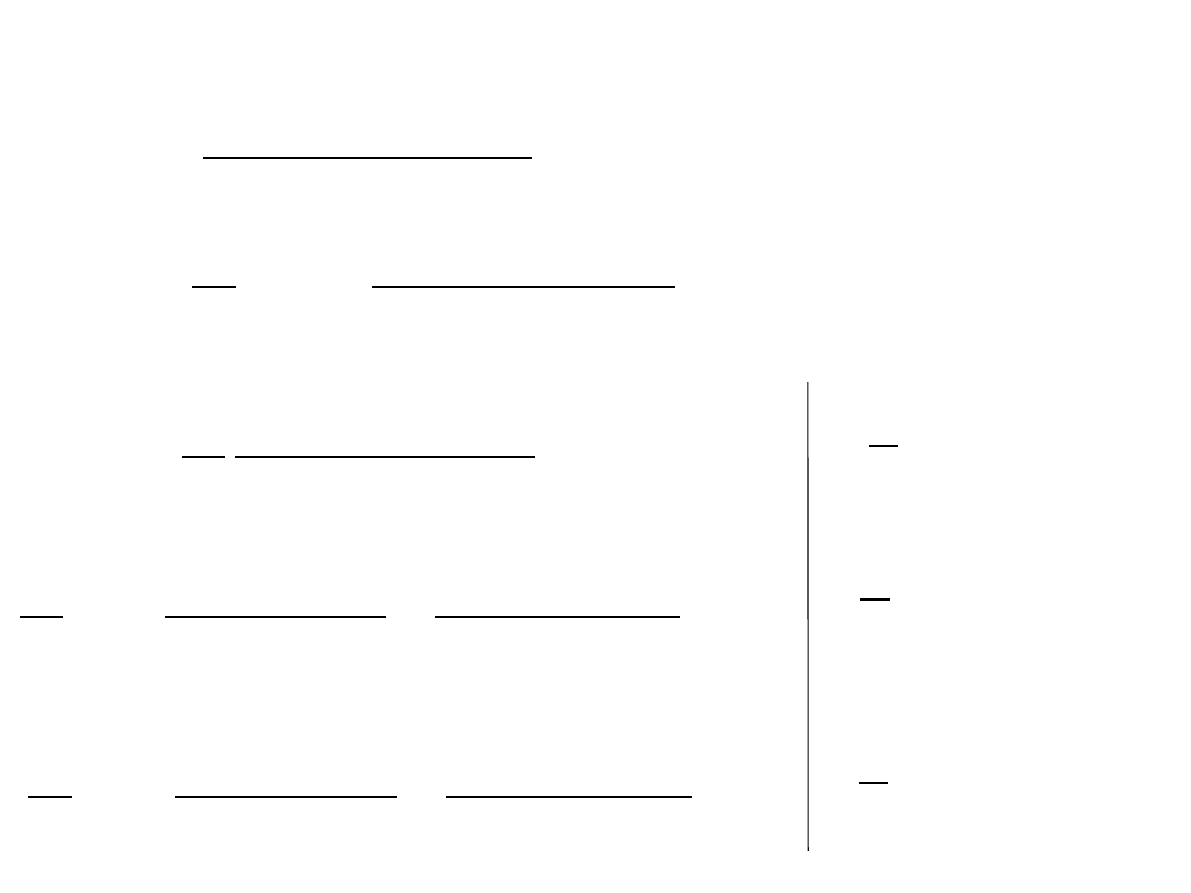
xt= A

e

jn

0

T

−e

− jn

0

T

2j

to:

Jeżeli nawejścieimpusatora podamysygnał sinusoidalny:

x t=

A

T

e

j 

0

T

−e

− j

0

T

2j



A

T



n=1

n=∞

[

e

jw

0

n

s

T

2j

−

e

− j

0

n

s

T

2j

]

A

T



n=1

n=∞

[

e

jw

0

−n

s

T

2j

−

e

− j

0

−n

s

T

2j

]

x t=

A

T



n=−∞

n=∞

e

j

0

T

−e

− j 

0

T

2j

e

jn

s

T

=

A

T

sin

0

t

A

T 

n=1

n=∞

sin

0

n

s

t

A

T 

n=1

n=∞

sin

0

−n

s

t

*

*

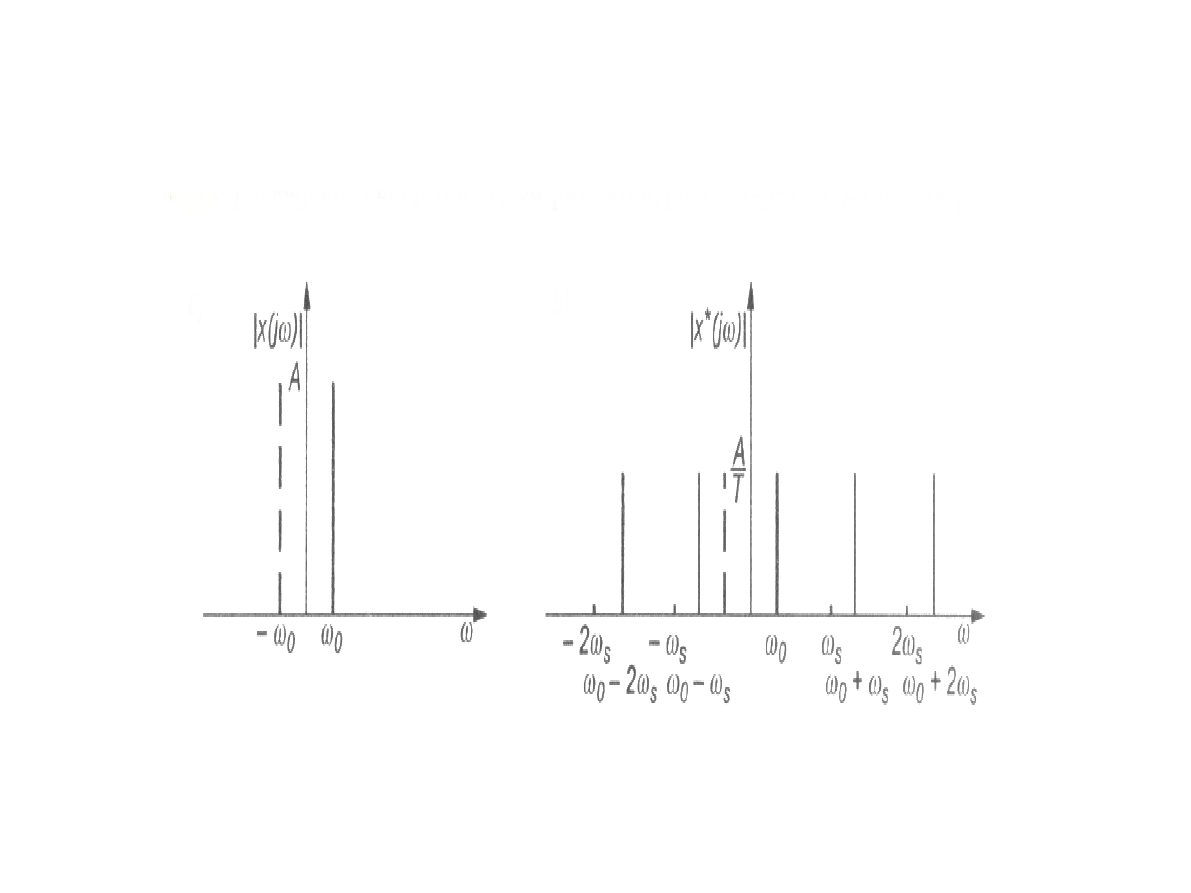
Widmasygnałówwejściowegoi wyjściowego

impulsatora idealnego przywejściusinusoidalnym

X s=L[ x t]=L[

1
T



n=−∞

n=−∞

xte

jn

s

t

]=

1
T



n=−∞

n=∞

X s− jn

s



Na podstawietwierdzeniao przesunięciuwdziedziniezmiennej

zespolonej:

Widać,żetransformatąLaplace' a sygnałuwyjściowego

impulsatora jest funkcjąokresową,awidmoamplitudowe

w funkcji pulsacji sygnałuwejściowegookreślazależność:

∣

X  j 

∣

=∣

1
T



n=−∞

n=∞

{X  j  jn

s

}∣

Widmaczęstotliwościoweimpulsatora przyograniczonym

widmiesygnałuwejściowego

*

*

*

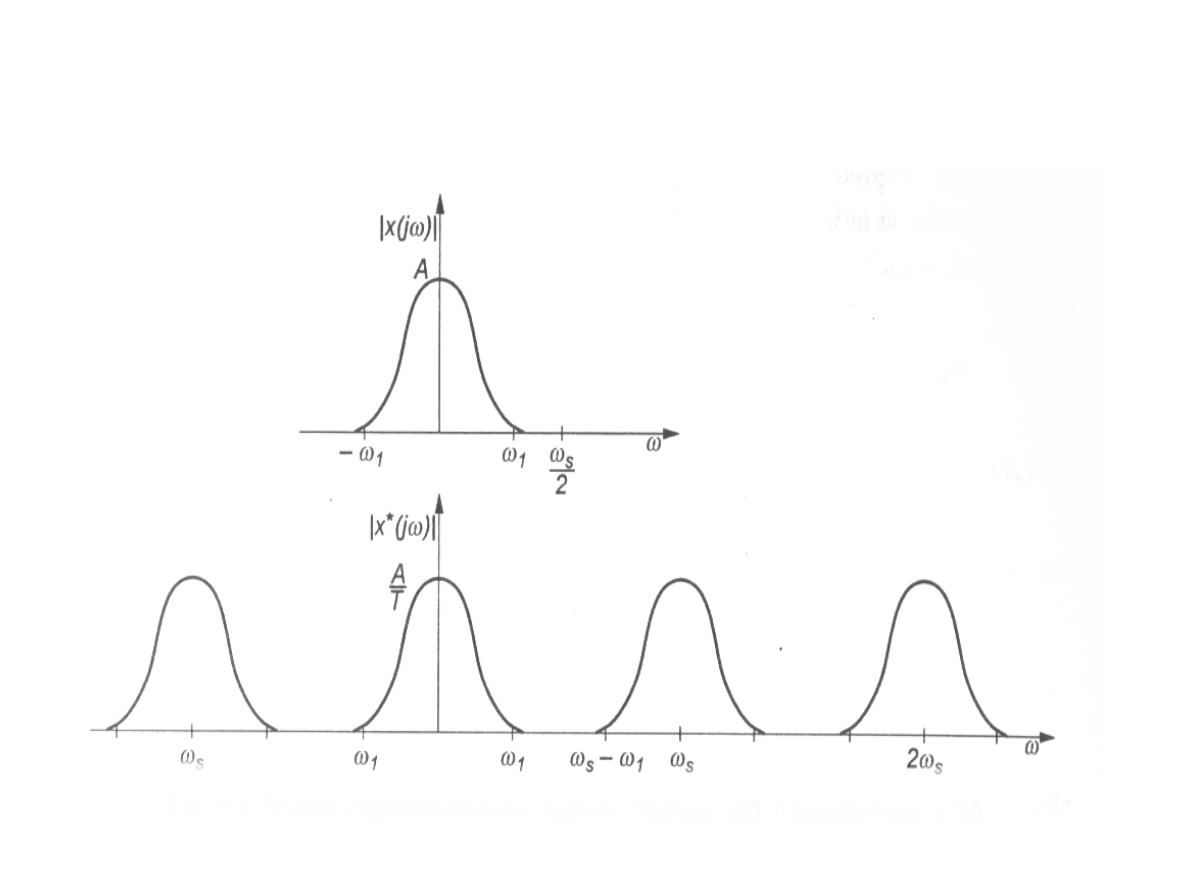
Widmaczęstotliwościoweimpulsatora przyograniczonym

widmiesygnałuwejściowego

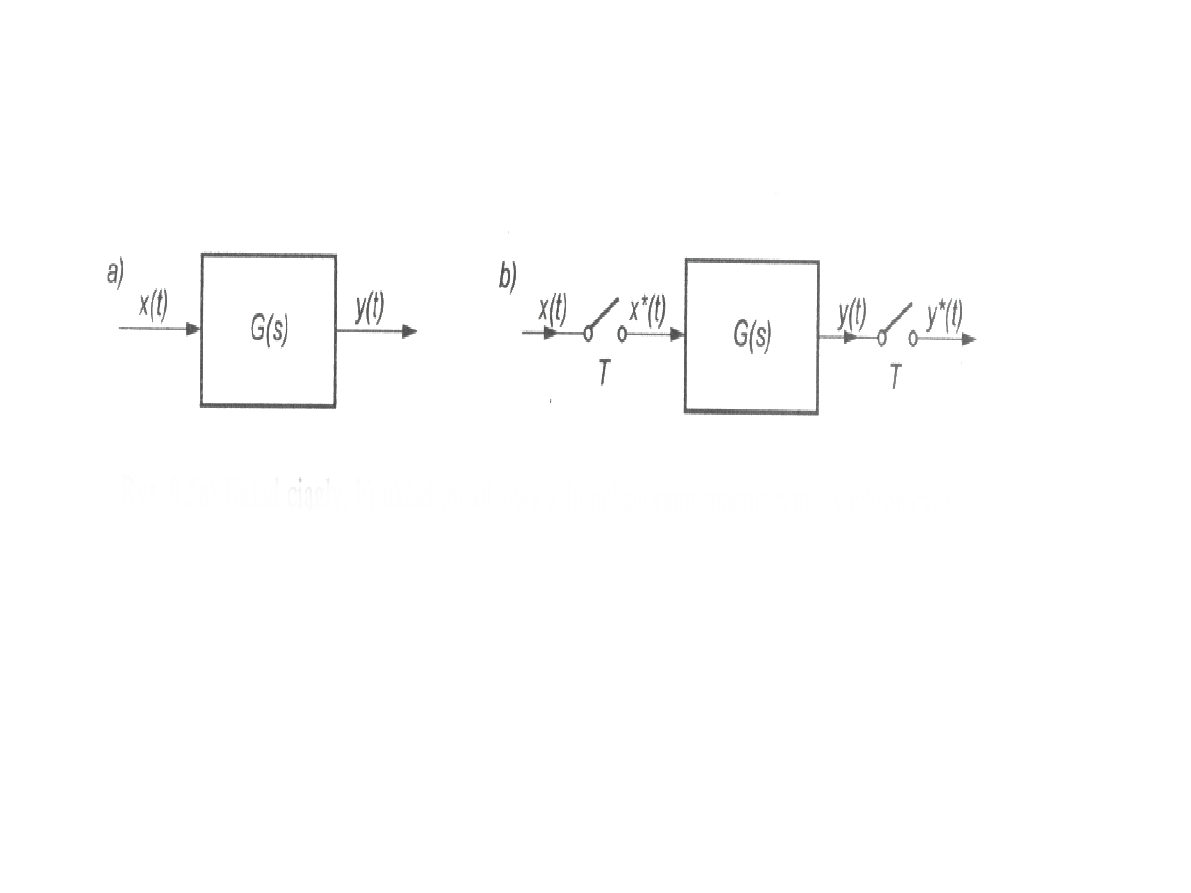
Układciągłyi dyskretny

Transmitancja impulsowa

Y s=Gs X  s

*

*

Transmitancja impulsowa cd.

Y s=

1
T



n=−∞

n=∞

Y s jn

s



Y s=

1
T



n=−∞

n=∞

∣

G s jn

s

 X s jn

s



∣

Ponieważ X  s jest funkcjąookresie j 

s

:

Y s= X s

∣

1
T



n=−∞

n=∞

Gs jn

s



∣

*

*

*

*

*

*

Transmitancja impulsowa cd.

przezanalogiędozależności X s=

1
T



n=−∞

n=∞

X s jn

s



G s=

1
T



n=−∞

n=∞

Gs jn

s

 ,a zatem:

Y s=X sG s,

wprowadzając zaśzmienną zespoloną zotrzymujemy:

Y z= X  zGz

TransmitancjaoperatorowaG z=

Y  z

X z

definiuje stosunek

transformatyZ sygnałuwyjściowegodo transformatyZ

sygnałuwejściowego, przyzerowychwarunkachpoczątkowych

*

*

*

*

*

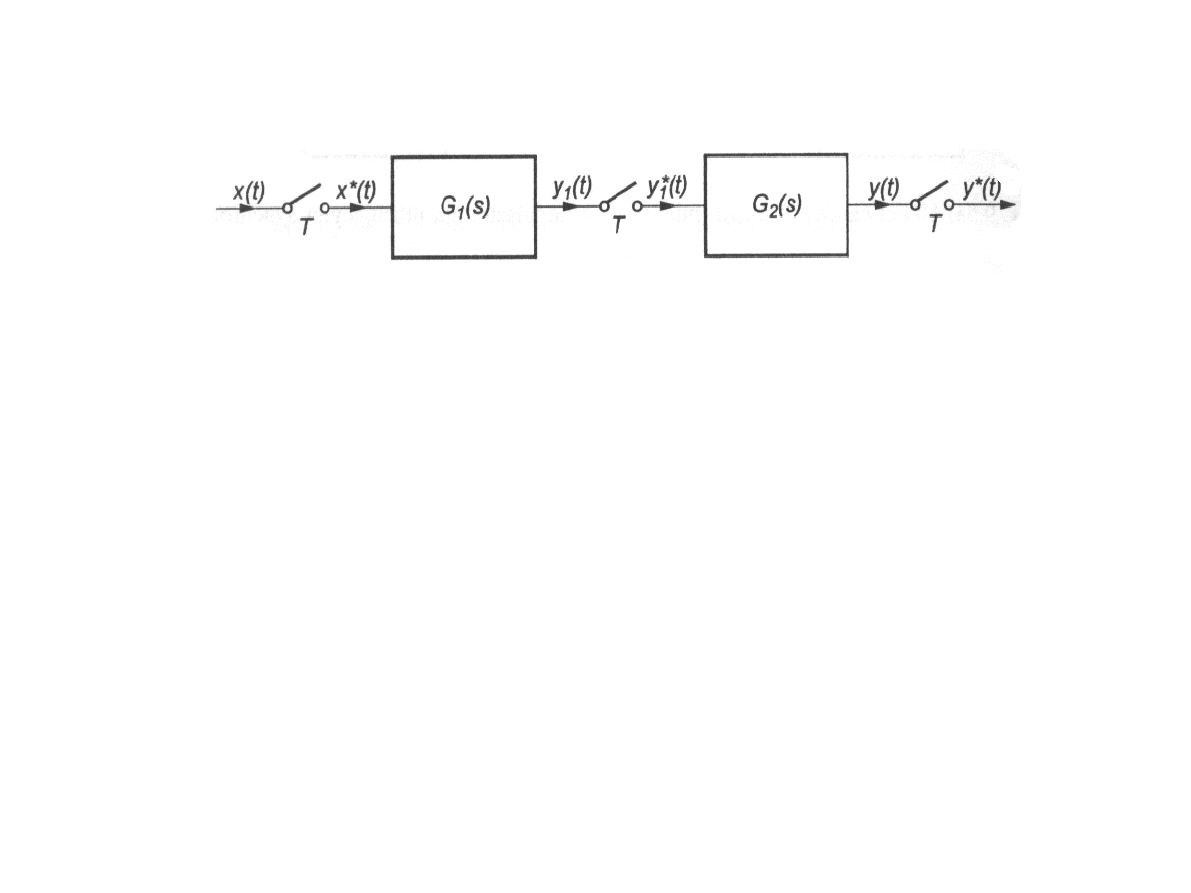
Transmitancjeimpulsoweukładówzłożonych

Układy połączoneszeregowo

Y

1

s=G

1

s X s

Y

1

s=G

1

s X s

Y

2

s=G

2

sY

1

s

Y

2

s=G

2

sY

1

s

Y

2

s=G

2

sG

1

s X sY z=G

2

 zG

1

 z X  z

Gz=G

1

 zG

2

z

*

*

*

*

*

*

*

*

*

*

*

*

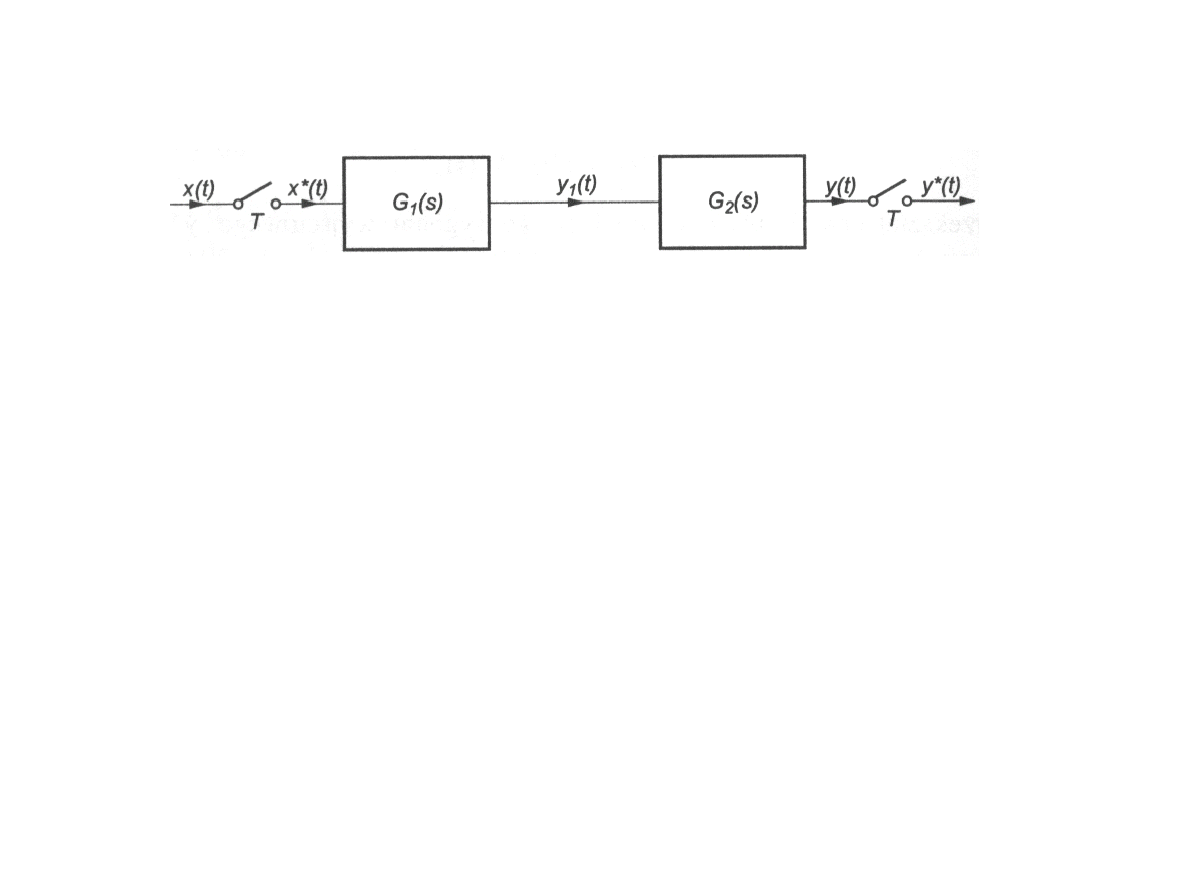
Y s=G

2

sG

1

s X s

Y s=[G

2

SG

1

S X s] =[G

2

sG

1

s] X s

Y z=Z{[G

1

sG

2

s]}X  z

Gz=Z[G

1

sG

2

s]

Transmitancjeimpulsoweukładówzłożonych

Układy połączoneszeregowocd.

*

*

*

*

*

*

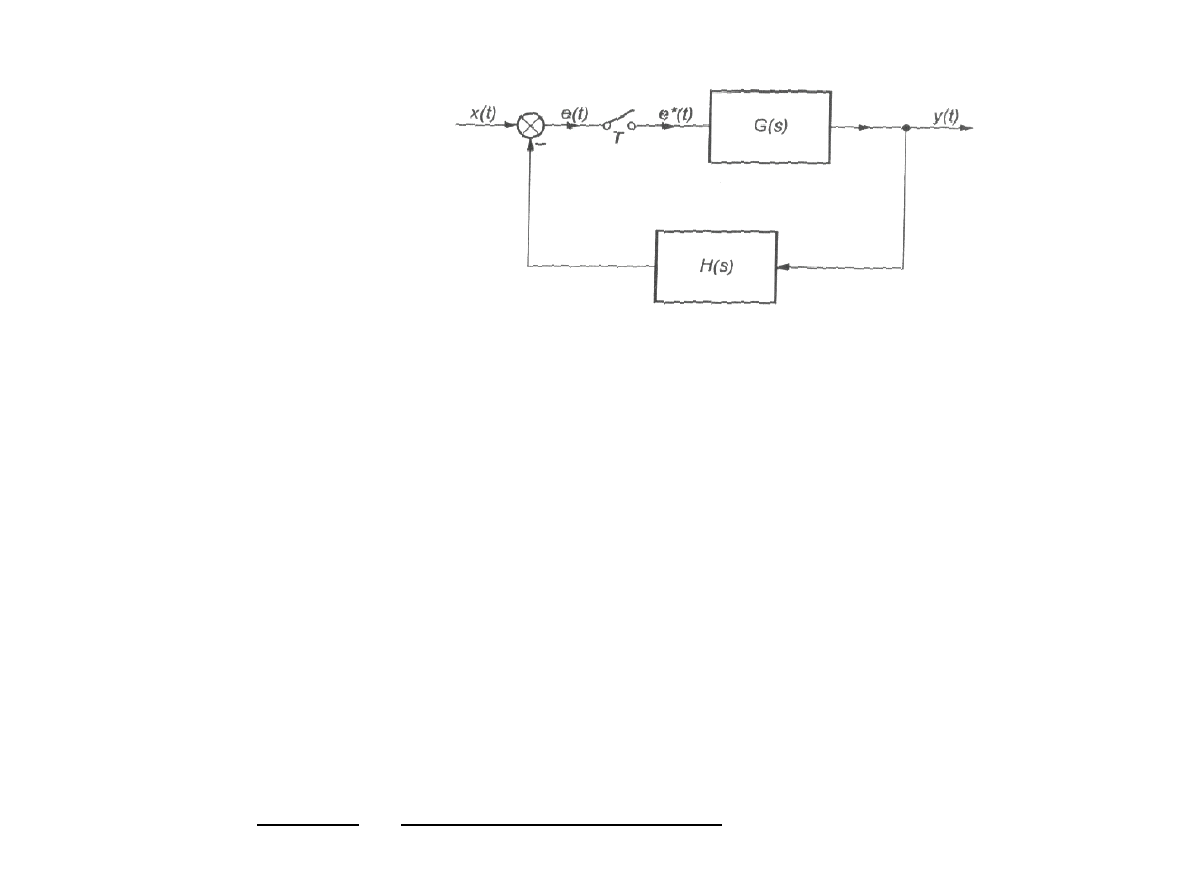
Transmitancjeimpulsoweukładówzłożonych

Układ zamknięty

Es= X s−Gs Hs E

¿

s ,

E s= X s−[Gs Hs] E s

Y s=Gs E s
Y s=G s E s
Y sY s{Gs Hs} =G s X s
Y zY zZ[Gs Hs]=Gz X z

G

z

 z=

Y  z

X z

=

G z

1Z[Gs Hs]

*

*

*

*

*

*

*

*

*

*

*

*

*

*

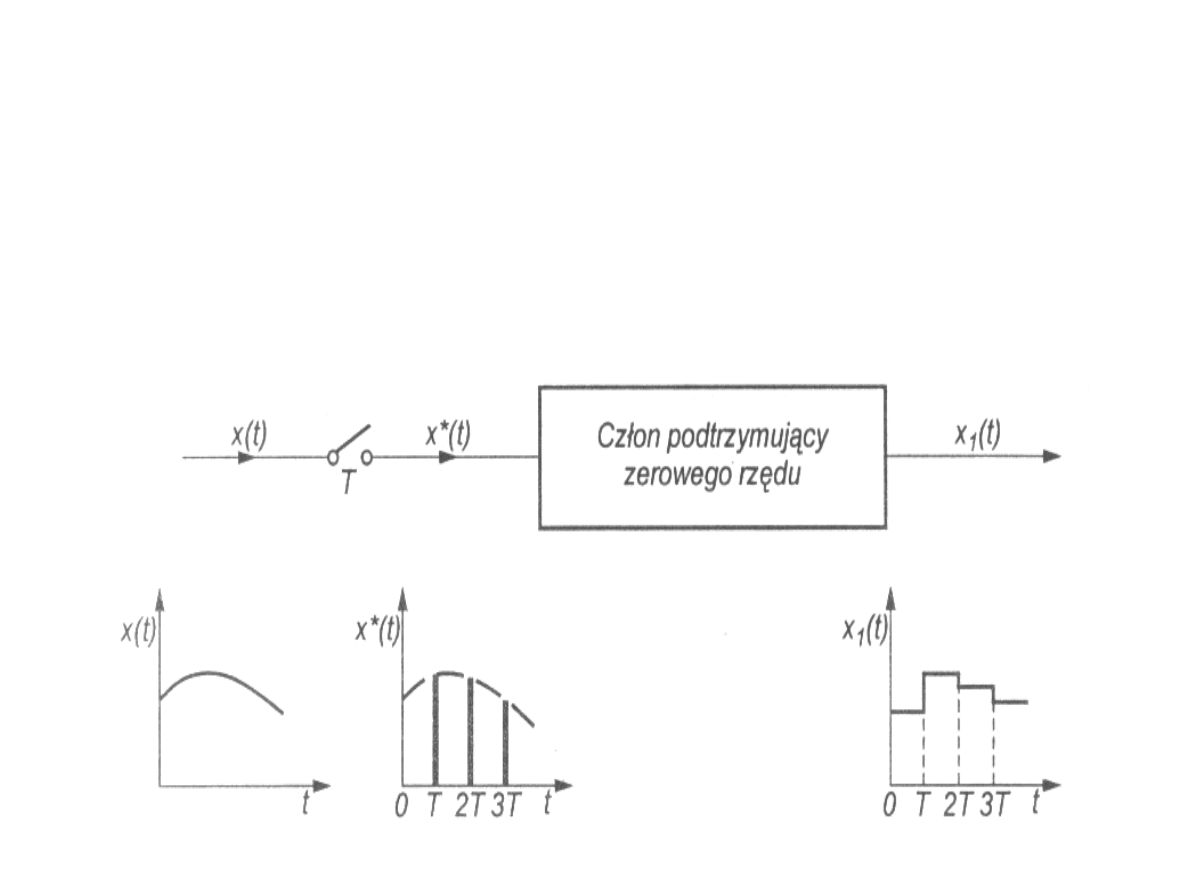
Wukładachrealizowanych fizyczniestosujesięczęsto

ekstrapolatorczłon podtrzymujący zerowegorzędu

Ekstrapolator zerowegorzędu

IdealnyimpulsatordajenawyjściuimpulsDiraca

T

Ekstrapolator zerowegorzędu cd.

x

1

t= 

n=0

∞

xnT[1t−nT−1t−nT−T]

X

1

s=

1

s

1−e

−sT

 

n=0

∞

xnTe

−snT



n=0

∞

xnTe

−snT

= X s

azatem:

G

h0

s=

1−e

−sT

s

Transmitancjawidmowaekstrapolatorazerowegorzędu

G

ho

 j =[G

hos

]

s= j

=

1−e

− jT

j 

,

po przekształceniach otrzymujemy :

G

ho

 j=Te

− j T

2

sin

T

2

T

2

skąd możemy obliczyć:

moduł i fazę transmitancji

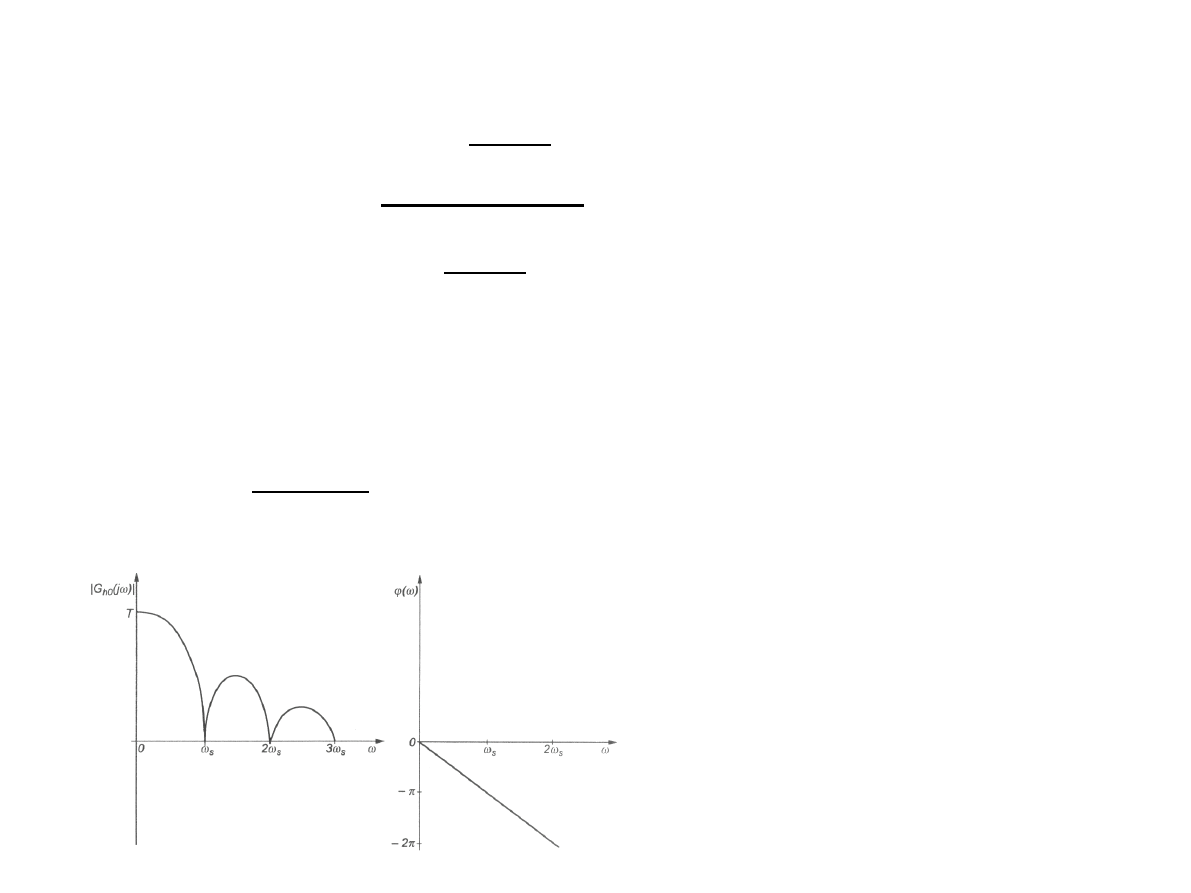
moduł jestrówny:

∣

G

ho

 j

∣

=T

∣

sin

T

2



∣

T

2

faza jestzaśrówna

=

−T

2

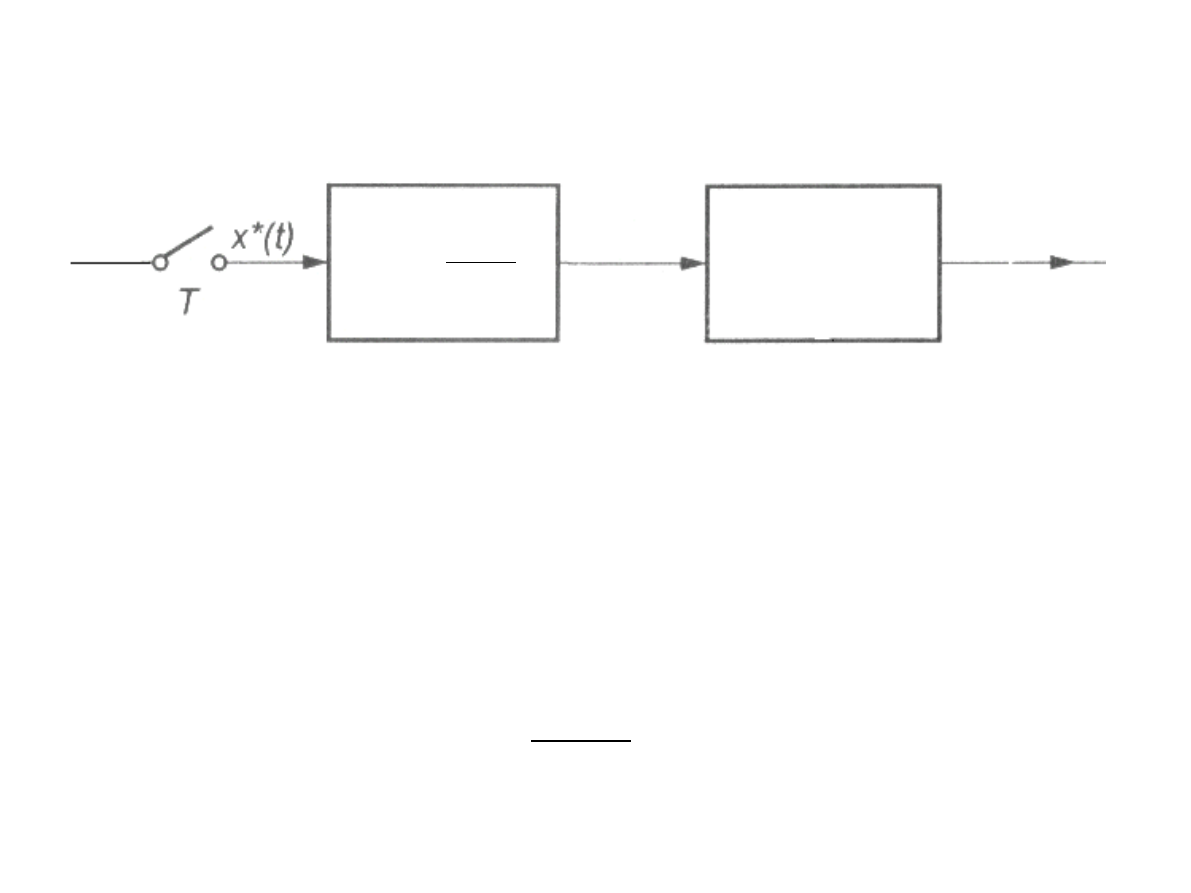
Ekstrapolator

Obiekt ciągły

G

1

 s=

1−e

sT

s

G

2

s

xt

xnT= Xe

jn T

= Xe

jnv

,gdziev=T − pulsacjabezwymiarowa

Dyskretnątransmitancją widmową G jV liniowegoukładuimpulsowego

nazywamy stosunekwartości zespolonychodpowiedzi Y  jv dowymuszenia X  jv

G jv=

Y  jv

X  jv

Dyskretnatransmitancjawidmowa

Dyskretnatransmitancjawidmowa cd.

Wukładzie jaknarysunkuzachodzi związekGs=G

1

sG

2

s

Międzydyskretnątransmitancjąwidmowąatransmitancją

dyskretnązachodzi związek:

G jv=[Gz]

z=e

jv

DyskretnatransmitancjawidmowaG jv jestwielkością
zespolonązależnąod parametrówukładui pulsacji v:

G jv=Pv jQv,gdzie:

Pv=real[G jv]

Qv=imag[G jv]

Dyskretnątransmitancjęwidmowąmozna przedstawićtakże

w postaciwykładniczej:

G jv=

∣

G jv

∣

e

j v

,gdzie:

∣

G jv

∣

−moduł dyskretnejtransmitancjiwidmowej

v−argumentdyskretnejtransmitancjiwidmowej

Pomiędzy postaciąalgebraicznąawykładniczązachodzą

związkianalogicznedotychdlaukładówciągłych:

∣

G jv

∣

=



 P

2

vQ

2

v

v=arctg

Qv

Pv

Dyskretnatransmitancjawidmowa cd.

Dyskretnatransmitancjawidmowacd.

Wodróżnieniuodukładówciągłychdyskretnatransmitancja

widmowa jest funkcjąokresową pulsacjiV ,gdyż:

G[ jv2 ]=G jv ,a

okrestej funkcjiwynosi 2 

Stabilnośćliniowychukładówimpulsowych

Podobnie jakdlaukładówciągłychrównieżdlaukładów

impulsowychistniejąróżnedefinicjestabilności ,według

Laplace' aukład jeststabilny, jezeli ograniczonemu

wejściuodpowiadaograniczonewyjście

Jeżeli transmitancjadyskretnaukładu jestrówna:

G z=

L z
M z

¿

ostabilnościukładudecyduje położeniepierwiastków

równaniacharakterystycznego:

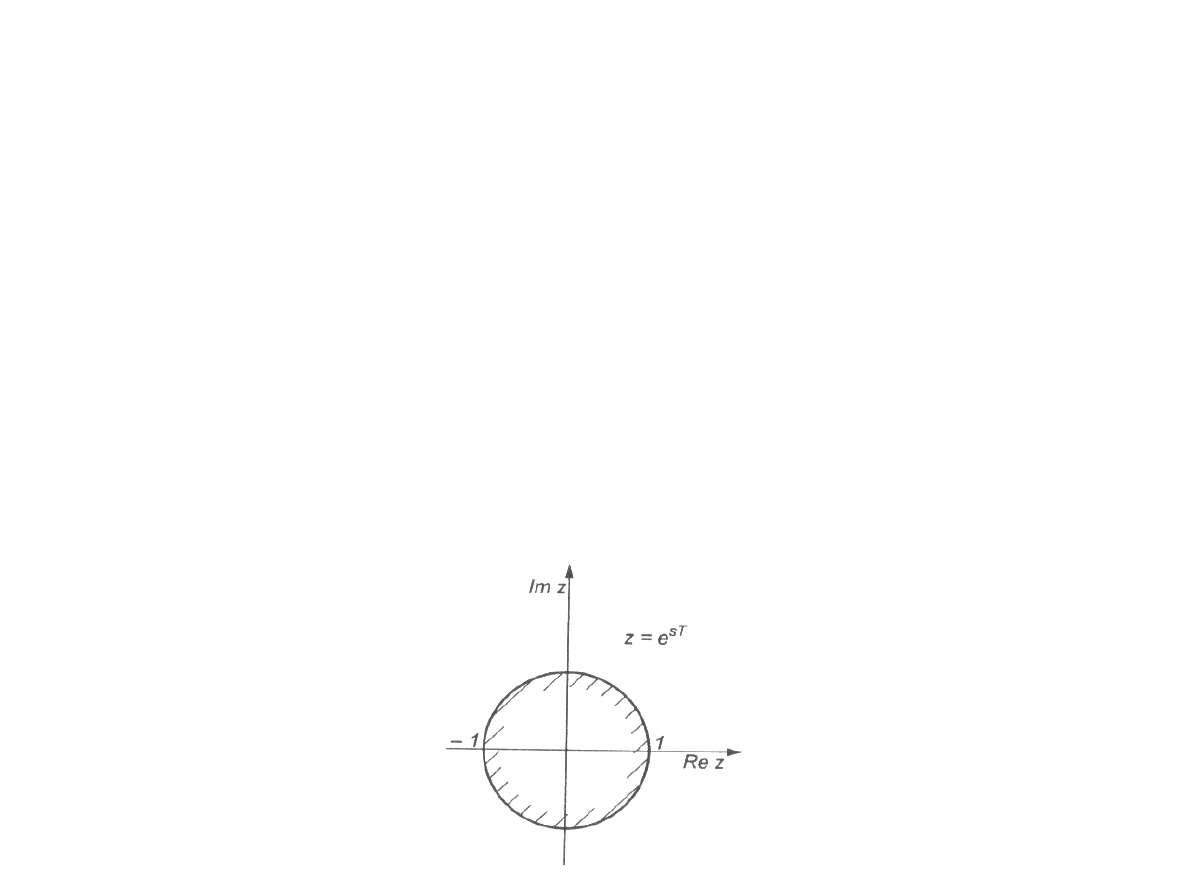
Stabilnośćliniowychukładówimpulsowych cd.

Równaniecharakterystyczneukładuma postać:

M z=0

Warunkiemstabilności układu jestabywszystkie pierwiastki

jegorównania charakterystycznegospełniaływarunek

∣

 z

i



∣

1, dlai=1,2....N ,gdzieNrządwielomianuM z

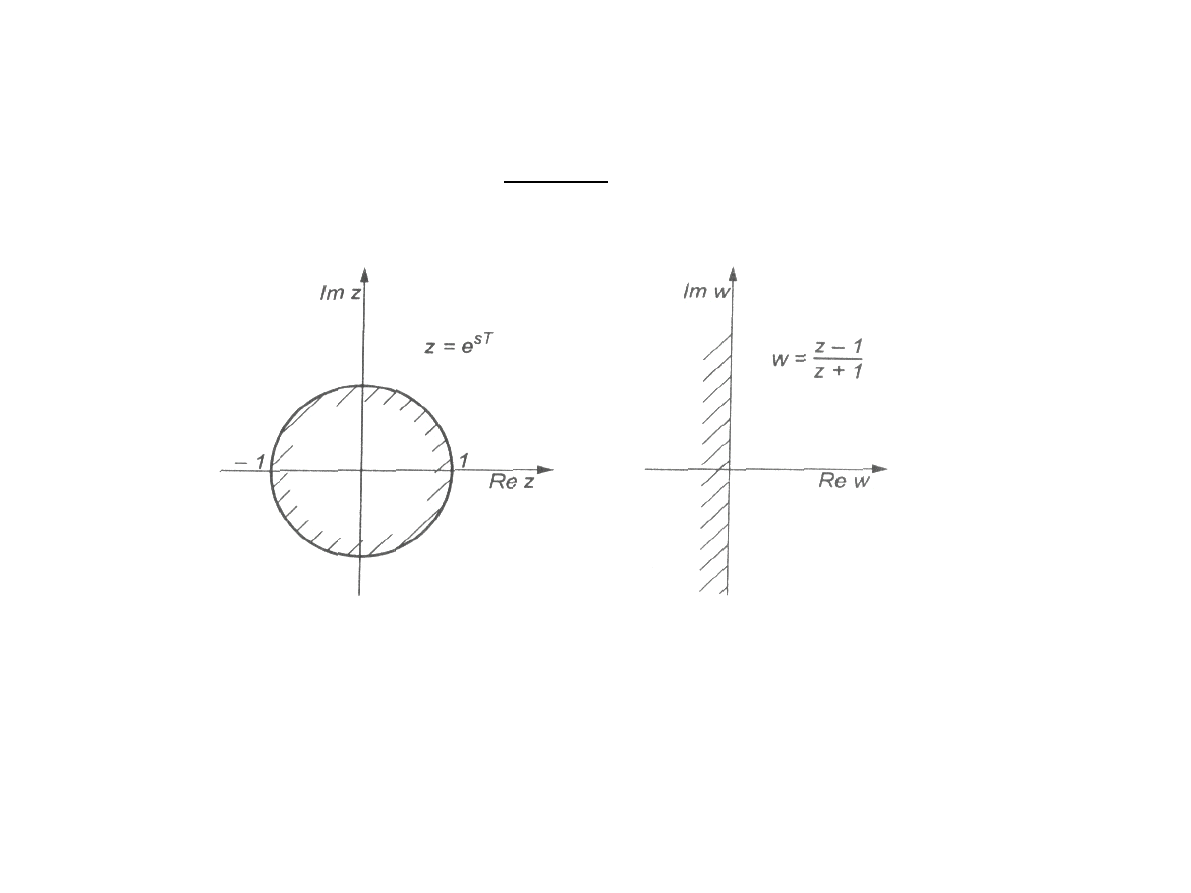
Przekształceniebliliniowe

z=

w1
w−1

Przekształcenietoodworowujewnętrzeokręgu

jednostkowegona płaszczyźniezwlewą półpłaszczyznę

płaszczyznyzmiennej zespolnej w

ponieważ przekształceniebiliniowezamieniawnętrze

okręgu jednostkowegowlewą półpłaszczyznętomożna

stosowaćdlanowej zmiennej zespolonej wkryteriatakie

jakdlaukładówciągłychnp:

KryteriumHurvitza

KryteriumRoutha

KryteriumMichajłowa

KryteriumNyquista

Dziękuję za uwagę