Część 1
11. METODA SIŁ - KRATOWNICA
1
11.
11. METODA SIŁ – KRATOWNICA
Sposób rozwiązywania kratownic statycznie niewyznaczalnych metodą sił omówimy rozwiązują
przykład liczbowy.
Zadanie 1
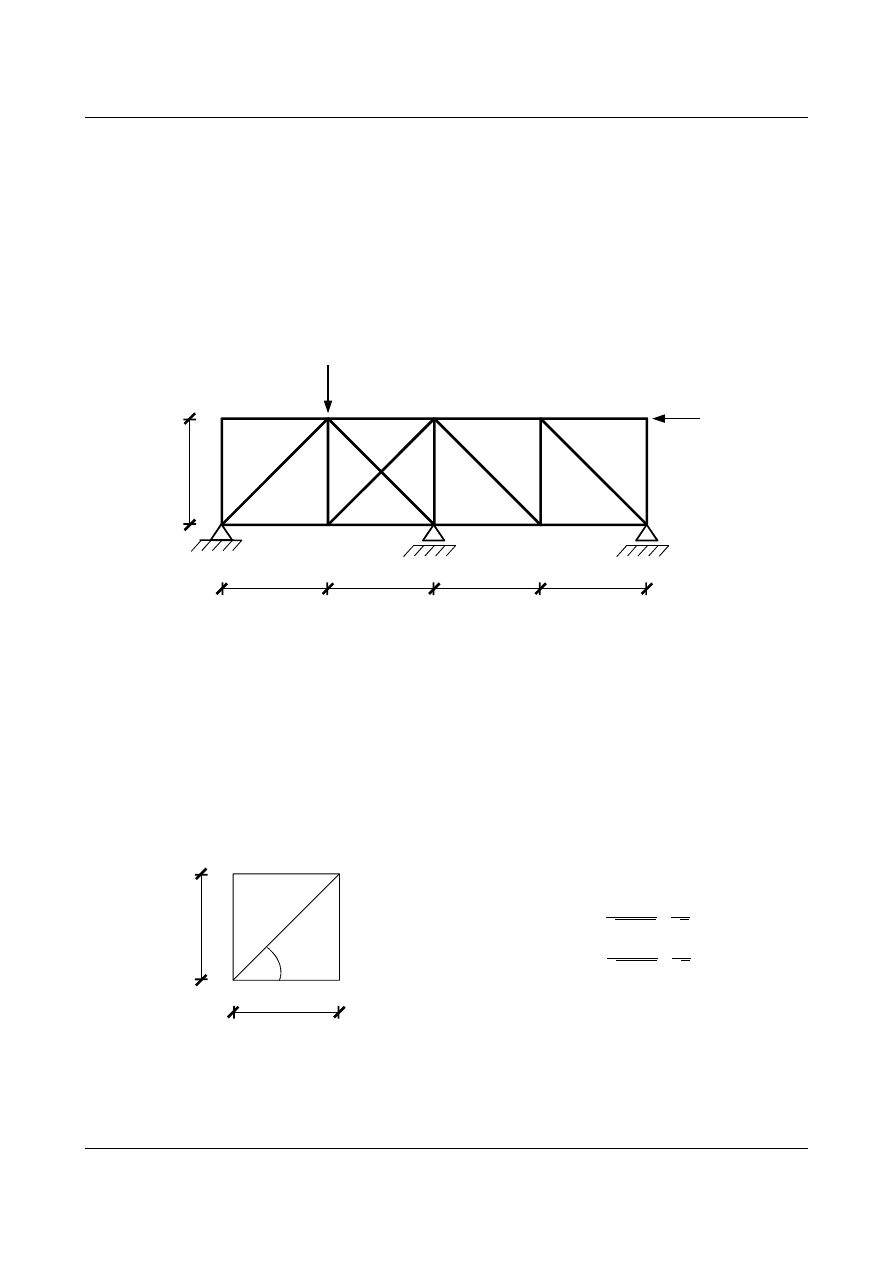
Dla kratownicy przedstawionej na rys.11.1 wyznaczyć siły wewnętrzne od podanego obciążenia.
40 kN
30 kN
3
3
3
3
3
[m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Rys. 11.1. Zadana kratownica statycznie niewyznaczalna
Dane geometryczne i fizyczne są takie same dla odpowiednich grup prętów. Po przyjęciu sztywności
porównawczej
EA
0
sztywności poszczególnych prętów są następujące:
dla pasa górnego
G
EA
G
=EA
0
dla pasa dolnego
D
EA
D
=EA
0
dla słupków
S
EA
K
=EA
0
dla krzyżulców
K
EA
S
=EA
0
Kąt pochylenia krzyżulca wynosi 45
o
, wobec tego:
3
3
α
[m]
sin
=
3
3
2
3
2
=
1
2
cos
=
3
3
2
3
2
=
1
2
Kratownica jest dwa razy statycznie niewyznaczalna (
SSN = 2), raz wewnętrznie i raz zewnętrznie. W
celu rozwiązania zadania metodą sił przyjmujemy układ podstawowy przedstawiony na rys. 11.2:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
2
40 kN
30 kN
3
3
3
3
3
[m]
X
2
X
1
X
1
A
B
C
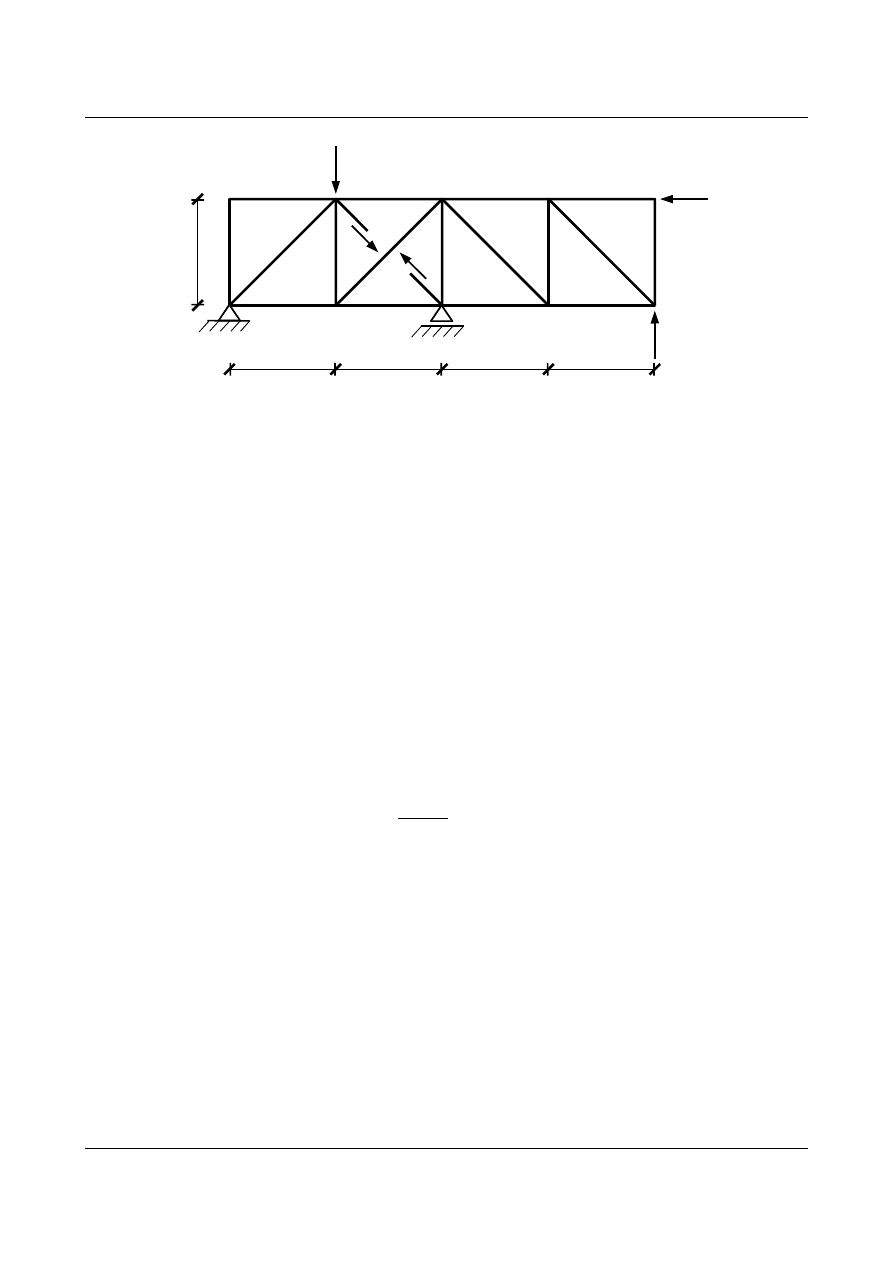
Rys. 11.2. Układ podstawowy
który musi spełniać warunki kinematycznej zgodności z układem wyjściowym. Oznacza to, że wzajemne
zbliżenie przekroi w rozciętym pręcie, oraz przemieszczenie pionowe węzła C muszą być równe zero.
=0
v
c
=0
(11.1)
Na powyższe przemieszczenia wpływ mają nadliczbowe sił
X
i
i obciążenie zewnętrzne.
Równania kanoniczne przyjmują postać:
= X
1
⋅
1 1
X
2
⋅
1 2
1 P
=0
v
c
= X
1
⋅
2 1
X
2
⋅
2 2
2 P
=0
(11.2)
Przemieszczenia w kratownicy obliczamy ze wzoru uwzględniającego tylko siły normalne:
ik
=
∑
j
=1
n
N
j
i
N
j
k
EA
j
l
j
(11.3)
gdzie:
N
j
i
- siła w pręcie
j- tym w stanie X
i
= 1,
N
j
k
- siła w pręcie
j- tym w stanie X
k
= 1,
n
- liczba prętów w kratownicy.
Kolejnym etapem jest wyznaczenie sił w prętach kratownicy od sił jednostkowych przyłożonych kolejno w
miejsca niewiadomych
X
1
i
X
2
, oraz od obciążenia zewnętrznego.
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
3
•
Stan od obciążenia
X
1
= 1
3
3
3
3
3
[m]
X
1
= 1
X
1
= 1
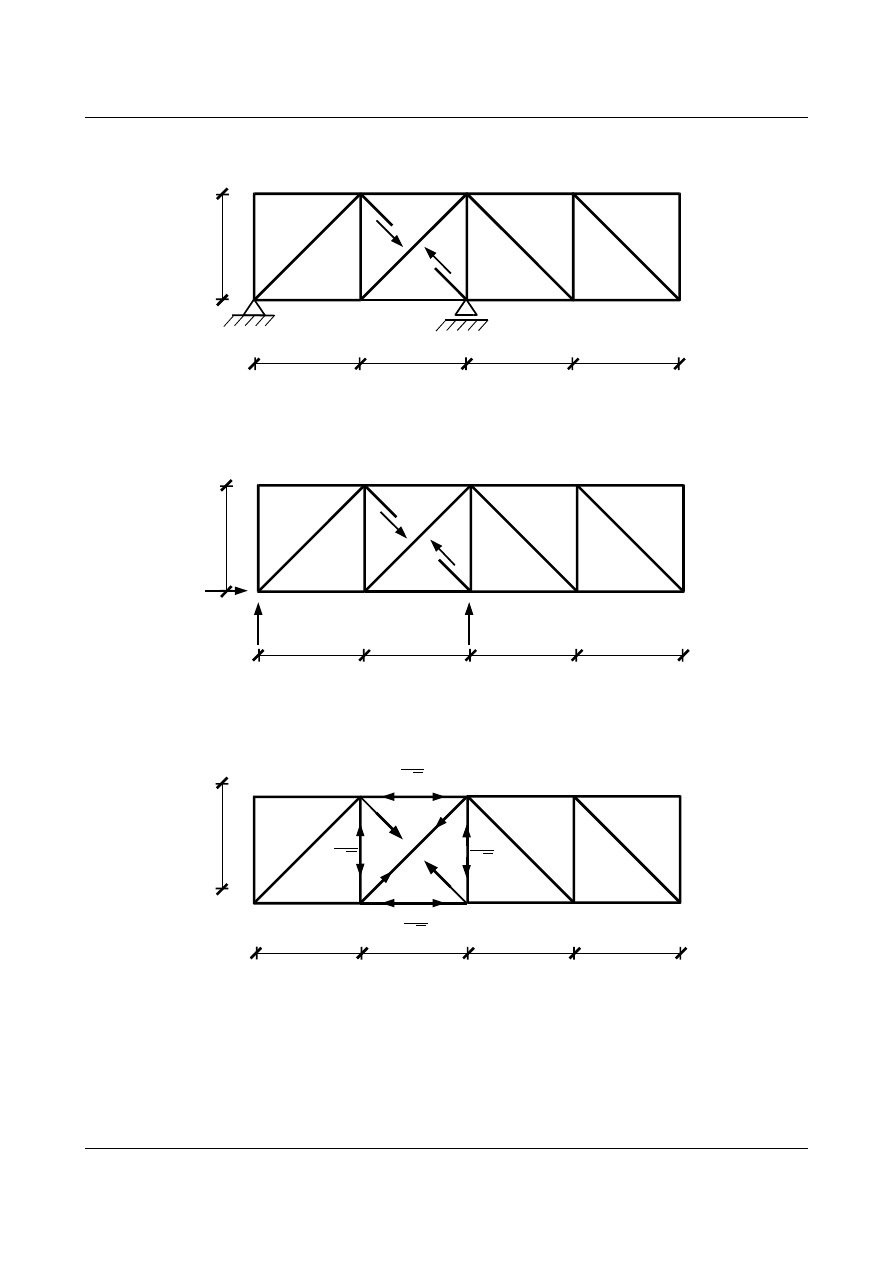
Rys. 11.3. Stan obciążenia X
1
=1
Obliczenie reakcji:
3
3
3
3
3
[m]
X
1
= 1
X
1
= 1
0
0
0
Siły w prętach obliczamy z równowagi węzłów. Ich rozkład przedstawia rys. 11.4:
3
3
3
3
3
[m]
O
O
O
O
1
1
O
O
O
O
O
O
O
O
1
1
N
1
[ - ]
1
2
1
2
1
2
1
2
Rys. 11.4. Rozwiązanie kratownicy w stanie X
1
=1
Należy zwrócić uwagę na fakt, że w pręcie 8 tylko w stanie
X
1
= 1 występuje siła normalna (N
8
(1)
=1).
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
4
•
Stan od obciążenia
X
2
= 1
3
3
3
3
3
[m]
X
2
= 1
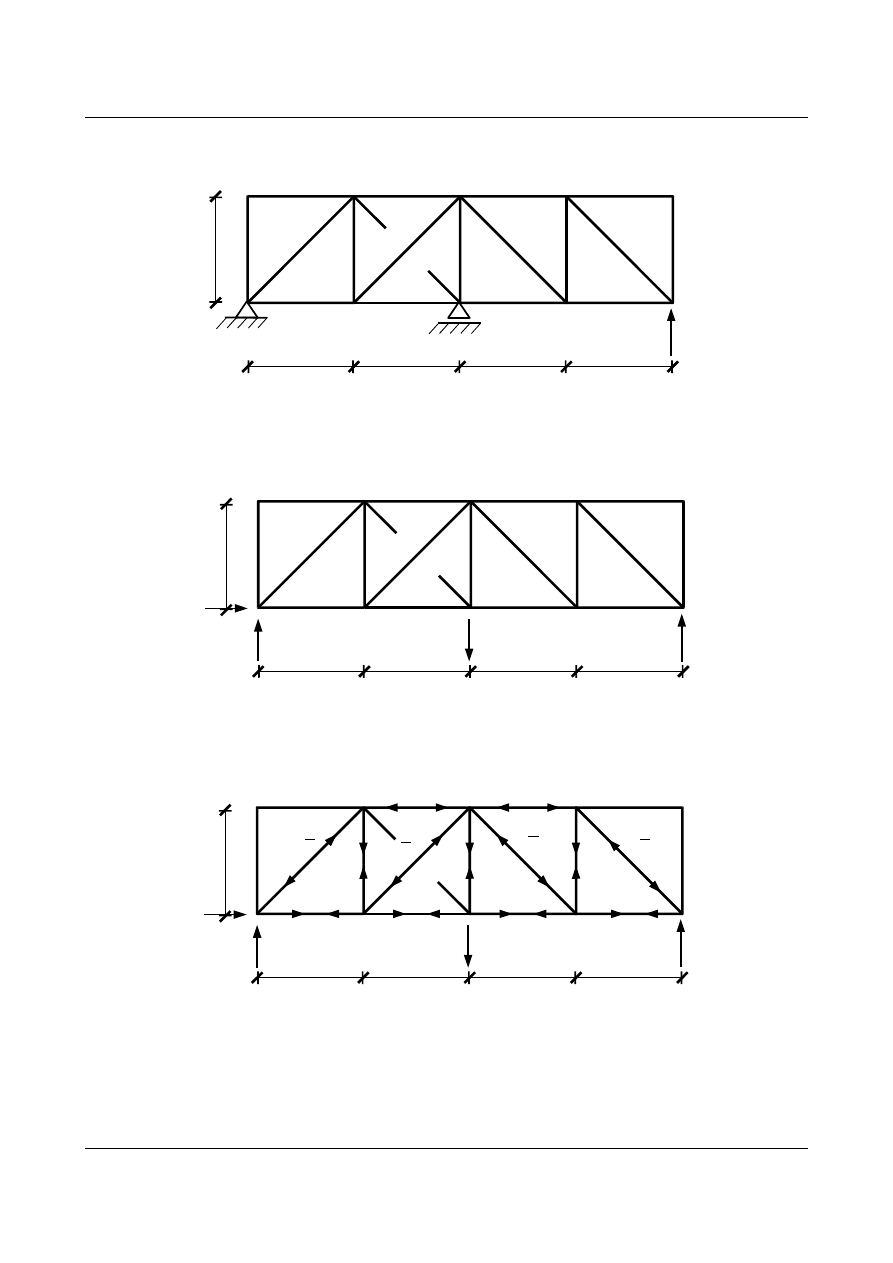
Rys. 11.5. Stan obciążenia X
2
=1
Obliczenie reakcji:
3
3
3
3
3
[m]
X
2
= 1
0
1
2
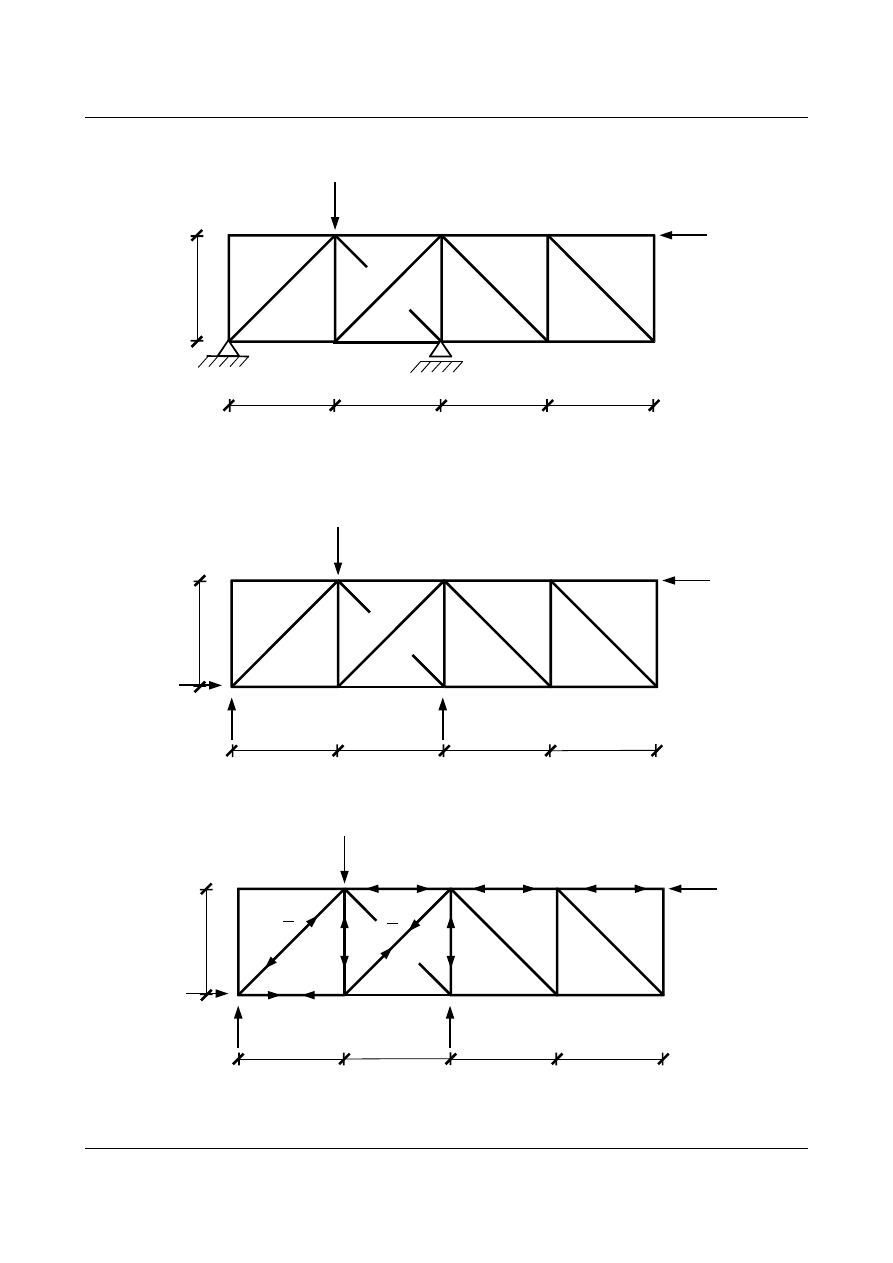
Siły w prętach obliczamy z równowagi węzłów. Ich rozkład przedstawia rys. 11.6:
3
3
3
3
3
[m]
1
0
1
2
O
O
O
O
O
O
1
1
2
1
1
2
2
2
1
1
N
2
[ - ]
2
2
2
Rys. 11.6. Rozwiązanie kratownicy w stanie X
2
=1
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
5
•
Stan od obciążenia
P
40 kN
30 kN
3
3
3
3
3
[m]
Rys. 11.7. Stan obciążenia P
Obliczenie reakcji:
40 kN
30 kN
3
3
3
3
3
[m]
30 kN
35 kN
5 kN
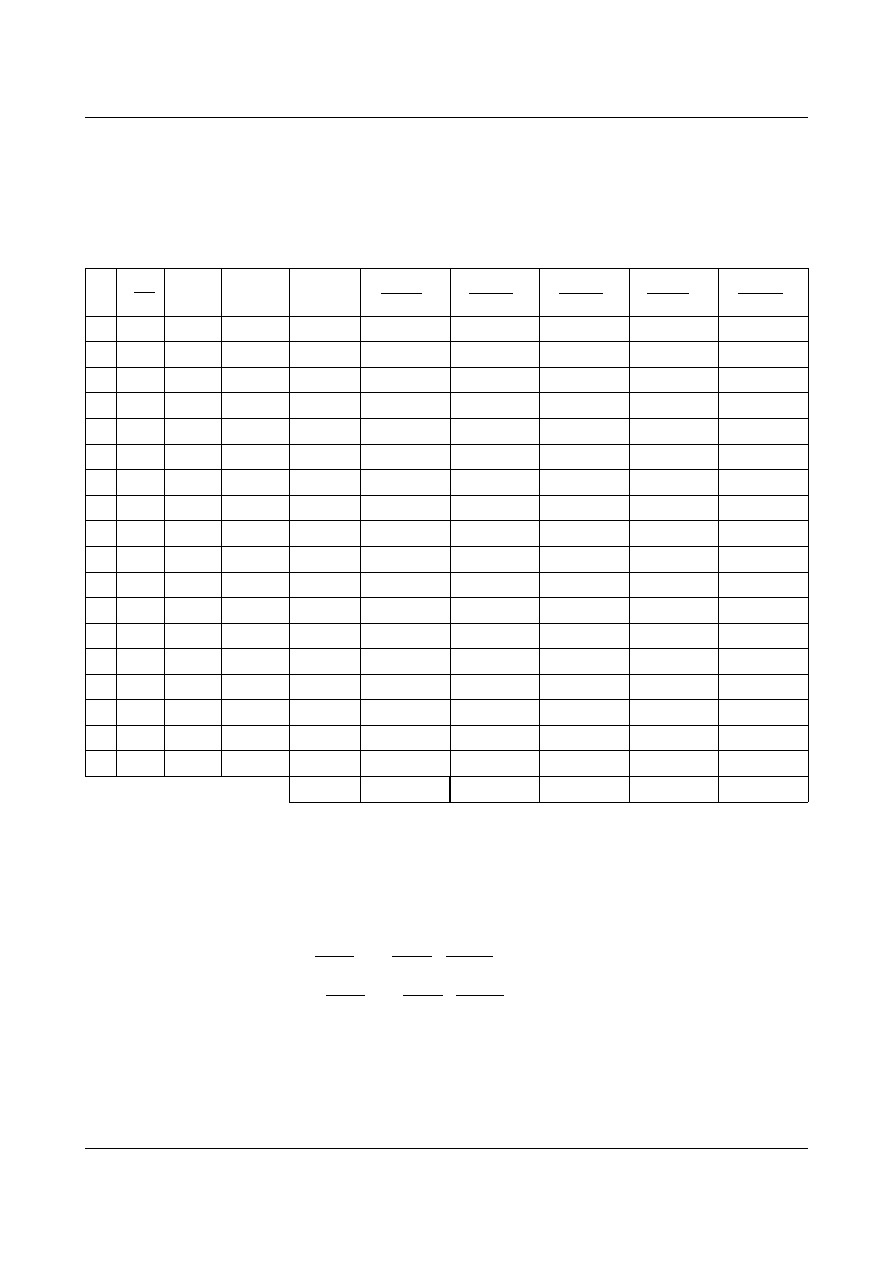
Siły w prętach obliczamy z równowagi węzłów. Ich rozkład przedstawia rys. 11.8:
40
30
3
3
3
3
3
[m]
30
35
5
N
P
[kN]
O
O
O
O
O
O
O
O
O
O
O
5
30
30
5
5
35
5
2
35
2
Rys. 11.8. Rozwiązanie kratownicy od stanu obciążenia zewnętrznego
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
6
W tabeli 11.1 zestawiono siły w prętach dla poszczególnych stanów obciążeń oraz iloczyny
odpowiednich wielkości. Wielkości zsumowane w odpowiednich kolumnach dają wartości przemieszczeń
zgodnie ze wzorem (11.3), (pomnożone przez sztywność porównawczą
EA
0
):
Tabela 11.1. Zestawienie wyników obliczeń
pręt
l
EA
N
P
[kN ]
N
1
[kN ]
N
2
[kN ]
N
1
N
1
EA
l
N
2
N
2
EA
l
N
1
N
2
EA
l
N
1
N
P
EA
l
N
2
N
P
EA
l
1
3,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
2
3,00 -35,00
-0,71
-1,00
1,50
3,00
2,12
74,25
105,00
3
3,00 -30,00
0,00
-1,00
0,00
3,00
0,00
0,00
90,00
4
3,00 -30,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
5
2,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
6
2,83 -49,50
0,00
-1,41
0,00
5,66
0,00
0,00
197,99
7
2,00
-5,00
-0,71
1,00
1,00
2,00
-1,41
7,07
-10,00
8
2,83
0,00
1,00
0,00
2,83
0,00
0,00
0,00
0,00
9
2,83
7,07
1,00
-1,41
2,83
5,66
-4,00
20,00
-28,28
10
2,00
-5,00
-0,71
2,00
1,00
8,00
-2,83
7,07
-20,00
11
2,83
0,00
0,00
-1,41
0,00
5,66
0,00
0,00
0,00
12
2,00
0,00
0,00
1,00
0,00
2,00
0,00
0,00
0,00
13
2,83
0,00
0,00
-1,41
0,00
5,66
0,00
0,00
0,00
14
2,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
15
3,00
5,00
0,00
1,00
0,00
3,00
0,00
0,00
15,00
16
3,00
0,00
-0,71
2,00
1,50
12,00
-4,24
0,00
0,00
17
3,00
0,00
0,00
2,00
0,00
12,00
0,00
0,00
0,00
18
3,00
0,00
0,00
1,00
0,00
3,00
0,00
0,00
0,00
Suma:
10,66
70,63
-10,36
108,39
349,71
EA
0
11
=10,66 ; EA
0
12
=−10,36 ; EA
0
22
=70,63 ; EA
0
1 P
=108,39 ; EA
0
2 P
=349,71
Obliczone wartości przemieszczeń podstawiamy do układu równań kanonicznych:
{
X
1
⋅
10,66
EA
0
− X
2
⋅
10,36
EA
0
108,39
EA
0
=0
−X
1
⋅
10,36
EA
0
X
2
⋅
70,63
EA
0
349,71
EA
0
=0
Mnożymy przez sztywność
EA
0
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
7
{
X
1
⋅10,66− X
2
⋅10,36108,39=0
−X
1
⋅10,36 X
2
⋅70,63349,71=0
i obliczamy wartości niewiadomych sił:
{
X
1
=−17,4807 [kN ]
X
2
=−7,5166 [kN ]
Po otrzymaniu wartości niewiadomych
dokonujemy analizy końcowej zadania, czyli obliczamy
rzeczywiste siły wewnętrzne obciążając układ podstawowy siłami zewnętrznymi oraz nadliczbowymi
X
1
i
X
2
.
40 kN
30 kN
3
3
3
3
3
[m]
7,52 kN
17,48 kN
17,48 kN
A
B
C
Rys. 11.9. Układ podstawowy obciążony zewnętrznie oraz przez siły X
1
i X
2
Ponieważ obliczenie sił normalnych wymaga ponownego rozwiązania układu, wygodniej jest skorzystać
z zasady superpozycji:
N
j
n
=N
P
j
X
1
⋅N
1
j
X
2
⋅N
2
j
(11.4)
gdzie:
N
j
(n)
– siła w
j- tym pręcie w układzie statycznie niewyznaczalnym
N
P
(j)
– siła w
j- tym pręcie od obciążenia zewnętrznego w układzie podstawowym
N
1
(j)
– siła w j- tym pręcie w stanie X
1
= 1
N
2
(j)
– siła w j- tym pręcie w stanie X
2
= 1
Dla ułatwienia obliczeń posłużymy się tabelą 11.2:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
8
Tabela 11.2. Zestawienie obliczeń do wyznaczenia N
j
n
l
EA
N
P
[kN ]
N
1
[−]
N
2
[−]
X
1
[kN ]
X
2
[kN ]
N
n
[kN ]
1
3,00
0,00
0,00
0,00
2
3,00
-35,00
-0,71
-1,00
3
3,00
-30,00
0,00
-1,00
4
3,00
-30,00
0,00
0,00
5
2,00
0,00
0,00
0,00
6
2,83
-49,50
0,00
-1,41
7
2,00
-5,00
-0,71
1,00
8
2,83
0,00
1,00
0,00
9
2,83
7,07
1,00
-1,41
10
2,00
-5,00
-0,71
2,00
11
2,83
0,00
0,00
-1,41
12
2,00
0,00
0,00
1,00
13
2,83
0,00
0,00
-1,41
14
2,00
0,00
0,00
0,00
15
3,00
5,00
0,00
1,00
16
3,00
0,00
-0,71
2,00
17
3,00
0,00
0,00
2,00
18
3,00
0,00
0,00
1,00
-17,48
-7,52
0,00
-15,12
-22,48
-30,00
0,00
-38,87
-0,16
-17,48
0,22
-7,67
10,63
-7,52
10,63
0,00
-2,52
-2,67
-15,03
-7,52
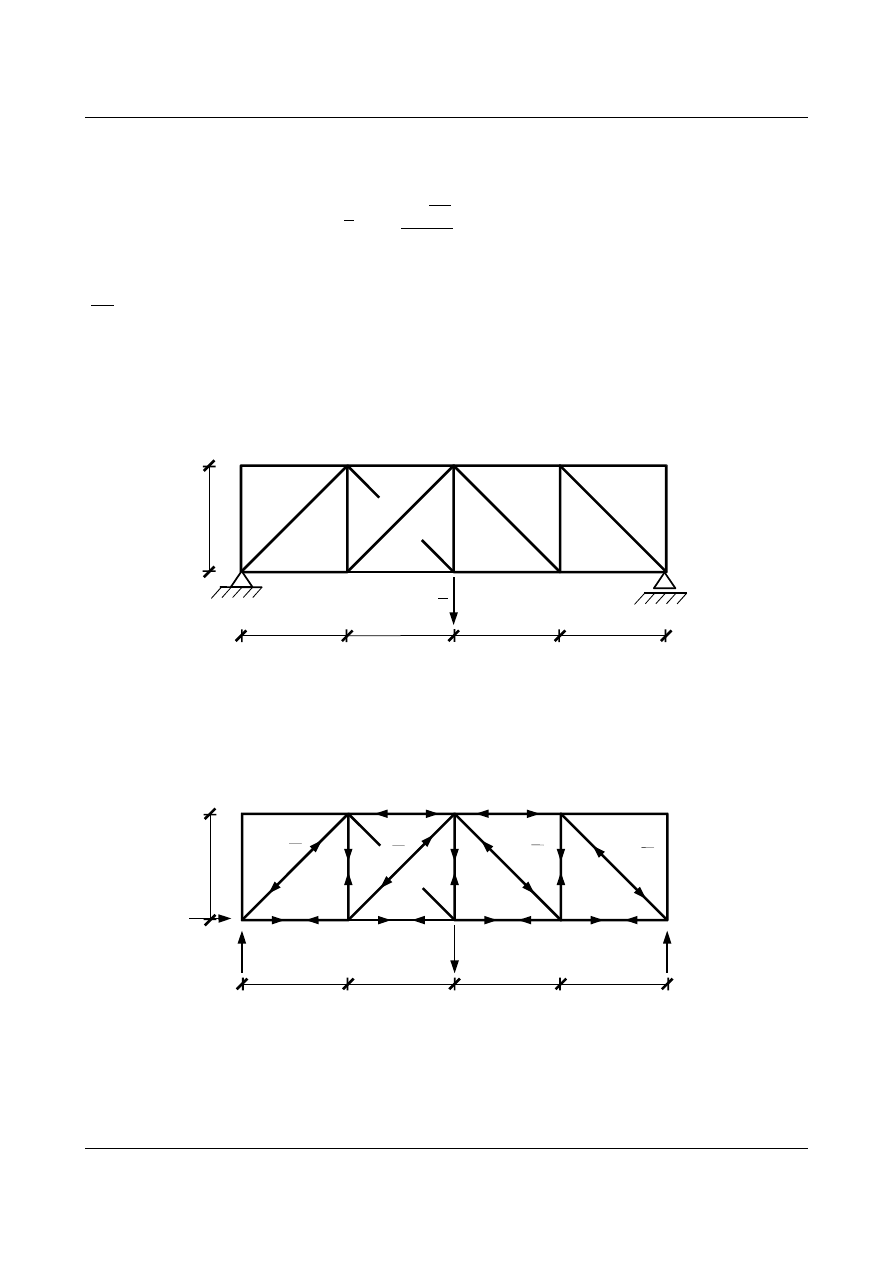
Posługując się wartościami zawartymi w tabeli 11.2 możemy określić rozkład sił w prętach zadanej
kratownicy statycznie niewyznaczalnej (rys. 11.10).
40,00
30,00
3
3
3
3
3
[m]
7,52
17,48
20,04
30,00
27,48
15,12
22,48
30,00
N
(n)
[kN]
O
O
O
2,52
2,67
15,03
7,52
38,87
0,16
0,22
7,67
10,63
7,52
10,63
Rys. 11.10. Rozkład sił w prętach kratownicy statycznie niewyznaczalnej
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
9
Sprawdzenie kinematyczne:
W celu wykonania sprawdzenia kinematycznego skorzystamy ze wzoru redukcyjnego:
1
⋅=
∑
j
N
j
n
N
k
j
EA
j
l
j
(11.5)
gdzie:
N
k
j
- siła w
j- tym pręcie w układzie statycznie wyznaczalnym od obciążenia wirtualnego.
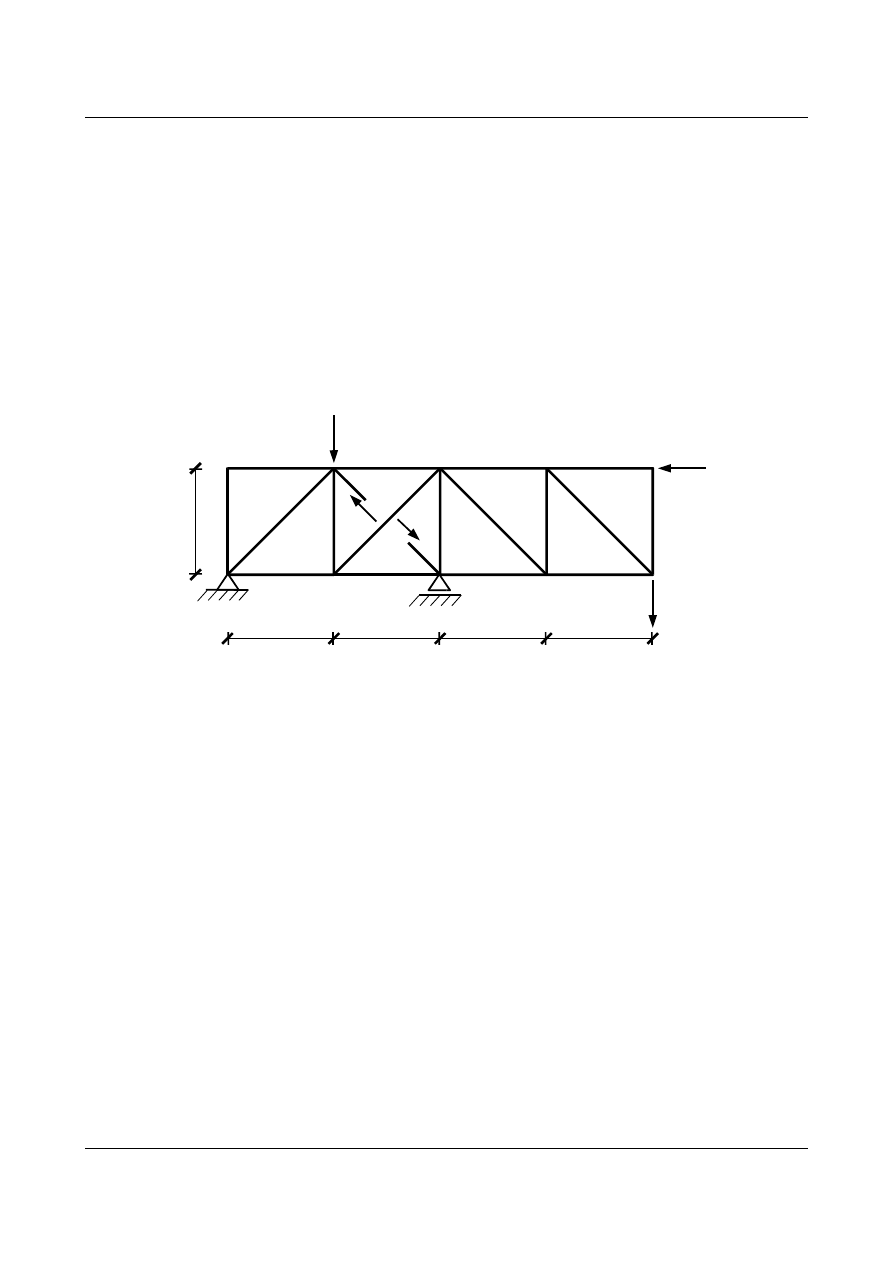
Musimy obliczyć znane przemieszczenie korzystając z innego układu podstawowego (rys. 11.11).
Liczymy przemieszczenie pionowe w węźle nr 3 (przykładamy wirtualną siłę pionową). W rzeczywistości jest
tam podpora, tak więc przemieszczenie pionowe jest równe zero.
3
3
3
3
3
[m]
1
Rys. 11.11. Inny układ podstawowy
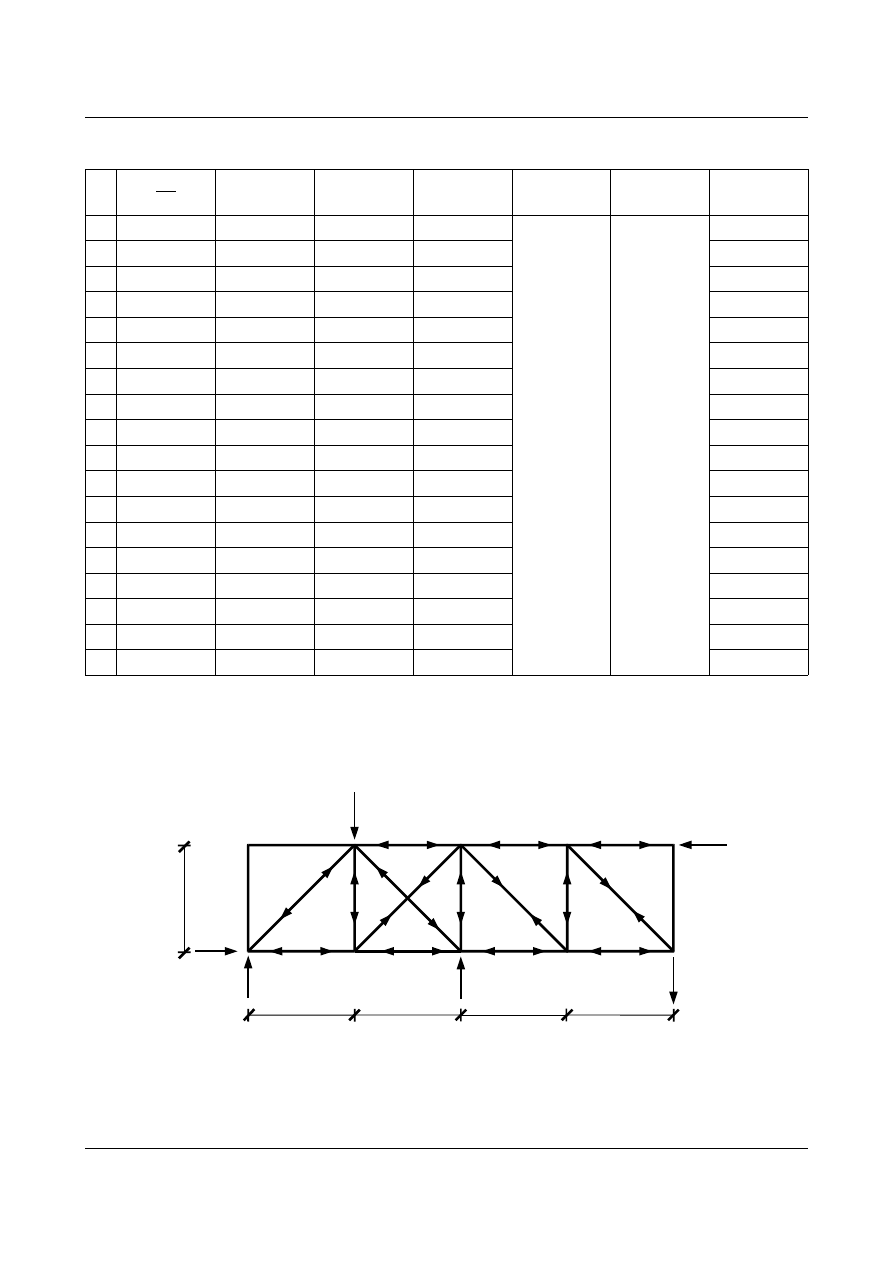
Siły w prętach obliczamy z równowagi węzłów. Ich rozkład przedstawia rys. 11.12:
3
3
3
3
3
[m]
1
0
0,5
0,5
B
O
O
O
O
O
O
1
1
1
0,5
0,5
0,5
2
0,5
0,5
0,5
0,5
N
k
[ - ]
0,5
2
0,5
2
0,5
2
Rys. 11.12. Rozkład sił w prętach kratownicy od siły wirtualnej w nowym układzie podstawowym
W tabeli 11.3 zestawiono wyniki kontroli kinematycznej sił z rys. 11.2 oraz dla sił wyznaczonych w
stanach
X
1
=1 i X
2
=1.
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
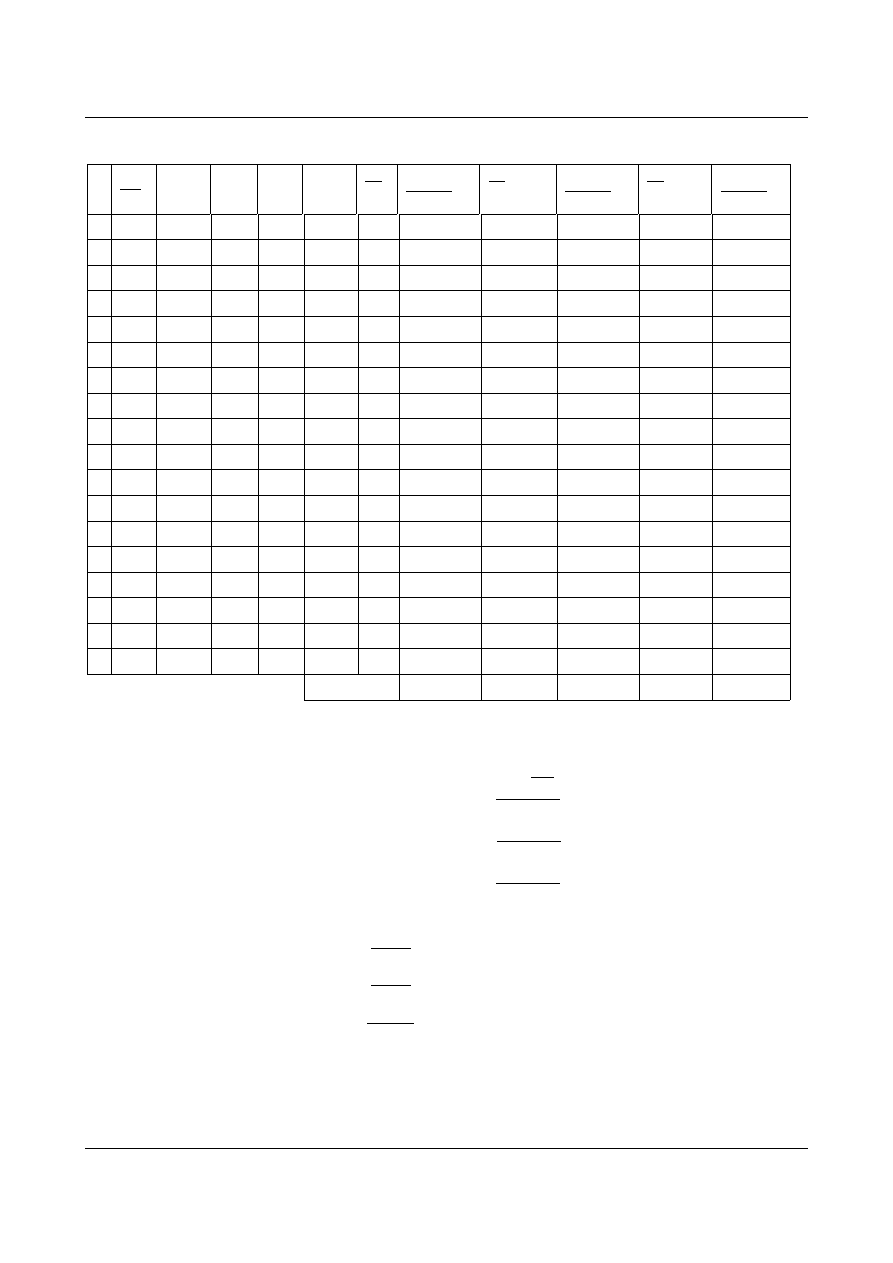
Część 1
11. METODA SIŁ - KRATOWNICA
10
Tabela 11.3. Wyniki kontroli kinematycznej
l
EA
N
P
[kN ]
N
1
[−]
N
2
[−]
N
n
[kN ]
N
k
N
n
N
k
EA
l
N
k
=N
1
N
n
N
1
EA
l
N
k
=N
2
N
n
N
2
EA
l
1
3,00
0,00
0,00
0,00
2
3,00 -35,00
-0,71 -1,00
3
3,00 -30,00
0,00 -1,00
4
3,00 -30,00
0,00
0,00
5
2,00
0,00
0,00
0,00
6
2,83 -49,50
0,00 -1,41
7
2,00
-5,00
-0,71
1,00
8
2,83
0,00
1,00
0,00
9
2,83
7,07
1,00 -1,41
10 2,00
-5,00
-0,71
2,00
11 2,83
0,00
0,00 -1,41
12 2,00
0,00
0,00
1,00
13 2,83
0,00
0,00 -1,41
14 2,00
0,00
0,00
0,00
15 3,00
5,00
0,00
1,00
16 3,00
0,00
-0,71
2,00
17 3,00
0,00
0,00
2,00
18 3,00
0,00
0,00
1,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-15,12 -0,50
22,68
-0,71
32,08
-1,00
45,37
-22,48 -0,50
33,73
0,00
0,00
-1,00
67,45
-30,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-38,87 -0,71
77,73
0,00
0,00
-1,41
155,47
-0,16
0,50
-0,16
-0,71
0,22
1,00
-0,31
-17,48
0,00
0,00
1,00
-49,44
0,00
0,00
0,22
-0,71
-0,44
1,00
0,62
-1,41
-0,88
-7,67
1,00
-15,34
-0,71
10,85
2,00
-30,69
10,63 -0,71
-21,26
0,00
0,00
-1,41
-42,52
-7,52
0,50
-7,52
0,00
0,00
1,00
-15,03
10,63 -0,71
-21,26
0,00
0,00
-1,41
-42,52
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-2,52
0,50
-3,77
0,00
0,00
1,00
-7,55
-2,67
1,00
-8,02
-0,71
5,67
2,00
-16,03
-15,03
1,00
-45,10
0,00
0,00
2,00
-90,20
-7,52
0,50
-11,27
0,00
0,00
1,00
-22,55
Suma:
-0,002
0,001
0,003
Dodatkowo obliczyć możemy jeszcze błędy, dzieląc wyniki przez sumy wartości bezwzględnych z
poszczególnych kolumn.
EA
0
V
=−0,002
EA
0
∑
∣N
j
n
∣∣N
k
j
∣
EA
⋅l=77,73
EA
0
1
=0,001
EA
0
∑
∣N
j
n
∣∣N
1
j
∣
EA
⋅l=49,44
EA
0
2
=−0,003
EA
0
∑
∣N
j
n
∣∣N
2
j
∣
EA
⋅l=155,47
0,002
77,73
⋅100 %=0,003 %
0,001
49,44
⋅100 %=0,002 %
0,003
155,47
⋅100 %=0,002 %
Warto dodać tutaj, iż błędy wyliczone powyżej mieszczą się w dopuszczalnej granicy 1%, zadanie
możemy więc uznać za rozwiązane prawidłowo.
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
11
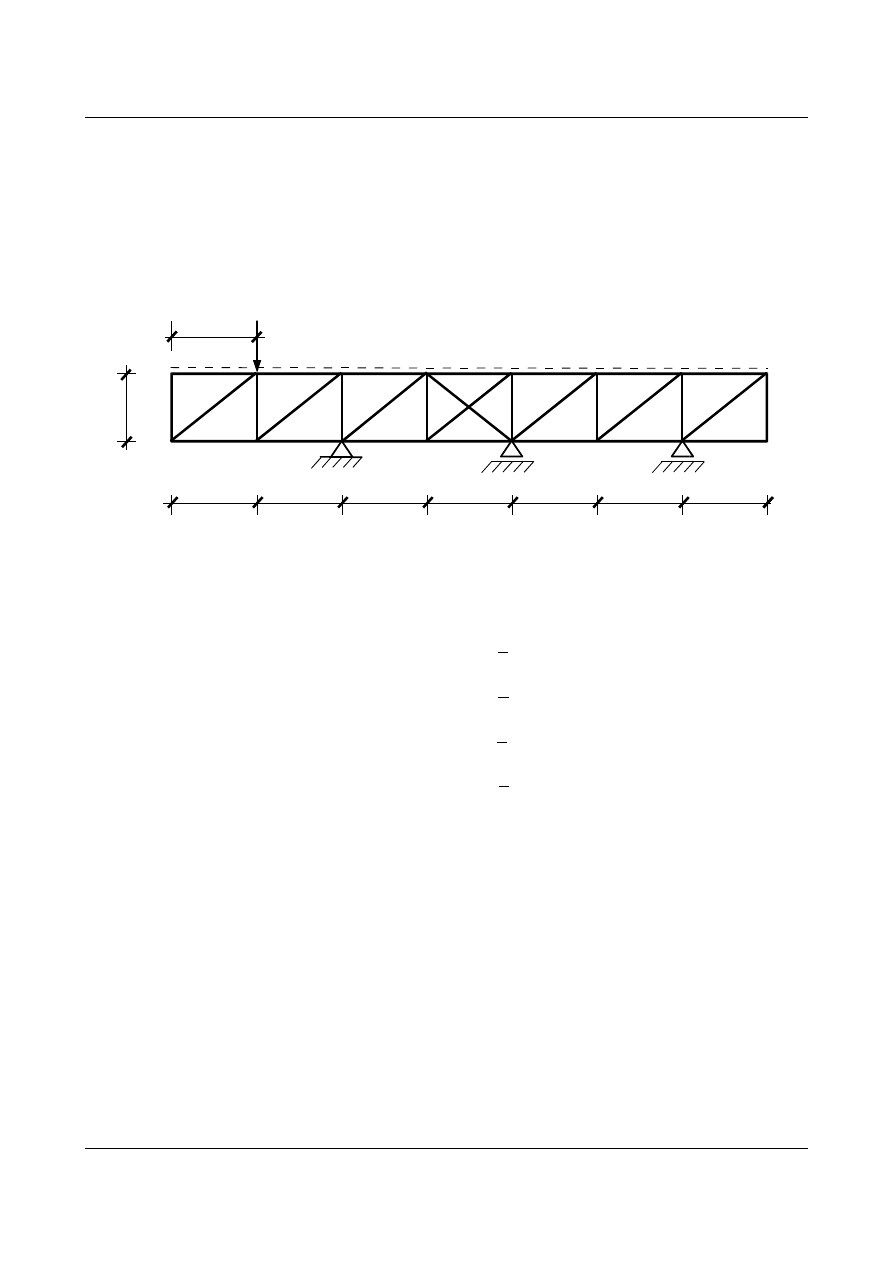
Zadanie 2
Wyznaczyć linie wpływu sił w prętach kratownicy statycznie niewyznaczalnej wykorzystując metodę
ciężarów sprężystych.
Dana jest kratownica:
4
4
4
4
4
4
4
3
S
2
S
3
S
4
S
5
S
6
S
7
S
8
S
1
G
1
G
2
G
3
G
4
G
5
G
6
G
7
D
7
D
6
D
5
D
4
D
3
D
2
D
1
K
1
K
2
K
3
K
4
K
5
K
6
K
7
P=1
K
n
[m]
x
Rys. 11.13. Zadana kratownica statycznie niewyznaczalna
Zależności między sztywnościami dla poszczególnych grup prętów są następujące:
dla pasa górnego
G
4
3
⋅EA
dla pasa dolnego
D
4
3
⋅EA
dla słupków
S
3
3
⋅EA
dla krzyżulców
K
5
3
⋅EA
Celem zadania jest wyznaczenie linii wpływu siły w pręcie
D
4
od poruszającej się po pasie górnym siły
jedynkowej. Zgodnie z zasadą superpozycji zapisujemy równanie linii wpływu w układzie statycznie
niewyznaczalnym:
lw D
4
n
=lw D
4
0
D
4
X
1
=1
⋅lw X
1
D
4
X
2
=1
⋅lw X
2
(11.6)
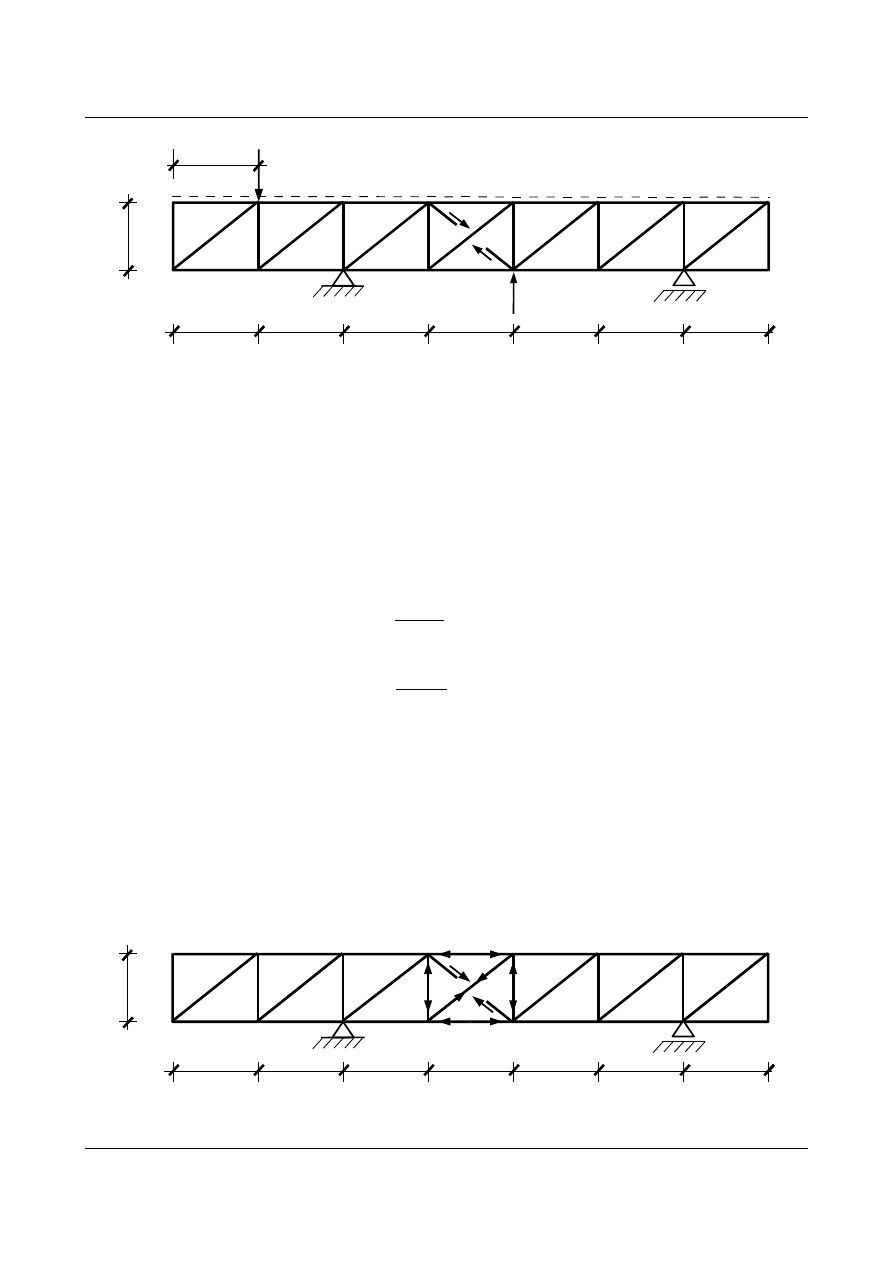
Dobrano układ podstawowy:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
12
4
4
4
4
4
4
4
3
S
2
S
3
S
4
S
5
S
6
S
7
S
8
S
1
G
1
G
2
G
3
G
4
G
5
G
6
G
7
D
7
D
6
D
5
D
4
D
3
D
2
D
1
K
1
K
2
K
3
K
4
K
5
K
6
K
7
P=1
[m]
x
X
1
X
2
X
1
Rys. 11.14. Układ podstawowy
który uzupełniamy układem równań kanonicznych:
{
11
⋅X
1
12
⋅X
2
1 P
=0
21
⋅X
1
22
⋅X
2
2 P
=0
(11.7)
W celu obliczenia współczynników korzystamy z zależności:
ik
=
∑
m
S
i m
⋅S
k m
EA
m
⋅l
m
(11.8)
iP
=
∑
m
S
i m
⋅S
P m
EA
m
⋅l
m
(11.9)
gdzie:
l
m
to długość pręta,
S
im
to siła w stanie
X
i
=1 w pręcie m,
S
Pm
to siła w pręcie
m od obciążenia zewnętrznego.
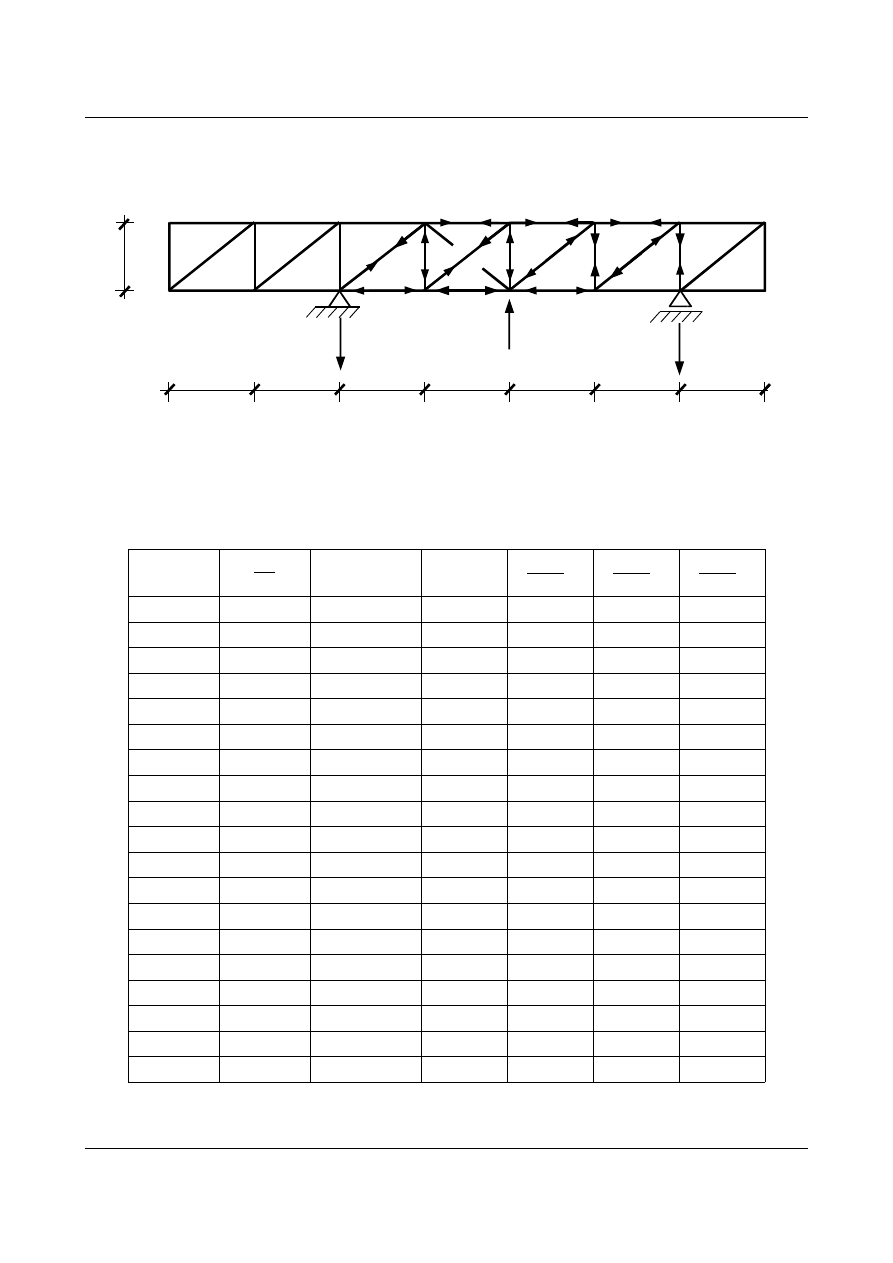
•
Stan
S
1
(obciążenie
X
1
=1)
4
4
4
4
4
4
4
3
-0.8
-0.8
-0.6
-0.6
1
1
1
1
[m]
Rys. 11.15. Stan obciążenia X
1
=1
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
13
•
Stan
S
2
(obciążenie
X
2
=1)
3
0,5
0,67
0,5
-0,5
-0,5
0,67
1,33
-0,67
-0,67
-1,33
-0.
83
-0.
83
0.8
3
0.8
3
X
2
=1
0,5
0,5
4
4
4
4
4
4
4
[m]
Rys. 11.16. Stan obciążenia X
2
=1
Do obliczenia przemieszczeń posłużono się tabelą:
Tabela 11.4. Siły w prętach w stanach jednostkowych
l
EA
S
1
S
2
S
1
⋅S
1
EA
⋅l
S
1
⋅S
2
EA
⋅l
S
2
⋅S
2
EA
⋅l
D
1
3,00
0,00
0,00
0,00
0,00
0,00
D
2
3,00
0,00
0,00
0,00
0,00
0,00
D
3
3,00
0,00
-0,6(6)
0,00
0,00
1,3(3)
D
4
3,00
-0,80
-1,3(3)
1,92
3,20
5,3(3)
D
5
3,00
0,00
-0,6(6)
0,00
0,00
1,3(3)
D
6
3,00
0,00
0,00
0,00
0,00
0,00
D
7
3,00
0,00
0,00
0,00
0,00
0,00
S
1
3,00
0,00
0,00
0,00
0,00
0,00
S
2
3,00
0,00
0,00
0,00
0,00
0,00
S
3
3,00
0,00
0,00
0,00
0,00
0,00
S
4
3,00
-0,60
-0,50
1,08
0,90
0,75
S
5
3,00
-0,60
-0,50
1,08
0,90
0,75
S
6
3,00
0,00
0,50
0,00
0,00
0,75
S
7
3,00
0,00
0,50
0,00
0,00
0,75
S
8
3,00
0,00
0,00
0,00
0,00
0,00
K
1
3,00
0,00
0,00
0,00
0,00
0,00
K
2
3,00
0,00
0,00
0,00
0,00
0,00
K
3
3,00
0,00
0,8(3)
0,00
0,00
2,08(3)
K
4
3,00
1,00
0,8(3)
3,00
2,50
2,08(3)
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
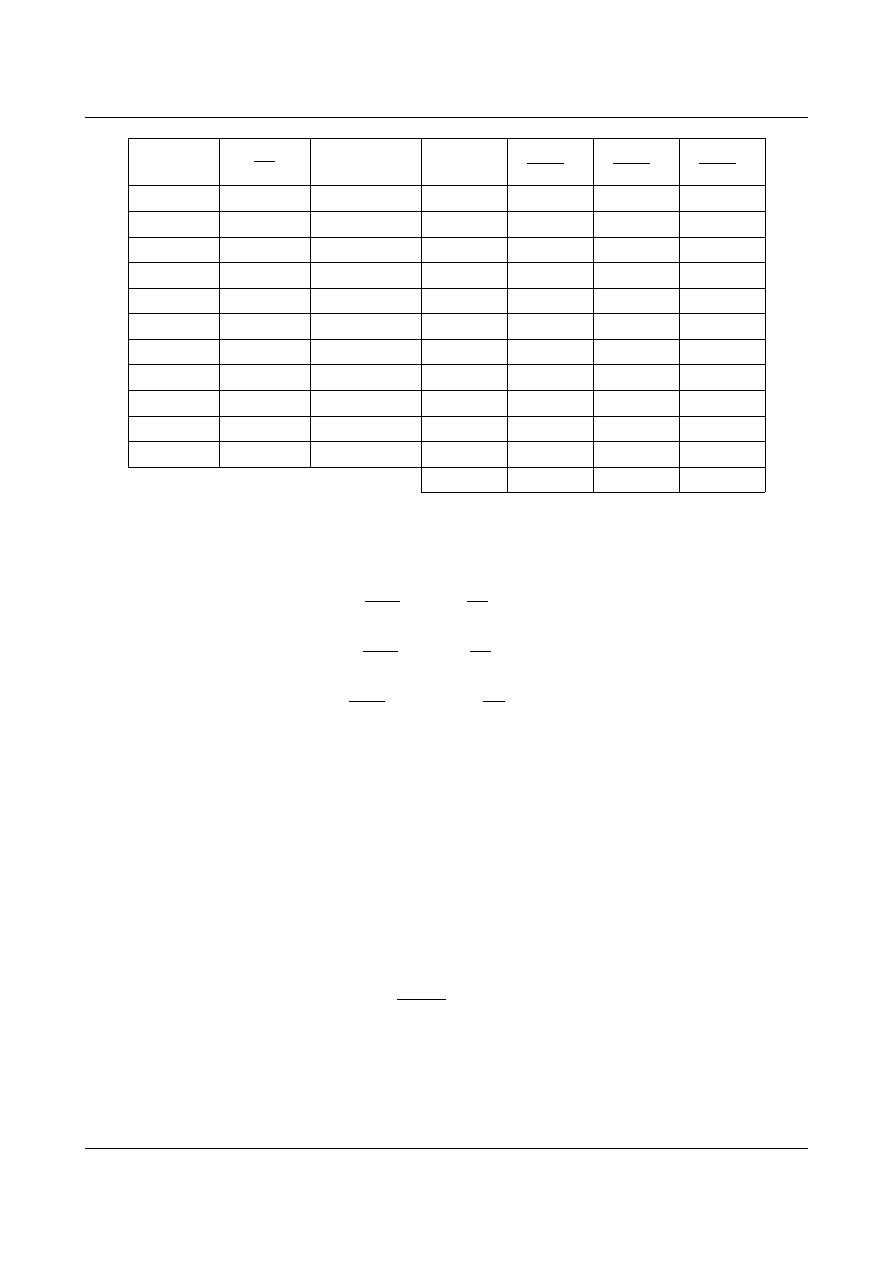
Część 1
11. METODA SIŁ - KRATOWNICA
14
l
EA
S
1
S
2
S
1
⋅S
1
EA
⋅l
S
1
⋅S
2
EA
⋅l
S
2
⋅S
2
EA
⋅l
K
5
3,00
0,00
-0,8(3)
0,00
0,00
2,08(3)
K
6
3,00
0,00
-0,8(3)
0,00
0,00
2,08(3)
K
7
3,00
0,00
0,00
0,00
0,00
0,00
G
1
3,00
0,00
0,00
0,00
0,00
0,00
G
2
3,00
0,00
0,00
0,00
0,00
0,00
G
3
3,00
0,00
0,00
0,00
0,00
0,00
G
4
3,00
-0,80
0,6(6)
1,92
-1,60
1,3(3)
G
5
3,00
0,00
1,3(3)
0,00
0,00
5,3(3)
G
6
3,00
0,00
0,6(6)
0,00
0,00
1,3(3)
G
7
3,00
0,00
0,00
0,00
0,00
0,00
K
n
3,00
1,00
0,00
3,00
0,00
0,00
Suma:
12,00
5,90
27,3(3)
Wyznaczone sumy oznaczają przemieszczenia:
11
=
∑
m
S
1
⋅S
1
EA
m
⋅l
m
=12
[
m
EA
]
12
=
∑
m
S
1
⋅S
2
EA
m
⋅l
m
=5,9
[
m
EA
]
22
=
∑
m
S
2
⋅S
2
EA
m
⋅l
m
=27,33
[
m
EA
]
Obciążeniem jest poruszająca się siła
P=1, zatem Δ
1P
i
Δ
2P
są wielkościami zmiennymi zależnymi od
x.
Zgodnie z twierdzeniem Maxwella (
Δ
iP
= Δ
Pi
) możemy wyznaczyć
Δ
P1
i Δ
P2
, czyli linie ugięć pasa górnego
kratownicy wywołane działaniem odpowiednio sił
X
1
i
X
2
.
Do ich wyznaczenia zastosujemy metodę ciężarów sprężystych. Musimy wyznaczyć dwie grupy
ciężarów sprężystych (siły
w
j
(1)
i
w
j
(2)
) i obciążyć nimi belkę zastępczą. Wyznaczone od tych sił dwa wykresy
momentów będą odpowiednio liniami ugięć
Δ
P1
i Δ
P2
.
Wartości sił wyliczymy ze wzoru:
w
j
i
=
∑
m
S
i m
⋅S
j m
EA
m
⋅l
m
(11.10)
gdzie:
w
j
i
to ciężar sprężysty obliczony dla węzła
j, dla obciążenia X
i
= 1,
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
15
S
j m
to siła w pręcie
m wywołana obciążeniem wirtualnym przyłożonym do węzłów j-1, j i j+1 w układzie
podstawowym,
S
i m
to siła w pręcie
m w stanie X
i
= 1.
w
1
(i)
w
2
(i)
w
3
(i)
w
4
(i)
w
5
(i)
w
6
(i)
1
0
2
3
4
5
6
7
4
4
4
4
4
4
4
[m]
Rys. 11.17. Belka zastępcza obciążona ciężarami sprężystymi
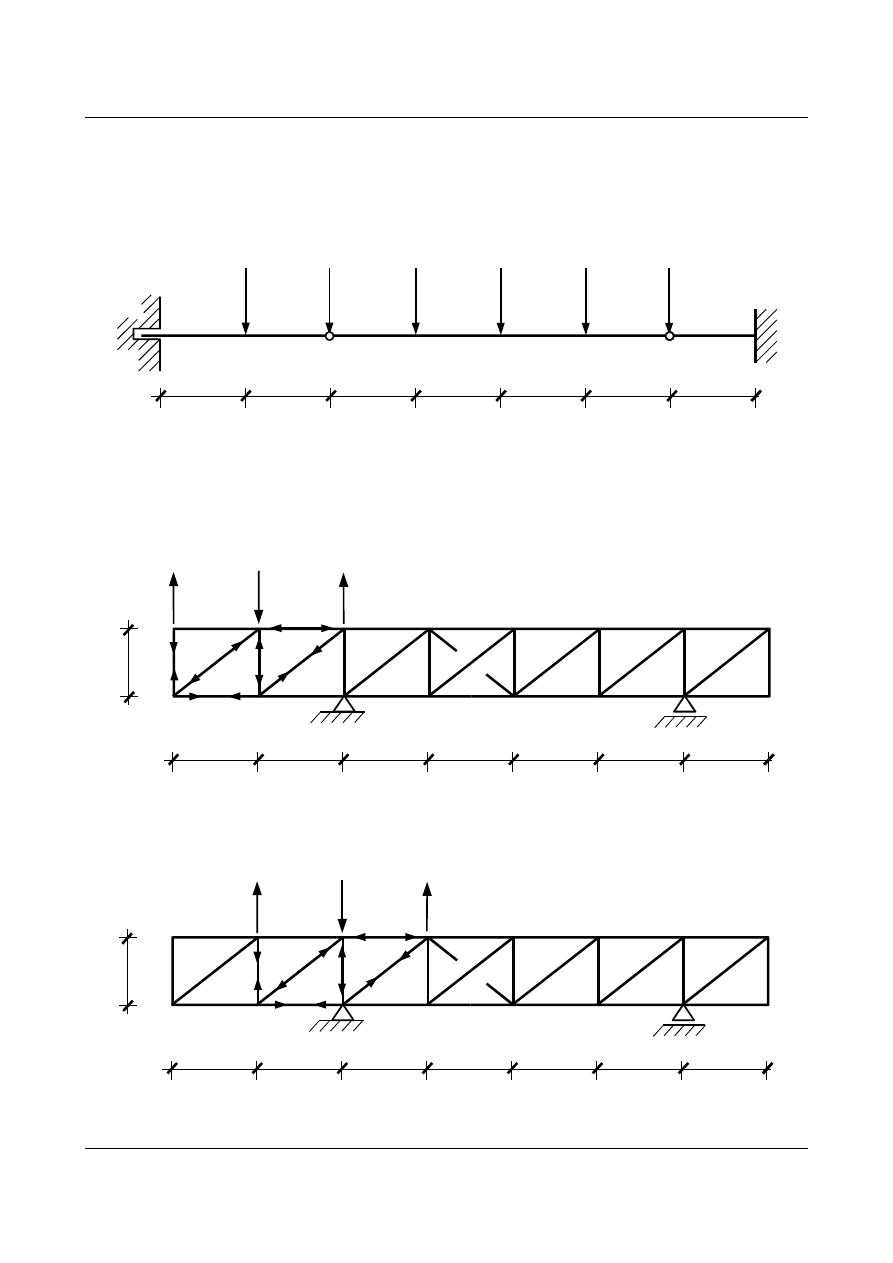
Najpierw musimy wyznaczyć siły S
jm
przykładając obciążenie wirtualne do kolejnych węzłów. Siły
S
1 m
otrzymamy przykładając obciążenie do węzłów 0, 1 i 2 (
m to numer pręta kratownicy):
3
-0,25
0,33
-0.
42
0,25
0,5
0,25
0.4
2
-0,33
0,25
4
4
4
4
4
4
4
[m]
Dalej wyznaczamy siły S
2 m
dla węzła
j = 2:
3
-0,25
0,33
-0.
42
0,25
0,5
0,25
0.4
2
-0,33
0,25
4
4
4
4
4
4
4
[m]
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
16
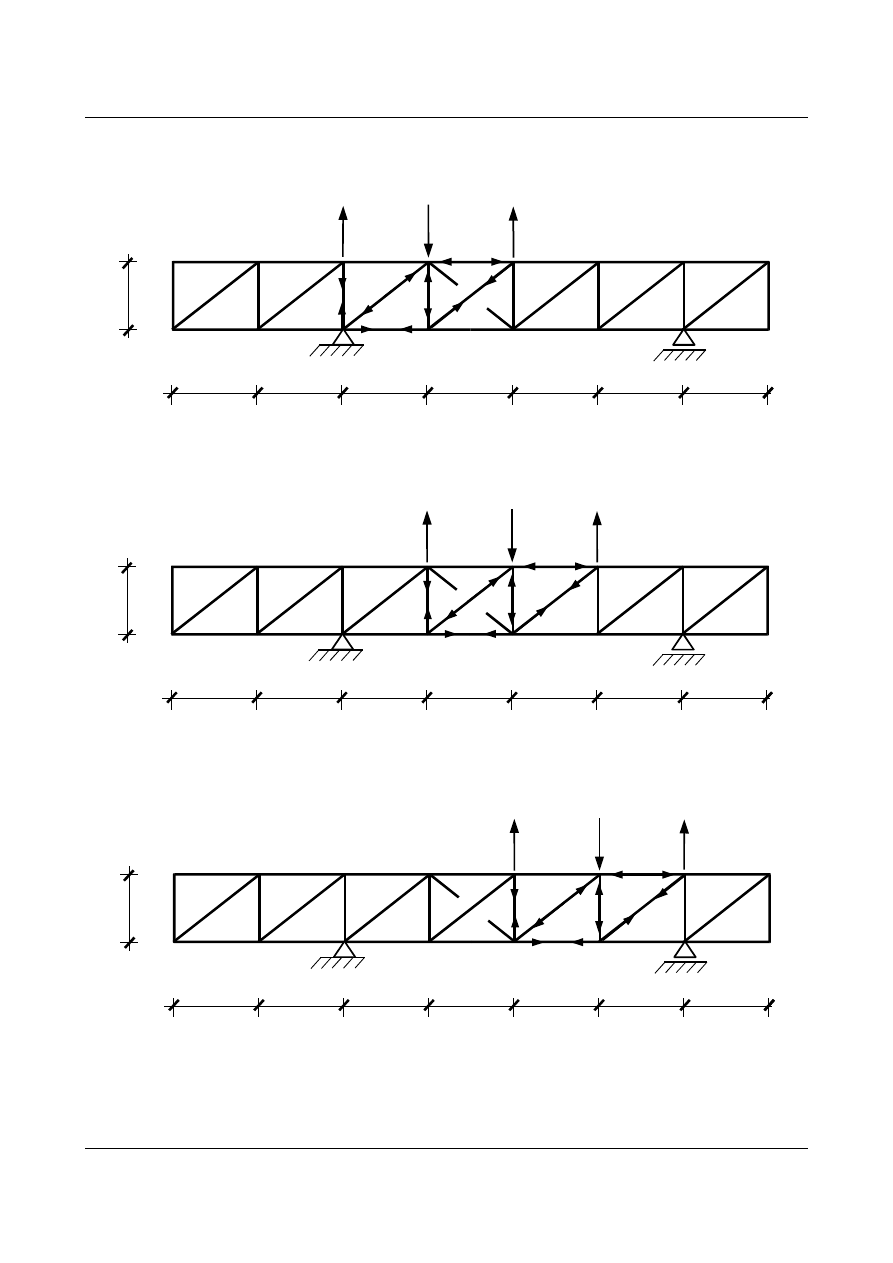
Dla
j = 3 siły S
3 m
:
3
-0,25
0,33
-0.
42
0,25
0,5
0,25
0.4
2
-0,33
0,25
4
4
4
4
4
4
4
[m]
Dla
j = 4 siły S
4 m
:
3
4
4
4
4
4
4
4
[m]
-0,25
0,33
-0.
42
0,25
0,5
0,25
0.4
2
-0,33
0,25
Dla
j = 5 siły S
5 m
:
3
4
4
4
4
4
4
4
[m]
-0,25
0,33
-0.
42
0,25
0,5
0,25
0.4
2
-0,33
0,25
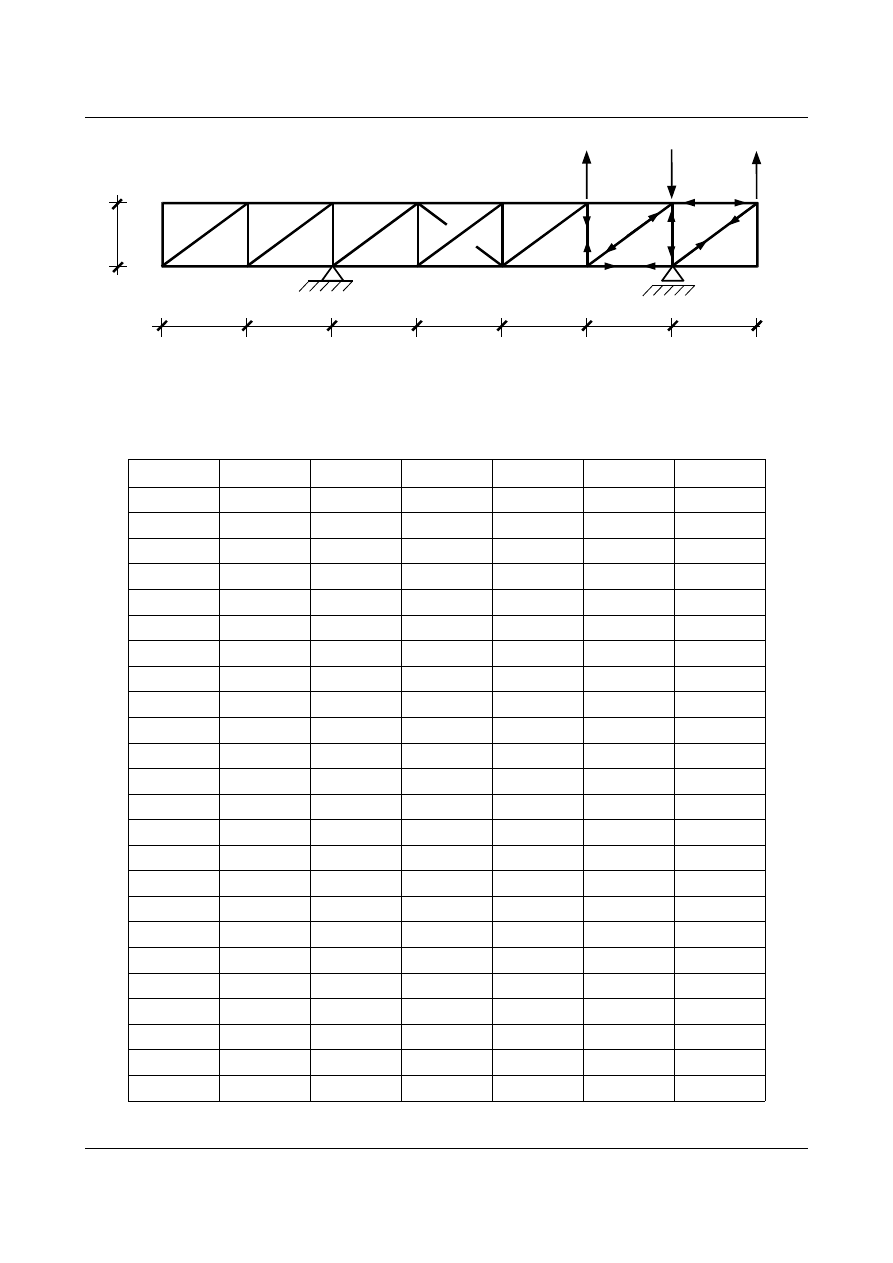
Dla
j = 6 siły S
6 m
:
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
17
3
4
4
4
4
4
4
4
[m]
-0,25
0,33
-0
.4
2
0,25
0,5
0,25
0.
42
-0,33
0,25
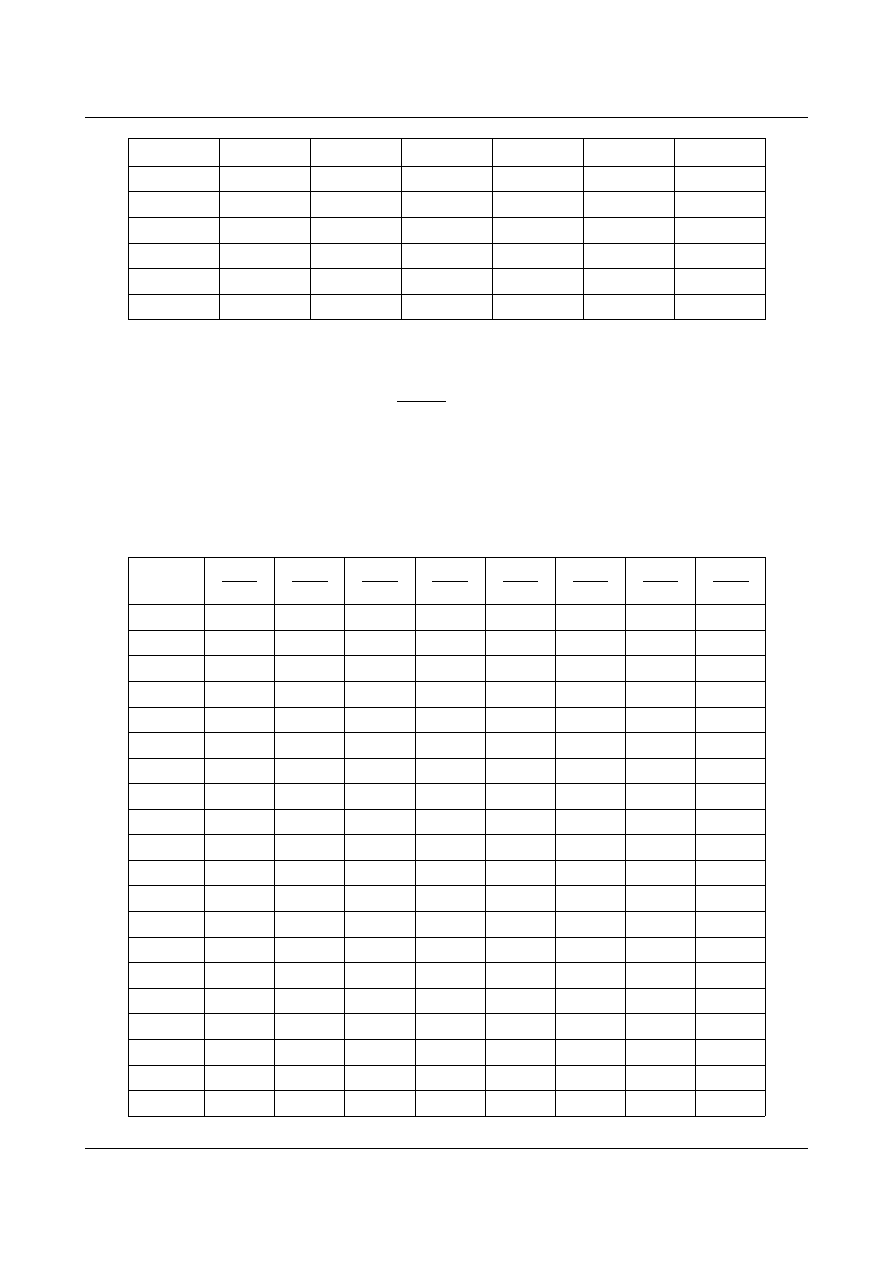
Wszystkie wartości sił przedstawiono w tabeli uwzględniając ściskanie i rozciąganie prętów:
Tabela 11.5. Siły w prętach od obciążeń wirtualnych
S
1
S
2
S
3
S
4
S
5
S
6
D
1
0,3(3)
0,00
0,00
0,00
0,00
0,00
D
2
0,00
0,3(3)
0,00
0,00
0,00
0,00
D
3
0,00
0,00
0,3(3)
0,00
0,00
0,00
D
4
0,00
0,00
0,00
0,3(3)
0,00
0,00
D
5
0,00
0,00
0,00
0,00
0,3(3)
0,00
D
6
0,00
0,00
0,00
0,00
0,00
0,3(3)
D
7
0,00
0,00
0,00
0,00
0,00
0,00
S
1
0,25
0,00
0,00
0,00
0,00
0,00
S
2
-0,25
0,25
0,00
0,00
0,00
0,00
S
3
0,00
-0,25
0,25
0,00
0,00
0,00
S
4
0,00
0,00
-0,25
0,25
0,00
0,00
S
5
0,00
0,00
0,00
-0,25
0,25
0,00
S
6
0,00
0,00
0,00
0,00
-0,25
0,25
S
7
0,00
0,00
0,00
0,00
0,00
-0,25
S
8
0,00
0,00
0,00
0,00
0,00
0,00
K
1
-0,41(6)
0,00
0,00
0,00
0,00
0,00
K
2
0,41(6)
-0,41(6)
0,00
0,00
0,00
0,00
K
3
0,00
0,41(6)
-0,41(6)
0,00
0,00
0,00
K
4
0,00
0,00
0,41(6)
-0,41(6)
0,00
0,00
K
5
0,00
0,00
0,00
0,41(6)
-0,41(6)
0,00
K
6
0,00
0,00
0,00
0,00
0,41(6)
-0,41(6)
K
7
0,00
0,00
0,00
0,00
0,00
0,41(6)
G
1
0,00
0,00
0,00
0,00
0,00
0,00
G
2
-0,3(3)
0,00
0,00
0,00
0,00
0,00
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
18
S
1
S
2
S
3
S
4
S
5
S
6
G
3
0,00
-0,3(3)
0,00
0,00
0,00
0,00
G
4
0,00
0,00
-0,3(3)
0,00
0,00
0,00
G
5
0,00
0,00
0,00
-0,3(3)
0,00
0,00
G
6
0,00
0,00
0,00
0,00
-0,3(3)
0,00
G
7
0,00
0,00
0,00
0,00
0,00
-0,3(3)
K
n
0,00
0,00
0,00
0,00
0,00
0,00
Wartości ciężarów sprężystych otrzymamy sumując odpowiednie iloczyny sił:
w
j
i
=
∑
m
S
i m
⋅S
j m
EA
m
⋅l
m
Porównując rozkład sił w stanie
X
1
= 1 i X
2
= 1 oraz przy obciążeniach wirtualnych zauważymy, że w
niektórych przypadkach siły nie pokrywają się w żadnym pręcie.
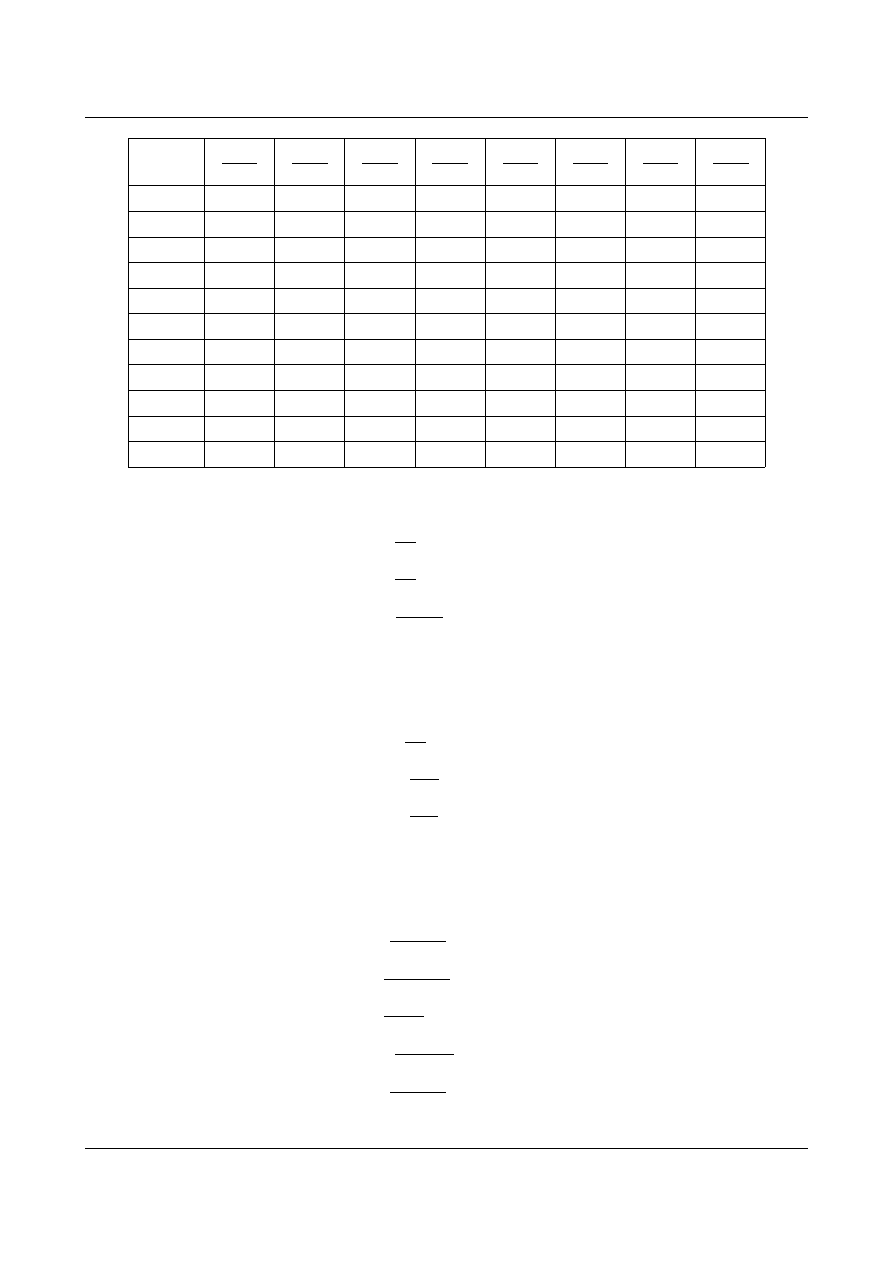
W tabeli 11.6 zestawiono tylko niezerowe iloczyny.
Tabela 11.6. Iloczyny od obciążeń jednostkowych i wirtualnych
S
1
⋅S
3
EA
⋅l
S
1
⋅S
4
EA
⋅l
S
1
⋅S
5
EA
⋅l
S
2
⋅S
2
EA
⋅l
S
2
⋅S
3
EA
⋅l
S
2
⋅S
4
EA
⋅l
S
2
⋅S
5
EA
⋅l
S
2
⋅S
6
EA
⋅l
D
1
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
D
2
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
D
3
0,00
0,00
0,00
0,00
-0,6(6)
0,00
0,00
0,00
D
4
0,00
-0,80
0,00
0,00
0,00
-1,3(3)
0,00
0,00
D
5
0,00
0,00
0,00
0,00
0,00
0,00
-0,6(6)
0,00
D
6
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
D
7
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
S
1
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
S
2
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
S
3
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
S
4
0,45
-0,45
0,00
0,00
0,375
-0,375
0,00
0,00
S
5
0,00
0,45
-0,45
0,00
0,00
0,375
-0,375
0,00
S
6
0,00
0,00
0,00
0,00
0,00
0,00
-0,375
0,375
S
7
0,00
0,00
0,00
0,00
0,00
0,00
0,00
-0,375
S
8
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
K
1
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
K
2
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
K
3
0,00
0,00
0,00
1,041(6) -1,041(6)
0,00
0,00
0,00
K
4
1,25
-1,25
0,00
0,00
1,041(6) -1,041(6)
0,00
0,00
K
5
0,00
0,00
0,00
0,00
0,00
1,041(6) -1,041(6)
0,00
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
19
S
1
⋅S
3
EA
⋅l
S
1
⋅S
4
EA
⋅l
S
1
⋅S
5
EA
⋅l
S
2
⋅S
2
EA
⋅l
S
2
⋅S
3
EA
⋅l
S
2
⋅S
4
EA
⋅l
S
2
⋅S
5
EA
⋅l
S
2
⋅S
6
EA
⋅l
K
6
0,00
0,00
0,00
0,00
0,00
0,00
1,041(6) -1,041(6)
K
7
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
G
1
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
G
2
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
G
3
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
G
4
0,80
0,00
0,00
0,00
-0,6(6)
0,00
0,00
0,00
G
5
0,00
0,00
0,00
0,00
0,00
-1,3(3)
0,00
0,00
G
6
0,00
0,00
0,00
0,00
0,00
0,00
-0,6(6)
0,00
G
7
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
K
n
0,00
0,00
0,00
0,00
0,00
0,00
0,00
0,00
Suma:
2,50
-2,05
-0,45
1,041(6) -0,958(3)
-4,75
-2,083(3) 1,041(6)
Odpowiednie sumy z tabel 11.4 i 11.6 prowadzą do wartości:
11
=
12
EA
12
=
5.0
EA
22
=
27,3
3
EA
dla obciążenia
X
1
= 1
w
1
= 0
w
2
= 0
w
3
=
2,5
EA
w
4
=−
2,05
EA
w
5
=−
0,45
EA
w
6
= 0
dla obciążenia
X
2
= 1
w
1
= 0
w
2
=
1,041
6
EA
w
3
=−
0,958
3
EA
w
4
=−
4,75
EA
w
5
=−
−2,08 3
EA
w
6
=
1,041
6
EA
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
20
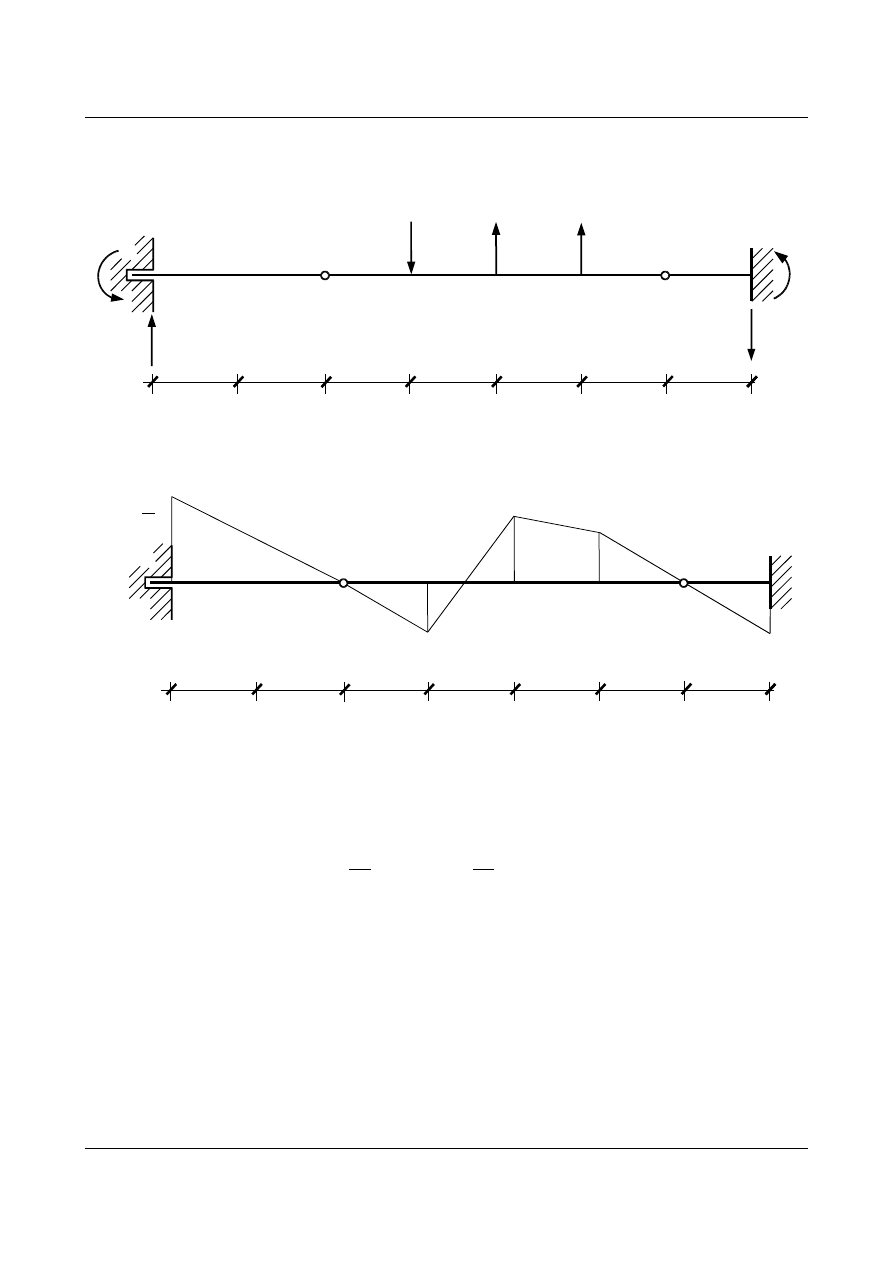
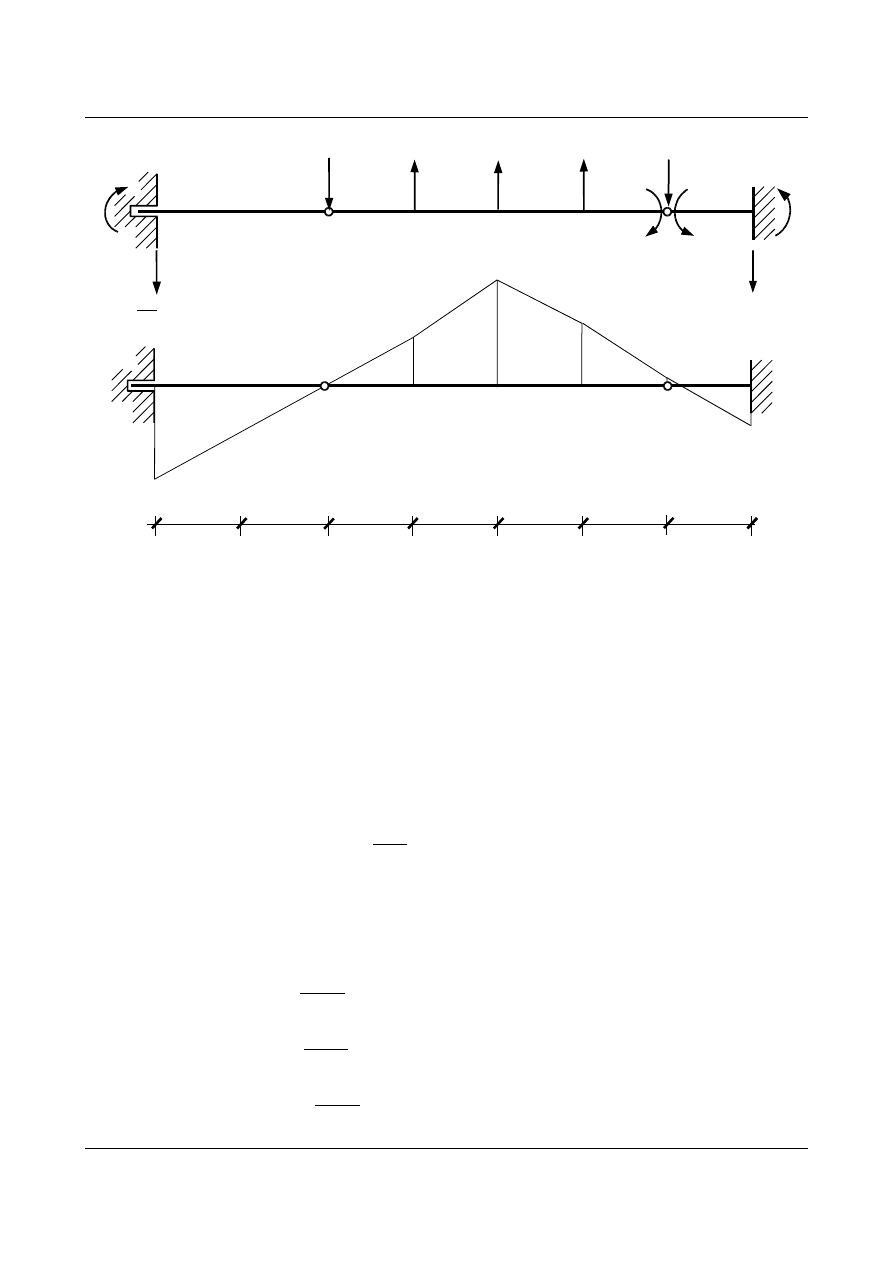
Wykres momentów w belce zastępczej od obciążenia ciężarkami sprężystymi
w
j
(1)
pokrywa się z linią ugięcia
P1
2,95
0,737
0,737
5,9
2,5
2,05
0,45
4
4
4
4
4
4
4
[m]
Rys. 11.18. Belka zastępcza obciążona ciężarami sprężystymi w
j
(1)
4
4
4
4
4
4
4
[m]
EA · M
1
4,1
2,95
2,95
5,9
2,95
Rys. 11.19. Wykres momentów w belce zastępczej od obciążenia ciężarkami sprężystymi w
j
(1)
Ponieważ siła porusza się po pasie górnym kraty należy w wykresie momentów uwzględnić w punkcie 7
wartość momentu wtórnego odpowiadającą rzeczywistemu skróceniu słupka
S'
7
przy obciążeniu kratownicy
X
2
= 1.
M
7
=
3
EA
⋅−1⋅0,5 ⋅1 =−
1,5
EA
Otrzymaliśmy wartość ujemną ponieważ słupek jest rozciągany oznacza to, że oś pasa górnego uniesie
się w tym miejscu o wartość
1,5/EA. W stanie X
1
= 1 w słupku podporowym siła była równa zero co
oznaczało, że pas górny nad podporą nie przemieszczał się.
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
21
4
4
4
4
4
4
4
[m]
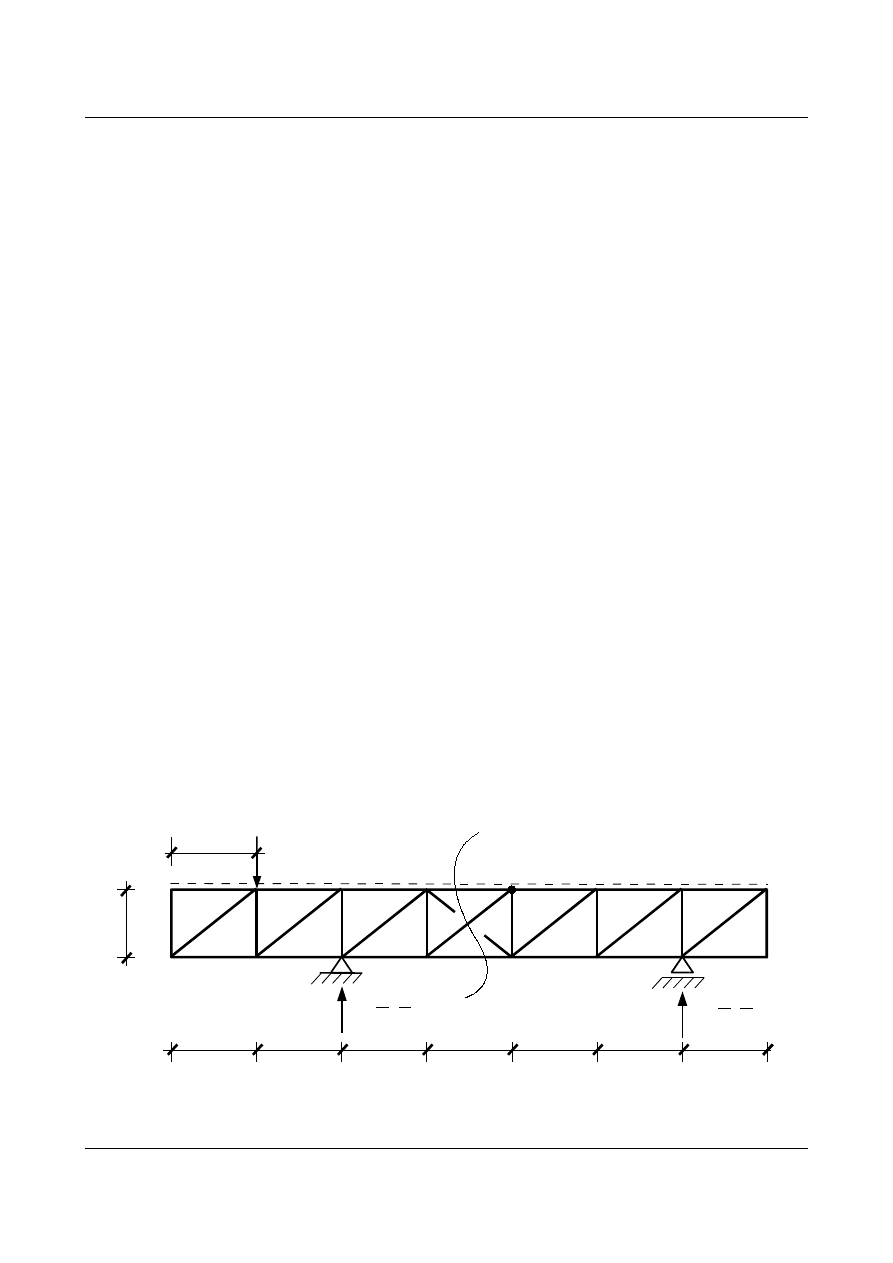
EA · M
2
21,33
14,83
25,83
17,83
1,5
10,67
1,042
1,042
10,667
3,041
2,667
20,33
0,958
4,75
2,083
M
7
=1,5
Rys. 11.20. Wykres momentów w belce zastępczej od obciążenia ciężarkami sprężystymi w
j
(2)
Aby znaleźć linie wpływu
X
1
i
X
2
trzeba rozwiązać układ równań kanonicznych można to zrobić
wyznaczając macierz odwrotną do macierzy podatności:
A
=
[
11
12
21
22
]
=
[
12
5,9
5,9 27,3
3
]
[ A][ X ]=[ P]
[ X ]=[ A]
−1
[ P]
(11.10)
Każdy wyraz macierzy odwrotnej policzymy ze wzoru:
A
ij
−1
=
1
det A
−1
i
j
A
ij
0
(11.11)
Czyli odwrotność wyznacznika macierzy pomnożona przez -1 do potęgi (
i+j) i pomnożona przez wyraz, który
pozostał po skróceniu
i-tego wiersza i j-tej kolumny:
det [A]= 293,19
A
11
−1
=
1
293,19
−1
1
1
⋅27,33=0,0932273725
A
12
−1
=
1
293,19
−1
1
2
⋅5,9=−0,02012344694
A
22
−1
=
1
293,19
−1
2
2
⋅12=0,0409290904
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
22
Otrzymujemy macierz odwrotną,
A
−1
=
[
0,0932273725
−0,0201234694
−0,0201234694
0,0409290904
]
która pomnożona przez macierz początkową musi dać macierz jedynkową:
[ A]
−1
[ A]=
[
0,0932273725
−0,0201234694
−0,0201234694
0,0409290904
]
⋅
[
12
5,9
5,9 27,3
3
]
=
[
1 0
0 1
]
Biorąc pod uwagę fakt, że
[ P]=col {−
1 P
;
−
2 P
}
wartości nadliczbowych wyliczamy z zależności:
X
1
=−0,0932273725 ⋅
1 P
0,020123469 ⋅
2 P
X
2
= 0,020123469 ⋅
1 P
0,0409290904 ⋅
2 P
Wyrazy wolne
iP
a co za tym idzie siły nadliczbowe
X
i
są funkcjami współrzędnej położenia siły
P = 1 (są
inne dla każdego
x). Oznacza to, że wyznaczyliśmy linie wpływu sił nadliczbowych (X
i
(x) = lw X
i
).
Aby stworzyć linię wpływu dowolnej wielkości w układzie statycznie niewyznaczalnym (np.
lw D
4
)
korzystamy z zasady superpozycji:
lw D
4
=lw D
4
0
D
4
x
1
=1
⋅lw X
1
D
4
X
2
=1
⋅lw X
2
Najpierw wyznaczymy wielkości w układzie statycznie wyznaczalnym (podstawowym).
Przy obciążeniu kratownicy siłą
X
1
= 1 otrzymaliśmy D
4
= -0,8, a przy obciążeniu siłą
X
2
= 1 było D
4
= -1,33.
Wobec tego:
D
4
X
1
=1
=−0,8
D
4
X
2
=1
=−1,33
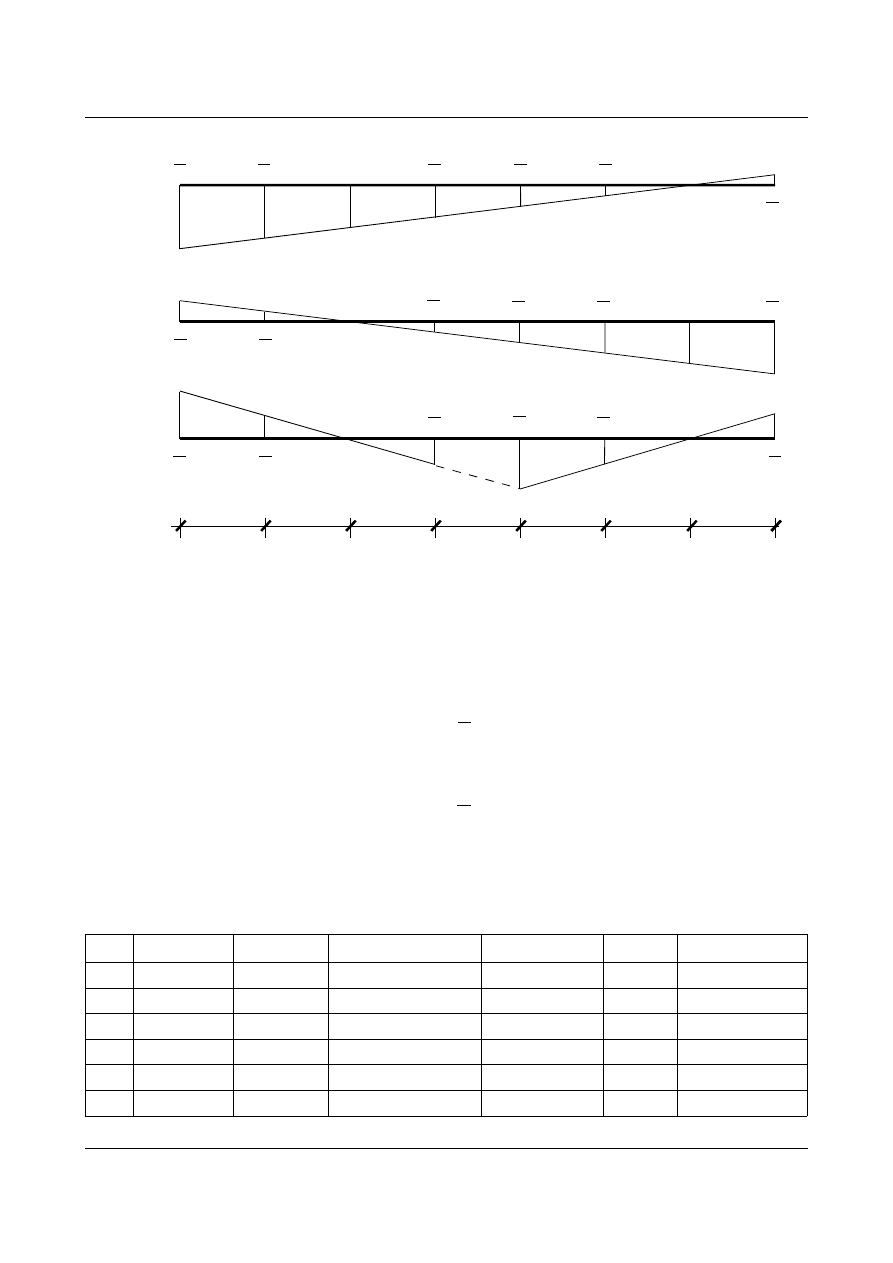
Dalej wyznaczamy linie wpływu w układzie podstawowym.
4
4
4
4
4
4
4
3
S
2
S
3
S
4
S
5
S
6
S
7
S
8
S
1
G
1
G
2
G
3
G
4
G
5
G
6
G
7
D
7
D
6
D
5
D
4
D
3
D
2
D
1
K
1
K
2
K
3
K
4
K
5
K
6
K
7
P=1
[m]
x
α
α
M
V
A
=
3
2
- x
16
V
B
=
x
16
- 1
2
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
23
4
4
4
4
4
4
4
[m]
lw V
B
0
1
0
1
0
0
0
lw D
4
0
lw V
A
0
6
4
5
4
3
4
2
4
1
4
-1
4
5
4
-1
4
-1
2
3
4
1
4
1
2
-4
3
-2
3
-2
3
2
3
2
3
4
3
Rys. 11.21. Linie wpływu w układzie podstawowym
Po wykonaniu przekroju
α-α równoważymy jedną z odciętych części zgodnie z metodą Rittera. Gdy siła
P=1 jest w przedziałach:
x
∈〈0,12 〉
∑
M
M
P
=0
D
4
=
8
3
⋅V
B
x
∈〈16,28 〉
∑
M
M
L
=0
D
4
=
8
3
⋅V
A
Na koniec w każdym węźle kratownicy policzono wartości nadliczbowych oraz siły w pręcie
D
4
(tab. 11.7)
Tabela 11.7. Linie wpływu sił
x
1 P
2 P
lwX
1
lwX
2
lwD
4
0
lwD
4
0
-5,900
21,333
0,97934218
-0,99188240
-1,333
-0,7942972120
4
-2,950
10,667
0,48967109
-0,49594120
-0,667
-0,3971486060
8
0,000
0,000
0,00000000
0,00000000
0,000
0,0000000000
12
2,950
-14,833
-0,57351888
0,66647908
0,667
0,2368430018
16
-4,100
-25,833
-0,13762407
0,97482861
1,333
0,1436611047
20
-2,900
-17,833
-0,08384779
0,67053788
0,667
-0,1603056055
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 1
11. METODA SIŁ - KRATOWNICA
24
x
1 P
2 P
lwX
1
lwX
2
lwD
4
0
lwD
4
24
0,000
-1,500
-0,03018520
0,06139364
0,000
-0,0577100175
28
2,950
10,633
-0,06104119
-0,37584843
-0,667
-0,1167024786
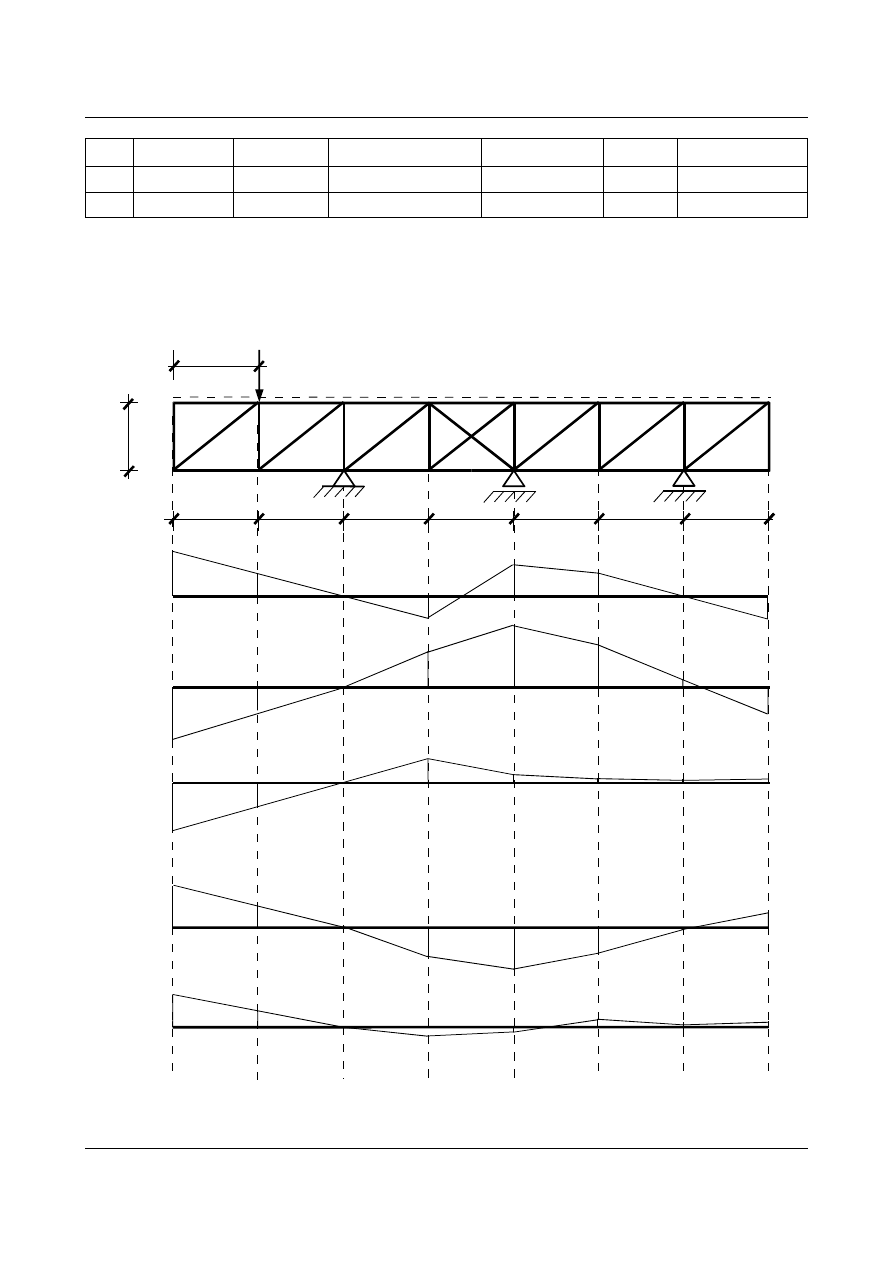
oraz przedstawiono graficznie rezultaty obliczeń.
Warto zwrócić uwagę na kształt funkcji
1 P
i
2 P
, które przedstawiają postać odkształconą (linię ugięcia)
pasa górnego kratownicy przy działaniu odpowiednio siły
X
1
= 1 i X
2
= 1.
4
4
4
4
4
4
4
0,979
0,49
0
-0,574
-0,138
-0,084
-0,03 -0,06
-0,998
-0,495
0
0,666
0,975
0,67
0,061
-0,376
-0,794
-0,397
0
0,237
0,144
-0,16
-0,058
-0,117
lw X
1
(n)
lw X
2
(n)
lw D
4
(n)
-5,9
-2,95
-2,95
-4,1
2,95
2,95
21,33
10,67
-14,83
-25,83
-17,83
1,5
10,63
Δ
1P
= Δ
P1
Δ
2P
= Δ
P2
3
S
2
S
3
S
4
S
5
S
6
S
7
S
8
S
1
G
1
G
2
G
3
G
4
G
5
G
6
G
7
D
7
D
6
D
5
D
4
D
3
D
2
D
1
K
1
K
2
K
3
K
4
K
5
K
6
K
7
P=1
x
K
n
[m]
Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Wyszukiwarka
Podobne podstrony:
2012 11 22 Document 001
2001 11 22
2006 11 22 3S pl na Broadband 2006
IMiUE, 9 11 22 zał VI
2001 11 22 kol 1
11,22
kolokwium 2006 11 22
11. 22.01.2014, TEMAT: NEGATYWNE I POZYTYWNE SKUTKI WYCHOWANIA W INSTYTUCJI TOTALNEJ (OPIEKI CAŁKOW
TPL PRAC 12 11 22 Jodyna
04 OZE 2013 11 22 en
GF 9,11,22 Bernat
TPL PRAC 13 11 22 Emulsje
2010.11.22 Liść, Rok I, Semestr I, Botanika
Wykład 2011-11-22, psychologia drugi rok, psychologia ról
cwiczenia 11 22.02.2008, cwiczenia - dr skladowski
biologia geol 2007 11 22 wyklad1 bez ilustr
cwiczenia 11 22.02.2008 praca domowa, cwiczenia - dr skladowski
BIOPIERWIASTKI 19.11 (22.11), Budownictwo PK, Chemia, Chemia nieorganiczna od Marysi
więcej podobnych podstron