Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

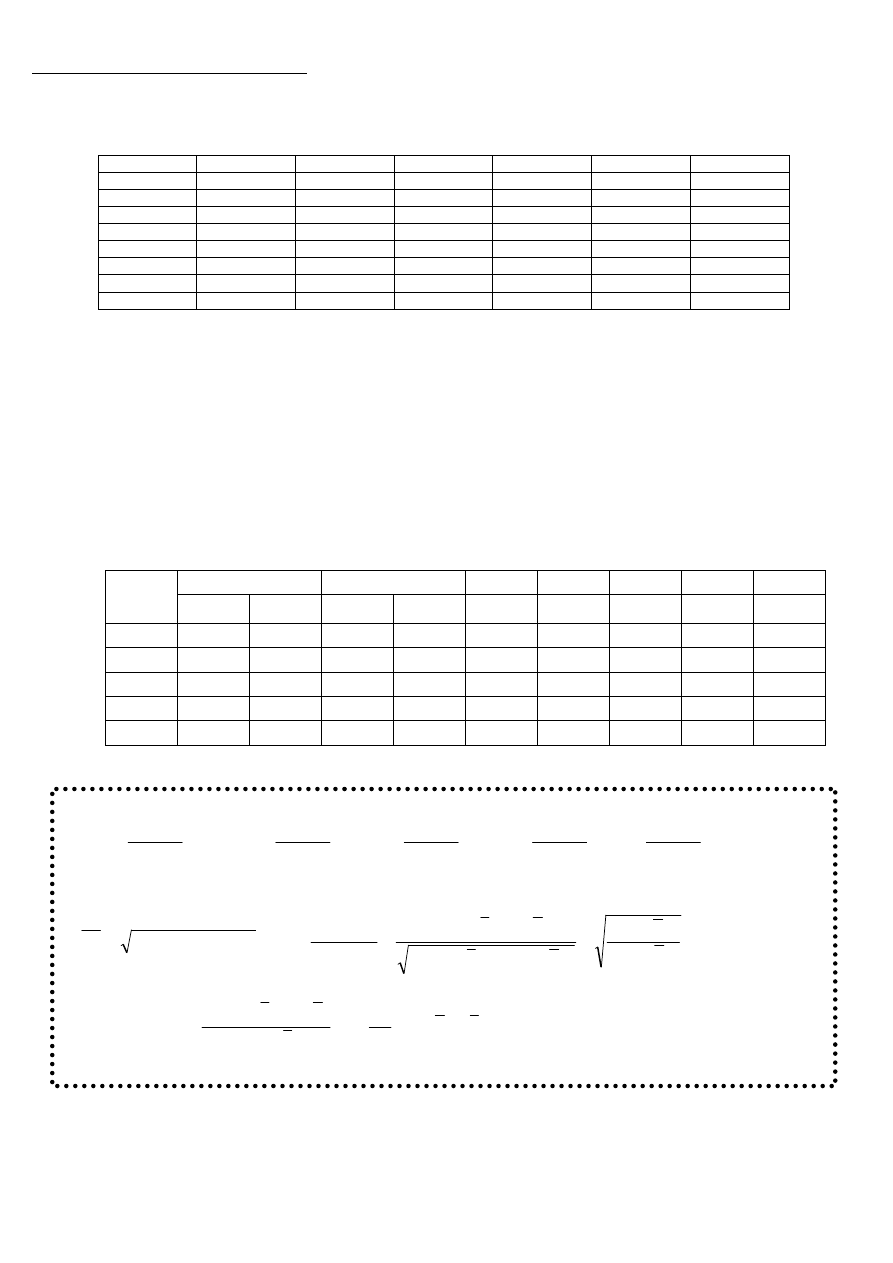
WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

VI a

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

18

10

18

16

19

21

19

25

20

23

21

40

25

40

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu 27
kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 3% rocznie,
1998 – 2001 malało średnio o 1,5% rocznie
2003 – 2009 rosło średnio o 5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 405 j.m. i 380 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2011. Po ilu
latach wielkość zjawiska potroi się przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

35

9

Mydło

120

2

100

2

Pasta

15

3

10

3

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

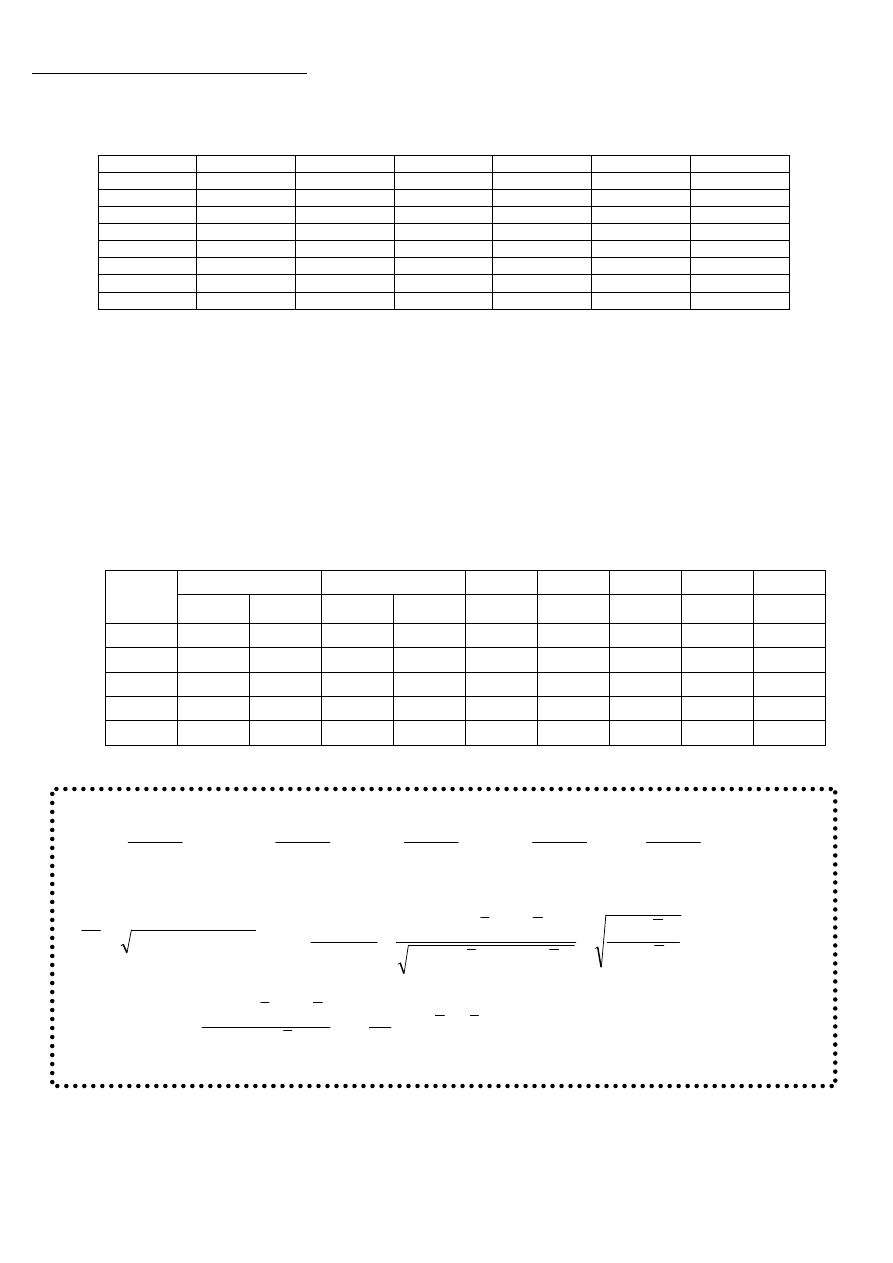
WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

XI a

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

25

16

26

21

25

20

29

21

30

22

31

31

30

30

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu
32,4 kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 1,2% rocznie,
1998 – 2001 malało średnio o 1,5% rocznie
2003 – 2009 rosło średnio o 5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 4105 j.m. i 5380 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2011. Po ilu
latach wielkość zjawiska potroi się przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

35

9

Mydło

120

2

112

2

Pasta

15

3

10

3

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

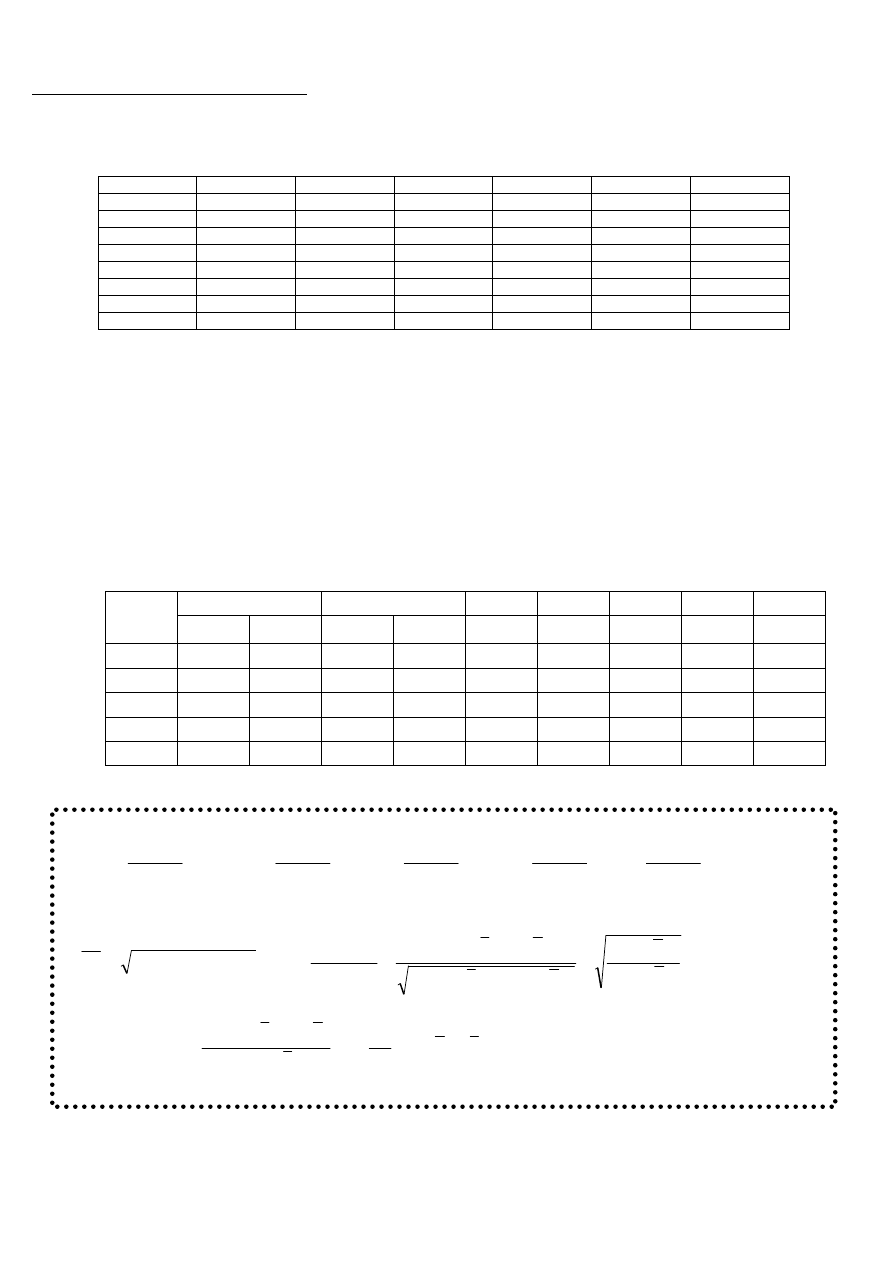
WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

V a

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

18

100

18

160

19

210

19

250

20

230

21

400

25

400

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu
128 kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 0,3% rocznie,
1998 – 2001 malało średnio o 11,5% rocznie
2003 – 2009 rosło średnio o 5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 455 j.m. i 580 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2011. Po ilu
latach wielkość zjawiska podwoi się przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

35

9

Mydło

120

2

105

2

Pasta

15

3

10

3

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

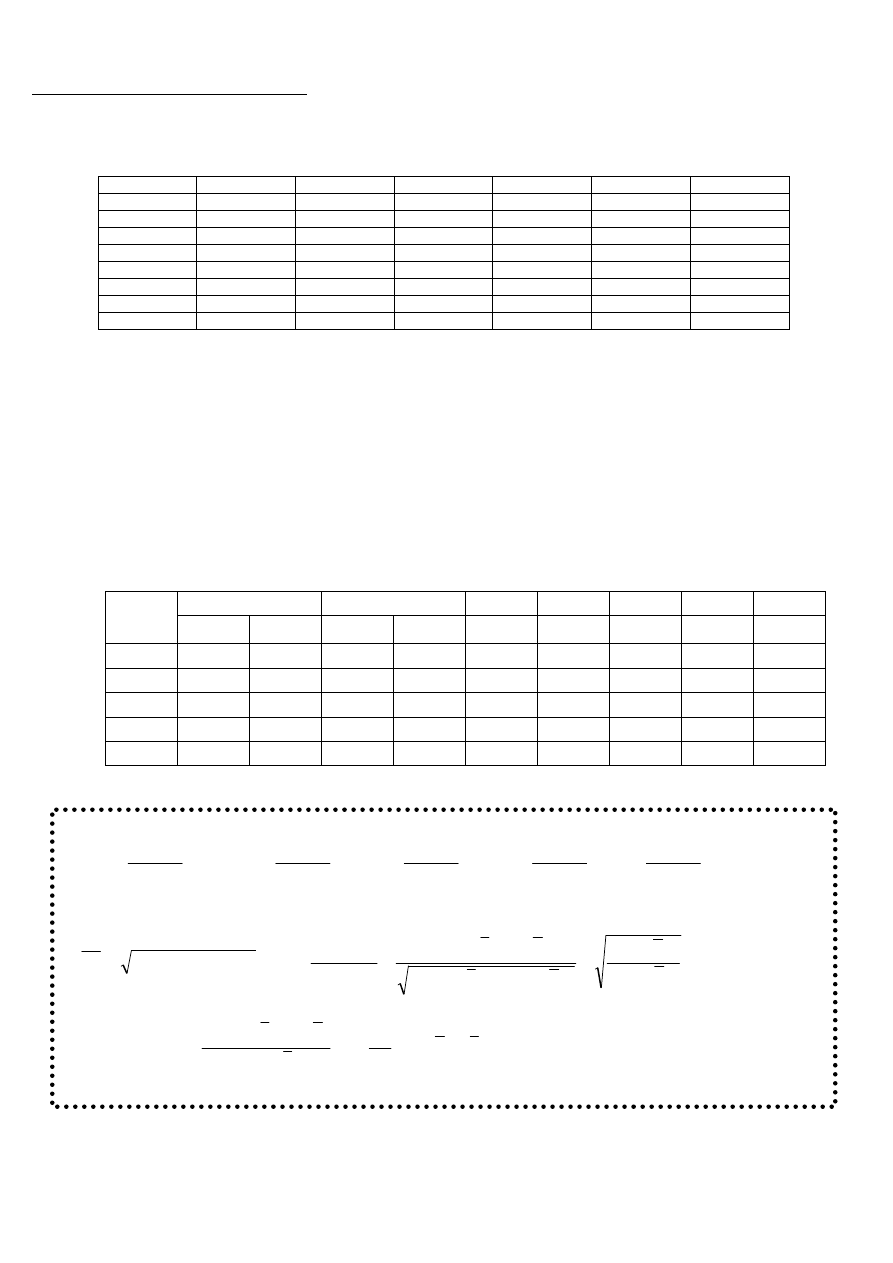
WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

IV a

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

18

150

18

155

19

156

19

158

20

158

21

160

25

162

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu
146 kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 3% rocznie,
1998 – 2001 malało średnio o 11% rocznie
2003 – 2009 rosło średnio o 5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 45 j.m. i 38 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2011. Po ilu
latach wielkość zjawiska powiększy się o 95% przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

35

9

Mydło

120

2

100

2

Pasta

15

3

13

3

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

VI b

ZAD.1.

Dane dotyczące zależności pomiędzy zużyciem pewnego surowca w kg (x), a produkcją wyrobu w tonach (y)
przedstawia tabela:

y

x

18

153

18

155

19

156

19

160

20

158

21

160

25

162

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakiej produkcji możemy spodziewać się przy zużyciu
132 kg surowca ?

ZAD.2.

Analizowane zjawisko w latach:
1980 – 1998 malało średnio o 0,3% rocznie,
1998 – 2001 malało średnio o 0,5% rocznie
2006 – 2009 rosło średnio o 3,5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 15 j.m. i 38 j.m.
Wyznacz średnie tempo zmian dla okresu 1980 – 2009. Oszacuj wielkość zjawiska w roku 2004 i 1977. Po ilu
latach wielkość zjawiska zmniejszy się o 60% przy założeniu spadku z pierwszego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

330

10,0

335

9,5

Mydło

120

2,5

100

2,3

Pasta

15

3,5

13

3,5

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

V b

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

16

153

18

155

19

156

19

160

20

158

21

160

27

162

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu
142 kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1995 – 1998 rosło średnio o 23% rocznie,
1998 – 2001 malało średnio o 15% rocznie
2005 – 2009 rosło średnio o 4,5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 4509 j.m. i 3802 j.m.
Wyznacz średnie tempo zmian dla okresu 1995 – 2009. Oszacuj wielkość zjawiska w roku 2004 i 2011. W którym
roku wielkość zjawiska przekroczy 5000 j.m. przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

35

9

Mydło

125

2

134

1

Pasta

15

10

11

14

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

XI b

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

16

15

18

16

21

18

19

18

20

21

21

19

25

26

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu 14
kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1975 – 1999 rosło średnio o 3% rocznie,
1999 – 2000 utrzymywało się na tym samym poziomie
2003 – 2009 rosło średnio o 5% rocznie.
W roku 1977 i 2005 odpowiednio wynosiło: 3405 j.m. i 5380 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2001 i 2011. Po ilu
latach wielkość zjawiska wzrośnie o 120% przy założeniu tempa wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

25

10

Mydło

120

2

160

2

Pasta

155

2

123

3

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

X b

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

26

15

28

16

31

18

29

18

30

21

31

19

35

26

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu 40
kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 9,3% rocznie,
1998 – 2001 malało średnio o 11,5% rocznie
2003 – 2009 rosło średnio o 0, 5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 105 j.m. i 200 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 1984.W którym
roku wielkość zjawiska osiągnie 50 j.m. przy założeniu spadku z okresu 1998 – 2001 ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10,2

35

9,3

Mydło

120

2,4

105

2,6

Pasta

15

3,6

13

3,4

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

IX h

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

26

25

28

26

31

28

29

28

30

31

31

29

35

36

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu 40
kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 1,3% rocznie,
1998 – 2001 malało średnio o 6,5% rocznie
2003 – 2009 rosło średnio o 7,5% rocznie.
W roku 1987 i 2005 odpowiednio wynosiło: 10005 j.m. i 10980 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2011. Po ilu
latach wielkość zjawiska zwiększy się o 75% przy założeniu wzrostu z pierwszego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

10

35

8

Mydło

120

2

100

2

Pasta

5

2

11

1

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

VI h

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

26

35

28

36

31

38

29

38

30

41

31

39

35

46

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu 42
kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1996 – 1998 rosło średnio o 31% rocznie,
1998 – 2001 malało średnio o 15% rocznie
2003 – 2009 rosło średnio o 8% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 309 j.m. i 480 j.m.
Wyznacz średnie tempo zmian dla okresu 1996 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2012. W którym
roku wielkość zjawiska osiągnie 1150 j.m. przy założeniu wzrostu z pierwszego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

30

9,4

35

9,9

Mydło

150

2,0

100

2,5

Pasta

15

3,5

13

3,1

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

V h

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

26

45

28

46

31

48

29

48

30

51

31

49

35

49

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu 42
kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1965 – 1998 rosło średnio o 0,43% rocznie,
1998 – 2000 malało średnio o 1,15% rocznie
2004 – 2009 rosło średnio o 0,25% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 900 j.m. i 1205 j.m.
Wyznacz średnie tempo zmian dla okresu 1965 – 2009. Oszacuj wielkość zjawiska w roku 2001 i 2013. W którym
roku wielkość zjawiska osiągnie 120 j.m. się przy założeniu spadku o 27% rocznie ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

20

10

25

7

Mydło

190

2

200

2

Pasta

45

3

43

3

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

III h

ZAD.1.

Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha (x)
dla 7 niezależnych upraw przedstawia tabela:

y

x

26

55

28

56

31

58

29

58

30

61

31

59

35

59

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakich plonów możemy spodziewać się przy zużyciu
62,5 kg nawozu ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 3% rocznie,
1998 – 2001 malało średnio o 1,5% rocznie
2003 – 2009 rosło średnio o 5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 3408 j.m. i 3803 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2012. Po ilu
latach wielkość zjawiska potroi się przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

12

11

15

9

Mydło

80

1

98

1

Pasta

11

3

10

4

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

VI ł

ZAD.1.

Liczbę dni (x) absencji chorobowej pracowników i wysokość miesięcznej premii w zł (y) dla losowo wybranej
grupy zatrudnionych przedstawia tabela:

y

x

1200

0

800

1

790

1

750

2

500

4

480

4

50

8

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakiej premii możemy spodziewać się przy 7 dniach
absencji ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 malało średnio o 3,8% rocznie,
1998 – 2001 malało średnio o 1,5% rocznie
2003 – 2009 malało średnio o 6,5% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 105 j.m. i 102 j.m.
Wyznacz średnie tempo zmian dla okresu 1989 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 1983. Po ilu
latach wielkość zjawiska zmniejszy się o 45% przy założeniu spadku z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

50

8,2

45

8,9

Mydło

170

0,9

190

0,8

Pasta

40

8,5

60

8,2

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

III ł

ZAD.1.

Liczbę dni (x) absencji chorobowej pracowników i wysokość miesięcznej premii w zł (y) dla losowo wybranej
grupy zatrudnionych przedstawia tabela:

y

x

1200

0

800

1

790

0

750

2

500

4

480

4

50

5

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakiej premii możemy spodziewać się przy 6 dniach
absencji ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1988 rosło średnio o 2,3% rocznie,
1988 – 2001 malało średnio o 1,5% rocznie
2004 – 2009 rosło średnio o 0,25% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 1425 j.m. i 1380 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2005. Oszacuj wielkość zjawiska w roku 1984 i 2011. W którym
roku wielkość zjawiska osiągnie 1900 j.m. się przy założeniu wzrostu 2,5 ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

78

3,5

98

3,4

Mydło

97

0,6

120

0,5

Pasta

65

8,5

36

10,2

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

IX ł

ZAD.1.

Liczbę dni (x) absencji chorobowej pracowników i wysokość miesięcznej premii w zł (y) dla losowo wybranej
grupy zatrudnionych przedstawia tabela:

y

x

1200

0

800

0

790

1

750

2

500

4

0

4

0

5

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakiej premii możemy spodziewać się przy 6 dniach
absencji ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 2,3% rocznie,
1998 – 2001 malało średnio o 1,9% rocznie
2003 – 2009 rosło średnio o 5,1% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 540 j.m. i 380 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2005. Oszacuj wielkość zjawiska w roku 2002 i 1983. O ile
procent rocznie powinna maleć wielkość zjawiska, aby w roku 2020 osiągnęła 200 j.m. ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

58

9,8

59

9,5

Mydło

210

0,4

215

0,4

Pasta

30

3,5

31

3,6

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

V ł

ZAD.1.

Liczbę dni (x) absencji chorobowej pracowników i wysokość miesięcznej premii w zł (y) dla losowo wybranej
grupy zatrudnionych przedstawia tabela:

y

x

1100

0

600

0

790

1

750

2

500

4

50

9

50

10

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakiej premii możemy spodziewać się przy 7 dniach
absencji ?

ZAD.2.

Analizowane zjawisko w latach:
1985 – 1998 rosło średnio o 0,53% rocznie,
1998 – 2001 malało średnio o 1,25% rocznie
2003 – 2009 rosło średnio o 5,65% rocznie.
W roku 1997 i 2005 odpowiednio wynosiło: 1345 j.m. i 1380 j.m.
Wyznacz średnie tempo zmian dla okresu 1985 – 2009. Oszacuj wielkość zjawiska w roku 2002 i 2011. Po ilu
latach wielkość zjawiska podwoi się przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

7

12,8

11

12,1

Mydło

12

0,9

9

0,9

Pasta

2

2,9

3

2,5

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU

Statystyka opisowa, kolokwium nr 2,29 stycznia 2010 roku

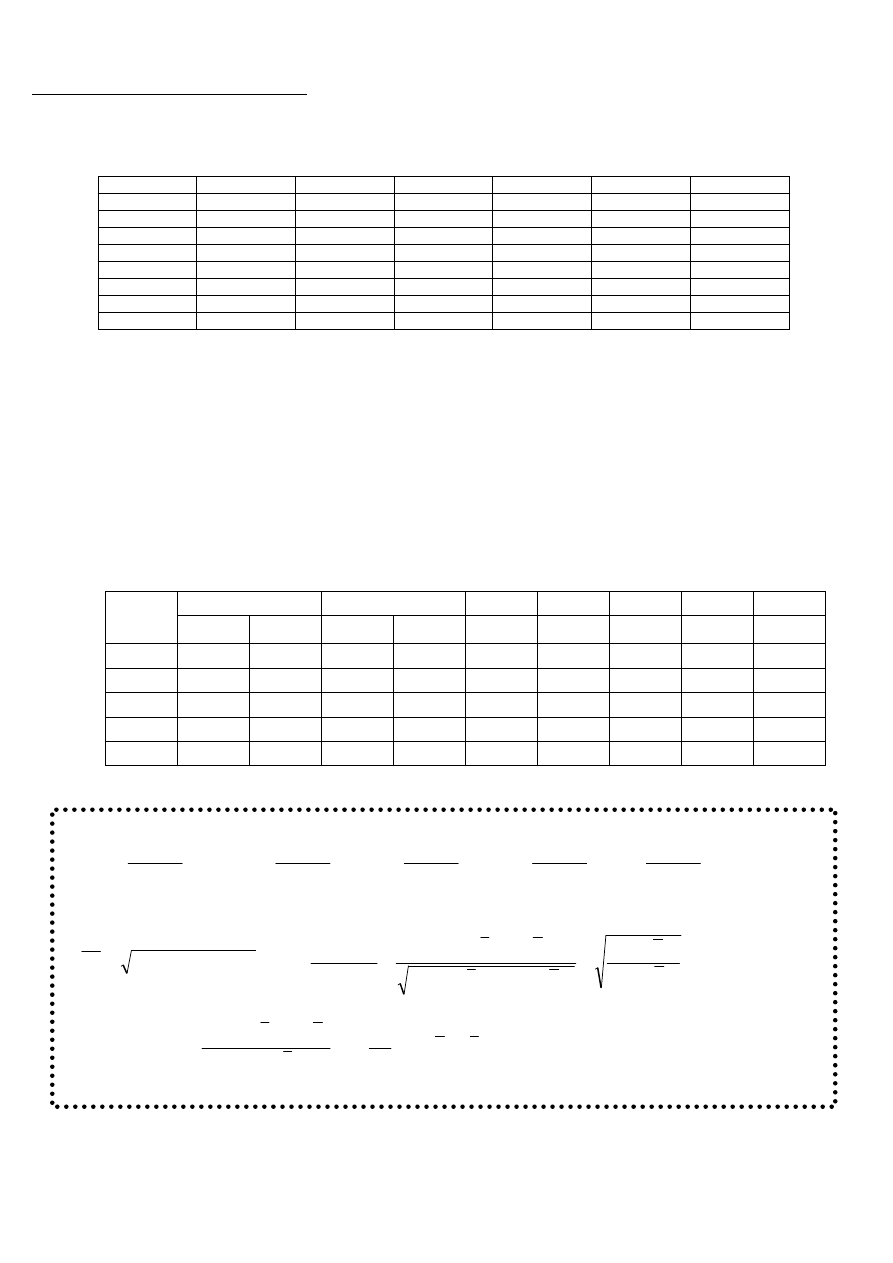
WZORY:

o

o

o

n

p

L

q

p

q

p

I

∑

∑

=

n

o

n

n

p

P

q

p

q

p

I

∑

∑

=

o

o

n

o

q

L

q

p

q

p

I

∑

∑

=

o

n

n

n

q

P

q

p

q

p

I

∑

∑

=

o

o

n

n

W

q

p

q

p

I

∑

∑

=

n

n

G

x

x

x

x

x

⋅

⋅

⋅

⋅

=

....

3

2

1

2

2

2

2

)

(

)

'

(

)

(

)

(

)

)(

(

)

,

cov(

y

y

y

y

y

y

x

x

y

y

x

x

y

x

r

i

i

i

i

y

x

xy

−

∑

−

∑

=

−

−

−

−

=

=

∑

∑

∑

σ

σ

bx

a

y

+

=

x

b

y

a

r

x

x

y

y

x

x

b

x

x

y

xy

i

i

i

x

−

=

=

−

−

−

=

∑

∑

;

)

(

)

)(

(

2

σ

σ

X ł

ZAD.1.

Liczbę dni (x) absencji chorobowej pracowników i wysokość miesięcznej premii w zł (y) dla losowo wybranej
grupy zatrudnionych przedstawia tabela:

y

x

1100

0

200

0

790

1

750

2

500

4

50

7

50

8

Naszkicuj wykres rozrzutu, oblicz i zinterpretuj współczynnik korelacji liniowej Pearsona, wyznacz linię regresji,
oceń dobroć dopasowania prostej do wyników obserwacji. Jakiej premii możemy spodziewać się przy 6 dniach
absencji ?

ZAD.2.

Analizowane zjawisko w latach:
1995 – 1998 rosło średnio o 31,2% rocznie,
1998 – 2001 malało średnio o 1,5% rocznie
2005 – 2009 rosło średnio o 5% rocznie.
W roku 1997 i 2006 odpowiednio wynosiło: 50 j.m. i 40 j.m.
Wyznacz średnie tempo zmian dla okresu 1995 – 2009. Oszacuj wielkość zjawiska w roku 2004 i 2011. W którym
roku wielkość zjawiska osiągnie 128 j.m. przy założeniu wzrostu z ostatniego okresu ?

ZAD. 3.

Przedsiębiorstwo prowadzi sprzedaż środków czyszczących. W październiku i listopadzie obroty artykułami
przedstawiały się następująco:

Październik 09

Listopad 09

Artykuł

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Ilość

(w tys. szt.)

Cena

(w zł/szt.)

Szampon

7

9

10

8

Mydło

19

1

15

1

Pasta

3

5

3

4

Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane
wyniki.

IMIĘ I NAZWISKO GRUPA NR INDEKSU