3
Zadanie 1. (
4 pkt)
Korzystajàc z w∏asnoÊci wartoÊci bezwzgl´dnej, uzasadnij, ˝e wyra˝enie
x
x
x
x
2
4
2
4
4
12
2
2
$
$
-
-
-
+
-
-
przedstawia liczb´ naturalnà. Podaj konieczne za∏o˝enia.
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
4
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 2. (
5 pkt)
Wyznacz wszystkie wartoÊci parametru
m
, dla których rozwiàzania
x
1
i
x
2
równania
(
)
x
x
m x
13
24
10
15
2
+
-
=
-
-
spe∏niajà warunek
x
x
x x
3
0
1
2
2
2
1
2
+
+
=
.
5
Zadanie 3. (
4 pkt)
Wyka˝, ˝e liczby
(
)
sin
cos
a
60
60
2
c
c
=
+
i
cos
b
tg45
30
c
c
=
-
sà pierwiastkami wielomianu
( )
W x
x
x
x
4
8
3
2
=
-
+
.
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
6
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 4. (
5 pkt)
Wyznacz
x
, tak aby liczby
,
,
x
x
x
x
3
3 11
2
2
+
+
-
by∏y w podanej kolejnoÊci wyrazami rosnàcego cià-
gu geometrycznego o wyrazach ca∏kowitych.
7
Zadanie 5. (
5 pkt)
Prosta
l
przechodzi przez poczàtek uk∏adu wspó∏rz´dnych. Napisz równanie tej prostej, wiedzàc, ˝e
jej odleg∏oÊç od punktu
,
A
3
4
= -
-
_
i jest równa
3
.
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
8
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
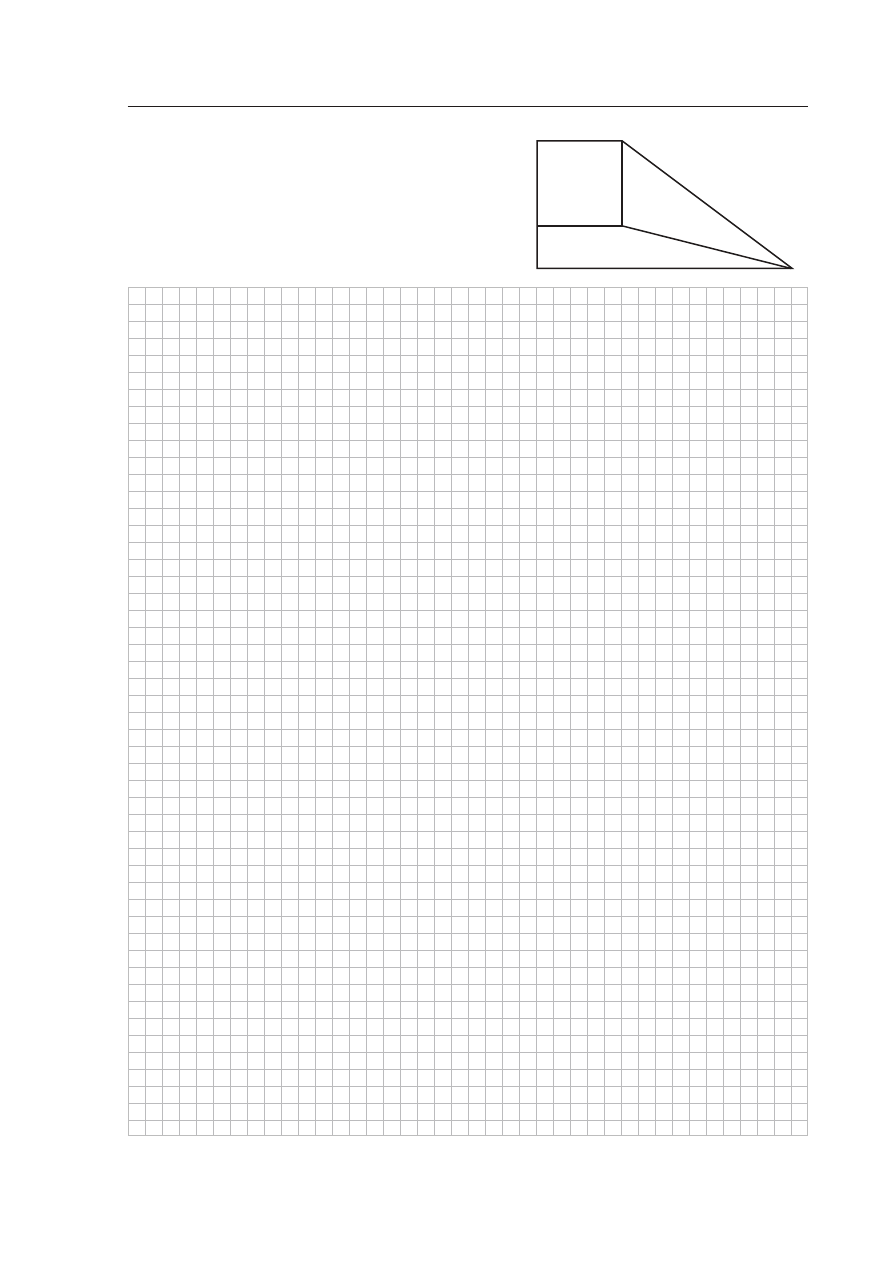
Zadanie 6. (
7 pkt)
Trapez
ABCD
podzielono na trzy figury o równych polach.
Sposób podzia∏u ilustruje rysunek. Wiedzàc, ˝e bok kwa-
dratu
CDEF
jest równy
6
, oblicz:
a) obwód trapezu
ABCD
,
b) cosinus kàta
CBF
.
A
B
E
F
D
C
9
Zadanie 7. (
4 pkt)
Wyznacz rozwiàzanie równania
cos
sin
x
x
2
3
2
=
nale˝àce do przedzia∏u
,
0
2
r
c
m
.
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
10
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 8. (
4 pkt)
Ciàg
a
n
_ i
jest arytmetyczny. Wiedzàc, ˝e
a
a
a
a
2
1
5
3
=
, wyznacz ró˝nic´ tego ciàgu.
11
Zadanie 9. (
5 pkt)
Dany jest ostros∏up trójkàtny, którego podstawà jest trójkàt równoramienny o bokach d∏ugoÊci
5
cm,
5
cm i
6
cm. WysokoÊç ostros∏upa jest równa
2
cm. Spodek wysokoÊci jest Êrodkiem okr´gu wpisa-
nego w podstaw´. Oblicz pole powierzchni ca∏kowitej tego ostros∏upa.
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
12
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 10. (
4 pkt)
Rozwià˝ równanie
P
V
P
10
(
)
(
)
x
x
x
2
2
1
$
$
=
-
-
, wiedzàc, ˝e:
P
n
– oznacza liczb´ wszystkich ró˝nych permutacji bez powtórzeƒ zbioru
n
-elementowego.
V
n
k
– oznacza liczb´ wszystkich ró˝nych
k
-elementowych wariacji bez powtórzeƒ zbioru
n
-elemen-
towego.
13
Zadanie 11. (
3 pkt)
Funkcja
f
okreÊlona jest wzorem
( )
f x
2
3
x
=
c m
. Funkcja
g
powstaje w wyniku przesuni´cia wykresu
funkcji
f
o wektor
,
1 2
-
7
A
.
a) Zapisz wzór funkcji
g
, uzyskanej w wyniku tego przesuni´cia.
b) Sporzàdê wykres funkcji
g
.
c) Wska˝ najwi´kszà liczb´
(
)
m m
R
!
takà, dla której równanie
( )
g x
m
=
nie ma rozwiàzania.
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
14
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
BRUDNOPIS
(nie podlega ocenie)