1.4 Moc na elementach RLC przy
wymuszeniu sinusoidalnym

Jeżeli odbiornikiem jest element o rezystancji R, to moc
chwilowa wydzielająca się w tym elemencie jest opisana
równaniem:

p(t) = u

R

(t) i(t) = R i

2

(t) = R I

m

2

sin

2

(

ω

t+

ψ

i

) =

=

1
2 R I

m

2

-

1
2 R I

m

2

cos(2

ω

t + 2

ψ

i

)] = R I

2

– R I

2

cos(2

ω

t + 2

ψ

i

)]

Wartość średnia mocy chwilowej jest w tym przypadku różna
od zera, a moc czynna elementu o rezystancji R wynosi:

P =

1
2

R I

m

2

= R I

2

Amplituda zmian mocy chwilowej na rezystorze jest równana
mocy czynnej:

S = R I

2

co oznacza, ze współczynnik mocy jest w tym przypadku równy
jedności.

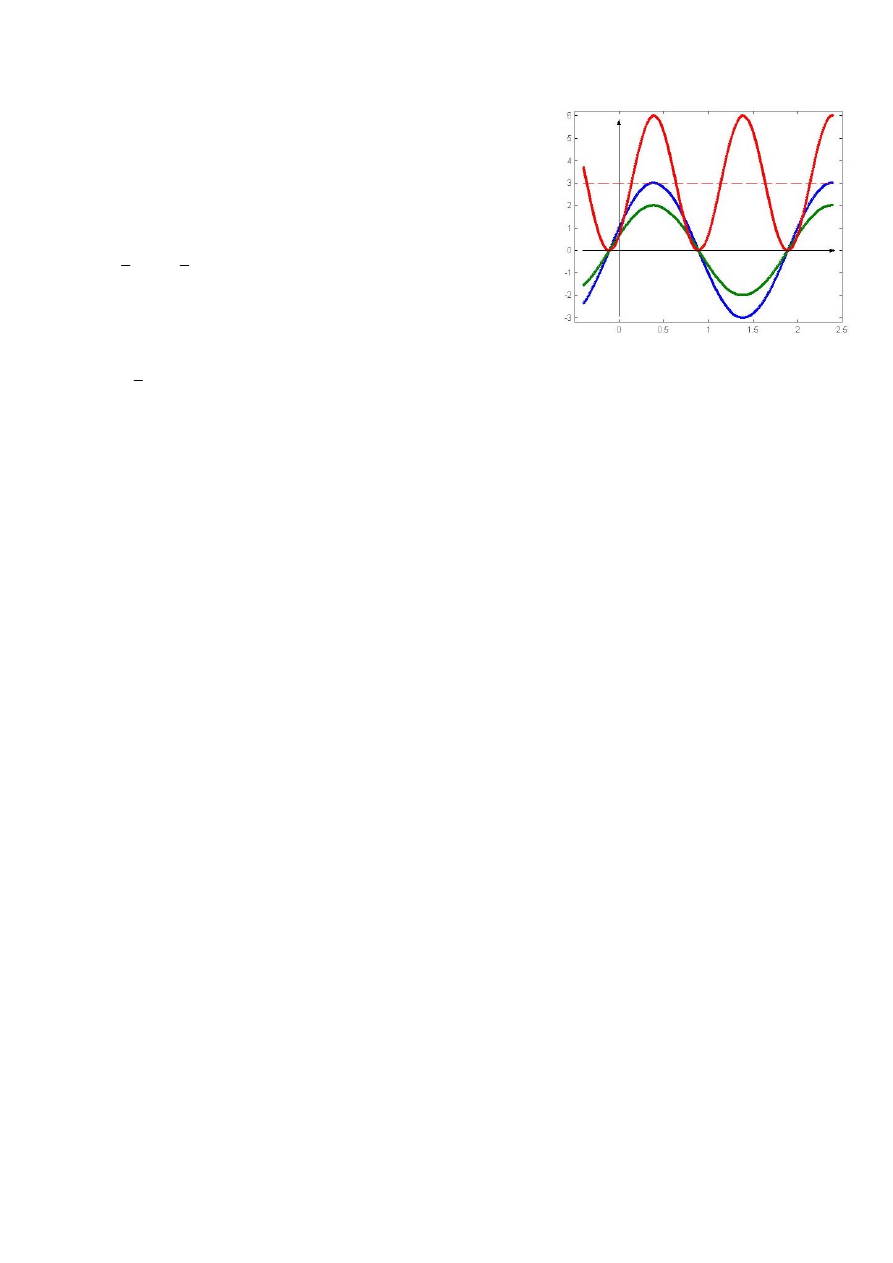
Na Rys. 6 przedstawiono zmiany chwilowe mocy na elemencie
rezystancyjnym.

Rys. 6. Wartość chwilowa mocy na rezystancji

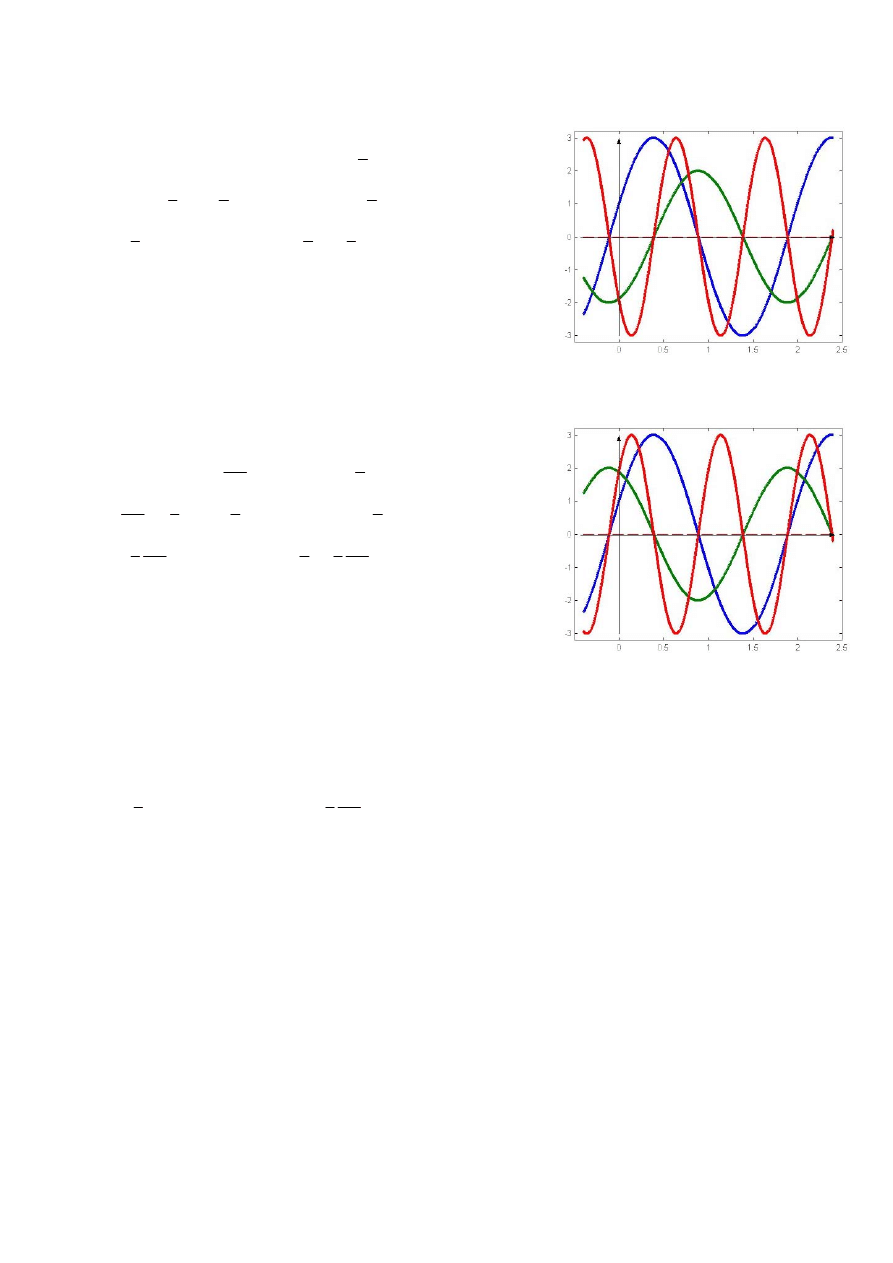
Jeżeli odbiornikiem jest element o indukcyjności L, to wartość
chwilowa mocy jest opisana równaniem:

p(t) = u

L

(t) i(t) =

ω

L I

m

sin(

ω

t +

ψ

i

+

π

2 ) I

m

sin(

ω

t +

ψ

i

) =

=

ω

L I

m

2

1
2 {cos(

π

2 ) – cos(2

ω

t + 2

ψ

i

+

π

2 )}=

=

-

1
2

ω

L I

m

2

cos(2

ω

t + 2

ψ

i

+

π

2 )= -

1
2

ω

L I

m

2

sin(2

ω

t + 2

ψ

i

) =

=

−

X

L

I

2

sin(2

ω

t + 2

ψ

i

)

Jak

widać na Rys. 7 oraz jak wynika z równania na wartość

chwilową mocy, w rozpatrywanym przypadku występują tylko
oscylacje mocy chwilowej między źródłem a cewką. Wartość
średnia mocy chwilowej jest równa zeru, czyli cewka nie pobiera
mocy czynnej ze źródła.

Jeżeli odbiornikiem jest element o pojemności C, to wartość
chwilowa mocy jest równa:

p(t) = u

C

(t) i(t) =

1

ω

C

I

m

sin(

ω

t +

ψ

i

-

π

2 ) I

m

sin(

ω

t +

ψ

i

) =

=

1

ω

C

I

m

2

1
2 {cos( -

π

2 ) – cos(2

ω

t + 2

ψ

i

-

π

2 )}=

=

-

1
2

1

ω

C

I

m

2

cos(2

ω

t + 2

ψ

i

-

π

2 )=

1
2

1

ω

C

I

m

2

sin(2

ω

t + 2

ψ

i

) =

=

X

C

I

2

sin(2

ω

t + 2

ψ

i

)

Jak

widać na Rys. 8 oraz jak wynika z równania na wartość

chwilową mocy odbiornik o pojemności C nie pobiera mocy
czynnej, ponieważ wartość średnia mocy chwilowej jest równa
zeru.

Należy zauważyć, że w obu przypadkach amplituda oscylacji
mocy chwilowej zależy od reaktancji elementu i kwadratu wartości
skutecznej prądu:

S =

1
2

ω

L I

m

2

= X

L

I

2

oraz S =

1
2

1

ω

C

I

m

2

= X

C

I

2

Ponieważ wartość średnia mocy P jest równa zeru, to
współczynnik mocy jest dla idealnej cewki i kondensatora równy
zeru.

Rys. 7. Wartość chwilowa mocy dla elementu

indukcyjnego

Rys. 8. Wartość chwilowa mocy dla elementu

pojemnościowego

1.5 Pomiar mocy dwójnika

Układ pomiarowy

Do pomiaru mocy pobieranej przez dwójnik wykorzystujemy
watomierz, czyli przyrząd pomiarowy, którego wskazanie P

w

jest

równe wartości średniej iloczynu wartości chwilowych napięcia
u

12

(t) doprowadzonego do napięciowych zacisków watomierza i

prądu i

ab

(t) przepływającego pomiędzy prądowymi zaciskami tego

watomierza:

P

w

=

1

T

⌡

⌠

0

T

u

12

(t) i

ab

(t) dt

W celu pomiaru mocy czynnej odbiornika należy do
odpowiednich zacisków watomierza doprowadzić prąd płynący
przez obciążenie oraz napięcie występujące na zaciskach tego
obciążenia (Rys. 12).

Jeżeli mierzone napięcia i prądy zmieniają się sinusoidalnie, to
moc czynna P pobierana przez odbiornik jest równa iloczynowi
wartości skutecznej napięcia U

12

na zaciskach odbiornika, wartości

skutecznej prądu I

ab

płynącego przez odbiornik oraz cosinusa kąta

przesunięcia fazowego

ϕ

między napięciem i prądem:

P = U

12

I

ab

cos

ϕ

Ponieważ zachodzi następująca równość:

P = UI cos

ϕ

= Re

{

U I

*

}

to w rozpatrywanym przypadku wskazanie watomierza można
obliczyć korzystając ze wzoru:

P

w

= Re{U

12

I

ab

*

}

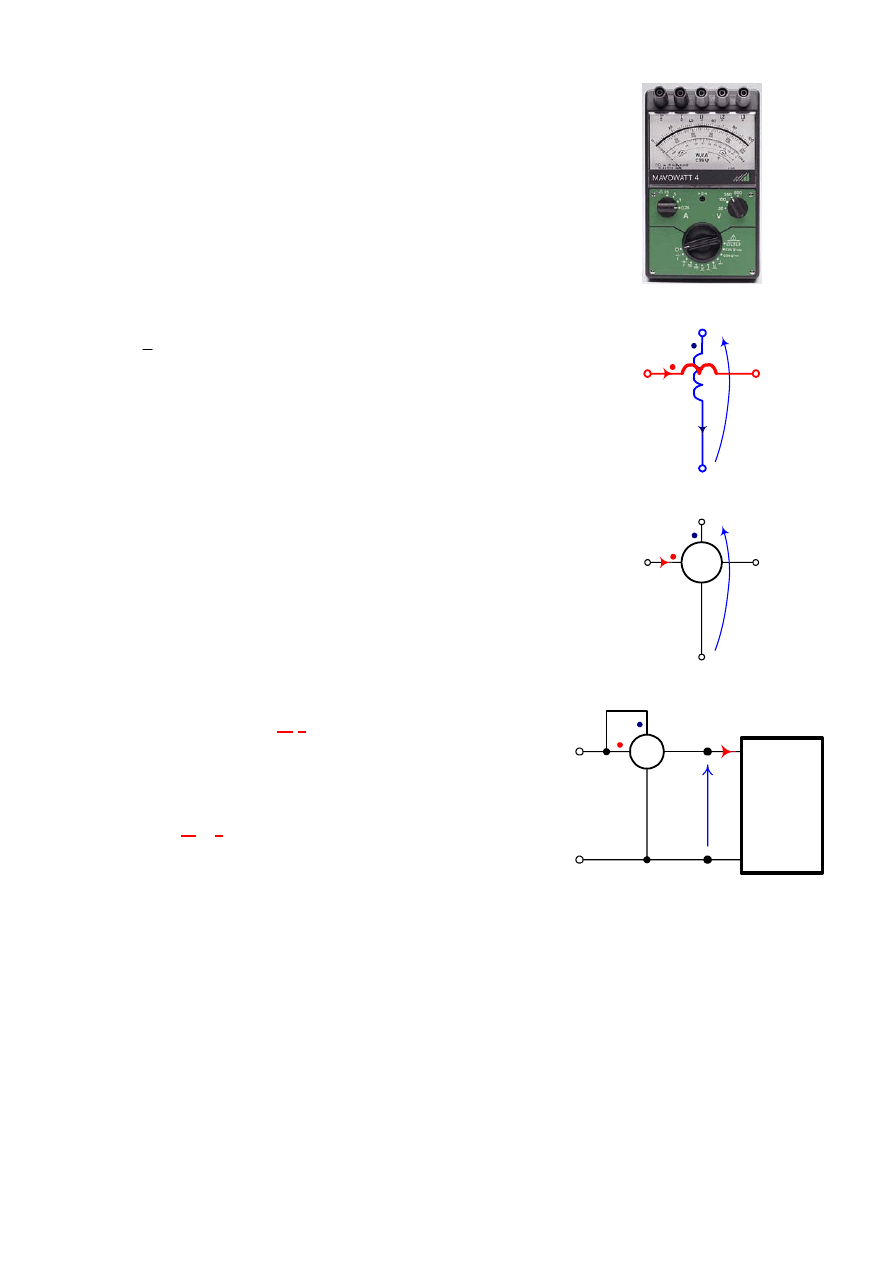
Rys. 9.

Watomierz

i(t)

i

u

(t)

a

b

1

2

u(t)

Rys. 10. Układ cewek watomierza

u(t)

i(t)

a

b

1

2

W

Rys. 11. Symbol watomierza

Odbiornik

u(t)

i(t)

W

Rys. 12. Układ do pomiaru mocy czynnej

dwójnika

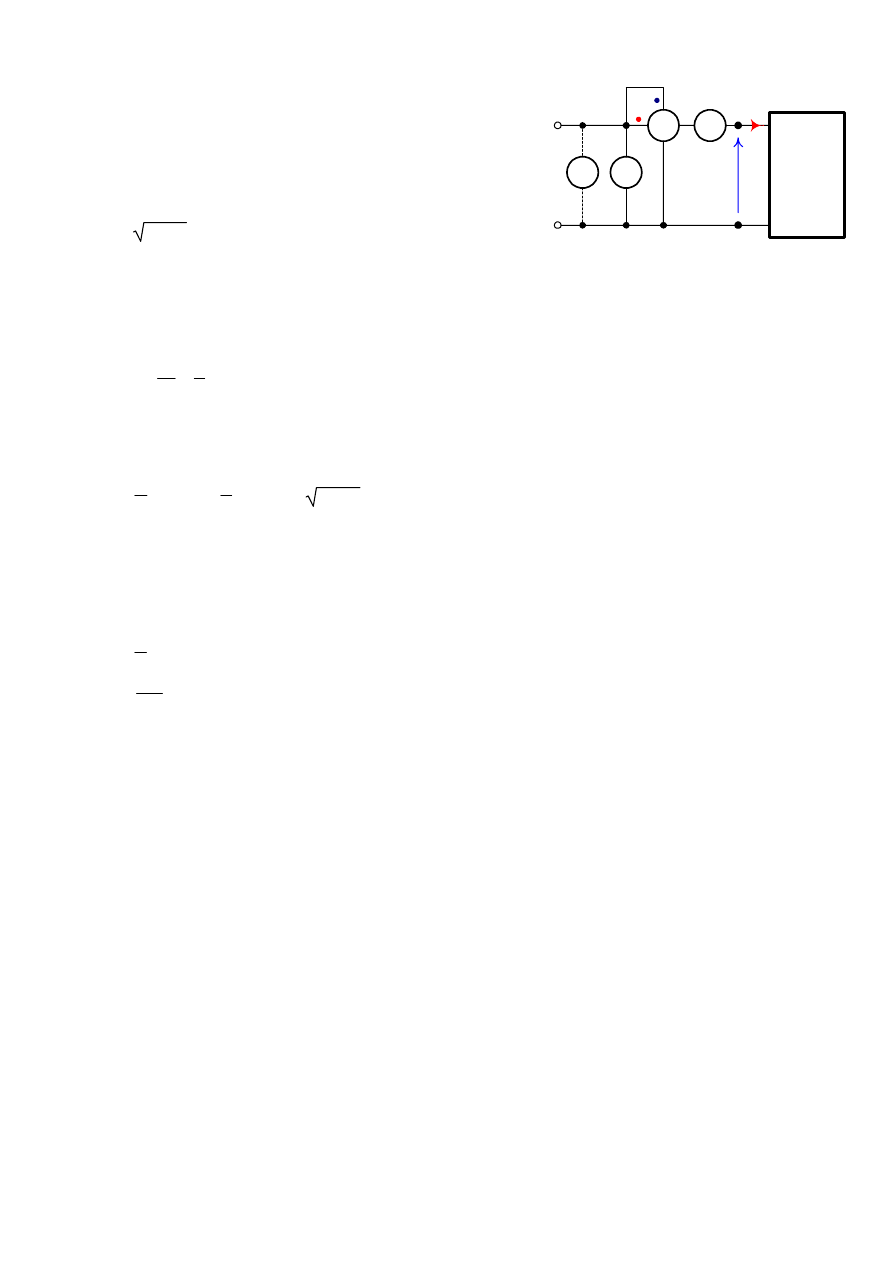
Uzupełniając dotychczasowy układ pomiarowy o amperomierz
i woltomierz (Rys. 13) możemy wyznaczyć moduł mocy pozornej
S pobieranej przez dwójnik:

S = U I

Moc

bierną obliczamy korzystając z następującej zależności:

Q = S

2

- P

2

Nie wiemy czy jest to moc indukcyjna czy pojemnościowa.

Kąt fazowy obwodu

(kąt przesunięcia fazowego) wyznaczamy

wiedząc, że

cos

ϕ

=

P

UI =

P

S

Moduł impedancji obwodu obliczamy korzystając ze wskazań
woltomierza i amperomierza:

Z

=

U

I R =

P
I

2

X = Z

2

- R

2

Znając natomiast częstotliwość mierzonych sygnałów możemy
obliczyć indukcyjność L lub pojemność C badanego dwójnika:

ω

= 2

π

f

L

=

X

ω

C

=

1

ω

X

Wyznaczone w powyższy sposób wartości rezystancji,
indukcyjności lub pojemności są wypadkowymi wartościami
opisującymi dwójnik.

Odbiornik

u

i

A

W

V

Hz

Rys. 13. Układ do pomiaru mocy czynnej i

pozornej dwójnika

Pomiar mocy

W przypadku, gdy napięcia i prądy na zaciskach układu lub
zmieniają się okresowo, to ilość energii dostarczonej do odbiornika
obliczamy za okres powtarzania sygnałów:

W(t

0,

t

o

+ T)

=

⌡

⌠

t

0

t

0

+T

p(t) dt =

⌡

⌠

0

T

p(t) dt

Powyższa równość wynika z faktu, że

⌡

⌠

t

0

t

0

+T

p(t) dt =

⌡

⌠

0

T

p(

τ

+t

0

) d

τ

= p(

τ

+t

0

)|

0

T

= p(T+t

0

) – p(t

0

) = W

T

Moc czynna może być obliczona dla dowolnej wielokrotności
okresu powtarzalności sygnałów:

P

=

1

nT

⌡

⌠

0

nT

p(t) dt =

1

nT n

⌡

⌠

0

T

p(t) dt =

1
T

⌡

⌠

0

T

p(t) dt

Trudno jest jednak dokładnie odmierzyć czas pomiaru tak aby
był on dokładnie wielokrotnością (n naturalne) okresu T napięcia i
prądu. Jeżeli pomiar trwa od chwili t

0

= 0, do chwili t = nT+

τ

,

gdzie

τ

należy do przedziału 0

≤

τ

≤

T, to ilość zmierzonej energii

wynosi:

W =

⌡

⌠

0

nT+

τ

p(t) dt =

⌡

⌠

0

nT

p(t) dt +

⌡

⌠

nT

τ

p(t) dt =

=

n

⌡

⌠

0

T

p(t) dt +

⌡

⌠

0

τ

p(t) dt = n W

T

+ W(

τ

)

gdzie W(

τ

) jest energią, która spełnia warunek 0

≤

W(

τ

)

≤

W

T

.

Ponieważ W(

τ

) jest co najwyżej równe W

T

, to błąd pomiaru

mocy będzie tym mniejszy im dłużej trwa pomiar, czyli im
większa jest liczba n. Dla n = 1000 błąd pomiaru mocy nie
przekracza 0,1 %.