2005-12-19
© Lesław ŁADNIAK
ENERGIA I MOC .........................................................................2
1.1
M
OC CHWILOWA I KIERUNEK PRZEKAZYWANIA ENERGII
......2
1.2
M
OC CZYNNA
.........................................................................4
1.3
M
OC SYGNAŁÓW SINUSOIDALNIE ZMIENNYCH
.....................5
1.4
M
OC NA ELEMENTACH
RLC
PRZY WYMUSZENIU
SINUSOIDALNYM
..........................................................................7
1.5
P
OMIAR MOCY DWÓJNIKA
.....................................................9
Układ pomiarowy ....................................................................9
Pomiar mocy..........................................................................11
2
© Lesław ŁADNIAK
E
NERGIA I MOC
1.1 Moc chwilowa i kierunek przekazywania
energii
Podstawowym zadaniem obwodu elektrycznego jest
przekazanie energii z jednej części obwodu do drugiej części tego
obwodu. Szybkość przekazywania energii z jednego układu do
drugiego układu poprzez wybrane zaciski opisuje wartość mocy
chwilowej:
p(t) = u(t) i(t)
Kierunek przepływu energii między poszczególnymi
fragmentami układu można określić znając napięcie na zaciskach
układu i kierunek prądu płynącego przez układ. Wyznaczając
kierunek przepływu energii należy pamiętać, że kierunek
przepływu prądu elektrycznego jest zgodny z kierunkiem ruchu
dodatnich ładunków elektrycznych, a strzałka napięcia wskazuje
punkt o potencjale wyższym. Iloczyn wartości chwilowych
napięcia i prądu jest większy od zera, czyli wartość chwilowa
mocy jest większa od zera, gdy potencjał punktu A jest wyższy niż
potencjał punktu B, a prąd płynie od punktu A do punktu B.
Korzystając z powyższych uwag, stwierdzamy, że w chwili t
układ pobiera energię elektryczną, jeżeli iloczyn wartości
chwilowych napięcia na zaciskach układu u(t) oraz prądu i(t)
płynącego przez układ jest dodatni, czyli wartość chwilowa mocy
p(t) jest większa od zera:
p(t) = u(t) i(t) > 0
⇒
energia dopływa do układu
Jeżeli w danej chwili czasu iloczyn napięcia u(t) na zaciskach
układu oraz wartości chwilowej prądu i(t) płynącego przez układ
jest ujemny, czyli gdy wartość chwilowa mocy p(t) jest mniejsza
od zera, to w chwili t rozpatrywany układ oddaje energię
elektryczną, czyli jest źródłem tej energii:
p(t) = u(t) i(t) < 0
⇒
energia odpływa z układu
Na
Błąd! Nie można odnaleźć źródła odwołania. oraz Rys. 1
pokazano jak kierunek przesyłu energii zależy od kierunków
napięć i prądów na zaciskach układu.
Układ B
i(t)
u(t)
Układ A
Energia
A
B
i(t)
u(t)
A
B
Układ B
Układ A
Energia
Rys. 1.
Kierunki przekazywania energii
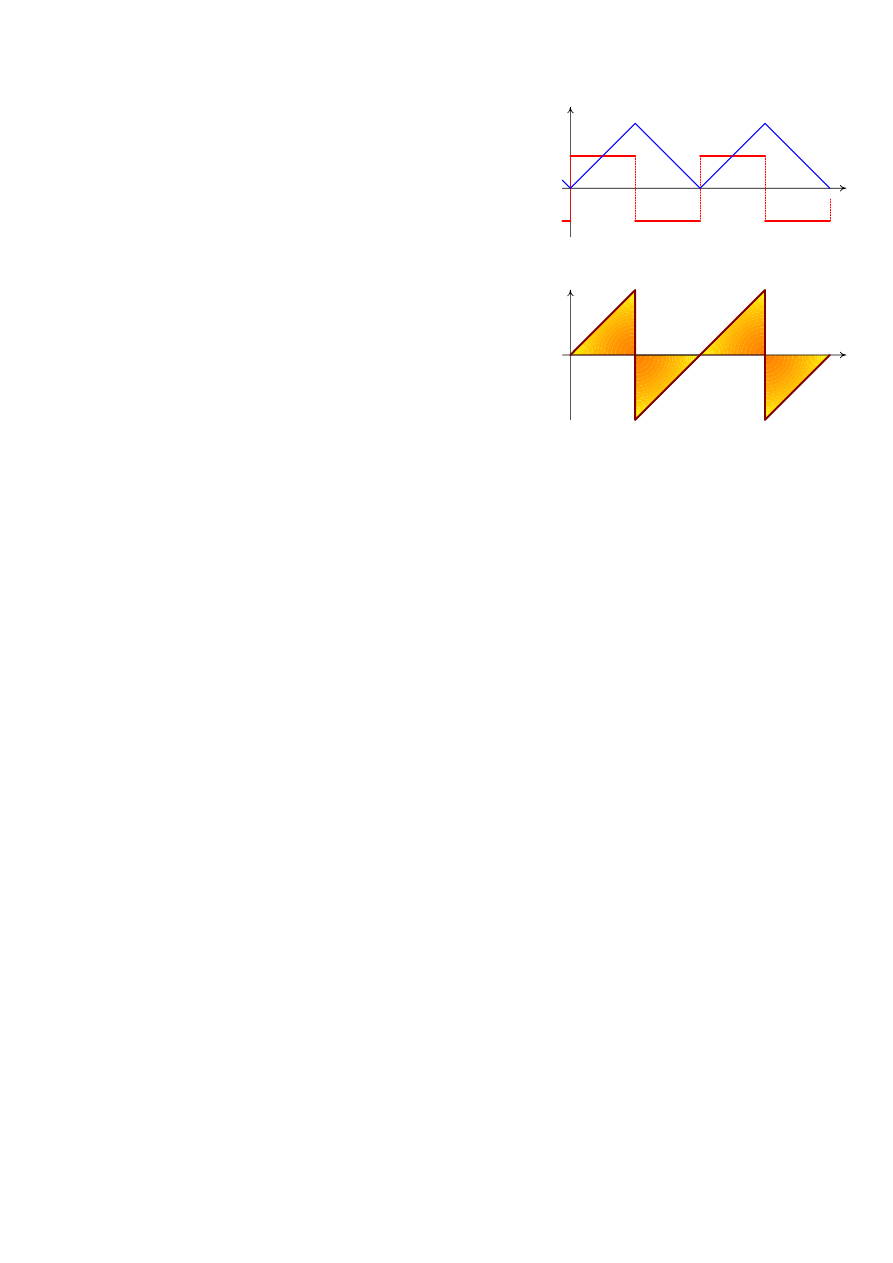
3
© Lesław ŁADNIAK
Ponieważ kierunek przepływu energii zależy od wartości
chwilowych napięcia na zaciskach układu u(t) oraz wartości
chwilowej prądu i(t) płynącego przez układ, to w przypadku, gdy
napięcia i prądy są przemienne, ulega zmianie kierunek przepływu
energii. Oznacza to, że występują na przemian przedziały czasu, w
których wartość chwilowa mocy jest większa od zera (dodatnia)
oraz przedziały czasu, gdzie wartość chwilowa mocy jest mniejsza
od zera (ujemna).
Na Rys. 2 przedstawiono wykres zmian wartości chwilowych
napięcia i prądu na zaciskach elementu obwodu, a na Rys. 3
odpowiadający im przebieg zmian wartości chwilowej mocy.
Analizując wykres zmian mocy chwilowej należy zauważyć, że
występują na przemian przedziały czasu, w których wartość mocy
chwilowej jest większa od zera (dodatnia) oraz przedziały czasu,
gdzie wartość chwilowa mocy jest mniejsza od zera (ujemna).
Okres zmian mocy chwilowej jest dwa razy mniejszy niż okres
napięcia lub prądu.
W tym przypadku amplituda zmian mocy chwilowej jest równa
iloczynowi amplitud zmian napięcia i prądu.
Jak wynika z Rys. 3 ilustrujacego zmain mocy chwilowej,
rozpatrywany element na przemian przyjmuje i oddaje taką samą
porcję energii elektrycznej. Moc czynna, czyli wartość średnia
mocy chwilowej jest w tym przypadku równa zeru. Jeżeli energia
elektryczna jest oddawana spowrotem do obwodu elektrycznego,
to znaczy, że element ten potrafi magazynować energię
elektryczną.
u(t), i(t)
t
u(t)
i(t)
Rys. 2.
Wartości chwilowe napięcia i prądu
p(t)
t
Rys. 3.
Wartości chwilowe mocy
(złożony z rezystora i cewki) (w stanie
przejściowym)
4
© Lesław ŁADNIAK
1.2 Moc czynna
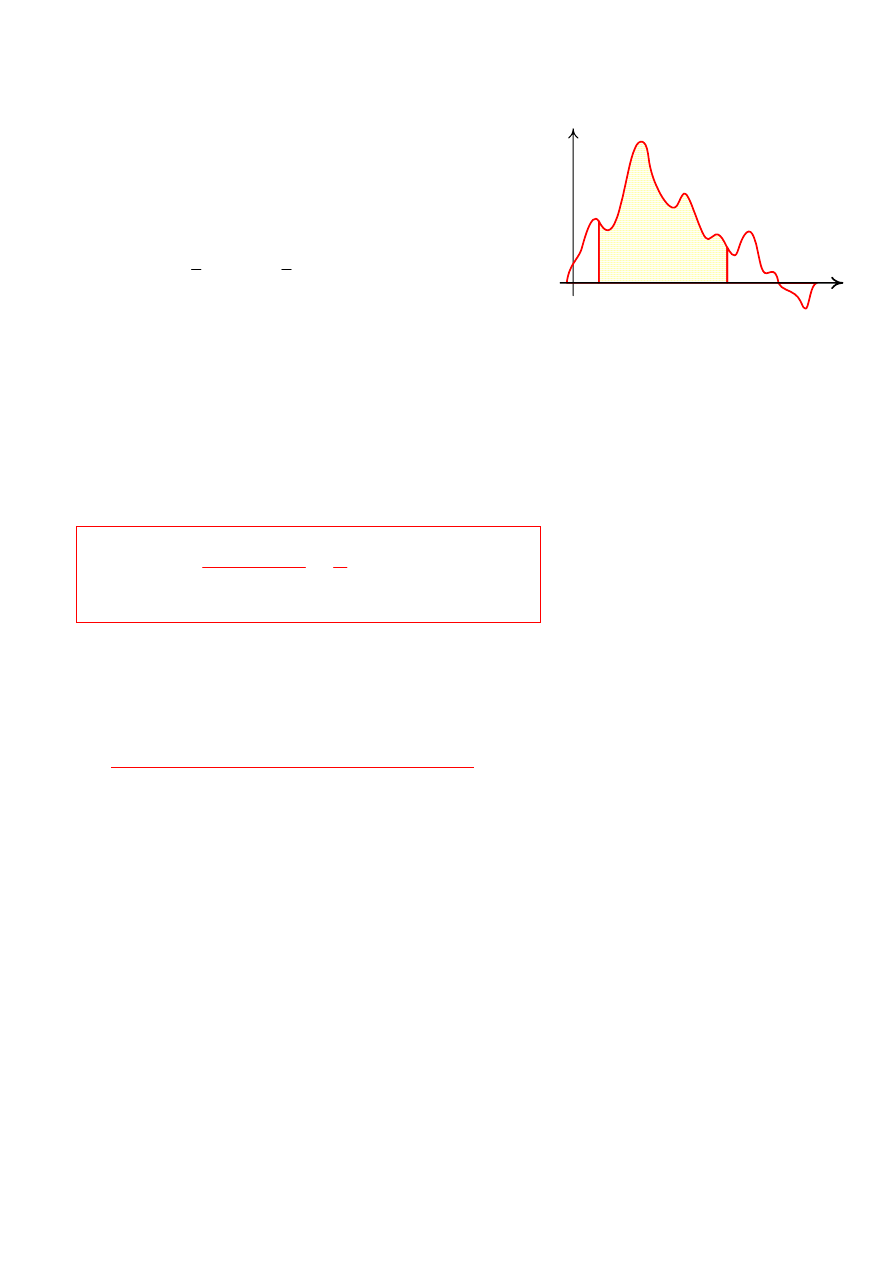
Miarą ilości energii dostarczonej do układu elektrycznego od
chwili t
0
do chwili t
0
+T jest pole powierzchni pod wykresem zmian
wartości chwilowej mocy p(t), czyli iloczyn wartości chwilowej
napięcia na zaciskach układu oraz prądu płynącego przez układ:
W(t
o,
t
o
+T)
=
1
T
⌡
⌠
t
o
t
o
+T
p(t) dt
=
1
T
⌡
⌠
t
o
t
o
+T
u(t) i(t) dt = W(t
o
+T)
-
W(t
0
)
Jeżeli ilość energii elektrycznej dostarczonej do układu
W(t
o
,t
o
+T) jest większa od zera, to znaczy, że w rozpatrywanym
układzie występuje przemiana energii elektrycznej na inną postać
energii np. cieplną lub mechaniczną.
Średnią szybkość przekazywania energii elektrycznej
obliczymy dzieląc ilość energii dostarczonej do układu W(t
o
,t
o
+T)
przez czas trwania dostawy energii T:
(A.1)
P =
W(t
o
;t
o
+T)
T
=
1
T
⌡
⌠
t
o
t
o
+T
p(t) dt
Średnią szybkość przekazywania energii elektrycznej
oznaczamy dużą lierą P nazywamy mocą czynną, ponieważ
dostarcza ona informacji o ilości energii elektrycznej, która uległa
przemianie na inną postać energii.
Moc czynna jest to wartość średnia mocy chwilowej.
Jeżeli napięcie i prąd zmieniają się okresowo, to wartością
średnią mocy chwilowej obliczoną za jeden okres powtarzania
sygnałów.
p(t)
t
t
o
t
x
W(t
o
,t
x
)
Rys. 4.
Wartość chwilowa mocy a energia
5
© Lesław ŁADNIAK
1.3 Moc sygnałów sinusoidalnie zmiennych
Rozpatrzmy dwa sygnały sinusoidalnie zmienne o tej samej
częstotliwości, różnych amplitudach i różnych fazach
początkowych. Jednym sygnałem jest napięcie o amplitudzie U
m
i
fazie początkowej
ψ
u
, czyli
u(t) = U
m
sin (
ω
t +
ψ
u
)
Drugim
sygnałem jest prąd o amplitudzie I
m
i fazie początkowej
ψ
i
, czyli przesunięcie w fazowe między napięciem i prądem jest
równe
ϕ
=
ψ
u
-
ψ
i
:
i(t) = I
m
sin (
ω
t +
ψ
i
)
Zgodnie z definicją, moc chwilowa jest iloczynem wartości
chwilowych napięcia i prądu:
p(t) = u(t) i(t)
czyli w przypadku sygnałów sinusoidalnie zmiennych
otrzymujemy:
p(t) = U
m
sin (
ω
t +
ψ
u
) I
m
sin (
ω
t +
ψ
i
)
Ponieważ sin
α
sin
β
=
1
2 cos(
α
-
β
) - cos(
α
+
β
),
oraz
ψ
u
-
ψ
i
=
ϕ
to zmiany mocy chwilowej są opisane rówaniem:
p(t)
=
1
2 U
m
I
m
[cos
ϕ
- cos(2
ω
t -
ϕ
)]
Jeżeli w powyższym równaiu uwzględnimy zależność między
wartością maksymalną, a wartością skuteczną dla sygnałów
sinusoidalnie zmiennych F
m
= 2 F, to równanie możemy zapisać
w postaci:
p(t) = U I cos
ϕ
- U I cos(2
ω
t -
ϕ
)
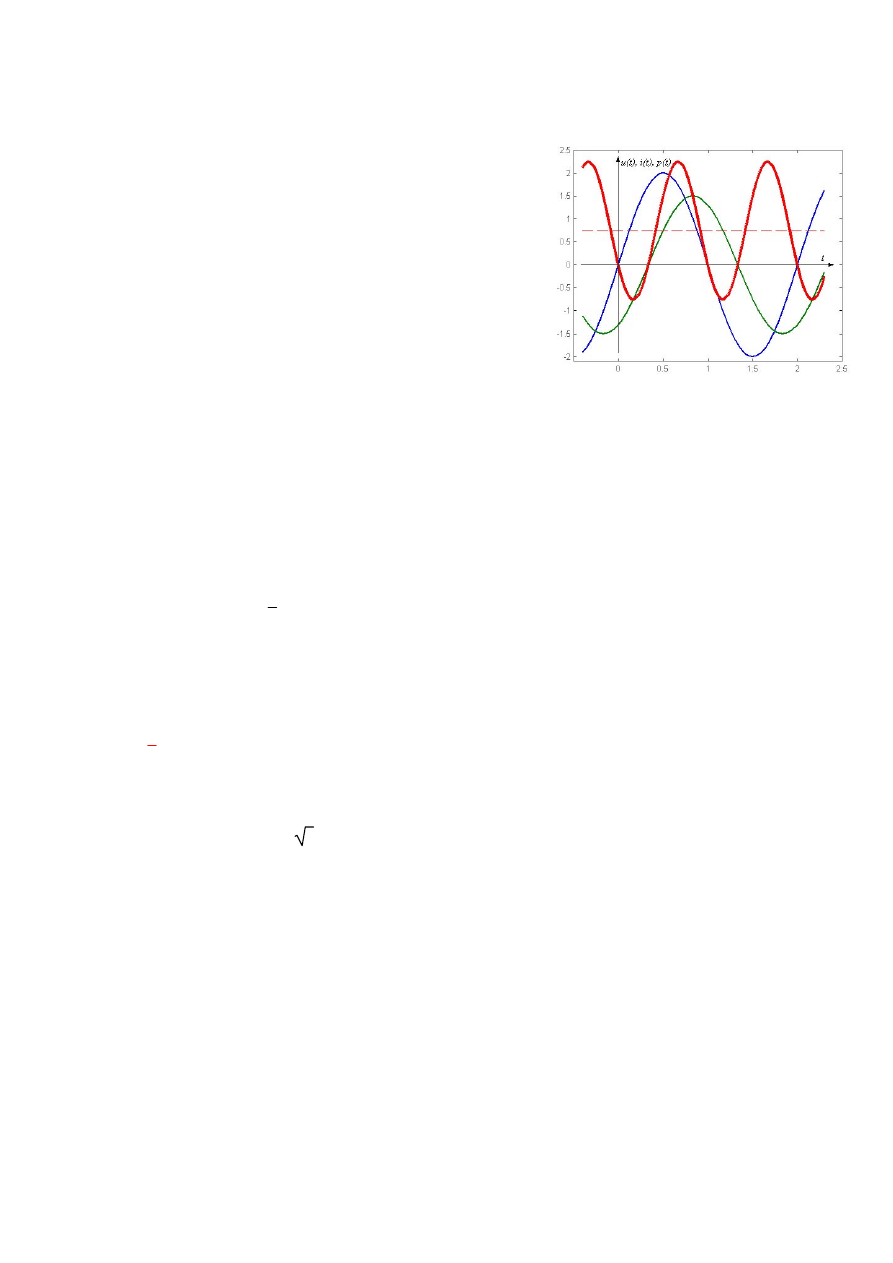
Na Rys. 5 przedstawiono wykres zmian wartości chwilowej
mocy dla przypadku, gdy napięcie i prąd zmieniają się
sinusoidalnie.
Rys. 5. Wartość chwilowa mocy sygnałów
sinusoidalnie zmiennych
6
© Lesław ŁADNIAK
Jak wynika z równania opisujacego zmiany mocy chwilowej,
gdy napięcie i prąd są sinusoidalnie zmienne, moc chwilowa p(t)
ma dwie składowe:
-
niezależną od czasu składową stałą UI cos
ϕ
,
-
składową zmienną UI cos (2
ω
t -
ϕ
).
Składowa stała jest to wartość średnia mocy chwilowej, czyli
moc czynna:
P
=
1
T
⌡
⌠
0
T
u(t) i(t) dt =
1
T
⌡
⌠
0
T
{U I cos
ϕ
- U I cos(2
ω
t -
ϕ
)} dt =
= U I cos
ϕ
=
1
2 U
m
I
m
cos
ϕ
gdzie
ϕ
=
ψ
u
-
ψ
i
Moc czynna sygnałów sinusoidalnie zmiennych jest równa
iloczynowi wartości skutecznych (połowie iloczynu wartości
maksymalnych) tych sygnałów pomnożonemu przez cosinus
kąta przesunięcia fazowego między nimi.
Składowa zmienna oscyluje sinusoidalnie wokół wartości
średniej mocy, czyli wokół mocy czynnej, z częstotliwością dwa
razy większą niż częstotliwość sygnałów napięcia i prądu (Rys. 5).
Amplituda oscylacji mocy chwilowej wokół wartośći średniej
mocy jest w rozpatrywanym przypadku równa iloczynowi wartości
skutecznych napięcia U oraz prądu I:
S = U I =
1
2 U
m
I
m
Znając amplitudę S oscylacji wartości chwilowej mocy i
wartość średnią mocy, czyli moc czynną P, można wyzanczyć
współczynnik mocy:
P
S = cos
ϕ
Współczynnik mocy określa stosunek mocy czynnej do
amplitudy zmian mocy chwilowej, czyli relację między ilością
energii elektrycznej, która w odbiorniku uległa przemianie na
inną postać energii, a energią elektryczną, która mogłaby być
dostarczona do odbiornika przy zachowaniu maksymalej mocy
przekazywania energii.
W przypadku przebiegów sinusoidlanych współczynnik mocy
jest równy cos
ϕ
odbiornika.
Z
zależności opisującej zmiany mocy
chwilowej
p(t) = UI cos
ϕ
- UI cos (2
ω
t -
ϕ
)
wynika, że przy danym przesunięciu
fazowym
ϕ
między prądem a napięciem
moc chwilowa osiąga wartość maksymalną,
gdy cos (2
ω
t -
ϕ
) jest równy jedności, czyli
gdy
2
ω
t -
ϕ
= k
π
gdzie k jest naturalną liczbą nieparzystą.
Oznacza
to,
że dla czasów t =
k
π
+
ϕ
2
ω
mocy chwilowa ma wartość maksymalną:
p
max
(t) = UI cos
ϕ
+ U I
Moc chwilowa osiąga wartość
najmniejszą w przypadku, gdy argument
składowej zmiennej jest równy zeru:
p(t) = p
min
= UI cos
ϕ
- U I
Pierwsze minimum wystąpi, gdy t =
ϕ
2
ω
.
7
© Lesław ŁADNIAK
1.4 Moc na elementach RLC przy
wymuszeniu sinusoidalnym
Jeżeli odbiornikiem jest element o rezystancji R, to moc
chwilowa wydzielająca się w tym elemencie jest opisana
równaniem:
p(t) = u
R
(t) i(t) = R i
2
(t) = R I
m
2
sin
2
(
ω
t+
ψ
i
) =
=
1
2 R I
m
2
-
1
2 R I
m
2
cos(2
ω
t + 2
ψ
i
)] = R I
2
– R I
2
cos(2
ω
t + 2
ψ
i
)]
Wartość średnia mocy chwilowej jest w tym przypadku różna
od zera, a moc czynna elementu o rezystancji R wynosi:
P =
1
2 R I
m
2
= R I
2
Amplituda zmian mocy chwilowej na rezystorze jest rówana
mocy czynnej:
S = R I
2
co oznacza, ze wspólczynnik mocy jest w tym przypadku równy
jedności.
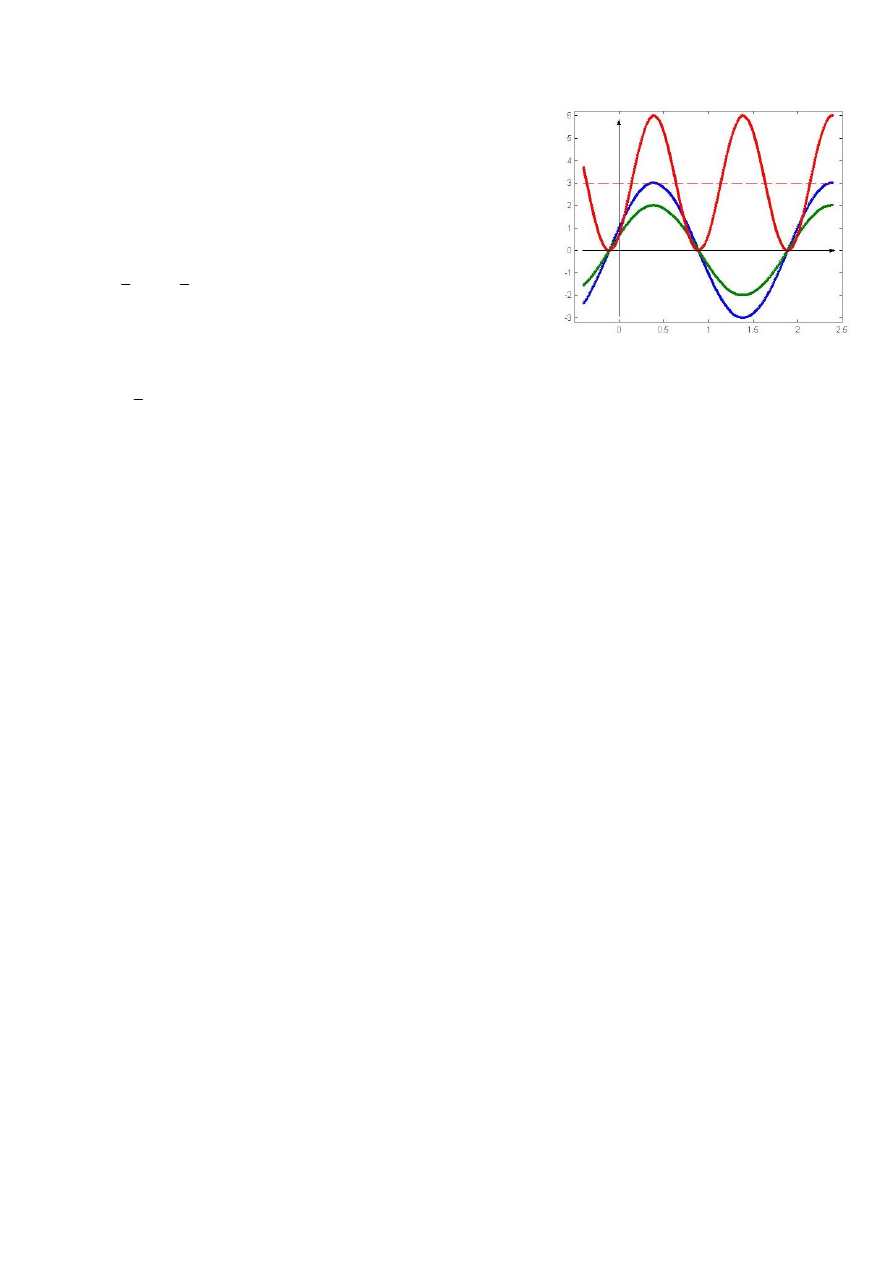
Na Rys. 6 przedstawiono zmiany chwilowe mocy na elemencie
rezystancyjnym.
Rys. 6. Wartość chwilowa mocy na rezystancji
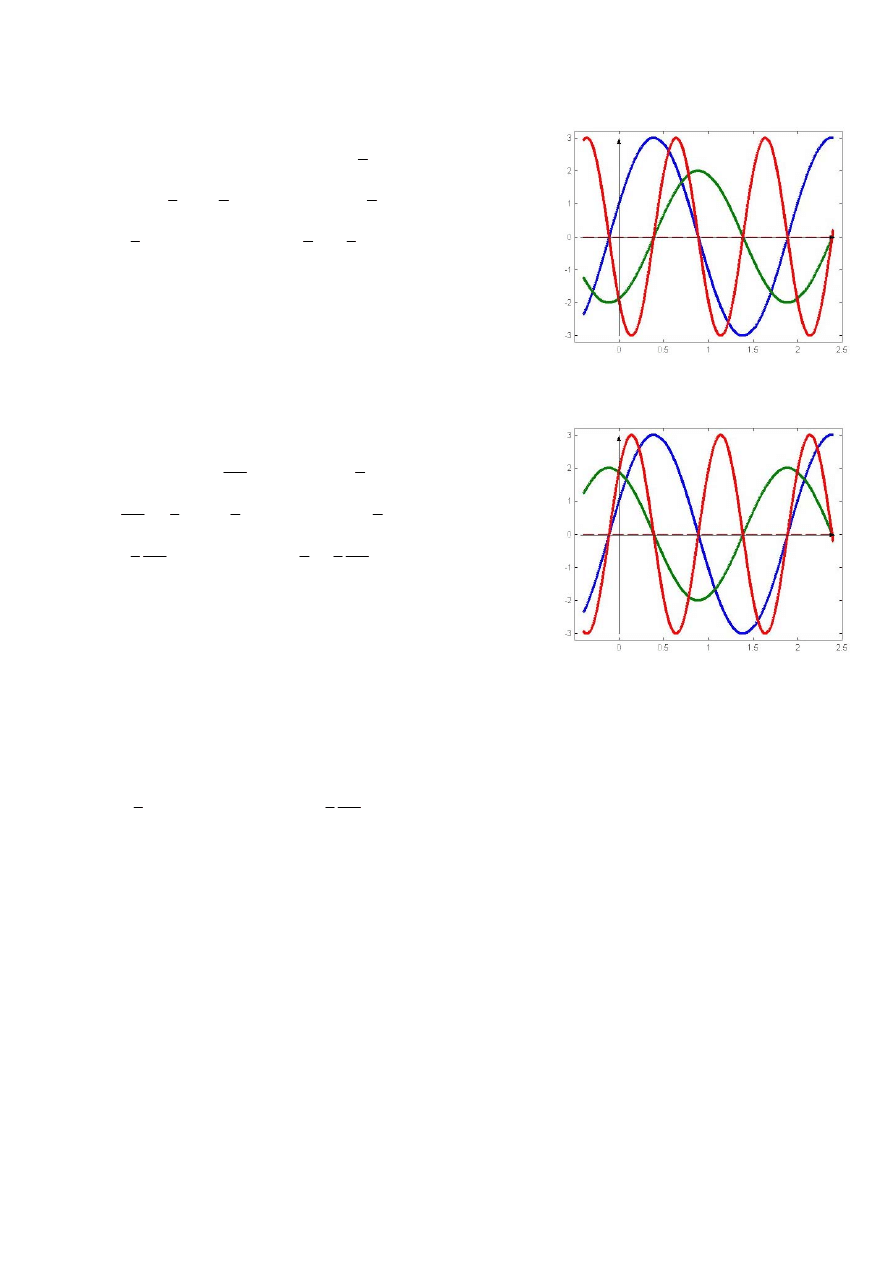
8
© Lesław ŁADNIAK
Jeżeli odbiornikiem jest element o indukcyjności L, to wartość
chwilowa mocy jest opisana równaniem:
p(t) = u
L
(t) i(t) =
ω
L I
m
sin(
ω
t +
ψ
i
+
π
2 ) I
m
sin(
ω
t +
ψ
i
) =
=
ω
L I
m
2
1
2 {cos(
π
2 ) – cos(2
ω
t + 2
ψ
i
+
π
2 )}=
=
-
1
2
ω
L I
m
2
cos(2
ω
t + 2
ψ
i
+
π
2 )= -
1
2
ω
L I
m
2
sin(2
ω
t + 2
ψ
i
) =
=
−
X
L
I
2
sin(2
ω
t + 2
ψ
i
)
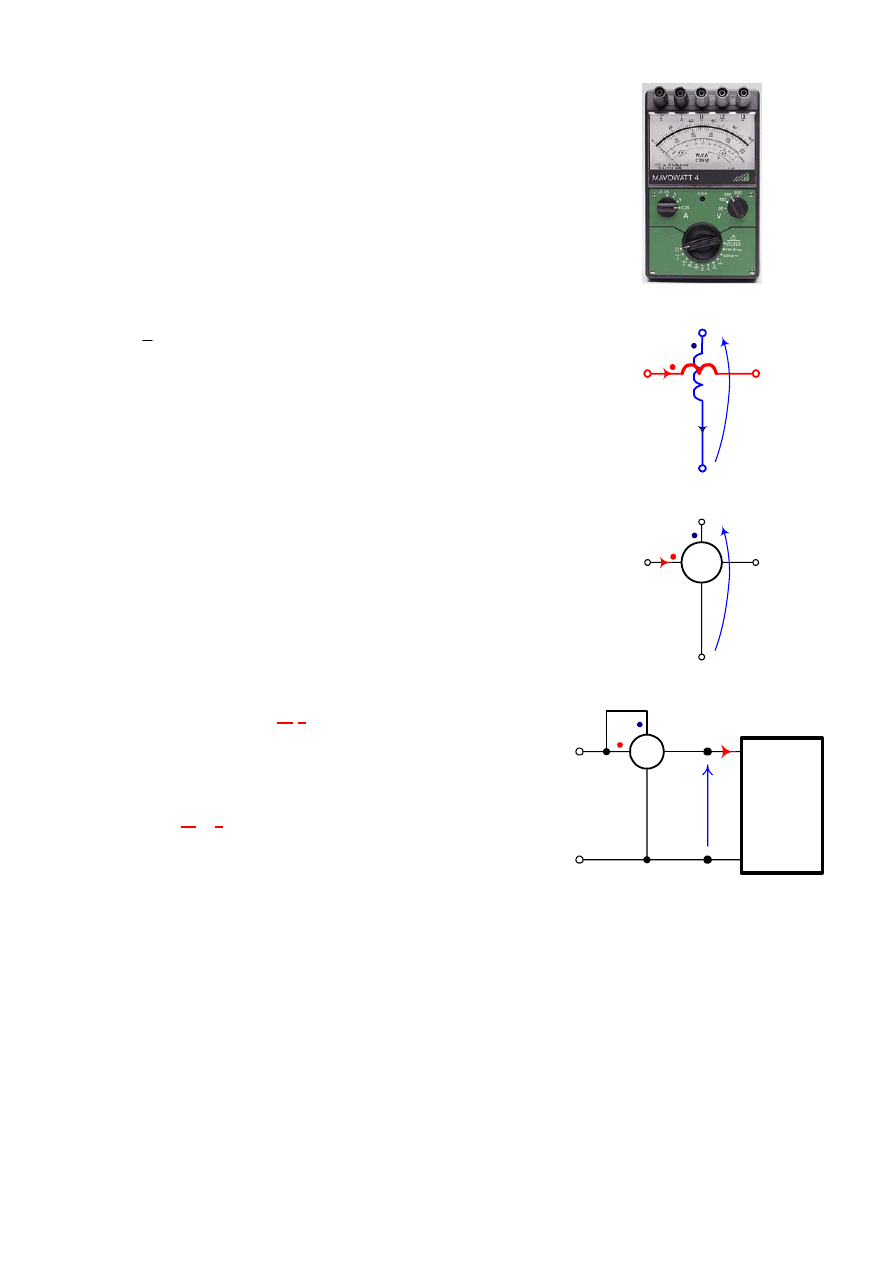
Jak
widać na Rys. 7 oraz jak wynika z równania na wartość
chwilową mocy, w rozpatrywanym przypadku występują tylko
oscylacje mocy chwilowej między źródłem a cewką. Wartość
średnia mocy chwilowej jest równa zeru, czyli cewka nie pobiera
mocy czynnej ze źródła.
Jeżeli odbiornikiem jest element o pojemności C, to wartość
chwilowa mocy jest równa:
p(t) = u
C
(t) i(t) =
1
ω
C
I
m
sin(
ω
t +
ψ
i
-
π
2 ) I
m
sin(
ω
t +
ψ
i
) =
=
1
ω
C
I
m
2
1
2 {cos( -
π
2 ) – cos(2
ω
t + 2
ψ
i
-
π
2 )}=
=
-
1
2
1
ω
C
I
m
2
cos(2
ω
t + 2
ψ
i
-
π
2 )=
1
2
1
ω
C
I
m
2
sin(2
ω
t + 2
ψ
i
) =
=
X
C
I
2
sin(2
ω
t + 2
ψ
i
)
Jak
widać na Rys. 8 oraz jak wynika z równania na wartość
chwilową mocy odbiornik o pojemności C nie pobiera mocy
czynnej, ponieważ wartość średnia mocy chwilowej jest równa
zeru.
Należy zauważyć, że w obu przypadkach amplituda oscylacji
mocy chwilowej zależy od reaktancji elementu i kwadratu wartości
skutecznej prądu:
S =
1
2
ω
L I
m
2
= X
L
I
2
oraz S =
1
2
1
ω
C
I
m
2
= X
C
I
2
Ponieważ wartość średnia mocy P jest równa zeru, to w
spółczynnik mocy jest dla idalnej cewki i kondensatora równy
zeru.
Rys. 7. Wartość chwilowa mocy dla elementu
indukcyjnego
Rys. 8. Wartość chwilowa mocy dla elementu
pojemnościowego
9
© Lesław ŁADNIAK
1.5 Pomiar mocy dwójnika
Układ pomiarowy
Do pomiaru mocy pobieranej przez dwójnik wykorzystujemy
watomierz, czyli przyrząd pomiarowy, którego wskazanie P
w
jest
równe wartości średniej iloczynu wartości chwilowych napięcia
u
12
(t) doprowadzonego do napięciowych zacisków watomierza i
prądu i
ab
(t) przepływającego pomiędzy prądowymi zaciskami tego
watomierza:
P
w
=
1
T
⌡
⌠
0
T
u
12
(t) i
ab
(t) dt
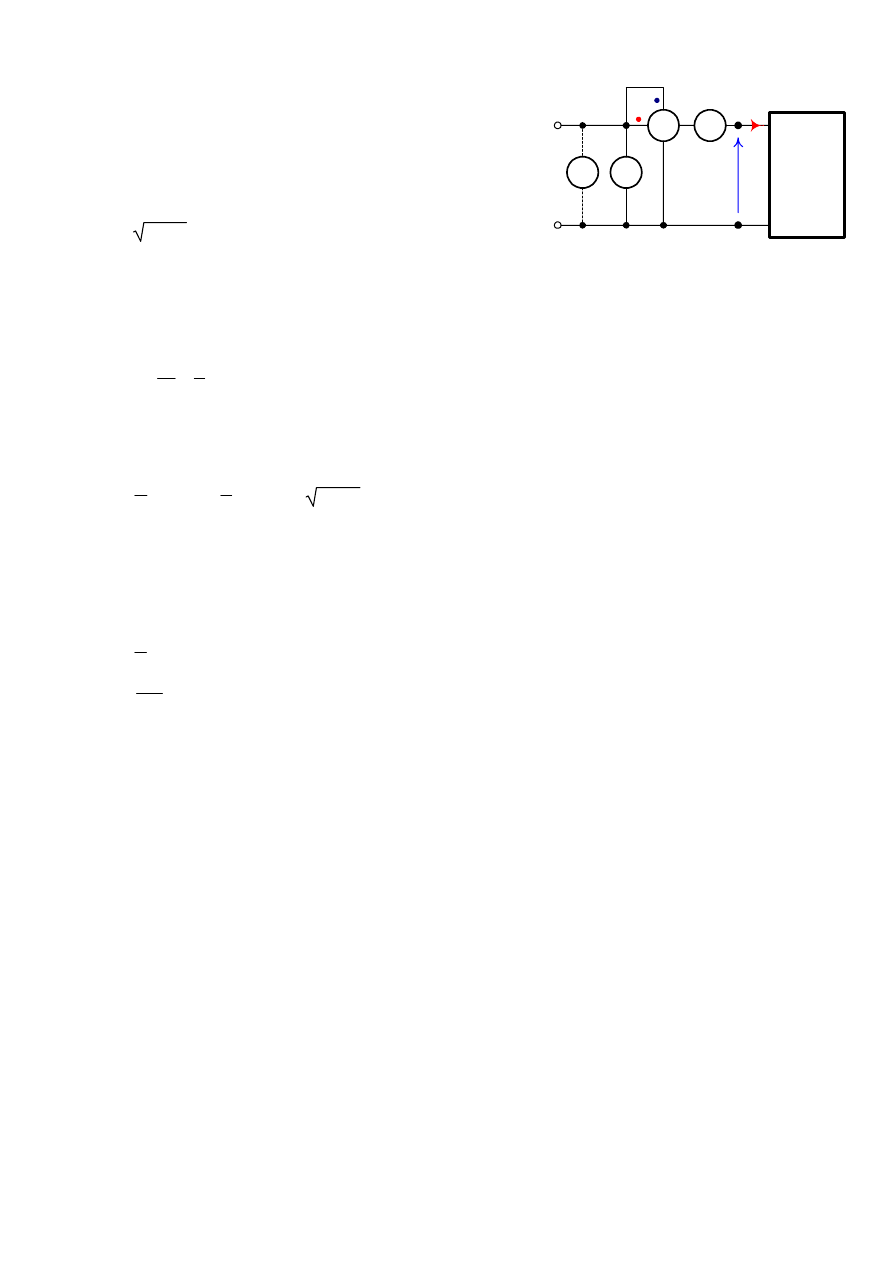
W celu pomiaru mocy czynnej odbiornika należy do
odpowiednich zacisków watomierza doprowadzić prąd płynący
przez obciążenie oraz napięcie występujące na zaciskach tego
obciążenia (Rys. 12).
Jeżeli mierzone napięcia i prądy zmieniają się sinusoidalnie, to
moc czynna P pobierana przez odbiornik jest równa iloczynowi
wartości skutecznej napięcia U
12
na zaciskach odbiornika, wartości
skutecznej prądu I
ab
płynącego przez odbiornik oraz cosinusa kąta
przesunięcia fazowego
ϕ
między napięciem i prądem:
P = U
12
I
ab
cos
ϕ
Ponieważ zachodzi następująca równość:
P = UI cos
ϕ
= Re
{
U I
*
}
to w rozpatrywanym przypadku wskazanie watomierza można
obliczyć korzystając ze wzoru:
P
w
= Re{U
12
I
ab
*
}
Rys. 9.
Watomierz
i(t)
i
u
(t)
a
b
1
2
u(t)
Rys. 10. Układ cewek watomierza
u(t)
i(t)
a
b
1
2
W
Rys. 11. Symbol watomierza
Odbiornik
u(t)
i(t)
W
Rys. 12. Układ do pomiaru mocy czynnej
dwójnika
10
© Lesław ŁADNIAK
Uzupełniając dotychczasowy układ pomiarowy o amperomierz
i woltomierz (Rys. 13) możemy wyznaczyć moduł mocy pozornej
S pobieranej przez dwójnik:
S = U I
Moc
bierną obliczamy korzystając z następującej zależności:
Q = S
2
- P
2
Nie wiemy czy jest to moc indukcyjna czy pojemnościowa.
Kąt fazowy obwodu
(kąt przesunięcia fazowego) wyznaczamy
wiedząc, że
cos
ϕ
=
P
UI =
P
S
Moduł impedancji obwodu obliczamy korzystając ze wskazań
woltomierza i amperomierza:
Z
=
U
I R =
P
I
2
X = Z
2
- R
2
Znając natomiast częstotliwość mierzonych sygnałów możemy
obliczyć indukcyjność L lub pojemność C badanego dwójnika:
ω
= 2
π
f
L
=
X
ω
C
=
1
ω
X
Wyznaczone w powyższy sposób wartości rezystancji,
indukcyjności lub pojemności są wypadkowymi wartościami
opisującymi dwójnik.
Odbiornik
u
i
A
W
V
Hz
Rys. 13. Układ do pomiaru mocy czynnej i
pozornej dwójnika
11
© Lesław ŁADNIAK
Pomiar mocy
W przypadku, gdy napięcia i prądy na zaciskach układu lub
zmieniają się okresowo, to ilość energii dostarczonej do odbiornika
obliczamy za okres powtarzania sygnałów:
W(t
0,
t
o
+ T)
=
⌡
⌠
t
0
t
0
+T
p(t) dt =
⌡
⌠
0
T
p(t) dt
Powyższa równość wynika z faktu, że
⌡
⌠
t
0
t
0
+T
p(t) dt =
⌡
⌠
0
T
p(
τ
+t
0
) d
τ
= p(
τ
+t
0
)|
0
T
= p(T+t
0
) – p(t
0
) = W
T
Moc czynna może być obliczona dla dowolnej wielokrotności
okresu powtarzalności sygnałów:
P
=
1
nT
⌡
⌠
0
nT
p(t) dt =
1
nT n
⌡
⌠
0
T
p(t) dt =
1
T
⌡
⌠
0
T
p(t) dt
Trudno jest jednak dokładnie odmierzyć czas pomiaru tak aby
był on dokładnie wielokrotnością (n naturalne) okresu T napięcia i
prądu. Jeżeli pomiar trwa od chwili t
0
= 0, do chwili t = nT+
τ
,
gdzie
τ
należy do przedziału 0
≤
τ
≤
T, to ilość zmierzonej energii
wynosi:
W =
⌡
⌠
0
nT+
τ
p(t) dt =
⌡
⌠
0
nT
p(t) dt +
⌡
⌠
nT
τ
p(t) dt =
=
n
⌡
⌠
0
T
p(t) dt +
⌡
⌠
0
τ
p(t) dt = n W
T
+ W(
τ
)
gdzie W(
τ
) jest energią, która spełnia warunek 0
≤
W(
τ
)
≤
W
T
.
Ponieważ W(
τ
) jest co najwyżej równe W
T
, to błąd pomiaru
mocy będzie tym mniejszy im dłużej trwa pomiar, czyli im
większa jest liczba n. Dla n = 1000 błąd pomiaru mocy nie
przekracza 0,1 %.
12
© Lesław ŁADNIAK