15
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
Prędkość chwilowa, prędkość średnia
We wcześniejszym przykładzie czterech samochodów nie braliśmy pod uwagę czasu ruchu. Ich
podróże mogły trwać godzinę, dwie lub nawet cały dzień. Czujemy intuicyjnie, że tym co będzie je
różniło jest kolejny ważny parametr – prędkość. Ogólnie prędkość będzie stosunkiem wykonanego
przesunięcia do czasu, w którym to przesunięcie zostało wykonane. Ale jak rozumieć
„przesunięcie”? W poprzednim rozdziale rozważaliśmy różne sposoby na określenie przesunięć
ciała:
– różniczki wektorów
zdające sprawę z „minimalnych” – chwilowych zmian wektora
wodzącego zachodzących w małych odstępach czasu
,
– różniczki skalarów
będące wartościami powyższych wektorów (czyli długościami
minimalnych – chwilowych przesunięć) równe różniczkom drogi
, zachodzące w małych
odstępach czasu
,
– posumowane (całkowane) różniczki wektorów dające całkowite – „globalne” przemieszczenie
, które ma miejsce w całkowitym czasie (wynikających z całkowania różniczek )
– posumowane (całkowane) różniczki skalarów dające całkowitą – „globalną” drogę
, również
pokonywaną w całkowitym czasie
.
Każde z tych przesunięć ma swój sens fizyczny i praktyczny. Dzieląc je przez odpowiadające im
czasy otrzymamy prędkości, które również będą miały głęboki i ważny sens. Omawiam je poniżej
po kolei.
Stosunek różniczki wektora
do odpowiadającego jej czasu :
nazywamy prędkością chwilową (niektóre podręczniki dopisują w jej oznaczeniu indeks „ch”:
). Jaki jest sens prędkości chwilowej? Zauważ, że powstaje z podzielenia różniczki wektora
wodzącego przez różniczkę czasu. Są to parametry obejmujące bardzo krótki fragment ruchu –
wręcz daną chwilę ruchu. W następnym momencie tak zdefiniowana prędkość może być już inna.
Dlatego nazywamy ją prędkością chwilową! Pamiętaj, że jest to wektor! Jaki będzie miał kierunek i
zwrot? Powstaje z podzielenia różniczki
przez dodatni skalar – czas. Zatem będzie miał kierunek
i zwrot taki sam jak
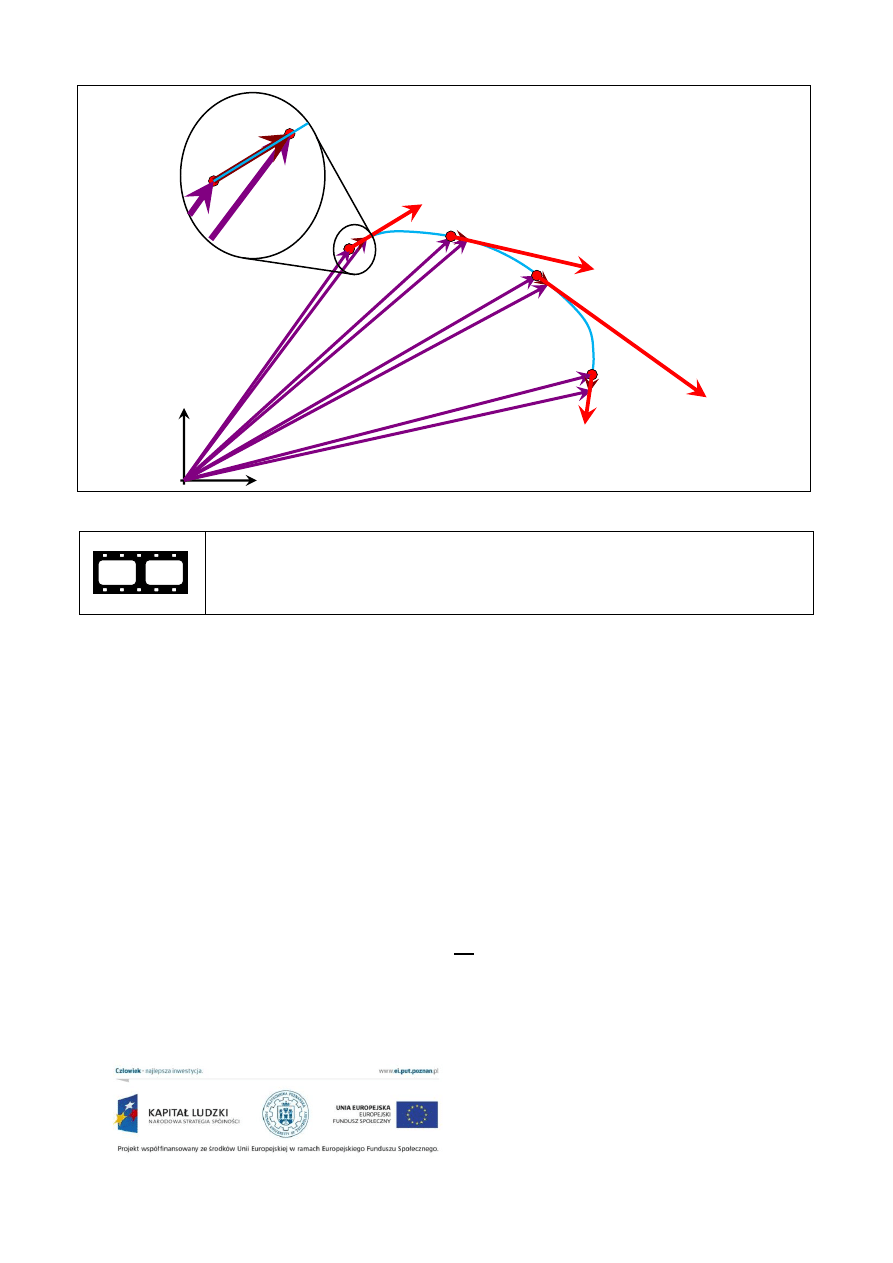
. Wektorowy sposób wyznaczania prędkości chwilowej pokazałem na
rysunku.
16
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
X
Y
r
d
V
V
V
V
Przeanalizuj animowaną wersję powyższego rysunku otwierając dokument
„ANIMACJA Prędkość chwilowa”.
U dołu obrazu znajduje się pasek postępu oraz przyciski,
które pozwalają uruchamiać kolejne etapy filmu.
Na obrazie przedstawiłem kilka chwil z niewielkimi zmianami wektora wodzącego
,
odpowiadającymi im różniczkami
oraz wektorami prędkości chwilowych . Pokazałem również
pierwszą różniczkę
w znaczącym powiększeniu. Widzimy, że wektor tej różniczki ma taki sam
kierunek jak lokalny przebieg drogi ciała (niebieska linia). Mówiliśmy już o tym wcześniej, że mały
przyrost wektora wodzącego
jest styczny do toru ruchu w danym miejscu (jego wartość jest też
równa przyrostowi drogi
). I tak samo będzie z prędkością chwilową: jako wielkość wektorowa
jest zawsze styczna do toru ruchu w danym punkcie!
Obliczmy teraz kolejny stosunek: wartości różniczki
do czasu :
17
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
Dzielimy tutaj skalar przez skalar, zatem dostajemy skalar. Dotyczy on też wielkości
obowiązujących w danym momencie – będzie to zatem wartość wcześniej obliczonej prędkości
chwilowej
. Przypominam Ci, że prędkość chwilowa jako wektor ma określoną długość – to jest
właśnie jej wartość! Właśnie z tego parametru „rozlicza” nas policja drogowa i tę wielkość mierzą
foto-radary. Wystarczy, że tylko na chwilę przekroczymy dozwoloną prędkość, już możemy
ponieść karę. W tym kontekście nazwanie tej prędkości „chwilową” staje się jeszcze bardziej
uzasadnione.
Jak wiemy różniczka
jest równa różniczce drogi . Zatem równanie na wartość prędkości
chwilowej możemy zapisać jako:
Zajmijmy się teraz kolejną wielkością. Podzielmy całkowite przemieszczenie
przez
odpowiadający mu czas
:
Otrzymaliśmy w ten sposób prędkość średnią. Jak każdą wartość średnią opatrzyłem ją dodatkową
kreską poziomą nad symbolem „
” (ale pod znakiem strzałki wektora): . Jest to wielkość
wektorowa, ponieważ powstała z podzielenia wektora przemieszczenia przez dodatni skalar – czas
całego ruchu. Oba te parametry „globalne” obejmują cały ruch od początku do końca. Zatem
uzasadnione jest nazwanie tak obliczonej prędkości – prędkością średnia. Po prostu zdaje sprawę ze
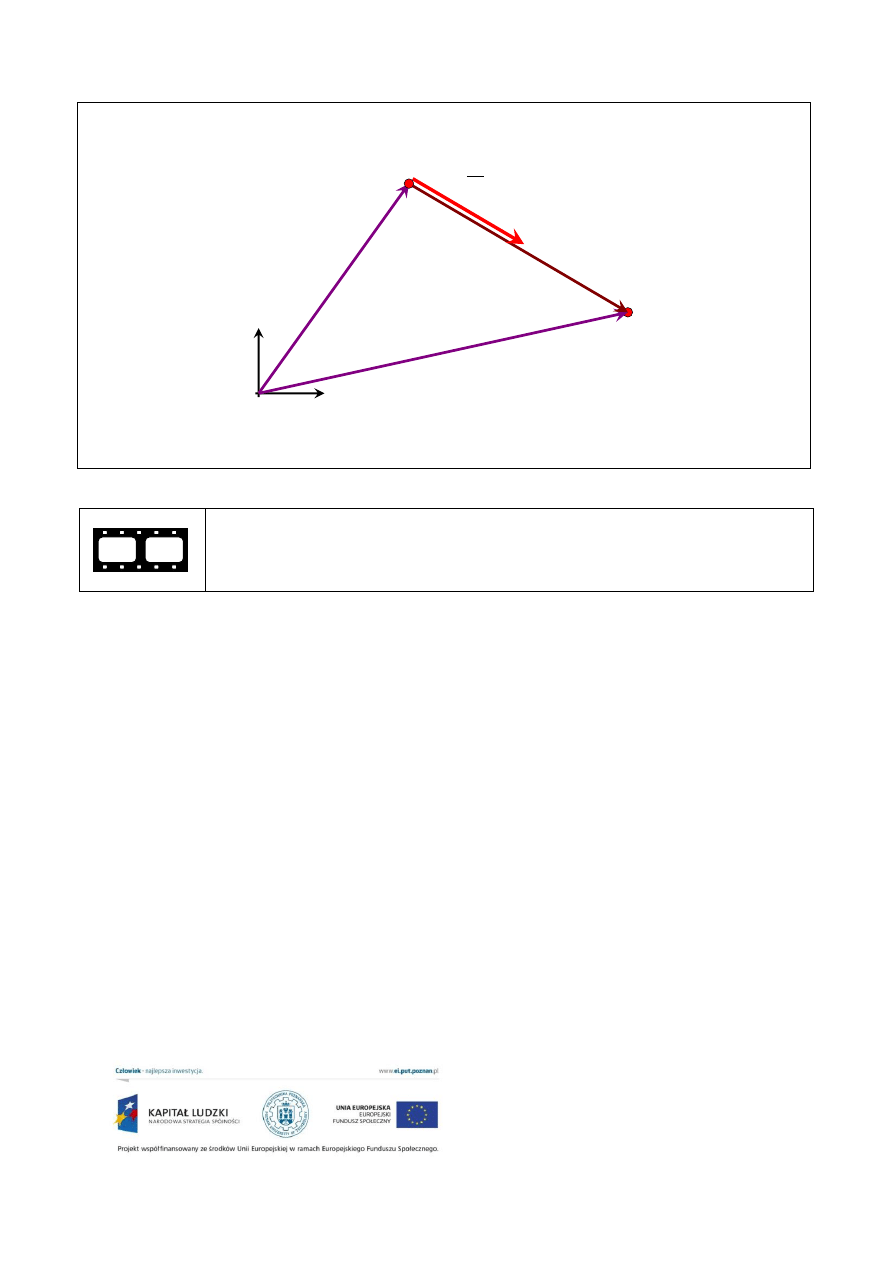
średniej wektorowej wartości tego parametru w całym czasie ruchu. Graficznie przedstawiłem ją na
kolejnym rysunku.
18
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
Przeanalizuj animowaną wersję powyższego rysunku otwierając dokument
„ANIMACJA Prędkość średnia”.
U dołu obrazu znajduje się pasek postępu oraz przyciski,
które pozwalają uruchamiać kolejne etapy filmu.
Powyższa wielkość ma również znaczenie praktyczne. Nieraz interesuje nas średnia prędkość
związana z określonym przemieszczeniem: na przykład podróży samochodu z miasta A do miasta
B. Nie zawsze droga biegnie prosto, samochód musi też omijać przeszkody i zatory, ale w końcu
dociera do miasta B. Logistycznie nie muszą interesować nas szczegóły kształtu całej drogi – tylko
czasowa możliwość dotarcia z jednej miejscowości do drugiej. Wówczas przydaje się właśnie
pojęcie i wartość „wektorowej” prędkości średniej związanej tylko z całkowitym „globalnym”
przemieszczeniem i czasem. Osoby pracujące w transporcie znają wręcz na pamięć czasowe
możliwości przebycia określonych przemieszczeń między miastami.
Zauważ, że gdy wektor przemieszczenia jest równy zeru, taką jest też prędkość średnia.
Przypominając sobie przykład z samochodami widzimy zatem, że prędkość średnia nie musi w
pełni oddawać specyfiki ruchu.
Dodajmy też, że gdy prędkość (jako wektor) jest stała, wówczas prędkość średnia jest równa
prędkości chwilowej.
V
X
Y
A
r
B
r
A
r
B
19
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
Pozostało nam jeszcze obliczenie stosunku całkowitej drogi
do czasu :
Dzielimy tutaj całkowitą „globalną” drogę przez czas. Jest to również prędkość średnia ale
uzyskana z podzielenia drogi (skalara) przez czas (też skalar). Zatem jest to skalarna prędkość
średnia. Zdaje ona sprawę ze średniej wartości (w czasie) jaką wyświetlał nam prędkościomierz
samochodu.
Uwaga: wartość „skalarnej” prędkości średniej
w ogólności nie jest równa wartości
„wektorowej” prędkości średniej
! Z przykładu z trzecim i czwartym samochodem wiemy
przecież, że przemieszczenie
może być równe zeru (i wówczas wektorowa prędkość średnia
jest równa zeru) a droga
może być większa od zera (i taką będzie prędkość średnia policzona w
postaci skalarnej
). Dlatego rozróżniam te dwie wielkości i wartość wektora prędkości średniej
oznaczam
a „skalarną” prędkość średnią jako
.
Podkreślmy jeszcze, że wszystkie powyższe wielkości (wektorowe i skalarne) będą miały konkretne
liczbowe wartości wyrażone w odpowiednich jednostkach. Wynikają one z podzielenia długości
przez czas. W układzie SI jest to [m/s], ale jak wiesz ogólnie dozwolone są również inne jednostki –
na przykład „motoryzacyjne” [km/h]. Dodać należy, że czasami wartość prędkości nazywa się
szybkością.
Nie bądź przerażony, że tyle rodzajów prędkości wymieniłem wcześniej. Podobnie jak z
przesunięciami ważne abyś rozumiał znaczenie tych pojęć – z jakich wielkości fizycznych i
operacji matematycznych powstają. Jak widzisz każda z nich ma sens praktyczny i masz z nimi do
czynienia na co dzień. W zależności od sytuacji będziemy się nimi stosownie posługiwać. Wiele
podręczników nie rozpisuje tak dokładnie zagadnień przesunięć i prędkości. Stąd często biorą się
nieporozumienia w rozwiązywaniu zadań.
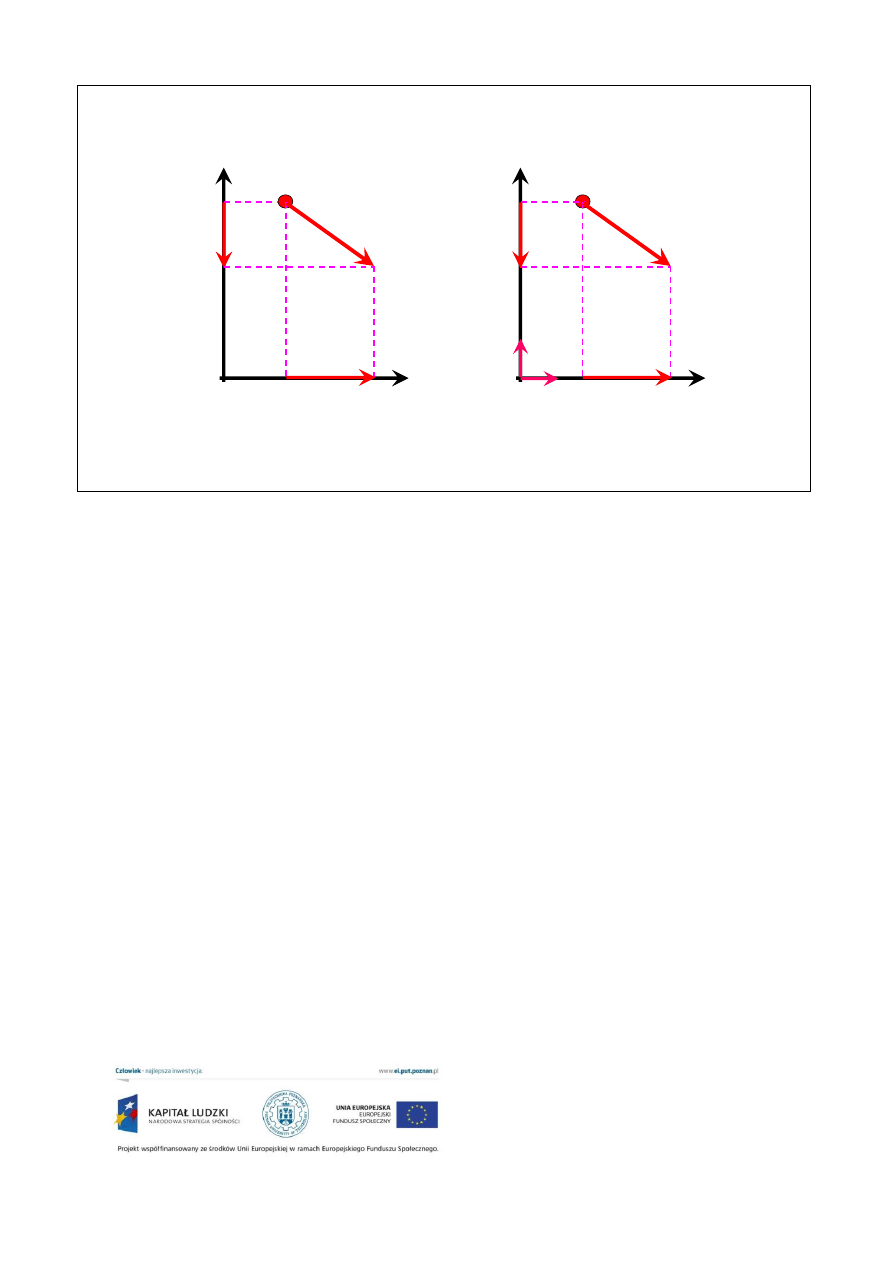
Prędkości jako wektory również możemy rzutować na osie układu współrzędnych otrzymując
stosowe składowe. Na rysunku przedstawiam taki rozkład dla prędkości chwilowej.
20
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
X
x
V
Y
Y
x
V
i
ˆ
y
V
j
ˆ
jˆ
iˆ
X
V
y
V
V
Ponownie składowa pionowa ma zwrot przeciwny do osi Y. Obie kładowe
oraz
wyznaczamy
zgodnie z zasadami prostopadłego rzutowania końca i początku wektora na osie X i Y. Z kolei
każdą taką składową możemy wyrazić za pomocą wektorów kierunkowych
oraz :
Oczywiście wektor
możemy zawsze znów „złożyć” ze sumy składowych:
Zapamiętaj ten „złożeniowy” wzór. Wkrótce nam się przyda! Minusy przed wartością
ponownie
wynikają z przeciwnego zwrotu odpowiadającej jej składowej w stosunku do osi Y.
Jak każdy wektor, również „wektorową” prędkość średnią
możemy rozłożyć na składowe
oraz
zgodnie z zasadami prostopadłego rzutowania końca i początku wektora na osie X i Y.
Obowiązują tutaj wzory analogiczne do wcześniejszych.
21
Kinematyka
Adam Buczek FIZYKA bez RYZYKA
Politechnika Poznańska Wydział Fizyki Technicznej
Nie przerażaj się powyższymi równaniami wektorowymi. Tak naprawdę rachunki dla wektora
wodzącego, jego różniczki, przemieszczeń i prędkości są do siebie bardzo podobne. Operujesz tutaj
obiektami geometrycznymi, zatem musisz „uszanować” ich kierunki i zwroty. Ten „szacunek”
okazujesz stosując wektory kierunkowe i rozróżniając czym jest wektor a czym jego wartość.