Pomiar prędkości lokalnej i średniej płynu
1
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Ćwiczenie 9
POMIAR PRĘDKOŚCI LOKALNEJ I ŚREDNIEJ PŁYNU
9.1. Wprowadzenie
Jeżeli w jednostajnym przepływie płynu z prędkością v
0
, w którym ciśnienie wynosi
p
0
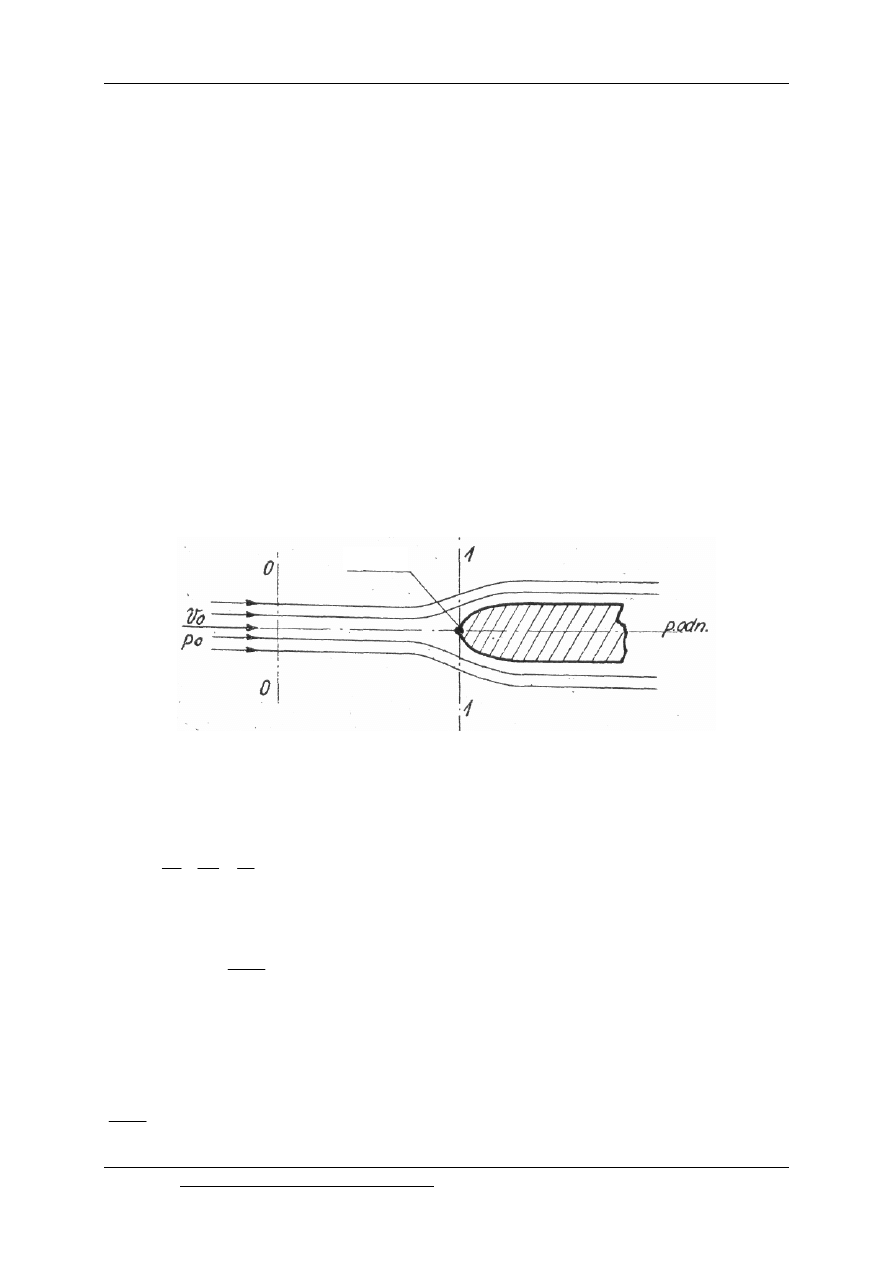
, znajdzie się przeszkoda w postaci zanurzonego ciała, to bezpośrednio przed nią następuje
spiętrzenie przepływu oraz opływ dookoła tej przeszkody.
W punkcie A znajdującym się w środku obszaru spiętrzenia, zwanym punktem
natarcia prędkość przepływu jest równa zeru: v
1
= 0. W pewnej dostatecznie dużej odległości
przed przeszkodą prędkość przepływu jest równa prędkości przepływu niezakłóconego v
0
,
a ciśnienie jest równe ciśnieniu p
0
. Ciśnienie w punkcie natarcia oznaczamy przez p
1
(rys.9.1).
Rys. 9.1. Opływ ciała stałego strumieniem płynu
Wówczas dla rozpatrywanej linii prądu równanie Bernoulliego ma postać:
2
0
0
1
p
v
p
2g
+
=
g
g
(9.1)
Stąd:
2
0
1
0
v
p
p
2
r×
=
+
(9.2)
gdzie:
p
1
- ciśnienie całkowite,
p
0
- ciśnienie statyczne,
2
0
v
2
r×
- ciśnienie dynamiczne.
v
1
=0, p
1
2
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Pod pojęciem ciśnienia statycznego rozumiemy jednostkową siłę powierzchniową,
z jaką działają na siebie dwa stykające się elementy przepływającego płynu, które znajdują się
w danej chwili w rozpatrywanym punkcie przestrzeni.
Ciśnienie dynamiczne jest to jednostkowa siła powierzchniowa, jaką przepływający
płyn wywiera na ciało w nim się znajdujące.
Przekształcając zależność (9.2) otrzymamy wzór określający prędkość niezakłóconego
strumienia płynu:
(
)
1
0
d
0
2 p
p
2p
v
-
=
=
r
r
(9.3)
Prędkościomierzami piętrzącymi /spiętrzającymi/ nazywamy przyrządy służące do
pomiaru miejscowych prędkości przepływu, których zasada pomiaru opiera się na
proporcjonalności miejscowej prędkości przepływu do pierwiastka kwadratowego zmierzonej
bezpośrednio wysokości ciśnienia dynamicznego lub różnicy wysokości ciśnienia całkowitego
i ciśnienia statycznego. Jeżeli więc w punkcie spiętrzenia rozpatrywanego ciała ustawionego
w przepływie wywiercony zostanie niewielki otwór o osi prostopadłej do powierzchni ciała,
wówczas ciśnienie wewnątrz tego otworu będzie równe p
1
, a wielkość jego może być
zmierzona przez doprowadzenie go do manometru. Na tej zasadzie oparty jest pomiar ciśnienia
całkowitego. Najprostszym przyrządem służącym do pomiaru tego ciśnienia jest tzw. rurka
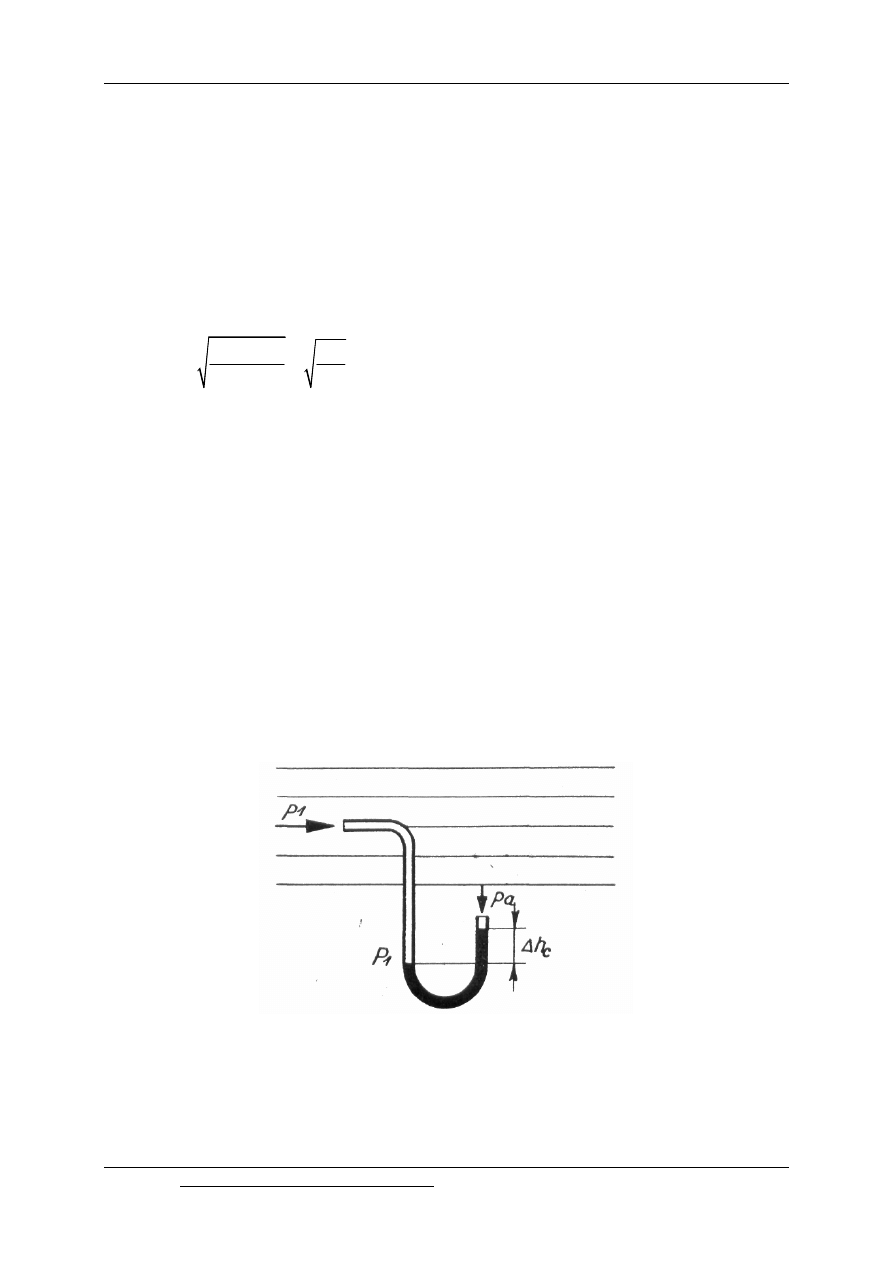
Pitota. Jest to zwykła rurka zgięta pod kątem prostym, którą skierowuje się jednym końcem
równolegle przeciw przepływowi, a drugi koniec łączy się z manometrem (rys.9.2).
Rys. 9.2. Zasada pomiaru ciśnienia całkowitego za pomocą rurki Pitota
Rozpatrzmy obecnie zasadę pomiaru ciśnienia statycznego. Niech na ścianie ciała sztywnego,
znajdującego się w przepływie, będzie wykonane wgłębienie w kształcie rowka o niewielkiej
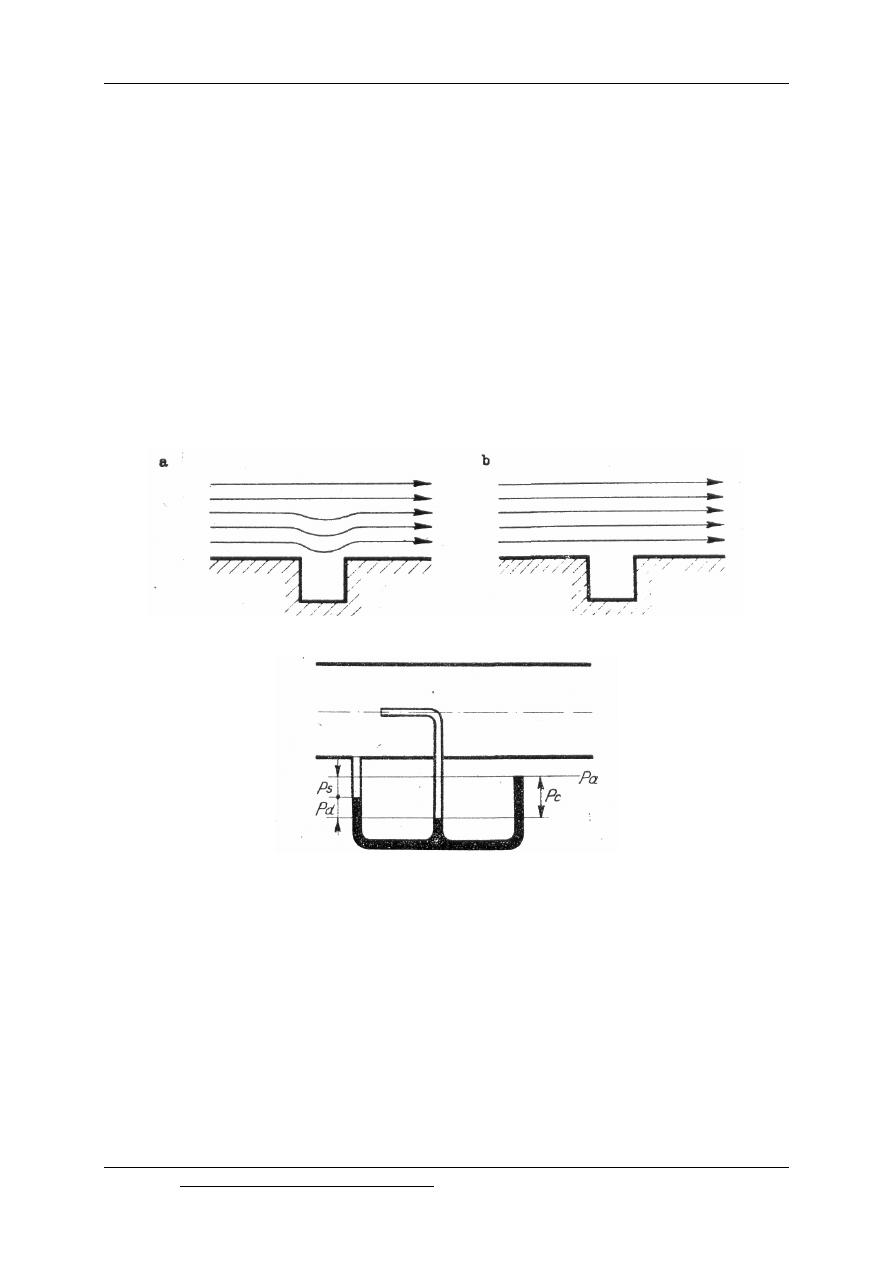
szerokości. W pierwszej chwili przy krawędziach będą tworzyły się wiry (rys.9.3a),
Pomiar prędkości lokalnej i średniej płynu
3
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
a następnie po ich oddaleniu się linie prądu przybiorą kształt uwidoczniony na rysunku
(rys.9.3b). Część płynu, która znalazła się we wgłębieniu jest - praktycznie biorąc –
w spoczynku. Ciśnienie tu panujące jest równe ciśnieniu statycznemu w płynie
przepływającym nad wgłębieniem. Gdyby istniała różnica ciśnień w płynie znajdującym się
w rowku i nad rowkiem, to musiałby nastąpić ruch w kierunku ciśnienia mniejszego, czego
doświadczenie nie potwierdza. Jeżeli teraz wnętrze tego wgłębienia połączymy
z manometrem, to będzie można zmierzyć wielkość ciśnienia statycznego, panującego
w przepływie w danym miejscu przy ścianie ciała sztywnego.
W technice do pomiarów ciśnienia statycznego łączy się manometr z otworami na
bocznej powierzchni walcowej. Zasadę pomiaru ciśnienia statycznego, dynamicznego
i całkowitego wyjaśnia rys. 9.4.
Rys. 9.3. Opływ wgłębienia w ściance
Rys. 9.4. Zasada pomiaru ciśnienia statycznego, dynamicznego i całkowitego
Pomiar ciśnienia statycznego i dynamicznego
Z inżynierskiego punktu widzenia interesuje nas zazwyczaj wartość prędkości
średniej, charakteryzującej przepływ płynu przez dany przewód. Przy pomiarach tego
ostatniego parametru przepływu należy mieć świadomość istotnej różnicy jakościowej,
wynikającej z charakteru samego przepływu /laminarny względnie turbulentny/.
Dla przepływu laminarnego, a więc takiego, w którym cząsteczki płynu
przemieszczają się po torach równoległych, znane jest ścisłe prawo rozkładu prędkości w
funkcji promienia.
4
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Np. dla przepływu w rurze:
( )
(
)
2
2
p
v r
R
r
4 L
D
=
-
h×
(9.4)
gdzie: r - odległość od osi rurociągu.
Na podstawie znajomości funkcji (9.4) potrafimy określić wielkość prędkości v
max
(tzn. prędkości w osi rurociągu) oraz wartości prędkości średniej
sr
max
1
v
v
2
=
.
Do pomiaru interesującej nas wartości lokalnej prędkości możemy zastosować rurki
piętrzące różnicowe, np. rurkę Prandtla, rurkę Brabbe-Rosenüllera (patrz rozdz. 9.2.1 i 9.2.2).
Inaczej zagadnienie to przedstawia się dla przypadku określania prędkości średniej dla
przepływu turbulentnego. Nie znamy tu ścisłego prawa rozkładu prędkości w funkcji
promienia. Traci również sens pojęcie ciśnienia statycznego ze względu na fakt istnienia
prędkości pulsacji oraz nieuporządkowanego ruchu cząsteczek płynu.
Stosowanie przez wielu badaczy dla przepływu turbulentnego różnicowych rurek
piętrzących powoduje w konsekwencji znaczne błędy pomiaru (rzędu 20 %). Chcąc zmierzyć
średnią prędkość ruchu burzliwego, należy przeprowadzić tzw. sondowanie rurociągu za
pomocą rurek piętrzących, np. rurki Pitota (patrz rozdz. 9.2.3).
9.2.
Omówienie przyrządów i metod pomiarowych
9.2.1. Rurka Prandtla /rys.9.5/
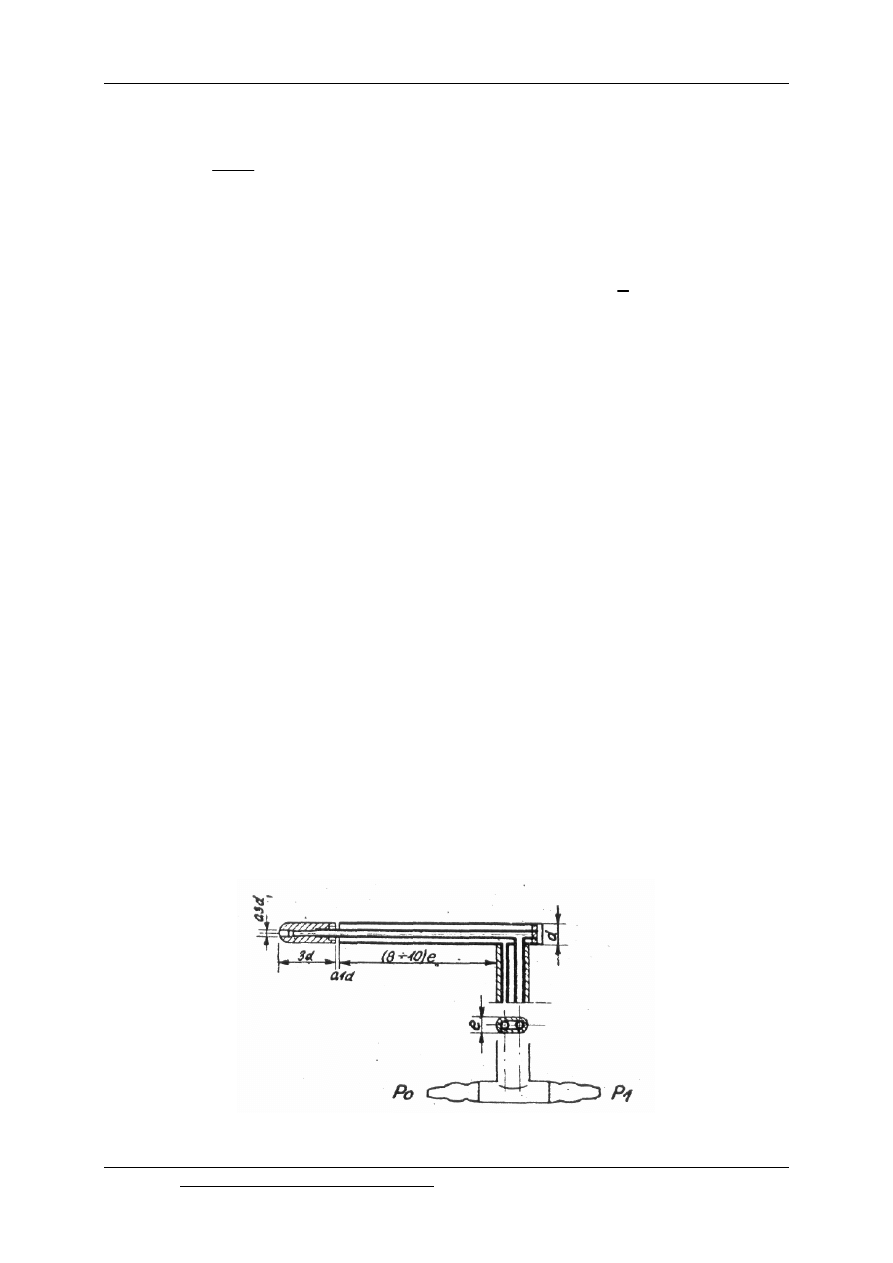
Rurka piętrząca Prandtla o średnicy zewnętrznej d posiada półkulistą główkę
zwróconą w czasie pomiaru przeciwnie do kierunku przepływu. Odbiór ciśnienia statycznego
odbywa się na pobocznicy rurki za pomocą szczeliny piezometrycznej o szerokości 0,1 d,
znajdującej się w odległości 3d poza punktem spiętrzenia i w odległości (8
¸10)e przed
trzonem przyrządu.
Rys. 9.5. Rurka Prandtla
Pomiar prędkości lokalnej i średniej płynu
5
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
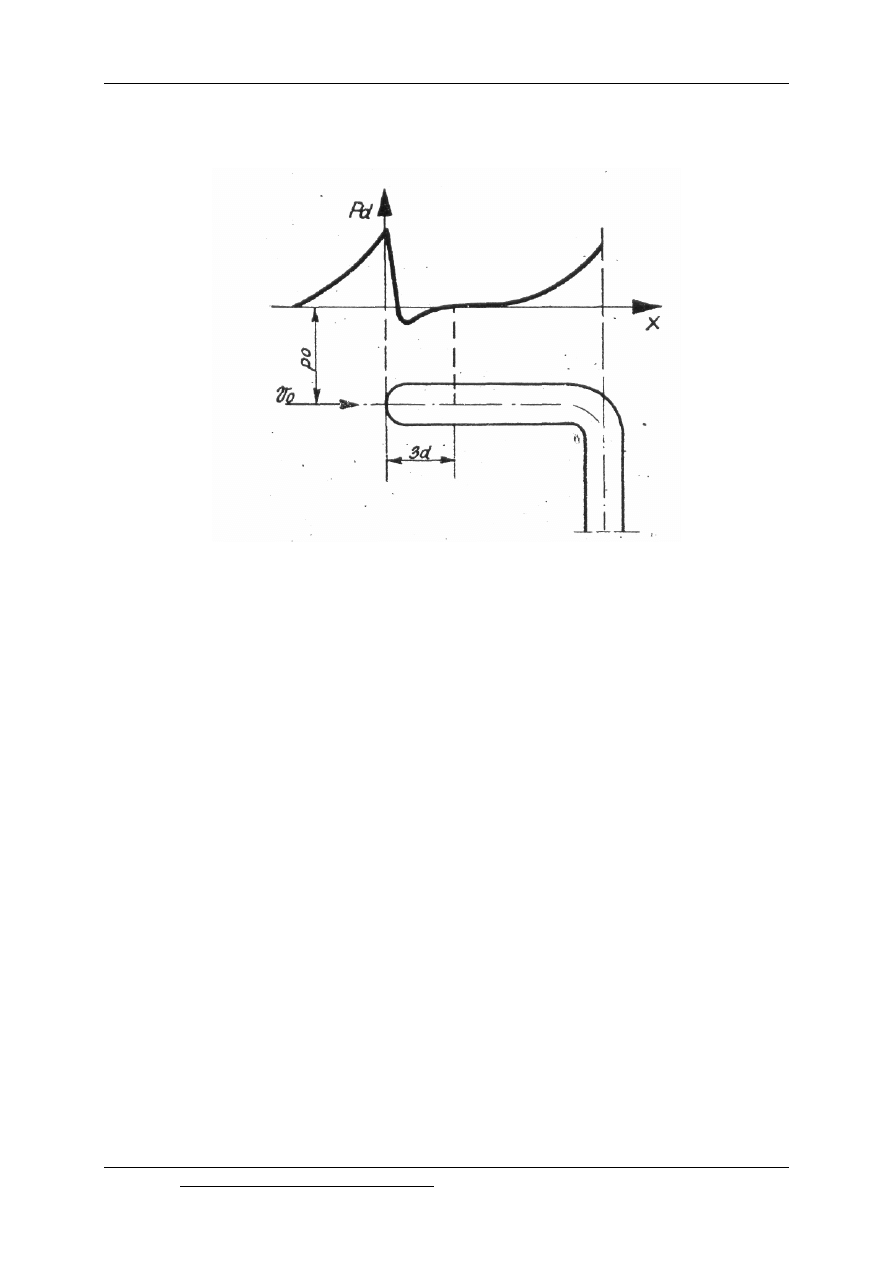
Położenie szczeliny piezometrycznej zależy od rozkładu ciśnienia wzdłuż poziomej
gałęzi rurki (rys.9.6).
Rys. 9.6. Rozkład ciśnienia p
d
wzdłuż rurki Prandtla
Jak wynika z tego wykresu, ciśnienie przed rurką piętrzącą wzrasta, osiągając
maksimum bezpośrednio u wlotu do rurki. Następnie ciśnienie gwałtownie maleje nieco-
poniżej wartości p, a potem łagodnie wzrasta, osiągając wartość p w przekroju, w którym
następuje odbiór ciśnienia statycznego. W dalszym ciągu na skutek istnienia trzona następuje
ponowny wzrost ciśnienia. Najczęściej używa się rurek wykonanych z mosiądzu - dla
temperatur płynu t < 500°C - lub ze stali chromoniklowej przy wyższych temperaturach.
Chcąc uniknąć wywołanych przez rurkę zaburzeń strumienia płynu, wpływających na jakość
pomiaru, należy spełnić warunek d ≤ 0,01·D (D - średnica wewnętrzna rurociągu). Ponieważ
wartości mierzonej różnicy ciśnień są małe, do pomiarów za pomocą rurek spiętrzających
różnicowych należy stosować czułe mikromanometry.
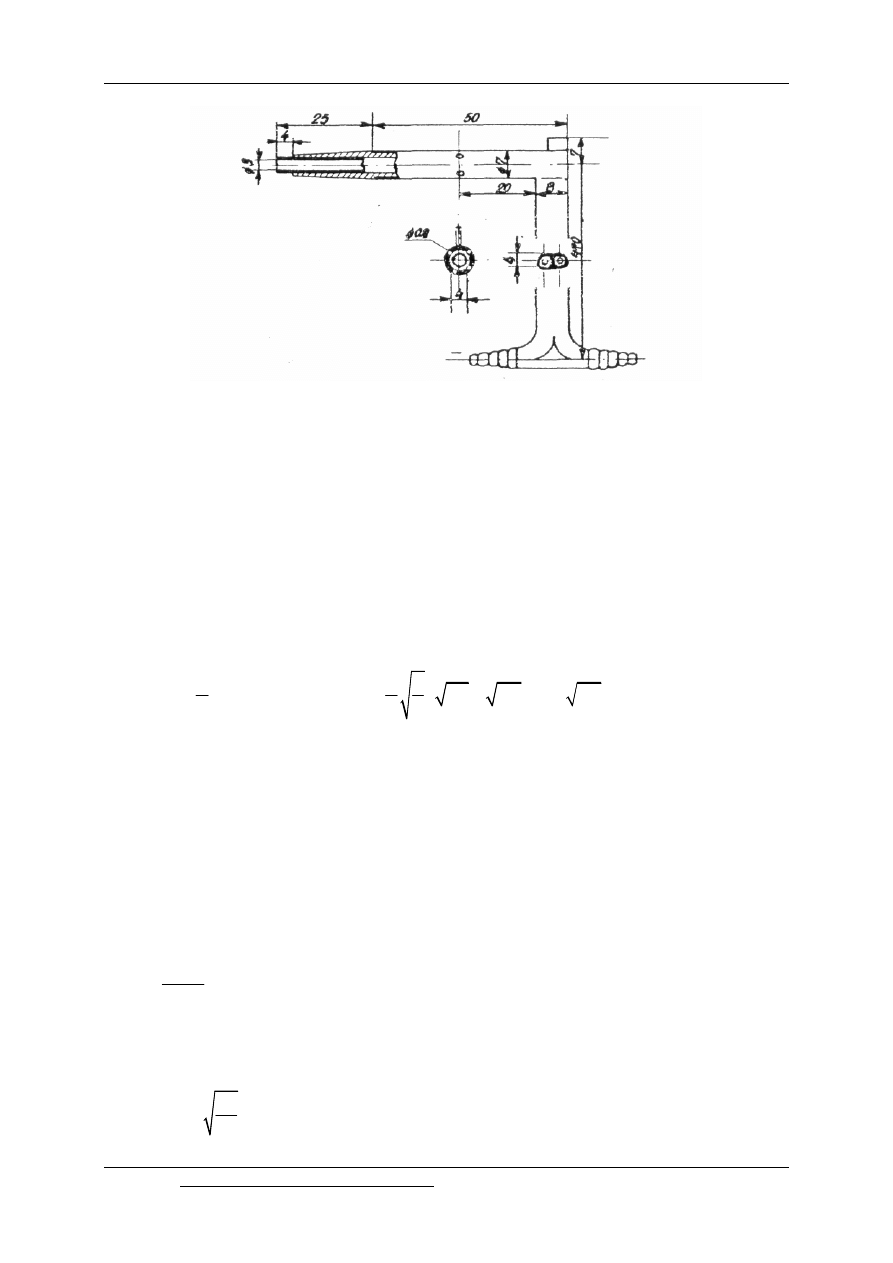
9.2.2. Rurka Brabbe-Rosenmüllera
Rurka Brabbe-Rosenmüllera jest przyrządem najczęściej używanym w Anglii i USA,
mniej rozpowszechnionym w Europie. Założenia budowy tego przyrządu są analogiczne jak
w przypadku rurki Prandtla.
Głowica tej rurki wykonana jest w kształcie ściętego stożka, cztery otwory na
powierzchni cylindrycznej końcówki służą do odbioru ciśnienia statycznego.
6
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Rys. 9.7. Rurka Brabbe-Rosenmüllera
9.2.3. Pomiar pośredni prędkości ruchu burzliwego płynu za pomocą rurek
spiętrzających
Chcąc mierzyć średnią prędkość ruchu burzliwego za pomocą rurek piętrzących,
mierzących prędkość lokalną, należy przeprowadzić tzw. sondowanie rurociągu. Przy
dokładnych pomiarach należy podzielić pole rozpatrywanego przekroju na części
o jednakowych powierzchniach i wyznaczyć prędkości w odpowiednich polach. Średnia
prędkość przepływu płynu wynosi wówczas:
(
)
(
)
s
1
2
3
n
d1
d 2
dn
1
1 2
v
v
v
v
... v
p
p
...
p
n
n
=
+
+
+ +
=
+
+ +
r
(9.5)
W celu wyznaczenia średniej prędkości przepływu przez rurociąg o przekroju
kołowym pole przekroju dzieli się na n części o jednakowych powierzchniach okręgami
zakreślonymi ze środka rurociągu. Pomiary prędkości wykonuje się wzdłuż linii
prostopadłych względem siebie średnic, w punktach dzielących każdy z poszczególnych
pierścieni na dwie części o jednakowych polach.
Dzieląc pole każdego kołowego przekroju rurociągu na 2n części o jednakowych
polach, otrzymujemy:
(
) (
)
(
)
2
2
2
2
2
2
2
2
1
2
1
3
2
2n 1
R
r
r
r
r
r
...
R
r
2n
-
p×
= p× = p
-
= p
-
= = p
-
(9.6)
Korzystając z powyższej zależności promienie okręgów, na których muszą znajdować
się wykonane punkty pomiarowe należy obliczać ze wzorów:
i
i
r
R
,
i 1,2,...,2n 1
2n
=
=
-
(9.7)
Pomiar prędkości lokalnej i średniej płynu
7
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
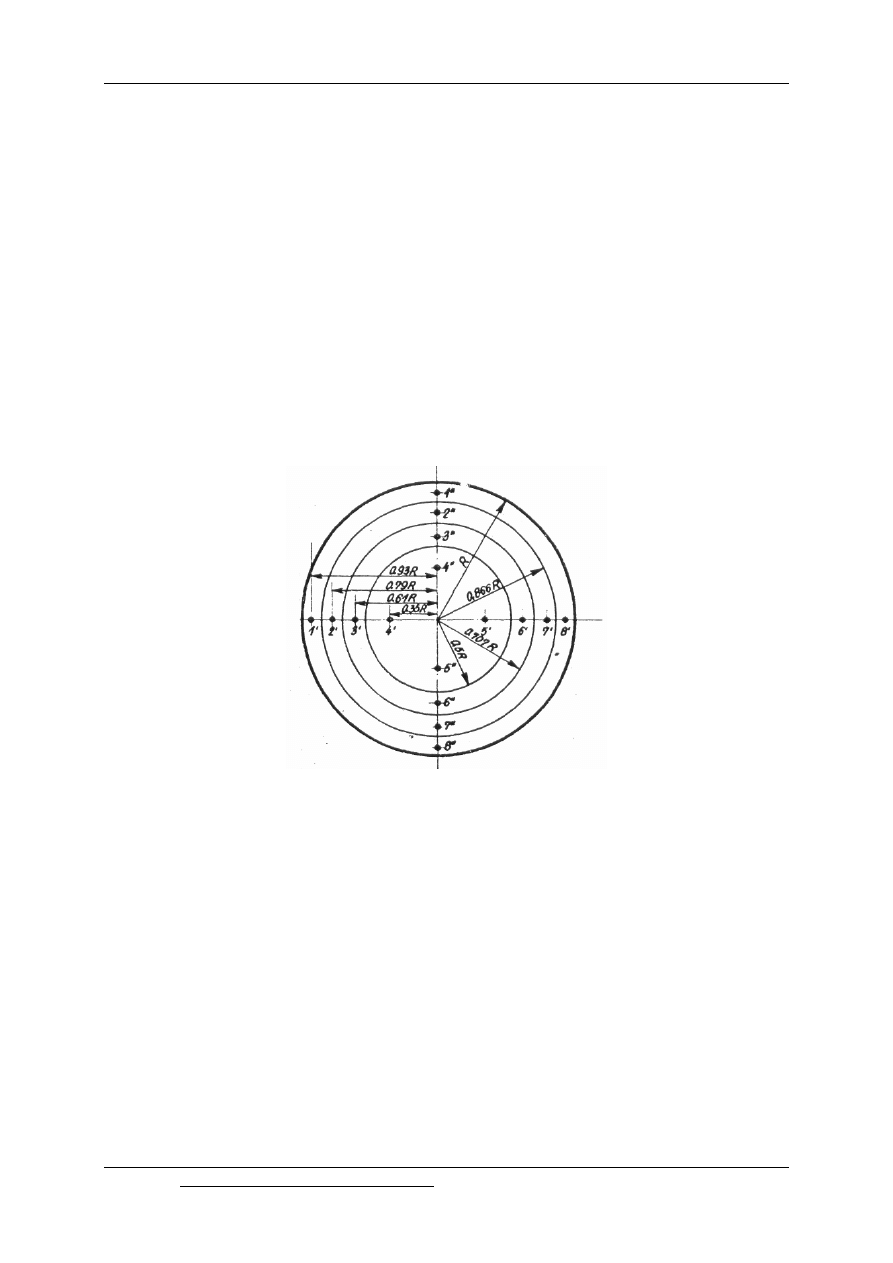
Przykładowo, jeżeli pole przekroju poprzecznego rurociągu podzielimy na cztery
części o równych polach, to punkty pomiarowe leżące w środkach tych pól będą leżały na
okręgach dzielących tak wydzielone obszary na połowy. W efekcie otrzymamy podział całego
przekroju na osiem części. Okręgi o numeracji parzystej będą okręgami podziału pól, okręgi
o numeracji nieparzystej będą wyznaczały położenie punktów pomiarowych.
2n 8
= - ilość części o jednakowych polach
1
2
3
4
5
6
7
8
r
0,35 R
r
0,5 R
r
0,61 R
r
0,707 R
r
0,79 R
r
0,86 R
r
0,93 R
r
R
=
=
=
=
=
=
=
=
Pomiar natężenia przepływu za pomocą rurek piętrzących jest uciążliwy i długotrwały.
Ponadto można go dokonywać przy spełnianiu warunku stałości natężenia przepływu
w czasie pomiaru.
Rys. 9.8. Podział pola przekroju poprzecznego rurociągu kołowego na cztery części o równych polach
9.2.4. Źródła błędów wskazań rurek piętrzących
Główne źródła błędów wskazań różnicowych rurek piętrzących są następujące:
- Trudność ustalenia właściwego położenia rurki względem kierunku przepływu, a zatem
możliwość występowania przy pomiarze odchylenia poziomej gałęzi rurki o kąt
a od
kierunku miejscowej prędkości przepływu. Rurka Prandtla charakteryzuje się dużą
niezależnością wskazań od kąta odchylenia
a, błąd wskazań w granicach a = ±17° nie
przekracza 1 %, Rurka Brabbe-Rosenmüllera przy nieprawidłowym położeniu daje
stosunkowo duże błędy wskazań ciśnienia dynamicznego dochodzące, przy kącie
nachylenia
a = 15° do 6 %.
8
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
- Przy pomiarze cieczy o dużej lepkości nie można pominąć wpływu lepkości płynącej
cieczy. Wzrost lepkości powoduje dodatnie błędy wskazań. Dla Re ≤ 100 (Re odniesione
do średnicy rurki piętrzącej) stosuje się wzór Barkera:
2
0
d
v
3
p
1
2
Re
r×
æ
ö
=
+
ç
÷
è
ø
(9.8)
- Przy pomiarze prędkości miejscowych zmieniających się okresowo o Dv
0
w kierunku
przepływu należy pamiętać o tym, że zmiana prędkości o ±
Dv
0
powoduje odpowiednią
zmianę ciśnienia dynamicznego w stosunku kwadratowym, tj.
(
)
2
d
0
0
p
v
v
2
r
=
± D
(9.9)
Gdy wartości chwilowej prędkości wahają się sinusoidalnie, powodując zmianę
ciśnienia dynamicznego w granicach ±10 %, błąd wskazania p
d
wynosi około 2 %. Przy
przepływach burzliwych charakteryzujących się wysokimi wartościami Re, na skutek silnego
wpływu pulsacji poprzecznych prędkości, błąd wskazań p
d
może dojść do 4 %.
9.2.5. Kule piętrzące
Kula piętrząca służy do pomiaru wartości i kierunku miejscowych prędkości
w przepływach trójwymiarowych. Główną zaletą kuli piętrzącej jest to, że umożliwia ona
pomiar prędkości miejscowych w obszarze o nieznanym polu prądu. Ponadto kula piętrząca
jest mniej wrażliwa na wpływ ścian ograniczających płynącą ciecz. Na rys. 9.9 przedstawiono
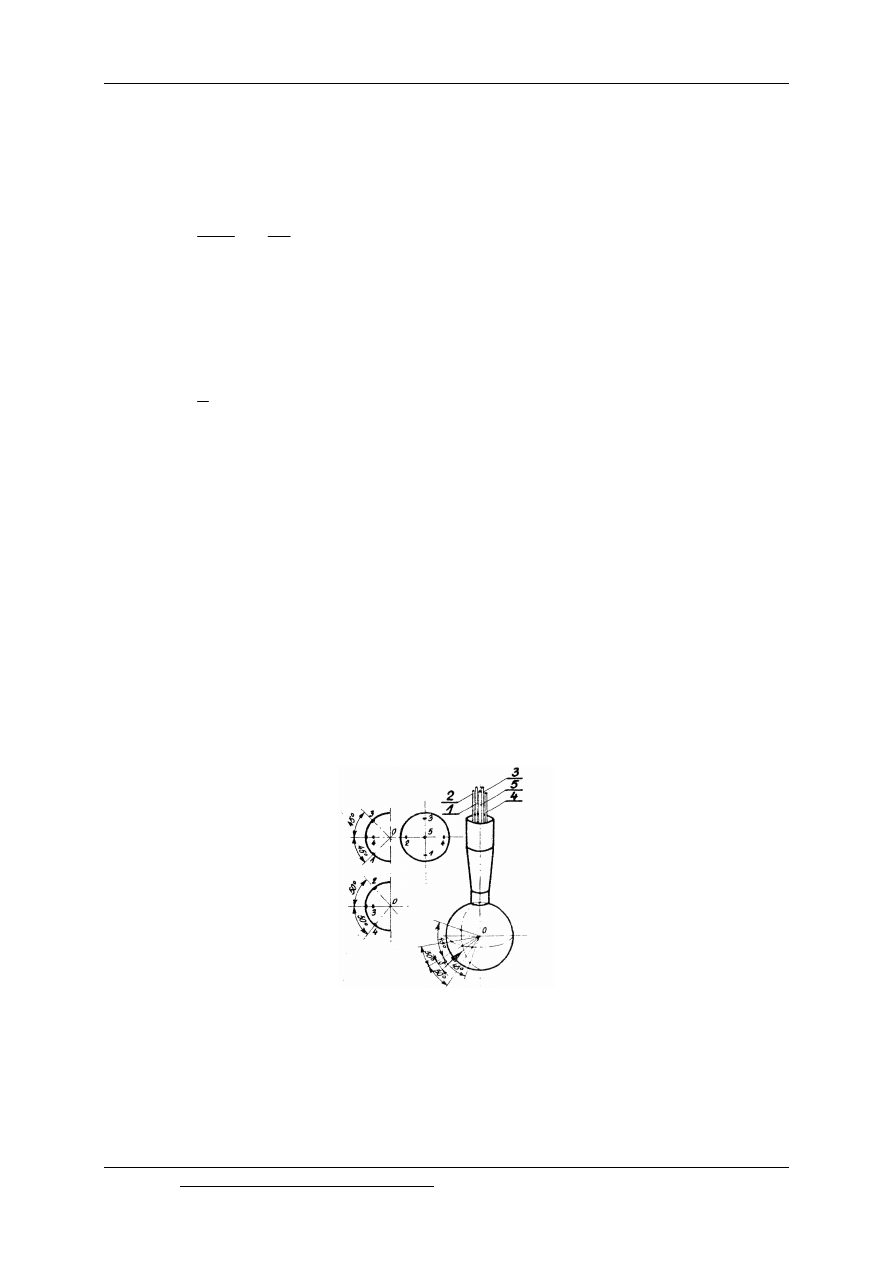
kulę piętrzącą w widoku i trzech rzutach prostokątnych.
Rys. 9.9. Kula piętrząca
W ściance wydrążonej kuli o średnicy zewnętrznej 8÷10 [mm] znajduje się pięć
otworów piezometrycznych 1÷5, przy czym otworki 1÷4 rozmieszczone są symetrycznie
w dwu wzajemnie prostopadłych płaszczyznach: płaszczyźnie południkowej przechodzącej
przez łuk º
13 i płaszczyźnie równikowej przechodzącej przez łuk º
24 .
Pomiar prędkości lokalnej i średniej płynu
9
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Odległość kątowa otworków 2 i 4 wynosi 100°, a odległość kątowa otworków 1 i 3
wynosi 90°. Otworek 5 znajduje się w punkcie przecięcia się łuków º
13 i º
24 . Promień kuli
przechodzący przez oś otworu 5 nazywa się osią dynamiczną kuli piętrzącej.
Położeniem zerowym kuli piętrzącej nazywamy położenie, przy którym oś
dynamiczna kuli pokrywa się z kierunkiem prędkości miejscowej. Otworki piezometryczne
połączone są za pomocą metalowych rurek z piezometrami lub manometrami. Kula jest
osadzona na końcu wydrążonego trzonka, którego położenie może być odczytywane na
podziałce kątowej tarczy. Przed przystąpieniem do pomiarów kulę piętrzącą należy poddać
wzorcowaniu. W czasie wzorcowania kulę piętrzącą ustawia się w takim położeniu, aby
ciśnienia w punktach 2 i 4 były jednakowe, a zatem by różnica ciśnień p
2
– p
4
= 0. Wówczas
wektor prędkości miejscowej v
r
leży w głównej, południkowej płaszczyźnie kuli. Położenie
kuli ustala się przez zamocowanie tarczy. Wzorcowanie kuli odbywa się przy różnych kątach
d pochylenia trzonka w głównej płaszczyźnie południkowej, a zatem przy y = 0. Dla różnych
wartości kąta nachylenia
d wyznaczamy doświadczalnie wartości następujących
współczynników prędkości:
1
0
2
0
4
0
v1
v2
v4
2
2
2
3
0
5
0
d
v3
v5
2
2
2
p
p
p
p
p
p
k
k
k
v
v
v
2
2
2
p
p
p
p
p
k
k
v
v
v
2
2
2
-
-
-
=
=
=
=
r
r
r
-
-
=
=
=
r
r
r
Otrzymawszy te wartości obliczamy wartość współczynnika kierunkowego k
d
dla
różnych kątów nachylenia:
v3
v1
3
1
3
1
v5
v2
5
2
5
2
k
k
p
p
h
h
k
k
k
p
p
h
h
d
-
-
-
=
=
=
-
-
-
(9.10)
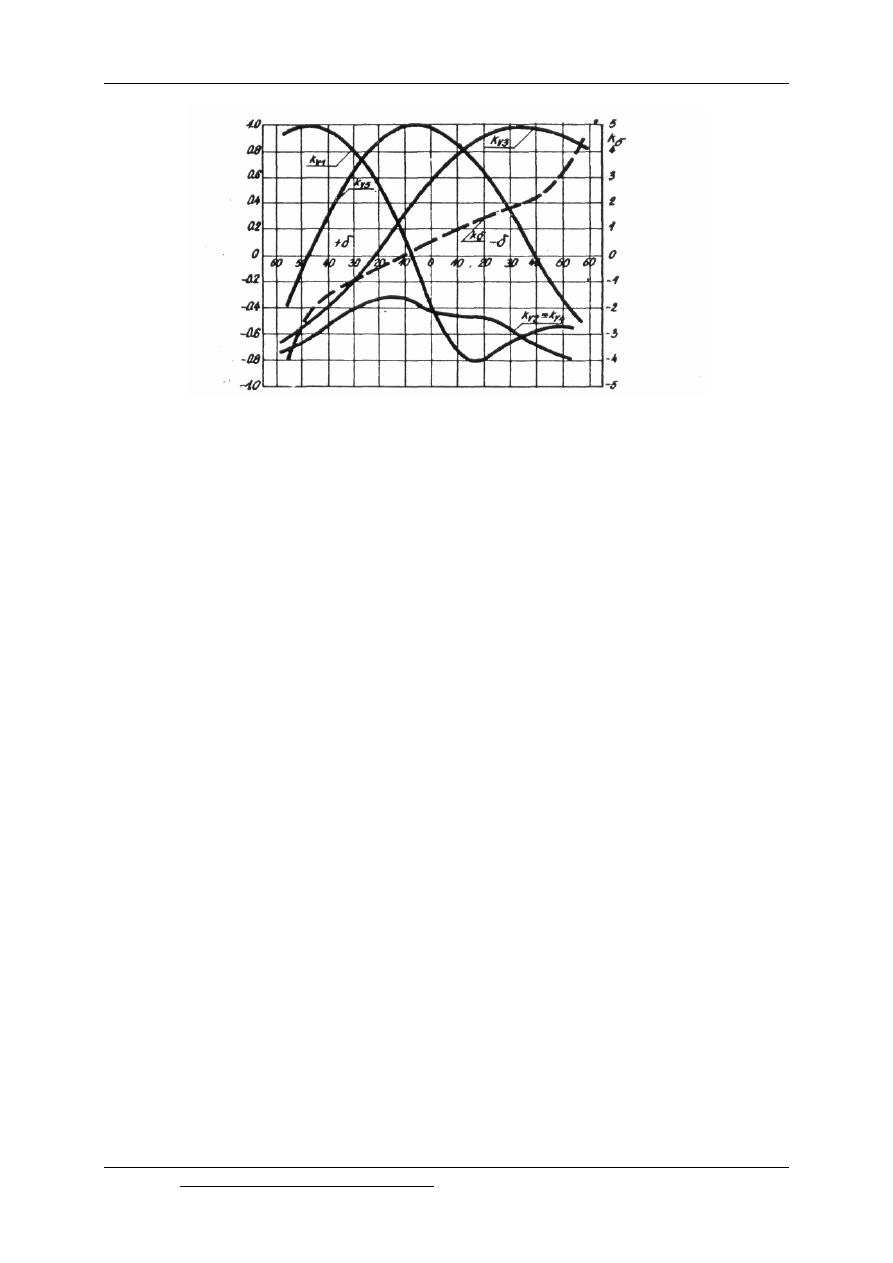
Wyniki kolejnych pomiarów w czasie wzorcowania ujęto na wykresie 9.10.
Celem dokonania pomiaru kierunku i wartości miejscowych prędkości wprowadzamy
kulę piętrzącą w obszar płynącego płynu i ustalamy jej położenie zerowe przez obrót dookoła
osi pionowego trzonka i jednoczesną obserwację manometru różnicowego, którego ramiona
są połączone z otworami piezometrycznymi 2 i 4. Gdy różnica ciśnień p
2
– p
4
= 0, ustalamy
położenie kuli i odczytujemy na tarczy wartość kąta
y. Następnie na manometrach
odczytujemy wysokości ciśnień h
1
, h
2
, h
3
, h
4
, h
5
i obliczamy wartość współczynnika
kierunkowego k
d
.
10
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Rys. 9.10. Krzywe wzorcowania kuli piętrzącej
Z wykresu k
d
= f(
d) wyznaczamy wartość kąta nachylenia d prędkości miejscowej
v względem dynamicznej osi kuli. W ten sposób położenie wektora prędkości w przestrzeni
jest określone położeniem kuli piętrzącej i wartościami kątów
d i y. Z wykresu 9.10
odczytujemy wartości współczynników prędkości k
v1
i k
v2
odpowiadające wartości kąta
nachylenia
d obliczamy wartości ciśnienia statycznego p i prędkości v.
Dokładność wskazań kuli piętrzącej zależy przede wszystkim od symetrii opływu względem
płaszczyzny południkowej przechodzącej przez łuk º
13 .
Dokładność pomiaru ciśnienia dynamicznego za pomocą kul piętrzących wynosi 4%,
a prędkości miejscowej około 2%. Ponieważ pomiar prędkości miejscowej za pomocą kuli
piętrzącej jest bardziej kłopotliwy niż za pomocą rurki piętrzącej, a dokładność pomiaru może
być obniżona wskutek asymetrii opływu, metodę tę stosujemy jedynie w przypadku
przepływu o nieznanym przebiegu linii prądu oraz przy wyraźnych zmianach kierunku
prędkości.
9.2.6. Anemometr skrzydełkowy
Widok przyrządu pokazano na rys. 9.11. Przyrząd jest przeznaczony do pomiaru
prędkości płynów w otwartych /w stosunku do wymiarów przyrządu/ przestrzeniach. Przyrząd
mierzy w zasadzie długość drogi gazu, który przypłynął prostopadle do płaszczyzny obrotu.
W celu uzyskania dużej czułości przyrządu konieczne jest zmniejszenie bezwładności jego
wirnika. Dlatego też elementy wirnika są bardzo lekkie, a przyrząd bardzo delikatny i podatny
na mechaniczne uszkodzenia. Przyrząd mierzy składową prędkości, prostopadłą do
płaszczyzny obrotu wirnika.
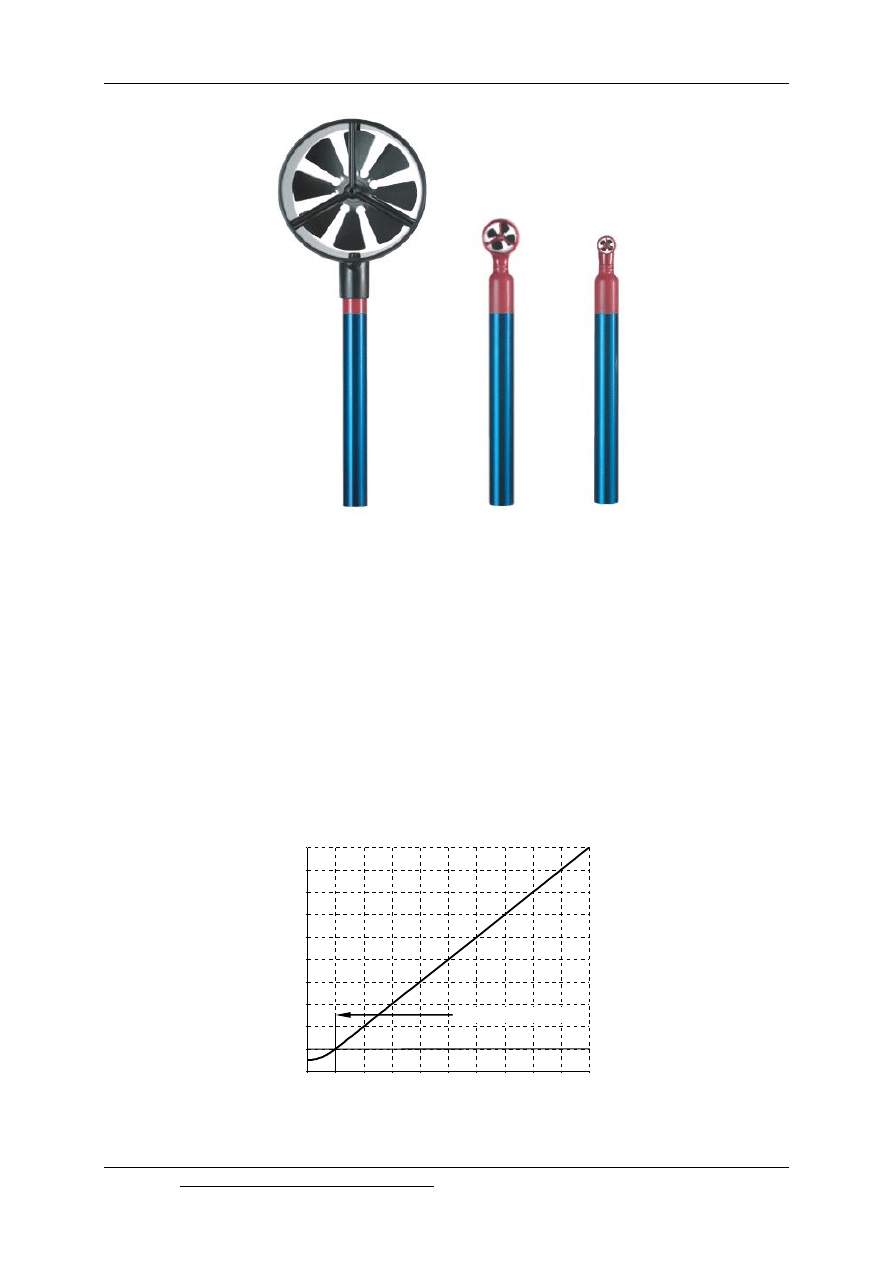
Pomiar prędkości lokalnej i średniej płynu
11
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Rys. 9.11. Widok anemometru skrzydełkowego firmy AHLBORN o rożnej średnicy głowicy
pomiarowej: a) 80 mm, b) 22 mm, c) 11 mm
Zasada działania anemometru skrzydełkowego polega na zamianie energii kinetycznej
przepływającej strugi gazu na ruch obrotowy wirnika pomiarowego. Prędkość obrotowa
wirnika jest proporcjonalna do prędkości przepływu gazu, a kierunek obrotów zależy od
kierunku przepływu. Informację o prędkości obrotów wirnika pomiarowego uzyskuje się
najczęściej dzięki odpowiednio usytuowanemu czujnikowi indukcyjnym, względem którego
przesuwają się krawędzie skrzydełek wirnika. Sygnał z czujnika, poddawane są analizie przez
układ pomiarowy. Możliwy jest pomiar chwilowej wartości prędkości (czas uśredniania
zwykle wynosi 1-2 [s]) lub wartość średnią w pewnym okresie czasu.
v
obl
[m/s]
v
rz
[
m
/s
]
Rys. 9.12. Charakterystyka anemometru skrzydełkowego
a)
b)
c)
obszar proporcjonalności
v
min
v
pmin
12
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Na rys 9.12 przedstawiono charakterystykę anemometru skrzydełkowego. Ze względu
na występowanie niewielkiego tarcia w łożyskach występuje pewien obszar nieczułości
przyrządów zależy od średnicy głowicy pomiarowej i wynosi 0,1-0,6 [m/s]. Występuje
również obszar nieliniowości charakterystyki anemometru, efekt ten może być
skompensowany przez układ pomiarowy. Zakres pomiarowy anemometrów ogranicza się do
30-40 [m/s] ze względu na ich delikatną budowę.
9.2.7. Anemometr czaszowy
Przyrząd ten jest jednym z podstawowych mierników stosowanych w meteorologii, do
pomiaru prędkości wiatru, ze względu na swoją mechaniczną odporność. Na rys. 9.13
pokazano schemat anemometru czaszowego.
Na osi (1) umocowane są cztery ramiona (2), na końcach których znajdują się czasze
(3) w postaci drążonych półkul. Przyrząd ustawia się osią obrotu prostopadle do kierunku
prędkości płynu, a więc mierzy on w zasadzie składową prędkości prostopadłą do swej osi,
lecz z dowolnego kierunku. Zasada pracy przyrządu polega na wykorzystaniu różnicy oporu
czołowego, który wywołują czasze kuliste w różnych położeniach.
Anemometr czaszowy ma duży obszar nieczułości, minimalna prędkość płynu
niezbędna do uruchomienia wirnika wynosi 1
¸2 [m/s]. Górna granica pomiarowa wynosi
około 50 [m/s], a w wykonaniach specjalnych - 100 [m/s]. Anemometr może być wyposażony
w tachometr. Najbardziej dogodną postacią tachometru jest prądnica elektryczna. W tym
przypadku wyniki pomiarów łatwo przekazać na dalsze odległości.
Rys. 9.13. Anemometr czaszowy: a) schemat, b) widok
a)
b)
Pomiar prędkości lokalnej i średniej płynu
13
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
9.2.8. Termoanemometr elektryczny (cieplny)
Anemometry cieplne znajdują zastosowanie przede wszystkim przy pomiarach
niewielkich prędkości przepływu niepalnych gazów. Zasada ich działania opiera się na
zależności pomiędzy ilością ciepła traconą przez nagrzany element pomiarowy a prędkością
chłodzącego go strumienia gazu. Ze względu na konstrukcję można termoanemometry
podzielić na dwie grupy.
Do pierwszej zaliczamy urządzenia, w których termoelement (cienki drut metalowy
lub powłoka) włącza się w charakterze jednej z gałęzi bezpośrednio w mostek pomiarowy.
Termoanemometry te mogą pracować tak przy stałej, jak i zmiennej temperaturze
termoelementu. Pomiar prędkości przepływu odbywa się przez pomiar zmiany oporu
termoelementu przy stałym natężeniu prądu zasilającego lub przez pomiar natężenia prądu
przy stałym oporze i stałej temperaturze termoelementu.
Do drugiej grupy należą urządzenia, składające się z podgrzewanego drutu i termopary
lub termistora mierzącego temperaturę tego drutu przy stałej mocy lub natężeniu prądu
zasilającego. Urządzenia tej grupy obarczone są znacznie większą bezwładnością w stosunku
do omówionych poprzednio. Czujniki termoelementów wykonane są z drutu platynowego
(niekiedy wolframowego lub niklowego) o średnicy 0,005
¸0,3 [mm]. Ze zmniejszeniem się
średnicy nici oporowej zmniejsza się jej bezwładność, ale równocześnie zmniejsza się jej
trwałość i wzrasta możliwość starzenia. Nić termoanemometru poddana jest obciążeniom
aerodynamicznym, zależnym; od stosunku jej długości do średnicy oraz obciążeniom
mechanicznym /udarowym/ pochodzącym od uderzających w nią twardych cząstek,
znajdujących się w przepływającym strumieniu. W wyniku drgań sondy, pojawiających się
w następstwie pulsacji prędkości przepływu strumienia, nić poddawana jest obciążeniom
dynamicznym, które mogą doprowadzić do jej zerwania. Jeżeli nawet obciążenie dynamiczne
nie spowoduje zerwania nici, to w jego następstwie pojawia się pulsacja oporu nici, która może
spowodować znaczne błędy pomiaru. W charakterze czujników znajdują również zastosowanie
cienkie, metaliczne powłoki naniesione na szklaną lub metaliczną powłokę. Posiadają one wiele
zalet w porównaniu z czujnikami wykonanymi z drutu. Zasadniczą wadą termoelementów,
ograniczającą znacznie zakres ich stosowania, jest reagowanie nie tylko na zmiany prędkości
gazu, ale również temperaturę i ciśnienie strumienia. Im wyższa temperatura termoelementu,
tym większa jest czułość urządzenia, a tym mniejszy wpływ na wskazania posiadają wahania
temperatury strumienia. Podwyższanie temperatury pracy czujnika jest jednak ograniczone ze
względu na możliwość zmiany struktury strumienia materiału, z którego został on wykonany.
14
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
Nić termoaneraometru można rozpatrywać jako walec (o znacznej, w porównaniu ze średnicą,
długości) wykonany z przewodnika elektrycznego. Przekazywanie ciepła od cylindra do
strumienia jest funkcją prędkości przepływu v oraz różnicy temperatur gazu i czujnika.
Temperaturę drutu t
d
, można wyznaczyć z równania:
(
)
(
)
2
d
g
q 0, 24 R I
t
t
k v
=
× × =
-
l +
(9.11)
gdzie:
v
k
2
c d
=
×r× ×
q - ilość ciepła oddawana przez nagrzane ciało czynnikowi w jednostce czasu,
t
g
- temperatura gazu,
R - opór nici,
I - natężenie prądu,
c
v
- ciepło właściwe gazu przy stałej objętości,
d - średnica drutu,
r - gęstość gazu,
l - współczynnik przewodnictwa cieplnego,
v - prędkość przepływu.
Przyjęte równanie dla obliczenia ilości oddanego ciepła przez nagrzaną prądem nić, po
uwzględnieniu przewodności warstwy przyściennej, przyjmie postać:
(
)
(
)
0.4
2
0.4
w
d
g
g
d
g
g
d
I R 1.35
t
t
2.2
t
t
v
æ
ö
× =
×l
-
+
×l
-
×
ç
÷
ç
÷
l
è
ø
(9.12)
gdzie:
l
w
- współczynnik przewodnictwa warstwy przyściennej,
l
g
- współczynnik przewodnictwa gazu.
Przy posługiwaniu się podanymi równaniami bilansu cieplnego (9.11) i (9.12) należy
wziąć pod uwagę, że są one słuszne wyłącznie dla warunków statycznych. Umieszczenie
nagrzanego walca w zmiennym strumieniu gazu prowadzi do nierówności pomiędzy ciepłem
dopływającym i odpływającym. W następstwie tego zmieni się temperatura walca.
W przypadku, gdy badany strumień posiada duże zmiany prędkości równanie bilansu
cieplnego jest następujące:
(
)
(
)
2
w
w
w
g
0
c
dR
0.24 I R
R
R
A b v
R
dt
× × =
-
+
+
a ×
(9.13)
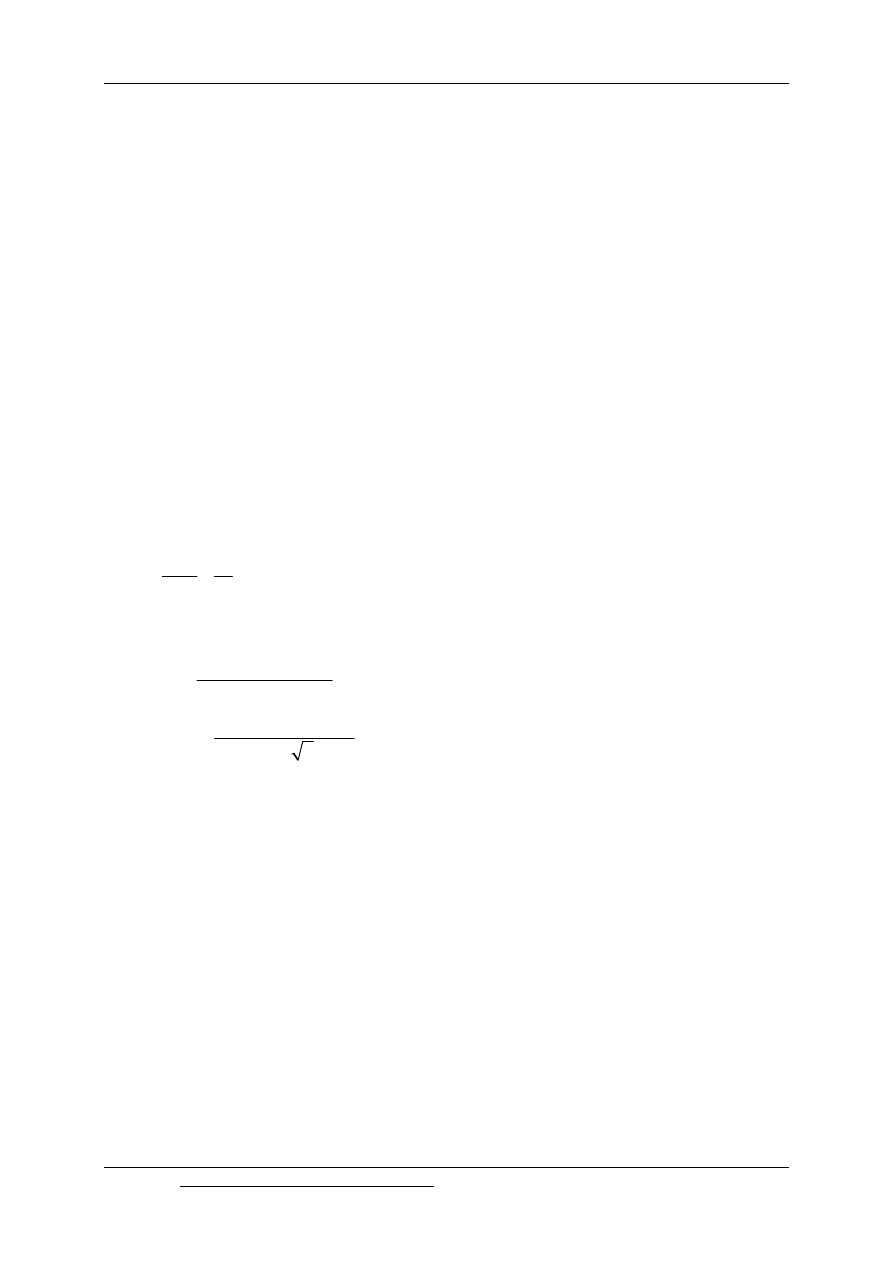
Pomiar prędkości lokalnej i średniej płynu
15
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
gdzie:
R
w
- opór nagrzanej nici,
R
g
- opór nici w temperaturze strumienia,
R
0
- opór nici w temperaturze 0°,
v - prędkość gazu,
a - współczynnik cieplny oporu,
c
w
- ciepło właściwe nici,
t - czas,
A, B- współczynniki zależne od własności fizycznych nici i gazu.
Lewa strona równania (9.13) wyraża wydzielające się w nici ciepło. Pierwszy i drugi
człon prawej strony równania przedstawia odpowiednio stratę ciepła przy chłodzeniu nici
w strumieniu oraz zmianę entalpii nici. Jeżeli założyć, że zmiany prędkości strumienia
w stosunku do jej średniej wartości są niewielkie, można dokonać linearyzacji równania
(9.13). Przyjmie ono wtedy postać:
( )
w
w
dR
1
R
f v
dt
M
+
=
(9.14)
gdzie:
(
)
( )
(
)
w
w
g
2
g
0
0
w
0
w
c
R
R
M
0.24
R R I
B
R R
R
f v
2 c
v
-
=
×a ×
× ×
×a ×
-
=
×
Z równania (9.13) wynika, że zmiana oporności przy małych i powolnych zmianach
prędkości strumienia zależy tylko od stałej M, która nazywa się stałą czasową bezwładności
cieplnej nici.
Jak wynika z przedstawionych równań przy zmianie prędkości strumienia v
(a w następstwie i t
d
) ulegnie zmianie tak natężenie prądu I, jak i opór termoelementu R.
W wyniku tego, że sygnał wychodzący w takim przyrządzie zwykle wyraża się w postaci
spadku napięcia na mostku pomiarowym, niezależność zmian natężenia prądu i oporu czyni
niemożliwym dany pomiar.
Dla wyeliminowania jednej ze zmiennych wielkości należy tak skonstruować zasilacz
całego przyrządu, aby natężenie prądu płynącego przez nagrzany termoelement było stałe bez
względu na jego opór. W tym przypadku wartość prędkości strumienia można określić, znając
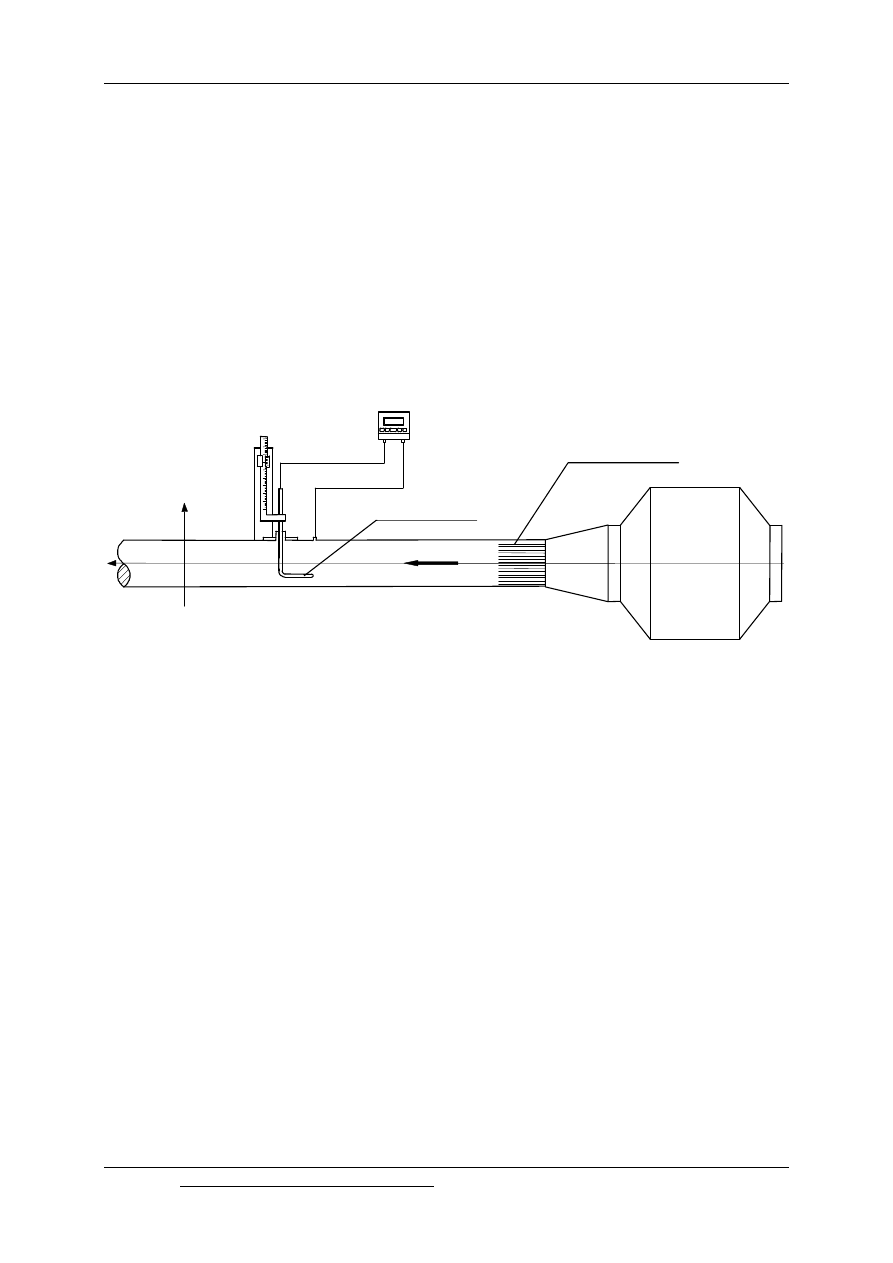
16
Pomiar prędkości lokalnej i średniej płynu
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
różnicę potencjałów na końcach termoelementu, temperaturę strumienia i charakterystykę
materiału termoelementu.
9.3. Stanowisko doświadczalne
Głównym elementem stanowiska jest rurociąg, przez który wymusza się przepływ
powietrza. W rurociągu znajduje się rurka Prandtla. Otworki piezometryczne rurki połączone
są z manometrami. Anemometr skrzydełkowy umożliwia wykonanie pomiarów prędkości
średniej. Celem, ćwiczenia jest wyznaczenie rozkładu prędkości w rurze o przekroju
kołowym i prostokątnym dla różnych liczb Reynoldsa.
rurka spiętrzająca
mikromanometr
różnicowy
wentylator
osiowy
prostownica strugi
r
Rys. 9.14. Schemat stanowiska pomiarowego
9.4. Opis ćwiczenia
Dokonać pomiaru prędkości lokalnych w wyznaczonych punktach przekroju
poprzecznego rury kołowej za pomocą rurki spiętrzającej Prandtla. Pomiary przeprowadzić
dla dwóch różnych natężeń przepływu.
Pomiar prędkości lokalnej i średniej płynu
17
download: http://www.mech.pk.edu.pl/~m52/pdf/[9_opis].pdf
10
4
10
5
10
6
10
7
1
6
1
8
1
9
1
10
1
7
1
11
1
12
1
13
1
n
n=f(Re)
1
n
= 2.1 lg(Re) – 1.9
Hydraulicznie gładka rura
staje się chropowatą
Re
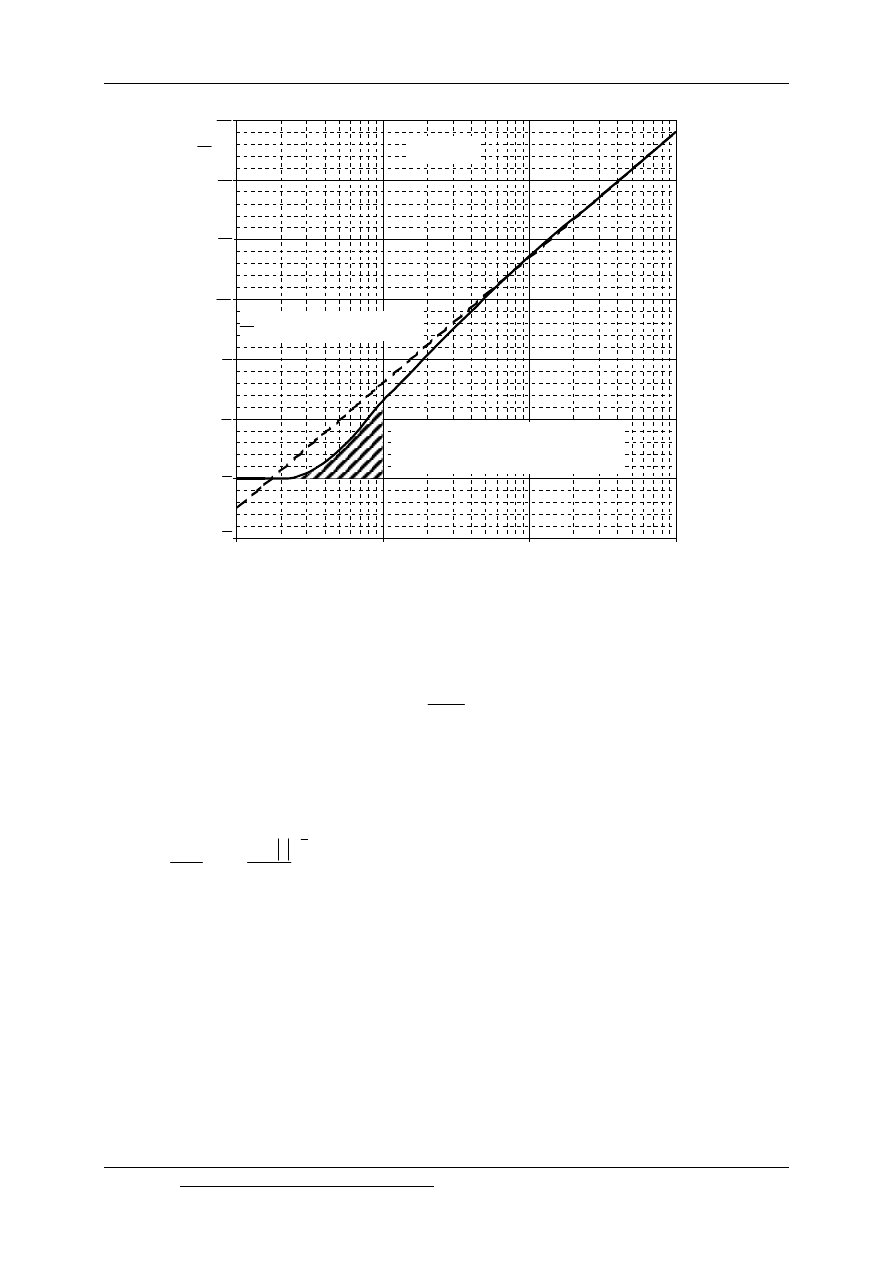
Rys. 9.15. Zależność wykładnika potęgowego n = f(Re) w funkcji liczby Reynoldsa
Dla rozpatrywanych przepływów o stałych wydatkach:
- zmierzyć prędkość średnią anemometrem,
- obliczyć wartość liczby Reynoldsa:
sr
v D
Re
×
=
n
,
- określić wartość wykładnika potęgowego n na podstawie wykresu
( )
n f Re
=
(rys. 9.15),
- obliczyć wartość wielkości bezwymiarowej
(
)
max T
v / v
z zależności:
1
n
max
T
R r
v
v
R
æ - ö
é
ù
= ç
÷
ê
ú
ë
û
è
ø
(9.15)
Zmierzyć za pomocą rurki Prandtla prędkości lokalne w wyznaczonych punktach
przekroju poprzecznego prostoosiowego przewodu o przekroju prostokątnym, dla dwóch
wartości natężenia przepływu.
9.5. Literatura
[1] Troskolański A. T.: Hydromechanika techniczna. t. I-III, Pomiary wodne PWT, Warszawa
1957.