W

W

Y

Y

K

K

Ł

Ł

A

A

D

D

8

8

P

P

R

R

Ę

Ę

D

D

K

K

O

O

Ś

Ś

Ć

Ć

D

D

E

E

F

F

O

O

R

R

M

M

A

A

C

C

J

J

I

I

,

,

T

T

E

E

N

N

S

S

O

O

R

R

P

P

R

R

Ę

Ę

D

D

K

K

O

O

Ś

Ś

C

C

I

I

D

D

E

E

F

F

O

O

R

R

M

M

A

A

C

C

J

J

I

I

,

,

Z

Z

W

W

I

I

Ą

Ą

Z

Z

K

K

I

I

K

K

O

O

N

N

S

S

T

T

Y

Y

T

T

U

U

T

T

Y

Y

W

W

N

N

E

E

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer

Równanie ruchu Cauchy’ego – Lagrange’a

opisuje ruch dowolnego ośrodka ciągłego

.

Dla płynu Pascala - płynu idealnego, w którym styczne siły
powierzc

hniowe są równe zero – tensor zależy jedynie od

ciśnienia

p

 

dv

F

dt







 

Aby otrzymać równanie ruchu konkretnego ośrodka należy

zdefiniować tensor



Naszym celem będzie określenie składnika prędkości

wynikającego z odkształcenia. Otrzymamy go odejmując od

całkowitej prędkości ośrodka ciągłego prędkość występującą

w ciele sztywnym.

Ciało sztywne: przemieszcza się i obraca

Płyn: przemieszcza się, obraca i ulega

odkształceniu

W rzeczywistości określenie



jest bardziej z

łożone. Tensory

naprężenia dla ośrodków ciągłych zależą od odkształcenia

oraz prędkości odkształcenia(deformacji).

Dla ciała sztywnego możemy zapisać:

 

0

v t, r

v (t)

(t) r









0

v

-

prędkość ciała określająca przesunięcie

r





-

iloczyn wektorowy prędkości kątowej



z wektorem

przesunięcia

r

. J

est to człon związany z obrotem.

Można pokazać, że dla obrotów z dowolną prędkością



jest

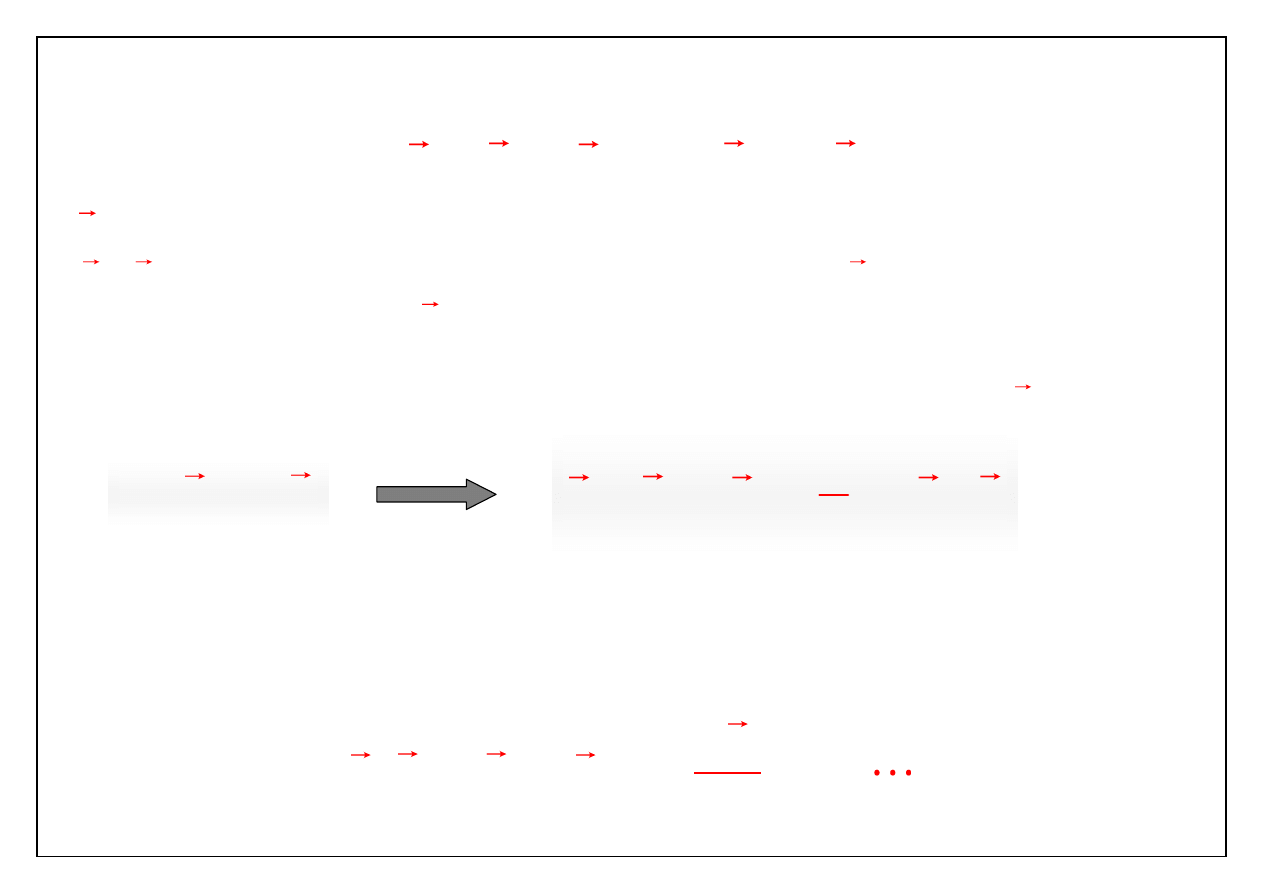
Rozpatrzmy teraz ruch dwu bliskich punktów materialnych w ciele
odkształcalnym. Odległość między nimi jest znikoma, a więc





i

i

v

v r

dr

v(r)

dx

x













rot v

2





0

1

v(t, r)

v

rot v r

2







wtedy

Dla

dr

→ 0

możemy zaniedbać wyrazy wyższego rzędu. Wtedy

powyższe równanie dla składowych

k

v (r)

przyjmuje postać:





k

k

k

i

i

v

v

r

dr

v (r)

dx

x











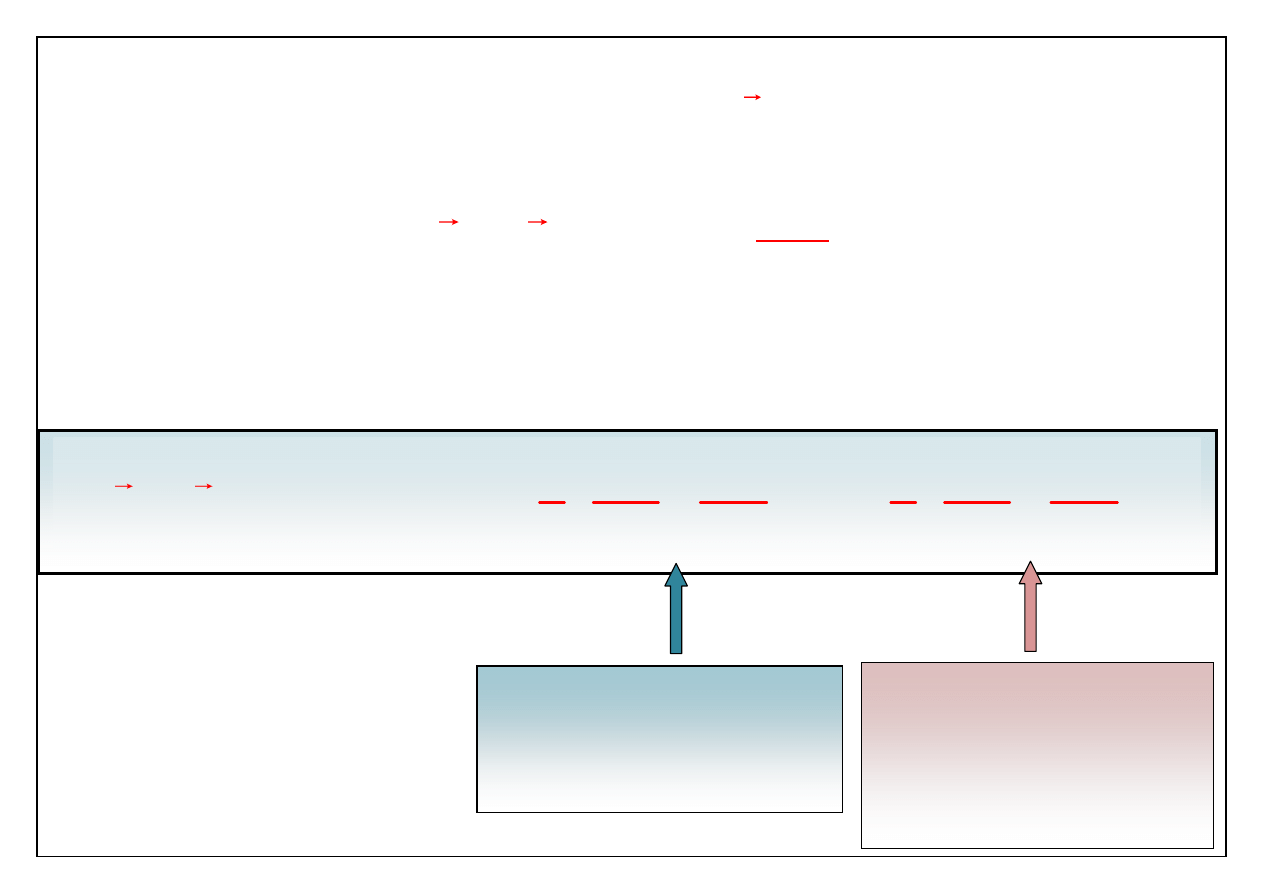
Zapiszmy to w nieco inny sposób

k

i

k

i

k

k

k

k

i

i

i

k

i

k

v

v

v

v

1

1

v (r

dr)

v

dv

v

dx

dx

2

x

x

2

x

x

























































Składnik związany z

odkształceniem

(dv

k

)

def

Składnik związany z

obrotem (w nawiasie są

składowe rotacji

prędkości)

(dv

k

)

rot

T

T

E

E

N

N

S

S

O

O

R

R

P

P

R

R

Ę

Ę

D

D

K

K

O

O

Ś

Ś

C

C

I

I

D

D

E

E

F

F

O

O

R

R

M

M

A

A

C

C

J

J

I

I

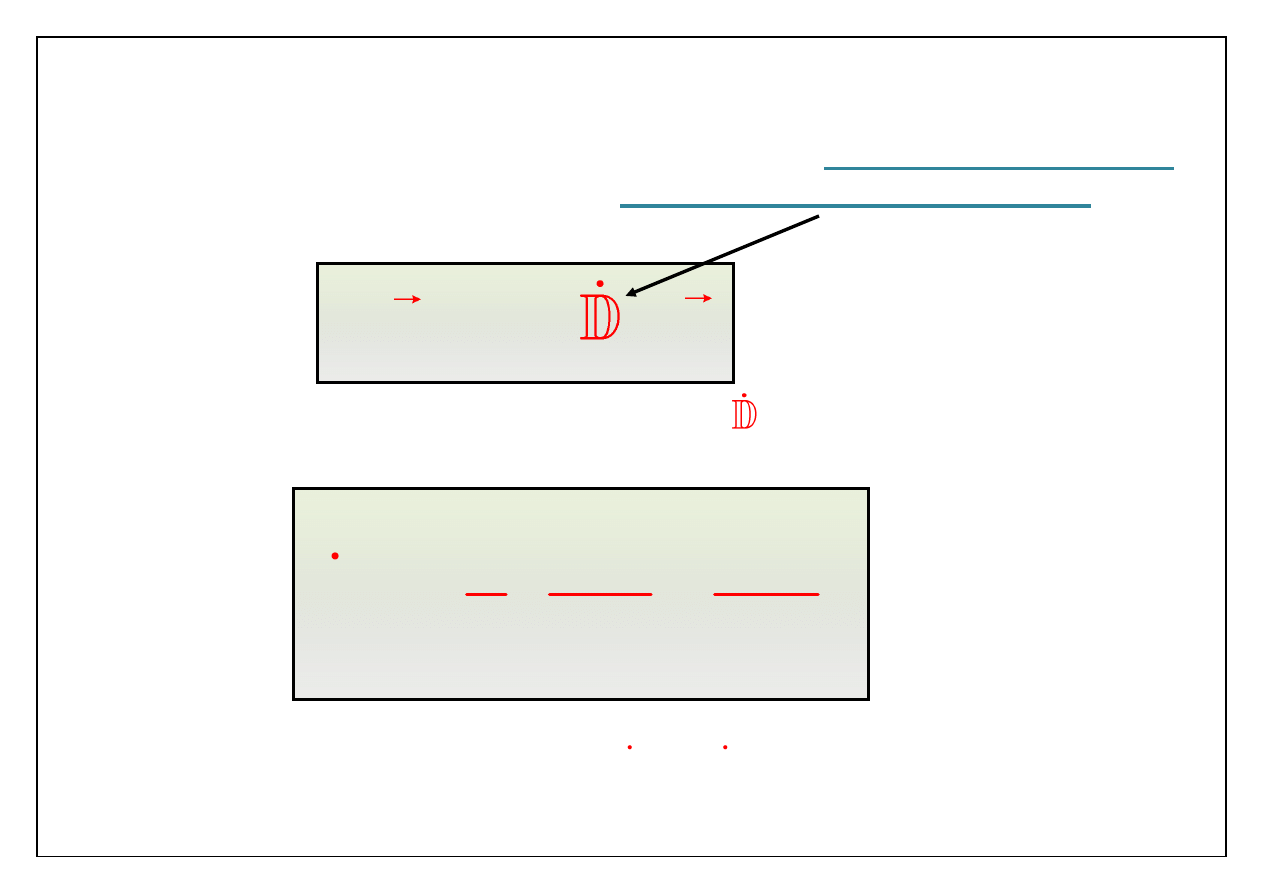
Składnik związany z odkształceniem nazywa się

prędkością deformacji

.

Zapiszmy go

wektorowo z użyciem

ten

sora prędkości deformacji:

Macierz tensora

prędkości deformacji

określa się następująco:

Tensor ten jest symetryczny bo

ki

ik

D

D



 

def

dv

dr

 

k

i

ki

i

k

v

v

1

D

2

x

x

























T

T

E

E

N

N

S

S

O

O

R

R

P

P

R

R

Ę

Ę

D

D

K

K

O

O

Ś

Ś

C

C

I

I

O

O

B

B

R

R

O

O

T

T

U

U

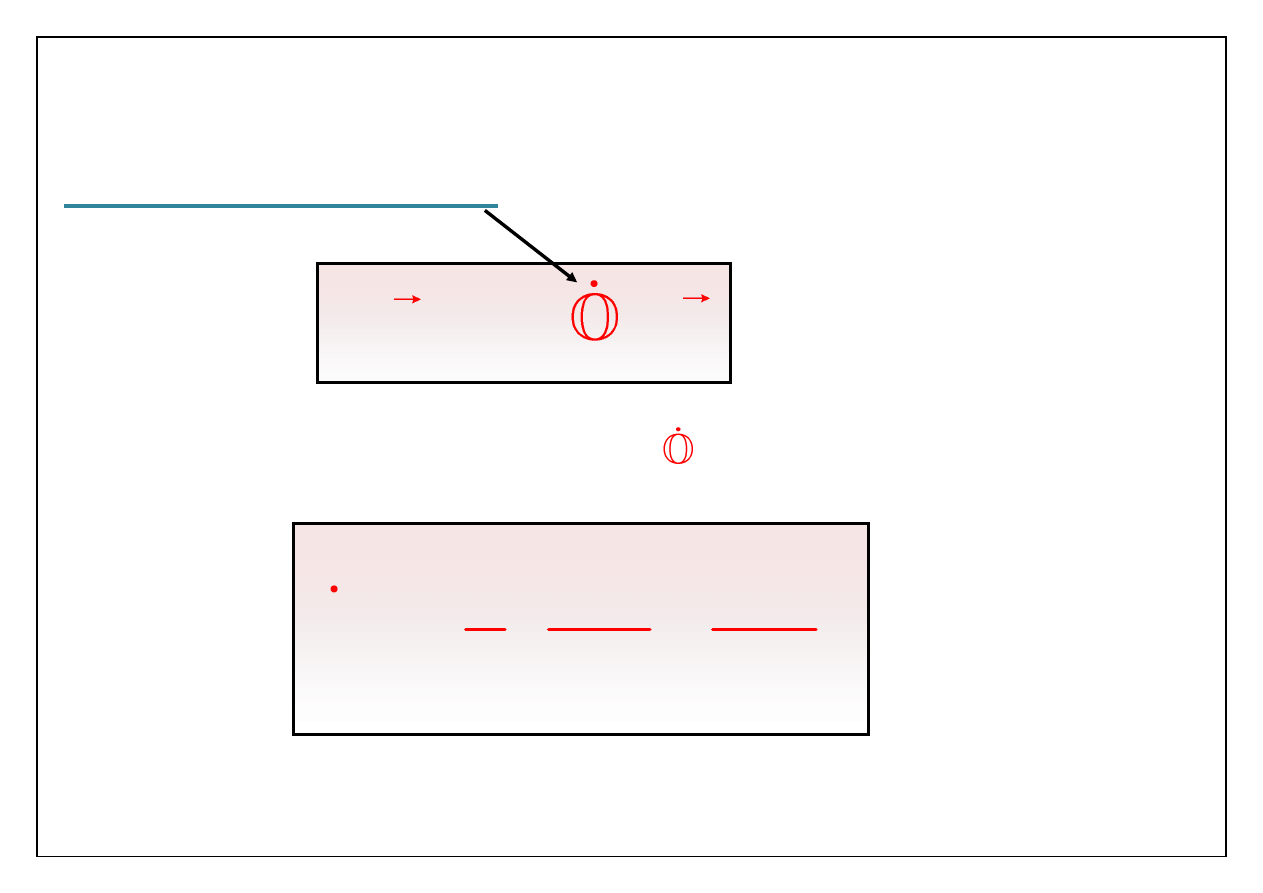
Składnik związany z obrotem zapiszmy wektorowo z użyciem

tensora prędkości obrotu

Macierz

tensora prędkości obrotu

określa się następująco:

 

rot

dv

dr

 

k

i

ki

i

k

v

v

1

O

2

x

x

























Z

Z

W

W

I

I

Ą

Ą

Z

Z

K

K

I

I

K

K

O

O

N

N

S

S

T

T

Y

Y

T

T

U

U

T

T

Y

Y

W

W

N

N

E

E

Dla ciała sprężystego podlegającemu prawu Hooke’a tensor



zależy od odkształceń. Tensor odkształcenia ma postać:

Gdzie wektor

w

to przemieszczenie.

Płyn prosty to ośrodek ciągły, w którym tensor

naprężenia



jest funkcją tensora prędkości

odkształcenia

( )



k

i

ki

i

k

w

w

1

D

2

x

x

























Dla ciał o dowolnych własnościach pośrednich można pisać:

Na

uka o własnościach naprężeniowo – odkształceniowych

ośrodków ciągłych nazywa się reologią.

Ciało proste to takie ciało, dla którego zachodzi związek

( )







, , ,

0



Jest to

równanie konstytutywne

wiążące



z

, ,

w sposób odpowiadający

własnościom rozważanego ciała