Materiały dydaktyczne, L-15, PK

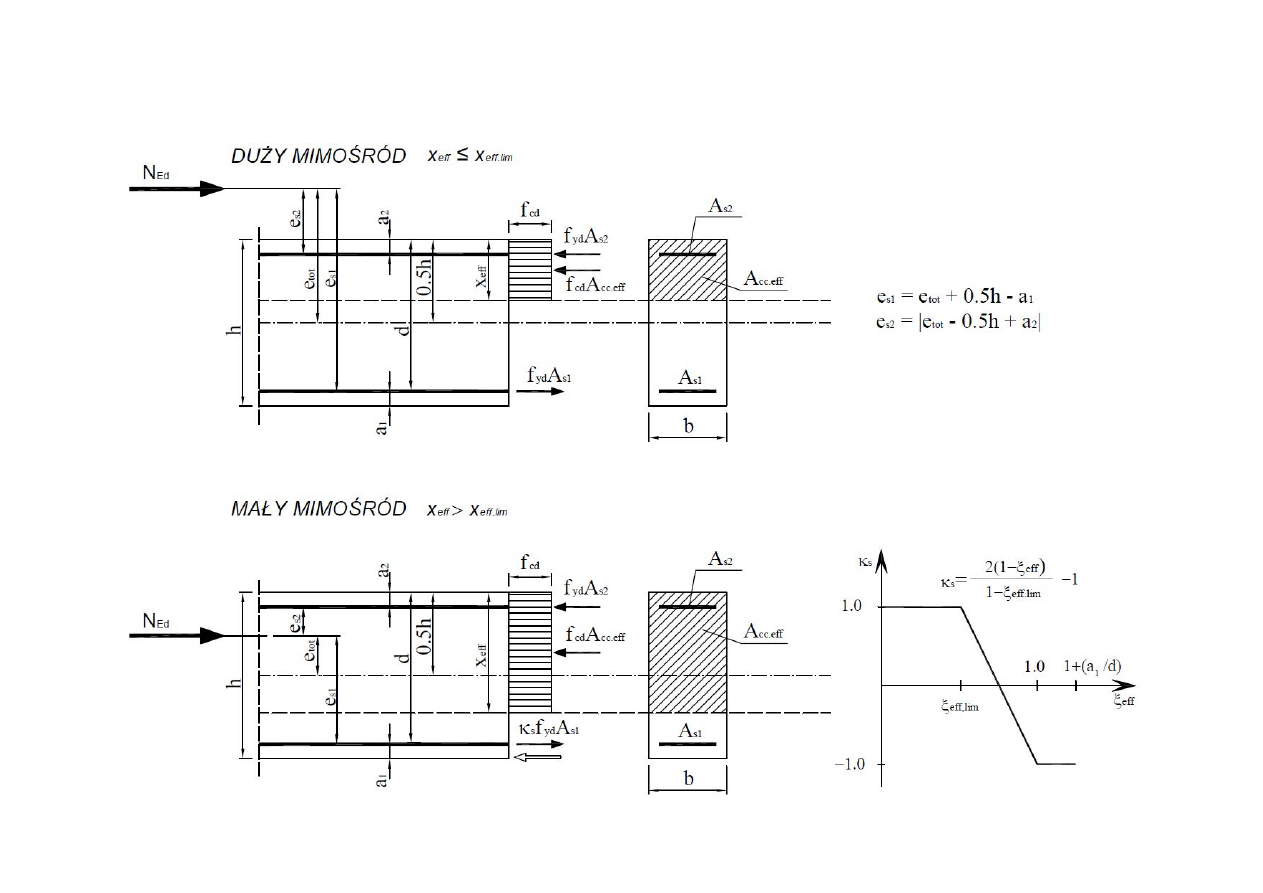
OGÓLNE WARUNKI RÓWNOWAGI PRZEKROJU MIMOŚRODOWO ŚCISKANEGO

(metoda uproszczona, zagadnienie płaskie)

Materiały dydaktyczne, L-15, PK

OBLICZANIE ZBROJENIA Z RÓWNAŃ RÓWNOWAGI SIŁ W PRZEKROJU

(metoda uproszczona, zagadnienie płaskie)

DANE:

a) geometria: b; d; a

1

; a

2

b) materiały: f

yd

; f

cd

; ξ

eff.lim

c) siły & mimośrody: N

Ed

; e

tot

(M

Ed.tot

)

SZUKANE:

A

s1

; A

s2

= ?

RÓWNANIA:

I. Zbrojenie A

s2

wyliczamy z sumy momentów względem osi zbrojenia A

s1

(

1

0

s

A

M





):

(A)

≤

.

+

( −

)

(1)

=

.

(

)

dla x

eff

> 2a

2

(2)

.

=

(

)

II. Zbrojenie A

s1

wyliczamy z równania równowagi sił poziomych (

0

H 



):

(B)

≤

.

+

(

− κ

)

(3)

=

κ

dla x

eff

> 2a

2

III. Zbrojenie A

s1

przy małej strefie ściskanej wylicza się z warunku sumy momentów względem A

s2

(



2

s

A

M

) zakładając x

eff

= 0:

(C)

≤

( −

)

(4)

=

(

)

dla x

eff

≤ 2a

2

→

x

eff

= 0

IV. W przypadku małego mimośrodu do wyznaczenia wielkości strefy ściskanej korzystamy z warunku sumy momentów względem

osi zbrojenia A

s2

przy założeniu, że A

s1

=0 (

2

0

s

A

M





):

(D)

− 0.5

−

−

= 0

(5)

=

+

+

Materiały dydaktyczne, L-15, PK

= 0.5 ∙

.

0.002 ℎ

= 0.04 ℎ

Zakł.: x

eff

=



eff,lim

d

A

s2

z wzoru (1)

A

s2

>0

x

eff

=



eff

d > 2a

2

A

s1

z wzoru (3) 

s

=1

A

s1

z wzoru (4)

A

s1

< 0

Przyjąć A

s1

KONIEC

Czy założony stopień

zbrojenia (do obliczenia

efektów II rzędu) różni się od

uzyskanego o ponad 20%

Ściskanie z małym

mimośrodem

Przyjąć średnią z powierzchni

założonej i otrzymanej
i powtórzyć obliczenia

Przekrój za duży

Zmniejszyć

przekrój

s

cc.eff

z wzoru (2)

A

s2

=max(A

s2,

A

smin

)

.

1

1 2

eff

cc eff

s



 



A

s2

=A

smin

TAK

NIE

NIE

TAK

TAK

NIE

NIE

TAK

NIE

TAK

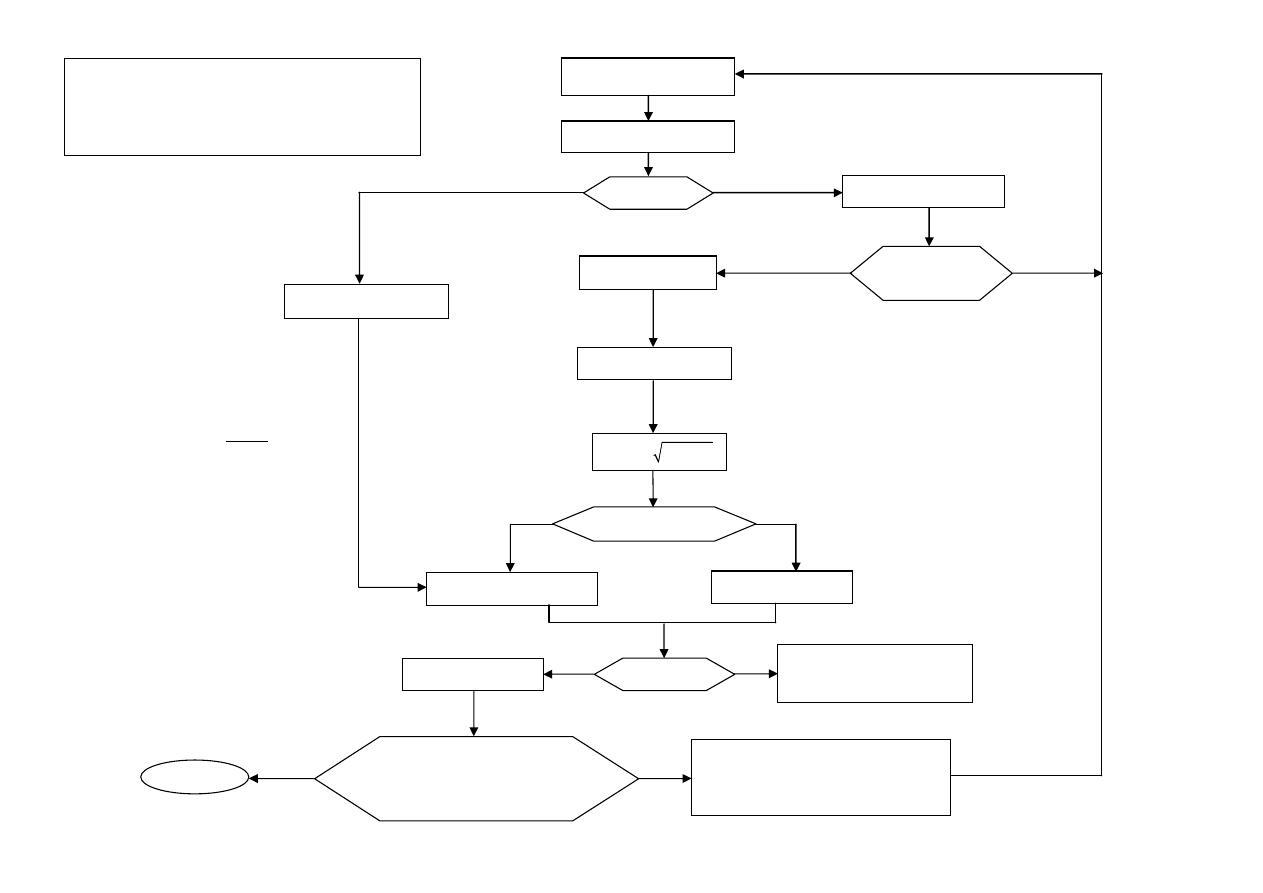
WYMIAROWANIE NA ŚCISKANIE

DUŻY MIMOŚRÓD (I)

ZBROJENIE NIESYMETRYCZNE

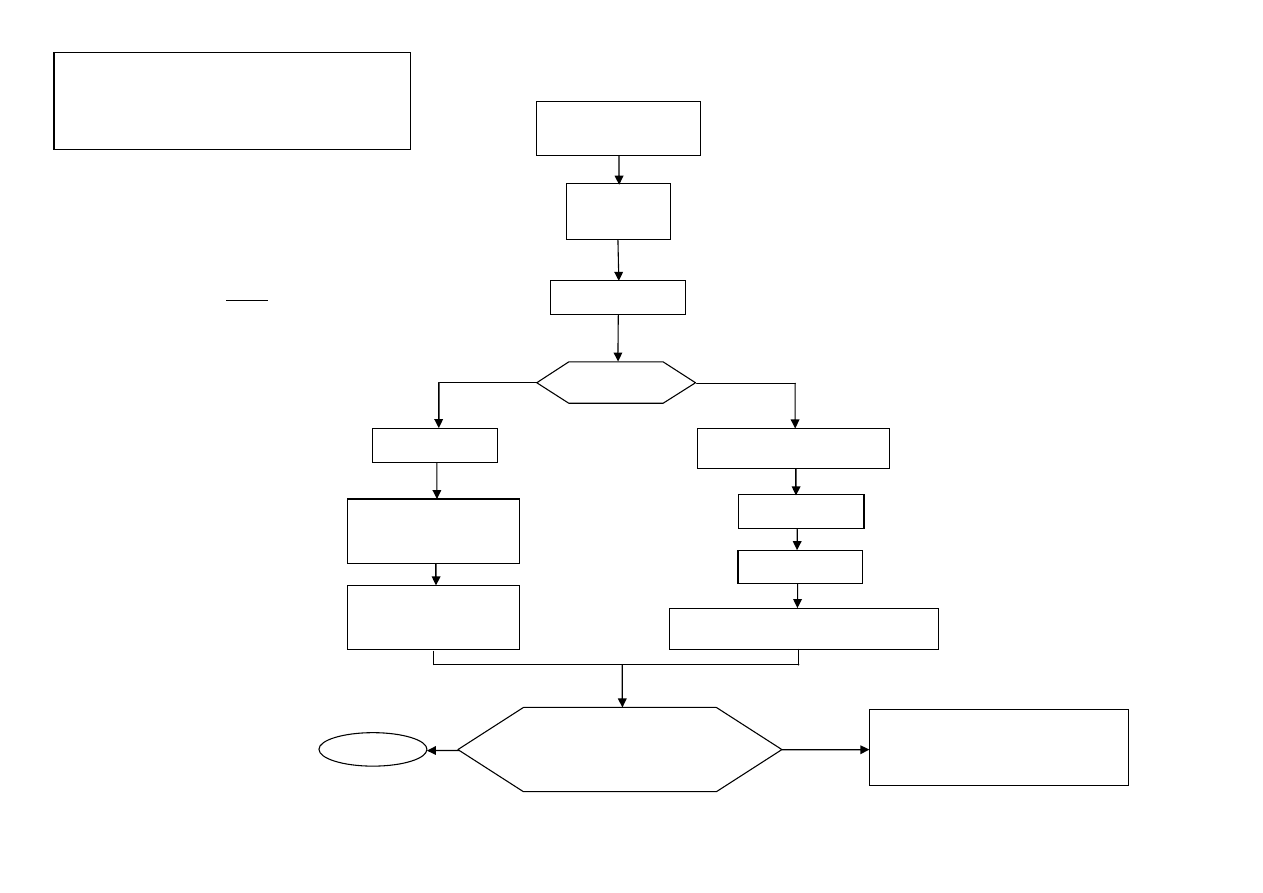
Materiały dydaktyczne, L-15, PK

= 0.5 ∙

.

0.002 ℎ

= 0.04 ℎ

Z (I) A

s1

< 0

Mały mimośród

Zakł.:

A

s1

= 0

x

eff

< h

x

eff

z wzoru (5)

A

s2

wzór (1)

Przyjąć:

min

2

s

rzecz

s

A

A



Przyjąć:

min

1

s

rzecz

s

A

A



Zakł.: x

eff

= h ,



s

= -1

A

s2

wzór (1)

A

s1

wzór (3)

max

min

2

1

,

,

s

s

s

rzecz

s

rzecz

s

A

A

A

A

A







KONIEC

Przyjąć średnią z powierzchni

założonej i otrzymanej
i powtórzyć obliczenia

Czy założony stopień

zbrojenia (do obliczenia

efektów II rzędu) różni się od

uzyskanego o ponad 20%

WYMIAROWANIE NA ŚCISKANIE

MAŁY MIMOŚRÓD (II)

ZBROJENIE NIESYMETRYCZNE

Materiały dydaktyczne, L-15, PK

= 0.5 ∙

.

0.002 ℎ

= 0.04 ℎ

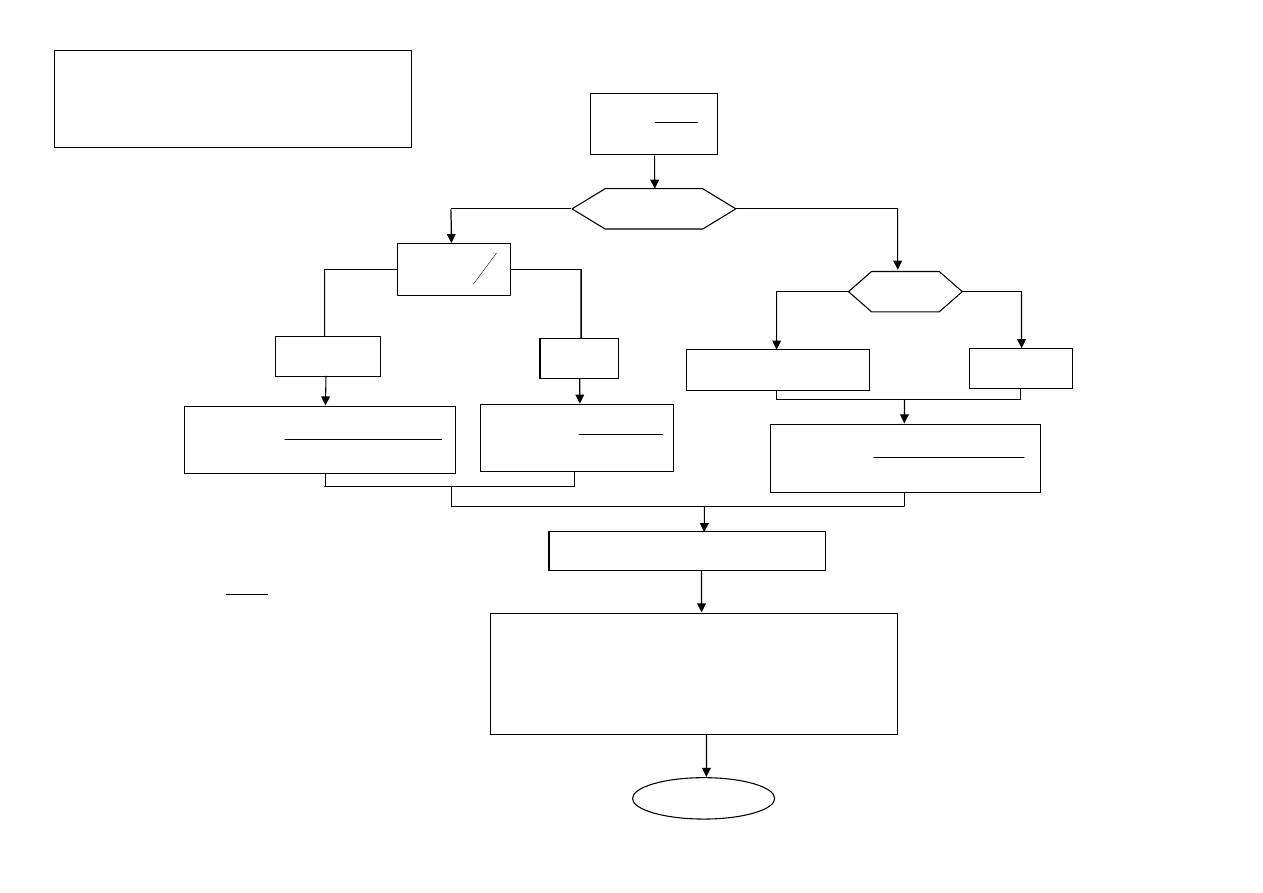
WYMIAROWANIE NA ŚCISKANIE

DOWOLNY MIMOŚRÓD (III)

ZBROJENIE SYMETRYCZNE

.lim

eff

eff







1



eff



d

a

eff

2

2





TAK

NIE

max

2

1

min

2

1

,

s

s

s

s

s

s

A

A

A

A

A

A









1) Jeśli A

s

> A

smax

– zmiana przekroju

2) Jeśli założony stopień zbrojenia (do obliczana

efektów II rzędu) różni się od obliczonego
o 20% - przyjąć średnią powierzchnię z
założonego i obliczonego i powtórzyć obliczenia

KONIEC

.

(1 0.5

)





cc eff

eff

eff

s





.

0.5



cc eff

s

TAK

TAK

NIE

NIE

eff

eff

d

x





0

eff

x



bd

f

N

ξ

cd

Ed

eff

=

)

a

d

(

f

)

x

5

.

0

d

e

(

N

A

A

2

yd

eff

1

s

Ed

2

s

1

s

-

+

-

=

=

)

a

d

(

f

e

N

A

A

2

yd

2

s

Ed

2

s

1

s

-

=

=

)

a

d

(

f

bd

f

s

e

N

A

A

2

yd

2

cd

eff

.

cc

1

s

Ed

2

s

1

s

-

-

=

=