1.

 

Dane są trzy siły P

1

 = -3i + 4j,  P

2

 = 2i – 3j,  P

3

 = 5i + 3j (gdzie składowe sił są 

wyrażone w niutonach), przecinające się w punkcie A (4,2). Zapisać wektor 
wypadkowej, obliczyć jej wartość oraz kąty nachylenia linii działania względem osi 
układu.  

 
2.

 

Dane są cztery siły zbieżne w przestrzeni P

1

 = -4i + 5j + 7k, P

2

 = 2i – 10j – 4k, P

3

 = 

3i - 8j + 2k, P

4

 = -4j – 9k (gdzie składowe sił są wyrażone w niutonach). Wyznaczyć 

wypadkową tych sił oraz kąty, jakie tworzy ona z osiami układu współrzędnych.  

 

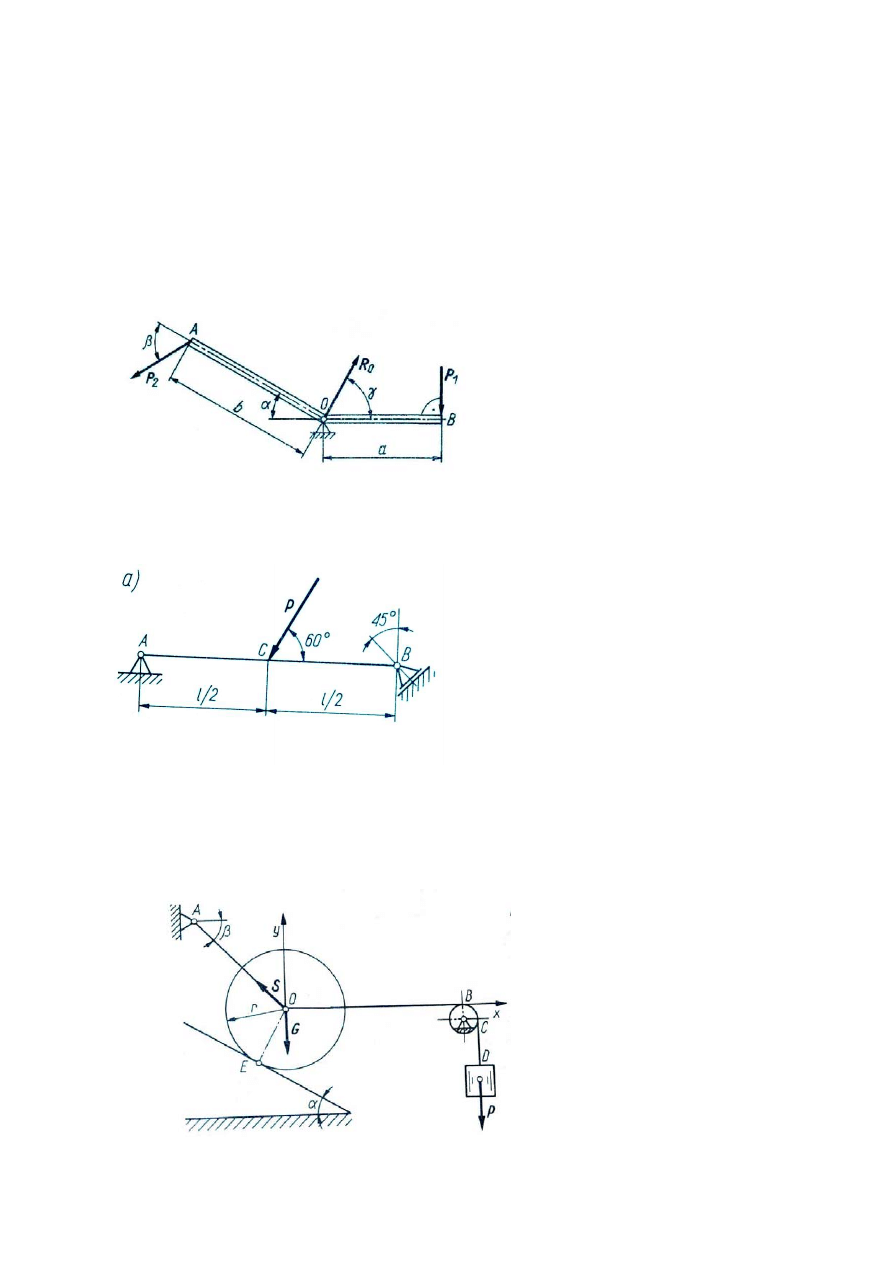
3.

 

Dźwignia AOB jest podparta przegubowo w punkcie O. Jaką siłę P

2

 należy przyłożyć 

w punkcie A (rys.), aby nie nastąpił obrót dźwigni wokół punktu O? Określić wartość 
i kierunek reakcji w punkcie podparcia, jeżeli: P

1

 = 50N, a = 0.6 m, b = 0.8 m, α = 30º, 

β = 60º. 

 

4.

 

Nieważka belka AB o długości l opiera się jednym końcem A na stałej podporze 
przegubowej. Drugi koniec B tej belki jest zamocowany na podporze przegubowej 
przesuwanej (rys.). Wyznaczyć reakcje podpór A i B, jeżeli belka jest obciążona w 
punkcie C siłą P.  

 

5.

 

Walec o promieniu r i ciężarze  G spoczywa na gładkiej równi pochyłej o kącie 
nachylenia  α = 30º i jest utrzymywany w położeniu równowagi za pomocą liny OA  
zgodnie z rysunkiem. Do środka walca przymocowano drugą linę, którą przerzucono 
przez nieważki krążek. Na końcu tej liny zawieszono ciężar  P. Obliczyć wartość 
reakcji N w punkcie E zetknięcia się walca z równią oraz napięcie w linie OA, jeżeli 
lina OB jest pozioma, a lina OA tworzy z poziomem kąt  β = 45º. 

 

 
 
 

 
 
 
 
 

6.

 

Układ dwóch nieważkich przegubowo połączonych 
prętów zamocowanych na stałych podporach 
przegubowych w punktach A i B (rys.) obciążono w 
punkcie C poziomą siłą  P. Wyznaczyć wartość 
reakcji w podporach A i B.  

 
 

 

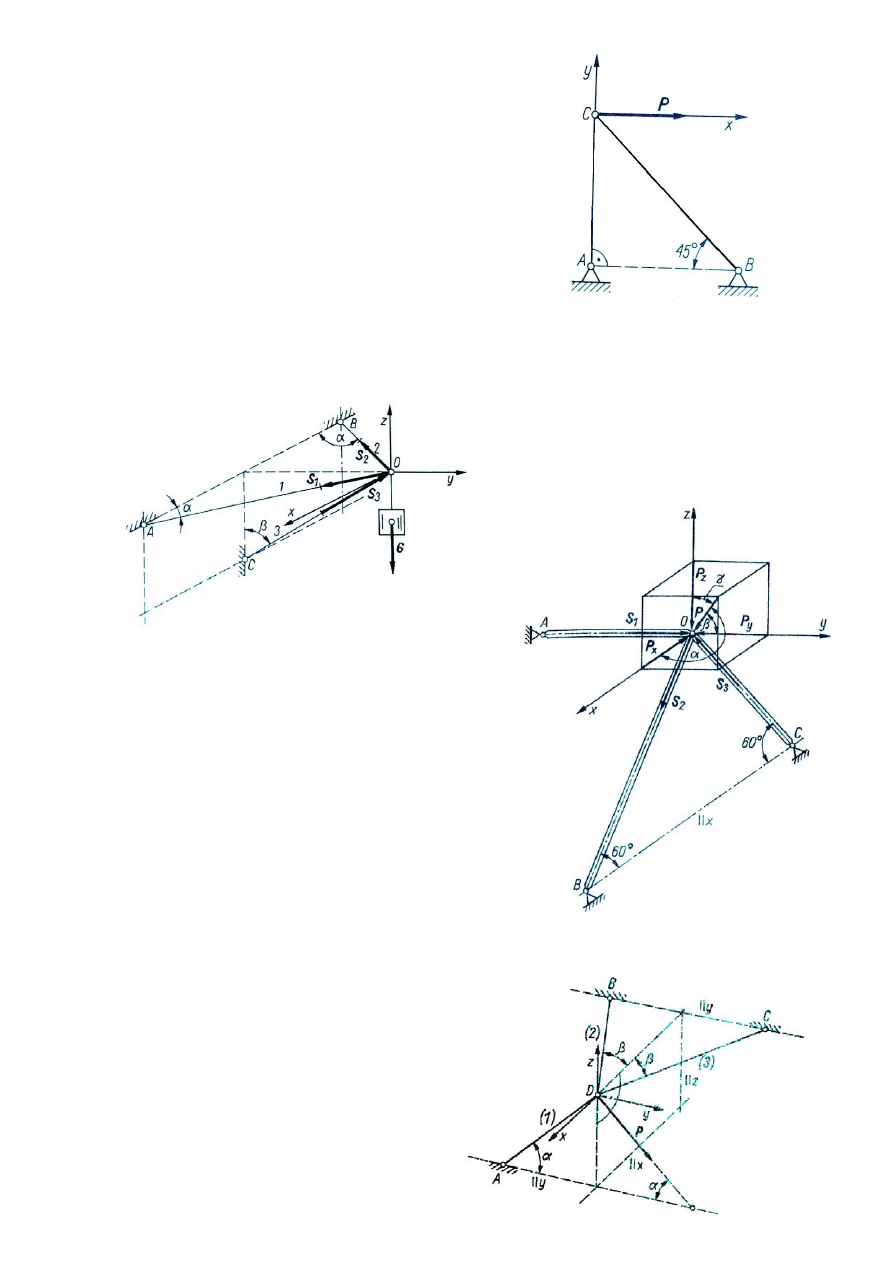
7.

 

Ciało o ciężarze G zawieszono na wsporniku składającym się z trzech prętów 
połączonych przegubowo w sposób pokazany na rysunku. Pręty OA i OB. leżące w 
płaszczyźnie prostopadłej do pionowej ściany, tworzą z tą  ścianą  kąty  α = 45º. Pręt 

OC tworzy z pionową  ścianą  kąt  β 
= 60º i również leży w płaszczyźnie 
prostopadłej do tej ściany. Obliczyć 
siły w prętach pomijając ich 
ciężary własne oraz tarcie w 
przegubach.  

 
 
 
 
 

8.

 

Na układ trzech nieważkich prętów OA, 
OB., OC działa wzdłuż głównej 
przekątnej prostopadłościanu siła P (rys). 
Obliczyć siły w prętach, jeżeli ich 
zamocowanie jest przegubowe.  

 
 
 
 

9.

 

Obliczyć siły w prętach układu pokazanego na rysunku. Siła P jest przyłożona w 
węźle D, w którym schodzą się trzy pręty AD, BD, CD. Końce tych prętów A, B i C 
zamocowane są przegubowo. Dane 
liczbowe: P = 100N, α = 45º, β = 30º.  

 
 
 
 
 
 
 
 
 

 
 
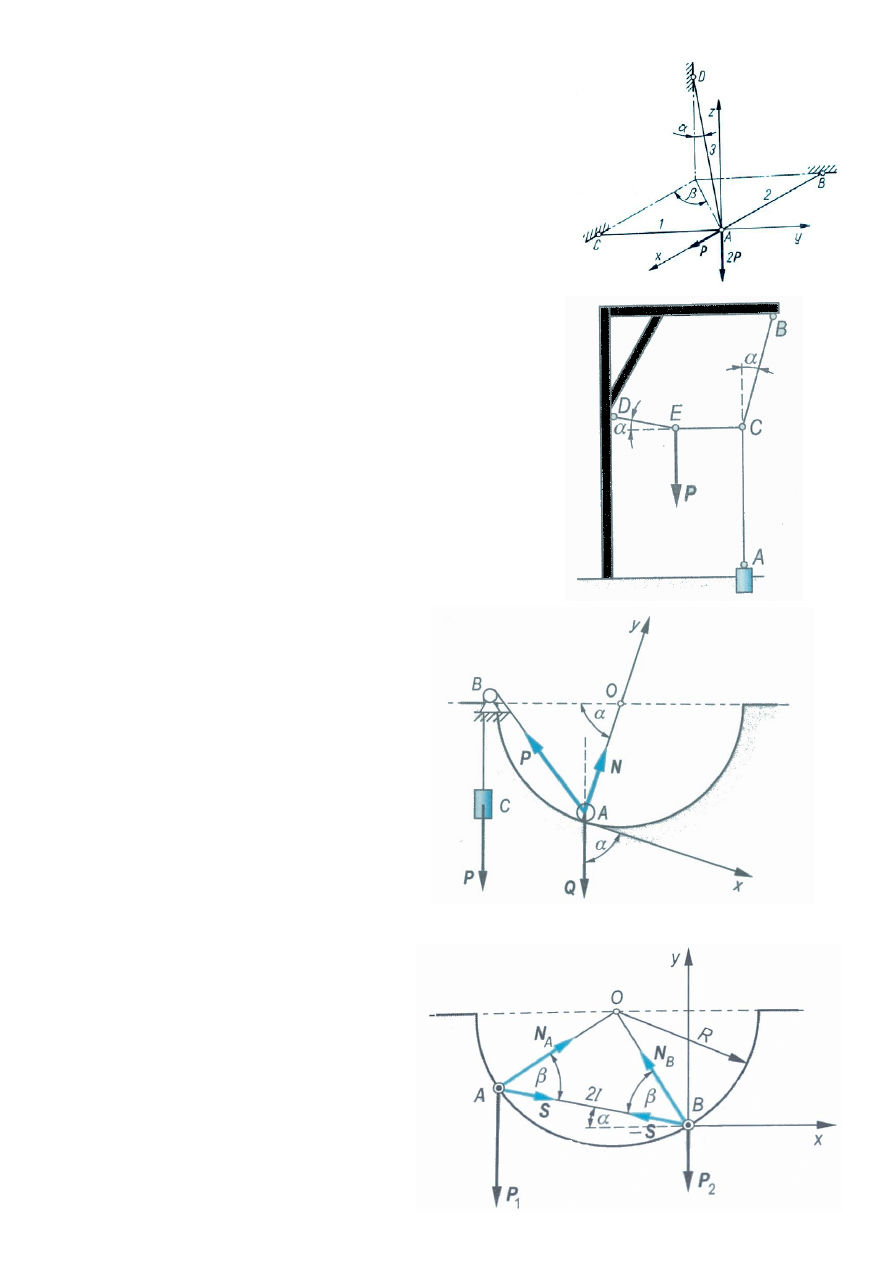
10.

 

Nieważkie pręty AB, AC, AD połączone są 
przegubowo w punktach A, B, C, D. W punkcie A 
przyłożono dwie siły: P wzdłuż osi Ax i 2P w 
kierunku pionowym (rys.). Wyznaczyć siły w 
prętach, jeżeli kąty α = 60º, β = 45º 

 
 
 
 
 
 

11.

 

Aby wyciągnąć z ziemi pal, robotnik przywiązał do 
niego linę w punkcie A. Po zamocowaniu drugiego 
końca liny B, przywiązał do niej drugą linę w punkcie 
C, zaczepioną w punkcie D, po czym uchwycił 
rękami linę CD w punkcie E i zawisł w powietrzu: 
część AC liny zajęła wtedy położenie pionowe, a 
część CE – poziome. Części CB i DE utworzyły 
jednakowe kąty  α, jedna z pionem, a druga z 
poziomem (rys.). Wyznaczyć siłę w linie AC, jeżeli 
ciężar robotnika jest równy P.  

 
 
 
 
12.

 

Na pionowej półkuli jest 
umieszczona kulka A, która może 
poruszać się tylko po okręgu. 
Kulka jest utrzymywana w 
równowadze za pomocą nici ABC. 
Na końcu nici uwieszono ciężar P. 
Ciężar kulki jest równy Q. Znaleźć 
kąt  α, jaki tworzy odcinek OA 
odcinkiem OB. w położeniu 
równowagi oraz nacisk kulki na 
powierzchnie półkuli. Średnicę 
bloku B zaniedbać.  

 
 
 
 
 

13.

 

Dwie kulki A i B o ciężarach P

1

 i 

P

2

 znajdują się położeniu 

równowagi wewnątrz gładkiej, 
sferycznej czaszy o promieniu R. 
Kulki są połączone nieważkim 
prętem o długości AB = 2l. 
Znaleźć naciski N

A

 i N

B

 kulek na 

czaszę, siłę  S w pręcie AB oraz 
kąt  α, jaki tworzy pręt AB z 
poziomem w położeniu 
równowagi (rys.).  

 

 
 

14.

 

Dwa jednorodne walce A i B, każdy o 
ciężarze  P, zawieszono w punkcie O na 
nieważkich niciach. Między walcami A i B 
położono walec C ciężarze  Q. Znaleźć 
zależność między kątami  α i β w położeniu 
równowagi.