1

Lista 2

1. Samochód o masie m = 900 kg pod działaniem stałej siły napędowej F = 300 N jechał ruchem
jednostajnie przyspieszonym po prostoliniowym odcinku drogi. Narysuj wykres zależności szybkości
tego samochodu od czasu.

2. Oblicz wartość siły, z jaką siłacz musiałby działać na ciężar o masie 100 kg, jeżeli chciałby
podnieść go na wysokość 0,5 m w czasie 1 sekundy ruchem jednostajnie przyspieszonym.

3. Człowiek o masie m = 50 kg wspina się po pionowej linie z przyspieszeniem równym
a = 0,2 m/s

2

. Oblicz napięcie liny. Masę liny zaniedbać, a przyspieszenie ziemskie przyjąć

g = 9,8 m/s

2

.

4. Balon o masie M opada w dół z prędkością v. Jaką masę balastu należy z niego wyrzucić, aby zaczął
się on wznosić z tą samą prędkością? Na balon działa siła wyporu powietrza W. Wskazówka: na balon
działa siła ciężkości, siła wyporu powietrza i siła oporu ośrodka proporcjonalna do prędkości.

5. Na stole przymocowano jedna za drugą masy m

1

, m

2

i m

3

.

Znaleźć: a) przyspieszenie a układu, b) naprężenia każdej z nici.
Tarcie mas o płaszczyznę stołu i tarcie w bloczku pominąć.

6. Prosiaczek, przyjaciel Kubusia Puchatka, zjeżdża po równi pochyłej w czasie dwa razy dłuższym
niż namydlony ( tarcie zaniedbywalnie małe) Kłapouch. Ile wynosi współczynnik tarcia między
ciałem Prosiaczka a równią?

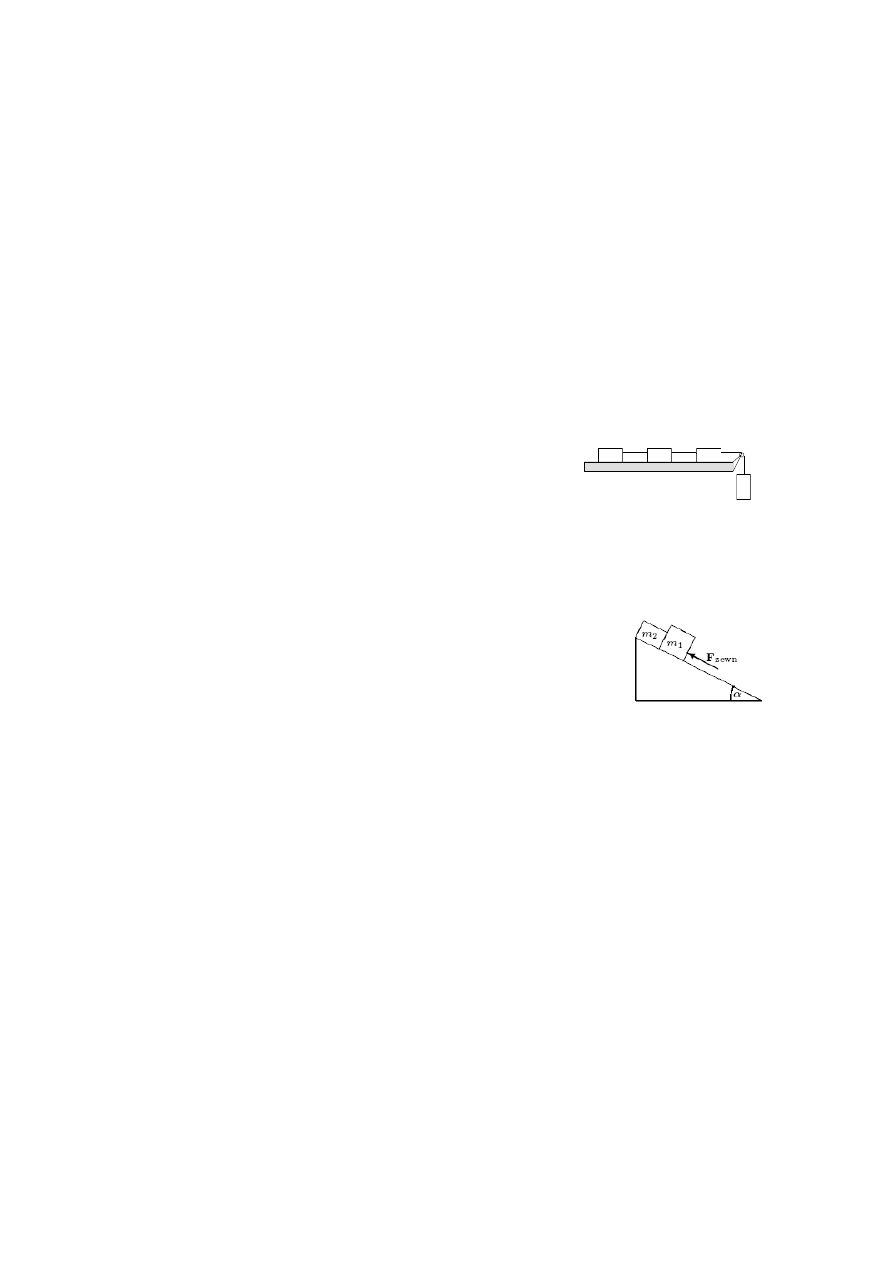
7. Na wierzchołku równi pochyłej o kącie



=30º utrzymywane są w

spoczynku przez siłę zewnętrzną F

z

dwa stykające się ze sobą bloczki o

masach m

1

= 70 kg i m

2

= 50 kg (patrz rysunek). Współczynniki tarcia

wynoszą odpowiednio f

1

= 0,1 i f

2

= 0,4. Wyznaczyć: minimalna i

maksymalną wartość F

z

, przy której klocki spoczywają; (b) przyspieszenia

obu klocków, gdy usuniemy siłę zewnętrzną; (c) odległość między
klockami po czasie t = 5 s; (d) ich przyspieszenia w przypadku, gdy
zamienimy je miejscami i usuniemy siłę zewnętrzną. Założyć, że wartości współczynników tarcia
statycznego są takie same jak współczynników tarcia kinetycznego.

8. Z równi pochyłej o wysokości h =1.8 m i kącie



= 30º zsuwa się skrzynia uzyskując na końcu

równi prędkość v = 2 m/s. Ile wynosi współczynnik tarcia f skrzyni o równię ?

9. Turysta, którego masa wraz z plecakiem wynosi m = 80 kg chce wejść na pagórek po oblodzonym
zboczu, nachylonym do poziomu pod kątem



= 15°. Współczynnik tarcia statycznego między

podeszwami jego butów, a zboczem wynosi f

s

= 0,3. a) Sprawdź, że turysta może wejść ruchem

jednostajnym na ten pagórek. b) Zbadaj, czy turysta, wchodząc po zboczu i chcąc zwiększyć nieco
szybkość, może podbiec z przyspieszeniem o wartości a = 0,5m/s

2

. c) Oblicz, jaki mógłby być

maksymalny kąt nachylenia oblodzonego zbocza pagórka, po którym turysta mógłby wchodzić w tych
butach.

10. Ciało o masie M przesuwane jest do góry po pionowej ścianie pod działaniem stałej siły F,
skierowanej pod kątem



do pionu. Wyznaczyć przyspieszenie ciała, jeżeli współczynnik tarcia ciała o

ścianę wynosi f.

11. Na końcach nieważkiej nici, przerzuconej przez nieważki blok, zawieszono ciężarki o masach M
oraz m, przy czym M > m. Lżejszy z nich znajduje się o l m niżej od cięższego. Wszelkie opory
ruchu pomijamy. Po jakim czasie ciężarki znajdą na tej samej wysokości jeśli puścimy je swobodnie?

m

m

m

M

2

1

3

2

13. Małpka o masie 10 kg wspina się po pionowej nieważkiej linie przerzuconej przez krążek o
znikomej masie. Do drugiego końca linki przymocowano skrzynię o masie 30 kg. Obliczyć
przyspieszenie, z jakim małpka może się wspinać, aby skrzynka pozostała nieruchoma.

14. Masywne ciało w kształcie prostopadłościanu porusza się w górę równi pochyłej o kącie 45

0

ze

stałą prędkością pod działaniem siły F = 15 N równoległej do równi. Wyznaczyć ciężar ciała.
Obliczyć minimalną wartość siły powodującej ruch ciała w dół równi, jeśli siła F nie będzie
przyłożona do ciała.

15. Na wózku o masie M spoczywa ciężarek o masie m, który jest ciągnięty siła F skierowaną pod
kątem



do poziomu. Jaką maksymalną wartość może mieć ta siła, aby ciężarek pozostawał w

spoczynku? Z jakim przyspieszeniem będzie się wówczas poruszał wózek? Współczynnik tarcia
między wózkiem i ciężarkiem wynosi



Zaniedbać inne siły oporu.

16. Worek wyrzucono z samolotu poruszającego się po poziomym torze na dużej wysokości.
Powietrze działa na worek siłą oporu F = -kv

3

(v/v), gdzie v – chwilowa wartość prędkości

spadochroniarza, a v długość wektora prędkości. Jaka jest prędkość worka po tym jak jego prędkość
osiągnie stałą wartość ?

17. Lampa wisi pionowo na linie w windzie, która jedzie w dół z opóźnieniem 2,4 m/s

2

. Naprężenie

liny wynosi wówczas 89 N. Jaka jest masa lampy? Ile wyniesie naciąg liny, gdy winda rusza do góry
z przyspieszeniem 2,4 m/s

2

?

18. Na gładkim stole położono dwa ciężarki o masach m

1

= 250 g i m

2

= 500 g połączone gumką.

W pewnej chwili ciężarki te rozsunięto, napinając gumkę, a następnie puszczono. Lżejszy z nich
zaczął poruszać się z przyspieszeniem o wartości a

1

= 0,2 2m/s

2

. Z jakim przyspieszeniem poruszał się

drugi ciężarek?

19. Samochód wpadł w poślizg na poziomym zakręcie o promieniu krzywizny 200 m, przed którym
stał znak ograniczenia prędkości do 40 km/h. O ile została przekroczona dozwolona prędkość.
Współczynnik tarcia między oponami i jezdnią wynosił 4/5? Wynik podać w km/h.

20. Wahadło o masie m wisi na podstawce umocowanej na wózku. Znaleźć kierunek nici wahadła, tj.
kąt α



nici z pionem oraz jej naprężenie T w przypadkach: a) wózek porusza się ruchem jednostajnym

po płaszczyźnie poziomej, b) wózek porusza się po płaszczyźnie poziomej z przyspieszeniem a,
c) wózek stacza się swobodnie z równi pochyłej, która tworzy kąt β z poziomem.

21. Wyznaczyć nacisk ciała pilota o masie M na fotel samolotu wykonującą pętlę o promieniu R = 6
km leżącą w płaszczyźnie pionowej, gdy samolot jest: a) w najniższym punkcie okręgu (fotel jest pod
ciałem pilota) a prędkość samolotu wynosi 280 m/s; b) w najwyższym punkcie pętli (fotel jest nad
pilotem) a prędkość samolotu wynosi 120 m/s. Obliczenia wykonać dla M = 62 kg. W jakim punkcie
pętli i przy jakich wartościach podanych parametrów pilot przez chwilę znajdzie się w stanie
nieważkości?

22. Współczynnik tarcia między torem a oponami samochodu wynosi 0,8. Z jaką maksymalną
prędkością może ten samochód pokonać bez poślizgu zakręt o promieniu 40 m?

23. Wiadro z wodą wprawiono w ruch po okręgu o promieniu R leżący w płaszczyźnie pionowej. Jaka
jest minimalna wartość prędkości wiadra w najwyższym punkcie toru ruchu, dla której woda nie
będzie wylewała się z niego?

3

24. Jarek o masie M = 40 kg buja się na huśtawce zawieszonej na dwóch linkach o długości L = 2 m
każda. W najniższym punkcie toru P siła naprężenia każdej z linek wynosi 300 N. Wyznaczyć
prędkość i przyspieszenie dośrodkowe Jarka oraz siłę jego nacisku na deskę huśtawki w punkcie P
toru.

25. Samochód porusza się po łuku drogi o promieniu R. Powierzchnia drogi jest nachylona pod kątem



względem poziomu w kierunku do wnętrza zakrętu. Współczynnik tarcia wynosi f. Pokazać, że

maksymalna prędkość, przy której samochód nie wypadnie z zakrętu na skutek poślizgu spełnia
równość (v

max

)

2

= Rg(f+tg



)/(1-ftg



).

26. Rowerzysta jedzie ze stałą prędkością v = 10 m/s po torze kołowym. Kąt nachylenia płaszczyzny
roweru do poziomu wynosi α=60˚. Oblicz promień toru.

27. Mała kulka stacza się po rynnie zakończonej pionową pętlą o promieniu r. Z jakiej wysokości
kulka ta powinna się stoczyć, aby nie odpaść od pętli?

28. Z wierzchołka gładkiej kuli o promieniu R zsuwa się bez tarcia małe ciało. Wyznacz położenie
punktu, w którym wspomniane ciało oderwie się od powierzchni kuli.

29. Ciężarek o masie m zawieszony na nici o długości d porusza się po okręgu ruchem jednostajnym,
w płaszczyźnie poziomej. W czasie ruchu nić odchylona jest od pionu o kąt



Oblicz siłę naprężenia

nici.