Praca, moc, energia mechaniczna, zasada zachowania energii mechanicznej.

Plan zajęć

1.

Rozkład sił na równi pochyłej.

2.

Definicja i sens fizyczny pracy, jednostki w układzie SI i pozaukładowe.

3.

Interpretacja geometryczna pracy w oparciu o wykres F

x

(x)

4.

Definicja i sens fizyczny mocy, jednostki mocy w układzie SI i pozaukładowe.

5.

Energia mechaniczna, rodzaje, jednostki.

6.

Zasada zachowania energii mechanicznej.

7.

Zastosowanie zasad zachowania energii i pędu do opisu zderzeń.

8.

Rozwiązywanie problemów z praktycznym wykorzystaniem w/w pojęć
fizycznych.

Zad.1. „ Ruch w górę równi” Samochód z wyłączonym silnikiem wjeżdżając na drogę
nachyloną pod kątem 15

0

do poziomu miał prędkość v = 10m/s. Jaką przebył on drogę do

chwili zatrzymania się, jeżeli współczynnik tarcia kół o drogę µ = 0,4.
Zad.2. „ Wbijanie pala” Młot o ciężarze 200N uderza z prędkością 5 m/s w pal i wbija go w
podłoże na głębokość 2cm. Oblicz średnia siłę oporu, jeżeli młot nie odbija się od pala. Pomiń
ciężar pala.
Zad.3. „ Diabelska pętla”; Z jakiej co najmniej wysokości musi zjeżdżać bez tarcia wózek z
pasażerami w wesołym miasteczku, aby mijał bezpiecznie najwyższy punkt pętli w kształcie
okręgu o promieniu r.
Zad.4. „Ruch na równi”; Samochód o masie 5t jedzie z prędkością 36km/h po drodze
nachylonej do poziomu pod kątem 30

0

. Współczynnik tarcia między kołami a drogą wynosi

0,2? Jaką moc powinien mieć silnik tego samochodu.
Zad.5. „Klocek” Jaką pracę należy wykonać, aby przewrócić z boku na bok sześcian o
krawędzi 0,1m i masie 1kg?
Zad.6. „Walec na równi” Na szczycie równi pochyłej o długości l = 10m i kącie nachylenia
30

0

znajduje się pełny walec o promieniu r =10 cm. Walec stacza się bez poślizgu. Znaleźć

prędkość środka masy walca u podstawy równi, jeżeli współczynnik tarcia podczas toczenia
się µ = 5*10

-4

m. Jaka byłaby prędkość walca gdyby nie było tarcia i walec by się ślizgał?

Zad.7. „Tarcie sanek o śnieg”; Sanki ześlizgujące się z górki o wysokości h zatrzymały się
w odległości d, mierzonej od punktu A’ będącego rzutem wierzchołka A górki na płaszczyznę
poziomą. Oblicz współczynnik tarcia sanek o śnieg.
Zad.8. „Ruch skrzyni po poziomym podłożu”. Na skrzynię o masie m = 40 kg działa siła o
wartości 100N, pod kątem 30

0

do poziomu. Współczynnik tarcia kinetycznego wynosi f

k

=

0,2. Oblicz pracę przy przemieszczaniu skrzyni na odległość 1m wykonaną przez:
a/siłę zewnętrzną,
b/ siłę tarcia,
c/ siłę ciężkości,
d/ wypadkową wszystkich sił działających na skrzynię.
Zad.9. „Zderzenia centralne sprężyste i niesprężyste” Oblicz prędkości dwóch kul o
masach m

1

i m

2

po ich centralnym zderzeniu sprężystym. Kule poruszają się z prędkościami

v

1

i v

2

w tę samą stonę.

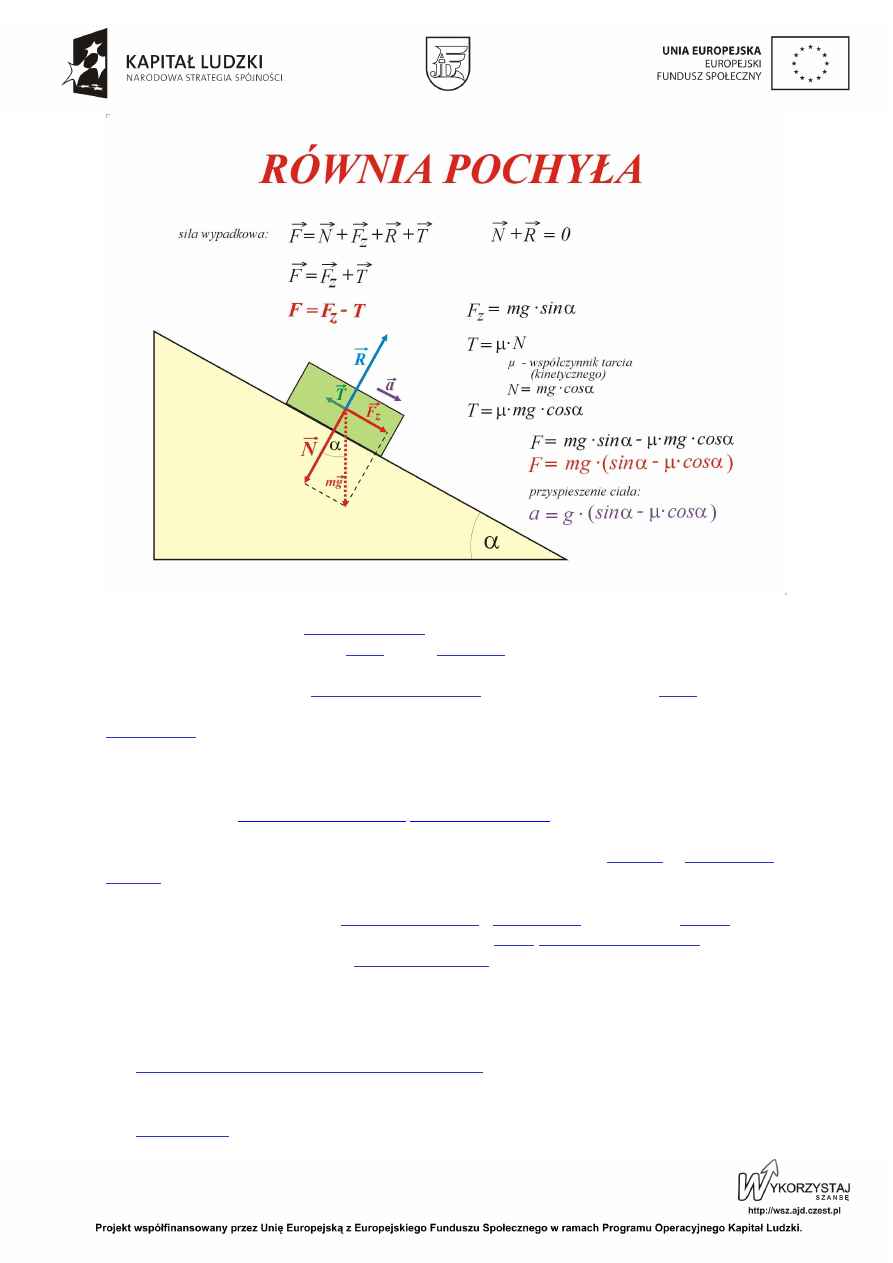
Równia pochyła – jedna z

maszyn prostych

. Równia to płaska powierzchnia nachylona do

poziomu pod pewnym kątem. W

XVII

wieku

Galileusz

wykorzystał obserwacje staczających

się po równi pochyłej kul o różnych ciężarach, do sformułowania rewolucyjnego na owe
czasy wniosku, że prędkość

spadającego swobodnie

ciała nie zależy od jego

masy

. Przeczyło

to przyjmowanym wtedy powszechnie (a spotykanym również obecnie!) poglądom

Arystotelesa

, że ciało spada tym prędzej im jest cięższe. Na podstawie tych obserwacji

Galileusz sformułował też swą regułę spadku swobodnego:

w jednakowych odstępach czasu spadające swobodnie ciało przebywa drogi będące
ilorazami

kolejnych naturalnych

liczb nieparzystych

Przyjmuje się powszechnie, że równie pochyłe posłużyły do budowy

piramid

w

starożytnym

Egipcie

.

Energia mechaniczna — suma

energii kinetycznej

i

potencjalnej

Jest postacią

energii

związaną z ruchem i położeniem obiektu fizycznego (

układ

punktów materialnych

, ośrodka

ciągłego itp.) względem pewnego

układu odniesienia

.

Rodzaje energii mechanicznej:

•

energia kinetyczna – skalar - pojęcie względne— dotyczy ciał będących w ruchu

postępowym, obrotowym lub obu równocześnie

względem przyjętego układu odniesienia,

•

energia potencjalna – wielkość skalarna — pojęcie względne, związana z wzajemnym
oddziaływaniem ciał lub układów ciał:

•

grawitacyjna

(ciała w polu grawitacyjnym),

•

sprężystości

(ciała odkształcone sprężyście)

Energia zwi

ą

zana z ruchem układu mechanicznego jako cało

ś

ci lub

poszczególnych jego cz

ęś

ci wzgl

ę

dem siebie (energia kinetyczna, energia

potencjalna).

Wszystkie zasady zachowania są bardzo użyteczne i pomocne z
zrozumieniu wielu problemów. Zasada zachowania energii mechanicznej
ułatwia rozwiązanie wielu problemów fizycznych. Jej zaletą jest to, że
układ fizyczny opisywany jest za pomocą wielkości skalarnych (energie są
skalarami),a to powoduje, że równania sprowadzają się do równań
algebraicznych. Zamiast posługiwać się kinematycznymi i dynamicznymi
równaniami ruchu w postaci wektorowej można spokojnie zapisać bilans
energetyczny, a ułożone równania w wielu wypadkach niemal od razu są
rozwiązaniem problemu fizycznego.

1. Praca

1.1. Definicja

Praca jest iloczynem skalarnym działającej siły i wektora przesunięcia
stycznego cały czas to toru ruchu (krzywej po jakiej porusza się ciało).

2.Moc

Moc jest skalarną

wielkością fizyczną

określającą

pracę

wykonaną przez układ fizyczny w

jednostce

czasu

. Z definicji, moc określa równanie:

gdzie:

P – moc,
W – praca,
t – czas.

Wzór ten jest prawdziwy, gdy praca wykonywana nie zmienia się w czasie. W przeciwnym
wypadku powyższy wzór określa moc średnią. Aby obliczyć moc chwilową należy skorzystać
z innego wzoru:

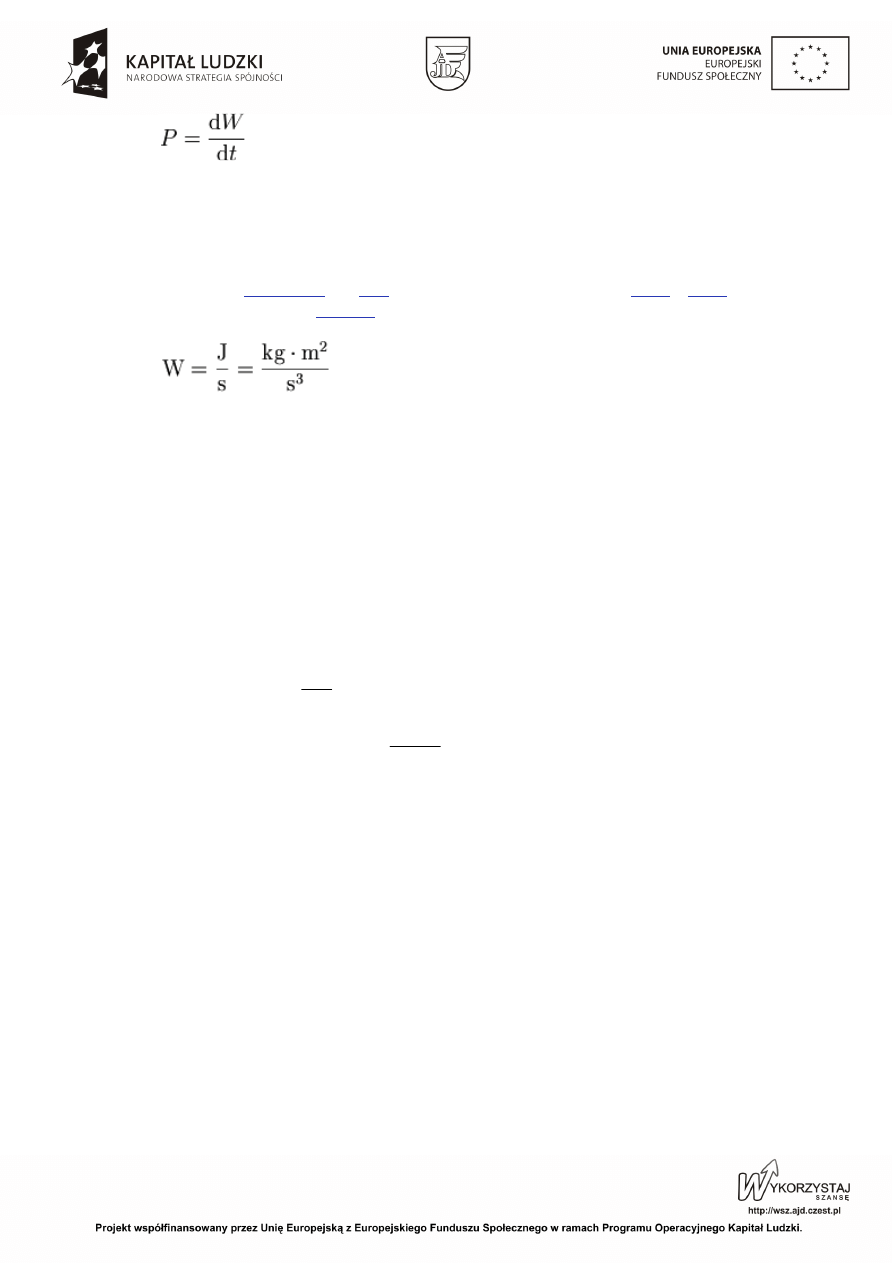
Jednostką pracy w układzie SI jest dżul;

J =N*m = kgm

2

s

-2

Jednostka mocy

Jednostką mocy w

układzie SI

jest

Wat

(W). Moc jest równa 1 wat, jeśli

praca

1

dżula

wykonywana jest w czasie 1

sekundy

.

Często używane wielokrotności:

1 mW = 0,001 W = 10

-3

W

1 kW = 1000 W = 10

3

W

1 MW = 1000000 W = 10

6

W

Pozaukładowe jednostki mocy: erg/s, kGm/s, koń mechaniczny KM

3.

ENERGIA MECHANICZNA, RODZAJE, JEDNOSTKI,

ZASADA

ZACHOWANIA ENERGII MECHANICZNEJ

Energia kinetyczna – E

k

=

2

2

mv

; energia potencjalna ciężkości - E

p

= mgh ;

energia potencjalna sprężystości E

ps

=

2

2

kx

; ∆E

m

= W

z

;

∆

E

k

+ ∆E

p

= W

z

E

mechaniczna

= E

potencjalna

+ E

kinetyczna

E

potencjalna

+ E

kinetyczna

= constans

Kiedy energia mechaniczna jest zachowana?
Gdy siły zewnętrzne nie wykonują pracy nad układem ciał (W

z

= 0)

∆E

k

+ ∆E

p

= W

z

; ∆E

k

+ ∆E

p

= 0