Spis treści

1.Cel projektu.........................................................................................................................2
2.Dane do projektu:................................................................................................................2

3.Obliczenia............................................................................................................................3

3.1.Cięgno o podporach podatnych...................................................................................3

3.2.Podpora podatna – słup utwierdzony w fundamencie.................................................5

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

CIĘGNO ZAKOTWIONE W KONSTRUKCJI PODATNEJ

1. Cel projektu

Zadanie projektowe obejmuje obliczenie siły naciągu cięgna, wskazanie równania linii zwisu tego
cięgna, a także obliczenie maksymalnego zwisu. Dodatkowo należy zaprojektować konstrukcję

wsporczą w postaci dwóch słupów wahaczowych wraz z odciągami oraz fundamenty dla tej
konstrukcji.

2. Dane do projektu:

–

pole powierzchni przekroju) –

A=2,60 cm

2

;

–

moduł sztywności podłużnej – E=190 GPa ;

–

sztywność cięgna – EA=49400 kN ;

–

rozstaw podpór cięgna – L=22,00 m ;

–

długość początkowa cięgna – s

0

=

22,10 m ;

–

wysokość konstrukcji – H =7,90 m ;

–

wysokość konstrukcji –

Δ

T =±30

o

C

;

–

współczynnik rozszerzalności cieplnej – α

t

=

0,000012

1

m⋅K

;

–

skończona sztywność gruntu – K

0

=

25,00

mN

m

3

;

–

obciążenie – ΣQ=80 kN → Q

i

=

80

7

=

11,43 kN .

2/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

3. Obliczenia

3.1. Cięgno o podporach podatnych

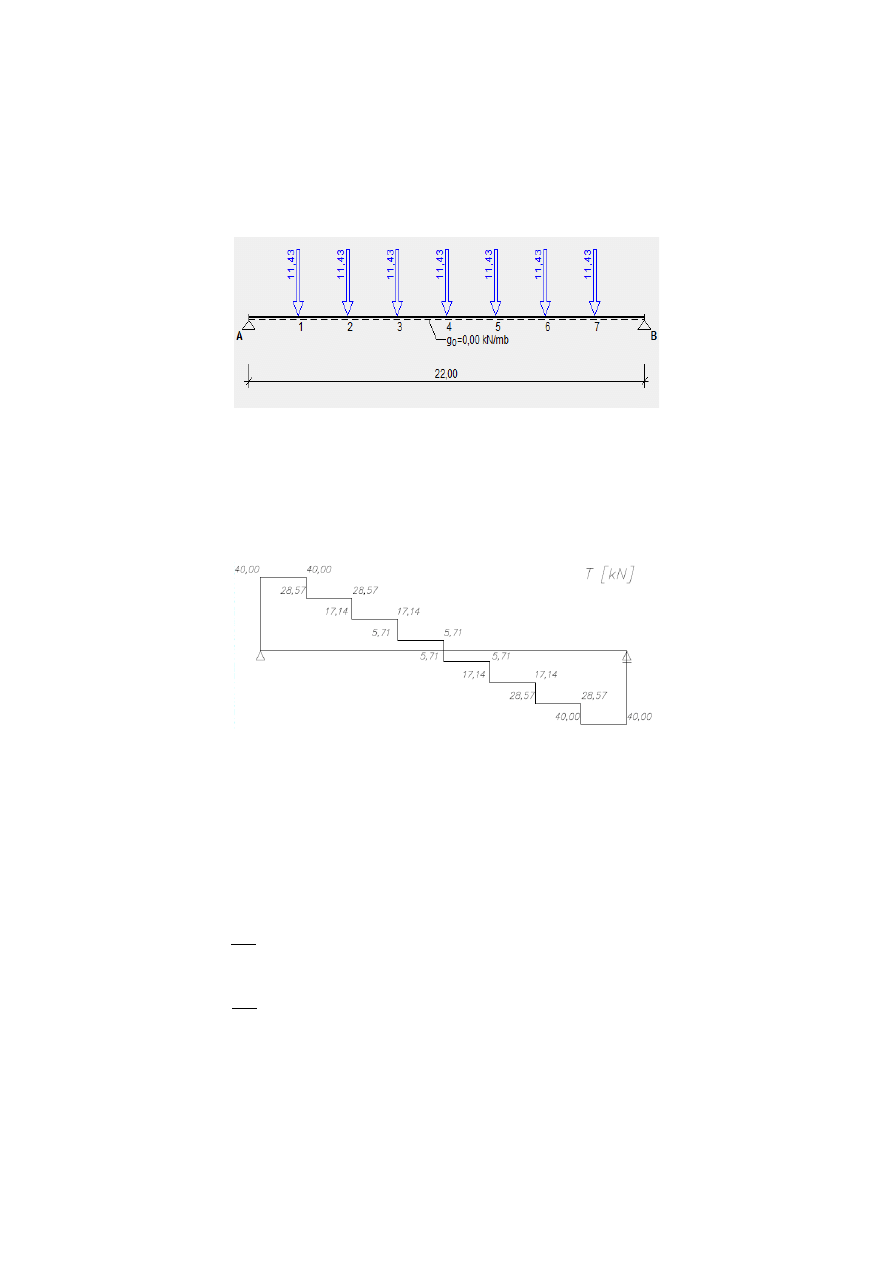
Szkic rozkładu projektowanego obciążenia

Wykresy sił przekrojowych

Wykres siły tnącej

Obciążenie zewnętrzne (wartość całki):

∫

Q( x)

2

=

685⋅L∗kN

2

m

Sztywności podpór cięgna

K

1

=

1 374

kN

m

K

2

=

1 374

kN

m

Równanie linii zwisu cięgna

Wartość siły naciągu H można wyznaczyć z równań:

3/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

–

metody 1: H

3

⋅

L

*

s

0

+

H

2

⋅

EA⋅

(

1−

L

*

s

0

+

α

t

⋅

Δ

T

)

+

H⋅

1

s

0

⋅

∫

0

L

*

Q( x)

2

dx −

EA

2 s

0

⋅

∫

0

L

*

Q( x)

2

dx=0 ;

–

metody 2: H

3

+

H

2

⋅

EA⋅

(

1−

L

*

s

0

+

α

t

⋅

Δ

T

)

−

EA

2⋅s

0

⋅

∫

0

L

*

Q( x)

2

dx =0 ,

gdzie: L

*

=

L−

(

H

K

1

+

H

K

2

)

.

Wartość siły naciągu H wyznaczono iteracyjnie, dążąc do wyzerowania reszty C(H) w

równaniach:

–

metoda 1: C (H )=−H

3

L

*

s

0

−

H

2

EA

(

1−

L

*

s

0

+

α

t

Δ

T

)

−

H

1

s

0

∫

0

L

*

Q(x )

2

dx+

EA

2 s

0

∫

0

L

*

Q(x )

2

dx

–

metoda 2: C (H )=−H

3

−

H

2

EA

(

1−

L

*

s

0

+

α

t

Δ

T

)

+

EA

2⋅s

0

∫

0

L

*

Q(x )

2

dx .

Wstępne oszacowanie siły naciągu H

Oszacowanie wstępne siły naciągu:

H

0

=

√

∫

0

L

Q(x )

2

dx

2⋅(s− L)

[

kN ]

Wstępnie oszacowana siła naciągu:

H

0

=

274,677 kN

Kres górny i dolny oraz średnia 1-szego oszacowania

Przyjęto kres górny i dolny 1-szego oszacowania wartości siły naciągu:

H

1,max

=

412,015 kN

H

1,min

=

137,338 kN

Średnia 1-szego oszacowania:

H

1

=

H

1,max

+

H

1,min

2

[

kN ]=

412,015+13 7,338

2

=

274,677 kN

W każdym kolejnym kroku zmniejszano przedział oszacowania o połowę, przyjmując za kres górny

lub dolny wartość średnią z poprzedniego oszacowania, zgodnie ze wzorami:

4/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

H

i , max

=

H

i −1

, H

i , min

=

H

i−1, min

, jeżeli C (H

i

) ≤

0 ;

H

i , min

=

H

i−1

, H

i , max

=

H

i−1, max

, jeżeliC ( H

i

) >

0 ;

Kres górny i dolny 20-tego oszacowania

Wartości kresu górnego i dolnego 20-tego oszacowania wartości siły naciągu:

–

metoda 1:

H =143,009 kN

;

–

metoda 2:

H =143,183 kN

.

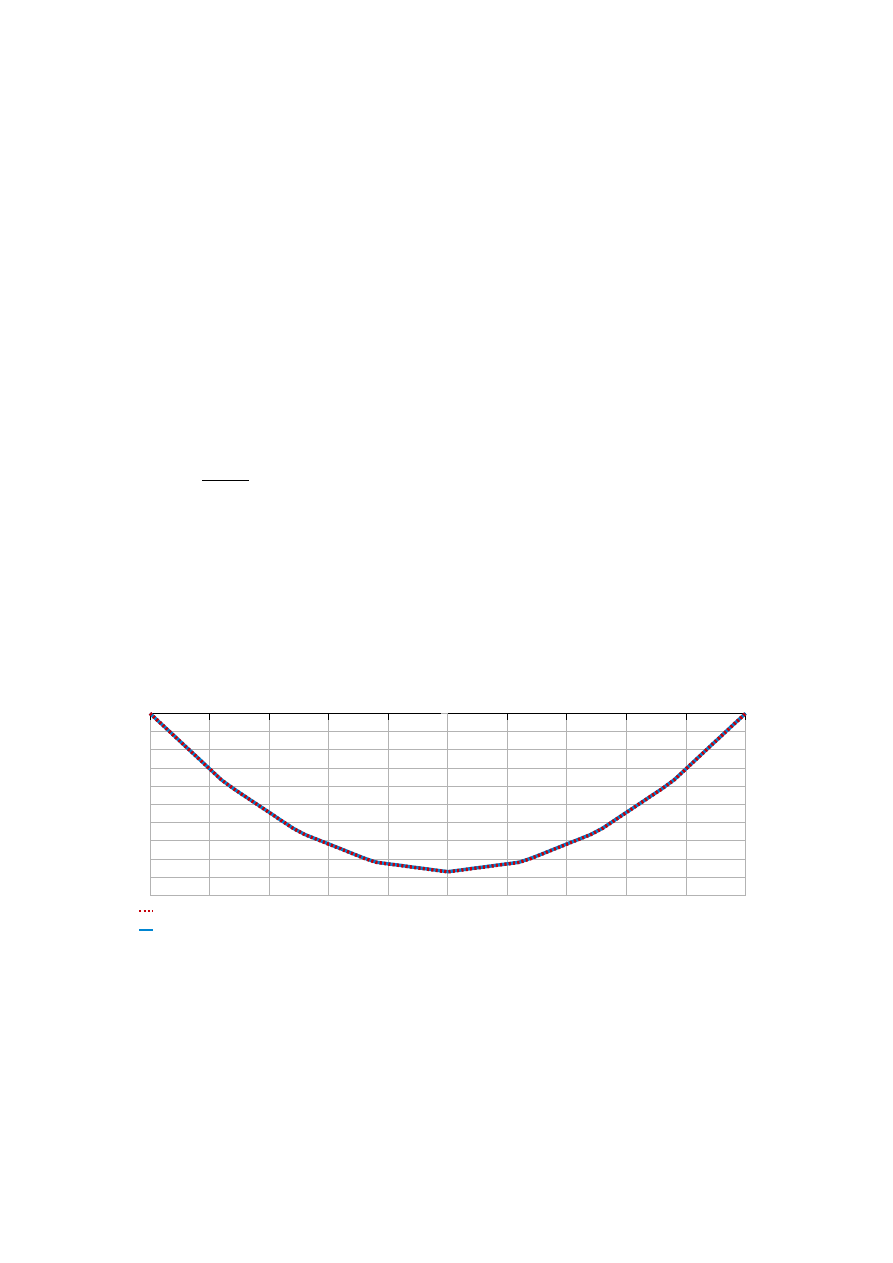
Linia zwisu cięgna

Linia zwisu cięgna w metodzie 1-szej i 2-giej:

z (ξ )=

M (ξ )

H

[

m]

Zwis maksymalny cięgna jest równy:

–

metoda 1:

z =1,742 m

;

–

metoda 2

z =1,740 m

.

Wykres linii zwisy cięgna

3.2. Podpora podatna – słup utwierdzony w fundamencie

Dane:

–

wysokość słupa – H =7,90 m ;

–

przekrój słupa – rura okrągła.

5/11

-0,5

-0,4

-0,3

-0,2

-0,1

0

0,1

0,2

0,3

0,4

0,5

-2

-1,8

-1,6

-1,4

-1,2

-1

-0,8

-0,6

-0,4

-0,2

0

metoda 1.
metoda 2.

ξ [-]

z [m]

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

Charakterystyki przekroju CHS 508 x 25:

–

średnica zewnętrzna – d =508,00 mm ;

–

grubość ścianki – t=25,00 mm ;

–

pole powierzchni przekroju poprzecznego –

A=379,35 cm

2

;

–

masa 1 m słupa – M =297,79

kg

m ;

–

moment bezwładności przy zginaniu – I =110 918 cm

4

;

–

wskaźnik sprężysty przy zginaniu – W =4 366,86cm

3

;

–

wskaźnik plastyczny przy zginaniu – W

p

=

5 837,43 cm

3

;

–

promień bezwładności –

i=17,10 cm

.

Charakterystyki stali:

–

klasa stali – S235 ;

–

granica plastyczności – f

y

=

235,00 MPa ;

–

wytrzymałość na rozciąganie – f

u

=

360,00 MPa ;

–

moduł sprężystości – E=210,00 GPa .

Wymiary fundamentu:

–

szerokość podstawy stopy fundamentowej –

b=3,50 m

;

–

długość podstawy stopy fundamentowej –

l=6,50 m

;

–

wysokość podstawy stopy fundamentowej –

h=0,60 m

;

–

długość i szerokość cokołu –

c=1,00 m

;

–

wysokość cokołu –

h=0,60 m

;

–

głębokość posadowienia –

z =1,20 m

;

–

moment bezwładności podstawy stopy – I =80,10 m

4

;

6/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

Parametry gruntu:

–

C=25,00

MN

m

3

;

–

γ=

22

kN

m

3

;

Sztywność na przesuw wierzchołka słupa

Sztywność na przesuw wierzchołka słupa wspornikowego o niepodatnym fundamencie
obciążonego siłą poziomą przyłożoną na końcu:

K

0

=

3 EI

H

3

=

0,03⋅210⋅110918

7,90

3

=

1 417

kN

m

Sztywność fundamentu na obrót:

C

y

=

i

y

⋅

C =80,10⋅25,00=2 002 474

kNm

rad

Sztywność na przesuw wierzchołka słupa wspornikowego o podatnym na obrót fundamencie,
obciążonego siłą poziomą przyłożoną na końcu:

K

1

=

1

1

K

0

+

H

2

C

y

=

1

1

1 417

+

7,90

2

2002474

=

1 357

kN

m

Siły wewnętrzne w słupie

Siła pionowa w wierzchołku słupa:

V =7⋅

11,43

2

=

40 kN

Siła pionowa w podstawie słupa:

V =40,00+

(

297,79⋅7,90)⋅9,81

1000

=

63,08 kN

Siła pozioma w słupie:

H =142,82 kN

7/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

Moment zginający w podstawie słupa:

M =142,82 kN⋅7,90 m=1 128,24 kNm

Stan graniczny nośności słupa

Klasa przekroju słupa przy zginaniu, ściskaniu i zginaniu ze ściskaniem:

–

stosunek średnicy zewnętrznej do grubości ścianki:

d

t

=

20,32≤50 ϵ

2

=

50

Przekrój przy zginaniu, ściskaniu i zginaniu ze ściskaniem jest klasy 1.

Nośność przekroju słupa przy ściskaniu:

N

c , Rd

=

A⋅f

y

γ

M0

=

379,35⋅235 MPa

10

=

8 915 kN

Obliczeniowa siła ściskająca:

N

Ed

=

63,08 kN

Warunek nośności przekroju przy ściskaniu:

N

Ed

N

c , Rd

=

63,08

8915

=

0,01<1,00

Warunek jest spełniony.

Nośność słupa przy wyboczeniu

Siła krytyczna wyboczenia sprężystego słupa wspornikowego o niepodatnym fundamencie:

ctg

(

√

N

cr ,0

EI

⋅

l

)

=

0 →

√

N

cr ,0

EI

= π

2

→

N

cr ,0

=

π

2

EI

4 l

2

Siła krytyczna wyboczenia:

N

cr ,0

=

210⋅110918⋅10

−

2

⋅π

2

2⋅7,90

2

=

9 209 kN

Siła krytyczna wyboczenia sprężystego słupa wspornikowego o podatnym na obrót fundamencie:

ctg

(

√

N

cr ,0

EI

⋅

l

)

=

√

N

cr,0

⋅

EI

C

y

8/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

Siła krytyczna wyboczenia:

N

cr

=

8 935 kN

Obliczeniowa siła ściskająca:

N

Ed

=

63,08 kN

Stosunek obliczeniowej siły ściskającej do siły krytycznej wyboczenia:

N

Ed

N

cr

=

63,08

8935

=

0,007<0,04

Warunek nośności przy wyboczeniu sprowadza się do warunku nośności przekroju.

Nośność przekroju słupa przy zginaniu

Nośność przekroju słupa przy zginaniu:

M

c,Rd

=

W

pl

⋅

f

y

γ

M 0

- klasa 1. i 2., M

c,Rd

=

W

el

⋅

f

y

γ

M0

- klasa 3.

Nośność przekroju słupa przy zginaniu:

M

c , Rd

=

1 371,8 kNm

Obliczeniowy moment zginający:

M

Ed

=

1 128,2 kNm

Warunek nośności przekroju przy zginaniu:

M

Ed

M

c , Rd

=

1128,2
1371,8

=

0,82<1,00

Warunek jest spełniony.

Nośność słupa przy zwichrzeniu
Słup nie jest narażony na zwichrzenie.

Warunek nośności przy zwichrzeniu sprowadza się do warunku nośności przekroju.
Nośność słupa przy ścinaniu

Nośność przekroju słupa przy ścinaniu:

V

pl , Rd

=

A

v

⋅

f

y

√

3⋅γ

M0

=

241,50⋅235

10⋅

√

3

=

3 277 kN

9/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

Obliczeniowa nośność przekroju przy ścinaniu:

V

Ed

V

pl , Rd

=

142,82

3277

=

0,044<1,00

Warunek jest spełniony.

Nośność przy zginaniu ze ścinaniem i siłą podłużną
Warunki normowe są spełnione.

Wpływ ścinania i ściskania na nośność przy zginaniu można pominąć.
Warunki stanu granicznego nośności są spełnione.

Stan graniczny użytkowalności
Maksymalne dopuszczalne przemieszczenie wierzchołka słupa:

u

dop

=

2H

150

=

2⋅7,90

150

=

105 mm

Przemieszczenie poziome wierzchołka słupa:

u=

1000⋅H

K

1

=

1000⋅143,18

1357

=

104 mm

Warunek stanu granicznego:

u

u

dop

=

0,99<1,00

Warunek jest spełniony.
Warunki stanu granicznego użytkowalności są spełnione.

Stateczność fundamentu
Wypadkowa siła pionowa (z ciężarem fundamentu, cokołu i gruntu nad fundamentem):

N =706,43 kN

Wypadkowy moment zginający:

M =1 109,81 kNm

Teoretyczny mimośród:

e=

M

N

=

1109,81

706,43

=

1,57 m

e

l

=

1,57
6,50

=

0,24

Maksymalne i minimalne naprężenia pod fundamentem:

σ

max

=

80,14 kPa

10/11

Konstrukcje cięgnowe - Zadanie 2 - Cięgno zakotwione w konstrukcji podatnej

σ

min

=

0,00 kPa

Długość części odrywanej:

x=1,46

x
l

=

0,23

Naprężenia nie przekraczają wartości 250 kPa .

Względna długość części odrywanej nie przekracza

0,30

.

Warunki stateczności fundamentu są spełnione.

11/11