GEOMETRIA I GRAFIKA INŻYNIERSKA

(3)

8. AKSONOMETRIA

8.1. Rzuty aksonometryczne prostokątne i ukośne

Rzuty prostokątne na wzajemnie prostopadłe rzutnie są elementem
każdego projektowania, jednakże wymagają wyobraźni przestrzennej dla
uchwycenia kształtów i położenia obiektów. Przy bardziej skomp-
likowanych obiektach uchwycenie rzeczywistego wyglądu obiektu może
być trudne. Pomocą dla wyobraźni są rzuty aksonometryczne pokazujące
obiekt w przestrzeni.

WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI

KATEDRA URZĄDZEŃ ELEKTRYCZNYCH I TECHNIKI ŚWIETLNEJ

Ponieważ z rzutów Monge’a można odczytać wszystkie współrzędne poszcze-
gólnych punktów obiektu, zatem można go narysować w układzie przestrzennym
przez odmierzanie współrzędnych.
Aksonometria jest (właśnie) metodą kreślenia rzutów w której korzysta się ze
współrzędnych rzutowanych punktów (axon – oś, metron – mierzyć). Rzut jest
konstruowany poprzez odmierzanie na osiach współrzędnych punktów obiektu
związanego z prostokątnym układem odniesienia

0xyz

(inny zapis:

0[x,y,z]

).

Definicja.

Rzut równoległy obiektu geometrycznego związanego

z prostokątnym układem odniesienia

0xyz

na płaszczyznę, w kierunku

nierównoległym do żadnej z osi tego układu ani do żadnej z płasz-
czyzn określonych tymi osiami, nazywamy rzutem aksonometrycz

-

nym, aksonometrią lub perspektywą aksonometryczną.

Patrząc na układ przestrzenny, sprowadzony jednak do płaszczyzny
rysunku, musimy zdawać sobie sprawę z tego, że w niektórych
kierunkach mamy do czynienia z deformacją liniową. Zmienia się
długość odcinków, następuje deformacja kształtu (np. koło – elipsa).

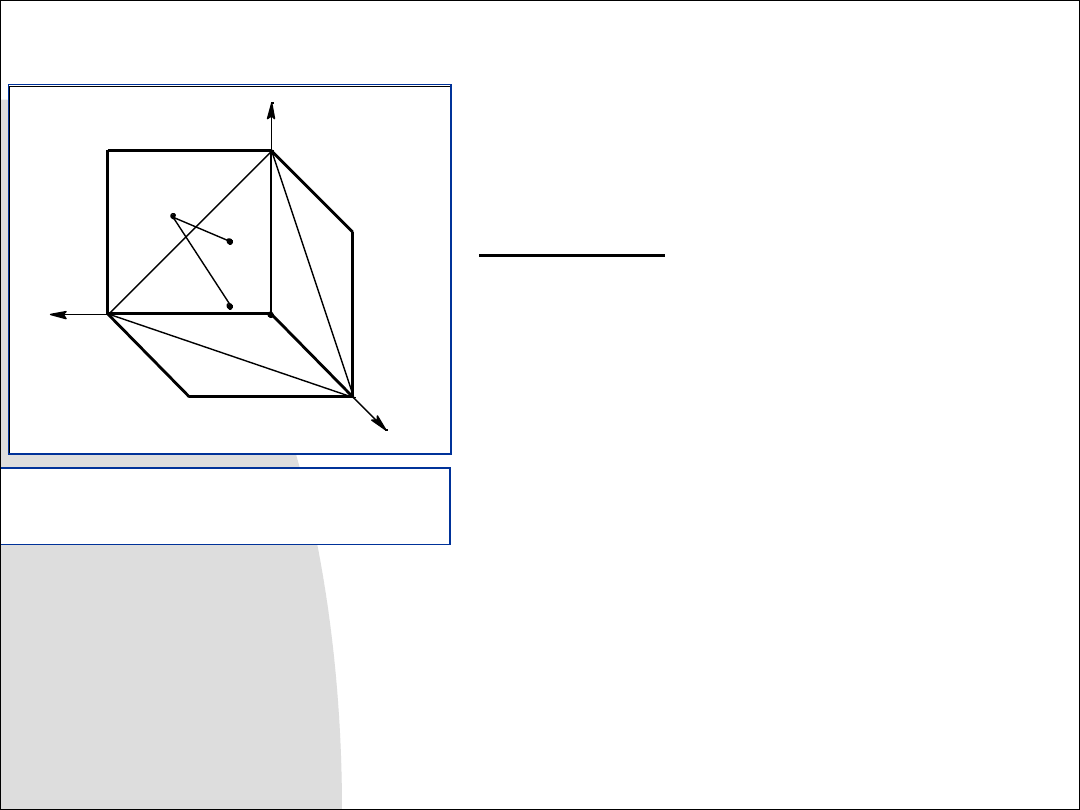
W metodzie rzutów aksonometrycznych nową
rzutnią jest płaszczyzna



a

dowolnie ustawiona

względem trzech rzutni



1

,



2

i



3

utworzonych

przez osie prostokątnego układu współrzędnych.
Rzutnię tę nazywamy rzutnią aksonometryczną.
Przecina ona płaszczyzny



1

,



2

i



3

tworzą

trójkąt śladów.

Rzut punktu

A

na płaszczyznę aksonometryczną

w kierunku prostopadłym do niej nazywamy
aksonometrią prostokątną punktu

A

. Rzut ten

oznaczmy indeksem n. Czyli

A

n

to aksonometria

prostokątna punktu

A

.

Przy rzucie w innym kierunku mamy do
czynienia z aksonometrią ukośną.

A

u

– to

aksonometria ukośna punktu

A

.

Rys. 8.1. Rzut punktu A na płaszczyznę
aksonometryczną

Możemy zauważyć, że przy danej rzutni



a

, mamy tylko jeden rzut prostokątny

punktu

A

, natomiast rzutów ukośnych jest nieskończenie wiele. Aby odwzorować

jednoznacznie kształt i położenie obiektu geometrycznego, wykreślamy na
płaszczyźnie rysunku aksonometrie trzech osi prostokątnego układu współrzędnych
dla danego kierunku rzutów

k

, trójkąt śladów pomija się.

1



2



A

x

A

n

u

A

3





a

z

y

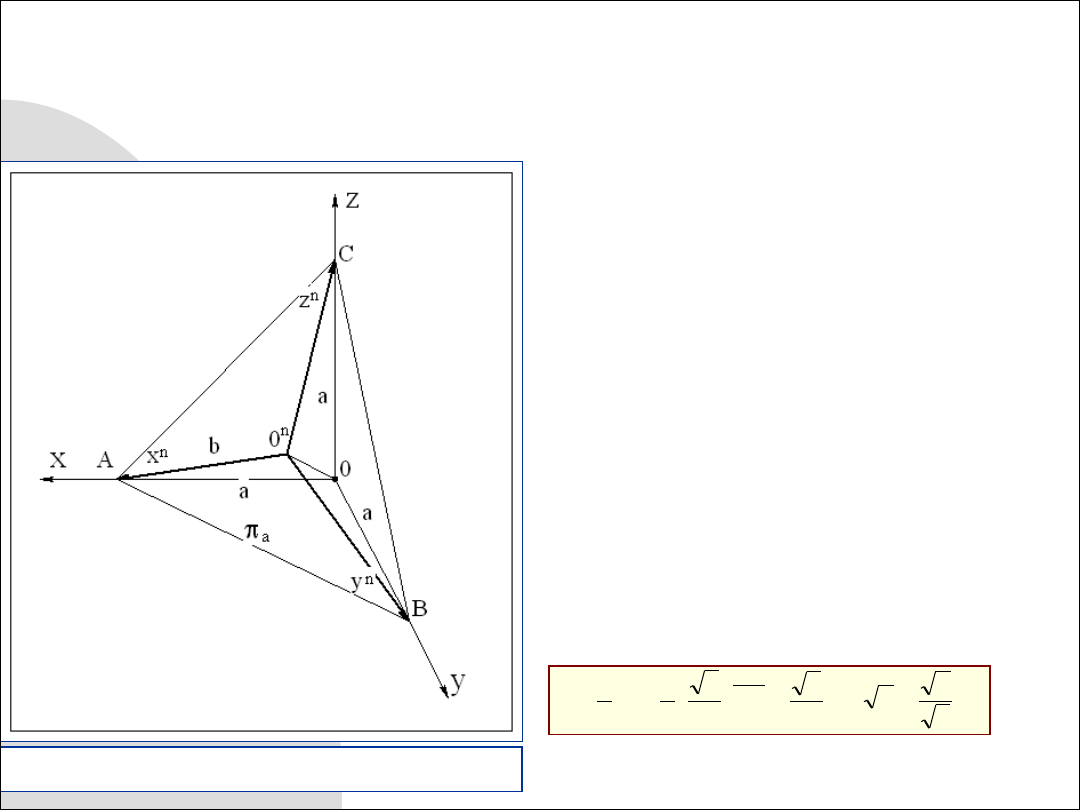
Rys. 8.2. Rzut aksonometryczny układu osi

Osie układu

x

a

,

y

a

i

z

a

leżące na rzutni aksonometrycznej



a

to osie aksonometryczne.

Każdej z tych osi przyporządkowany jest współczynnik deformacji liniowej



x

,



y

,



z

.

Spróbujmy określić te współczynniki dla konkretnego układu (rys. 8.2).

Niech rzutnia aksonometryczna



a będzie

ustawiona tak aby trójkąt śladów był
trójkątem równobocznym. Punkt

0

n

jest

rzutem aksonometrycznym prostokątnym
środka układu współrzędnych a osie

x

n

,

y

n

,

z

n

rzutami aksonometrycznymi osi

x

,

y

i

z

.

Oznaczmy długości odcinków

b = A0

n

= B0

n

= C0

n

,

a = A0 = B0 = C0

,

h

– wysokość trójkąta śladów

Współczynniki deformacji na osiach
aksonometrycznych są jednakowe
i wynoszą



x

=



y

=



z

= b/a

czyli



x

=



y

=



z

= b/a = 0,816

a

3

2

2

a

3

3

AB

2

3

3

2

h

3

2

b





















Jeżeli w pewnym przestrzennym układzie współrzędnych

0xyz

punkt

A

ma współrzędne

x

A

,

y

A

,

z

A

to w danym układzie aksonome-

trycznym

0

a

x

a

y

a

z

a

punkt ten ma współrzędne



x



x

A

,



y



y

A

,



z



z

A

.

Przyjętym współczynnikom deformacji odpowiada tylko jeden układ osi. Przy
aksonometrii prostokątnej współczynniki deformacji liniowej zależą tylko od
położenia rzutni aksonometrycznej.
W przypadku rzutów aksonometrycznych ukośnych współczynniki deformacji
zależą zarówno od położenia płaszczyzny aksonometrycznej jak i kierunku rzutów.
Swoboda wyboru płaszczyzny rzutów jak i kierunku rzutowania sprawia, że istnieje
nieskończenie wiele ustawień osi aksonometrycznych a współczynniki deformacji
mogą być także większe od 1.

Można skonstruować układ aksonometryczny prostokątny z dowol-
nymi współczynnikami deformacji liniowej. Muszą być jednak
spełnione warunki

2

2

z

2

y

2

x













2

z

2

y

2

x











2

x

2

z

2

y











2

y

2

z

2

x











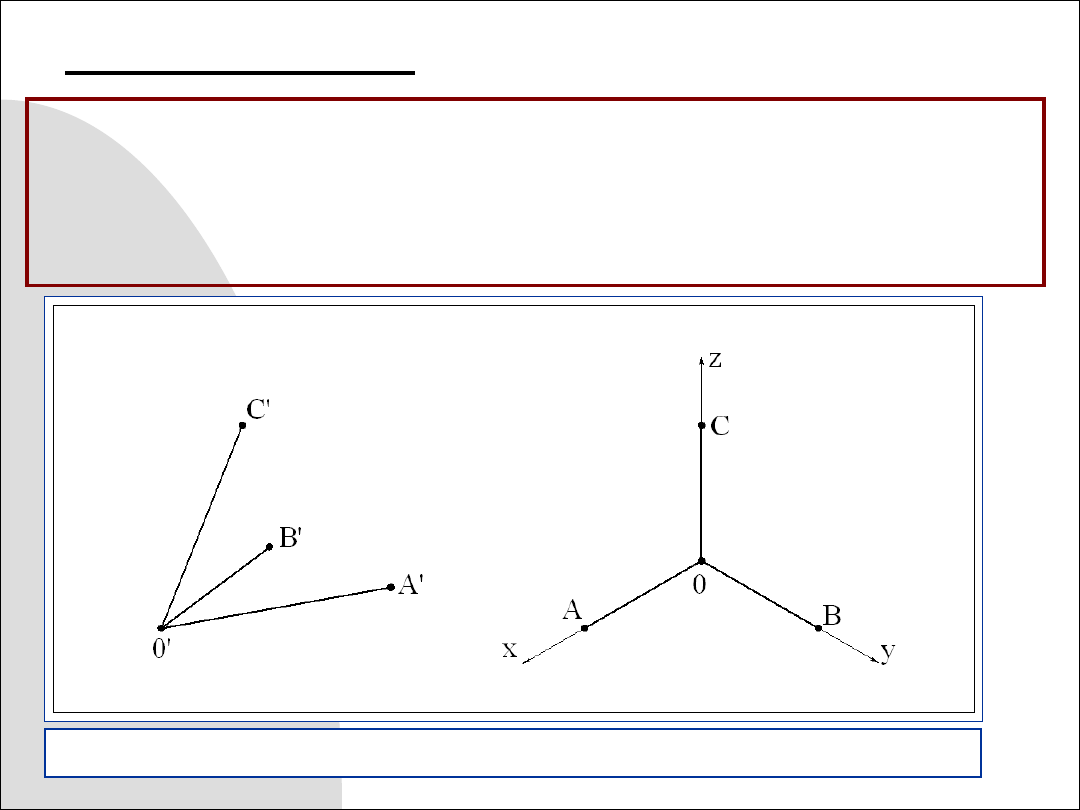
Rys. 8.3. Ilustracja twierdzenia Pohlke’go

Twierdzenie Pohlke’go

Trzy odcinki dowolnej długości, leżące na płaszczyźnie, wychodzą-
ce z jednego punktu i tworzące dowolne kąty między sobą, są rzuta-
mi równoległymi trzech równych odcinków odmierzonych na trzech
osiach prostokątnego układu współrzędnych od jego początku.

Z twierdzenia tego wynika, że przyjmując dowolną długość odcinka

0A=0B=0C=a

(rys. 8.3b) możemy obliczyć współczynniki deformacji

dla układu osi odpowiadającym kierunkom z rysunku 8.3a

i skonstruować rzut aksonometryczny.

Nic nie stoi na przeszkodzie aby przyjąć

0’A’=0’B’=0’C’

, te odcinki

są przecież dowolnej długości, otrzymując jednakowe współczynniki
deformacji na osiach. Można w końcu przyjąć dla dowolnego układu
osi



x

:



y

:



z

= 1 : 1 : 1

.

Swoboda kształtowania rzutów aksonometrycznych ukośnych
sprawia, że są one częściej stosowane od aksonometrii prostokątnej.

,

a

'

A

'

0

x





,

a

'

B

'

0

y





,

a

'

C

'

0

z





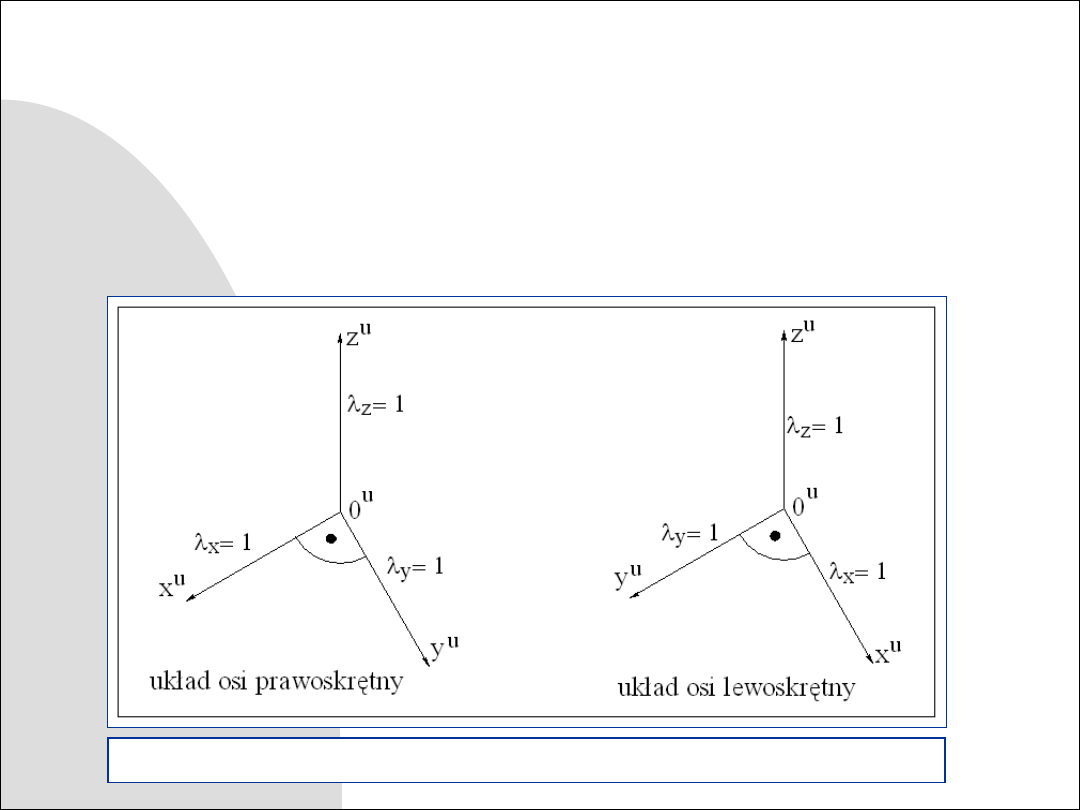
8.2. Układy osi aksonometrycznych

Najczęściej stosowane są dwa szczególne przypadki aksonometrii ukośnej
odznaczające się kątem prostym między dwiema osiami. Są to:

a) aksonometria wojskowa (rzut aksonometryczny ukośny jednomiarowy):

- układ osi prawoskrętny (izometria prawoskrętna),

- układ osi lewoskrętny (izometria lewoskrętna),

Rys. 8.4. Aksonometria wojskowa – układy osi aksonometrycznych

W aksonometrii wojskowej między osiami

x

i

y

jest kąt 90



, oś

z

jest

pionowo skierowana do góry a kąty między osiami

x

i

z

oraz

y

i

z

nie są

określone. Układ osi

xy

można dowolnie ustawić względem osi

z

– obracać

wokół osi

z

.

Obiekty płaskie leżące na płaszczyznach równoległych do rzutni poziomej
(

xy

) odwzorowują się bez zniekształceń. Współczynniki deformacji liniowej

na osiach

x, y

i

z

są równe jedności. Chociaż



z

może być w zasadzie

dowolny (w zakresie 0 - 1). Zmniejszanie współczynnika



z

,

wtedy nie jest to

rzut izometryczny, można interpretować patrzeniem na obiekt coraz bardziej
z góry. W granicznym przypadku przy



z

= 0

oś

z

staje się punktem i rzut

aksonometryczny staje się rzutem poziomym – widok z lotu ptaka.

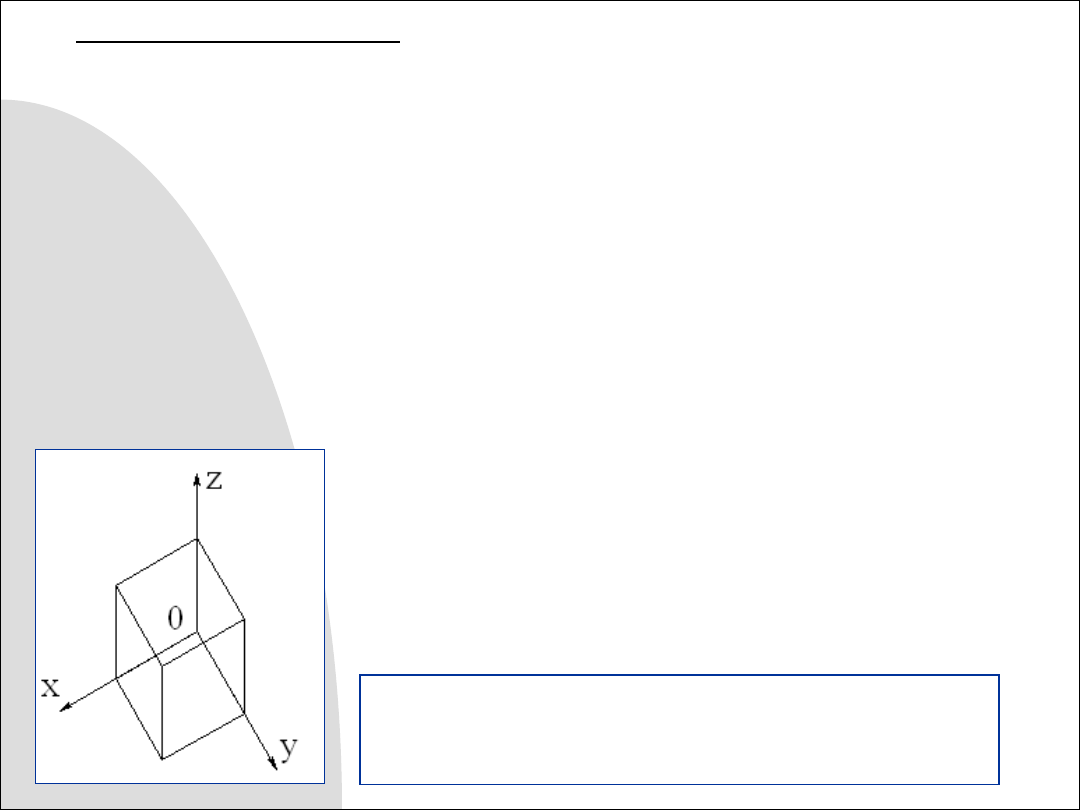
Rys. 8.5. Aksonometria (izometria) wojskowa sześcianu.
Figury (ściany) równoległe do płaszczyzny xy mają
rzeczywisty kształt i rozmiary

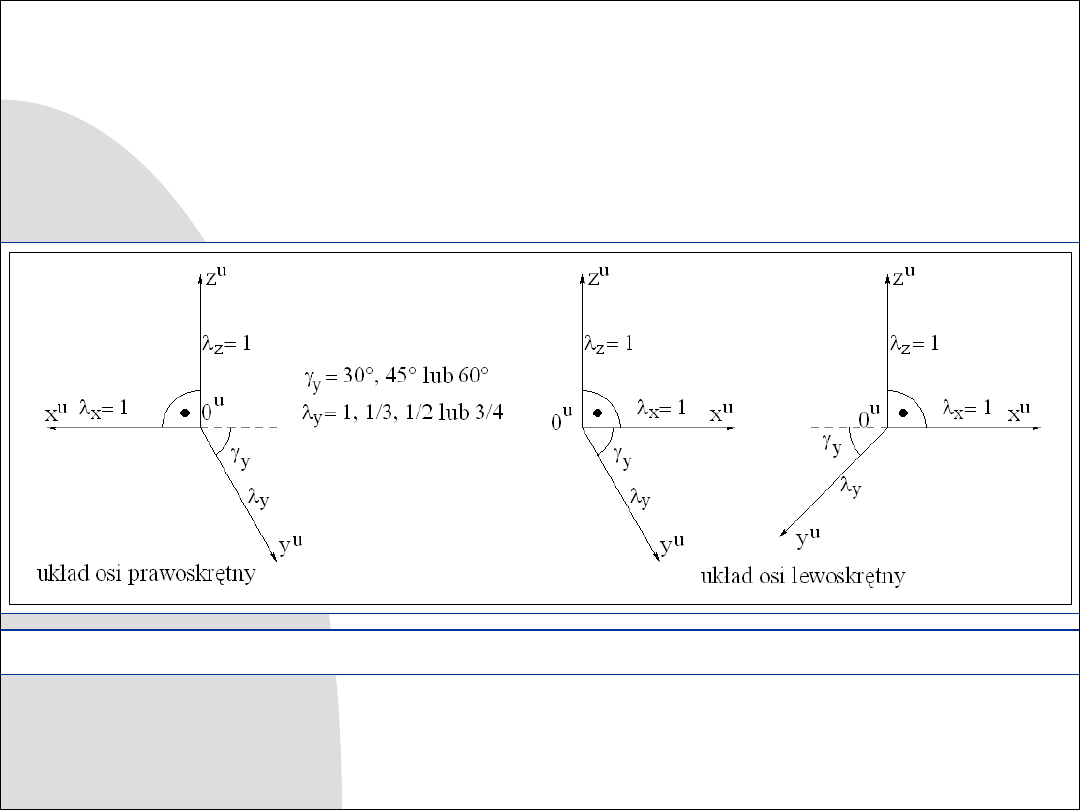
Rys. 8.6. Aksonometria kawalerska – układy osi aksonometrycznych

b) aksonometria kawalerska (układ aksonometryczny ukośny dwu-
miarowy):

- dimetria prawoskrętna,

- dimetria lewoskrętna.

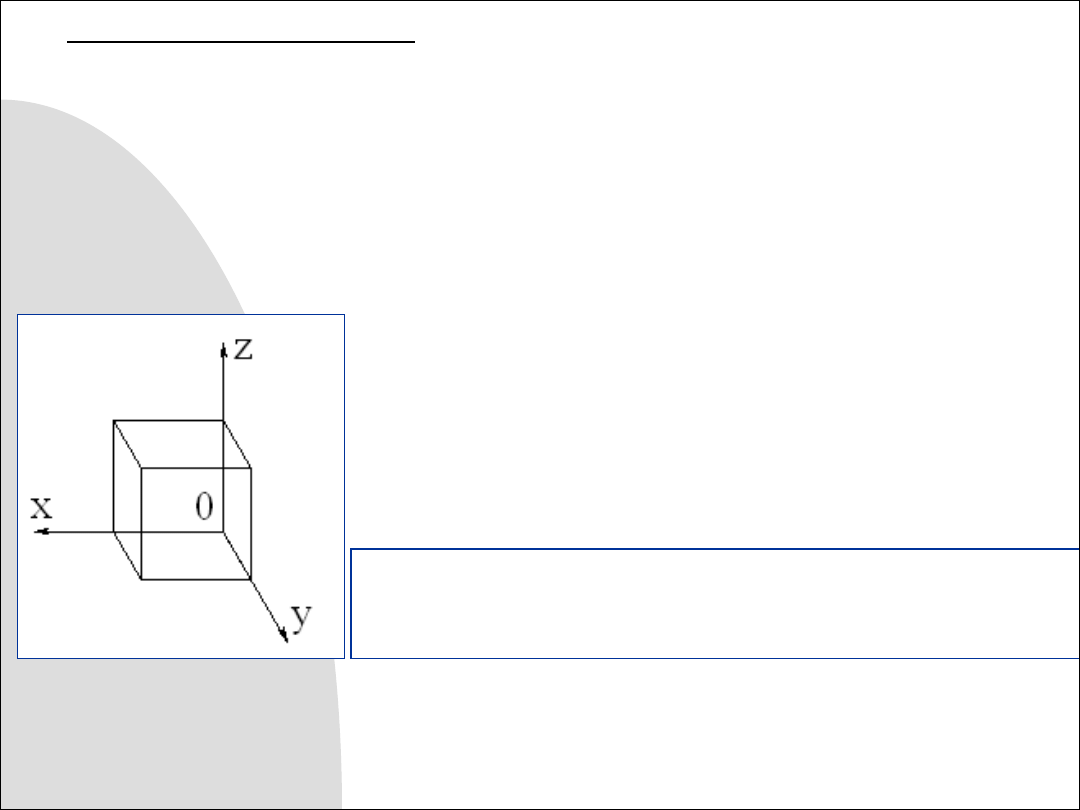
Rys. 8.7. Aksonometria kawalerska sześcianu przy l

y

= 1/2 i g

y

=

60°. Figury równoległe do płaszczyzny xz mają rzeczywisty
kształt i rozmiary

W aksonometrii kawalerskiej między osiami

x

i

z

jest kąt

90



, oś

y

jest

nachylona pod kątem

30



,

45



lub

60



do osi

x

. Współczynniki deformacji

liniowej na osiach

x

i

z

są równe

1

, natomiast na osi

y

przyjmuje się

najczęściej



y

= ¼

,

1/3

,

½

lub

¾

choć też może być równy

1

. Obiekty płaskie

równoległe do płaszczyzny

xz

odwzorowywane są bez zniekształceń. Ma to

znaczenie np. w przypadku okręgów (rzutowanie walca).

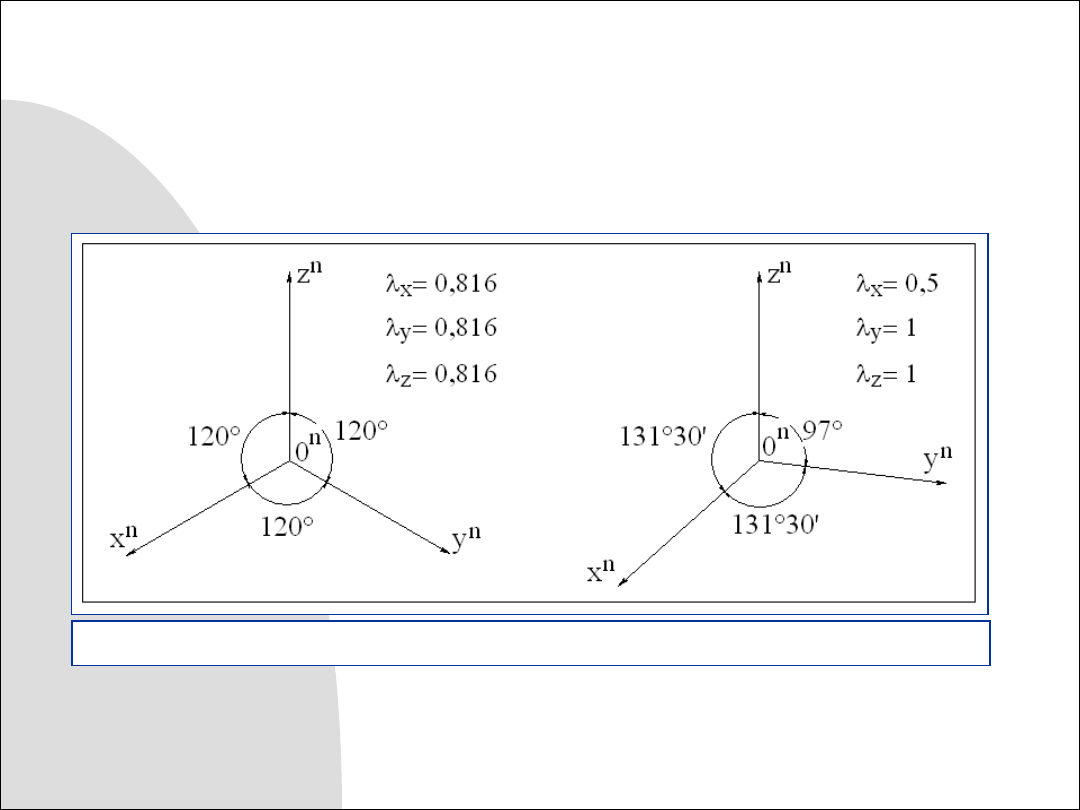
Układy osi aksonometrii prostokątnej

Zastosowanie znajdują również inne układy osi aksonometrycznych, także
związane z aksonometrią prostokątną – zależy to od rodzaju odwzorowywa-
nego obiektu. Aksonometria prostokątna jest mniej wygodna – współczynniki
deformacji i układy osi są ściśle ze sobą związane.

Rys. 8.8. Aksonometria prostokątna – przykłady układów osi aksonometrycznych

W przypadku układu z rys. 8.8a najczęściej przyjmuje się współczynniki deformacji
liniowej równe 1 – są przecież jednakowe a rozmiar obiektu przy rysunkach poglądo-
wych nie ma znaczenia.

Rysowanie rzutów aksonometrycznych w powyższych układach nie jest wygodne,
nie ma możliwości rzutowania obiektów płaskich bez zniekształceń.
Przy rysowaniu rzutów aksonometrycznych obowiązują niezmienniki rzutowania
równoległego wraz z konsekwencjami z nich wynikającymi.

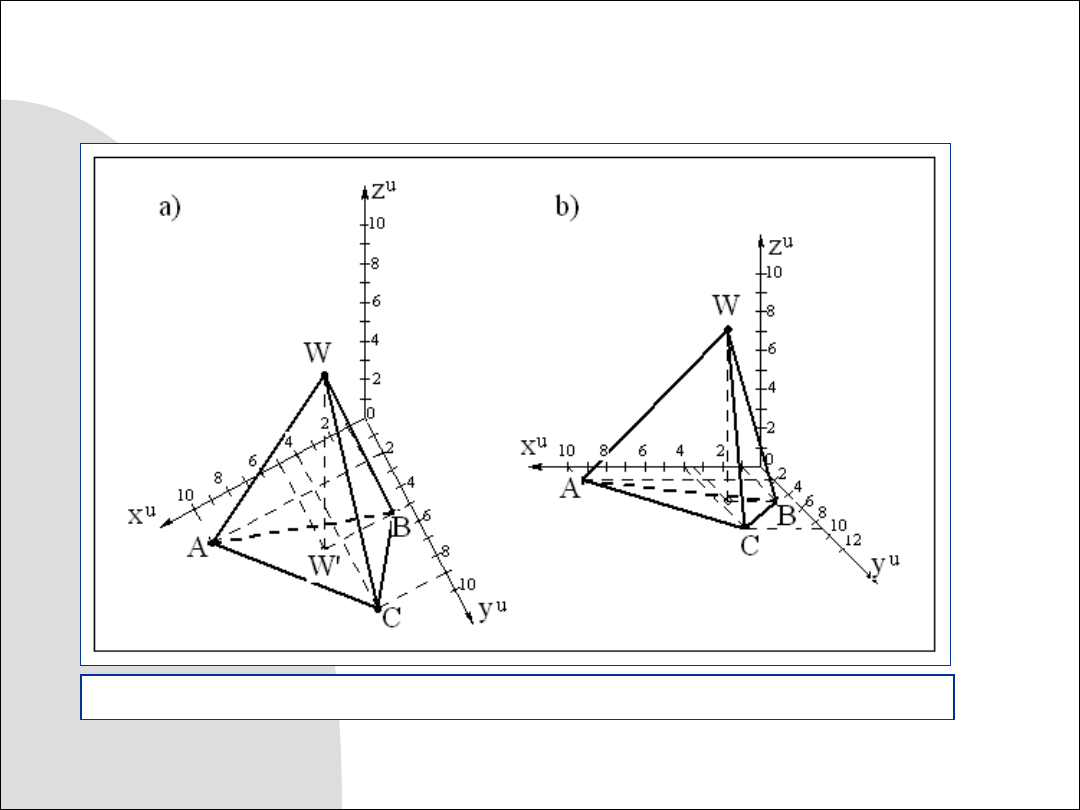
Zadanie 8.1. Wykreślić aksonometrię wojskową ostrosłupa o współ-
rzędnych podstawy

A(10, 2, 0)

,

B(1, 5, 0)

,

C(4, 9, 0)

i wierzchołka

W(5,5,9)

. Współczynniki deformacji liniowej na wszystkich osiach

są równe 1.

Należy zacząć od narysowania układu osi aksonometrii wojskowej i naniesienia na
nie podziałki. Poprzez odmierzanie współrzędnych na osiach układu należy
znaleźć położenia punktów A, B, C i W. Łącząc ze sobą punkty otrzymamy
krawędzie szukanego ostrosłupa. Należy pamiętać o tym, że krawędzie
niewidoczne rysujemy linią kreskową cienką.

Zadanie 8.2. Wykreślić aksonometrię kawalerską prawoskrętną
ostrosłupa o współrzędnych jak w poprzednim zadaniu. Nachylenie
osi

y

,



y

= 45



, współczynniki deformacji liniowej



x

= 1

,



y

= ½

,



z

=1

.

Należy pamiętać, że współrzędne punktów należy mnożyć przez odpowiednie
współczynniki deformacji liniowej. Skrócenie występuje jedynie na osi

y

i wynosi

½.

Zamiast mnożyć współrzędne y przez



y

można zagęścić dwukrotnie skalę osi

y.

Rys. 8.9. Aksonometrie ukośne ostrosłupa: a) wojskowa, b) kawalerska

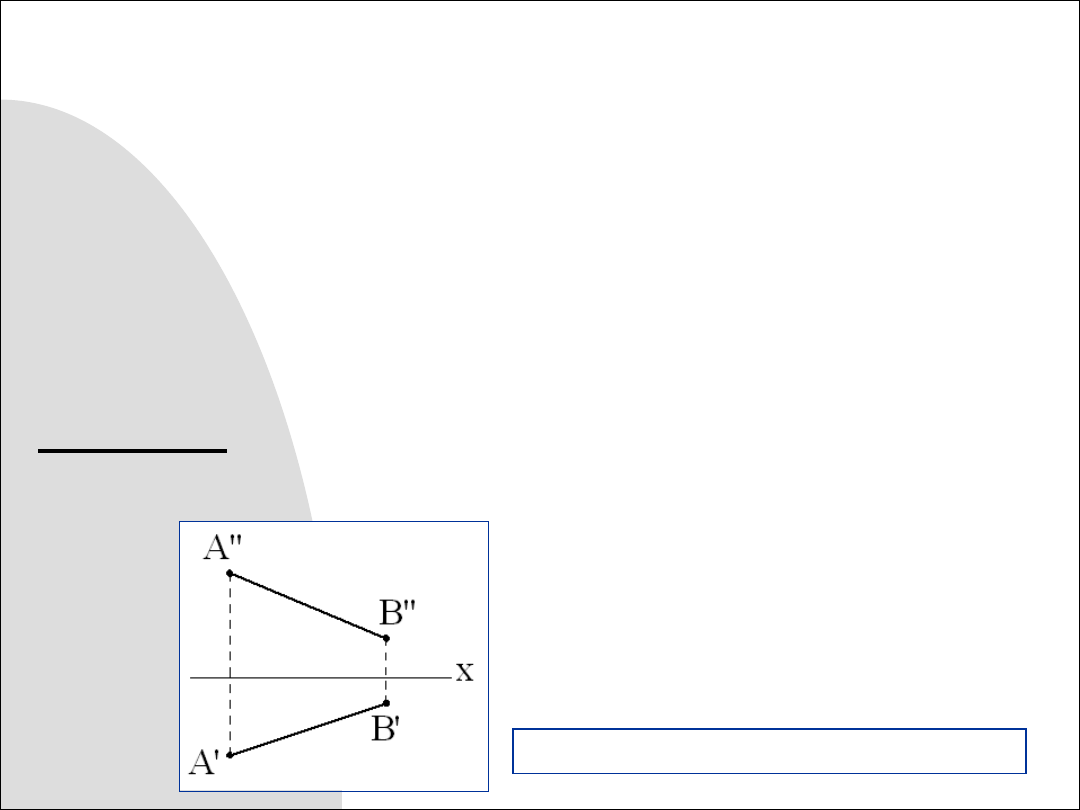
Rys. 9.1. Rzuty odcinka: poziomy i pionowy

9. WYKREŚLANIE AKSONOMETRII NA PODSTAWIE
RZUTÓW MONGE’A

Mając przynajmniej dwa rzuty prostokątne obiektu możemy wykreślić
jego aksonometrię. Wiemy, że z dwóch rzutów na płaszczyzny
wzajemnie prostopadłe można odczytać wszystkie współrzędne
punktów. Aby ujawnić współrzędne punktów trzeba rzutowany obiekt
związać z układem współrzędnych prostokątnych. Na rysunkach
technicznych nie rysuje się osi układu współrzędnych, musimy zatem
dorysować je sami.

Zadanie 9.1. Wykreślić aksonometrię wojskową odcinka danego
dwoma rzutami. Współczynniki deformacji na wszystkich osiach są
równe 1.

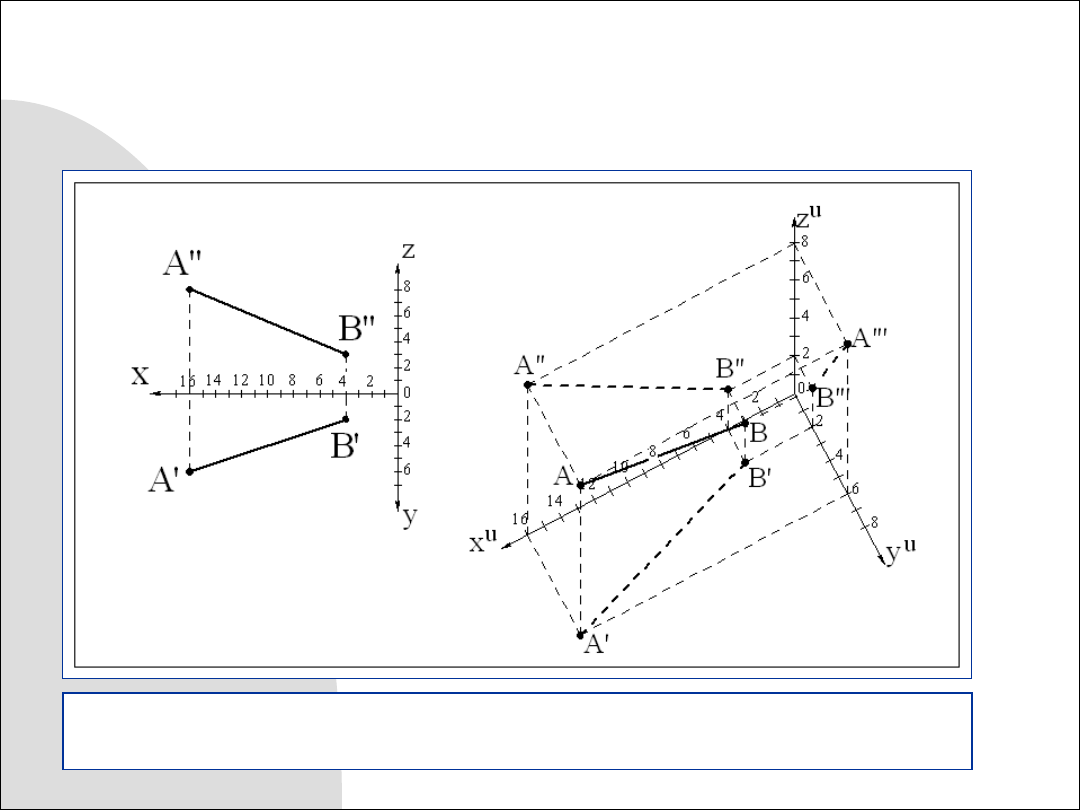
Na osi

x

musimy obrać środek układu współrzędnych, dorysować osie

z

i

y

,

a następnie je wyskalować w dowolnych jednostkach miary.
Odmierzając współrzędne punktów

A

i

B

otrzymamy aksonometrię odcinka. Na

rysunku dodatkowo narysowano również aksonometrie trzech rzutów odcinka.

Rys. 9.2. Wykreślanie aksonometrii odcinka na podstawie dwóch rzutów
prostokątnych: poziomego i pionowego

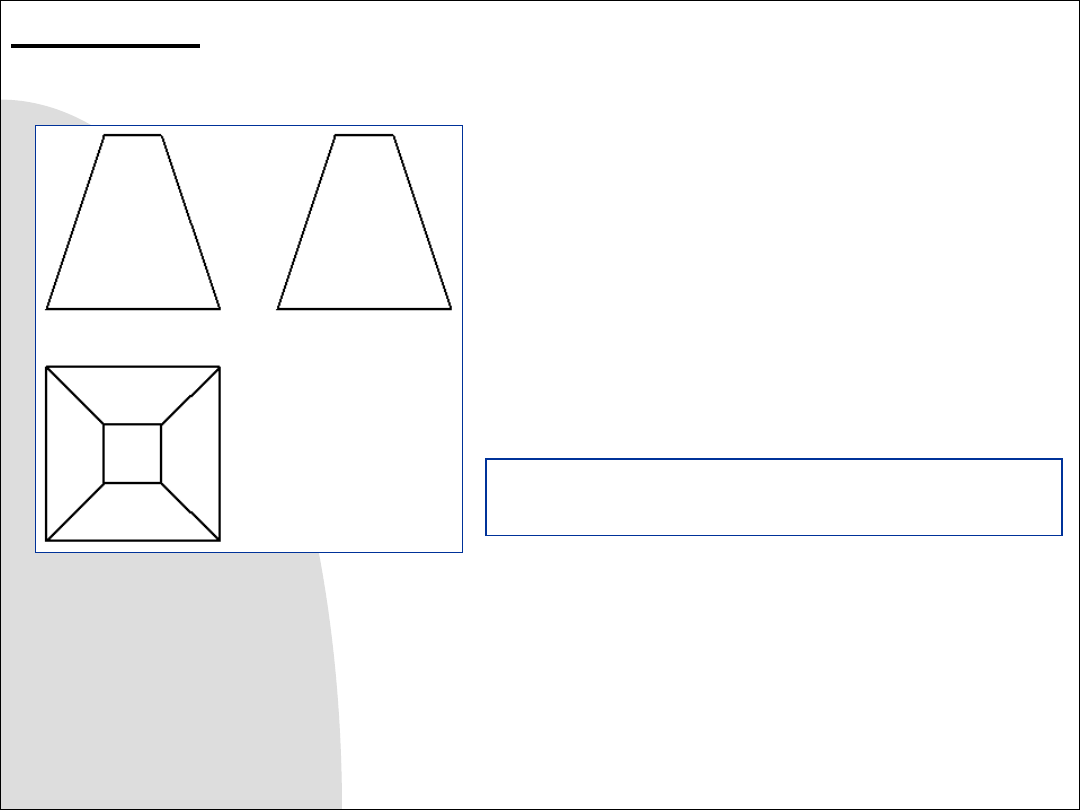
Zadanie 9.2. Wykreślić aksonometrię kawalerską prawoskrętną (



y

= ½

,



y

= 45



) bryły mając dane jej trzy rzuty główne pokazane na rysunku.

Rys. 9.3. Rzuty główne bryły powstałej przez
wycięcia z sześcianu

Rzuty główne bryły należy umieścić w układzie współrzędnych prostokątnych
i wyznaczyć współrzędne wszystkich jej wierzchołków. Odmierzając współrzędne
na osiach można wyznaczyć położenie tych punktów. Łącząc ze sobą punkty
otrzymamy krawędzie bryły. Trzeba pamiętać o współczynniku deformacji liniowej
na osi

y

.

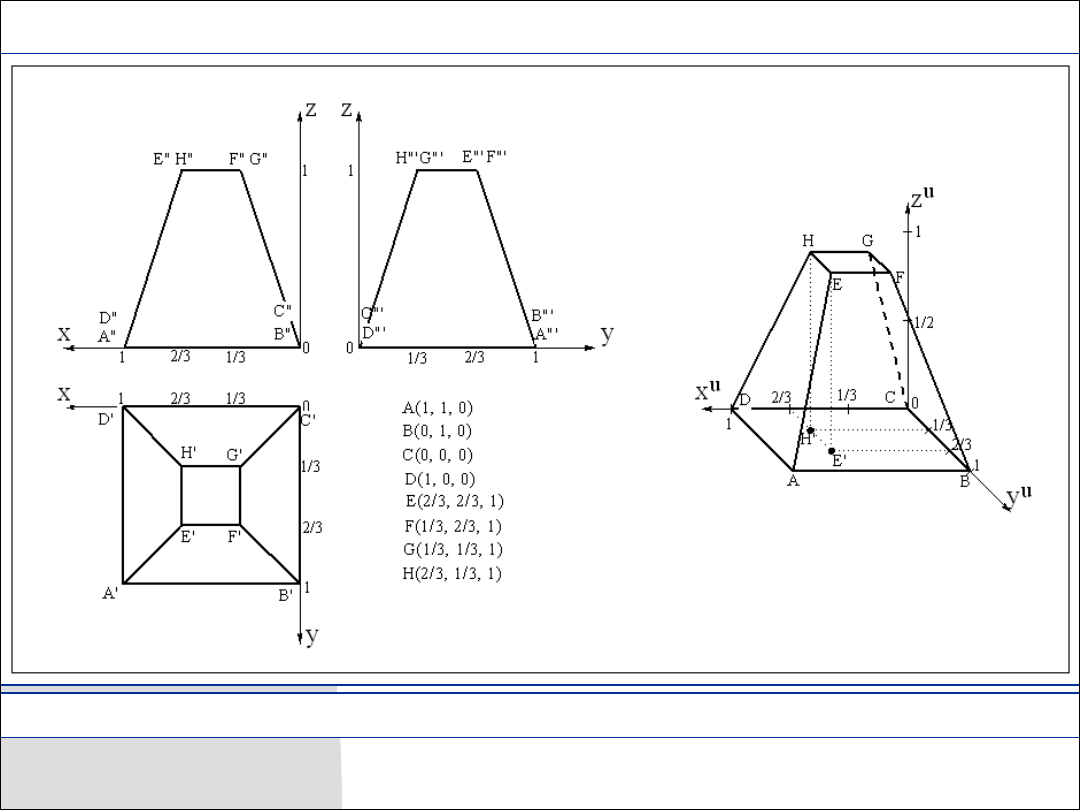
Rys. 9.4. Wykreślanie aksonometrii bryły z rzutów Monge’a

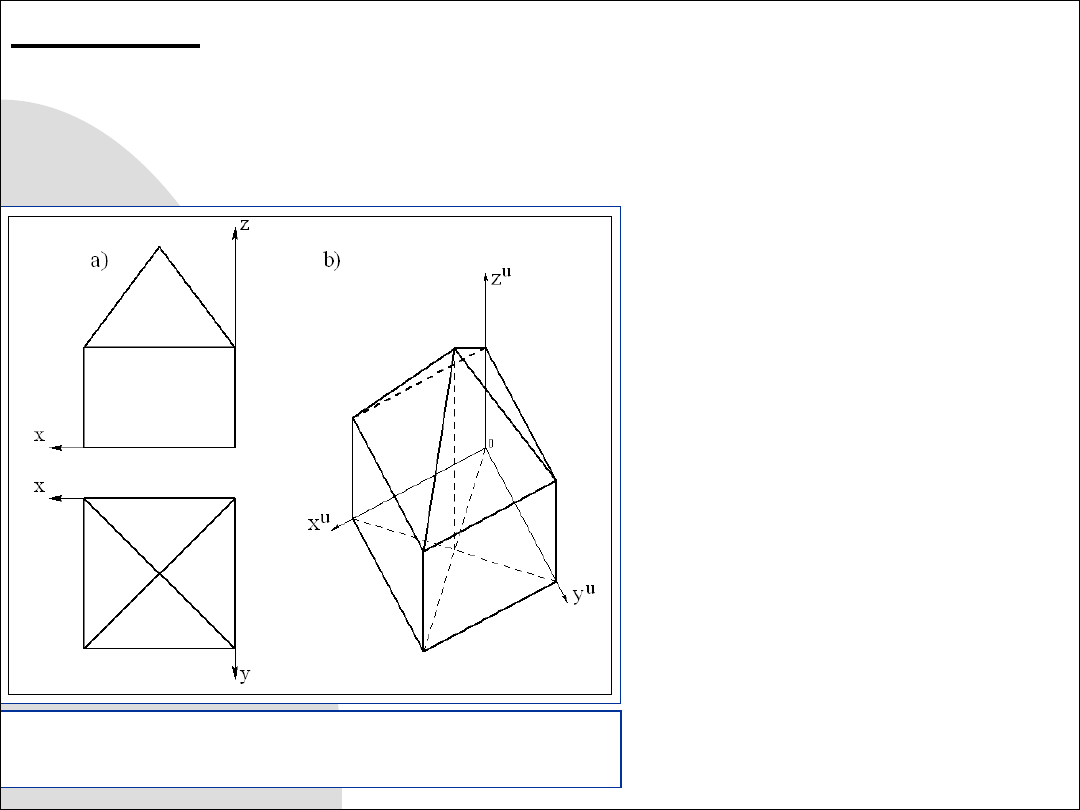
Zadanie 9.3. Wykreślić aksonometrię wojskową bryły mając dane jej
dwa rzuty.

Rys. 9.5. Wykreślanie aksonometrii bryły z dwóch
rzutów prostokątnych

Narysowanie aksonometrii bryły jest łatwiejsze jeśli istnieje już ona w naszej
wyobraźni. Można wtedy rysować ją jak gdyby od razu, nawet bez wyskalowywania
osi, potrzebne wymiary przenosząc za pomocą cyrkla.

Mimo danych tylko widoku z
przodu i widoku z góry, bryłę tę
łatwo sobie wyobrazić.
Wierzchołek “domku”
znajdujemy odmierzając jego
współrzędną ‘

z

’ pionowo do

góry od punktu przecięcia
przekątnych podstawy.

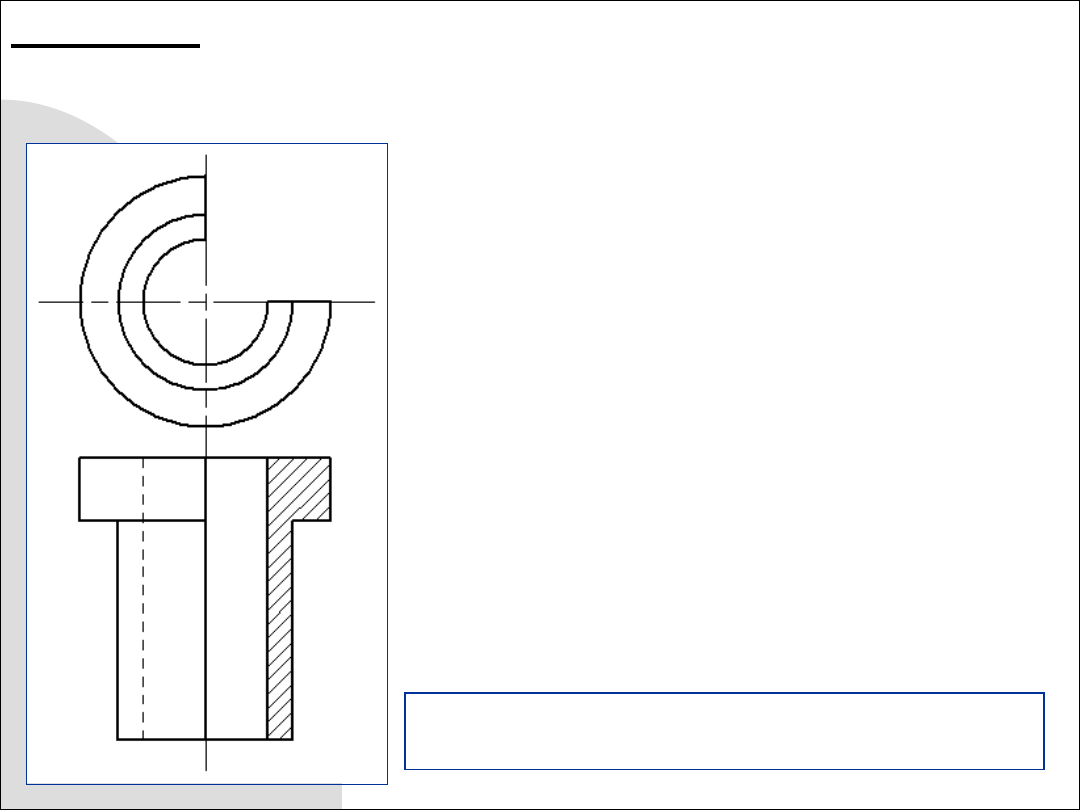
Zadanie 9.4. Wykreślić aksonometrię kawalerską bryły mając dane jej
dwa rzuty. Przyjąć



y

= 1

,



y

= 45



.

Rys. 9. 6. Rzuty poziomy i pionowy bryły o symetrii
obrotowej

Bryła dana dwoma rzutami ma symetrię obrotową.
Właściwe usytuowanie bryły w układzie
współrzędnych może ułatwić jej narysowanie.
Najwłaściwszym wyborem jest aksonometria
kawalerska. Wszystkie okręgi (części okręgu)
zawarte w tej bryle są równoległe do płaszczyzny
pionowej (

xz

). Przy aksonometrii kawalerskiej nie

zmieniają swoich rozmiarów i kształtu.

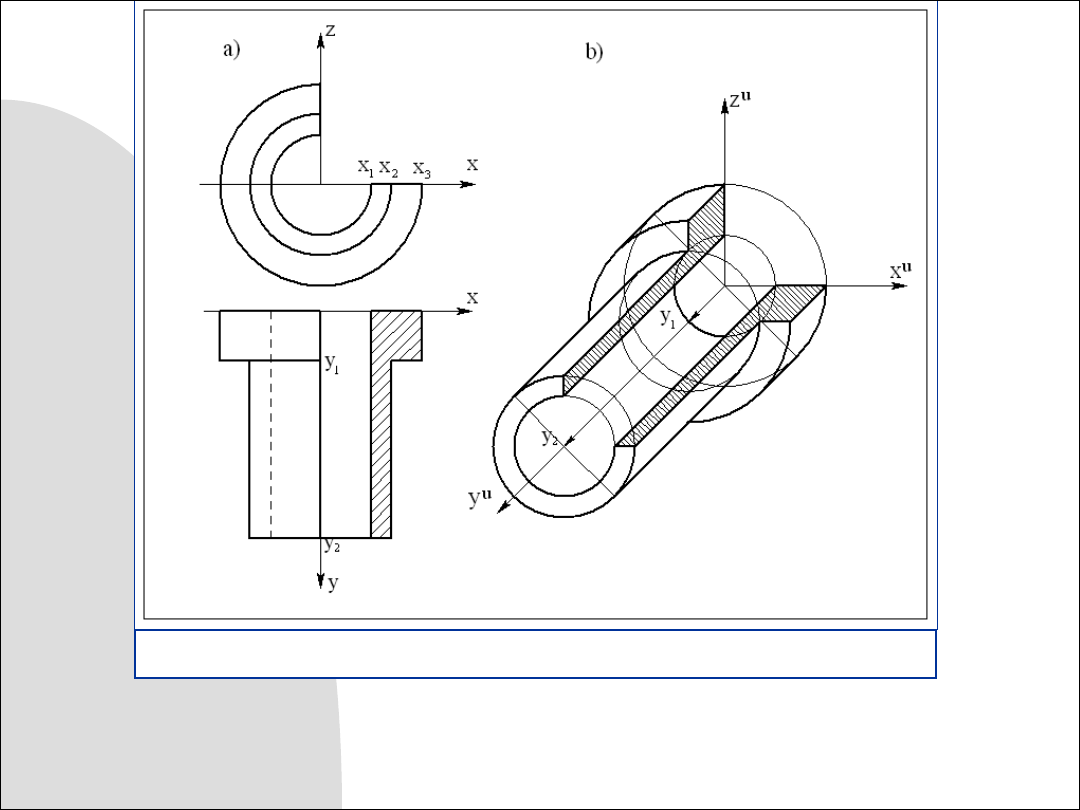
Rys. 9.7. Wykreślanie aksonometrii bryły o symetrii obrotowej

Środki okręgów o promieniach

x

1

,

x

2

i

x

3

leżą na osi

y

, przy czym przy

y = 0

znajdują

się środki okręgów

x

1

i

x

3

, przy

y = y

1

środki

x

2

i

x

3

, a przy

y = y

2

należy narysować

okręgi o promieniach

x

1

i

x

2

.

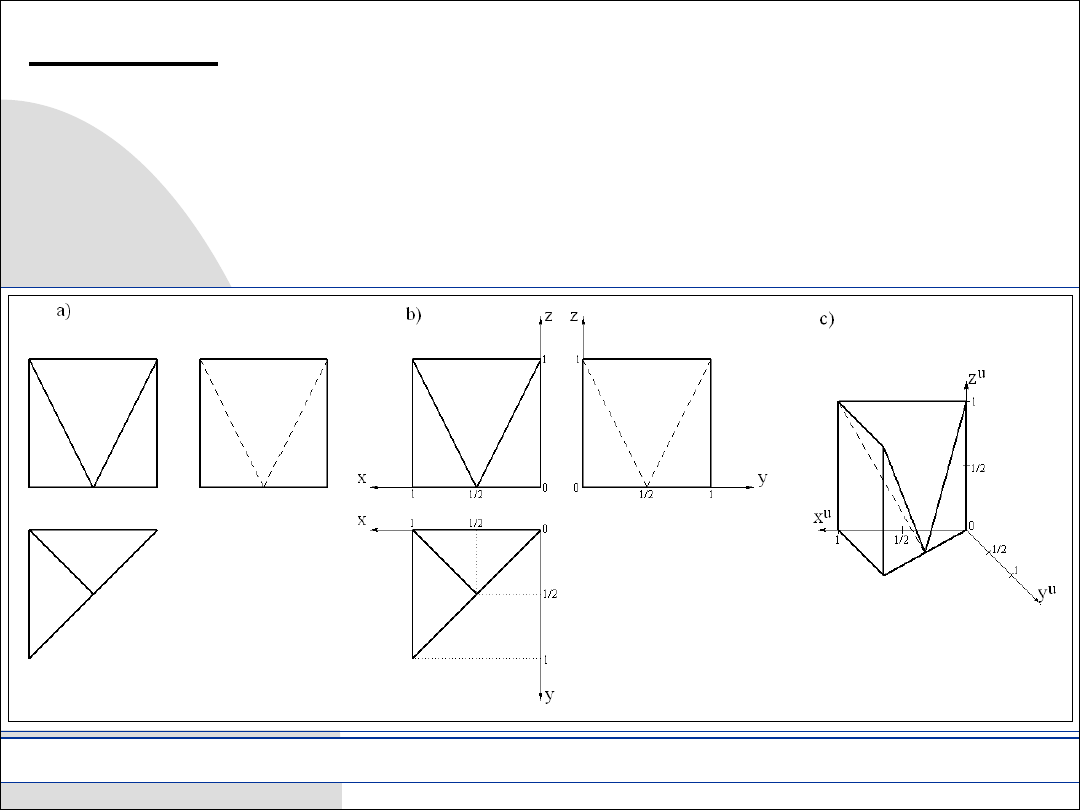
Zadanie 9.5. Wykreślić aksonometrię kawalerską prawoskrętną (



y

=

½

,



y

= 45



) bryły mając dane jej trzy rzuty główne.

Rys. 9.8. Wykreślanie aksonometrii bryły z rzutów Monge’a

Wiedząc, że bryła powstała przez wycięcia z sześcianu, możemy jej aksonometrię
wykreślić szkicując najpierw sześcian a następnie zrealizować wycięcia tak, aby
widoki bryły w kierunku płaszczyzn wyznaczonych przez osie zgadzały się
z danymi rzutami.

Dziękuję za uwagę