1

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – ekstremum funkcji liniowej przy liniowych

ograniczeniach

Opracowanie modelu programowania linowego:

●

określenie zmiennych zadania,

●

określenie ograniczeń w postaci liniowych równań lub nierówności,

●

wyznaczenie linowej funkcji celu podlegającej minimalizacji lub
maksymalizacji

Programowanie liniowe

Metody:

metoda graficzna,
metoda algebraiczna,
metoda simpleks.

2

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – przykład

Zadanie: Pewien zakład produkuje dwa typy płytek chodnikowych.
Oba typy wymagają zużycia jednakowej ilości surowców (piasek,
woda, żwir, cement). Jeden typ jest barwny i do jego produkcji
potrzebna jest farba. Wyprodukowanie 1 tony płytek barwnych
wymaga 2h pracy maszyn, 3h pracy ludzkiej i 2l barwnika. Produkcja
tony płyt bezbarwnych wymaga 1h pracy maszyn, 3h pracy ludzkiej.
Zysk: płyty barwne 300 zł/t, płyty bezbarwne 200 zł/t. Dysponujemy
10h pracy urządzeń, 24h pracy ludzkiej i 8l barwnika. Ile
wyprodukować płyt i jakich aby osiągnąć maksymalny zysk.

3

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – przykład

Oznaczenia:

x

1

= płyty barwne ,

x

2

= płyty bezbarwne.

Funkcja celu:

Z

=300 x

1

200 x

2

 max

Ograniczenia:

{

2 x

1

x

2

10

3 x

1

3 x

2

24

2 x

1

8

x

i

0 i=12

4

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

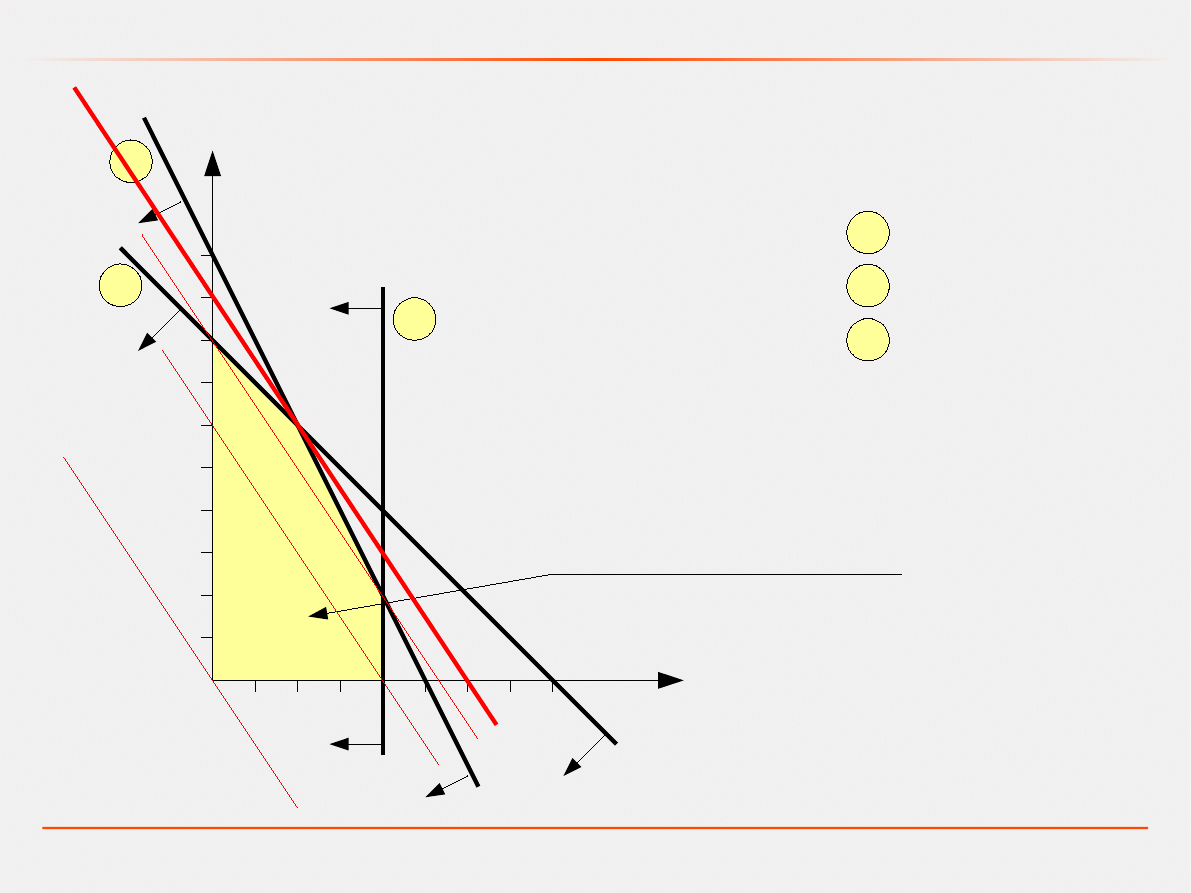
Programowanie liniowe – metoda graficzna

Funkcja celu:

Z

=300 x

1

200 x

2

 max

Ograniczenia:

{

2 x

1

x

2

10

3 x

1

3 x

2

24

2 x

1

8

2

1

1

2

3

4

5

6

7

8

0

1

3

2

4

5

6

7

8

9

10

3

2

1

3

x

2

x

1

obszar rozwiązań dopuszczalnych

Z=

0

Z=

12

00

Z=

16

00

Z=

18

00

5

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

- zmienne dopełniające

Programowanie liniowe – metoda algebraiczna

Funkcja celu:

Z

=300 x

1

200 x

2

 max

Ograniczenia:

{

2 x

1

x

2

10

3 x

1

3 x

2

24

2 x

1

8

Postać kanoniczna – zamieniamy nierówności na równości:

{

2 x

1

x

2

x

3

=10

3 x

1

3 x

2

x

4

=24

2 x

1

x

5

=8

x

i

0 i=15

Z

=300 x

1

200 x

2

0 x

3

0 x

4

0 x

5

Przekształcamy ograniczenia, tak aby wszystkie wyrazy wolne były

nieujemne i zapisujemy postać kanoniczną.

Uwzględniamy zmienne dopełniające w funkcji celu:

6

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – metoda algebraiczna

{

2 x

1

x

2

x

3

=10

3 x

1

3 x

2

x

4

=24

2 x

1

x

5

=8

Z

=300 x

1

200 x

2

0 x

3

0 x

4

0 x

5

Mamy 3 równania i 5 niewiadomych:

1

x

1

=x

2

=0  zmienne wolne

{

x

3

=10

x

4

=24

x

5

=8

x

1

=0, x

2

=0, x

3

=10, x

4

=24, x

5

=8  rozw. bazowe dopuszczalne

Z

=0  wartość funkcji celu

x

3,

x

4,

x

5

 zmienne bazowe

7

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – metoda algebraiczna

2

x

1

=x

3

=0  zmienne wolne

{

x

2

=10

x

4

=−6

x

5

=8

x

1

=0, x

2

=10, x

3

=0, x

4

=−6, x

5

=8  rozw.bazowe niedopuszczalne

x

2,

x

4,

x

5

 zmienne bazowe

3

x

1

=x

4

=0  zmienne wolne

{

x

2

=8

x

3

=2

x

5

=8

x

1

=0, x

2

=8, x

3

=2, x

4

=0, x

5

=8  rozw. bazowe dopuszczalne

Z

=1600  wartość funkcji celu

x

2,

x

3,

x

5

 zmienne bazowe

8

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – metoda algebraiczna

4

x

1

=x

5

=0  zmienne wolne

{

x

2

x

3

=10

3 x

2

x

4

=24

0

=8

 układ sprzeczny

zmienne x

2,

x

3,

x

4

−nie mogą być zmiennymi bazowymi

x

2,

x

3,

x

4

 zmienne bazowe

5

x

2

=x

3

=0  zmienne wolne

x

1

=5, x

2

=0, x

3

=0, x

4

=9, x

5

=−2  rozw. bazowe niedopuszczalne

x

1,

x

4,

x

5

 zmienne bazowe

6

x

2

=x

4

=0  zmienne wolne

x

1

=8, x

2

=0, x

3

=−6, x

4

=0, x

5

=−8  rozw. bazowe niedopuszczalne

x

1,

x

3,

x

5

 zmienne bazowe

9

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – metoda algebraiczna

7

x

2

=x

5

=0  zmienne wolne

x

1

=4, x

2

=0, x

3

=2, x

4

=12, x

5

=0  rozw. bazowe dopuszczalne

Z

=1200  wartość funkcji celu

x

1,

x

3,

x

4

 zmienne bazowe

8

x

3

=x

4

=0  zmienne wolne

Z

=1800  wartość funkcji celu

x

1,

x

2,

x

5

 zmienne bazowe

9

x

3

=x

5

=0  zmienne wolne

x

1

=4, x

2

=2, x

3

=0, x

4

=6, x

5

=0  rozw.bazowe dopuszczalne

Z

=1600  wartość funkcji celu

x

1,

x

2,

x

4

 zmienne bazowe

x

1

=2, x

2

=6, x

3

=0, x

4

=0, x

5

=4  rozw.bazowe dopuszczalne

10

METODY OPTYMALIZACJI, Informatyka

Szczecin - 2008-03-16

Programowanie liniowe – metoda algebraiczna

10

x

4

=x

5

=0  zmienne wolne

x

1

=4, x

2

=4, x

3

=−2, x

4

=0, x

5

=0  rozw. bazowe niedopuszczalne

x

1,

x

2,

x

3

 zmienne bazowe

C

n

m

=

n !

m !

n−m!

C

5

3

=

5 !

3 !

5−3!

=10

Ilość możliwych rozwiązań jakie należy sprawdzić:

n – liczba zmiennych,

m – liczba ograniczeń