2008-03-16

Szczecin

1

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych

Z OGRANICZENIAMI

2008-03-16

Szczecin

2

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

Zadanie optymalizacji warunkowej – zminimalizować

f(x) przy ograniczeniach:

h

k

 x=0

g

j

x0

x

i

U 

x

i

x

i

D

k

=1,2 , , K

j

=1,2 , , J

i

=1,2 ,, N

2008-03-16

Szczecin

3

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

h

k

 x=0

k

=1,2 , , K

Rozwiązywanie zadania poszukiwania minimum warunkowego:

równanie

K

n

wykorzystujemy do wyeliminowania dowolnych K zmiennych.
Funkcję f(x) doprowadza się do postaci:

f

x

1,

x

2,

, x

n

= f

1

 y

1,

y

2,

 , y

n

−K



y

1

, y

2

, ..., y

n-K

– niewyeliminowane zmienne

2008-03-16

Szczecin

4

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

Rozwiązywanie zadanie poszukiwania minimum warunkowego
przekształcamy w zadanie poszukiwania wartości zmiennych

y

1

, y

2

, ..., y

n-K

dla których funkcja f

1

(y) osiąga minimum i na które

nie nałożono żadnych ograniczeń.

zadanie minimalizacji

warunkowej

zadanie minimalizacji

bezwarunkowej

2008-03-16

Szczecin

5

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

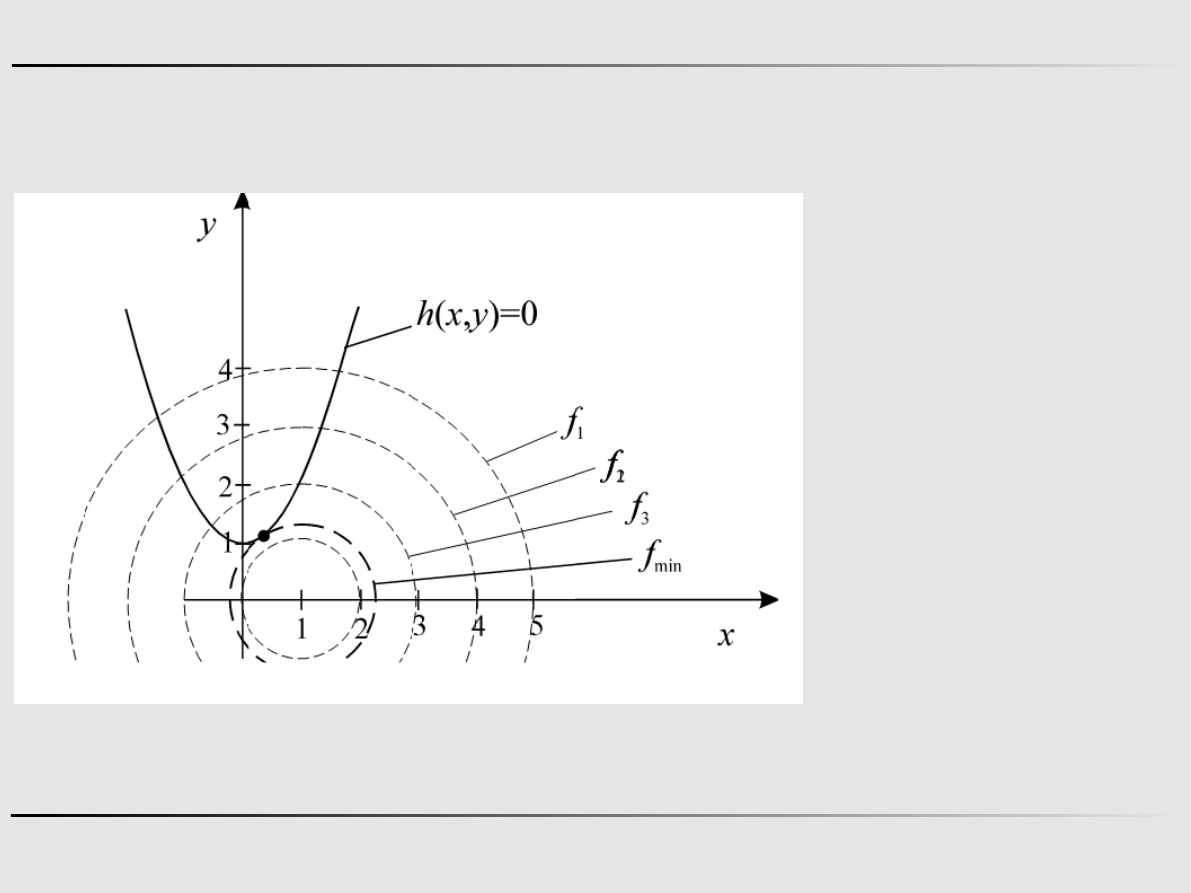
Przykład 1. Dana jest funkcja dwóch zmiennych i ograniczenie.

Znajdź minimum tej funkcji.

f

x , y=x−1

2

 y

2

h

 x , y=x

2

− y1=0

x

2

− y1=0  y=x

2

1

f

x , x

2

1= f  x= x−1

2

 x

2

1

2

min f

 x ∂

f

 x

∂ x

=0 2 x

3

3 x−1=0  x

m

=0.313

y

m

=x

m

2

1=1.098

f

x

m

, y

m

=1.678

2008-03-16

Szczecin

6

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

Przykład 1. Dana jest funkcja dwóch zmiennych i ograniczenie.

Znajdź minimum tej funkcji.

f

 x , y= x−1

2

 y

2

h

 x , y=x

2

− y1=0

y

m

=x

m

2

1=1.098

f

 x

m

, y

m

=1.678

2008-03-16

Szczecin

7

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

Przykład 2. Dana jest funkcja dwóch zmiennych i ograniczenie.

Znajdź minimum tej funkcji.

f

x , y , z=x⋅y⋅z

h

 x , y , z=x

2

⋅z y⋅z

2

 y

−1

⋅x=0

✔ uzyskanie wyrażenia analitycznego dowolnej zmiennej za

pomocą innych w tym wypadku nie jest możliwe.

2008-03-16

Szczecin

8

Metody optymalizacji, Informatyka

Ekstremum funkcji wielu zmiennych z ograniczeniami

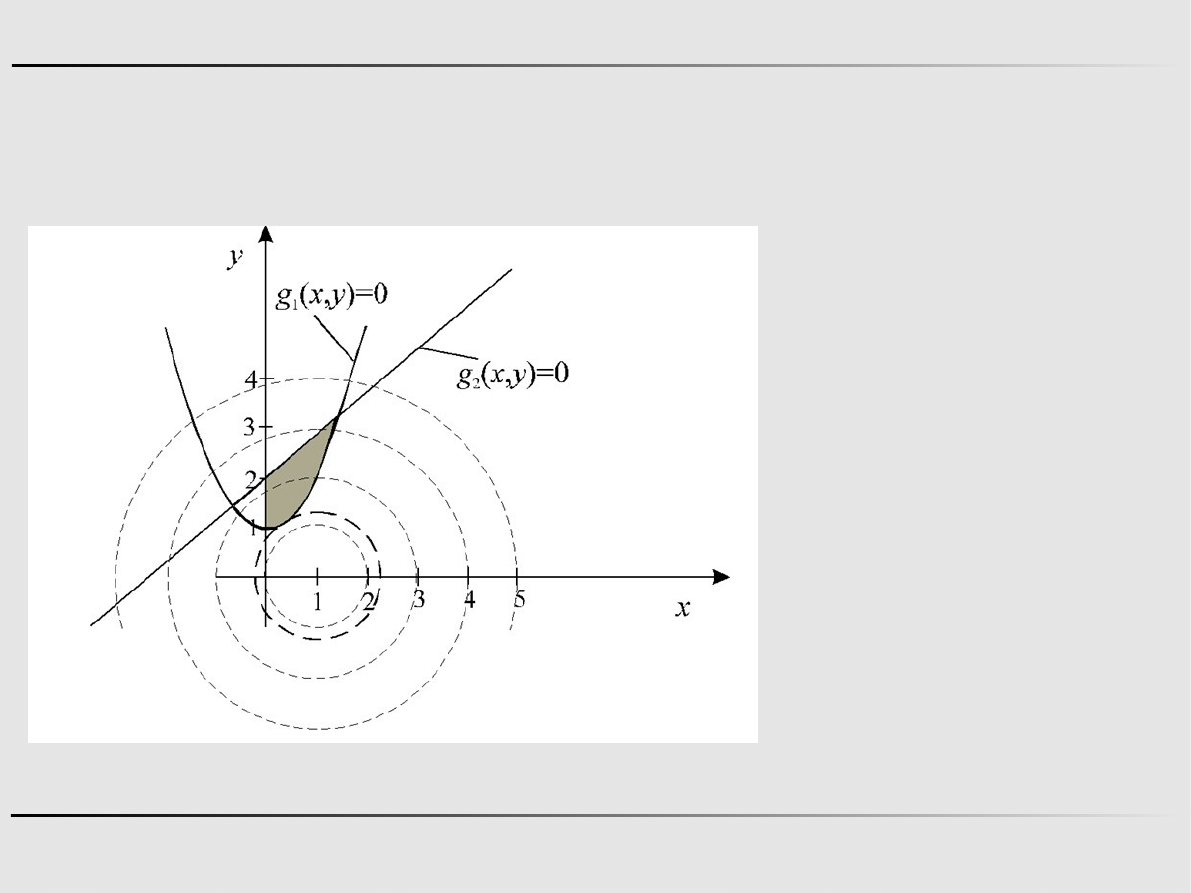
Przykład 3. Dana jest funkcja dwóch zmiennych i ograniczenia.

Znajdź minimum tej funkcji.

f

 x , y= x−1

2

 y

2

{

g

1

 x , y=−x

2

 y−10

g

2

 x , y=x− y20

x

0

y

0

2008-03-16

Szczecin

9

Metody optymalizacji, Informatyka

Metody poszukiwania ekstremum funkcji

wielu zmiennych z ograniczeniami

metody graficzne

metoda systematycznego przeszukiwania,

metody losowe,

metoda mnożników Lagrange'a,

warunki Kuhna-Tuckera

,

metoda funkcji kary,

Ekstremum funkcji wielu zmiennych z ograniczeniami

2008-03-16

Szczecin

10

Metody optymalizacji, Informatyka

Metoda mnożników Lagrange'a pozwala przekształcać
zadanie poszukiwania ekstremum warunkowego do postaci
zadania poszukiwania ekstremum bezwarunkowego w
przypadku istnienia ograniczeń w postaci równości.

Metoda mnożników Lagrange'a

2008-03-16

Szczecin

11

Metody optymalizacji, Informatyka

Metoda mnożników Lagrange'a

Znaleźć min f(x)

x

=[ x

1,

x

2,

... , x

n

]

T

Przy ograniczeniach

h

k

x=0

k

=1,2 ,... , K

K

n

=[

1,



2,

... ,



K

]

Wprowadzamy wektor

L

 x , = f x

∑

k

=1

K



k

h

k

 x

Budujemy funkcję Lagrange'a

Nieokreślone

mnożniki Lagrange'a

Punkty stacjonarne funkcji Lagrange'a

znajdziemy rozwiązując układ równań:

∂ Lx ,
∂ x

j

=0 j=1,2 ,... , n

∂ Lx ,
∂ 

k

=h

k

x=0 k=1,2 ,... , K

2008-03-16

Szczecin

12

Metody optymalizacji, Informatyka

Metoda mnożników Lagrange'a – ograniczenia równościowe

Znaleźć

Przy ograniczeniu

min f

 x=x

1

2

x

2

2

h

x=x

1

x

2

=1 1−x

1

−x

2

=0

L

 x

1,

x

2,

=x

1

2

x

2

2

1−x

1

−x

2



Budujemy funkcję Lagrange'a

∂ L
∂ x

1

=2x

1

−=0

∂ L
∂ x

2

=2x

2

−=0

∂ L
∂

=1−x

1

−x

2

=0

Rozwiązanie:

x

1

=

1
2

x

2

=

1
2

=1

Przykład

2008-03-16

Szczecin

13

Metody optymalizacji, Informatyka

Metoda mnożników Lagrange'a – ograniczenia równościowe

Znaleźć

Przy ograniczeniu

min f

 x=x

1

2

x

2

2

h

x=x

1

x

2

=1 1−x

1

−x

2

=0

x

1

x

2

1

1

2

2

2008-03-16

Szczecin

14

Metody optymalizacji, Informatyka

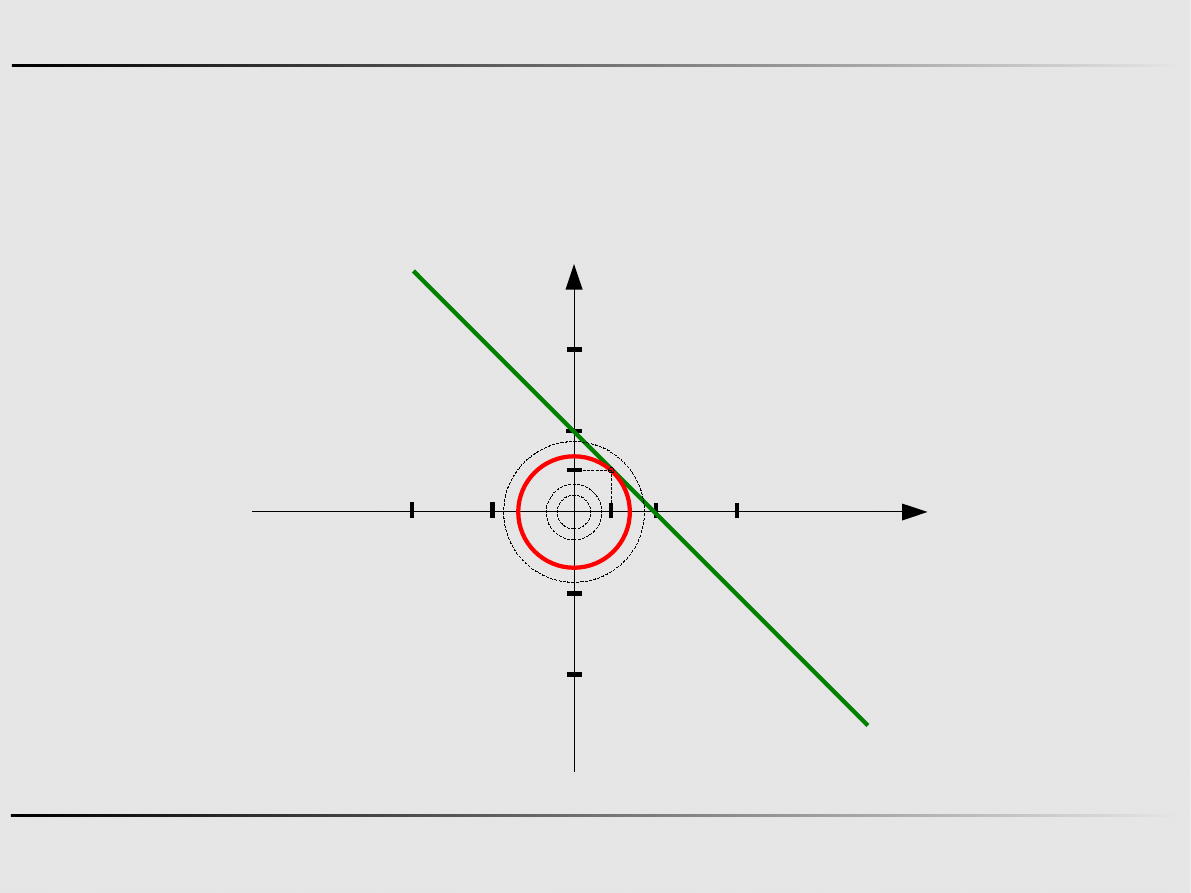
Metoda mnożników Lagrange'a – dowolne ograniczenia

Znaleźć

Przy ograniczeniu

min f

 x=x

1

⋅x

2

g

x=25−x

1

2

−x

2

2

0

L

 x ,  , u=x

1

⋅x

2

25−x

1

2

−x

2

2

−u

2



Budujemy funkcję Lagrange'a

Przykład.

Przekształcamy ograniczenie do równości

g

x=25−x

1

2

−x

2

2

0 gx=25−x

1

2

−x

2

2

−u

2

=0

∂ L
∂ x

1

=x

2

−2 x

1

=0

∂ L
∂ x

2

=x

1

−2 x

2

=0

∂ L
∂

=25−x

1

2

−x

2

2

−u

2

=0

∂ L
∂ u

=u=0