1

9.05.2013

Szczecin

Metody optymalizacji

Ekstremum funkcji wielu zmiennych

Z OGRANICZENIAMI

2

9.05.2013

Szczecin

Metody optymalizacji

Metody poszukiwania ekstremum funkcji

wielu zmiennych z ograniczeniami

metody graficzne

metoda systematycznego przeszukiwania,

metody losowe,

metoda mnożników Lagrange'a,

warunki Kuhna-Tuckera,

metoda funkcji kary,

Ekstremum funkcji wielu zmiennych z ograniczeniami

3

9.05.2013

Szczecin

Metody optymalizacji

Metoda mnożników Lagrange'a

Znaleźć min f(x)

x=[ x

1,

x

2,

... , x

n

]

T

Przy ograniczeniach

h

k

(

x)=g

k

k =1,2 ,... , m

m<n

λ=[λ

1,

λ

2,

... , λ

m

]

Wprowadzamy wektor

L( x , λ)= f (x)+

∑

k=1

m

λ

k

h

k

(

x)

Budujemy funkcję Lagrange'a

Nieokreślone

mnożniki Lagrange'a

Punkty stacjonarne funkcji Lagrange'a
znajdziemy rozwiązując układ równań:

∂

L( x , λ)

∂

x

j

=

0 j=1,2 ,... , n

∂

L( x , λ)

∂ λ

k

=

h

k

(

x)=0 k=1,2 ,... , m

4

9.05.2013

Szczecin

Metody optymalizacji

Metoda mnożników Lagrange'a – ograniczenia równościowe

Znaleźć

Przy ograniczeniu

min f ( x)=x

1

2

+

x

2

2

h( x)=x

1

+

x

2

=

1

1−x

1

−

x

2

=

0

L( x

1,

x

2,

λ)=

x

1

2

+

x

2

2

+λ (

1− x

1

−

x

2

)

Budujemy funkcję Lagrange'a

∂

L

∂

x

1

=

2x

1

−λ=

0

∂

L

∂

x

2

=

2x

2

−λ=

0

∂

L

∂ λ

=

1−x

1

−

x

2

=

0

Rozwiązanie:

x

1

=

1

2

x

2

=

1
2

λ=

1

5

9.05.2013

Szczecin

Metody optymalizacji

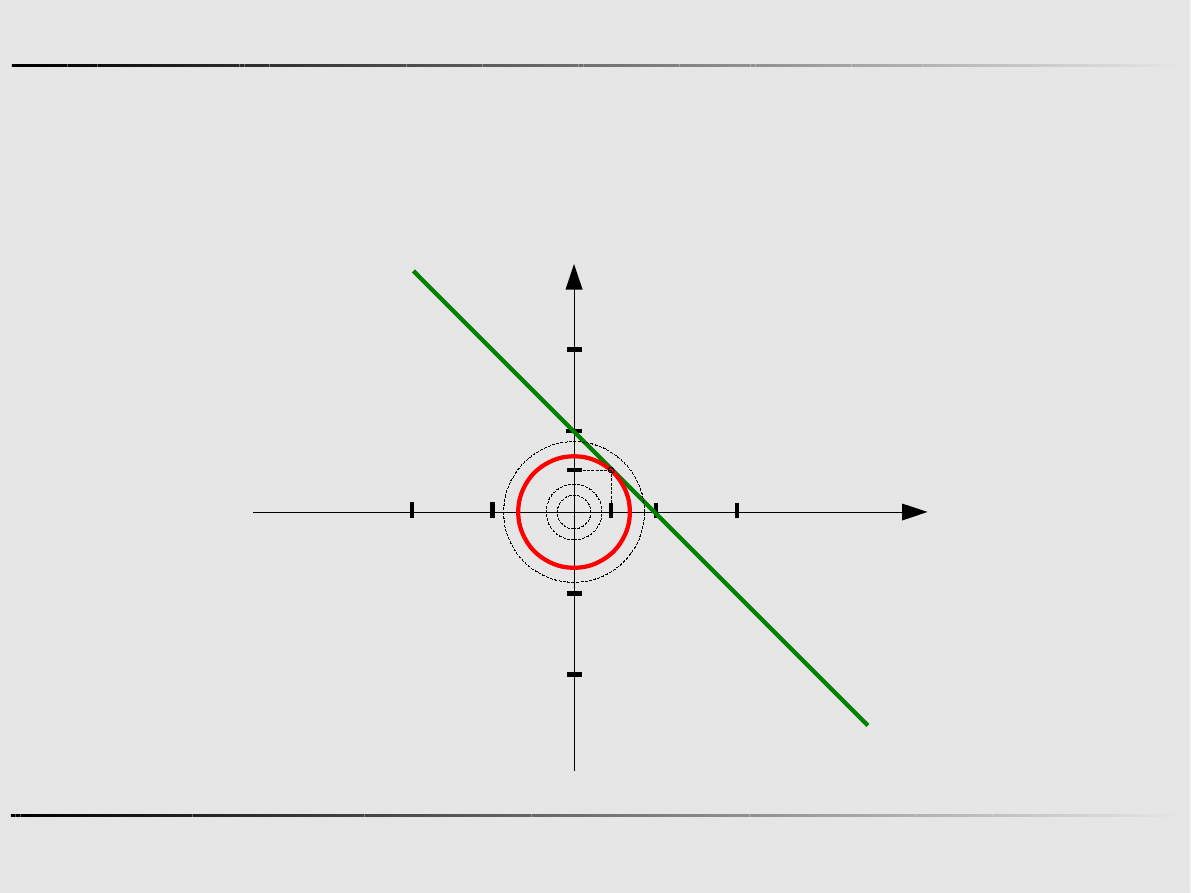
Metoda mnożników Lagrange'a – ograniczenia równościowe

Znaleźć

Przy ograniczeniu

min f ( x)=x

1

2

+

x

2

2

h( x)=x

1

+

x

2

=

1

1−x

1

−

x

2

=

0

x

1

x

2

1

1

2

2

6

9.05.2013

Szczecin

Metody optymalizacji

Metoda mnożników Lagrange'a – ograniczenia równościowe

Znaleźć

Przy ograniczeniach:

min f ( x)=x

1

2

+

x

2

2

+

x

3

2

h

1

(

x)=x

1

+

x

2

=

1

h

2

(

x)=x

2

+

x

3

=

1

Rozwiązanie:

x

1

=

1

3

x

2

=

2
3

x

3

=

1

3

λ

1

=

2
3

λ

2

=

2
3

7

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – ograniczenia nierównościowe

Znaleźć max f(x)

x=[ x

1,

x

2,

... , x

n

]

T

Przy ograniczeniach:

b

i

−

g

i

(

x)⩾0 i=1,... , u

b

i

−

g

i

(

x)⩽0 i=u+1,... , v

b

i

−

g

i

(

x)=0 i=v+1,... , m

oraz:

x

j

⩾

0

j=1,... , s

x

j

⩽

0

j=s+1,... t

x

j

nieograniczonego znaku

j=t+1, ... , n

L( x , λ)= f ( x)+

∑

i=1

m

λ

i

[

b

i

−

g

i

(

x)]

Budujemy funkcję Lagrange'a

8

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – ograniczenia nierównościowe

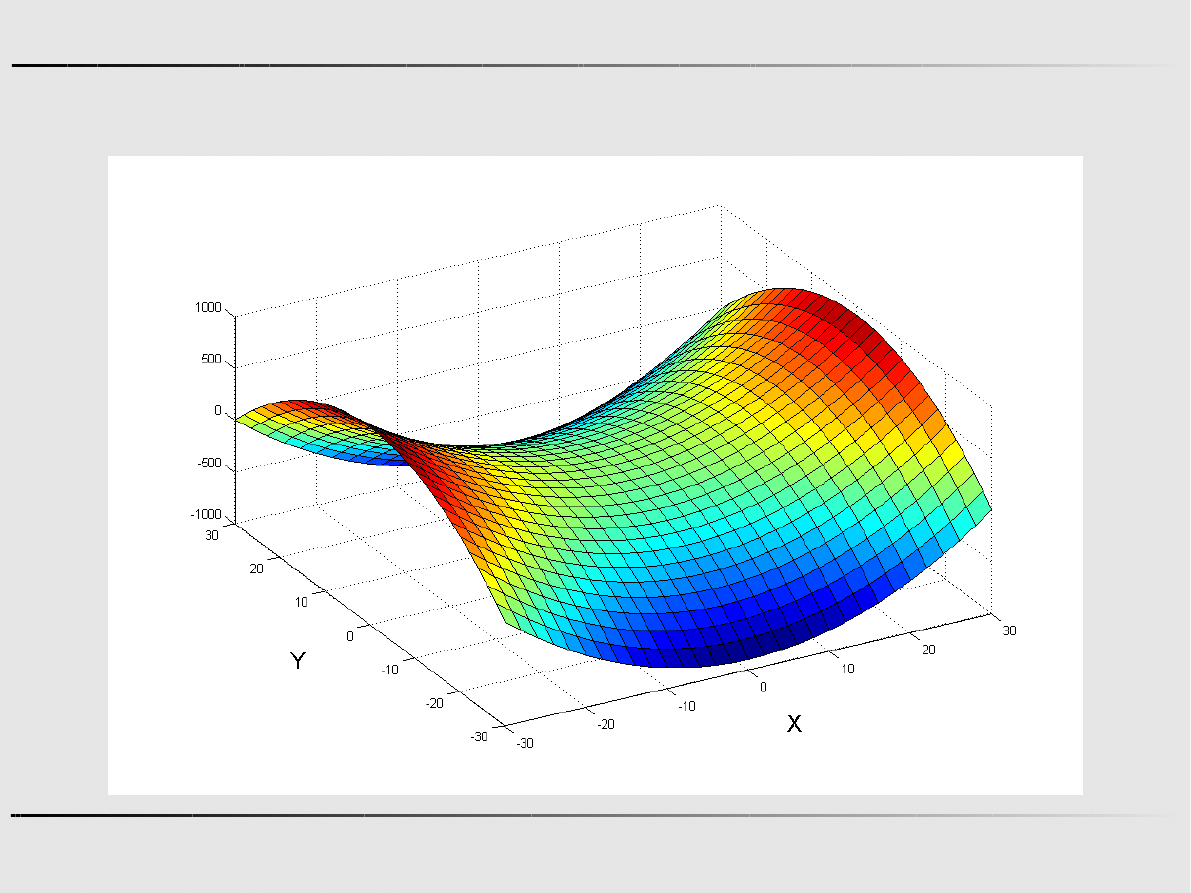
Funkcja ma punkt siodłowy jeśli istnieje takie otoczenie

że dla wszystkich ,

oraz dla wszystkich obowiązuje:

Punkt siodłowy

L(x ,λ)

[

x

✷

, λ

✷

]

ε>

0

x

∣

x− x

✷

∣<ε

λ

∣λ−λ

✷

∣<ε

L( x , λ

✷

)⩽

L( x

✷

, λ

✷

)⩽

L( x

✷

, λ)

Poszukiwanie punktu siodłowego można uważać za poszukiwanie:

min

λ

max

x

L(x , λ)

9

9.05.2013

Szczecin

Metody optymalizacji

Funkcja siodłowa

Warunki Kuhna – Tuckera – ograniczenia nierównościowe

10

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – ograniczenia nierównościowe

Warunki konieczne istnienia punktu siodłowego dla funkcji L(x,

λ

):

x

j

⩾

0

x

j

⩽

0

x

j

nieograniczonego znaku

∂

L

∂

x

j

⩽

0,

j=1,... , s

∂

L

∂

x

j

⩾

0,

j=s+1,... t

∂

L

∂

x

j

=

0,

j=t+1,... , n

x

j

∂

L

∂

x

j

=

0

j=1,... , n

11

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – ograniczenia nierównościowe

Warunki konieczne istnienia punktu siodłowego dla funkcji L(x,

λ

) c.d.

λ

i

∂

L

∂ λ

i

=

0

i=1,... , m

∂

L

∂ λ

i

⩾

0 i=1,... , u

∂

L

∂ λ

i

⩽

0 i=u+1,... , v

∂

L

∂ λ

i

=

0 i=v+1,... , m

λ

i

⩾

0

λ

i

⩽

0

λ

i

nieograniczonego znaku

12

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 1

Znaleźć

Przy ograniczeniach

max f ( x)=−( x

1

−

2)

2

−(

x

2

−

4)

2

x

1

+

x

2

⩽

4

Bez ograniczenia znaku

x

1,

x

2

L( x , λ)=−( x

1

−

2)

2

−(

x

2

−

4)

2

+λ (

4−x

1

−

x

2

)

4−x

1

−

x

2

⩾

0

13

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 1

Warunki konieczne istnienia punktu siodłowego dla funkcji L(x,

λ

):

L( x , λ)=−( x

1

−

2)

2

−(

x

2

−

4)

2

+λ (

4−x

1

−

x

2

)

∂

L

∂

x

1

=

0

∂

L

∂

x

2

=

0

x

1

∂

L

∂

x

1

=

0

x

2

∂

L

∂

x

2

=

0

∂

L

∂ λ

⩾

0

λ⩾

0

λ

∂

L

∂ λ

=

0

Ostatecznie otrzymamy:

∂

L

∂

x

1

=

0

∂

L

∂

x

2

=

0

λ

∂

L

∂ λ

=

0

∂

L

∂ λ

⩾

0

λ⩾

0

14

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 1

L( x , λ)=−( x

1

−

2)

2

−(

x

2

−

4)

2

+λ (

4−x

1

−

x

2

)

∂

L

∂

x

1

=−

2( x

1

−

2)−λ=0

∂

L

∂

x

2

=−

2( x

2

−

4)−λ=0

λ

∂

L

∂ λ

=λ (

4−x

1

−

x

2

)=

0

∂

L

∂ λ

=

4−x

1

−

x

2

⩾

0

λ⩾

0

15

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 1

−

2 x

1

+

4−λ=0

λ (

4−x

1

−

x

2

)=

0

4−x

1

−

x

2

⩾

0

wyznaczamy

λ

z I równania i wstawiamy do pozostałych:

−

2 x

2

+

8−λ=0

−

2 x

2

+

8+2 x

1

−

4=0

λ=−

2 x

1

+

4

2 x

2

=

2 x

1

+

4/: 2

x

2

=

x

1

+

2

(−

2 x

1

+

4)⋅(4−x

1

−

x

2

)=

0

(−

2 x

1

+

4)⋅(4−x

1

−

x

1

−

2)=0

(−

2 x

1

+

4)=0 lub (4−x

1

−

x

1

−

2)=0

x

1

=

2

x

2

=

4

λ=

0

x

1

=

1

x

1

=

3

λ=

2

16

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 1

I

II

x

1

2

1

x

2

4

3

λ

0

2

λ⩾

0

TAK TAK

4−x

1

−

x

2

⩾

0 NIE TAK

x

1

=

1

x

1

=

3

λ=

2

Rozwiązaniem jest:

17

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 2

Znaleźć

Przy ograniczeniach

max f ( x , y)=( x−3)

2

+(

2 y−2)

2

x+2 y⩾2

Bez ograniczenia znaku

x , y

L( x , y , λ)=( x−3)

2

+(

2 y−2)

2

+λ (

2−x−2 y)

2−x−2 y⩽0

18

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 2

Warunki konieczne istnienia punktu siodłowego dla funkcji L(x,

λ

):

∂

L

∂

x

=

0

∂

L

∂

y

=

0

x

∂

L

∂

x

=

0

y

∂

L

∂

y

=

0

∂

L

∂ λ

⩽

0

λ⩽

0

λ

∂

L

∂ λ

=

0

Ostatecznie otrzymamy:

∂

L

∂

x

=

0

∂

L

∂

y

=

0

λ

∂

L

∂ λ

=

0

∂

L

∂ λ

⩽

0

λ⩽

0

L( x , y , λ)=( x−3)

2

+(

2 y−2)

2

+λ (

2−x−2 y)

19

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 2

∂

L

∂

x

=

2 x−6−λ=0

∂

L

∂

y

=

8 y−8−2 λ=0

λ

∂

L

∂ λ

=λ (

2−x−2 y)=0

λ⩾

0

L( x , y , λ)=( x−3)

2

+(

2 y−2)

2

+λ (

2−x−2 y)

20

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 2

2 x−6−λ=0

λ (

2−x−2 y)=0

2−x−2 y⩽0

na podstawie III równania

8 y−8−2 λ=0

2 x=6/: 2

λ=

0

x=2

y=1

8 y=8/:8

2−x−2 y=0

x=2−2 y

2(2−2 y)−6−λ=0

−

4 y−2−λ=0

λ=−

4 y−2

λ=−

4⋅

1
4

−

2=−3

8 y−8−2(−4 y−2)=0

8 y−8+8 y+4=0

y=

1

4

x=2−2⋅

1
4

=

3
2

16 y−4=0

21

9.05.2013

Szczecin

Metody optymalizacji

Warunki Kuhna – Tuckera – zadanie 2

I

II

x

3

3
2

y

1

1
4

λ

0

−

3

λ⩽

0

TAK TAK

2−x−2 y⩽0 TAK TAK

f (3,1)=0

Aby znaleźć rozwiązanie, trzeba obliczyć f(x,y)

f

(

3
2

,

1

4

)

=

4.5

22

9.05.2013

Szczecin

Metody optymalizacji

Metoda funkcji kary

minimalizujemy f(x) przy ograniczeniach

g

i

(

x)⩾0, i=1,… , I

h

k

(

x)=0, k=1,… , K

przekształcamy to zadanie do postaci zadania optymalizacji bezwarunkowej
albo do sekwencji takich zadań równoważnych. W tym celu wprowadza się
funkcję kary:

P(x , R)= f (x)+Ω( R , g (x) , h( x))

Ω−

kara

Kara może mieć różną postać. Najczęściej – kara kwadratowa:

Ω=

R(h( x))

2

23

9.05.2013

Szczecin

Metody optymalizacji

Metoda funkcji kary – zadanie 1

Znaleźć

Przy ograniczeniu

min f ( x)=( x

1

−

4)

2

+(

x

2

−

4)

2

h( x)=x

1

+

x

2

−

5=0

Wprowadzamy funkcję kary

P( x , R)=( x

1

−

4)

2

+(

x

2

−

4)

2

+

R( x

1

+

x

2

−

5)

2

dalej rozwiązujemy jak zadanie bezwarunkowej minimalizacji dla funkcji P(x,R)

24

9.05.2013

Szczecin

Metody optymalizacji

Metoda funkcji kary – zadanie 1

P( x , R)=( x

1

−

4)

2

+(

x

2

−

4)

2

+

R( x

1

+

x

2

−

5)

2

dalej rozwiązujemy jak zadanie bezwarunkowej minimalizacji dla funkcji P(x,R)

∂

P( x , R)

∂

x

j

=

0

(

x

1

−

4)+R( x

1

+

x

2

−

5)=0

(

x

2

−

4)+R( x

1

+

x

2

−

5)=0

x

1

=

x

2

x

j

=

4+5 R

1+2 R

,

j=1,2

25

9.05.2013

Szczecin

Metody optymalizacji

Metoda funkcji kary – zadanie 1

po przejściu do granicy przy

x

j

=

4+5 R

1+2 R

,

j=1,2

R →∞

lim

R →∞

x

j

=

2.5 ,

j=1,2

Rozwiązanie zbiega się do punktu (2.5, 2.5), f(2.5,2.5)=4.5

26

9.05.2013

Szczecin

Metody optymalizacji

Metoda funkcji kary

Przy rozwiązywaniu zadań z ograniczeniami w postaci nierówności należy
przekształcić je do postaci równości. Zadanie ma postać:

min f ( x),

x=[ x

1,

x

2,

…

, x

n

]

T

przy ograniczeniach

g

i

(

x)−u

i

2

=

0, i=1,…, I

h

k

(

x)=0, k=1,…, K

funkcja Lagrange'a

L( x ,φ ,ψ ,u)= f ( x)+∑

i=1

I

φ[

g

i

(

x)−u

i

2

]+∑

k=1

K

ψ

k

h

k

(

x)

27

9.05.2013

Szczecin

Metody optymalizacji

Metoda funkcji kary

nieujemne i niezależne od x współczynniki, określa się je z warunków:

φ

i

, ψ

k

∂

L( x ,φ , ψ,u)

∂

x

j

=

0, ∀ j(1,n)

L( x ,φ ,ψ ,u)= f ( x)+∑

i=1

I

φ[

g

i

(

x)−u

i

2

]+∑

k=1

K

ψ

k

h

k

(

x)

∂

L( x ,φ , ψ,u)

∂ φ

i

=

0, ∀i(1, I )

∂

L( x ,φ , ψ,u)

∂ ψ

=

0, ∀k (1, K )

∂

L( x ,φ , ψ,u)

∂

u

i

=

0, ∀i(1, I )