9.05.2013
Szczecin
1
Metody optymalizacji
METODY OPTYMALIZACJI
dr inż. Anna Barcz
Zakład Matematyki Stosowanej
kontakt: pok. 28,
abarcz@wi.zut.edu.pl
9.05.2013
Szczecin
1
Metody optymalizacji
METODY OPTYMALIZACJI
dr inż. Anna Barcz
Zakład Matematyki Stosowanej
kontakt: pok. 28,
abarcz@wi.zut.edu.pl
9.05.2013
Szczecin
2
Metody optymalizacji
Zasady zaliczenia:
✔
kolokwium na ostatnim (pełnym 90min) wykładzie
✔
23.05.2013 lub 13.06.2013
Ocena końcowa:
✔
2 ECTS,
✔
średnia arytmetyczna ocen
z lab (waga 0.6) i wykładów (waga 0.4)
Konsultacje: piątek, 12:15-13:30
9.05.2013
Szczecin
3
Metody optymalizacji
Literatura:
✔
Popov O., Metody numeryczne i optymalizacja, Szczecin 2003
✔
Findeisen W., Szymanowski J., Wierzbicki A., Teoria i metody
obliczeniowe optymalizacji, PWN, Warszawa 1980
✔
Seidler I., Badach A., Molisz W., Metody rozwiązywania zadań
optymalizacji, WNT,Warszawa, 1980
✔
Gass S., Programowanie linowe, PWN, Warszawa 1980
✔
Brandt S., Analiza danych, PWN, Warszawa 1999
9.05.2013
Szczecin
4
Metody optymalizacji
Cele:
✔
Ukształtowanie umiejętności poprawnego formułowania
zagadnienia optymalizacyjnego.
✔
Ukształtowanie umiejętności wyboru właściwej metody
rozwiązania zadań optymalizacyjnych, algorytmizacji
zagadnienia, rozwiązania i analizy wyników.
✔
Ukształtowanie umiejętności dostrzegania w życiu codziennym
zagadnień, dla których można sformułować zadania
optymalizacyjne.
✔
Ukształtowanie umiejętności tworzenia programów
komputerowych wykorzystujących algorytmy poszukiwania
ekstremów funkcji.
9.05.2013
Szczecin
5
Metody optymalizacji
Treść:
✔
Wprowadzenie. Ogólne sformułowanie zadań optymalizacji.
✔
Ekstremum funkcji jednej zmiennej. Warunki istnienia. Metody poszukiwań:
metoda połowienia, złotego podziału, aproksymacji kwadratowej, aproksymacji
sześciennej, metoda Newtona.
✔
Bezwarunkowe ekstremum funkcji wielu zmiennych. Warunki istnienia ekstremum
funkcji wielu zmiennych. Metody bezgradientowe: metoda spadku względem
współrzędnych, metoda Gaussa-Seidla.
✔
Metody gradientowe poszukiwania ekstremum funkcji wielu zmiennych: metoda
najszybszego spadku, metoda Newtona.
✔
Ekstremum funkcji w zadaniach z ograniczeniami. Mnożniki Lagrange'a, warunki
Khuna-Tuckera. Funkcja kary.
✔
Programowanie liniowe. Ogólne sformułowanie zadania. Metoda graficzna i
algebraiczna.
✔
Metoda simpleks. Ogólny schemat. Rozwiązania dopuszczalne i bazowe.
9.05.2013
Szczecin
6
Metody optymalizacji
Bardzo krótka historia optymalizacji:
●
Analityczne metody klasyczne z wykorzystaniem
pochodnych.
●
Rozwój obliczeń komputerowych: modyfikacje metod
klasycznych, algorytmizacja obliczeń.
●
Algorytmy ewolucyjne, genetyczne, sieci neuronowe:
zastosowanie metod optymalizacji do złożonych modeli
systemów rzeczywistych.
9.05.2013
Szczecin
7
Metody optymalizacji
Optymalizacja to:
●
Problemy logistyczne,
●
Tworzenie nowych konstrukcji,
●
Sterowanie ruchem różnych obiektów,
●
Alokacja produktów,
●
Skład portfela inwestycyjnego,
●
Zatrudnianie pracowników,
●
Gry strategiczne
(zwłaszcza te, które przeszkadzają w studiowaniu)
,
●
Sesja egzaminacyjna,
●
Impreza po sesji,
●
i wiele innych sytuacji
9.05.2013
Szczecin
8
Metody optymalizacji
Dlaczego zadania optymalizacyjne są takie trudne?
●
Wielkość przestrzeni rozwiązań.
●
Nieciągłość przestrzeni rozwiązań.
●
Nieliniowość.
●
Ograniczenia.
np. problem magazynowy: 400 lokalizacji i 200
produktów
Liczba rozwiązań 400
200
≈ 10
520
9.05.2013
Szczecin
9
Metody optymalizacji
Problemy NP-trudne
●
czas znalezienia optimum rośnie bardzo szybko
(wykładniczo) wraz ze wzrostem rozmiaru problemu,
●
w praktyce oznacza to, że nie można znaleźć
rozwiązania optymalnego w realnym czasie dla zadań o
rzeczywistych rozmiarach,
●
wszystkie problemy NP-trudne są w pewnym sensie
równoważne.
9.05.2013
Szczecin
10
Metody optymalizacji
Praktyczne przykłady problemów NP-trudnych:
●
Połącz ludzi w zespoły wedle kompetencji
●
Rozmieść biura w budynku firmy
●
Ustal trasę dla śmieciarki (lub rozwozu towarów ze
sklepu)
●
Zadecyduj gdzie w tekście umieścić rysunki
●
Ustal położenie układów scalonych na płytce
drukowanej
●
Wybierz część działów/pracowników biura do
przeniesienia do innej lokalizacji
●
Wybierz najlepszy przebieg linii metra
●
Rozmieść w najkorzystniejszych miejscach przystanki
autobusowe
9.05.2013
Szczecin
11
Metody optymalizacji
Praktyczne przykłady problemów NP-trudnych:
●
Zaprojektuj najwygodniejszy układ klawiszy na
klawiaturze
●
Przydziel zadania do procesorów
●
Przypisz oddziały szpitala do posiadanych lokalizacji
●
Ułóż plan zajęć
●
Zaprojektuj najlepszą antenę lub skrzydło samolotu
●
Podaj wartości zmiennych, dla których wyrażenie
logiczne jest prawdą
●
Określ kolejność i czas nadawania reklam w radiu/TV
●
Poprowadź sieć tak, by jak najtaniej połączyć budynki
●
Wybierz akcje, w które zainwestujesz posiadane środki
●
Wybierz pliki do nagrania/archiwizacji na DVD
9.05.2013
Szczecin
12
Metody optymalizacji
Tym się nie będziemy zajmować:
●
Metody przybliżone – heurystyki
–
z reguły bardzo krótki czas pracy,
–
wyniki zwykle dość odległe od optimum,
–
każda stworzona specjalnie dla konkretnego problemu.
●
Metaheurystyki – bazują na analogiach do procesów ze
świata rzeczywistego (fizyki, biologii), które można
interpretować w kategoriach optymalizacji, a które często
prowadzą do wyników bliskich optimum.
–
lokalna optymalizacja (wspinaczka),
–
symulowane wyżarzanie,
–
przeszukiwanie tabu,
–
algorytmy ewolucyjne i genetyczne,
–
algorytmy mrówkowe.
9.05.2013
Szczecin
13
Metody optymalizacji
Zaczniemy od metod klasycznych ...
9.05.2013
Szczecin
14
Metody optymalizacji
W zasadzie wszystkie praktyczne zadania optymalizacyjne,
niezależnie od ich treści można przedstawić jako zadania
minimalizacji funkcji rzeczywistej f(x) n-wymiarowego
argumentu wektorowego którego
współrzędne spełniają układ równań , układ
nierówności , jak również są ograniczone od góry
i od dołu, czyli .
x=[ x
1,
x
2,
…
, x
n
]
T
h
k
(
x)=0
g
j
(
x)⩾0
x
i
(
U )
⩾
x
i
⩾
x
i
(
D)
9.05.2013
Szczecin
15
Metody optymalizacji
Zadanie optymalizacji warunkowej – zminimalizować
f(x) przy ograniczeniach:
h
k
(
x)=0
g
j
(
x)⩾0
x
i
(
U )
⩾
x
i
⩾
x
i
(
D)
k =1,2 ,…, K
j=1,2 ,…, J
i=1,2 ,…, N
9.05.2013
Szczecin
16
Metody optymalizacji
Zadanie optymalizacji bezwarunkowej
x
i
(
U )
=−
x
i
(
D)
=∞
K =J =0
9.05.2013
Szczecin
17
Metody optymalizacji
Klasyfikacja zadań optymalizacji:
ze względu na funkcję celu f(x),
ze względu na rodzaj ograniczeń h
k
i g
j
,
ze względu na wymiarowość wektora x.
9.05.2013
Szczecin
18
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Zadanie minimalizacji funkcji jednej zmiennej f(x) na zbiorze X,
który jest dowolnym podzbiorem jednowymiarowej przestrzeni
euklidesowej E
1
:
min
x∈ X ⊂E
1
f (x)
9.05.2013
Szczecin
19
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Definicja
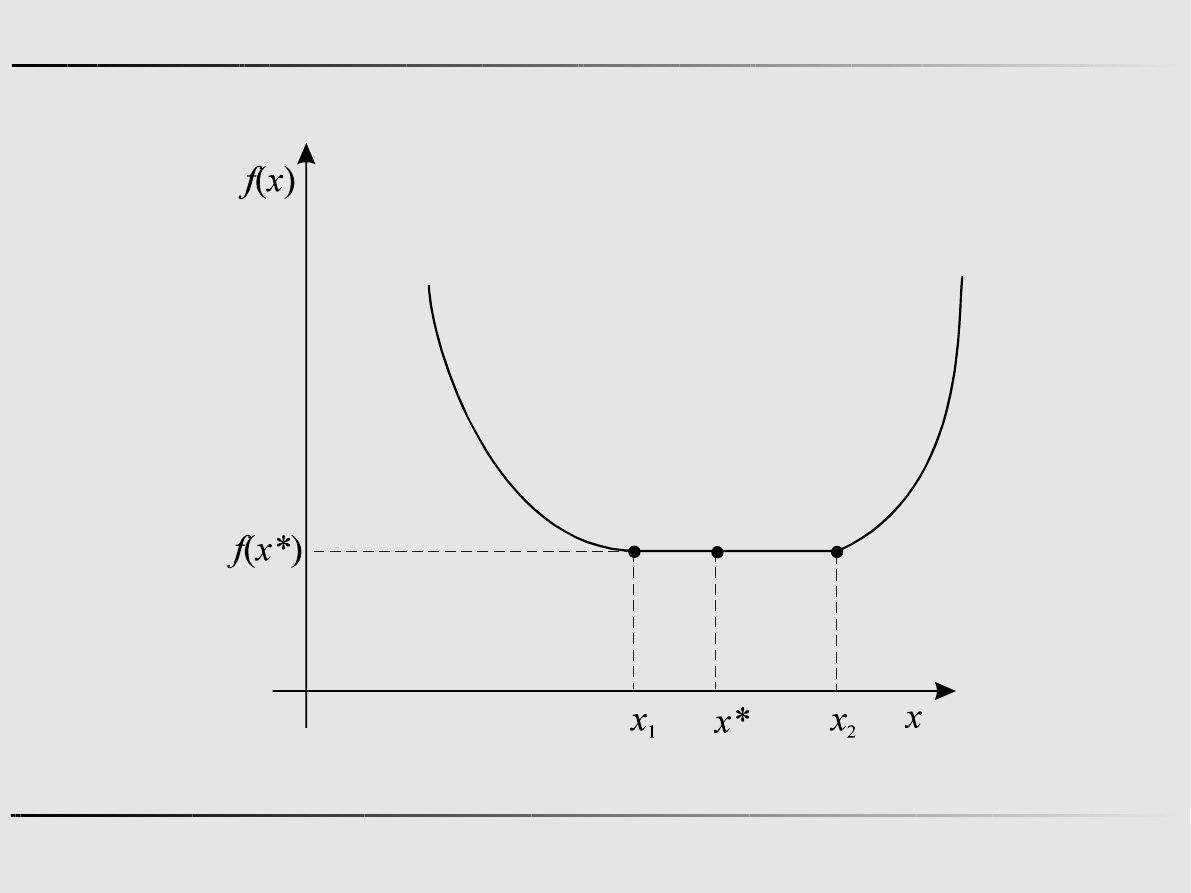
Punkt x* jest punktem, w którym funkcja f(x) osiąga minimum
globalne na zbiorze X, jeśli:
dla wszystkich
x
∗
∈
X
i
f (x
∗
)⩽
f (x)
x∈ X
9.05.2013
Szczecin
20
Metody optymalizacji
Ekstremum funkcji jednej zmiennej – minimum globalne
9.05.2013
Szczecin
21
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Definicja
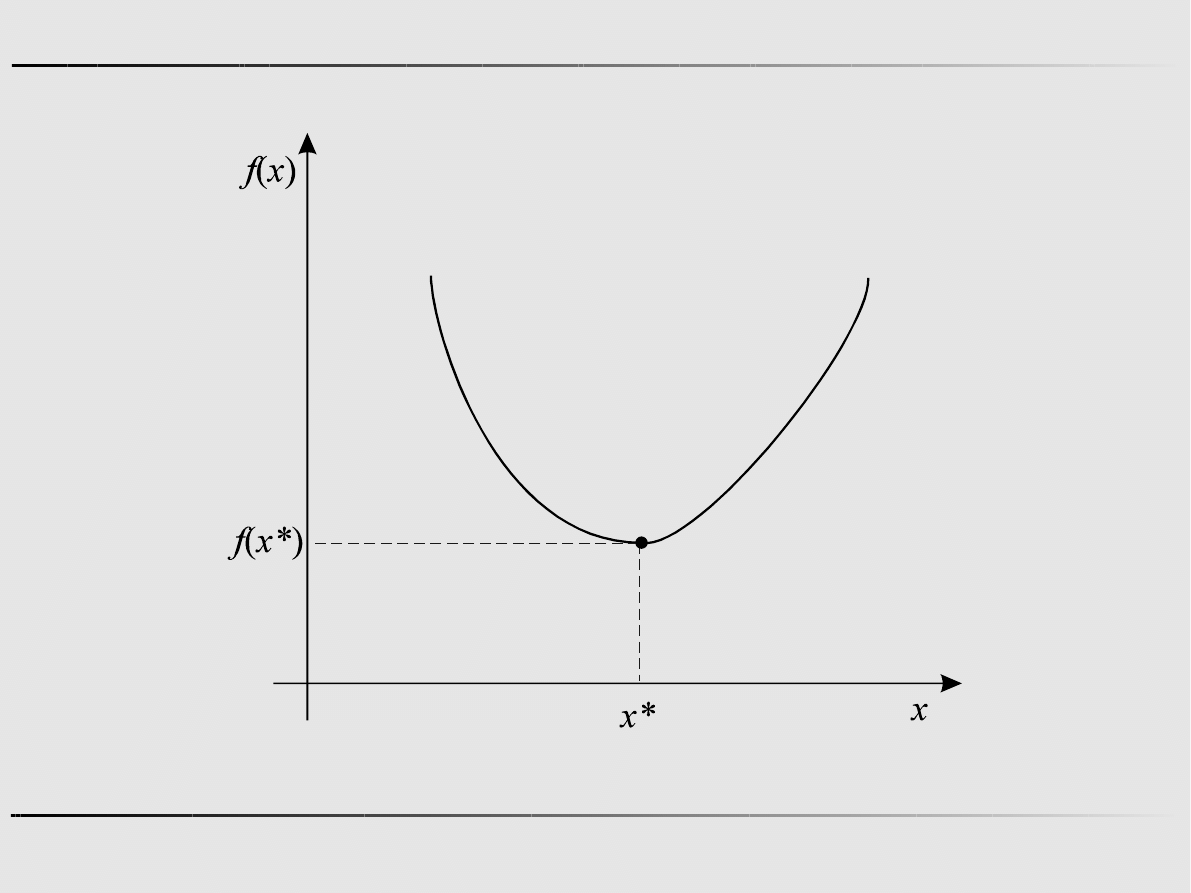
Punkt x* jest punktem właściwego minimum globalnego
funkcji f(x) na zbiorze X, jeśli:
dla wszystkich
x
∗
∈
X
i
f (x
∗
)<
f (x)
x∈ X , x≠x
∗
9.05.2013
Szczecin
22
Metody optymalizacji
Ekstremum funkcji jednej zmiennej – właściwe minimum globalne
9.05.2013
Szczecin
23
Metody optymalizacji
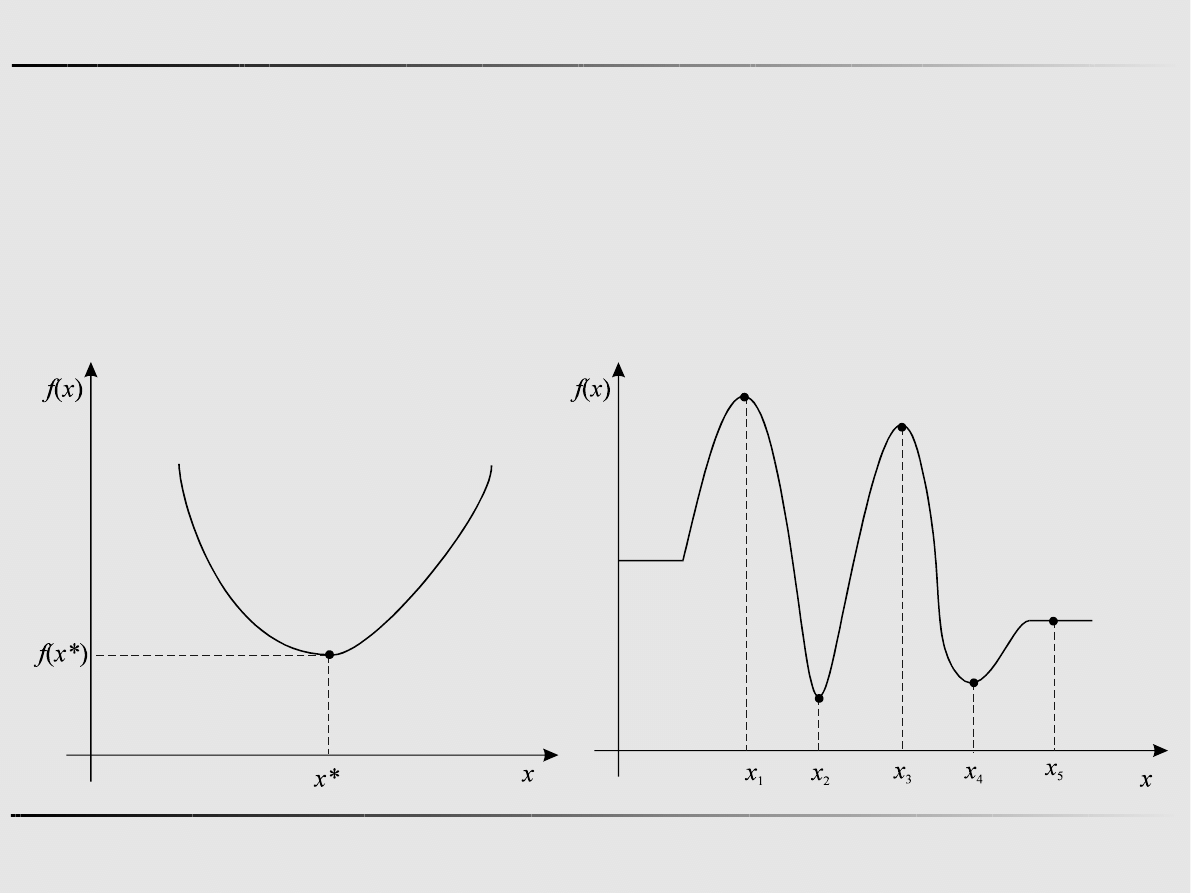
Ekstremum funkcji jednej zmiennej
Definicja
Punkt jest punktem, w którym funkcja f(x) osiąga
minimum lokalne na zbiorze X, jeśli przy dowolnym
wystarczająco małym
ε
> 0 dla wszystkich
spełniających warunek
spełniona jest nierówność
x
∗
∈
X
x≠x
∗
, x∈ X
∣
x−x
∗
∣⩽ε
f ( x
∗
)⩽
f ( x)
9.05.2013
Szczecin
24
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Definicja
Funkcję f(x) nazywa się unimodalną na odcinku [a,b], jeśli jest
ona monotoniczna z obydwu stron od jedynego, na
rozpatrywanym
przedziale,
punktu
ekstremum
x*.
9.05.2013
Szczecin
25
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
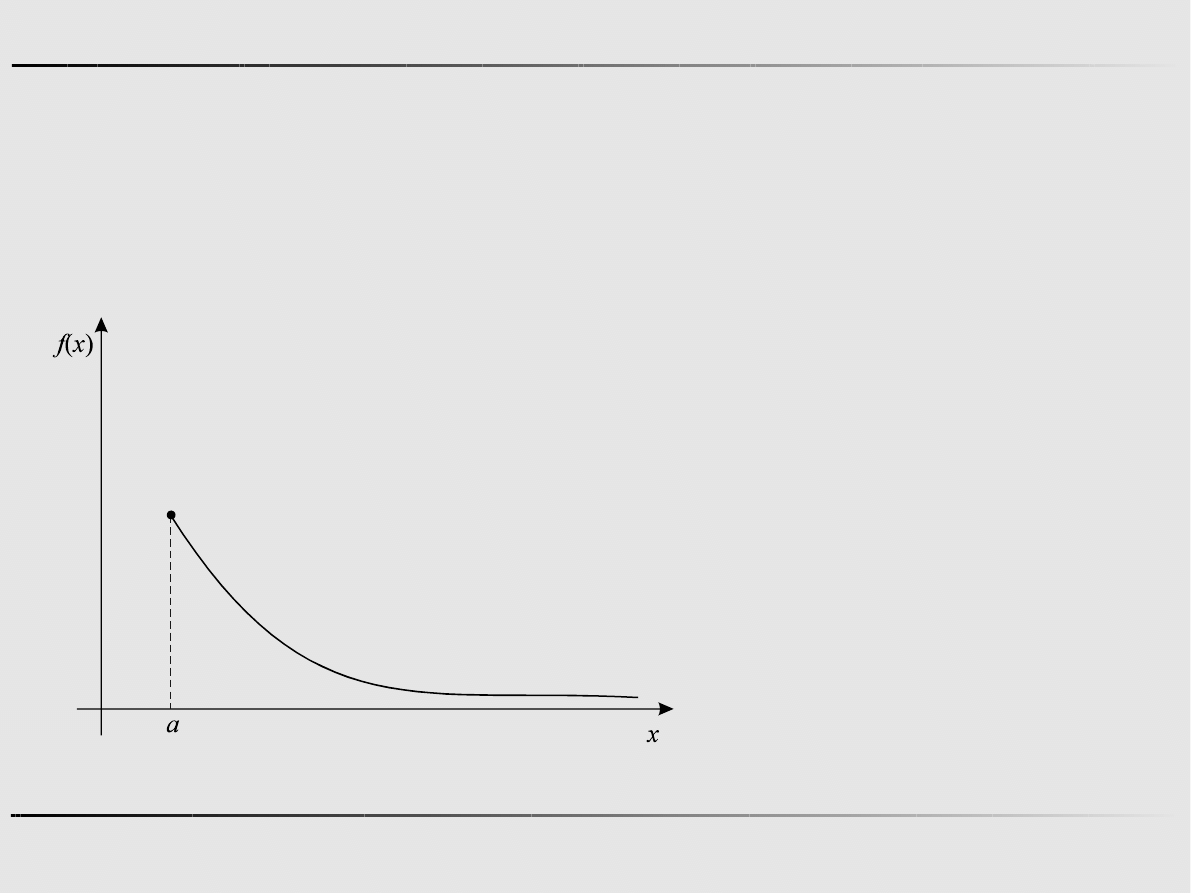
Problem istnienia rozwiązania zadania minimalizacji -
przykład
f ( x)=e
−
x
, X =
{
x : x⩾a
}
9.05.2013
Szczecin
26
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Twierdzenie Weierstrassa
Funkcja ciągła określona na niepustym, domkniętym i
ograniczonym zbiorze osiąga minimum (maksimum) w co
najmniej jednym punkcie tego zbioru.
9.05.2013
Szczecin
27
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Aby punkt x* był punktem lokalnego minimum dwukrotnie
różniczkowalnej funkcji f(x) na otwartym przedziale (a,b),
konieczne jest spełnienie następujących warunków:
{
df
dx
∣
x=x
∗
=
0
d
2
f
dx
2
∣
x= x
∗
⩾
0
warunek konieczny I rzędu
warunek konieczny II rzędu
9.05.2013
Szczecin
28
Metody optymalizacji
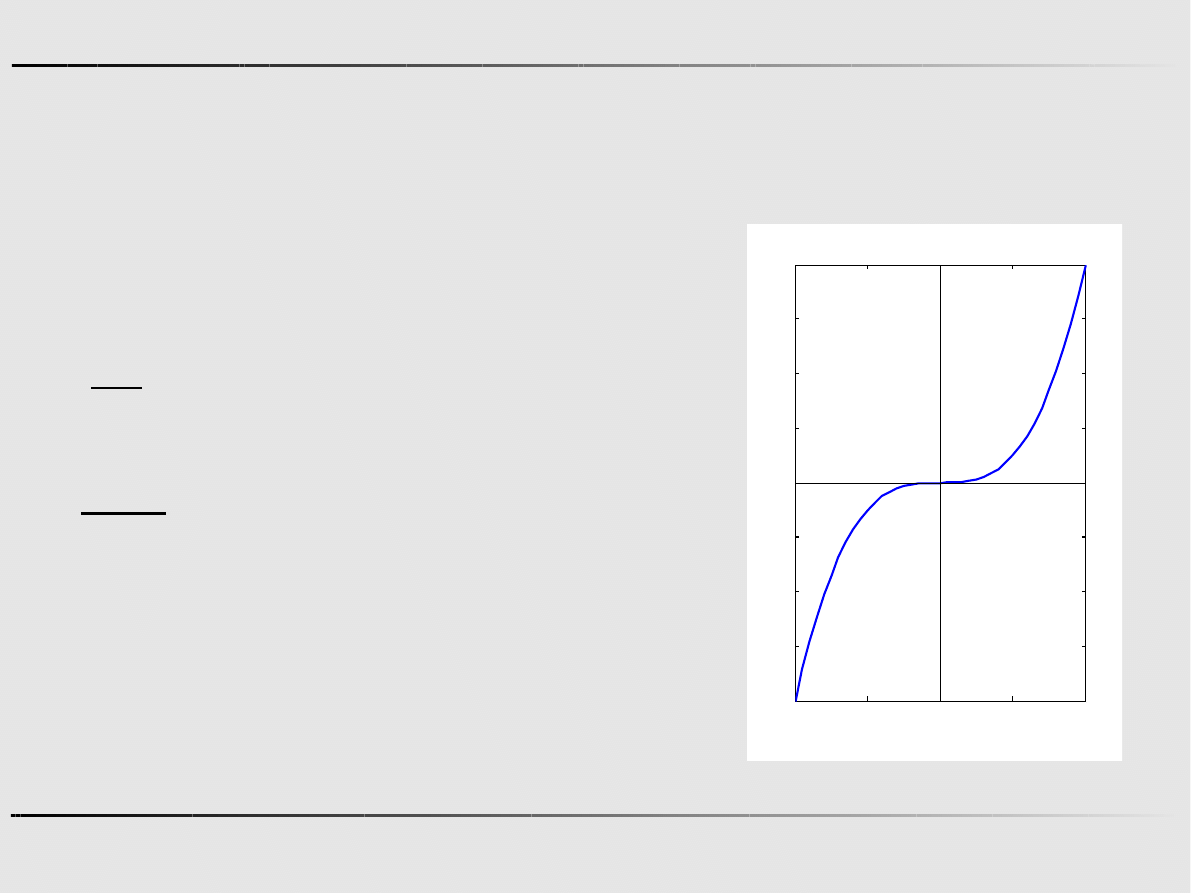
Ekstremum funkcji jednej zmiennej
Przykład
Niech f(x)=x
3
. Wówczas punkt x*=0 spełnia konieczne warunki
minimum.
{
df
dx
∣
x=0
=
3 x
2
∣
x=0
=
0
d
2
f
dx
2
∣
x=0
=
6 x
∣
x=0
=
0
Punkt x=0 jest punktem przegięcia,
nie zaś punktem minimum funkcji.
- 2
- 1
0
1
2
- 8
- 6
- 4
- 2
0
2
4
6
8
9.05.2013
Szczecin
29
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Definicja
Punkt x*, w którym spełniony jest warunek
nazywa się punktem stacjonarnym funkcji f(x).
df
dx
∣
x= x
∗
=
0
9.05.2013
Szczecin
30
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Niech w punkcie x=x* pochodne funkcji f(x) do rzędu(n-1)
włącznie przyjmują wartość zero, natomiast pochodna rzędu
(n) jest różna od zera. Wówczas następujące warunki są
wystarczającymi warunkami istnienia ekstremum:
1. jeśli n jest liczbą nieparzystą to x* jest punktem przegięcia,
2. jeśli n jest liczbą parzystą to x* jest punktem ekstremum
lokalnego
d
n
f
dx
n
∣
x=x
∗
>
0 → minimum
d
n
f
dx
n
∣
x=x
∗
<
0 → maximum
9.05.2013
Szczecin
31
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
df
dx
∣
x=0
=
d
2
f
dx
2
∣
x=0
=
0
Ponieważ rząd pierwszej różnej od zera pochodnej wynosi 3
(liczba
nieparzysta),
to
zgodnie
z
warunkiem
wystarczającym punkt x*=0 jest punktem przegięcia.
Przykład
f(x)=x
3
d
3
f
dx
3
∣
x=0
=
6
9.05.2013
Szczecin
32
Metody optymalizacji
Ekstremum funkcji jednej zmiennej
Algorytmy zerowego rzędu:
metoda połowienia,
metoda oparta na liczbach Fibonacciego,
metoda złotego podziału,
aproksymacja kwadratowa.
Algorytmy pierwszego rzędu:
aproksymacja sześcienna,
algorytm stycznych,
algorytm siecznych.
Algorytm drugiego rzędu:
algorytm Newtona.
9.05.2013
Szczecin
33
Metody optymalizacji
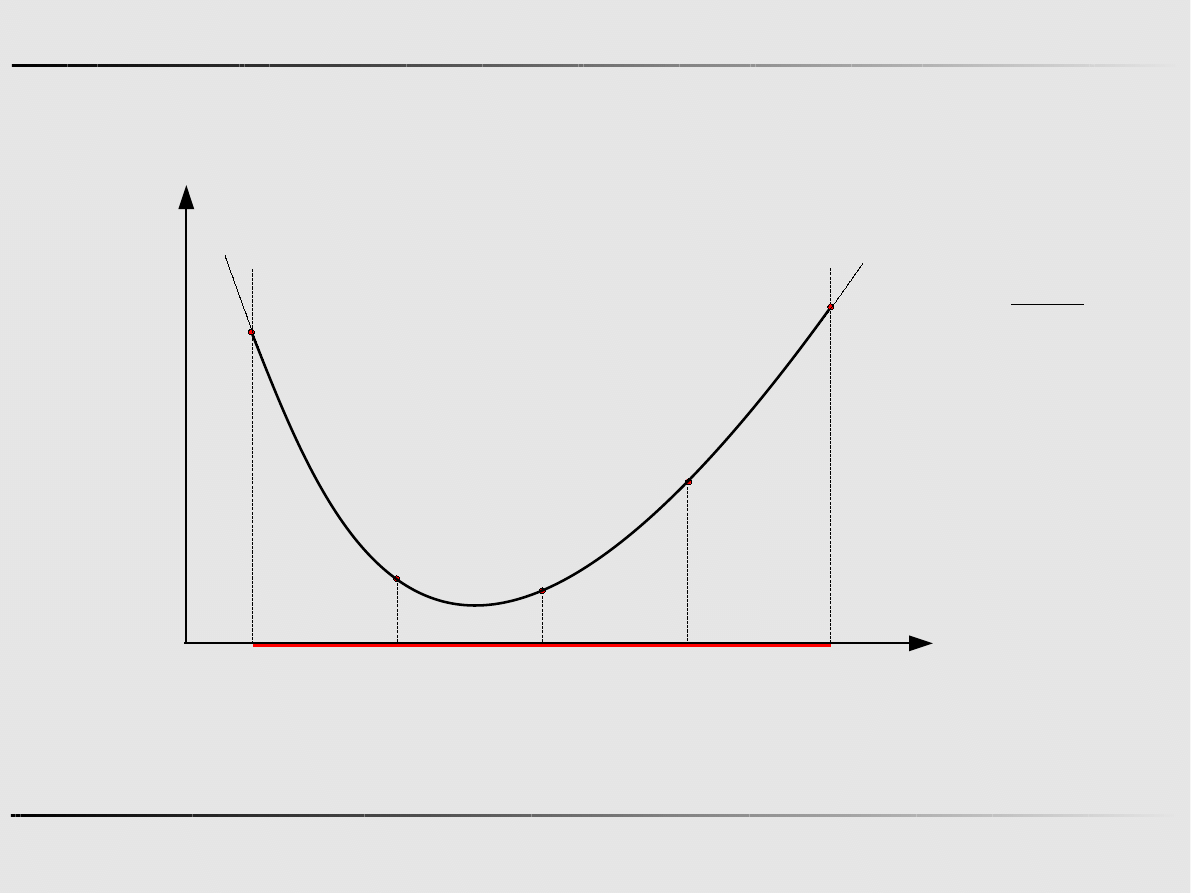
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia
x
m
f(x
m
)
x
1
x
2
f(x
1
)
f(x
2
)
x
m
=
(
a+b)
2
x
1
=
a+0.25⋅L
x
2
=
b−0.25⋅L
L=b−a
L
a
b
f(a)
f(b)
X
f(x)
Krok 0
9.05.2013
Szczecin
34
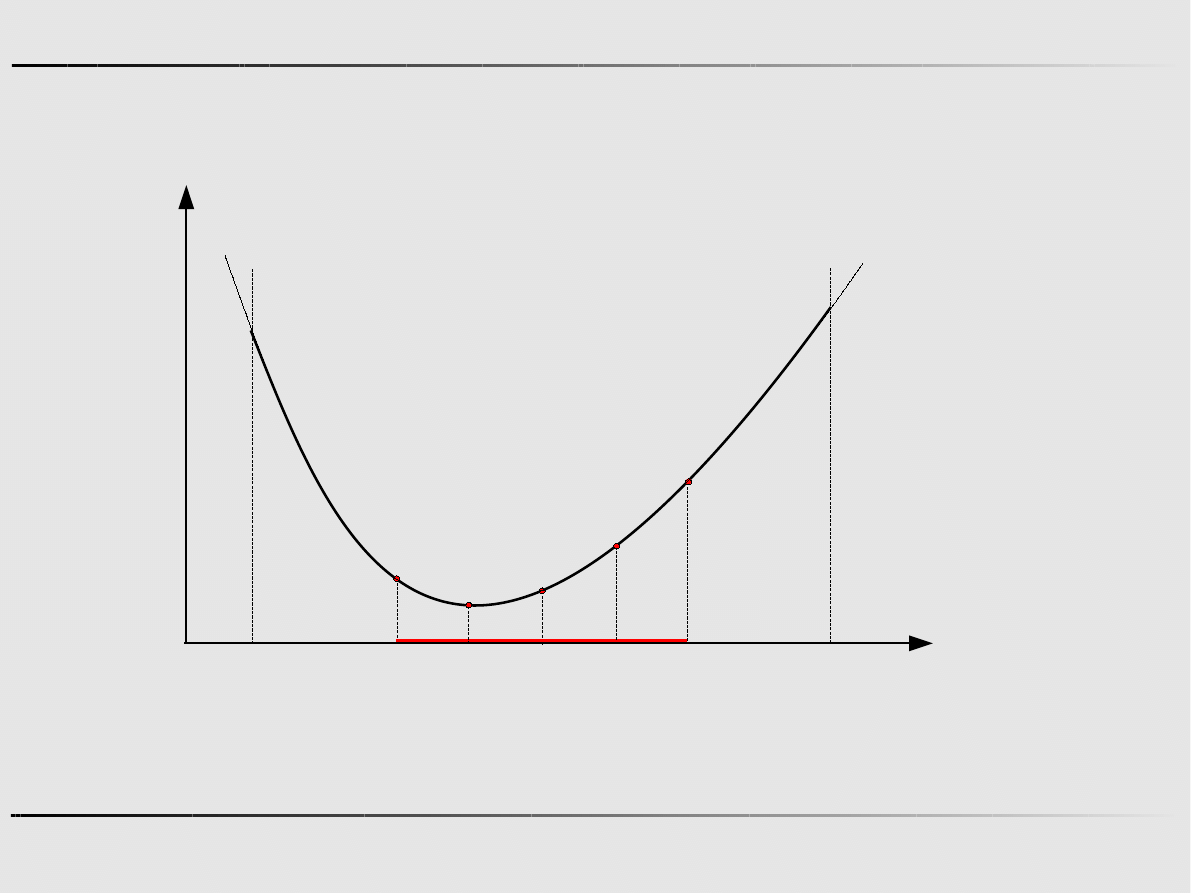
Metody optymalizacji
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia
x
m
f(x
m
)
a
b
f(a)
f(b)
L
X
f(x)
Krok 1
x
1
f(x
1
)
x
2
f(x
2
)
x
1
=
a+0.25⋅L
x
2
=
b−0.25⋅L
L=b−a
9.05.2013
Szczecin
35
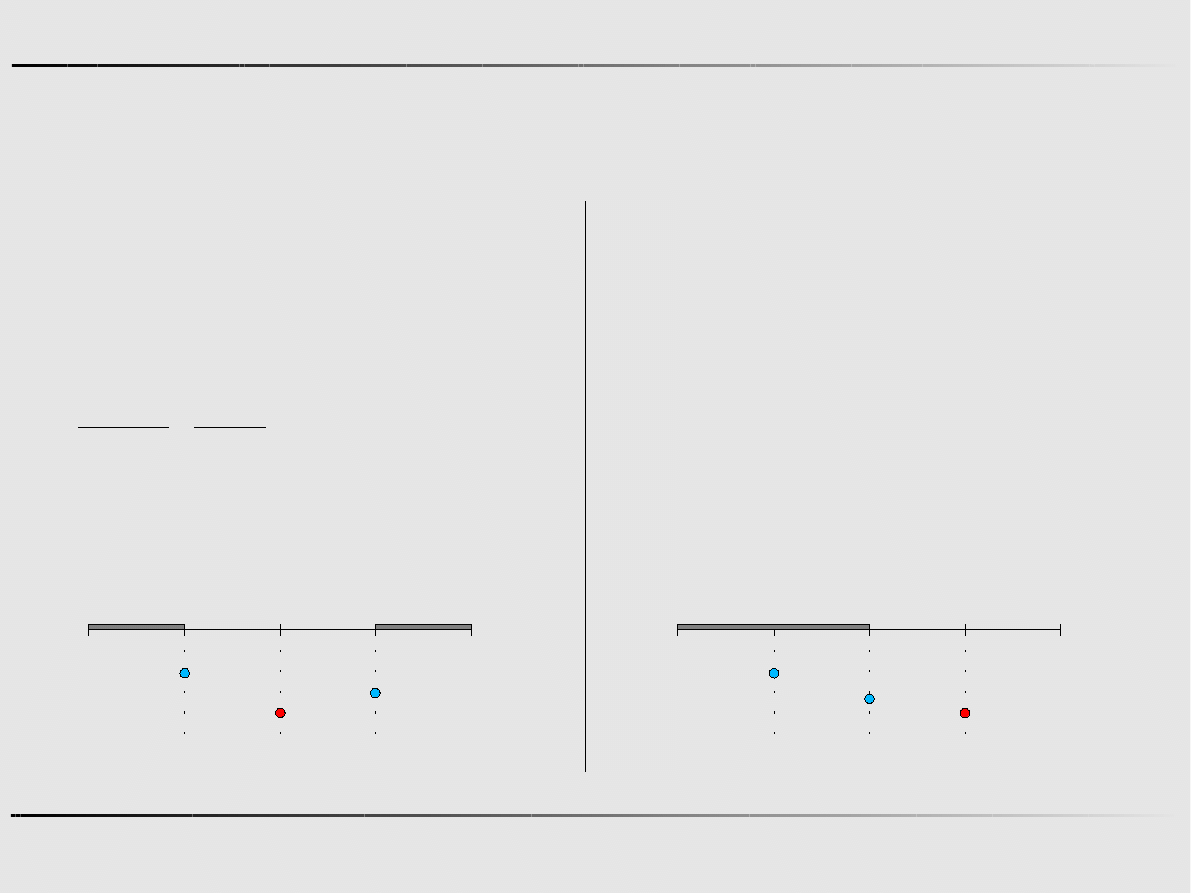
Metody optymalizacji
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 0
x
m0
=
(
a
0
+
b
0
)
2
=
(
0+2)
2
=
1,
f (1)=−10
x
10
=
a
0
+
0.25⋅L
0
=
0+0.25⋅2=0.5 , f (0.5)=−7.75
x
20
=
b
0
−
0.25⋅L
0
=
2−0.25⋅2=1.5 , f (1.5)=−9.75
L
0
=
b
0
−
a
0
=
2−0=2
a
x
10
x
m0
x
20
b
0
a
0
a
0
=
0,
f (0)=−3
b
0
=
2,
f (2)=−7
Krok 1
x
11
=
a
1
+
0.25⋅L
1
=
0.75 , f (0.75)=−9.1875
L
1
=
b
1
−
a
1
=
1.5−0.5=1
a
1
=
x
10
=
0.5
b
1
=
x
20
=
1.5
x
21
=
b
1
−
0.25⋅L
1
=
1.25 , f (1.25)=−10.1875
x
m1
=
x
m0
=
1
a
x
11
x
m1
x
21
b
1
a
1
9.05.2013
Szczecin
36
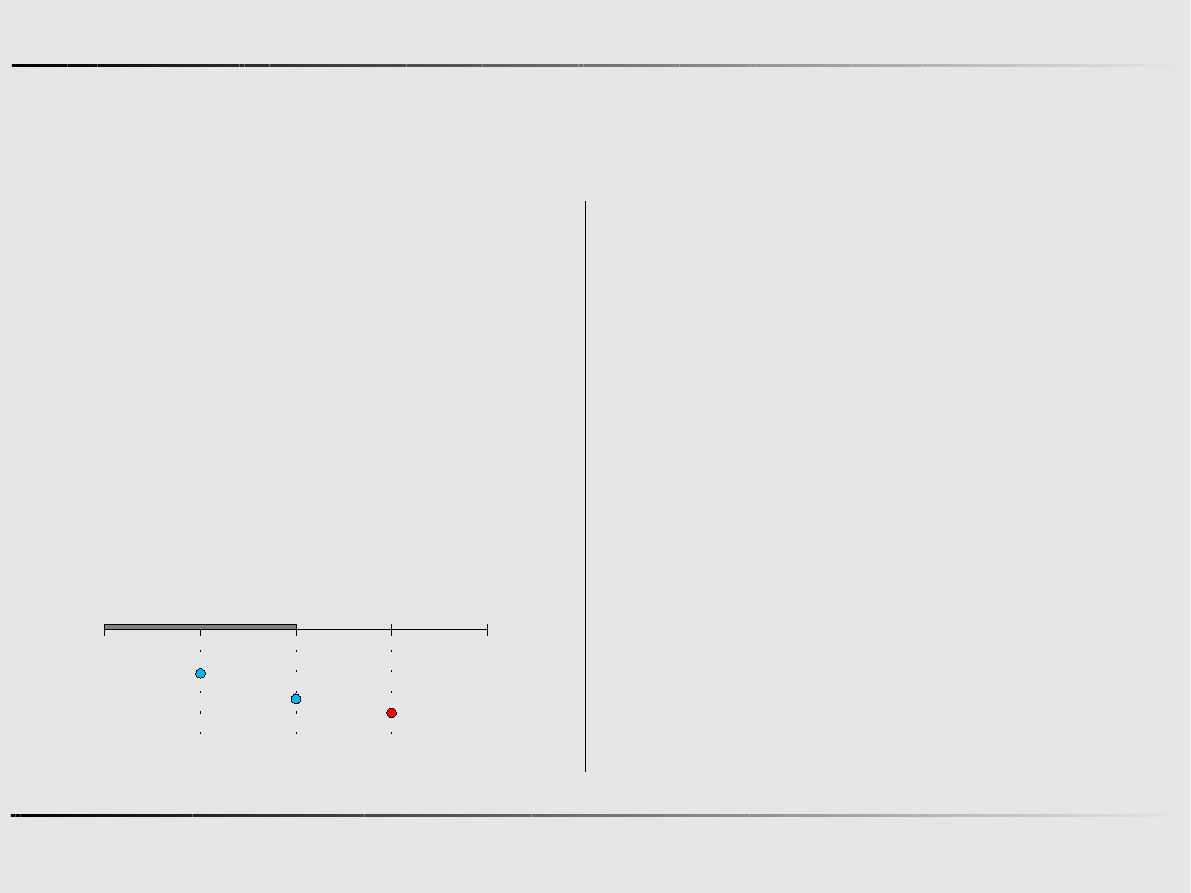
Metody optymalizacji
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 1
x
11
=
a
1
+
0.25⋅L
1
=
0.75 , f (0.75)=−9.1875
L
1
=
b
1
−
a
1
=
1.5−0.5=1
a
1
=
x
10
=
0.5
b
1
=
x
20
=
1.5
x
21
=
b
1
−
0.25⋅L
1
=
1.25 , f (1.25)=−10.1875
x
m1
=
x
m0
=
1
a
x
11
x
m1
x
21
b
1
a
1
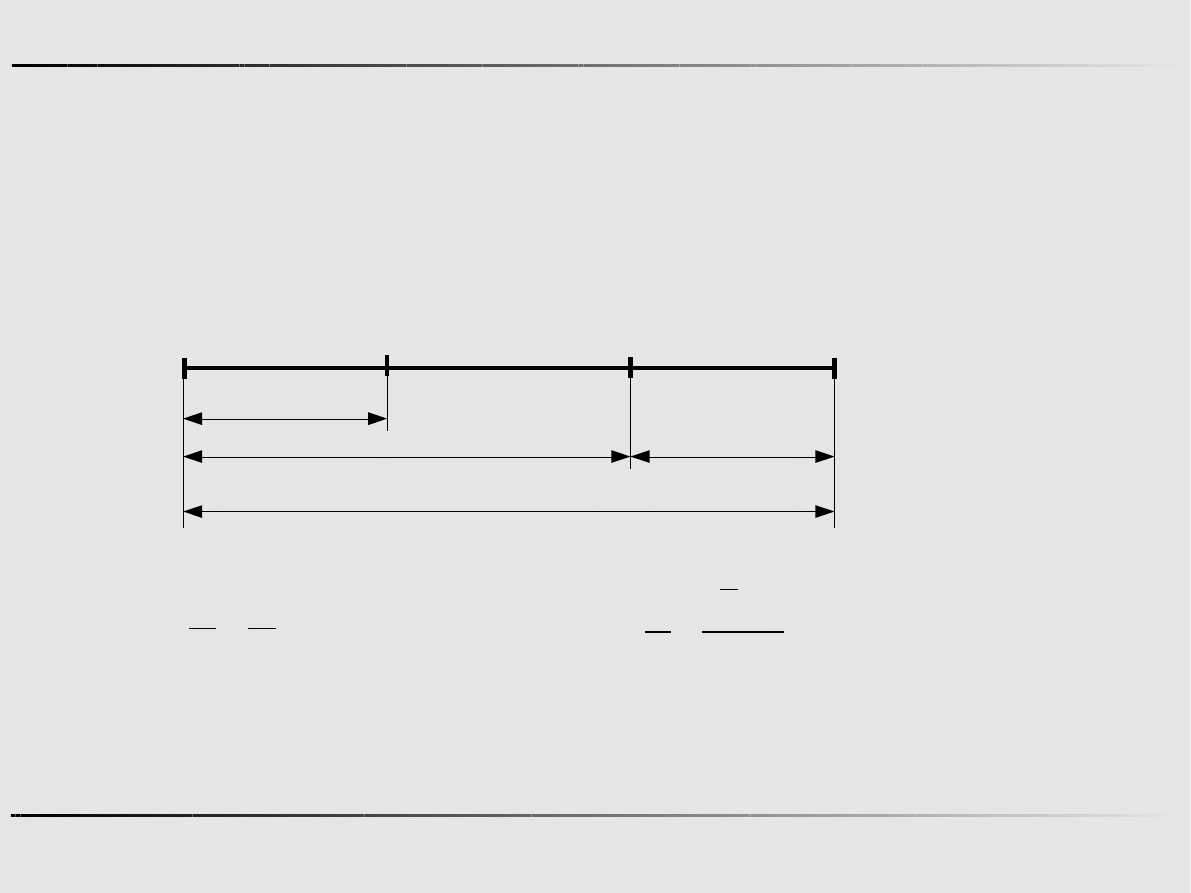
Krok 2
x
12
=…
L
2
=
b
2
−
a
2
=
0.5
a
2
=
x
m1
=
1
b
2
=
b
1
=
1.5
x
22
=…
x
m2
=
x
21
=
1.25
9.05.2013
Szczecin
37
Metody optymalizacji
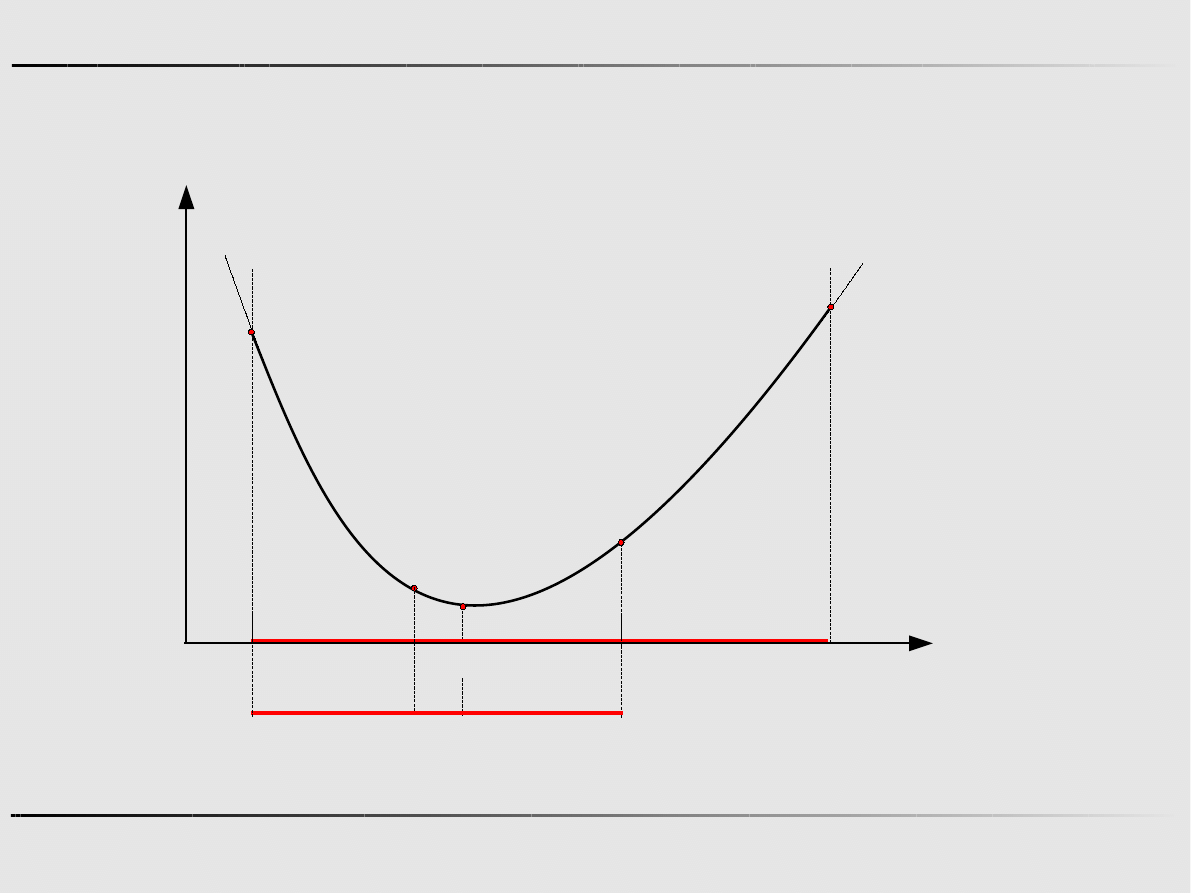
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda złotego podziału
Idea złotego podziału odcinka
A
C
B
a
β
b
C
α
B
A
=
C
B
gdzie:
C=A−B
B
A
=
√
5−1
2
≈
0.618
9.05.2013
Szczecin
38
Metody optymalizacji
α
β
α=
b−0.618⋅L
β=
a+0.618⋅L
L=b−a
L
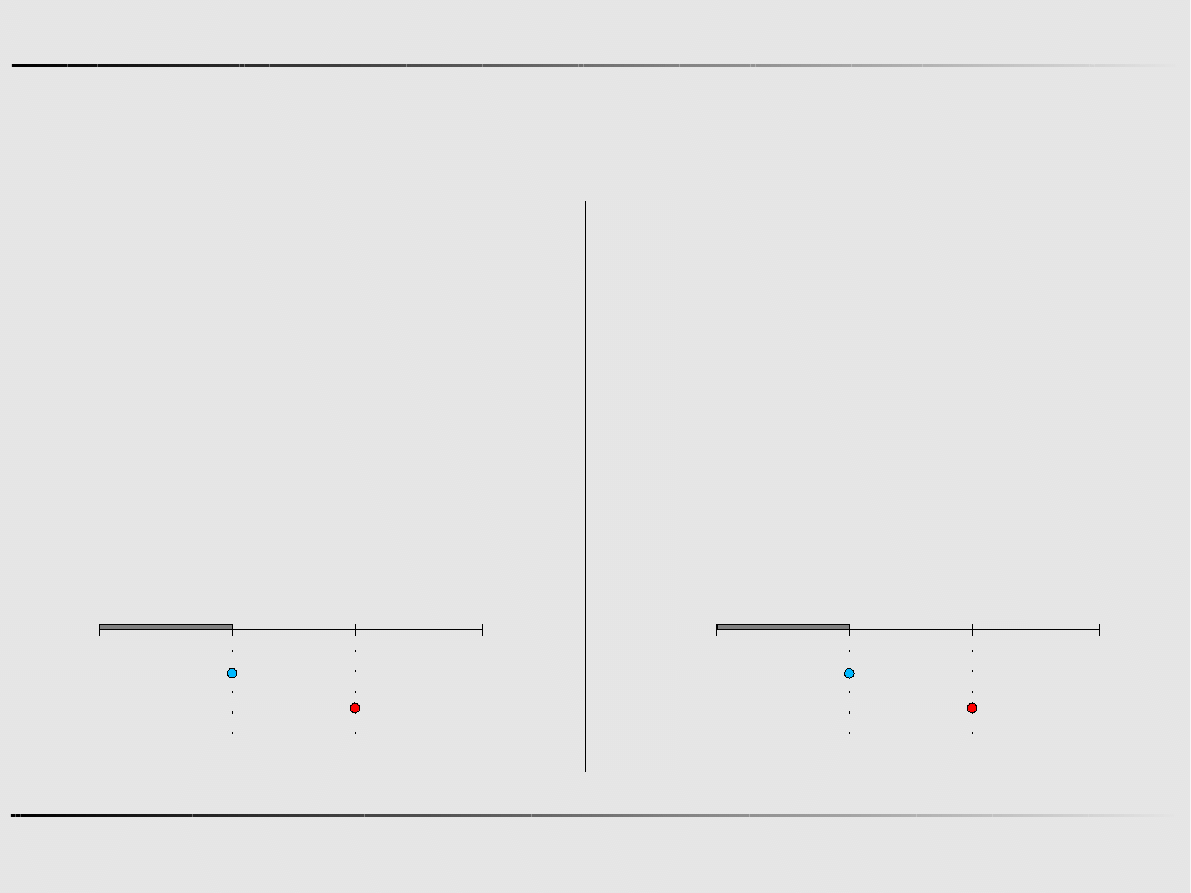
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda złotego podziału
a
b
X
f(x)
f(b)
f(a)
f(
α
)
f(
β
)
f(
α1
)
α1 β1
b1
L1
a1
Krok 0
β
1=α
α
1=b1−0.618⋅L1
a 1=a
Krok 1
b 1=β
L1=b1−a1
9.05.2013
Szczecin
39
Metody optymalizacji
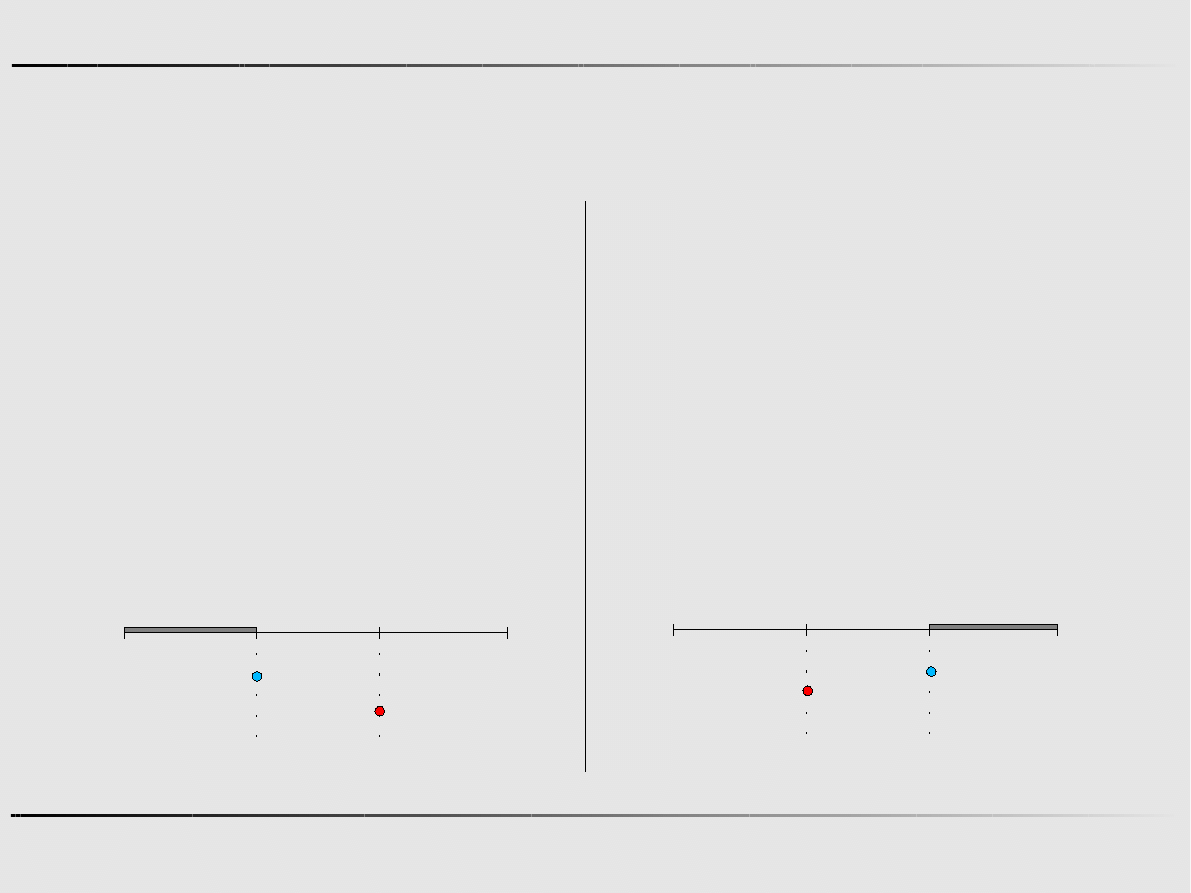
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda złotego podziału - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 0
L
0
=
b
0
−
a
0
=
2−0=2
a
α
0
β
0
b
0
a
0
a
0
=
0,
f (0)=−3
b
0
=
2,
f (2)=−7
Krok 1
α
0
=
b
0
−
0.618⋅L
0
=
0.764 ,
f (0.764)=−9.2495
β
0
=
a
0
+
0.618⋅L
0
=
1.236 ,
f (1.236)=−10.1935
L
1
=
b
1
−
a
1
=
1.236
a
1
=α
0
=
0.764 ,
b
1
=
b
0
=
2
α
1
=β
0
=
1.236
β
1
=
a
1
+
0.618⋅L
1
=
1.5278 ,
f (1.5278)=−9.6626
a
α
1
β
1
b
1
a
1
9.05.2013
Szczecin
40
Metody optymalizacji
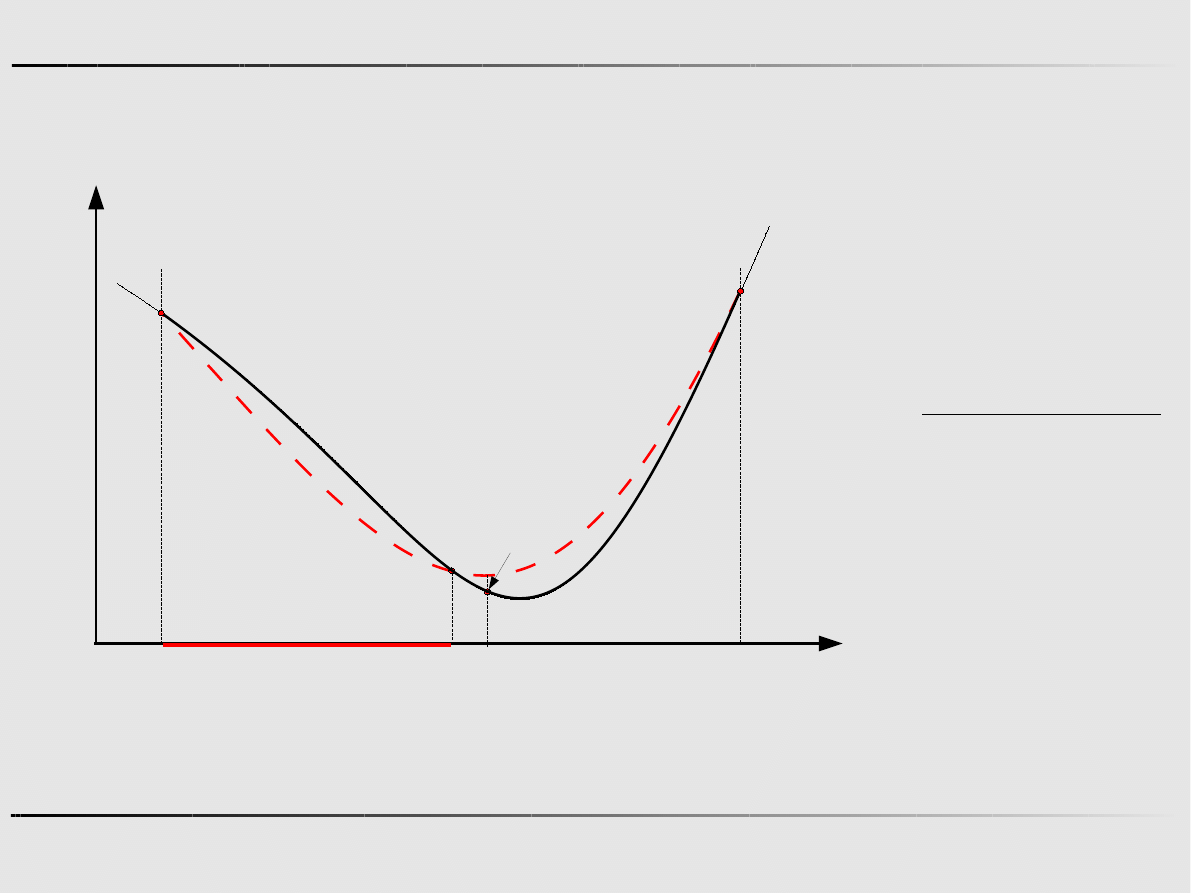
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 1
Krok 2
L
1
=
b
1
−
a
1
=
1.236
a
1
=α
0
=
0.764 ,
b
1
=
b
0
=
2
α
1
=β
0
=
1.236
β
1
=
a
1
+
0.618⋅L
1
=
1.5278 ,
f (1.5278)=−9.6626
a
α
1
β
1
b
1
a
1
L
2
=
b
2
−
a
2
=
0.764
a
2
=α
1
=
1.236 ,
b
2
=
b
1
=
2
α
2
=β
1
=
1.5278
β
2
=
a
2
+
0.618⋅L
2
=
1.7082 ,
f (1.7082)=−8.909
a
α
2
β
2
b
2
a
2
9.05.2013
Szczecin
41
Metody optymalizacji
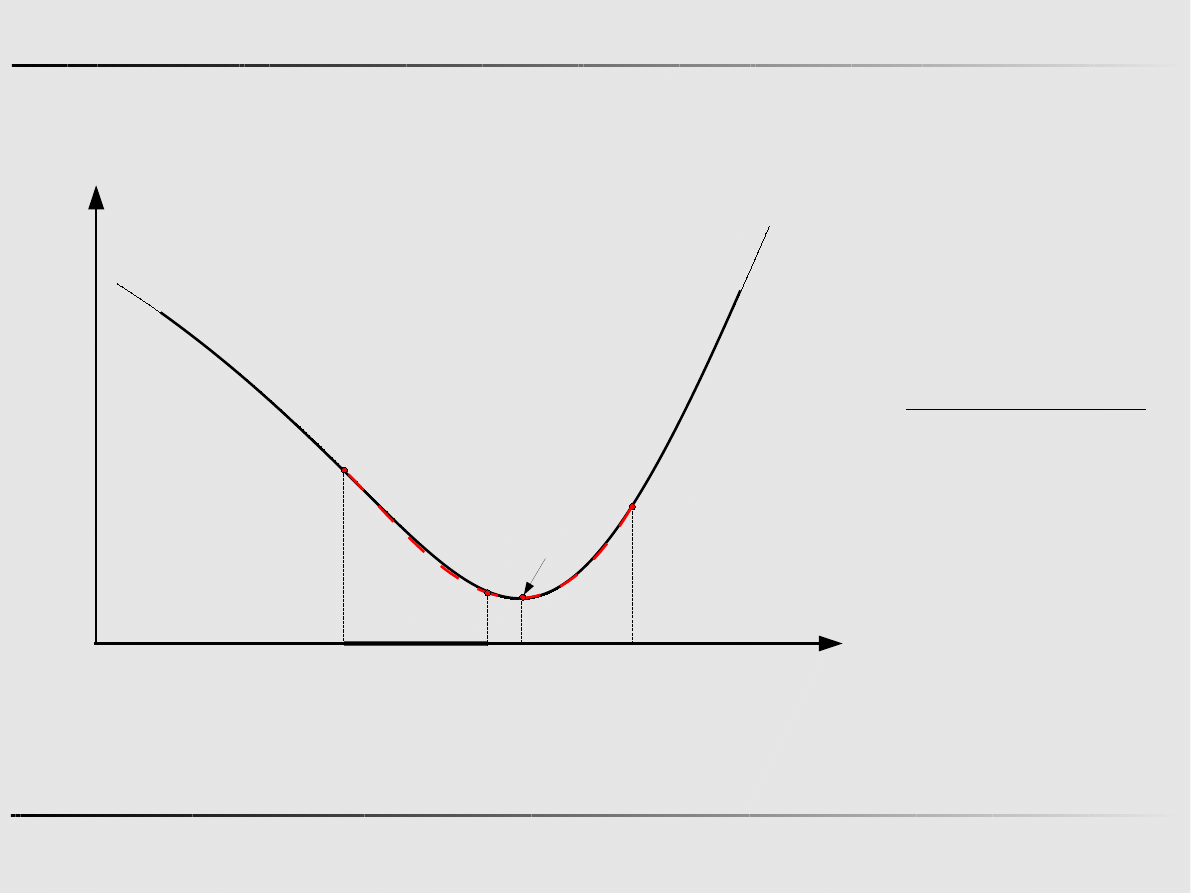
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja kwadratowa funkcji – algorytm Powella
x
1
<
x
2
<
x
3
Krok 0
x
2
Δ=
x
2
−
x
1
=
x
3
−
x
2
x
m
f(x
m
)
f(x
2
)
x
1
x
3
X
f(x)
f(x
3
)
f(x
1
)
x
m
=
x
2
−
0.5⋅Δ
f ( x
3
)−
f ( x
1
)
f ( x
1
)−
2 f ( x
2
)+
f ( x
3
)
∆
9.05.2013
Szczecin
42
Metody optymalizacji
x
1
x
3
∆
X
f(x)
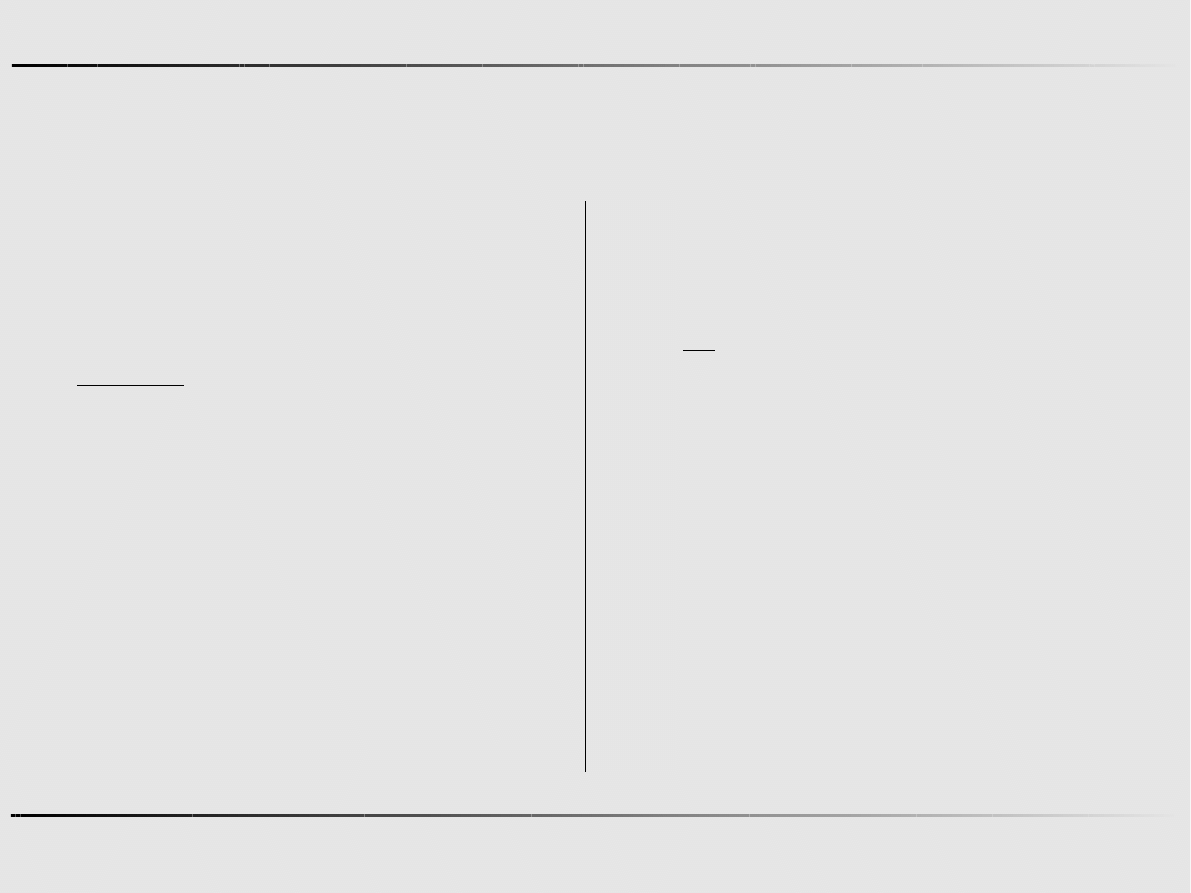
Krok 1
f(x
3
)
x
2
x
m
f(x
m
)
f(x
2
)
f(x
1
)
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja kwadratowa funkcji – algorytm Powella
x
1
<
x
2
<
x
3
Δ=
x
2
−
x
1
=
x
3
−
x
2
x
m
=
x
2
−
0.5⋅Δ
f ( x
3
)−
f ( x
1
)
f ( x
1
)−
2 f ( x
2
)+
f ( x
3
)
9.05.2013
Szczecin
43
Metody optymalizacji
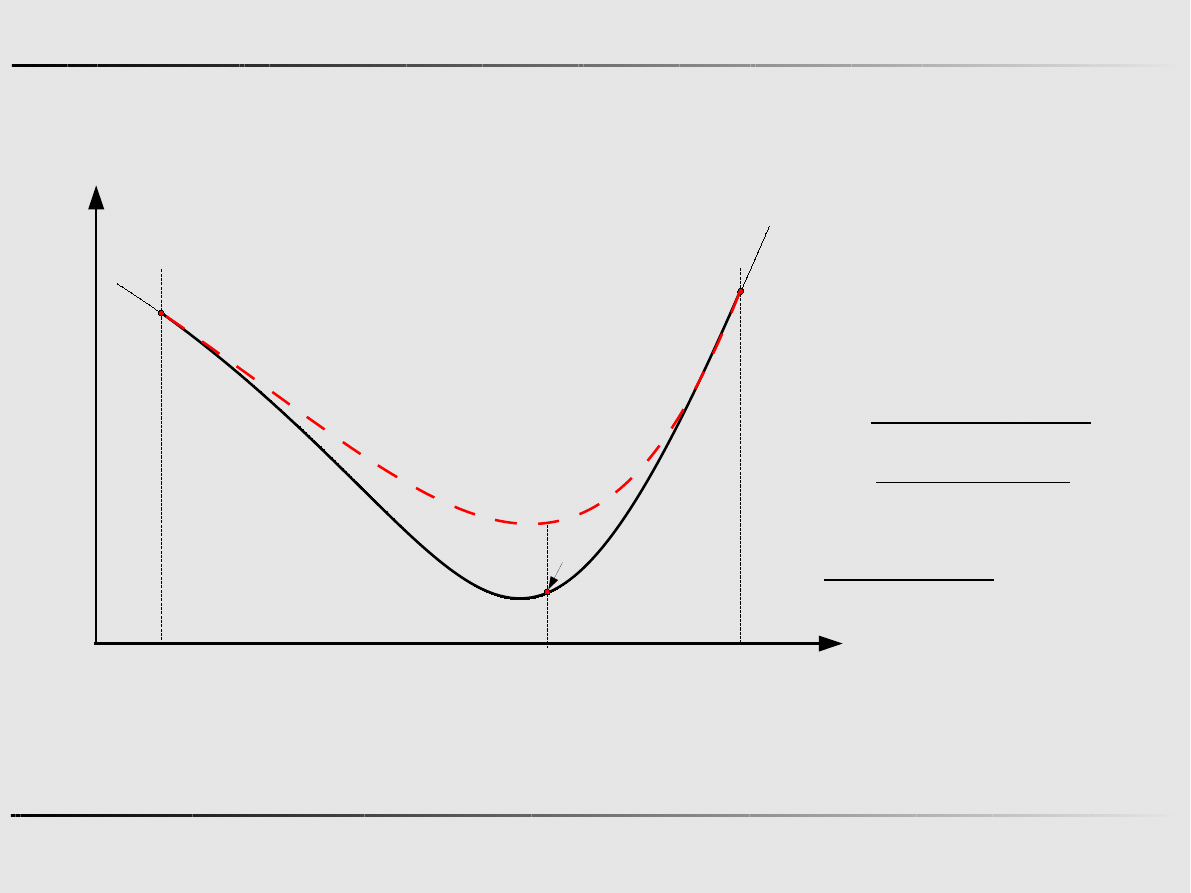
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja kwadratowa - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 0
x
20
=
(
x
10
+
x
30
)
2
=
1,
f (1)=−10
x
10
=
0,
f (0)=−3
x
30
=
2,
f (2)=−7
Krok 1
x
m0
=
1.2 ,
f (1.2)=−10.2
x
21
=
x
m0
=
1.2 ,
f (1.2)=−10.2
x
11
=
x
21
−Δ
1
=
0.7 ,
f (0.7)=−8.95
x
31
=
x
22
+Δ
1
=
1.7 ,
f (1.7)=−8.95
x
m1
=
1.2 ,
f (1.2)=−10.2
Δ
0
=
x
20
−
x
10
=
1
Δ
1
=
Δ
0
2
=
0.5
9.05.2013
Szczecin
44
Metody optymalizacji
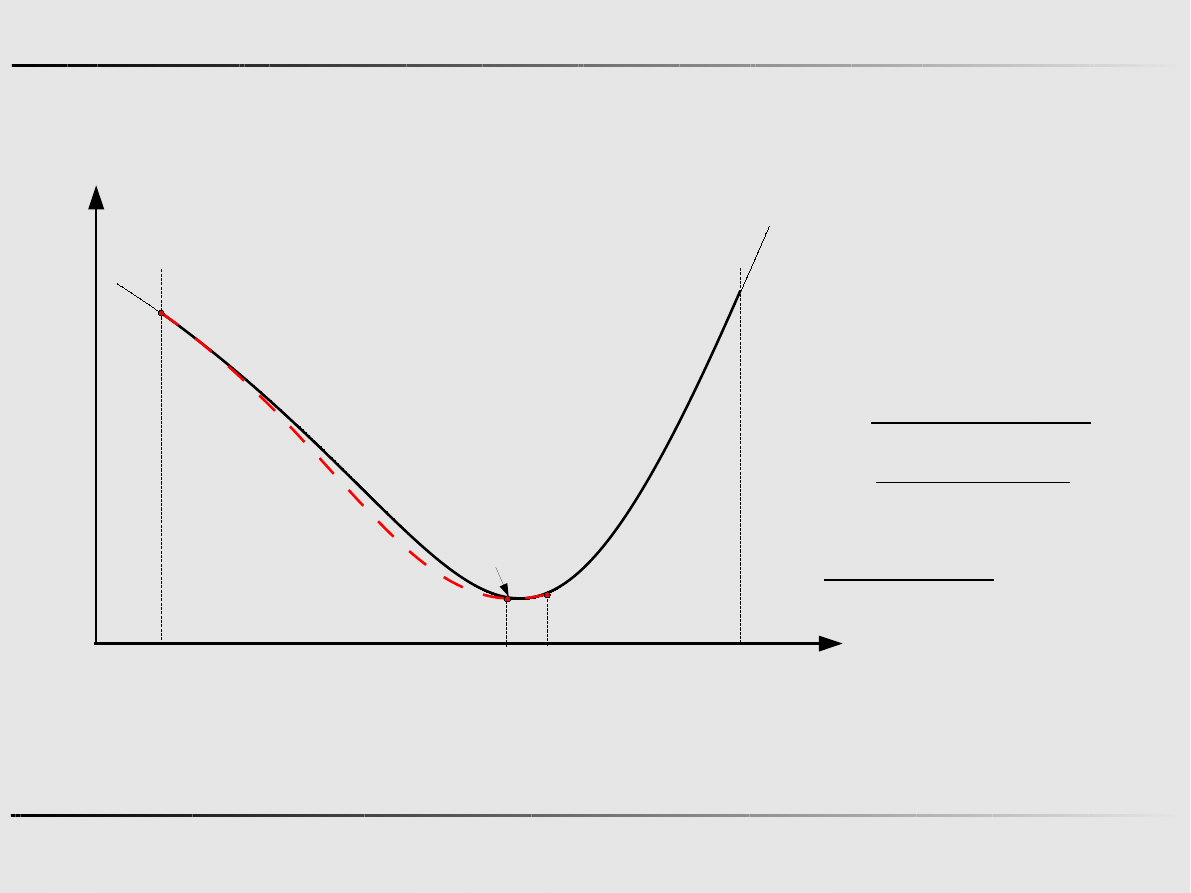
Ekstremum funkcji jednej zmiennej - algorytmy pierwszego rzędu
Aproksymacja sześcienna funkcji – algorytm Davidona
a
b
f ' (a)<0, f ' (b)>0
X
f(x)
Krok 0
f(b)
x
m
f(x
m
)
f(a)
x
m
=
b−
f ' (b)+Q−Z
f ' (b)− f ' (a)+2 Q
(
b−a)
Q=
√
Z
2
−
f ' (a)⋅f ' (b)
Z =
3[ f (a)− f (b)]
b−a
+
f ' (a)+ f ' (b)
9.05.2013
Szczecin
45
Metody optymalizacji
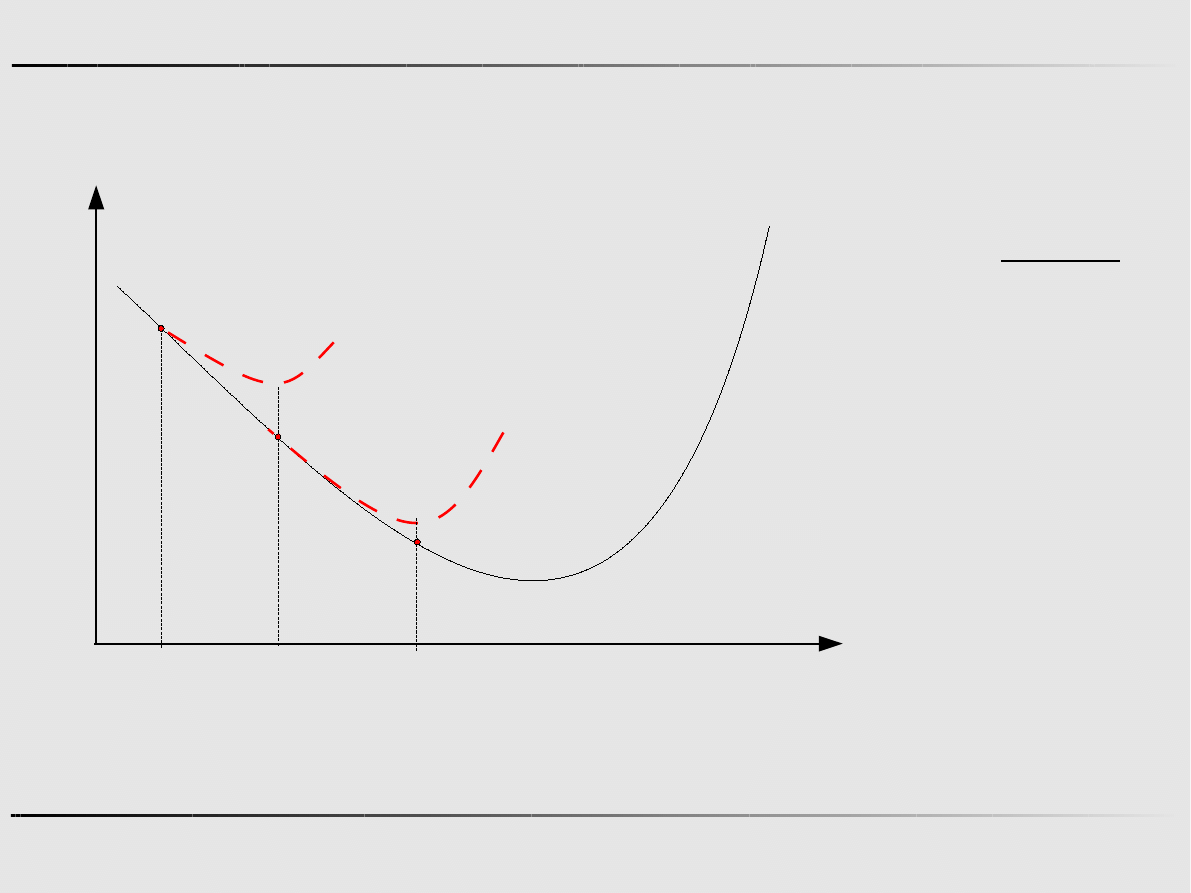
Ekstremum funkcji jednej zmiennej - algorytmy pierwszego rzędu
Aproksymacja sześcienna funkcji – algorytm Davidona
a
X
f(x)
Krok 1
b
f(x
m
)
f(a)
x
m
f(b)
f ' (a)<0, f ' (b)>0
x
m
=
b−
f ' (b)+Q−Z
f ' (b)− f ' (a)+2 Q
(
b−a)
Q=
√
Z
2
−
f ' (a)⋅f ' (b)
Z =
3[ f (a)− f (b)]
b−a
+
f ' (a)+ f ' (b)
9.05.2013
Szczecin
46
Metody optymalizacji
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja sześcienna - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 0
f ' ( x)=10 x−12
x
m
=
b−
f ' (b)+Q−Z
f ' (b)− f ' (a)+2 Q
(
b−a)=1.2 , f (1.2)=−10.2
Q=
√
Z
2
−
f ' (a)⋅f ' (b)=10
Z =
3[ f (a)− f (b)]
b−a
+
f ' (a)+ f ' (b)=2
a
0
=
0,
f (0)=−3,
f ' (0)=−12
b
0
=
2,
f (2)=−7,
f ' (2)=8
f ' (a)<0, f ' (b)>0
f ' (1.2)=0
9.05.2013
Szczecin
47
Metody optymalizacji
Ekstremum funkcji jednej zmiennej - algorytmy drugiego rzędu
algorytm Newtona
x
0
X
f(x)
f(x
0
)
x
1
f(x
1
)
x
2
f(x
2
)
x
n+1
=
x
n
−
f ' ( x
n
)
f ' ' ( x
n
)
9.05.2013
Szczecin
48
Metody optymalizacji
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda Newtona - przykład
Znajdz minimum funkcji f ( x)=5 x
2
−
12 x−3, w przedziale <0,2> .
Krok 0
f ' ( x)=10 x−12,
f ' ' ( x)=10
a=0,
f (0)=−3,
f ' (0)=−12,
f ' ' (0)=10
b=2,
f (2)=−7,
f ' (2)=8,
f ' ' (2)=10
x
1
=
x
0
−
f ' (x
0
)
f ' ' ( x
0
)
=
0−
−
12
10
=
1.2 ,
f (1.2)=−10.2
x
0
=
a
x
0
=
b
x
1
=
x
0
−
f ' (x
0
)
f ' ' ( x
0
)
=
2−
8
10
=
1.2 ,
f (1.2)=−10.2