
1
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Metody optymalizacji
dr inż. Anna Barcz
Zakład Matematyki Stosowanej
kontakt: pokój 28
abarcz@wi.zut.edu.pl

2
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Niech dany będzie układ m liniowo niezależnych równań z n niewiadomymi
x
1
,x
2
,...,x
n
, który będziemy nazywali układem ograniczeń zadania
programowania liniowego
Programowanie liniowe
{
a
11
x
1
a
12
x
2
a
1n
x
n
=
b
1
a
21
x
1
a
22
x
2
a
2n
x
n
=
b
2
a
m1
x
1
a
m2
x
2
a
mn
x
n
=
b
m
gdzie, nie zmniejszając ogólności, można założyć, że b
i
≥
0.
Należy znaleźć nieujemne wartości zmiennych x
j
≥
0, (j=1,...,n), które
minimalizują (maksymalizują) funkcję celu
Z =c
1
x
1
c
2
x
2
c
n
x
n

3
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Każdy zbiór zmiennych x
j
(j=1,...,n) spełniający układ równań będziemy
nazywali rozwiązaniem.
Jednak na x
j
nałożono dodatkowy warunek x
j
≥
0 (j=1,...,n).
Rozwiązania, które spełniają ten warunek będziemy nazywali
rozwiązaniami dopuszczalnymi.
Sens zadania programowania liniowego polega na tym, aby ze zbioru
rozwiązań dopuszczalnych wybrać to, które minimalizuje (maksymalizuje)
funkcję celu.
Programowanie liniowe

4
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Bazą nazywamy dowolny zbiór m zmiennych takich, że wyznacznik
składający się ze współczynników przy tych zmiennych jest różny od zera.
m zmiennych x
1
, x
2
, ..., x
m
nazywa się zmiennymi bazowymi.
pozostałe (n-m) zmiennych x
m+1
,x
m+2
,...,x
n
nazywa się zmiennymi
niebazowymi.
dla układu równań można zadać kilka różnych baz o różnych zmiennych
bazowych.
rozwiązanie bazowe nazywa się dopuszczalnym rozwiązaniem
bazowym, jeżeli wartości należących do niego zmiennych bazowych są
nieujemne.
Programowanie liniowe

5
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – ekstremum funkcji liniowej przy liniowych
ograniczeniach
Opracowanie modelu programowania liniowego:
●
określenie zmiennych zadania,
●
określenie ograniczeń w postaci liniowych równań lub nierówności,
●
wyznaczenie linowej funkcji celu podlegającej minimalizacji lub
maksymalizacji
Programowanie liniowe
Metody:
metoda graficzna,
metoda algebraiczna,
metoda simpleks.

6
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Metoda simpleks – iteracyjna procedura rozwiązywania zadania
programowania liniowego, zapisanego w postaci znormalizowanej.
Algorytm metody simpleks:
Wybór początkowego dopuszczalnego rozwiązania bazowego.
Przejście od początkowego rozwiązania do innego dopuszczalnego
rozwiązania bazowego o lepszej wartości funkcji celu.
Kontynuacja
poszukiwań
kolejnych
dopuszczalnych
rozwiązań
bazowych, polepszających wartości funkcji celu. Sąsiednie dopuszczalne
rozwiązanie bazowe różni się od poprzedniego tylko o jedną zmienną
bazową.
Jeśli nie ma możliwości polepszenia uzyskanego dopuszczalnego
rozwiązania bazowego, to można wywnioskować, że jest ono optymalne.
Programowanie liniowe – metoda simpleks

7
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – przykład
Zadanie: Pewien zakład produkuje dwa typy płytek chodnikowych.
Oba typy wymagają zużycia jednakowej ilości surowców (piasek,
woda, żwir, cement). Jeden typ jest barwny i do jego produkcji
potrzebna jest farba. Wyprodukowanie 1 tony płytek barwnych
wymaga 2h pracy maszyn, 3h pracy ludzkiej i 2l barwnika. Produkcja
tony płyt bezbarwnych wymaga 1h pracy maszyn, 3h pracy ludzkiej.
Zysk: płyty barwne 300 zł/t, płyty bezbarwne 200 zł/t. Dysponujemy
10h pracy urządzeń, 24h pracy ludzkiej i 8l barwnika. Ile
wyprodukować płyt (jakich) aby osiągnąć maksymalny zysk.

8
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – przykład
Oznaczenia:
x
1
=
płyty barwne ,
x
2
=
płyty bezbarwne.
Funkcja celu:
Z =300 x
1
200 x
2
max
Ograniczenia:
{
2 x
1
x
2
10
3 x
1
3 x
2
24
2 x
1
8
x
i
0 i=12
9
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
- zmienne dopełniające
Programowanie liniowe – metoda simpleks
Funkcja celu:
Z =300 x
1
200 x
2
max
Ograniczenia:
{
2 x
1
x
2
10
3 x
1
3 x
2
24
2 x
1
8
Postać kanoniczna – zamieniamy nierówności na równości:
{
2 x
1
x
2
x
3
=
10
3 x
1
3 x
2
x
4
=
24
2 x
1
x
5
=
8
x
i
0 i=15
Z =300 x
1
200 x
2
0 x
3
0 x
4
0 x
5
Przekształcamy ograniczenia, tak aby wszystkie wyrazy wolne były
nieujemne i zapisujemy postać znormalizowaną (kanoniczną).
Uwzględniamy zmienne dopełniające w funkcji celu:

10
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – metoda simpleks
Postać kanoniczna:
{
2 x
1
x
2
x
3
=
10
3 x
1
3 x
2
x
4
=
24
2 x
1
x
5
=
8
x
i
0 i=15
Z =300 x
1
200 x
2
0 x
3
0 x
4
0 x
5
Funkcja celu:
Ograniczenia:
{
2 x
1
1 x
2
1 x
3
0 x
4
0 x
5
=
10
3 x
1
3 x
2
0 x
3
1 x
4
0 x
5
=
24
2 x
1
0 x
2
0 x
3
0 x
4
1 x
5
=
8
Ograniczenia w postaci macierzowej:
2 1 1 0 0
3 3 0 1 0
2 0 0 0 1
A
⋅
x
1
x
2
x
3
x
4
x
5
X
=
10
24
8
b
A⋅X =b
11
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
a
1
a
2
a
3
a
4
a
5
2 1 1 0 0
3 3 0 1 0
2 0 0 0 1
A
⋅
x
1
x
2
x
3
x
4
x
5
X
=
10
24
8
b
Programowanie liniowe – metoda simpleks
Ograniczenia w postaci macierzowej:
Z =300 x
1
200 x
2
0 x
3
0 x
4
0 x
5
Funkcja celu:
Wektory bazowe
c
b
0
0
0
a
3
a
4
a
5
wiersz wskaźnikowy
c
j
b
10
24
8
300
a
1
2
3
2
200
a
2
1
3
0
0
a
3
1
0
0
0
a
4
0
1
0
0
a
5
0
0
1
Pierwsza tablica simpleksów
12
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
-200
F
j
−
c
j
=
c
b
T
⋅
a
j
−
c
j
-300
0
0
0
0
F
0
=
c
b
T
⋅
b
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
0
0
0
a
3
a
4
a
5
wiersz wskaźnikowy
0
2
c
j
b
10
24
8
300
a
1
2
3
200
a
2
1
3
0
0
a
3
1
0
0
0
a
4
0
1
0
a
5
0
0
1
b
a
1
10/2=5
24 /3=8
8/2=4
Pierwsza tablica simpleksów
kolumna kluczowa (KK)
wiersz kluczowy (WK)
2
element rozwiązujący (ER)
13
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
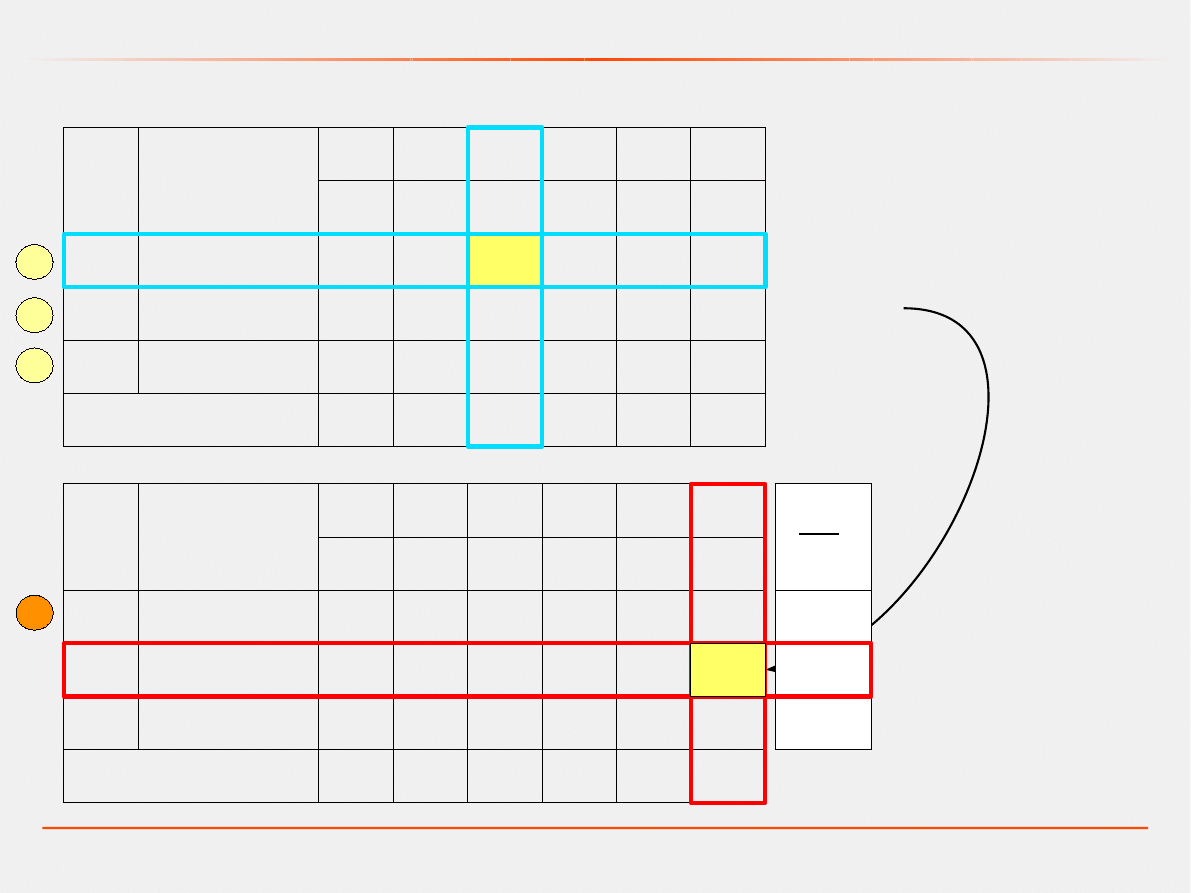
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
0
0
300
a
3
a
4
a
1
wiersz wskaźnikowy
c
j
b
300
a
1
200
a
2
0
a
3
0
a
4
0
a
5
Druga tablica simpleksów
Pierwsza tablica simpleksów
W1
W2
WK
0
1200
-200
0
0
150
1
4
0
0
0
1/2
WK / ER
NW3
12
0
3
0
1
-3/2
W2 - 3*NW3
2
0
1
1
0
-1
W1 - 2*NW3
b
a
2
2/1=2
12/3=4
2
Wektory bazowe
c
b
0
0
0
a
3
a
4
a
5
wiersz wskaźnikowy
c
j
b
10
24
8
300
a
1
2
3
200
a
2
1
3
0
0
a
3
1
0
0
0
a
4
0
1
0
0
a
5
0
0
1
-300
0
-200
0
0
0
1
14
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
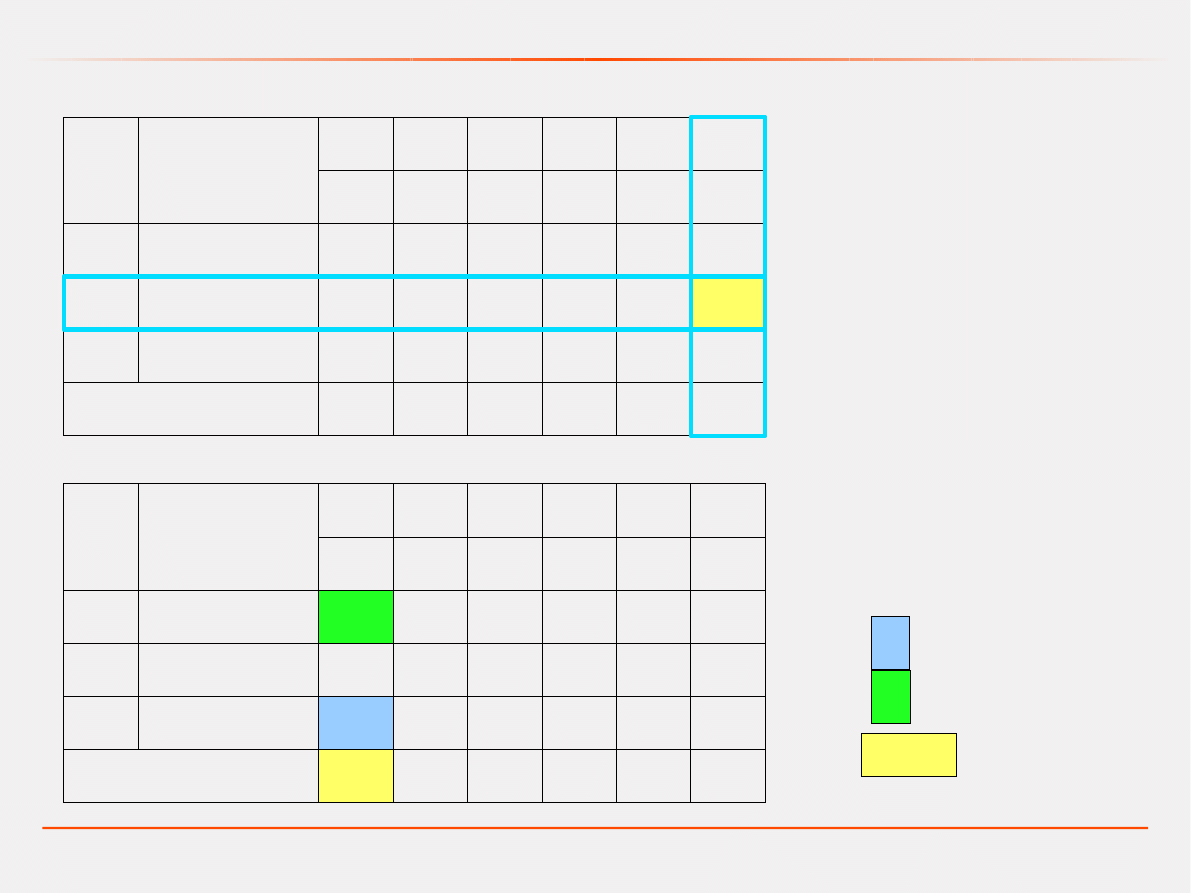
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
200
0
300
a
2
a
4
a
1
wiersz wskaźnikowy
c
j
b
300
a
1
200
a
2
0
a
3
0
a
4
0
a
5
Trzecia tablica simpleksów
Druga tablica simpleksów
WK
W2
W3
0
1600
0
200
0
-50
1
4
0
0
0
1/2
6
0
0
-3
1
3/2
W2 - 3*NW1
b
a
5
6: 3/2=4
4 :1/2=8
1
Wektory bazowe
c
b
0
0
300
a
3
a
4
a
1
wiersz wskaźnikowy
c
j
b
2
12
4
300
a
1
0
0
200
a
2
1
3
0
0
a
3
1
0
0
0
a
4
0
1
0
0
a
5
-1
-3/2
1/2
0
1200
-200
0
0
150
2
0
1
1
0
-1
NW1
3/2
15
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
200
0
300
a
2
a
5
a
1
wiersz wskaźnikowy
c
j
b
300
a
1
200
a
2
0
a
3
0
a
4
0
a
5
Czwarta tablica simpleksów
0
1800
0
100
33.3
0
0
4
0
-2
2/3
1
0
6
1
-1
2/3
0
1
2
0
1
-1/3
0
Wektory bazowe
c
b
200
0
300
a
2
a
4
a
1
wiersz wskaźnikowy
c
j
b
300
a
1
200
a
2
0
a
3
0
a
4
0
a
5
Trzecia tablica simpleksów
0
1600
0
200
0
-50
1
4
0
0
0
1/2
6
0
0
-3
1
3/2
2
0
1
1
0
-1
ROZWIĄZANIE:
x
1
=
2
x
2
=
6
Z =1800

16
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – postać kanoniczna
Przy realizacji metody simpleks mogą powstać pewne problemy
obliczeniowe, związane z tak zwanym zwyrodnieniem zadania.
Zwyrodniałym dopuszczalnym rozwiązaniem bazowym nazywa się
dopuszczalne rozwiązanie bazowe, w którym jedna lub kilka
zmiennych bazowych przybierają wartość zerową.
W tym przypadku może się okazać, że zmiana bazy nie zmienia
wartości funkcji celu.

17
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
- zmienne dopełniające
Programowanie liniowe – postać kanoniczna
Funkcja celu:
Z =300 x
1
200 x
2
max
Ograniczenia:
{
−
2 x
1
−
x
2
−
10
3 x
1
3 x
2
24
2 x
1
=
8
Postać kanoniczna – zamieniamy nierówności na równości:
{
2 x
1
x
2
−
x
3
=
10
3 x
1
3 x
2
x
4
=
24
2 x
1
=
8
x
i
0 i=14
Z =300 x
1
200 x
2
0 x
3
0 x
4
Przekształcamy ograniczenia, tak aby wszystkie wyrazy wolne były
nieujemne i zapisujemy postać kanoniczną.
Uwzględniamy zmienne dopełniające w funkcji celu:
{
2 x
1
x
2
10
3 x
1
3 x
2
24
2 x
1
=
8

18
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – metoda simpleks
Postać kanoniczna:
x
i
0 i=14
Z =300 x
1
200 x
2
0 x
3
0 x
4
max
Funkcja celu:
Ograniczenia:
Ograniczenia w postaci macierzowej:
2 1−1 0
3 3 0 1
2 0 0 0
A
⋅
x
1
x
2
x
3
x
4
X
=
10
24
8
b
A⋅X =b
{
2 x
1
x
2
−
x
3
=
10
3 x
1
3 x
2
x
4
=
24
2 x
1
=
8
Brak bazy startowej !

19
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – metoda simpleks
Dodajemy zmienne sztuczne:
x
i
0 i=16
Z =300 x
1
200 x
2
0 x
3
0 x
4
−
M x
5
−
M x
6
Funkcja celu:
Ograniczenia:
Ograniczenia w postaci macierzowej:
2 1−1 0 1 0
3 3 0 1 0 0
2 0 0 0 0 1
A
⋅
x
1
x
2
x
3
x
4
x
5
x
6
X
=
10
24
8
b
A⋅X =b
{
2 x
1
x
2
−
x
3
x
5
=
10
3 x
1
3 x
2
x
4
=
24
2 x
1
x
6
=
8
Zmienne sztuczne
M – liczba dużo większa od pozostałych
współczynników funkcji celu
20
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
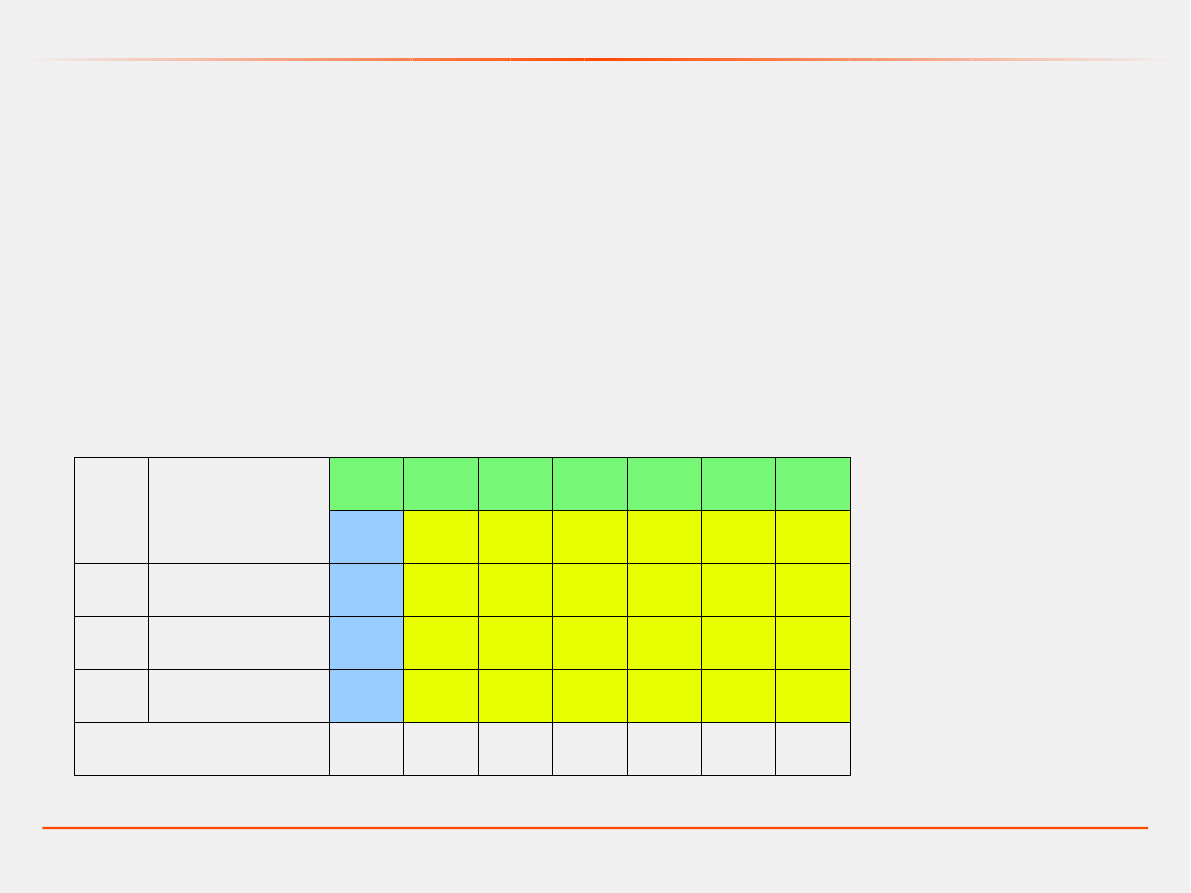
Programowanie liniowe – metoda simpleks
Ograniczenia w postaci macierzowej:
Funkcja celu:
Wektory bazowe
c
b
-1000
0
-1000
a
5
a
4
a
6
wiersz wskaźnikowy
c
j
b
10
24
8
300
a
1
2
3
2
200
a
2
1
3
0
0
a
3
-1
0
0
0
a
4
0
1
0
-1000
a
5
1
0
0
Pierwsza tablica simpleksów
2 1−1 0 1 0
3 3 0 1 0 0
2 0 0 0 0 1
A
⋅
x
1
x
2
x
3
x
4
x
5
x
6
X
=
10
24
8
b
Z =300 x
1
200 x
2
0 x
3
0 x
4
−
M x
5
−
M x
6
Z =300 x
1
200 x
2
0 x
3
0 x
4
−
1000 x
5
−
1000 x
6
-1000
a
6
0
0
1

21
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – przykład 2
Funkcja celu:
Z =5 x
1
3 x
2
max
Ograniczenia:
{
3 x
1
5 x
2
15
−
5 x
1
−
2 x
2
−
10
x
i
0 i=12

22
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
Programowanie liniowe – przykład 2
Funkcja celu:
Ograniczenia (postać znormalizowana):
{
3 x
1
5 x
2
x
3
=
15
5 x
1
2 x
2
x
4
=
10
x
i
0 i=14
Z =5 x
1
3 x
2
0 x
3
0 x
4
23
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
-3
F
j
−
c
j
=
c
b
T
⋅
a
j
−
c
j
-5
0
0
0
F
0
=
c
b
T
⋅
b
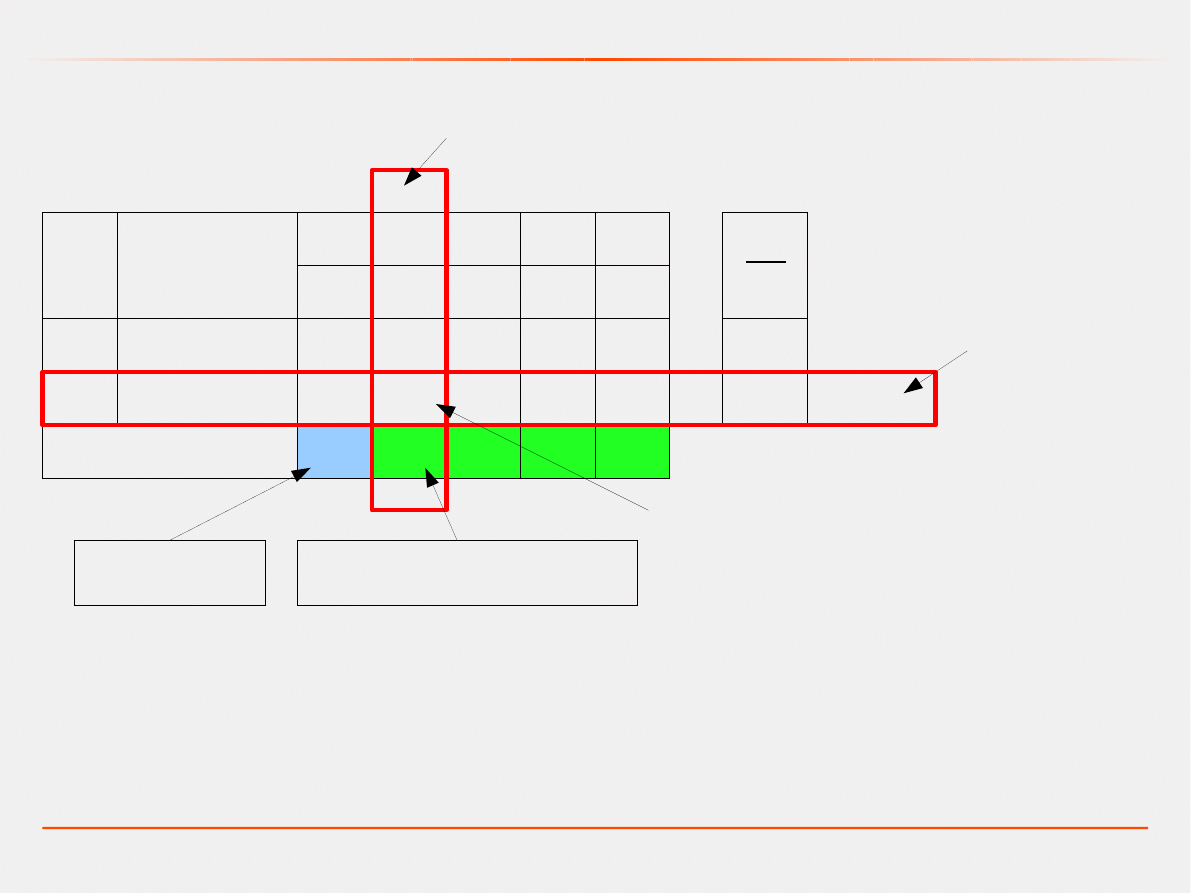
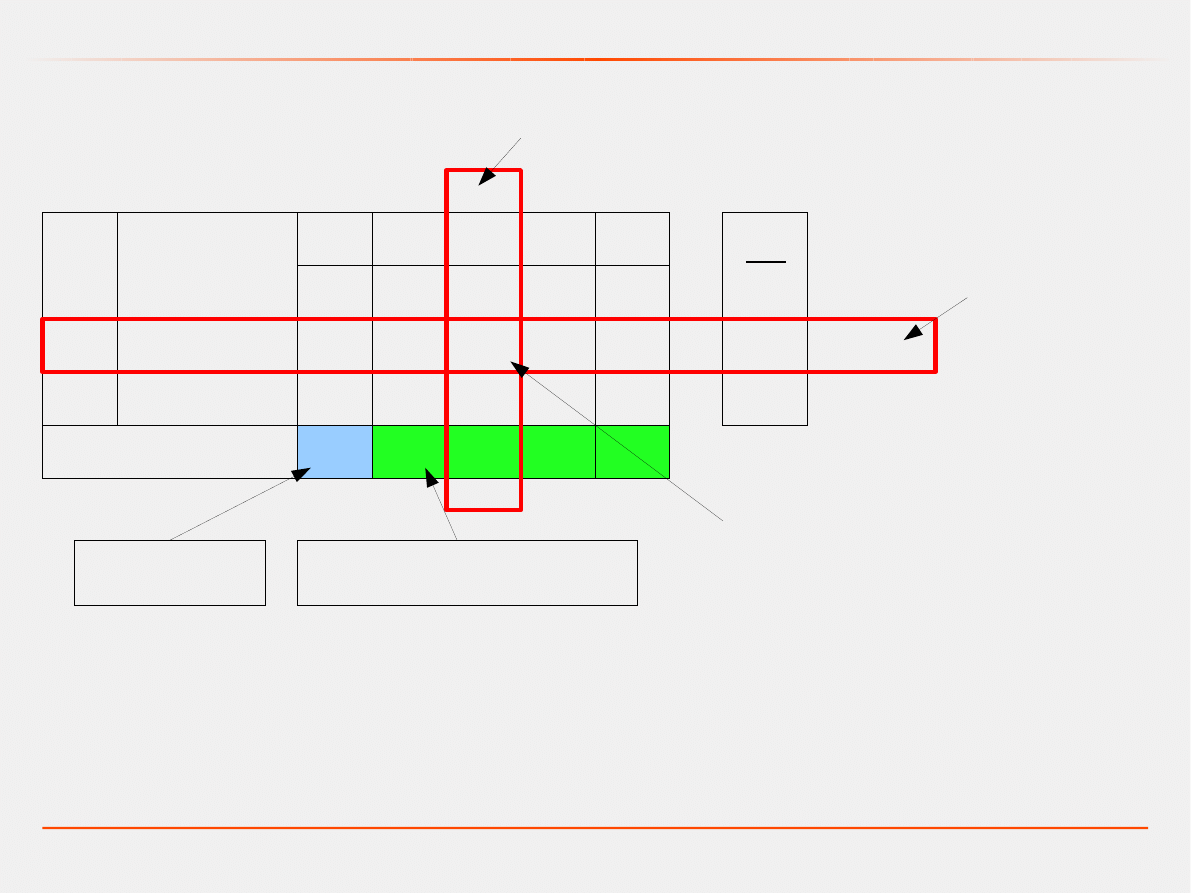
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
0
0
a
3
a
4
wiersz wskaźnikowy
c
j
b
15
10
5
a
1
3
5
3
a
2
5
2
0
a
3
1
0
0
a
4
0
1
b
a
1
15/3=5
10/5=2
Pierwsza tablica simpleksów
kolumna kluczowa (KK)
wiersz kluczowy (WK)
element rozwiązujący (ER)
24
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
-1
F
j
−
c
j
=
c
b
T
⋅
a
j
−
c
j
0
0
1
10
F
0
=
c
b
T
⋅
b
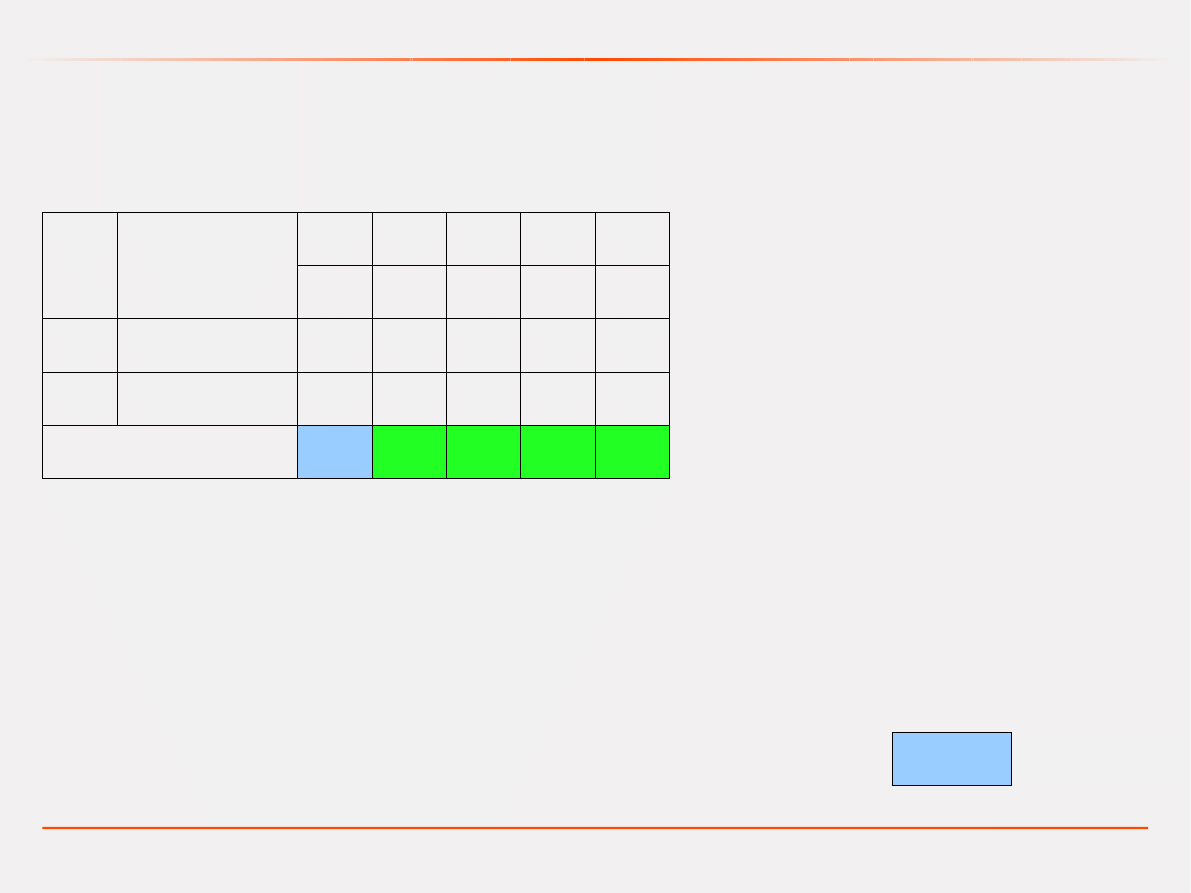
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
0
5
a
3
a
1
wiersz wskaźnikowy
c
j
b
9
2
5
a
1
0
1
3
a
2
3.8
2/5
0
a
3
1
0
0
a
4
-3/5
1/5
b
a
2
2.638
5
Druga tablica simpleksów
kolumna kluczowa (KK)
wiersz kluczowy (WK)
element rozwiązujący (ER)
25
METODY OPTYMALIZACJI
Szczecin - 9.05.2013
0
0
0.263 0.842
12.368
Programowanie liniowe – metoda simpleks
Wektory bazowe
c
b
3
5
a
2
a
1
wiersz wskaźnikowy
c
j
b
2.368
1.053
5
a
1
0
1
3
a
2
1
0
0
a
3
0.263
-0.105
0
a
4
-0.158
0.263
Trzecia tablica simpleksów
ROZWIĄZANIE:
x
1
=
1.053 ,
x
2
=
2.368
Z =12.368
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
- Slajd 19
- Slajd 20
- Slajd 21
- Slajd 22
- Slajd 23
- Slajd 24
- Slajd 25
Wyszukiwarka
Podobne podstrony:
psychologia ogólna W5 2013
Optymalizacja w4 2013
Logika W5 2013 14 ppt
Optymalizacja w1 2013
Optymalizacja w2 2013
ZJ w5 2013
Optymalizacja w3 2013
psychologia ogólna W5 2013
Optymalizacja w4 2013
PPS 2013 W5
GF w5 4.11, Geologia GZMiW UAM 2010-2013, I rok, Geologia fizyczna, Geologia fizyczna - wykłady, 03,
GF w5 16.03, Geologia GZMiW UAM 2010-2013, I rok, Geologia fizyczna, Geologia fizyczna - wykłady, 05
PPS 2013 W5
więcej podobnych podstron