Zarządzanie jakością
dr inż. Anna Olszewska
a.olszewska@pb.edu.pl
Instrumentarium zarządzania
- statystyczne metody sterowania jakościa
Zarządzanie jakością
dr inż. Anna Olszewska
a.olszewska@pb.edu.pl
Instrumentarium zarządzania
- statystyczne metody sterowania jakościa
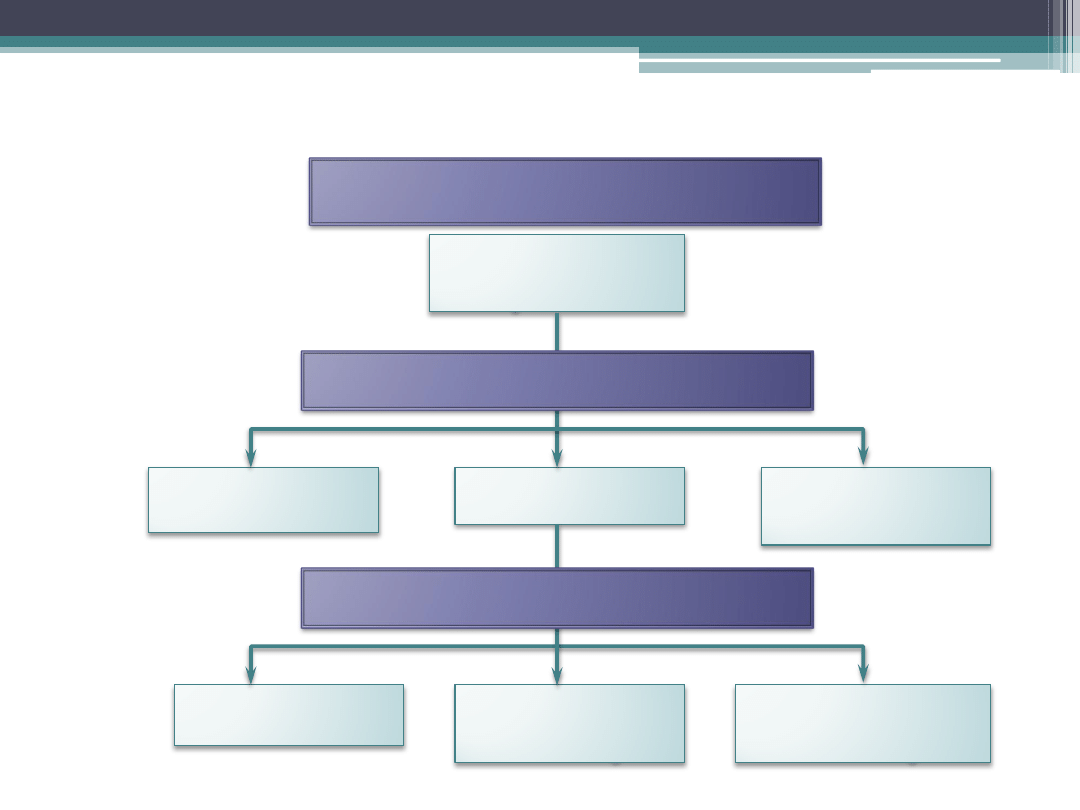
Narzędzia statystyczne
Zbieranie danych
Analiza
wariancji
Pobieranie
próbek
Statystyki
Rozkłady
Przedziały
ufności
Hipotezy
Analiza regresji
i korelacji
Charakterystyka populacji
Wnioskowanie
Pobieranie próbek
Zanim dane do analizy zostaną pobrane, należy podjąć decyzję o
sposobie doboru, jak też liczebności próby. Przede wszystkim
wybierana próba powinna być reprezentatywna, czyli z przyjętą z góry
dokładnością opisująca strukturę zbiorowości. Reprezentatywność
można osiągnąć poprzez dobór celowy lub losowy. Ponieważ wybór
celowy jest decyzją badacza, nie podlega działaniu praw wielkich liczb,
większość badań oparta jest na doborze próby w sposób losowy.
Losowanie może się odbywać w sposób zwrotny (mówimy wówczas o
losowaniu niezależnym) lub bez zwracania (losowanie zależne).
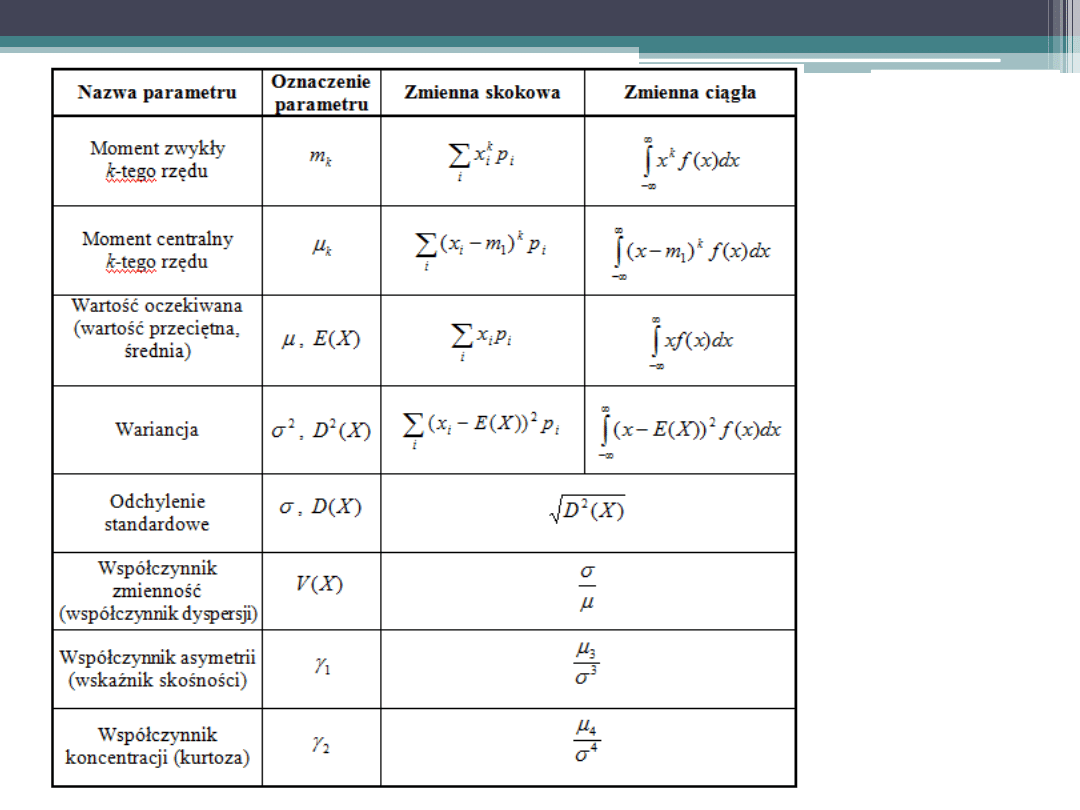
Statystyki wykorzystywane w pomiarze jakości
Zbiorowość można opisywać za pomocą różnych statystyk, nazywanych
charakterystykami, takich jak:
•
średnia
•
wariancja
•
odchylenie standardowe
•
współczynniki asymetrii
•
współczynnik koncentracji
•
współczynnik korelacji
•
współczynnik regresji
•
frakcja
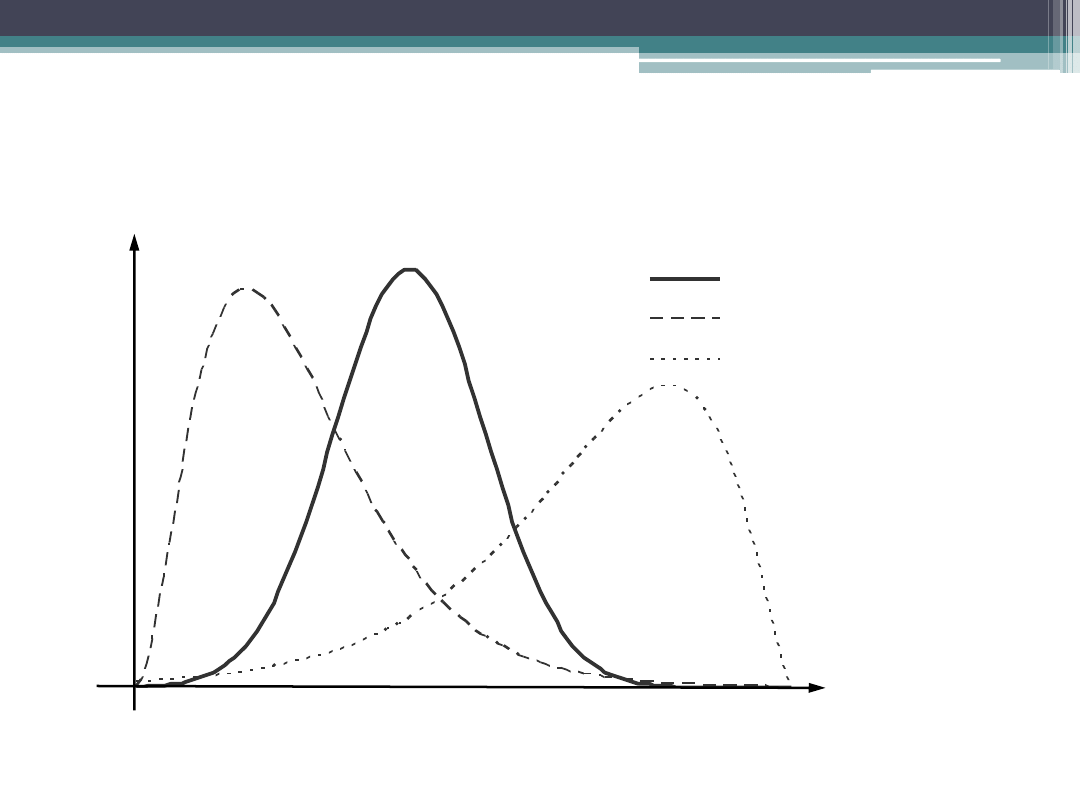
Rozkłady przy różnych wartościach miary
asymetrii (
1
)
1
=0
1
=1,1
1
= -0,9
x
f(x)
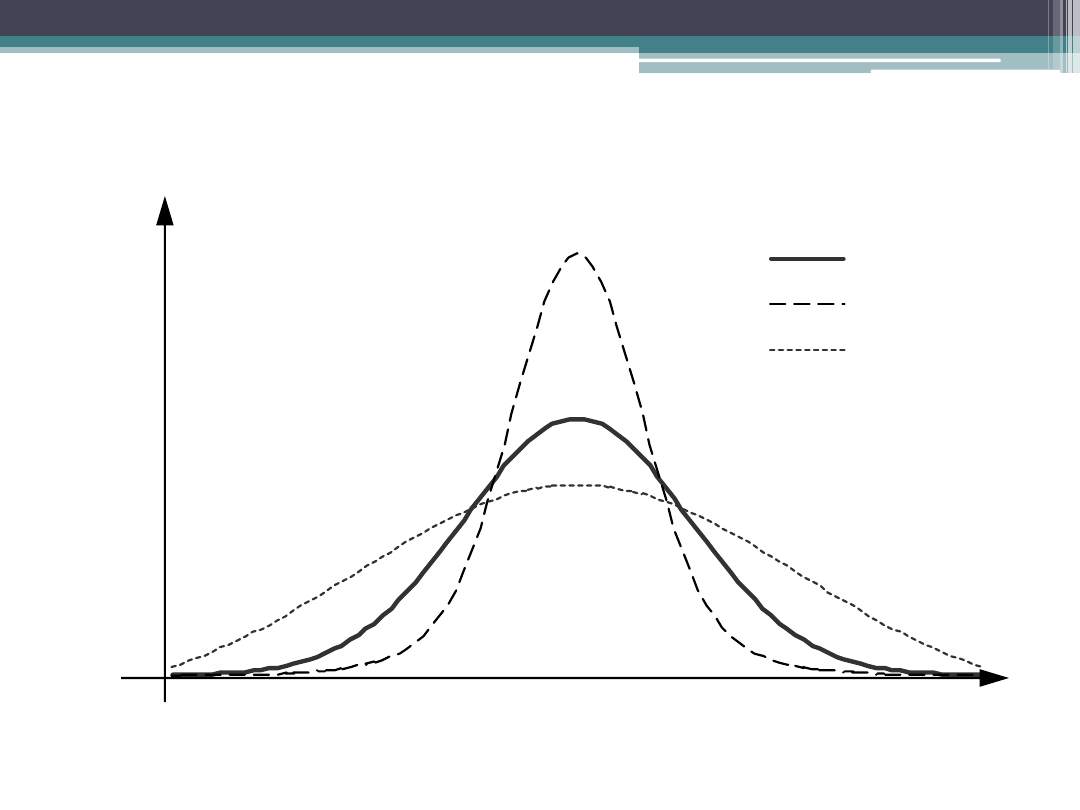
Rozkłady przy różnych wartościach
miary koncentracji (
2
)
2
=3,0
2
=2,2
2
=4,6
x
f(x)
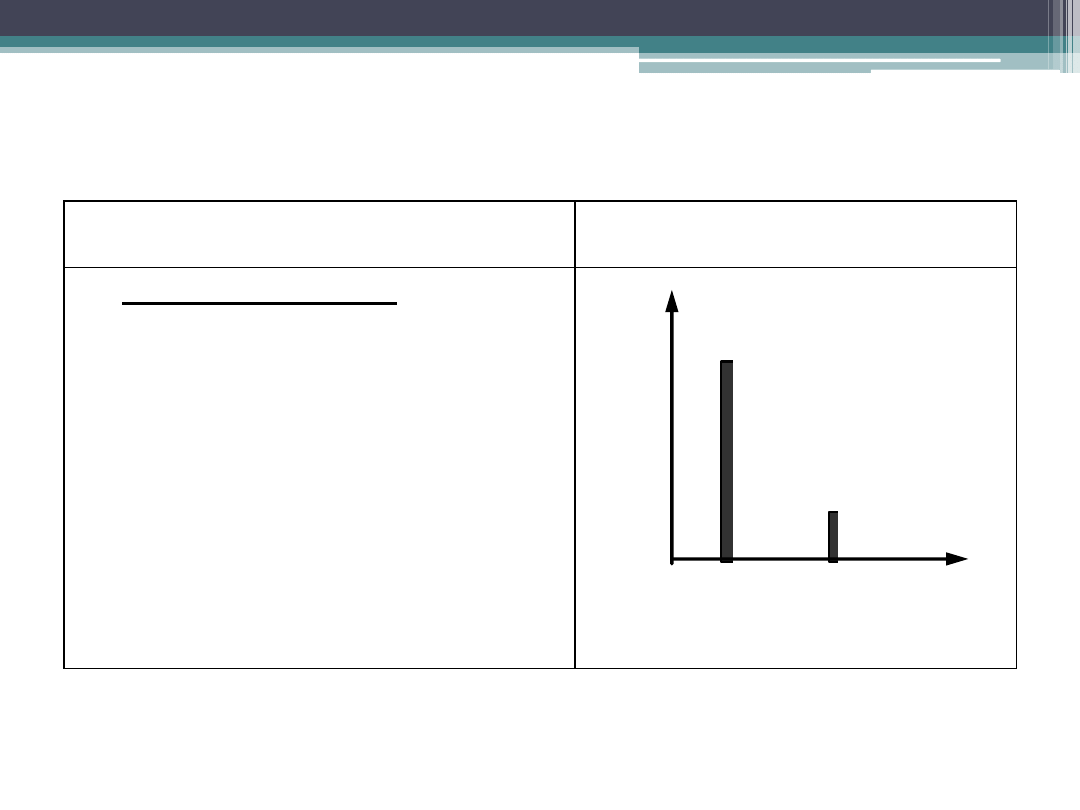
Podstawowe rozkłady zmiennej losowej
skokowej
Funkcja gęstości
Wykres
Rozkład zero–jedynkowy określony jest
następującymi prawdopodobieństwami:
,
gdzie p jest prawdopodobieństwem
wylosowania sztuki wadliwej (nazywane także
prawdopodobieństwem sukcesu,
).
p
X
P
)
1
(
1
0
p
0
0,2
0,4
0,6
0,8
0
1
p =0,2
p
x
p
X
P
1
)
0
(
Podstawowe rozkłady zmiennej losowej
skokowej
Podstawowe rozkłady zmiennej losowej
skokowej
Podstawowe rozkłady zmiennej losowej
ciągłej
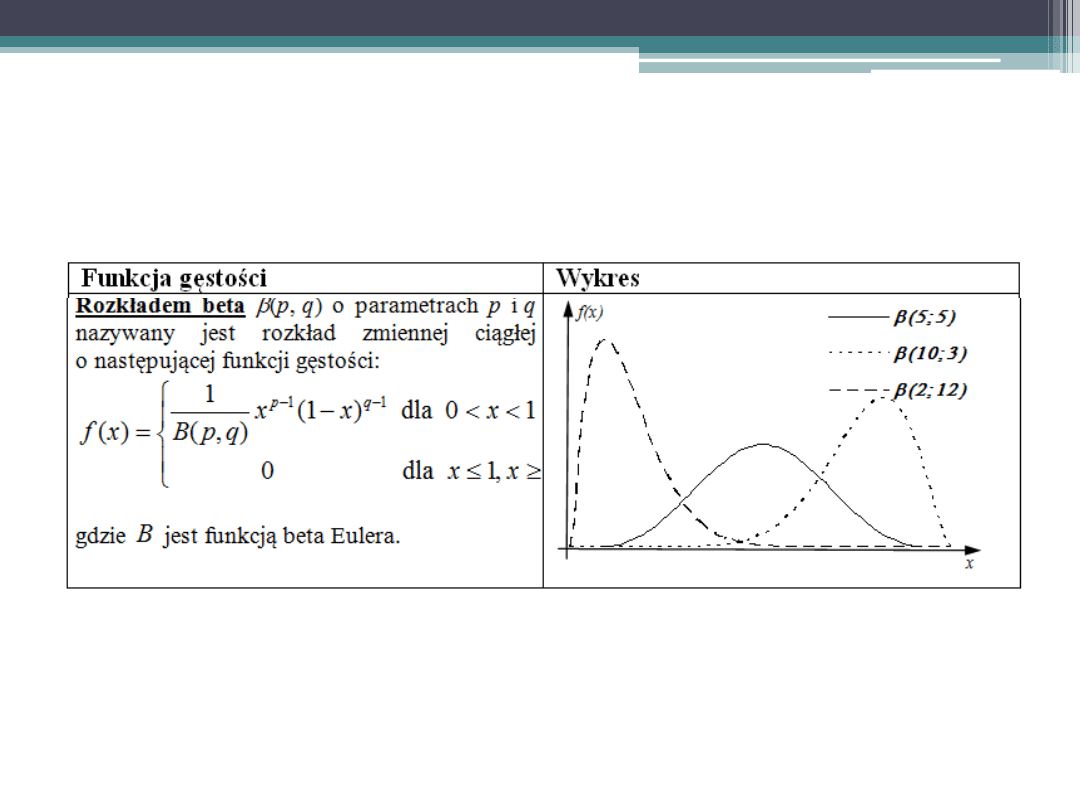
Podstawowe rozkłady zmiennej losowej
ciągłej
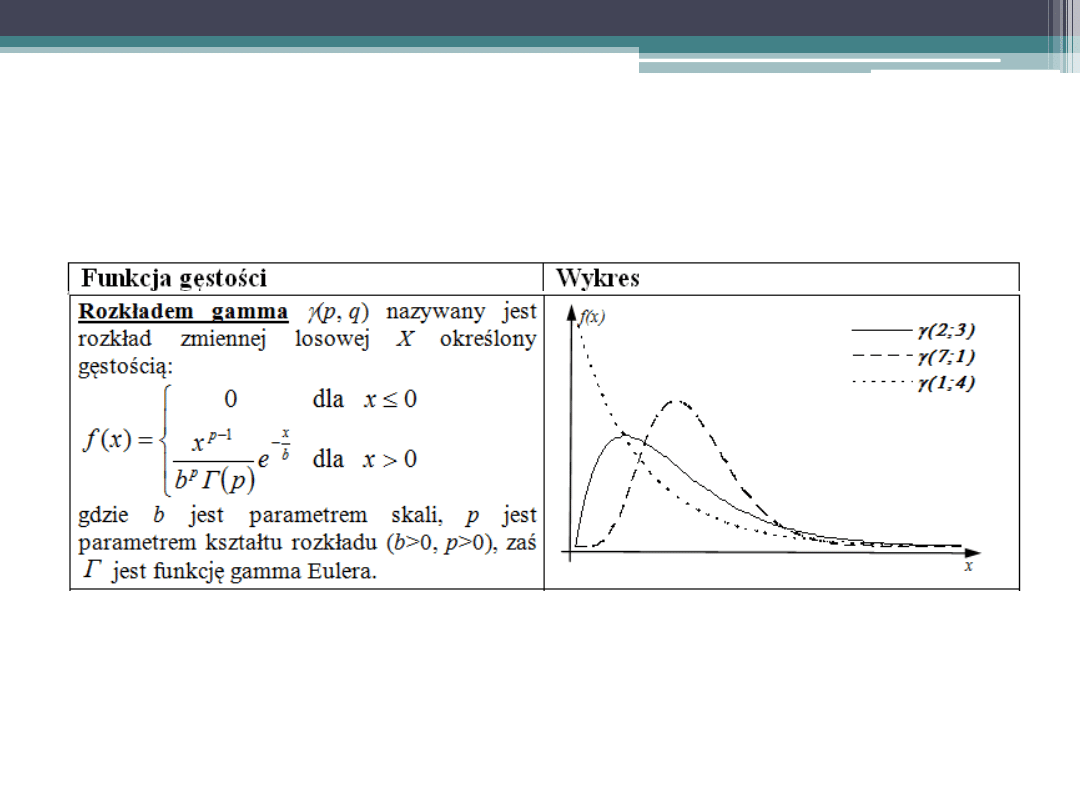
Podstawowe rozkłady zmiennej losowej
ciągłej
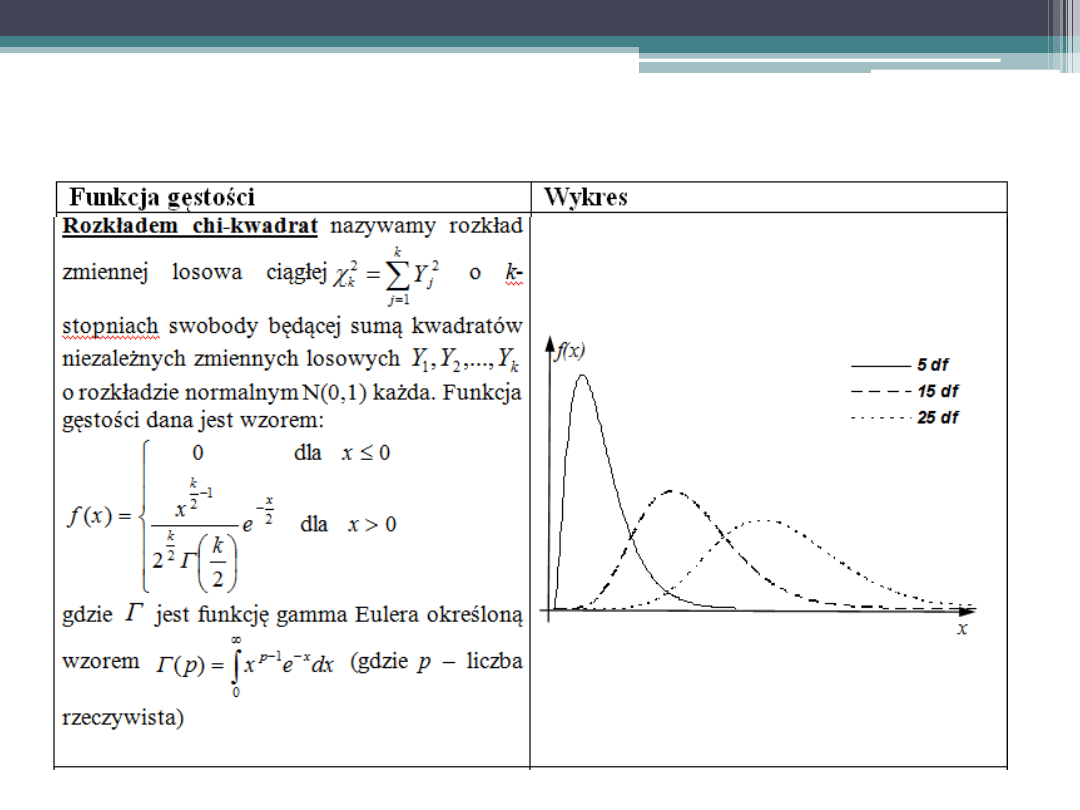
Podstawowe rozkłady zmiennej losowej
ciągłej
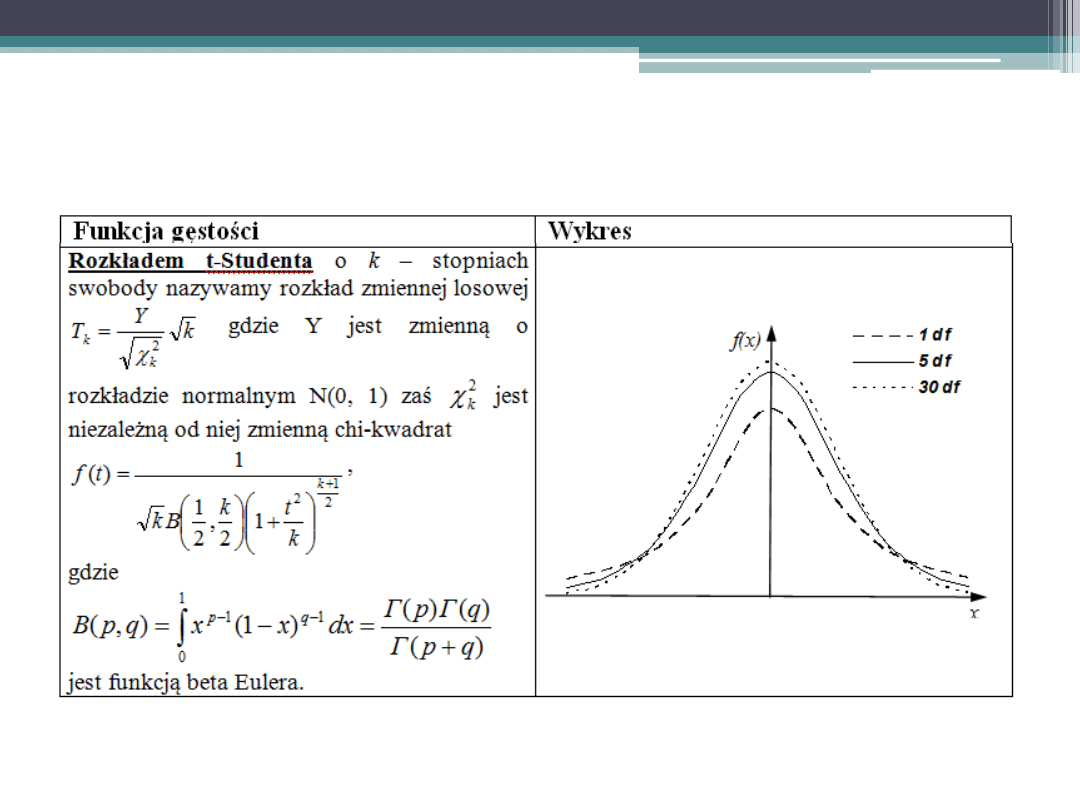
Podstawowe rozkłady zmiennej losowej
ciągłej
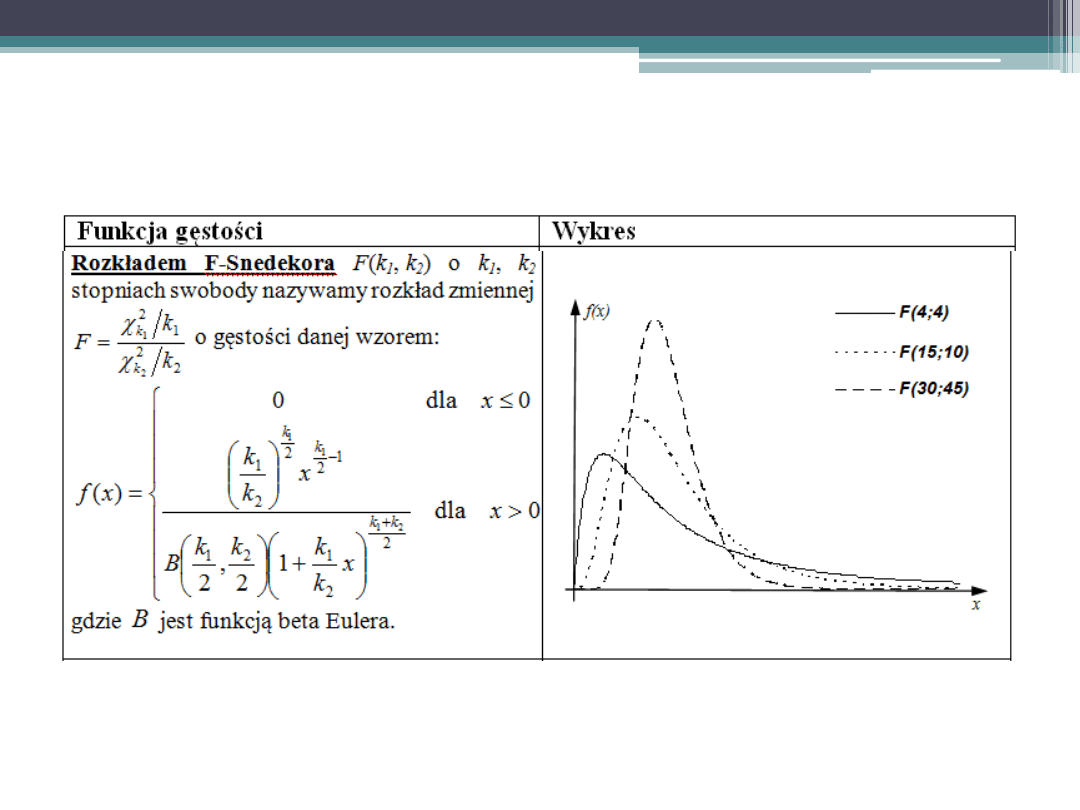
Podstawowe rozkłady zmiennej losowej
ciągłej
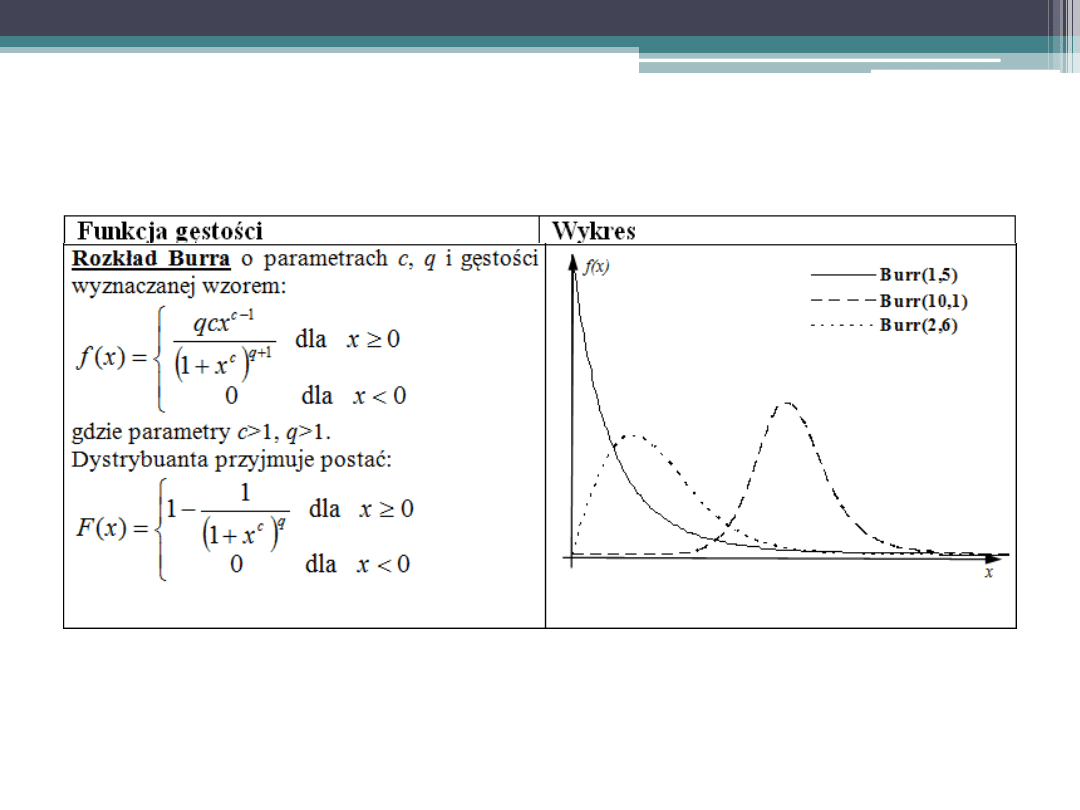
Podstawowe rozkłady zmiennej losowej
ciągłej
Podstawowe pojęcia
Pojęciem populacji określana jest zbiorowość (skończona lub nie)
poddawana obserwacji. Ze zbiorowości tej wybierana jest w określony
sposób (najczęściej losowy) próba. Wybór taki dokonywany jest
wówczas, gdy niemożliwe jest całościowe przeprowadzenie analizy
populacji. Zebrane dane (populacji lub próby) grupowane są w szereg
rozdzielczy.
Szereg rozdzielczy składa się przynajmniej z dwóch kolumn (lub
wierszy), z których pierwsza reprezentuje wartości cech lub przedziały
klasowe, zaś druga – liczba ich wystąpień (liczebność). Liczebność
można zastąpić częstością, co ma miejsce zwłaszcza przy znacznych
wielkościach liczebności.
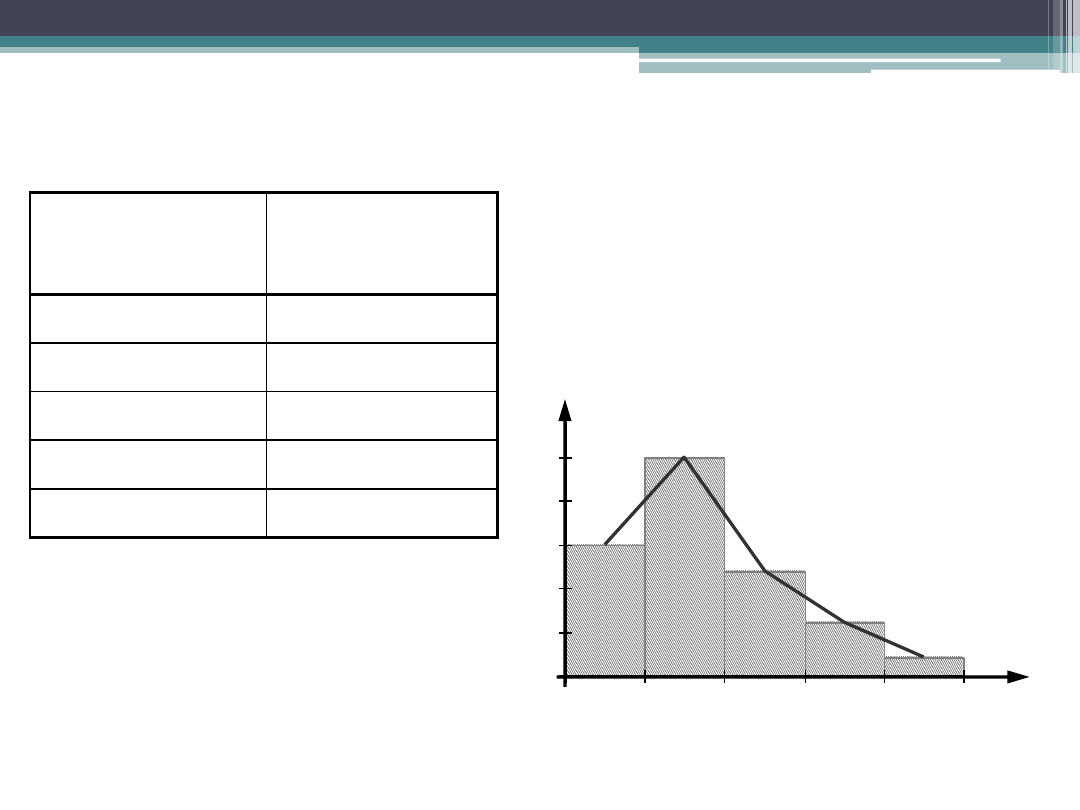
Szereg rozdzielczy
Odsetek braków
[x
i0
– xi
1
)
Liczba partii
towaru n
i
0,00 – 0,02
15
0,02 – 0,04
25
0,04 – 0,06
12
0,06 – 0,08
6
0,08 – 0,10
2
0
5
10
15
20
25
0
0,02
0,04
0,06
0,08
0,10
x
n
i
Estymacja
Z pojęciem populacji i próby ściśle związane jest pojęcie estymatora.
Estymator jest to statystyka wyznaczona na podstawie próby przybliżająca
nieznany parametr populacji.
Estymatory powinny posiadać przynajmniej trzy własności: zgodność,
nieobciążoność i efektywność.
Pierwsza oznacza, że zwiększając liczebności próby wzrasta dokładność
szacunków. Symbolicznie zapis ten można przedstawić następująco:
gdzie oznacza estymator, – szacowany parametr, n – liczebność próby.
Nieobciążonością nazywana jest własność zgodnie, z którą estymator jest
pozbawiony błędu systematycznego, czyli wartość oczekiwana jest równa
szacowanemu parametrowi ( ). Jeżeli natomiast estymator ma
możliwie małą wariancję, to nazywany jest on efektywnym.
1
lim
0
n
n
T
P
n
T
)
(
n
T
E
Estymatory
Na podstawie próby wyznaczana jest pewna statystyka. Może nią być
np. średnia, odchylenie standardowe lub wskaźnik struktury. Jest ona
oszacowaniem punktowym odpowiedniego parametru całej zbiorowości.
Estymator punktowy średniej procesu wyznaczany jest jako średnia z
próby. Jeżeli jest to szereg punktowy, wówczas wzór średniej przyjmuje
postać:
gdzie oznacza i-ty pomiar, natomiast n to liczebność próby.
W przypadku szeregów rozdzielczych, gdy dane pogrupowane zostały w
przedziały, wykorzystywany jest wzór:
gdzie to środek przedziału, zaś jego liczebność.
n
i
i
x
n
x
1
1
n
i
i
i
o
n
x
n
x
1
1
i
o
x
Estymatory
Wariancja z próby jest estymatorem punktowym wariancji zbiorowości.
Wyznaczana jest ona zgodnie z następującym wzorem dla szeregu
punktowego:
lub przedziałowego:
Wariancja podana powyższymi wzorami jest wariancją obciążoną. Chcąc
otrzymać wariancję pozbawioną błędu systematycznego należy
zastosować następujące przekształcenie:
Estymatorem punktowym wskaźnika struktury jest frakcja wyznaczona
na podstawie próby:
gdzie m jest liczbą elementów wyróżnionych z n-elementowej próby.
n
i
i
x
x
n
s
1
2
2
1
n
i
i
i
o
n
x
x
n
s
1
2
2
1
2
2
1
ˆ
s
n
n
s
n
m
p
Estymatory
Chcąc podać parametr zbiorowości z dużym, określonym z góry
prawdopodobieństwem należy wyznaczyć przedział ufności.
Prawdopodobieństwo, z jaką podejmuje się taką decyzję jest określane
mianem współczynnika ufności i oznaczane 1-
(
to poziom
istotności).
Estymat
ory
prze
działowe
Hipotezy statystyczne
Hipoteza może być związana z wartością parametru rozkładu lub z
postacią rozkładu zmiennej, czy losowością pomiarów. Pierwszą
grupę nazywa się hipotezami (testami) parametrycznymi, zaś dwie
pozostałe – nieparametrycznymi.
Proces weryfikacji hipotez rozpoczyna się od postawienia hipotezy
zerowej, oznaczanej jako H
0
Jeżeli
oznacza parametr populacji, a
0
jego wartość, to hipoteza
zerowa przyjmuje postać:
W odniesieniu do hipotezy zerowej, jako jej zaprzeczenie stawiana jest
hipoteza alternatywna H
1
. Hipoteza alternatywna przy teście
parametrycznym może przybrać jedną z postaci:
0
0
:
H
0
1
:
H
0
1
:
H
0
1
:
H
Błąd I i II rodzaju
Weryfikując hipotezy można popełnić jeden z dwóch rodzajów
błędów. Błąd pierwszego rodzaju podlega na odrzuceniu hipotezy
prawdziwej i oznaczany jest jako
, zaś błąd drugiego rodzaju
polegający na przyjęciu hipotezy fałszywej i oznaczany jest jako
.
Pierwszy z błędów jest nazywany ryzykiem producenta, zaś drugi
ryzykiem konsumenta.
W odniesieniu do kontroli procesu produkcyjnego,
oznacza
prawdopodobieństwo błędnej regulacji w przypadku, gdy proces
działa poprawnie, natomiast
– prawdopodobieństwo
niezauważenia powstałego rozregulowania.
Prawdopodobieństwo popełnienia błędu I rodzaju (nazywane też
poziomem istotności) uznawane jest jako bardziej niebezpieczne
dla badań, dlatego podczas konstrukcji testu jest ono brane pod
uwagę. Najczęściej jest to wartość wynosząca 0,05
Decyzje i ich konsekwencje w teście
sprawdzającym hipotezę H
0
:
Sytuacje
Decyzje
przyjęcie H
0
odrzucenie H
0
Hipoteza zerowa
prawdziwa
decyzja prawidłowa
błąd I rodzaju
Hipoteza zerowa
fałszywa
błąd II rodzaju
decyzja prawidłowa
Weryfikacja hipotez statystycznych
Reguła postępowania podczas weryfikacji hipotez statystycznych nosi
nazwę testu statystycznego. Praktyczne zastosowanie ma grupa testów
nazywanych testami istotności, które pozwalają na odrzucenie hipotezy
sprawdzanej z małym prawdopodobieństwem popełnienia błędu I
rodzaju. Przy tej konstrukcji nie podejmuje się decyzji o przyjęciu
hipotezy zerowej, a jedynie o braku podstaw do jej odrzucenia.
Konstrukcja testu przebiega następująco:
1.
stawiana są hipotezy: zerowa, będąca hipotezą sprawdzaną i
alternatywna, będąca jej zaprzeczeniem lub związana z celem
badania.
2.
wybór sprawdzianu hipotezy (Z
n
) i obliczenie go na podstawie próby
losowej.
3.
podjęcie decyzji o odrzuceniu hipotezy lub braku podstaw do jej
odrzucenia na podstawie obszaru krytycznego Q, dla którego
spełniona jest relacja:
Jeżeli wartość statystyki znajdzie się w obszarze krytycznym
podejmowana jest decyzja o odrzuceniu sprawdzanej hipotezy, zaś w
przeciwnym przypadku o braku podstaw do jej odrzucenia.
0
| H
Q
Z
P
n
Weryfikacja hipotez statystycznych
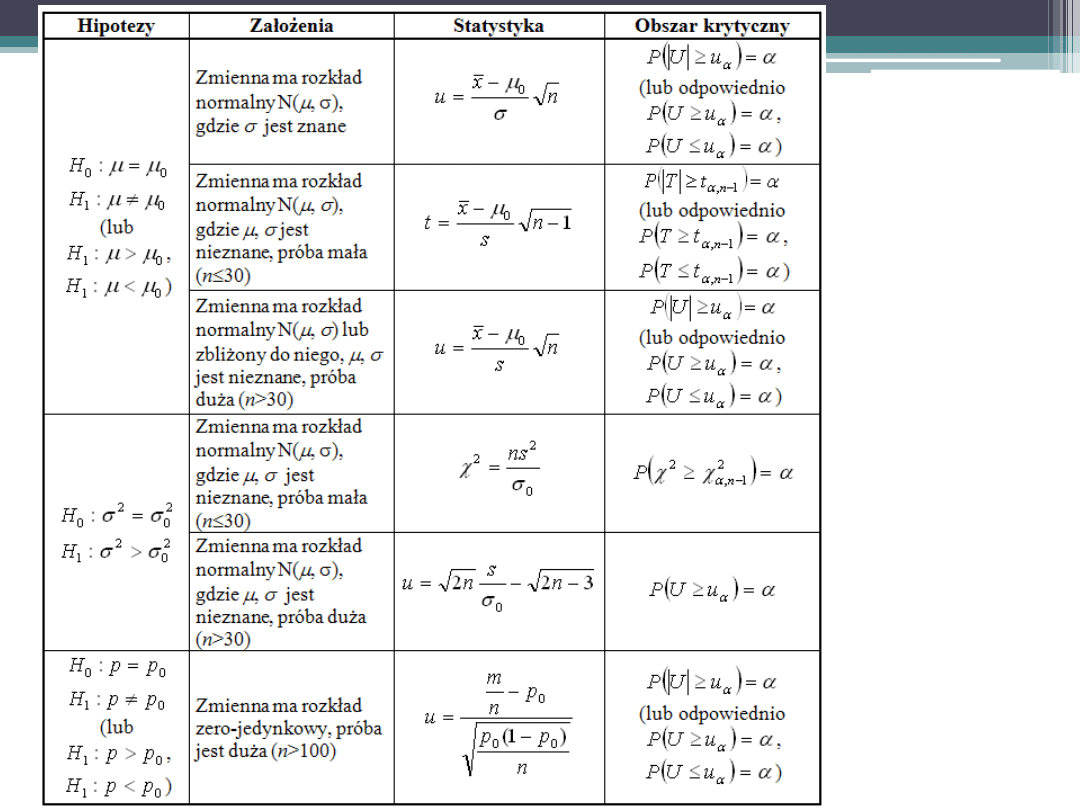
Testy
parame
tryczn
e
Testy nieparametryczne
Przy zdecydowanej większości testów istotne jest założenie o zgodności
pomiarów z rozkładem normalnym, jak też o ich losowości i
niezależności. Niespełnienie jednego z tych założeń uniemożliwia
korzystanie z podanych powyżej testów istotności. Jeżeli jednak test
taki mimo niespełnienia założeń jest przeprowadzany, konstruowane
wnioski mogą prowadzić do błędnych decyzji. Stąd ważność i
konieczność korzystania z nieparametrycznych testów zgodności.
Jednymi z częściej wykonywanych z tej grupy są testy zgodności
pomiarów z rozkładem normalnym. W literaturze i praktyce
stosowanych jest wiele testów weryfikujących normalność pomiarów.
Wśród nich najczęściej stosowane są testy zgodności
chi-kwadrat, czy testy Kołmogorowa.
Testy zgodności – test chi-kwadrat
Za pomocą testu zgodności chi-kwadrat można zweryfikować czy
obserwowana cecha posiada rozkład zgodny z określonym
rozkładem teoretycznym. Aby wykonać ten test dane muszą być
pogrupowane i przedstawione w postaci szeregu rozdzielczego.
Symboliczny zapis hipotez jest następujący:
gdzie – jest dystrybuantą rozkładu teoretycznego. Zatem
sprawdzana jest hipoteza zgodności dystrybuanty analizowanego
rozkładu, z którego pobrano próbę losową z rozkładem
teoretycznym, najczęściej z rozkładem normalnym.
)
(
)
(
:
)
(
)
(
:
0
1
0
0
x
F
x
F
H
x
F
x
F
H
)
(
0
x
F
Testy zgodności – test chi-kwadrat
Sprawdzianem hipotezy H
0
jest statystyka podlegająca rozkładowi chi-
kwadrat o stopniach swobody:
gdzie
r – liczba przedziałów klasowych,
l – liczba parametrów, które należy wstępnie wyznaczyć na podstawie
próby (jeżeli średnia i odchylenie standardowe było szacowane,
to l = 2),
n
i
– liczebność empiryczna i-tego przedziału,
p
i
– prawdopodobieństwo odpowiadające wartości badanej cechy w i-
tej klasie,
np
i
– liczebność teoretyczna w i-tym przedziale.
r
i
i
i
i
np
np
n
1
2
2
)
(
Testy zgodności – test chi-kwadrat
Aby wnioski z wykonanego testu zgodności chi-kwadrat były
wiarygodne, liczebności w przedziałach, jak i liczba przedziałów
powinna być większa lub równe 5.
Wyznaczoną zgodnie ze wzorem statystykę należy porównać z
wartością krytyczna zmiennej losowej chi-kwadrat o k stopniach
swobody, spełniającą warunek:
)
(
2
;
2
k
P
2
;
k
Testy zgodności – test chi-kwadrat
W teście zgodności Kołmogorowa weryfikowane są hipotezy identyczne,
jak w testach zgodności
2
.
Test ten stosuje się w celu porównania danych rozkładów z wybranymi
rozkładami ciągłymi. Sprawdzianem testu jest charakterystyka:
gdzie:
D to statystyka wyznaczona wzorem:
– dystrybuanta empiryczna.
Wartość krytyczną potrzebną do weryfikacji hipotezy otrzymuje się z
rozkładu Kołmogorowa, tak aby spełniony był warunek:
n
D
)
(
)
(
sup
0
x
F
x
F
D
n
x
)
(x
F
n
)
(
P
Testy losowości – test serii
Zgodność pomiarów z rozkładem normalnym jest jedynie jednym z
założeń stosowania testów parametrycznych czy estymacji
przedziałowej. Drugim jest losowość pomiarów. Założenie to możne być
sprawdzone np. testem serii.
Serią nazywany jest podciąg identycznych elementów jednego rodzaju
znajdujący się w ciągu składającym się z dwóch rodzajów elementów. W
teście serii z populacji o dowolnym rozkładzie pobrana jest próba n-
elementowa. Z próby tej wyznaczana jest mediana (wartość środkowa –
oznaczona jako Me). Następnie nie zmieniając kolejności pobierania
pomiarów, każdemu pomiarowi x
i
przypisywana jest określona litera
(np. a) jeżeli , zaś gdy inna (np. b) bądź też pomiar jest
pomijany, gdy .
Me
x
i
Me
x
i
Me
x
i
Testy losowości – test serii
W tak utworzonym ciągu wyznaczana jest liczba serii oznaczana jako k.
Zakładając, że hipoteza zerowa dotycząca losowości pomiarów jest
prawdziwa, to liczba serii ma rozkład nazwany rozkładem serii. Jest on
zależy od dwóch parametrów: n
1
i n
2
oznaczających liczebności
odpowiednio elementów a i b. Jeżeli wyznaczona liczba serii k znajduje
się pomiędzy wartościami k
1
, k
2
będącymi odczytem z tablic serii,
spełniającymi relacje:
gdzie
jest poziomem istotności, wówczas formułowany jest wniosek o
braku podstaw do odrzucenia hipotezy zerowej dotyczącej losowości
pomiarów. Jeżeli lub , wówczas hipotezę o losowości należy
odrzucić, a zatem liczba serii jest zbyt mała lub zbyt duża by dobór
można było uznać za losowy.
2
1
k
k
P
2
1
1
k
k
P
1
k
k
2
k
k
Analiza wariancji (ANOVA)
ij
i
ij
y
i
a
i
,...,
2
,
1
ij
i
n
j
,...,
2
,
1
Analiza wariancji (ANOVA – ang. Analysis of Variance) jest jednym
z zaawansowanych narzędzi statystycznych, wykorzystywanych do
porównywania różnic w poziomie średniej w kilku populacjach.
Założeniami jej stosowania są: niezależność doboru prób i normalność
pomiarów z nich pochodzących (są to próby o rozkładzie normalnym z
identyczną wariancją, ale o dowolnych średnich).
W jednoczynnikowej wariancji, przyjmuje się, że każdy z pomiarów jest
postaci:
gdzie
jest średnią ogólną, identyczną dla wszystkich populacji, z których
pobierane są próby,
jest efektem i –tgo zabiegu (
) zaś
jest składnikiem losowym dla
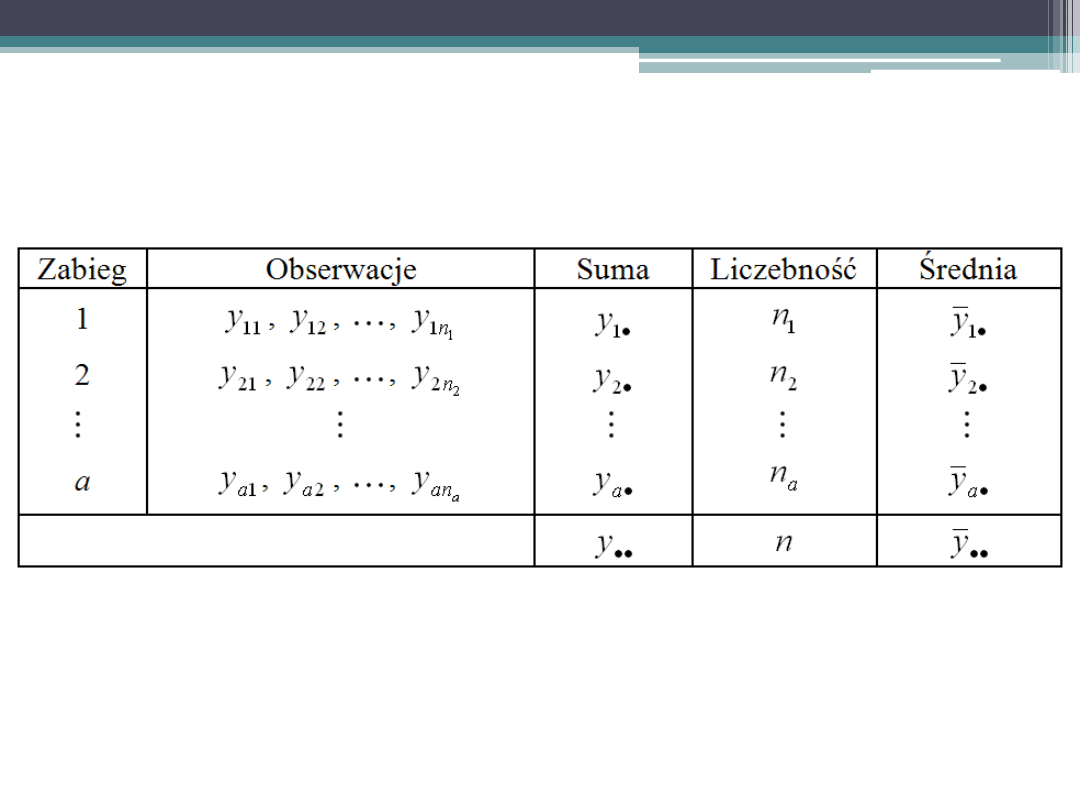
Przykładowa tabela danych
w jednoczynnikowej analizie wariancji
Analiza wariancji (ANOVA)
Analiza oparta została na następujących hipotezach zerowej i
alternatywnej:
dla przynajmniej jednego i
Sprawdzaną hipotezą jest, iż wpływ wszystkich zabiegów jest zerowy,
czyli wszystkie populacje mają taką samą średnią równą średniej
ogólnej
. Hipoteza alternatywna, informuje, że istnieje taki zabieg,
który jest istotnie różny od zera, czyli przynajmniej jedna średnia różni
się od pozostałych.
:
0
H
:
1
H
0
2
1
a
0
i
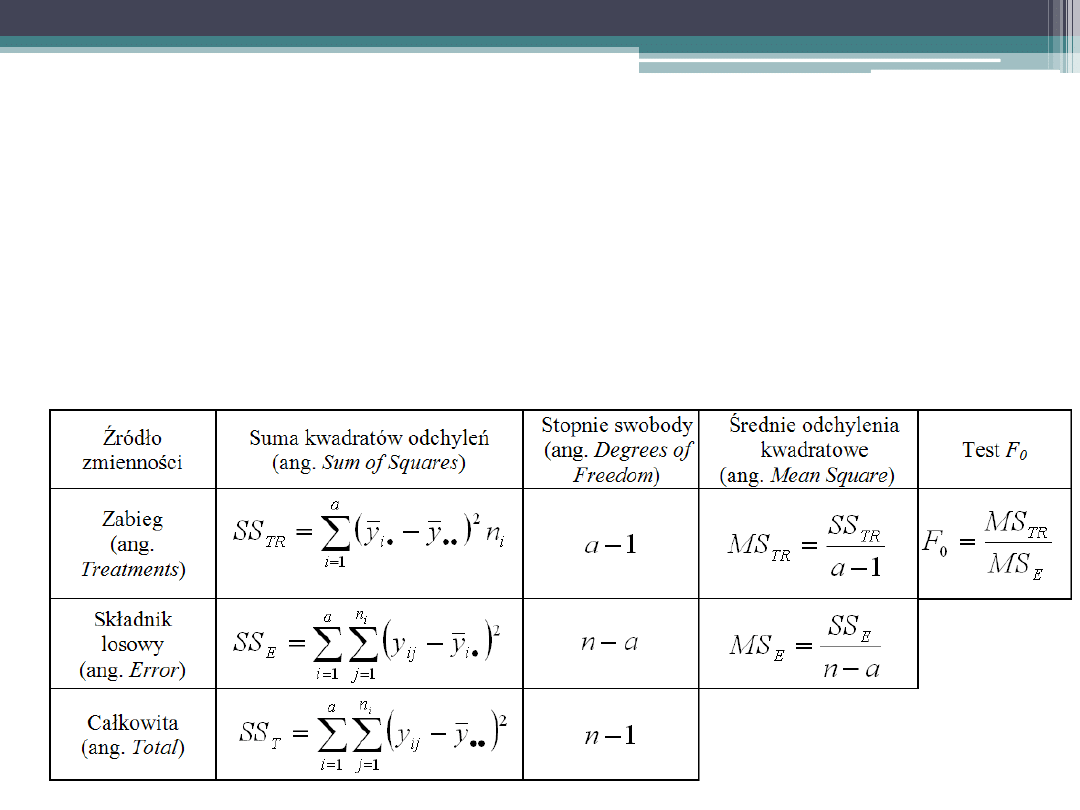
Analiza wariancji (ANOVA)
Analiza wariancji opiera się na zasadzie sum kwadratów, zgodnie z
którą całkowita suma kwadratów odchyleń (SS
T
) równa jest sumie
składników: sumy kwadratów odchyleń wynikających z zabiegu, czyli
między populacjami (SS
TR
) i sumy kwadratów błędów (SS
E
).
Sprawdzianem hipotezy zerowej jest statystyka F, która przy
prawdziwości hipotezy zerowej posiada rozkład F-Snedekcora o (a-1) i
(n-a) stopniach swobody.
Analiza wariancji (ANOVA)
Jeżeli nie ma podstaw do odrzucenia H
0
, co w efekcie prowadzi do
zakończenia działania testu ANOVA stwierdzeniem, iż na podstawie
zgromadzonych danych nie można wskazać na wyraźnie widoczny,
różny od zera wpływ jednego z czynników.
W przeciwnym przypadku, gdy H
0
jest odrzucana, czyli przynajmniej
jedna średnia różni się od pozostałych, wykonywana jest w kolejnym
kroku klasyfikacja szczegółowa. Jej celem jest wskazanie grup, dla
których zachodzi różnica pomiędzy średnimi i dla których nie jest ona
zauważalna przy przyjętym poziomie istotności
.
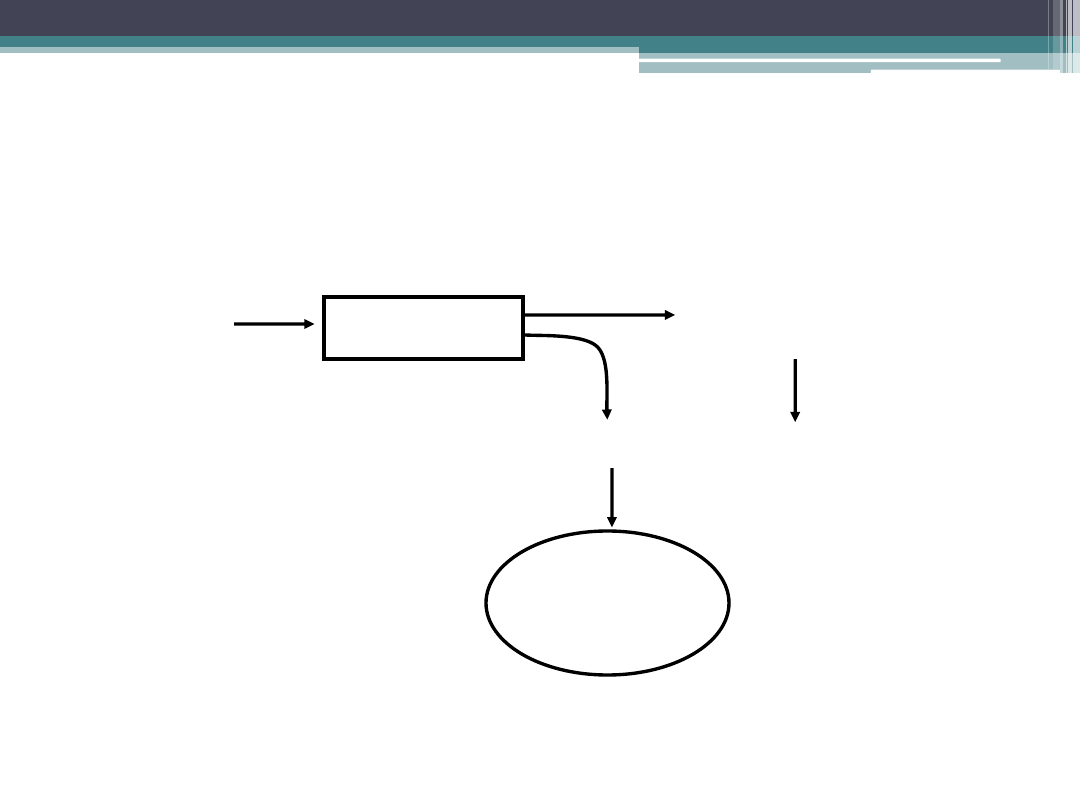
Analiza wariancji (ANOVA)
Dane
ANOVA
STOP
Odrzuć H
0
Brak podstaw
do odrzucenia H
0
Dalsza
analiza
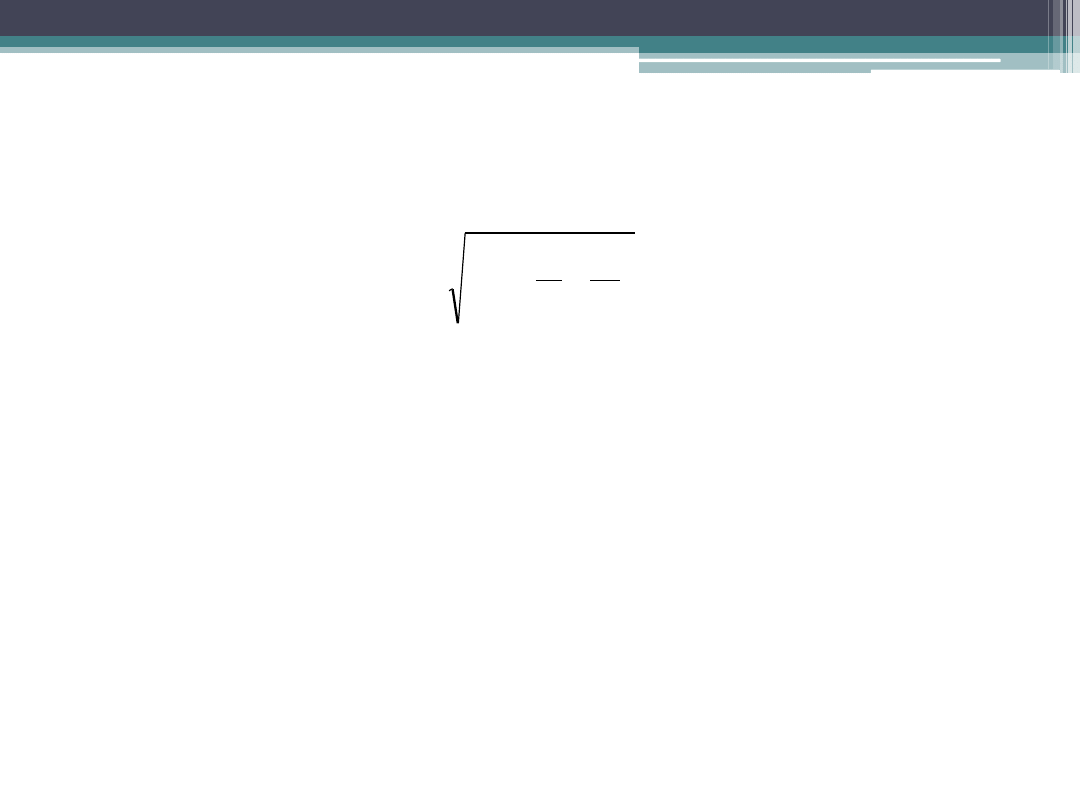
Test NIR
Funkcjonuje kilka testów sprawdzających istotność różnic, jednym z
nich jest test NIR (najmniejszej istotnej różnicy). Przyjmuje on postać:
dla prób i-tej i j-tej ( ), gdzie jest odczytem z tablic rozkładu
t-Studenta o (n-1) stopniach swobody.
Jeżeli bezwzględna różnica pomiędzy średnimi i-tej i j-tej próby jest
mniejsza od NIR, wówczas średnie nie różnią się istotnie między sobą.
Analogicznie, jak jednoczynnikowa przebiega dwu- lub
wieloczynnikowa analiza wariancji. Podstawowa różnica polega na tym,
że w dwuczynnikowej weryfikowanych jest jednocześnie nie jedna, ale
trzy hipotezy zerowe, zaś w wieloczynnikowej odpowiednio więcej.
Hipotezy te dotyczą zarówno czynników, jak też zachodzącej między
nimi interakcji.
j
i
E
n
n
n
MS
t
NIR
1
1
|
|
1
,
j
i
1
,
n
t
Założenia analizy wariancji
1.
Analizowana zmienna i wydzielone podpopulacje podlegają
rozkładowi normalnemu
2.
Spełniona jest hipoteza o równości warunkowych wariancji na
wszystkich poziomach czynnika
Testy nieparametryczne
Test jednorodności wariancji