Mechanika ciała stałego i wytrzymałość materiałów – odpowiedzi. | 20.01.2009 | AiR

1. Podać definicję punktu materialnego

Jest to punkt geometryczny o nieskończenie małych wymiarach i skończonej masie

2. Podać definicję ciała sztywnego

Jest to ciało materialne, nieodkształcalne, w którym wzajemne odległości cząstek nie ulegają zmianie
pod wpływem działających na nie sił. W rzeczywistości wszystkie ciała są odkształcalne. Założenie
takie przyjęto dla celów statyki.

3. Podać definicję dwójki zerowej

Dwójką zerową nazywamy dwie siły P i P' przyłożone do ciała sztywnego lub punktu materialnego,
działające wzdłuż tej samej prostej o równych wartościach i przeciwnych zwrotach. Jest to najprostszy
układ sił zrównoważonych. Aksjomat: do każdego układu sił działających na bryłę sztywną można
dodać lub odjąć układ sił zrównoważonych, nie zmieniając stanu ruchowego bryły.

4. Podać twierdzenie o przesuwaniu siły wzdłuż prostej jej działania

Nie naruszając równowagi bryły sztywnej możemy punkt zaczepienia siły przenieść dowolnie wzdłuż
prostej działania tej siły.

5. Omówić sposób wyznaczania wypadkowej dwóch sił nierównoległych na płaszczyźnie

Przesuwamy obie siły tak, aby były zaczepione w punkcie przecięcia kierunków działania tych sił.
Stosujemy zasadę równoległoboku. Jego przekątna jest wypadkową sił P1 i P2. Możemy też skorzystać
z twierdzenia cosinusów – Carnota |W| = sqrt(|P1|^2+|P2|^2+2|P1||P2|cosa). W szczególnym wypadku
może to być przekątna prostokąta (dla sił prostopadłych) lub bezpośrednie sumowanie (dla sił na tej
samej prostej).

6. Podać wzór na wyznaczanie wartości liczbowej wypadkowej dwóch sił nierównoległych na

płaszczyźnie
Twierdzenie cosinusów – Carnota: |W| = sqrt(|P1|^2+|P2|^2+2|P1||P2|cosa)

7. Omówić zagadnienie wypadkowej dwóch sił działających wzdłuż tej samej prostej:

Jeśli dwie siły działają wzdłuż tej samej prostej (cos kąta między nimi to 0) to możemy po prostu
zsumować algebraicznie ich wartości (sumowanie dla zwrotów zgodnych, odejmowanie dla
przeciwnych).

8. Wyjaśnić pojęcie sił zewnętrznych i podać ich podział.|

Są to siły przyłożone do poszczególnych brył układu, pochodzące od brył nie wchodzących w skład
rozpatrywanego układu. Wśród sił zewnętrznych można wyróżnić siły czynne (powodujące ruch brył)
oraz reakcje, czyli siły pochodzące od brył zewnętrznych będących więzami (ograniczeniami ruchu).

9. Podać trzecie prawo sformułowane przez Newtona

Jeżeli ciało A, działo na ciało B siłą P to ciało B oddziałuje na ciało A taką samą co do modułu i
kierunku siłą P' lecz zwróconą przeciwnie

10. Co to jest reakcja

Reakcja jest to siła, za pomocą której uwalniamy ciało od więzów. Po tej operacji nie musimy brać pod
uwagę więzów. W obliczeniach używamy tylko reakcji.

11. Co rozumiesz przez więzy

Połączenia, które ograniczają swobodę brył. Typy więzów:
1 niewiadoma
- cięgna (pręty, łańcuchy, liny) – wzdłuż liny
- podpory gładkie (idealnie gładka powierzchnia) – prostopadle do powierzchni
- podpory przegubowe ruchome (uchwyt kulowy) – prostopadle do powierzchni
2 niewiadome
- podpory chropowate (każda rzeczywista powierzchnia) – normalna i tarcie
- podpory przegubowe stałe (połączenie przegubowe) – prostopadła i równoległa do pow.
- przeguby walcowe (łożysko ślizgowe) – dwie prostopadłe reakcje
3 niewiadome
- przeguby kuliste (przegub) – trzy prostopadłe reakcje
- utwierdzenie (zamurowana belka) – dwie prostopadłe reakcje i moment utwierdzenia

12. Podać zasadę uwalniania od więzów

Ciała uwalniamy od więzów za pomocą odpowiedniej ilości i typu reakcji w zależności od typu więzów.
Aby uwolnić ciało musimy zlikwidować wszystkie więzy – zastąpić je odpowiednimi reakcjami.

13. Wymienić rodzaje więzów i narysować je wraz z zaznaczonymi reakcjami

1 niewiadoma

- cięgna (pręty, łańcuchy, liny) – wzdłuż liny
- podpory gładkie (idealnie gładka powierzchnia) – prostopadle do powierzchni
- podpory przegubowe ruchome (uchwyt kulowy) – prostopadle do powierzchni
2 niewiadome
- podpory chropowate (każda rzeczywista powierzchnia) – normalna i tarcie
- podpory przegubowe stałe (połączenie przegubowe) – prostopadła i równoległa do pow.
- przeguby walcowe (łożysko ślizgowe) – dwie prostopadłe reakcje
3 niewiadome
- przeguby kuliste (przegub) – trzy prostopadłe reakcje
- utwierdzenie (zamurowana belka) – dwie prostopadłe reakcje i moment utwierdzenia

14. Podać twierdzenie o trzech siłach

Trzy siły są w równowadze jeżeli ich proste działania przecinają się w jednym punkcie, leżą w jednej
płaszczyźnie, a trójkąt sił z nich utworzony jest trójkątem zamkniętym.

15. Podać analityczny sposób przedstawienia siły i wieloboku sił

Siłę można przedstawić analitycznie rzutując ją na wszystkie osie rozpatrywanego układu. Wielobok sił
jest to układ sił zrównoważonych (połączone tworzą wielokąt zamknięty). Każdą siłę możemy
przedstawić za pomocą jej składowych

16. Co rozumiemy pod pojęciem wektora głównego.

Wektor główny jest to suma geometryczna wszystkich sił działających na ciało. Można wykazać, że rzut

wektora głównego na dowolną oś równa się sumie rzutów na tą oś sił składowych. ∣W∣=

∑

i=1

n

∣

P

i

∣

i

odpowiednio dla wszystkich osi. Prostą działania Wg wyznaczamy za pomocą funkcji. Analogicznie dla
układu przestrzennego.

17. Jaki układ nazywamy układem zbieżnym

Zbieżny układ sił (płaski lub przestrzenny). Jest to układ, w którym proste działania sił przecinają
się w jednym punkcie. Taki układ sił można zastąpić jedną siłą wypadkową.

18. Określić analityczne warunki równowagi zbieżnego układu sił (płaskiego i przestrzennego)

płaski W

gx

=

0 ; W

gy

=

0 ;

∑

i=1

n

P

ix

=

0 ;....

przestrzenny W

gx

=

0 ; W

gy

=

0 ;W

gz

=

0 ;

∑

i =1

n

P

ix

=

0 ;....

19. Jak wyznaczamy wypadkową dwóch sił równoległych

Wypadkowa sił równoległych jest sumą algebraiczną tych sił i leży na prostej ich działania (równoległej
do ich kierunków). Jeżeli siły mają te same zwroty to prosta ta leży między nimi. Jeśli zwroty są
przeciwne – prosta leży poza nimi. Możemy wyznaczyć ją stosując dwójkę zerową (aby wypadkowe sił
i składowych dwójki nie były równoległe). Przydatna okazuje się zasada dźwigni dwustronnej lub
podobieństwa trójkątów. Zwrot jak w sile większej.

20. Co rozumiemy przez parę sił

Układ dwóch sił równoległych nie leżących na jednej prostej o równych wartościach, lecz przeciwnych
zwrotach. Pary sił nie można zastąpić jedną siłą. Powoduje ona obrót ciała sztywnego wokół osi
prostopadłej do płaszczyzny działania pary. Parę sił można zastąpić inną parą o tym samym działaniu.

21. Co rozumiemy przez ramię pary sił.

Ramieniem pary sił nazywamy najkrótszą odległość między kierunkami działania sił pary – odległość
między prostymi równoległymi.

22. Co rozumiemy przez moment pary sił

Moment pary sił jest wektorem prostopadłym do płaszczyzny działania pary sił. Przyjęła się konwencja
znaków zgodna ze śrubą prawoskrętną (w prawo „-”, w lewo „+”). Wartość tego momentu jest równa
iloczynowi wartości siły i ramienia d. Możemy też definiować go jako iloczyn wektorowy M(P,P')=r x P

23. Czy można przenieść parę sił do dowolnej płaszczyzny równoległej do jej działania

tak

24. Czy działanie pary sił na ciało sztywne ulegnie zmianie, jeżeli parę przesuniemy na dowolne

położenie w jej płaszczyźnie działania?
Nie

25. Do czego sprowadza się układ par sił działających na ciało sztywne na w jednej płaszczyźnie?

Układ par sił możemy się sprowadza do jednej pary sił. Najpierw sprowadzamy wszystkie pary do

jednego ramienia d, a następnie 'składamy' w jedną parę sił (zachowując jej moment).

26. Jaki jest warunek równowagi par sił działających na ciało sztywne

Aby pary sił działających w jednej płaszczyźnie na ciało sztywne znajdowały się w równowadze suma

momentów tych par musi się równać zeru M =

∑

i=1

n

M

i

=

0

27. Moment sił względem punktu jako iloczyn wektorowy. Podać jego własności.

Momentem siły względem punktu (bieguna) nazywamy wektor M(P) prostopadły do płaszczyzny
wyznaczonej przez prostą działania tej siły i punkt. Wartość tego momentu to P*d, gdzie

d =r×sin r , P . Odległość d nazywamy ramieniem. Zwrot wyznaczamy z reguły śruby

prawoskrętnej. Moment siły względem bieguna jest zerem, gdy prosta działania siły przechodzi przez
ten punkt. Z definicji momentu siły względem punktu wynika, że moment nie zmieni się, jeżeli siłę
przesuniemy wzdłuż prostej jej działania.

28. Co to jest moment siły względem osi

Jest to moment rzutu siły na na płaszczyznę prostopadłą do danej osi względem punktu przebicia tej
płaszczyzny przez oś. Rzut siły P na płaszczyznę prostopadła do osi oznaczony przez Pxy, a punkt
przebicia płaszczyzny Oxy przez oś z oznaczony symbolem O. Z powyższego określenia momentu sily
względem osi wynika, że moment siły względem osi jest zerem, gdy siła i oś leżą w jednej płaszczyźnie
(gdy siła jest równoległa do osi lub gdy prosta przecina oś).

29. Określić analityczne warunki równowagi płaskiego i przestrzennego układu sił.

W=0 i M=0 czyli:
Płaski – Wx=0, Wy = 0, M = 0
Przestrzenny – Wx=0, Wy=0, Wz=0, Mx=0, My=0, Mz=0

30. Podać równania równowagi układu sił równoległych

Układ sił równoległych jest w równowadze, jeżeli Wg i Mg są równe 0.

31. Co rozumiemy przez redukcję układu sił

Przez redukcję dowolnego układu sił rozumiemy przekształcenie układu w równoważny układ złożony
z siły i pary sił (zastępujemy działanie układu sił jedną siłą i parą sił (momentem)).

32. Jakie są możliwe przypadki redukcji płaskiego dowolnego układu sił.

Wg=/=0, Mg=/=0, zostaje moment i para sił (moment)
Wg=/=0, Mg=0, zostaje wektor główny
Wg=0, Mg=/=0, zostaje moment główny
Wg=0, Mg=0, układ pozostaje w równowadze

33. Kiedy płaski dowolny układ sił redukuje się do pary sił

Mg=/=0 i Wg = 0

34. Kiedy płaski dowolny układ sił pozostaje w równowadze

Wx=0, Wy=0, M=0 lub Wx,y=0, Ma=0,Mb=0, czyli W=0 i M=0
Warunkiem koniecznym i dostatecznym równowagi płaskiego dowolnego układu sił jest, aby sumy
algebraiczne rzutów wszystkich sił na każdą z dwóch nierównoległych osi równały się zeru i suma
momentów wszystkich sił względem dowolnego obranego bieguna na płaszczyźnie działania tych sił
była równa zeru (trzy równania równowagi). Jedno z równań na rzut sił możemy zastąpić momentem
względem innego punktu.

35. Co rozumiemy przez redukcję przestrzennego układu sił

jak w 31

36. Wymienić wszystkie przypadki, które zachodzą przy redukcji przestrzennego dowolnego układu

sił.
Wg =/= 0, Mg=/=0, Wg || Mg – sprowadza się do skrętnika (śruba statyczna) – układ sił i pary sił
działających w płaszczyźnie prostopadłej do tej siły. Skrętnik może być prawy albo lewy. Prostą
działania wektora głównego Wg nazywamy osią centralną skrętnika.
Wg =/= 0, Mg =/= 0, Wg _|_ Mg układ sił redukuje się do wypadkowej. Wartość siły wypadkowej jest
równa wartości wektora głównego, ma jego zwrot, prostą i jest przesunięta od bieguna redukcji o ramię
d = Mg/Wg tak, aby moment siły wypadkowej względem bieguna redukcji był równy momentowi
głównemu
Wg =/= 0, Mg = 0 redukuje się do wypadkowej = Wg
Wg = 0, Mg =/= 0 sprowadza się do pary sił. Mg nie zależy od bieguna – jest niezmiennikiem układu.
Wg=/=0, Mg=/= 0- sprowadza się do skrętnika, ale o osi przesuniętej względem bieguna redukcji o
ramię d.

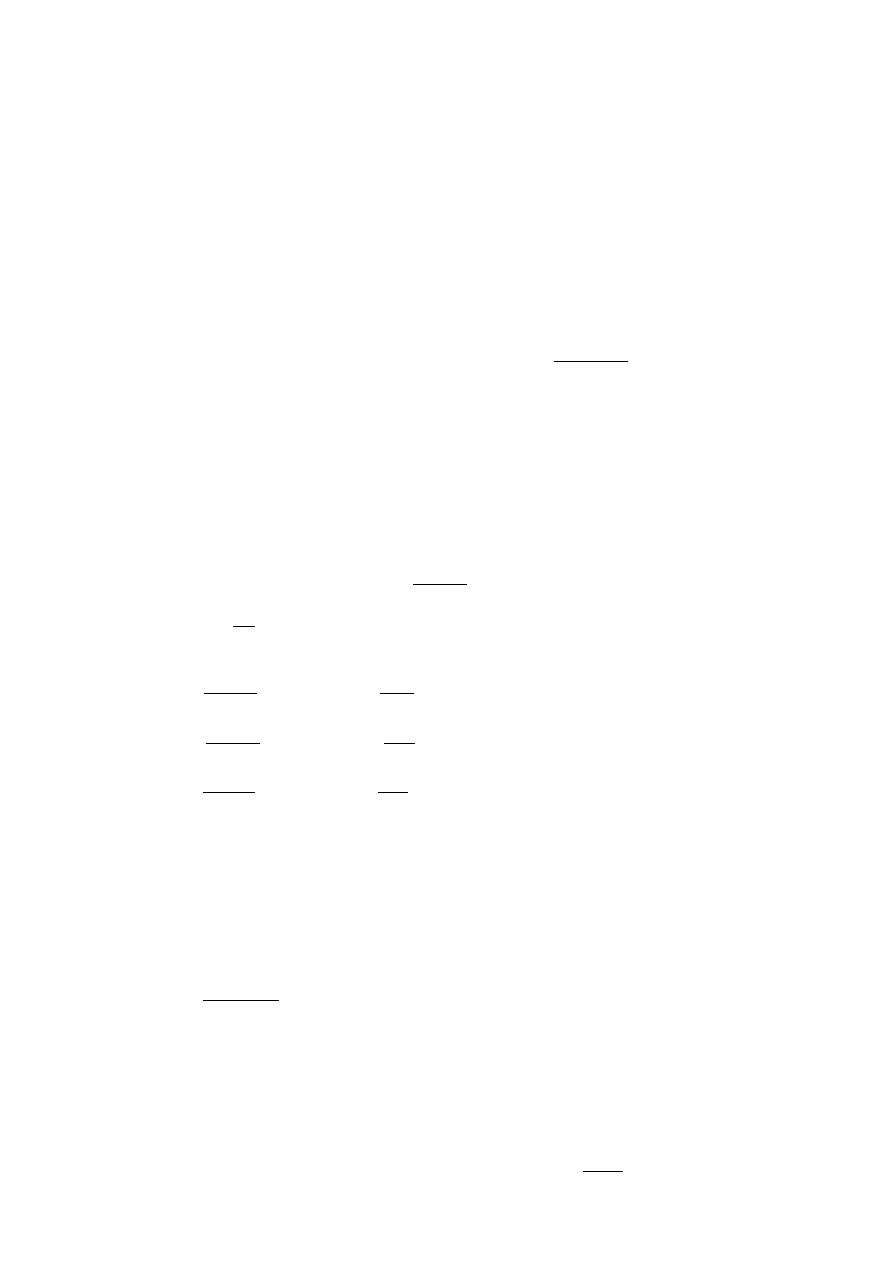
37. Kiedy przestrzenny dowolny układ sił redukuje się do wypadkowej.

Wg =/= 0, Mg =/= 0, Wg _|_ Mg
Wg =/= 0, Mg = 0

38. Kiedy przestrzenny dowolny układ sił redukuje się do pary sił

Wg = 0, Mg =/= 0

39. Kiedy przestrzenny dowolny układ sił redukuje się do skrętnika

Wg =/= 0, Mg=/=0, Wg || Mg, Wg=/=0, Mg=/= 0

40. Co to jest skrętnik (śruba statyczna).

Układ sił składający się z pary sił i momentu prostopadłego do płaszczyzny tej pary. Skrętnik może być
lewy albo prawy.

41. Co to jest środek sił równoległych

Jest to punkt, w którym przecina się wypadkowa dwóch równoległych sił i wypadkowa tych samych sił
obróconych o ten sam kąt α. Punkt S dzieli odcinek AB na części odwrotnie proporcjonalne do

działających sił. Jego położenie można obliczyć z wzoru X

s

=

∑

i=1

n

x

i

∗

∣

P

i

∣

∑

i=1

n

∣

P

i

∣

analogicznie dla Ys i Zs.

Położenie tego punktu nie zależy od kierunku sił. Dlatego jeżeli wszystkie siły obrócimy o ten sam kąt
zachowując ich równoległość, to położenie środka sił równoległych nie ulegnie zmianie.

42. Określić pojęcie siły ciężkości i środka ciężkości

Środek ciężkości to środek równoległych sił ciężkości. Wyznaczamy go za pomocą podziału bryły na
elementarne (znane) objętości. Wówczas to ciężary oddzielnych objętości będą przedstawiać
przestrzenny układ sił równoległych. Jeżeli przez G oznaczymy ciężar (wywołany przez pole
grawitacyjne Ziemi) bryły to środek ciężkości jest punktem, przez który przechodzi prosta działania tej

siły. Zapisując w rachunku całkowym x

s

=

∫

x dV

V

, y

s

.... , gdzie V jest objętością ciała. Dla figur

płaskich

x

s

=

∫

x

dA

A

, gdzie A jest powierzchnią całkowitą.

43. Podać wzory na wyznaczanie środków ciężkości brył, figur i linii

bryły x

s

=

∑

i =1

n

x

i

∗

dVi

V

, ys... lub X

s

=

∫

xdV

V

figur x

s

=

∑

i=1

n

x

i

∗

dAi

A

, ys ...lub X

s

=

∫

xdA

A

linii x

s

=

∑

i=1

n

x

i

∗

dLi

L

, ys... lub X

s

=

∫

xdL

L

44. Podać twierdzenia pomocne przy wyznaczaniu środków ciężkości

Środek ciężkości układu mającego środek symetrii leży w tym środku
Jeżeli układ ma płaszczyznę symetrii to środek ciężkości leży na tej płaszczyźnie
Jeżeli układ ma oś symetrii to środek ciężkości leży na tej osi
Jeżeli układ ma dwie lub więcej osi symetrii, to środek ciężkości leży w punkcie przecięcia się tych osi.
Rzut środka ciężkości figury płaskiej na płaszczyznę jest środkiem ciężkości rzutu tej figury na daną
płaszczyznę.

45. Podać prawa tarcia sformułowane przez Coulomba

Siła tarcia jest niezależna od wielkości powierzchni stykających się ze sobą ciał i zależy jedynie od ich
rodzaju.
Wartość siły tarcia dla ciała znajdującego się w spoczynku może zmienić się od zera do granicznej
wartości, proporcjonalnej do całkowitego nacisku normalnego.
W przypadku gdy ciało ślizga się po pewnej powierzchni, siła tarcia jest zawsze skierowana przeciwnie
do kierunku ruchu i jest mniejsza od granicznej wartości statycznej (zazwyczaj?)

46. Omówić pojęcia tarcia kinetycznego i statycznego

Tarcie statyczne to reakcja styczna przeciwdziałająca przesunięciu ciał względem siebie.

T=u*N, Ciała pozostaną w równowadze dopóki PT ; =tg p=

T

stmax

N

(stożek tarcia)

Tarcie kinetyczne jest to siła przeciwdziałająca ruchowi ciała (już będącego w ruchu). Zazwyczaj jest

ona mniejsza od tarcia statycznego np. dla stali us=0,15 a uk=0,1

47. Podać definicję tarcia statycznego

Jest to reakcja styczna przeciwdziałająca przesunięciu ciał względem siebie.

T = ∗N

48. Kiedy ciała pozostają w stanie równowagi względnej (tarcie statyczne)

Gdy siła działająca na ciało jest mniejsza od reakcji (z uwzględnieniem tarcia)

P ∗N

49. Co to jest kąt tarcia

Kąt tarcia jest to kąt utworzony przez reakcję Rmax z normalną (największy z możliwych kątów

wychylenia). Tangens kąta tarcia jest równy współczynnikowi tarcia statycznego.  =tg p=

T

stmax

N

50. Co to jest stożek tarcia

Jest to bryła zakreślona przez reakcję Rmax skierowaną kolejno we wszystkich kierunkach - dookoła. W
szczególnym przypadku izotropowych własności ciernych jest to stożek kołowy.

51. Jaki jest związek między napięciami w cięgnie nawiniętym na chropowaty krążek (wzór Eulera)

ln 

S

2

S

1

=∗

lub S

2

=

S

1

∗

e

 ∗

, gdzie S2 i S1 są to siły, u -współczynnik tarcia cięgna o walec, a α

kąt opasania,

52. Omówić istotę tarcia toczenia

Tarcie toczenia powstaje przy usiłowaniu przetoczenia walca o ciężarze G po poziomej płaszczyźnie. W
rozważaniu tego tarcia nie możemy przyjąć idealnej sztywności wałca, gdyż nie występowałaby
składowa pozioma siły nacisku równoważąca siłę ciągnącą P.

53. Co to jest ramię oporu toczenia (współczynnik tarcia tocznego)

Minimalna siła potrzebna do przesunięcia walca to P

gr

=

F
R

∗

G , gdzie F to ramię oporu toczenia

(zależy od plastyczności materiału walca). Jest to odległość między prostymi działania siły G i N
mierzona przy podłożu. Przykładowe wartości F dla stali jest to 0,005, a dla koła samochodowego po
asfalcie 0,24

Wytrzymałość materiałów:

1. Co to jest wytrzymałość?

Jest to odporność materiału na odkształcenia spowodowane naprężeniami. Rozróżniamy różne rodzaje
wytrzymałości: na skręcanie, na zginanie itp

2. Czym zajmuje się wytrzymałość materiałów?

Zadaniem wytrzymałości materiałów jest opracowanie metod oceny zachowania spotykanych w
praktyce inżynierskiej typowych elementów konstrukcyjnych poddanych działaniu obciążeń. Jest to
jeden z działów mechaniki.

3. Wymień podstawowe materiały konstrukcyjne.

*Sprężysto plastyczne (stal i inne metale poza żeliwem)
*lepko-sprężyste (tworzywa sztuczne, beton)
*sprężysto kruche (kryształy np. szkło lub żeliwo)

4. Omów podstawowe założenia wytrzymałości materiałów.

*Ciało materialne pod wpływem obciążeń ulega odkształceniom: sprężystym ustępującym po odjęciu
obciążenia i trwałe zwane plastycznymi – pozostają w materiale nawet po usunięciu przyczyny.
*Dodatkowo przyjmuje się, że w większości przypadków wszelkie odkształcenia w stosunku do
wymiarów ciała są znikomo małe, co zresztą odpowiada praktycznym warunkom eksploatacji
elementów konstrukcyjnych.

5. Co to są odkształcenia, sklasyfikuj rodzaje odkształceń?

Odkształceniem nazywamy chwilową lub trwałą zmianę wymiarów całego ciała lub jego części
wywołaną przyłożonym do niego obciążeniem. Rozróżniamy dwa rodzaje odkształceń:
*sprężyste – ustępujące po odjęciu obciążenia,
*trwałe – plastyczne, które pozostają po usunięciu przyczyny odkształcenia. Odkształcenia stałe
towarzyszą procesowi obciążenia od samego początku, ale ich wartość zaczyna mieć praktyczne
znaczenie (dla liniowo sprężystych) dopiero po przekroczeniu granicy sprężystości.
Dodatkowo trzeba pamiętać, że odkształcenia względem wymiarów materiału są znikomo małe
-----
*czysto postaciowe (zmienia się kształt, objętość nie)
*czysto objętościowe (zmienia się objętość, względne wymiary pozostają te same)

*mieszane.

6. Co to są naprężenia, podaj ich rodzaje?

Naprężenie to miara gęstości powierzchniowej sił wewnętrznych występujących w materiale. Jest
podstawową wielkością mechaniki. Jednostka to [Pa].
Naprężenia mogą być styczne (τ) do powierzchni przekroju (np. przy skręcaniu) lub normalne (δ) (np.
przy rozciąganiu).

7. Co to są równania konstytutywne?

Są to równania pozwalające ustalić wzajemne zależności matematyczne pomiędzy odkształceniami
ciała, a obciążeniami zewnętrznymi. Budowane są w oparciu o mechaniczne własności materiału.

8. Podaj zależność pomiędzy naprężeniami a odkształceniami w trójosiowym stanie naprężeń.

Jest to uogólnione prawo Hooka E

x

=

1

E

∗[

x

−

V 

y



z

]

;

y

;

z

,Y

xy

=



zy

G

,Y

xz

;Y

yz

9. Omów znane rodzaje obciążeń.

*Obciążenia stałe – ciężar własny konstrukcji, ciężar elementów podtrzymywanych przez konstrukcję.
Obciążenie to ma w okresie eksploatacji stałą wartość
*Obciążenia użytkowe (zmienne) – obciążenia zasadnicze, dla których projektuje się daną konstrukcję
np. wyposażenie technologiczne, siły bezwładności działających urządzeń, wpływ prędkości
odkształceń, wpływ czasu obciążenia, wpływ obciążeń wielokrotnych. Oszacowanie tych obciążeń
należy do najbardziej istotnych fragmentu projektowania.
*Wpływ otoczenia – śnieg, wiatr, temperatura, napromieniowanie. Zwykle odczytujemy z
odpowiednich norm. W rzadkich przypadkach analizowane indywidualnie
*Obciążenia transportowe i montażowe – w czasie transportu i montażu, elementy nie są ostatecznie
złożone w maszynie/urządzeniu

10. Podaj i omów zasadę de Saint-Venanta.

Równoważne układy sił działające na mały obszar ciała wywołują takie same stany naprężenia w całym
ciele z wyjątkiem bezpośredniego otoczenia przyłożonych sił (odmienny stan naprężeń w pobliżu
punktu przyłożenia pomijamy). Oznacza to, że możemy analizować np. pręt tak samo dla dwóch sił P/2
i jednej P przyłożonych na końcach.

11. Jaka jest różnica pomiędzy jednorodnością a izotropią materiału?

Jednorodność materiału oznacza, że w każdym jego punkcie jego właściwości mechaniczne są takie
same (np. gęstość jest taka sama).
Izotropowość – właściwości mechaniczne nie zależą od orientacji elementarnych objętości ciała (np.
stal jest izotropowa, drewno z włóknami NIE)

12. Co to są stałe materiałowe?

Są to mechaniczne parametry materiału. Przykładem może być moduł Kirchoffa G, Moduł Younga E,
Współczynnik Poissona v.

13. Na czym polega liniowa sprężystość materiału?

Zakłada się, że do pewnej granicy obciążenia ciało zachowuje ciągłość struktury oraz że istnieje
jednoznaczny, bez naprężeniowy (początkowy) stan ciała, do którego badane ciało powraca po
usunięciu sił zewnętrznych – obciążenia.

14. Wymień podstawowe stałe materiałowe dla materiału liniowo sprężystego.

*Kirchoffa G – moduł sprężystości poprzecznej/odkształcalności postaciowej [Pa]. Określa ona
sprężystość materiału (stal 0,8, beton 0,13, alu 0,27)*10^5. G=(τ/γ)
*Moduł Younga E – uzależnia odkształcenia liniowe od naprężenia. Moduł Younga jest hipotetycznym
naprężeniem, które wystąpiłoby przy dwukrotnym wydłużeniu próbki materiału, przy założeniu, że jej
przekrój nie ulegnie zmianie (stal 2, beton 0,3, alu 0,72). E=δ/ε
*Współczynnik Poissona V - stosunek odkształcenia poprzecznego do odkształcenia podłużnego przy

osiowym naprężeniu. Określa w jaki sposób ciało się odkształca. V =

−

E

y

E

x

=

−

E

z

E

x

(stal 0,29, beton

0,17, alu 0,34)*10^5
*(wytrzymałość doraźna Rm, granica plastyczności Re, wydłużalność A5, twardość H, wytrzymałość
zmęczeniowa Z)

15. Podaj definicje: momentów statycznych przekroju oraz promieni bezwładności.

Momenty statyczne przekroju są to inaczej momenty bezwładności powierzchni [m^4]
- moment względem osi przechodzącej przez środek ciężkości I =

∫

y

2

dA

-biegunowy moment bezwładności I

o

=

∫

r

2

dA=I

y



I

z

-moment dewiacji – odśrodkowy I

yz

=

∫

yz dA , gdzie A to powierzchnia, y, z współrzędne w

układzie współrzędnych elementarnej powierzchni dA

16. Co to jest moment dewiacji?

I

yz

=

∫

yz dA inaczej moment odśrodkowy. Moment dewiacji jest to moment względem układu osi, z

których co najmniej jedna jest osią symetrii figury jest równy 0.

17. Co to jest biegunowy moment bezwładności przekroju?

I

o

=

∫

r

2

dA=I

y



I

z

jest to moment względem obranego punktu

18. Podaj twierdzenia Steinera dla momentów statycznych i momentów bezwładności przekroju.

I '= I A∗b

2

– gdzie I – moment w osi przechodzącej przez środek ciężkości powierzchni, A -

Powierzchnia całej figury, b – odległość od tej osi. I

yz

'=I

yz



A∗bc

19. Scharakteryzuj stan naprężenia w pręcie rozciąganym.

W pręcie rozciąganym występują naprężenia normalne równomiernie w całej objętości i przekroju. Są
one proporcjonalne do przyłożonej siły P i odwrotnie proporcjonalne do pola przekroju poprzecznego A,

 =

P
A

20. Podaj wzór na naprężenia normalne w pręcie rozciąganym.

 =

P
A

, P – przyłożona siła, A – pole przekroju poprzecznego

21. Scharakteryzuj stan odkształcenia w pręcie rozciąganym.

Podczas rozciągania następuje wydłużenie pręta



L=

P∗L

E∗A

, L- długość pręta i zwężenie przekroju



y

=−

V ∗



x

E

22. Podaj interpretację fizykalną liczby Poissona.

Współczynnik Poissona V jest stosunkiem odkształcenia poprzecznego do odkształcenia podłużnego
przy osiowym naprężeniu. Określa w jaki sposób ciało się odkształca.

23. Podaj wzór na wydłużenie pręta rozciąganego stałą siłą.



L=

P∗L

E∗A

, P- siła, L- długość pręta, A- pole przekroju, E- moduł Younga

24. Czym różni się czyste ścinanie od ścinania technologicznego?

W ścinaniu czystym nie występują naprężenia normalne (od zginania), odległość między krawędziami
tnącymi wynosi 0. W praktyce występuje tylko ścinanie techniczne, lecz np. w nitach przyjmujemy, że
występują tylko naprężenia styczne (pomijamy normalne).

25. Podaj warunki wytrzymałościowe do projektowania nitów jedno i dwuciętych.

1 cięte: k

t



T

A

, T – siła, A – pole przekroju, kt – naprężenie dopuszczalne na ścinanie

2 cięte k

t



T

2A

(dwie powierzchnie ścinane) A=

∗

d

4

26. Z jakiego warunku wyznaczamy długość spoiny pachwinowej?

L

s



T

A∗k

s

=

T

0,7∗a∗k

s

, ks – naprężenie dopuszczalne w spoinie, zwykle ks = 0,65kr materiału

łączonego

27. Jaka jest zależność jednostkowego kąta skręcania od momentu skręcającego?



i

=

M

s

∗

L

I

o

∗

G

, gdzie Ms – moment skręcający, L – długość pręta, Io – wskaźnik odporności na

skręcanie, G – stała Kirchoffa

28. Podaj wzór na moment bezwładności na skręcanie.

Io = W * R, Io – moment bezwładności, R – promień wału, W – wskaźnik przekroju na skręcanie

29. Określ rozkład naprężeń stycznych przy skręcaniu.

Wartości naprężeń stycznych zwiększają się proporcjonalnie do odległości od osi wału, poczynając od
zera w jego środku do wartości maksymalnych we włóknach skrajnych.
Są prostopadłe do odpowiednich okręgów przekroju – prostopadłe do odpowiednich promieni.

30. Podaj warunki projektowania przekroju przy skręcaniu.

Warunek wytrzymałościowy k

s



M

s

W

o

Warunek odkształceniowy 

max

=

M

s

∗

L

G∗I

o



dop

31. Podaj definicję kąta skręcenia i jednostkowego kąta skręcenia.

Kąt skręcenia jest to suma wszystkich jednostkowych kątów skręcenia wału.

Jednostkowy kąt skręcenia jest to kąt skręcenia na jednostkowej długości   =

M

s

∗

L∗ l

I

o

∗

G

32. Co wiesz o stanie naprężenia i rozkładzie naprężeń przy skręcaniu?

Naprężenia są styczne i prostopadłe do przekroju – odpowiednich promieni. Są maksymalne na
włóknach zewnętrznych, a zerowe w środku wału. Rosną liniowo wraz z odległością od środka wału.

33. Co to jest moment bezwładności na skręcanie?

Io = W * R, Io – moment bezwładności, R – promień wału, W – wskaźnik przekroju na skręcanie,
określa odporność danego przekroju na skręcenie

34. Scharakteryzuj stan naprężenia przy czystym zginaniu.

W czystym zginaniu występuje tylko moment gnący prostopadły do osi pręta.

35. Podaj wzór na naprężenia normalne przy czystym zginaniu.

 =

Z


⇒ 

z =

E∗z

 ∗

z

, z – odległość od osi obojętnej, ρ – promień zginania

36. Określ rozkład naprężeń normalnych w przekroju poprzecznym przy czystym zginaniu.

Naprężenia są zerowe w płaszczyźnie obojętnej, po wewnętrznej stronie gięcia (bliżej 'środka okręgu')
następuje ściskanie, a 'za' osią obojętną rozciąganie. Im te odległości są większe tym naprężenia
większe.

37. Opisz położenie osi obojętnej przy czystym zginaniu.

Jest to oś, w której naprężenia są równe 0, jest to przecięcie się płaszczyzny naprężeń z płaszczyzną
przekroju poprzecznego. -skomplikowany wzór-

38. Gdzie występują największe naprężenia w przekroju przy czystym zginaniu?

Przy powierzchni – najdalej od osi obojętnej.

39. Scharakteryzuj stan odkształcenia przy czystym zginaniu.

Przekroje poprzeczne pozostają niezmienione (teoria niezmiennych przekrojów), zmienia się tylko kąt
między nimi - przestają być równoległe.

40. Co wiesz o deformacji przekroju poprzecznego przy czystym zginaniu?

Zgodnie z przyjętymi hipotezami przekrój poprzeczny przy czystym zginaniu nie zmienia się.

41. Co to jest wskaźnik wytrzymałości?

Jest to parametr uzależniający właściwości mechaniczne przedmiotu od jego kształtu geometrycznego
(np. przekroju). Przykładem może być Wo – na skręcanie, Wy – na zginanie

42. Jaki przekrój najlepiej pracuje na zginanie?

Najlepiej znosi (radzi sobie) - drążony (rury kwadratowe), ceowniki ustawione dłuższą krawędzią
równolegle do działającego obciążenia, dwuteowniki.

43. Jak zaprojektować optymalny przekrój zginany?

Należy pamiętać o zachowaniu współczynników bezpieczeństwa, sprawdzeniu wydłużeń
przewidywanych, dążenie do najniższej masy i najniższej ceny. Przekrój powinien być ustawiony
dłuższą krawędzią równolegle do przyłożonego obciążenia. Najlepiej gdyby to był dwuteownik,
ceownik lub rura kwadratowa.

44. Jak określić naprężenia w dowolnym punkcie przekroju?

Należy obliczyć odległość od osi obojętnej, moment gnący działający na dany przekrój oraz znaleźć
(np. w polskich normach, tabelach) moment bezwładności na zginanie Iy oraz moduł Younga naszego

materiału. Wzór   z =

M

s

∗

z

E∗I

y

45. Podaj założenia technicznej teorii zginania.

W czystym zginaniu zakładamy istnienie tylko momentu gnącego. W zginaniu technicznym musimy
uwzględnić jeszcze siły tnące (będące pochodnymi momentów gnących). ???

46. Co to są ugięcia i kąty obrotu?

Ugięcie jest to odkształcenie pręta przenoszącego obciążenia gnące (belki).
Kąt obrotu jest to pochodna ugięcia: (w(x))'x = tg δ x Dla małych kątów tg δ x = δ x (w radianach).

Inaczej mówiąc jest to styczna do linii ugięcia w punkcie.

47. Jak zależność różniczkowa istnieje pomiędzy ugięciami a momentem zginającym?



x

2



w x=

M

g



x

E∗I

y

, pochodna drugiego stopnia po x

48. Omów warunki brzegowe dla równania różniczkowego opisujące ugięcie belki.

*Podpora przegubowa lub przesuwna w = 0 zerowe przemieszczenie poprzeczne
*Wspornik – w =0 i (w)'=kąt ugięcia = 0 zerowe przemieszczenie poprzeczne i zerowy kąt obrotu
*Koniec swobodny: moment gnący i siły tnące = 0

49. Opisz metodę analityczną obliczania ugięć.

Mając wyznaczoną funkcję opisującą przemieszczenie poprzeczne w(x) dla danego przedziału belki, w
który EI_y=const (stały wskaźnik na zginanie) oraz moment gnący Mg(x) całkujemy dwukrotnie

równanie: 

x

2



w x=

M

g



x

E∗I

y

⇒

E∗I

y

∗

w x=

∫



∫

M

g



x  dxC dx D

50. Opisz metodę Clebscha obliczania ugięć

Metoda ta ma zaletę nad analityczną metodą obliczania ugięć, gdyż stałe całkowania są niezmienne.
Można ją tylko stosować do belek o stałej sztywności.
1. Jeżeli występuje obciążenie ciągłe to przedłużamy je do końca belki, a z przeciwnej strony belki
dodajemy takie obciążenie ciągłe o ile przedłużyliśmy(zrównoważenie przedłużenia).
2. Piszemy jedno równanie ugięcia belki EI y= (wszystkie wyrazy wynikłe z założenia 1)
3. Dwa razy całkujemy przestrzegając założenia 2.
4. Ustalamy warunki początkowe i wyliczamy stałe całkowania.
Składniki wypisujemy w postaci: M(x-a)^0, P(x-a)^1, q/2(x-2)^2, M – moment, P – siła, q – obciążenie
ciągłe

51. Podaj znane hipotezy wytrzymałościowe

największych naprężeń normalnych
największych naprężeń tnących
największego wydłużenia względnego
Hubera

52. Które hipotezy stosuje się dla materiałów sprężysto-plastycznych, a które do sprężysto-kruchych?

*plastyczne
-największych naprężeń tnących (głównie stale niskowęglowe)
-Hubera
*kruche
-największych naprężeń normalnych (historyczna)

53. Scharakteryzuj stan naprężenia przy zginaniu z rozciąganiem.

Naprężenia od zginania i rozciągania są normalne, sumują się algebraicznie, w związku z tym
największe naprężenia będą występowały we włóknie skrajnym (zewnętrznym). W zależności od
stosunku naprężeń gnących i rozciągających możemy otrzymać figurę obrazującą naprężenia w postaci:
podwójny trójkąt, trapez lub trójkąt.



max

=

P

A



M

g

W

y



k

r

54. Podaj wzór na naprężenia normalne przy zginaniu z rozciąganiem.



max

=

P

A



M

g

W

y



k

r

P – siła, A – przekrój poprzeczny, Mg – moment gnący, Wy – wskaźnik

przekroju na zginanie.

55. Opisz rozkład naprężeń normalnych w przekroju poprzecznym przy zginaniu z rozciąganiem.

Maksymalne naprężenia będą występowały we włóknie skrajnym (zewnętrznym). W zależności od
stosunku naprężeń gnących punkt o najmniejszym naprężeniu może występować w środku lub na skraju
przedziału (przeciwnym do naprężeń maksymalnych). Dla silniejszego zginania będzie to wnętrze, dla
silniejszego rozciągania brzeg.

56. Określ położenie osi obojętnej przy zginaniu z rozciąganiem.

Położenie osi obojętnej zależy od stosunku naprężeń zginających i rozciągających. Leży w przecięciu
się płaszczyzn obu naprężeń. Może wypadać we wnętrzu materiału lub w jego zewnętrznych włóknach.

57. Jakie są możliwe położenia osi obojętnej przy zginaniu z rozciąganiem?

Może wypadać we wnętrzu materiału lub w jego zewnętrznych włóknach – zależnie od stosunku

naprężeń pochodzących od zginania i rozciągania.

58. Gdzie występują największe naprężenia normalne w przekroju przy zginaniu z rozciąganiem?

W zewnętrznym włóknie (którym to zależy od stosunku naprężeń rozciągających i gnących).

59. Scharakteryzuj stan naprężenia przy zginaniu ze skręcaniem.

W dowolnym punkcie wału występują naprężenia od zginania δ (normalne) i skręcania τ (styczne).
Przyjmują one wartości maksymalne w skrajnych włóknach (tam naprężenia składowe są największe).
W zależności od przyjętej hipotezy istnieją różne wzory na wyznaczenie naprężeń w materiale. np. dla
Hubera 

z

=





2



3∗

2

60. Opisz rozkład naprężeń normalnych i stycznych w przekroju poprzecznym przy zginaniu ze

skręcaniem.
Naprężenia styczne rosną liniowo od środka wału, aż do jego zewnętrznych włókien. Analogicznie
zachowują się naprężenia normalne (również rosną wraz ze wzrostem odległości od osi wału).

61. Podaj wzór na naprężenia zredukowane według znanych Ci hipotez przy zginaniu ze skręcaniem.

*największych naprężeń normalnych 

z

=

1
2

 





2



4∗

2



*największych naprężeń tnących 

z

=





2



4∗

2

*największego wydłużenia względnego … - skomplikowany wzór-
*Hubera 

z

=





2



3∗

2

62. Opisz zjawisko zmęczenia materiału.

Zmęczenie materiału jest to obniżanie się wytrzymałości przy zmiennych naprężenia (materiał poddany
zmiennym obciążeniom).

63. Jakie wielkości opisują naprężenia w cyklu zmęczeniowym?

naprężenia średnie 

m

=

max



min

/

2

amplituda naprężeń 

a

=

max

−

min

/

2

częstotliwośćcyklu 

Często zamiast podawać te wartości podaje:

współczynnik asymetrii cyklu R=



m

−

a



m



a

współczynnik stałości obciążenia X =



m



a

=

1 R
1− R

64. Jakie rozróżniamy rodzaje cykli obciążenia?

* cykl jednostronny o wartościach dodatnich (X=1, R=0) lub ujemnych (X=-1, R=inf)
* cykl obustronny (X=0,R=-1)
* cykl mieszany

65. Co to jest wytrzymałość zmęczeniowa?

Wytrzymałością zmęczeniową Z (granicą zmęczenia) nazywamy maksymalne naprężenie δ_max dla
danego cyklu naprężeń, przy którym element nie ulegnie zniszczeniu po osiągnięciu umownej
granicznej liczby cykli naprężeń (dla stali 10*10^6).

66. Naszkicuj wykres Wohlera.

Dla obciążeń rozciągających, skręcających,
zginających, cykli jedno i obustronnych wykresy te
będą różne.

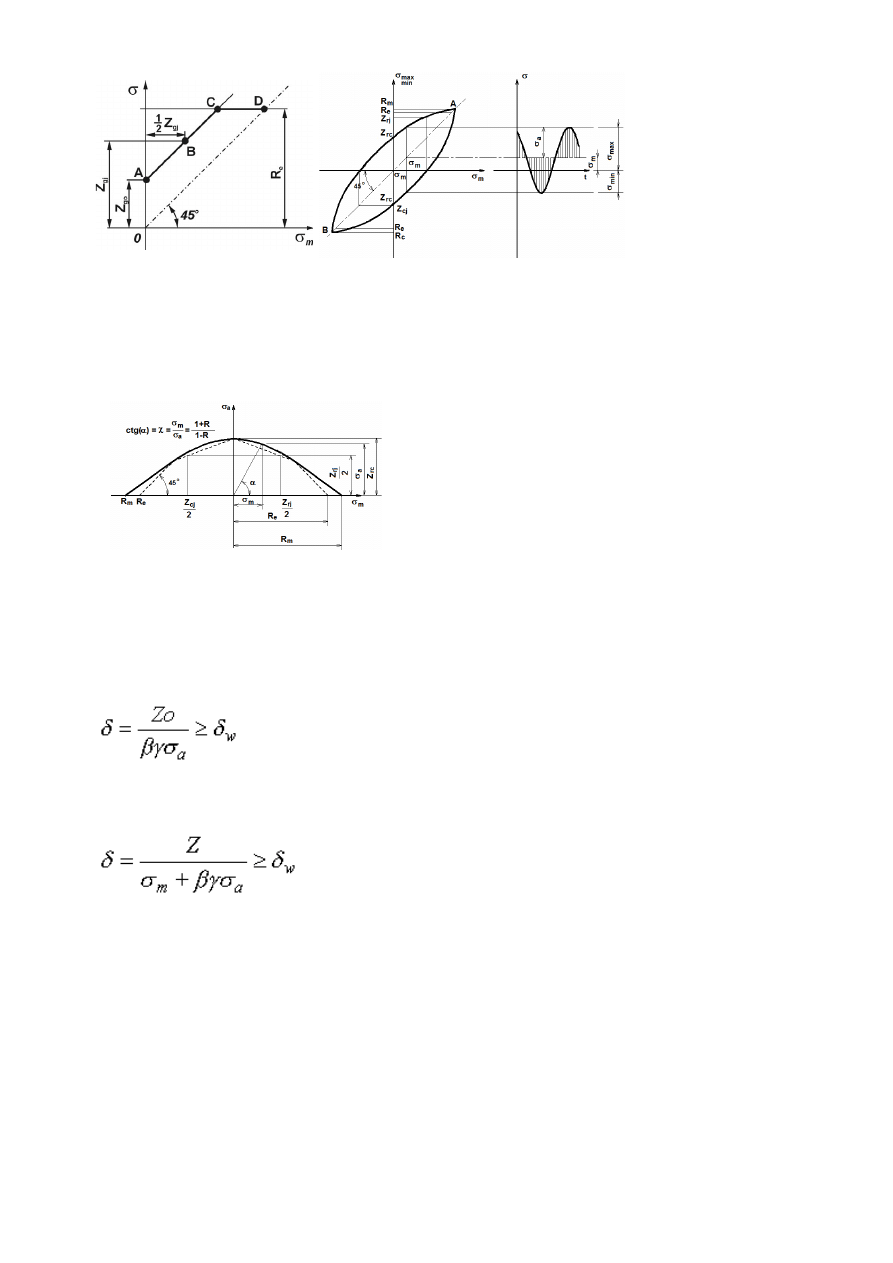
67. Opisz wykres Smitha i krzywą Haigha dla innych rodzajów cykli.

np. dla zginania Rysunek po prawej przedstawia rzeczywisty wykres Smitha (z histerezą). Po lewej
wersja uproszczona (aproksymowana).
Punkt A – odpowiada wytrzymałości zmęczeniowej dla obustronnego zginania.
B – (1/2Zgj, Zgj) i przeprowadzamy prostą AB aż do przecięcia z linią poziomą odpowiadającą granicy
plastyczności Re. W ten sposób powstaje nam łamana.
Otrzymany w ten sposób wykres pozwala na przeprowadzanie obliczeń dla materiałów sprężysto-
plastycznych

Wykres Haigha powstaje z części wykresu Smitha obróconego o 45st. Jeszcze łatwiej z niego odczytać
dopuszczalne wartości naprężeń. Linia przerywana pokazuje jego uproszczoną postać.

68. Podaj sposób wyznaczania współczynnika bezpieczeństwa przy cyklach niesymetrycznych.

Najpewniejszym sposobem jest wykonanie badań doświadczalnych. Możemy też sprawdzić za pomocą
wzoru δw – przyjmujemy zazwyczaj 2.5-4.0

69. Podaj sposób wyznaczania współczynnika bezpieczeństwa przy cyklach symetrycznych.

Najpewniejszym sposobem jest wykonanie badań doświadczalnych. Możemy też sprawdzić za pomocą
wzoru δw – przyjmujemy zazwyczaj 2.5-4.0

70. Pęknięć materiałów NIE OBEJMUJE.