1
LICZBY PIERWSZE
Liczba pierwsza, to liczba naturalna większa od 1, która jest podzielna tylko przez 1 i samą
siebie.
Liczby pierwsze były badane od czasów starożytnych. Euklides w IV w. p.n.e. poświęcił im
księgę w Elementach. Zaprezentował w nich m.in. algorytm znajdowania największego wspólnego
dzielnika oraz udowodnił, że liczb pierwszych jest nieskooczenie wiele. Przy dowodzie tego
twierdzenia posłużył się metodą sprowadzania do absurdu i jest to jeden z pierwszych przykładów
zastosowania praktycznego tej metody.
Euklides pokazał, że żaden skooczony zbiór nie zawiera wszystkich liczb pierwszych:
Niech będzie skooczonym zbiorem liczb pierwszych. Niech będzie iloczynem wszystkich liczb
występujących w (gdy jest puste, to ). Jedynym wspólnym dzielnikiem liczb oraz
jest . Zatem żadna liczba pierwsza, występująca w , nie jest dzielnikiem liczby . Ale
. Więc ma dzielnik , który jest liczbą pierwszą. Liczba pierwsza nie należy do (bo
jest dzielnikiem liczby x+1).
Każda liczba naturalna większa od 1 daje się jednoznacznie zapisad w postaci iloczynu
skooczonego niemalejącego ciągu pewnych liczb pierwszych. Twierdzenie to był w stanie udowodnid
już Euklides (stworzył niezbędne narzędzia), ale uczynił to dopiero Gauss. Twierdzenie to oznacza, że
liczby pierwsze są w pewnym sensie atomami, z których przy pomocy mnożenia zbudowane są
pozostałe liczby.
W 240 p.n.e. Eratostenes użył algorytmu nazwanego sitem Eratostenesa do szybkiego
znajdowania liczb pierwszych. Łatwo szukad kolejnych liczb pierwszych nie większych od danej liczby
naturalnej n. Wypisuje się kolejno liczby naturalne od 2 do n. Liczba 2, pierwsza z wypisanych liczb,
jest liczbą pierwszą; pozostawia się ją i wykreśla się wszystkie dalsze liczby podzielne przez 2, gdyż nie
są to liczby pierwsze. Z liczb pozostałych po tym wykreśleniu kolejną po liczbie 2 jest liczba 3.
Pozostawia się ją jako liczbę pierwszą i wykreśla się wszystkie dalsze liczby podzielne przez 3, które
nie zostały poprzednio wykreślone. Z pozostałych teraz liczb kolejną po 2 i 3 jest liczba 5; pozostawia
się ją i wykreśla wszystkie dalsze liczby podzielne przez 5, które nie zostały dotychczas wykreślone.
Kontynuując to wykreślanie, dojdzie się wreszcie do tego, że wszystkie liczby, które nie są pierwsze
zostaną wykreślone, pozostaną tylko liczby pierwsze nie większe od n.
Ta metoda, znacznie dzisiaj udoskonalona pozwala wyłuskad wszystkie liczby pierwsze
z początkowych kilkudziesięciu milionów liczb.
Dalszy ciąg historii liczb pierwszych następuje dopiero w XVII wieku, gdy Fermat udowadnia
hipotezę znaną jako małe twierdzenie Fermata.
Małe twierdzenie Fermata:
jeżeli jest liczbą pierwszą, to dla dowolnej liczby całkowitej , liczba
jest podzielna przez .
,
lub inaczej
jeśli jest liczbą pierwszą, a jest taką liczbą całkowitą, że liczby i są względnie pierwsze,
to
dzieli się przez . Innymi słowy,
albo
Test pierwszości Fermata: by stwierdzid czy jest pierwsza, możemy wybrad kilka losowych wartości
i sprawdzid czy ta równośd jest dla nich spełniona. Jeśli dla któregokolwiek nie jest, wiemy na
pewno że jest liczbą złożoną. Jeśli wszystkie ją spełniają, jest prawdopodobnie liczbą pierwszą
albo pseudopierwszą, czyli taką która spełnia niektóre własności charakteryzujące liczby pierwsze, ale
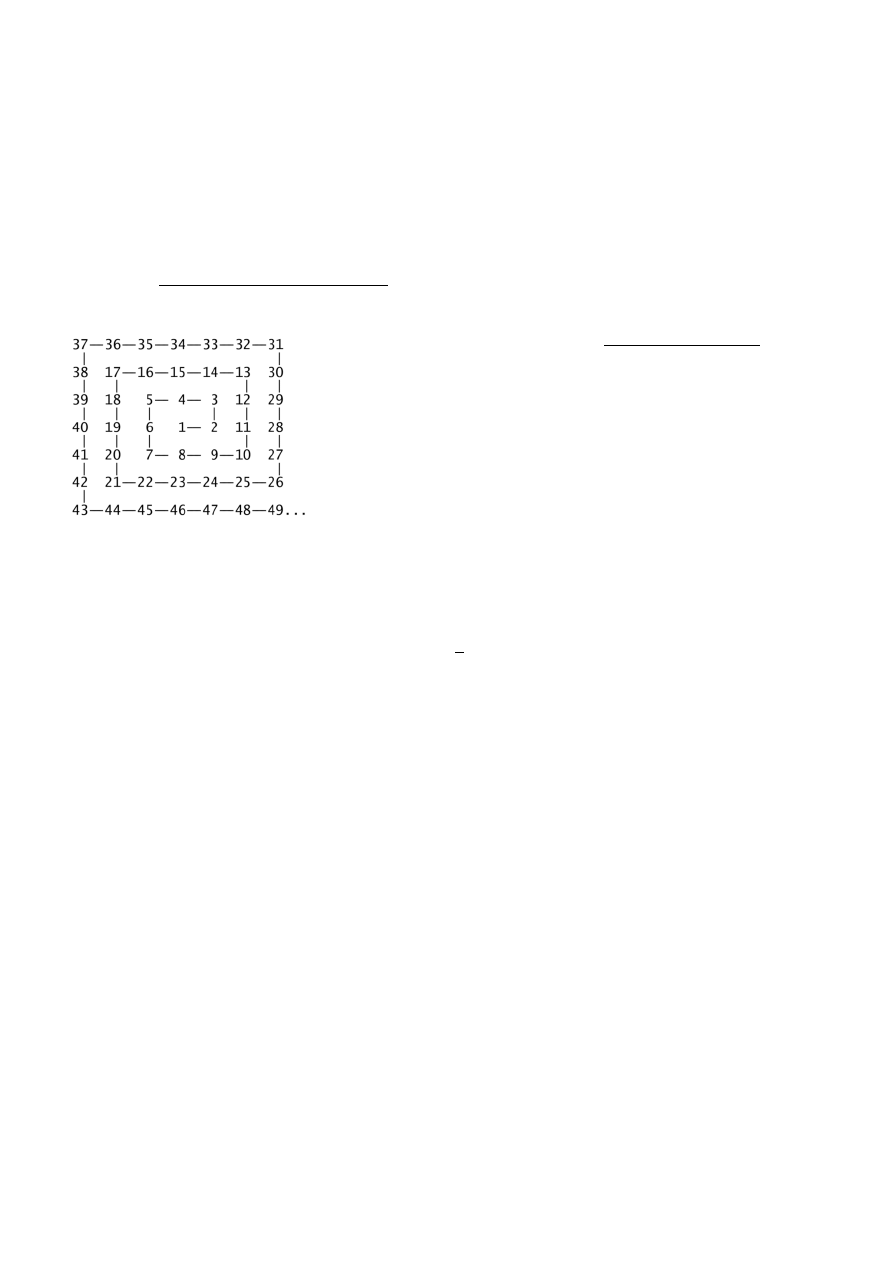
2
sama nie jest liczbą pierwszą. Liczby złożone spełniające Małe twierdzenie Fermata nazywa się
liczbami Carmichaela.
Dalszy postęp w dziedzinie teorii liczb nastąpił w epoce Renesansu. W 1796 Legendre podał
wzór na gęstośd rozmieszczenia liczb pierwszych. Wzór został ostatecznie udowodniony przez
Hadamarda i de la Vallée-Poussina w 1896. W 1859 Riemann stworzył słynną hipotezę, do dziś
nieudowodnioną, dotyczącą pierwiastków funkcji dzeta.
Rozmieszczenie liczb pierwszych wśród liczb naturalnych spełnia pewne prawidłowości
statystyczne, ale nie jest znany żaden wzór, który pozwalałby wyznaczad liczby pierwsze w sposób
bardziej efektywny niż metoda Eratostenesa.
Jest coś takiego, jak spirala Ulama lub spirala liczb pierwszych - to
graficzna metoda pokazywania pewnych niewyjaśnionych do dziś
różnic w rozkładzie liczb pierwszych, zaproponowana przez
polskiego matematyka Stanisława Ulama w 1963 roku. Natomiast
już w 1964 Martin Gardner opisał spiralę Ulama w czasopiśmie
Scientific American.
Na kwadratowej tablicy zaczynając od 1 w środku spiralnie
wypisuje się kolejne liczby naturalne. Na niektórych przekątnych
liczby pierwsze częściej grupują się niż na innych. Fakt ten nie
został do tej pory wyjaśniony. Zjawisko występuje także, jeśli
rozpoczyna się od innych wartości niż 1.
Kilka poniższych twierdzeo przybliża zagadnienia związane z badaniem rozmieszczenia liczb
pierwszych na osi liczbowej:
Szereg odwrotności wszystkich liczb pierwszych:
Leonhard Euler udowodnił, że szereg liczbowy
odwrotności wszystkich liczb pierwszych jest rozbieżny. Sugeruje to, że liczby pierwsze nie mogą byd
rozłożone zbyt "rzadko" na osi liczbowej. Rozbieżnośd tego szeregu daje też nowy dowód na istnienie
nieskooczenie wielu liczb pierwszych.
Postulat Bertranda – Twierdzenie Czebyszewa:
Dla dowolnej liczby naturalnej większej od 1, między liczbami a istnieje co najmniej jedna
liczba pierwsza.
Wariacja Erdősa:
Paul Erdős wzmocnił twierdzenie Czebyszewa dowodząc, że dla dowolnej liczby naturalnej ,
między liczbami , a , znajdują się co najmniej dwie liczby pierwsze – co najmniej jedna postaci
, oraz co najmniej jedna postaci .
Twierdzenie Dirichleta:
W dowolnym ciągu arytmetycznym liczb naturalnych: takim, że i są
względnie pierwsze, występuje nieskooczenie wiele liczb pierwszych. (Przy ustalonym , ilośd liczb
pierwszych dla różnych , względnie pierwszych z liczbą , jest w pewnym asymptotycznym sensie
taka sama.)
Twierdzenie o liczbach pierwszych:
Podstawowe twierdzenie o rozmieszczeniu liczb pierwszych wśród liczb naturalnych sformułował
Gauss, który na podstawie badao empirycznych zasugerował, że liczba liczb pierwszych
w przedziale opisana jest zależnością
3
gdzie symbol oznacza resztę logarytmu całkowego, a oznacza równośd
asymptotyczną rozumianą jako
Rozwinięcie logarytmu całkowego w szereg daje oszacowanie:
Gauss nie udowodnił tego twierdzenia – dopiero pod koniec XIX wieku zostało ono udowodnione
przez Hadamarda i de la Vallee Poussina.
Najprostszą postacią przybliżenia funkcji jest pierwszy element tego szeregu:
W tym wypadku także zachodzi asymptotyczna równośd:
Z twierdzenia wynika, że gęstośd rozłożenia liczb pierwszych na osi liczbowej jest odwrotnie
proporcjonalna do ich logarytmu, co oznacza, że jest ich mniej więcej tyle samo w każdej dekadzie
(między 10 000 a 100 000, między 100 000 000 a 1 000 000 000 itd.)
Szczególne rodzaje liczb pierwszych:
Liczby pierwsze bliźniacze
Liczby pierwsze i są bliźniacze jeśli . Przykłady: 3 i 5, 5 i 7, 11 i 13, 17 i 19, 29 i 31, 41
i 43, 59 i 61, 71 i 73...
5 jest bliźniacza zarówno z 3 jak i z 7.
Nie wiadomo, czy istnieje nieskooczenie wiele bliźniaczych liczb pierwszych.
Największa znana para liczb pierwszych bliźniaczych (stan na listopad 2007) to
. Liczby te, znalezione w 2007 roku, mają 58711 cyfr w zapisie dziesiętnym.
Liczby pierwsze czworacze
Liczby czworacze – liczby pierwsze, mające postad , , , , np. 5, 7, 11 i 13 lub 101,
103, 107 i 109, czyli dwie pary liczb bliźniaczych w najbliższym możliwym sąsiedztwie. Największe
znane liczby czworacze to 4104082046 4799! + 5651, 4104082046 4799! + 5653, 4104082046
4799! + 5657 oraz 4104082046 4799! + 5659.
Liczby pierwsze izolowane
Liczba pierwsza jest izolowana, jeśli najbliższa jej liczba pierwsza różni się od p co najmniej o 4.
Przykłady: 23, 89, 157, 173.
Liczby pierwsze Mersenne'a
Liczby pierwsze Mersenna są to liczby pierwsze, będące jednocześnie liczbami Mersenne'a.
Przykłady: 3, 7, 31, 127, 8191...
Warunkiem koniecznym, żeby liczba Mersenne'a była pierwsza jest pierwszośd liczby . Jednak
nie dla każdej liczby pierwszej , liczba jest pierwsza; na przykład
W sierpniu 2008 roku największą znaną liczbą pierwszą była liczba 47-ma Mersenne'a
– do jej zapisania w układzie dziesiętnym trzeba użyd 12978189 cyfr. Wygrano w ten sposób 100
tysięcy dolarów ufundowane przez Electronic Frontier Foundation dla odkrywcy liczby pierwszej o co
najmniej 10 milionach cyfr. Odkrywcą był Edson Smith.
4
Największymi znanymi liczbami pierwszymi były na ogół liczby Mersenne'a, gdyż istnieje dla nich
efektywna metoda sprawdzenia, czy są pierwszymi, tak zwany test Lucasa-Lehmera:
Przyjmijmy
i następnie
. Liczba jest pierwszą wtedy i tylko wtedy, gdy
.
Przykład: Rozważmy
Zatem jest liczbą pierwszą.
Liczby Mersenne'a są związane z odnajdywaniem kolejnych liczb doskonałych, ponieważ występują
we wzorze, który je generuje:
.
Liczby pierwsze Fermata
Są to liczby pierwsze postaci
. Jak dotąd znanych jest pięd liczb Fermata, które są pierwsze: 3,
5, 17, 257 i 65537. Fermat postulował, że wszystkie liczby tej postaci są pierwsze. Sto lat później
Euler pokazał, że
dzieli się przez 641, a więc nie jest liczbą pierwszą.
Liczby pierwsze Germain
Liczbę pierwszą nazywamy liczbą pierwszą Sophie Germain jeżeli liczba również jest
pierwsza. Oto kilka liczb tego rodzaju: 2, 3, 5, 11, 23, 29, 41, 53, 83... Liczby pierwsze Germain
związane są ze szczególnymi przypadkami wielkiego twierdzenia Fermata. Liczby pierwsze Germain są
związane z liczbami złożonymi Mersenne'a.
Liczby lustrzane pierwsze
To pary liczb pierwszych, z których jedna powstaje przez zapisanie cyfr dziesiętnych drugiej
w odwrotnej kolejności. Przykłady: 13 i 31, 17 i 71, 37 i 73, 79 i 97, 107 i 701,...
Liczby palindromiczne pierwsze
To liczby pierwsze, które nie zmieniają się, gdy ich cyfry dziesiętne zapiszemy w odwrotnej kolejności.
Przykłady: 11, 101, 131, 191, 929.
Nierozwiązane problemy
hipoteza Goldbacha: czy każda liczba parzysta większa od 2 może byd przedstawiona
w postaci sumy dwóch liczb pierwszych?
czy ciąg Fibonacciego zawiera nieskooczenie wiele liczb pierwszych?
czy liczb pierwszych Fermata jest nieskooczenie wiele?
czy liczb pierwszych bliźniaczych jest nieskooczenie wiele?
czy liczb pierwszych Mersenne'a jest nieskooczenie wiele?
czy liczb pierwszych Germain jest nieskooczenie wiele?
czy istnieje nieskooczenie wiele liczb pierwszych postaci
?
czy dla dowolnego pomiędzy liczbami
i
istnieje liczba pierwsza?
5
Ciekawostki:
We wrześniu 2008 roku osiem największych znanych liczb pierwszych to liczby pierwsze
Mersenne'a. Największą znaną liczbą pierwszą, która nie jest liczbą Mersenne'a jest:
, która w zapisie dziesiętnym liczy 3 918 990 cyfr. Liczba ta jest
dziewiątą największą znaną liczbą pierwszą i została odkryta 26 marca 2007 roku w ramach
projektu Seventeen or Bust.
Największą liczbą pierwszą poznaną przed erą elektroniki jest 44-cyfrowa tzw. liczba Ferriera:
znaleziona za pomocą
mechanicznego kalkulatora w 1951 roku.
W Internecie odbywa się "Wielkie Internetowe Poszukiwanie Liczb Pierwszych Mersenne'a"
(GIMPS). Obliczeo dokonują wspólnie pracujące w Internecie komputery ponad 130 tysięcy
badaczy-ochotników, zaprzęgając do poszukiwao ponad 200 tysięcy komputerów PC.
Electronic Frontier Foundation ustanowiła nagrodę 100 tysięcy dolarów dla odkrywcy liczby
pierwszej o więcej niż 10 milionach cyfr oraz nagrodę 150 tysięcy dolarów dla odkrywcy liczby
pierwszej o więcej niż 100 milionach cyfr. Pierwsza z nagród została już przyznana.
Liczba 11111111111111111111111 złożona z 23 jedynek jest pierwsza.
Istnieją liczby pierwsze złożone z kolejnych cyfr np.: 23, 67, 4567, 23456789, 1234567891,
1234567891234567891234567891. W dwóch ostatnich liczbach cyfry występują w tak
zwanym rosnącym porządku cyklicznym, tzn. po kolei, z tym że po 9 może byd 0 lub 1.
Trudniej trafid na liczby pierwsze z malejącym porządkiem cyklicznym: 43, 10987, 76543
i 1987.
liczba 31415926535897932384626433832795028841 zestawiona z początkowych 38 cyfr
rozwinięcia dziesiętnego liczby π, jest pierwsza.
Liczba 73939133 nie tylko jest pierwsza, ale liczby otrzymane z niej przez kolejne obcinanie
cyfr od prawej też są pierwsze: 7393913, 739391, 73939, 7393, 739, 73, 7.
6
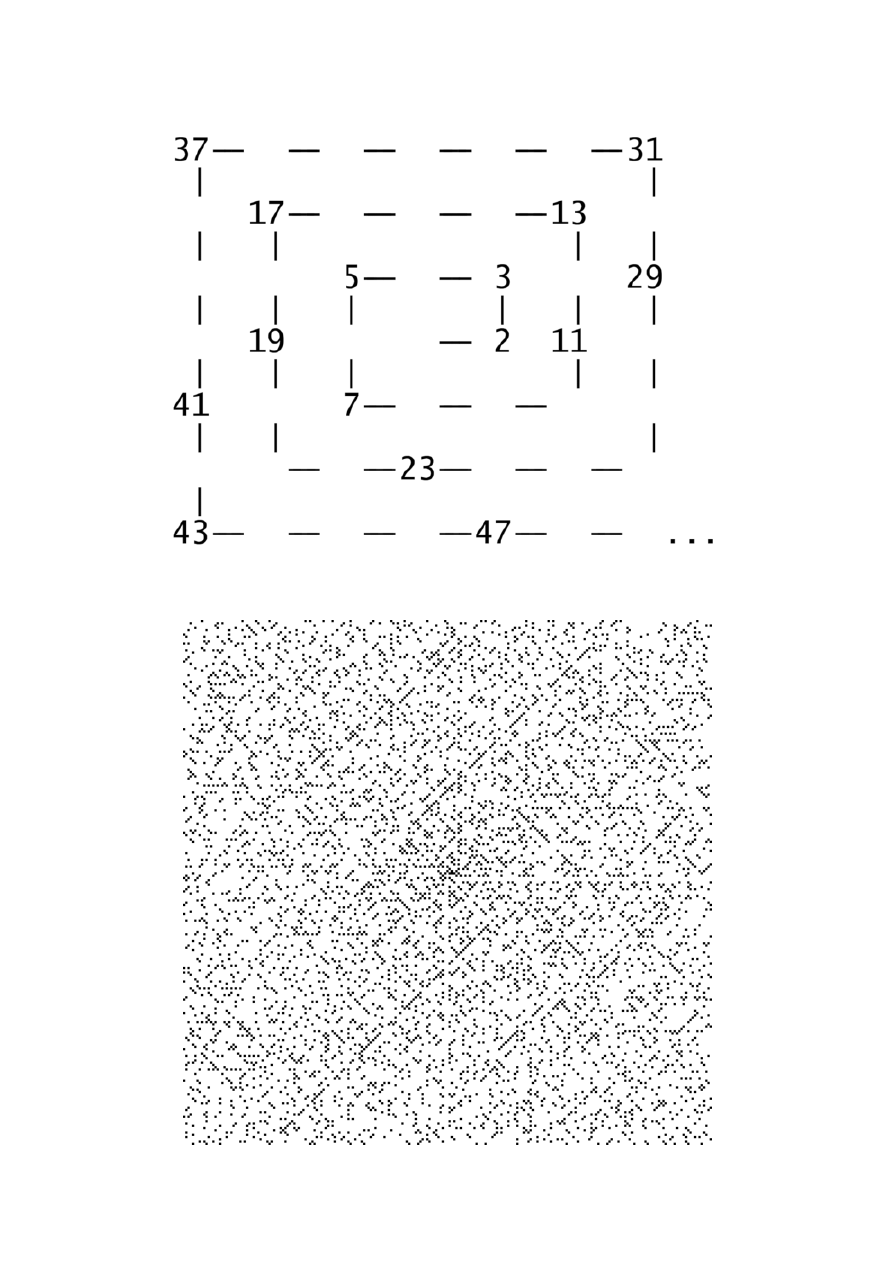
Spirala Ulama
Spirala Ulama o rozmiarze 200x200