Multimedia

Dr hab. inż. Ewa Świercz

Kompresja danych multimedialnych



Co to jest kompresja?



W jakim celu dokonujemy kompresji danych?



Z czym związana jest kompresja – co zyskujemy a co
tracimy?



Jakie mechanizmy są podstawą algorytmów kompresji
danych?



Jakie algorytmy są wykorzystywane do kompresji
obrazu, dźwięku i wideo? Jak działają? Jakie są ich
wady i zalety? Gdzie znajdują zastosowanie?

Kompresja danych multimedialnych



Co zyskujemy a co tracimy?



Zmniejszenie zajmowanej powierzchni na nośniku lub

oszczędność przepustowości łącza. Szczególnie ważne przy

materiale wideo, zajmującym najwięcej zasobów spośród

wszystkich składników systemu multimedialnego.



Konieczność dekompresji przed końcowym wykorzystaniem, a

więc niezbędne jest poświęcenie czasu i części mocy
obliczeniowych maszyny

– co może stanowić problem,

zwłaszcza, jeżeli potrzebne jest odtwarzanie „w locie”.



Kompresja stratna i bezstratna. Czy możemy sobie

pozwolić na utratę części informacji? Jak bardzo będzie

to zauważalne? Jak wpłynie na przydatność

skompresowanego zbioru do naszych celów?

Dlaczego kompresja jest tak istotna?



Nieskompresowany obraz kolorowy w trybie „true color” – 24 bity na
piksel:



Nieskompresowana sekwencja wideo, 25 klatek/s, w jakości

telewizyjnej (PAL 704x576, po 12 bitów/piksel):



121 651 kbit/s (121,6 Mbit/s)



Dwugodzinny film PAL, 25 klatek/s, 12 bitów/piksel:



Blisko 120 GB!

wymiary

352x288 CIF

Common

Intermediate

Format

704x576 PAL

Phase

Alternating Line

1600x1200

BMP

Format plików
z grafiką
bitmapową

rozmiar

297 kB

1,16 MB

5,5 MB

Przykład obrazu w formacie BMP , wymiar 549X601, 967.29 kB

Dlaczego można cokolwiek skompresować?



Redundancja (nadmiarowość)



Informacje w danych powtarzają się, jest ich więcej, niż to absolutnie
konieczne

– np. w dowodzie osobistym jest zarówno PESEL jak i data

urodzenia, chociaż PESEL ją zawiera, w formularzach często należy

wpisać adres zameldowania i zamieszkania, chociaż mogą być takie

same, itd…



Różne sposoby reprezentacji



np.reprezentacja grafiki: rastrowa i wektorowa. Często można coś

krócej opisać za pomocą wzoru lub metody postępowania, niż

dosłownej listy. „Kwadrat o boku 500 i górnym-lewym wierzchołku w

punkcie (0,0) ” jest krótszym zapisem niż lista współrzędnych

wszystkich pikseli składających się na ten kwadrat.



Ograniczenia percepcji



wzrokowej

– nie jesteśmy w stanie dostrzec niektórych szczegółów,

więc nie zauważymy różnicy, jeżeli zostaną wycięte z obrazu.



słuchowej – nie jesteśmy w stanie usłyszeć niektórych częstotliwości

występujących w sygnale dźwiękowym, więc nie zauważymy, jeżeli

zostaną wycięte.

Czy każde dane można skompresować

?



Nie zawsze!!

Możliwe, że używając danej metody kompresji

dla specyficznego tekstu nie osiągniemy
żadnego zysku!

Kompresja danych multimedialnych

Podstaw teoretyczne



Podstawowe definicje:



Kompresja

– proces zmiany sposobu zapisu

informacji, mający na celu zmniejszenie zajmowanej

przez nie przestrzeni w nośniku (nośnik fizyczny,

kanał transmisyjny, itd…)



Koder

– implementacja algorytmu kodowania i

kompresji.



Dekoder

– implementacja algorytmu dekodowania i

dekompresji.



Kodek

– koder + dekoder, w kontekście multimediów

rozumiane jako kompletna implementacja kompresji i

dekompresji danych określonego formatu

.

Kompresja danych multimedialnych

Podstaw teoretyczne c.d.



Podstawowe definicje:



Symbol

– w kontekście kodowania: unikalny,

niepodzielny i jednoznacznie odróżnialny składnik
strumienia danych, niosący informację. Przykłady:
litera w tekście, bit w pliku binarnym.



Alfabet

– zbiór wszystkich symboli, z których może

być złożona wiadomość.



Kodowanie

– przyporządkowanie każdemu

symbolowi z alfabetu A unikalnego ciągu symboli z
alfabetu B.

Kompresja danych multimedialnych

Miary jakości algorytmu kompresji



Współczynnik kompresji:



Jest to stosunek liczby bitów po kompresji do liczby bitów przed

kompresją.



Bitrate



Średnia liczba bitów na symbol w skompresowanej wiadomości.



Czas kompresji i dekompresji



Średni czas wykonania operacji dla określonej porcji danych

(np. 1kB)



Zapotrzebowanie na dodatkowe zasoby-

np. dodatkową

pamięć na buforowanie danych.



Subiektywna ocena odbiorcy

– nie zawsze parametry

liczbowe algorytmu dobrze opisują postrzeganą jakość

zbioru wynikowego! Można wskazać obraz subiektywnie

„lepszy”, „wyraźniejszy” , „ostrzejszy”.

Kompresja bezstratna



Kompresja bezstratna wykorzystuje redundancję
(nadmiarowość) danych w strumieniu i pozwala
ograniczyć ich rozmiar bez jakiejkolwiek straty informacji.
Skompresowany zbiór danych po dekompresji jest w
100% zgodny z oryginałem- identyczność bitowa!



Algorytmy kompresji mogą być zatem wykorzystane do
dowolnego typu danych, także np. plików
wykonywalnych czy danych pomiarowych.



Kompresja bezstratna jest całkowicie odwracalna!

Kompresja bezstratna



Wydajność algorytmów kompresji bezstratnej zależy od
stopnia redundancji strumienia wejściowego – od ilości
nadmiarowych informacji w nim zawartych.



Strumień o wysokim stopniu redundancji danych:



AAAA

BBB

CCCCC

DD

AAAA

BBBBBBB



Strumień o niskim stopniu redundancji danych:



A

BB

C

D

A

B

C

B

C

A

DD

B

A

C

A

B

D

A

C

Kompresja bezstratna



Przykłady zbiorów danych o wysokim stopniu
redundancji:



Tekst w języku naturalnym



Zdjęcia



Sekwencje wideo, film



Mowa, muzyka

Takie zbiory dadzą się zwykle silnie skompresować!

Kompresja bezstratna



Przykłady zbiorów danych o niskiej redundancji:



Ciągi liczb pseudolosowych



Szum



Dane skompresowane innym algorytmem

bezstratnym

Takie zbiory nie dadzą się silnie skompresować!

Kompresja bezstratna



Klasy algorytmów kompresji bezstratnej:



Algorytmy proste

– nie dokonują analizy strumienia

wejściowego przed kompresją, wykorzystują podobieństwo

sąsiedztwa.



Algorytmy statystyczne

– przed kompresją cały strumień jest

buforowany i analizowany pod kątem częstości występowania

poszczególnych elementów, na podstawie wyników dobierana
jest odpowiednia strategia kompresji



Algorytmy słownikowe

– kompresja oparta jest na stworzeniu

słownika podciągów w strumieniu danych i zastąpieniu ich

krótszymi „numerami” swojej pozycji w słowniku.

Algorytmy proste



Najmniej wydajne, ale szybkie i łatwe w
implementacji, mają bardzo małe wymagania
pamięciowe – nie potrzebują bufora.



Przykłady algorytmów należących do grupy
algorytmów prostych:



ByteRun



RLE (Run Length Encoding)

Algorytm ByteRun



Operuje na pojedynczych bajtach (symbol ma reprezentację bajtową),

opiera się na eliminacji redundancji lokalnej. Zasada działania:



Grupa bajtów ze strumienia wejściowego może zostać

zakodowana na jeden z dwóch sposobów:



Sposób pierwszy: oznaczamy

n

następnych bajtów, które mają

zostać skopiowane bez zmian i umieszczamy tę liczbę wraz z

bajtami, których dotyczy w strumieniu wyjściowym, czyli:

A

B

C

D => 4

A

B

C

D

n musi się zawierać w przedziale <1, 127>



Sposób drugi: jeżeli znajdziemy powtarzające się, sąsiednie

symbole, zastępujemy je symbolem
K [ -n+1, A

x

], gdzie: n -

liczba powtórzeń, A

x

- powtarzany symbol,

czyli:

AAAA

=> -3

A

, ponieważ: - (-3) +1 = 4*

A

=

AAAA

n musi się zawierać w przedziale <1, 127>

Algorytm ByteRun



Przykład:



Strumień oryginalny

:



AAAA

BBB

C

D

A

BBBBBB

– 16 bajtów



Strumień skompresowany

:



-3

A

-2

B

3

C

D

A

-5

B

– 10 bajtów



Dekodowanie jest bardzo proste, sprawdzamy znak pierwszego

bajtu, rozpoznajemy rodzaj sekwencji, a później albo powielamy

albo kopiujemy określoną liczbę bajtów.



Wady:

w najbardziej pesymistycznym przypadku

– brak grup

powtarzających się symboli skompresowany strumień będzie

dłuższy niż strumień oryginalny!

Algorytm Run Length Encoding



Podobny do algorytmu ByteRun, ale zawiera
dodatkowe sekwencje sterujące.



Kopiowanie oznaczane jest symbolem [0, n, A

1

, A

2

, …, A

n

], gdzie

n -

liczba kolejnych bajtów do skopiowania bez zmian.



Przykład:



A

B

C

D

=> 04

A

B

C

D



Powielanie oznaczane jest symbolem [n, A] , gdzie n

– liczba

powtórzeń, A – powtarzany symbol



AAAA

=> 4

A

n może zawierać się w przedziale <1, 255> , zysk przy długich

sekwencjach w porównaniu do ByteRun

Algorytmy proste

– podsumowanie



Szybkie w działaniu, nie zajmujące zasobów,
umiarkowanie wydajne.



Wykorzystywane między innymi w formatach grafiki
PCX, wariantach formatu GIFF, Truevision TGA (format
grafiki rastrowej), PackBits, czy ILBM.



Mogą w niekorzystnych warunkach generować
strumienie dłuższe niż oryginalny.

Algorytmy statystyczne



Dokonują analizy strumienia wejściowego pod kątem
częstości występowania poszczególnych symboli i
przyporządkowują najczęściej występującym najkrótsze
słowa kodowe.



Jest to grupa algorytmów o zmiennej długości słowa
kodowego.



Zysk w kodowaniu statystycznym polega na tym, że
symbole występujące częściej niż średnia otrzymują
słowa kodowe krótsze niż średnia długość słowa
kodowego dla symbolu. Część symboli otrzymuje co
prawda słowa kodowe dłuższe niż średnia, ale ponieważ
występują rzadziej – całość strumienia jest krótsza!

Kodowanie Huffmana najczęściej wykorzystywany

statystyczny algorytm kompresji bezstratnej



Opracowany przez Davida Huffmana w Massachusetts
Institute of Technology, ogłoszony w 1952 roku, prosty,
efektywny jest jednym z najbardziej
rozpowszechnionych algorytmów kompresji bezstratnej.



Podstawą jego działania jest analiza statystyczna danej
wiadomości pod kątem częstotliwości występowania w
niej poszczególnych symboli. Każda wiadomość musi
być indywidualnie analizowana!



Stosowany także jako jeden z etapów wielu algorytmów
kompresji stratnej

– np. JPEG czy MP3.

Kodowanie Huffmana



Zasada działania:



Etap 1:



Analiza częstości występowania symboli (liter) w wiadomości

(tekście) i uszeregowanie ich od najrzadziej do najczęściej

występujących,



HELLO WORLD



L

– 3 wystąpienia



O

– 2 wystąpienia



H

– 1 wystąpienie



E

– 1 wystąpienie



W

– 1 wystąpienie



R

– 1 wystąpienie



D -

1 wystąpienie

Kolejność: L, O, H, E, W, R, D



Każdy tekst ma swój charakterystyczny rozkład częstości występowania znaków,
dlatego przy kodowaniu algorytmem Huffmana konieczna jest indywidualna

analiza każdej wiadomości!

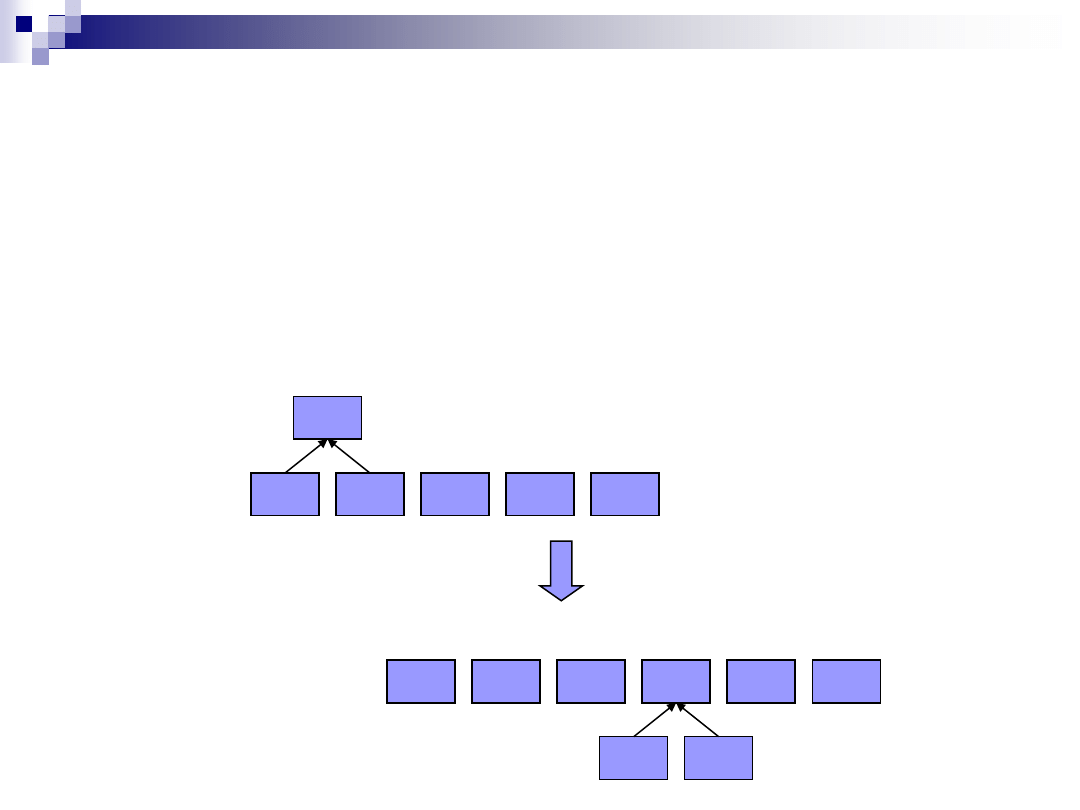
Kodowanie Huffmana



Etap 2:



Budowa drzewa binarnego, w którym liśćmi będą litery pojawiające

się w tekście. Każdemu węzłowi przyporządkowywana jest waga – na

początku węzłami są występujące w tekście litery a ich wagami-

częstość ich wystąpienia. Drzewo budowane jest przez łączenie

dwóch węzłów o najmniejszych wagach w jeden węzeł- rodzic, i

przypisanie mu wagi będącej sumą jego potomków

.

R(1)

E(1)

W(1)

H(1)

O(2)

L(3)

(2)

D(1)

R(1)

(2)

D(1)

E(1)

W(1)

H(1)

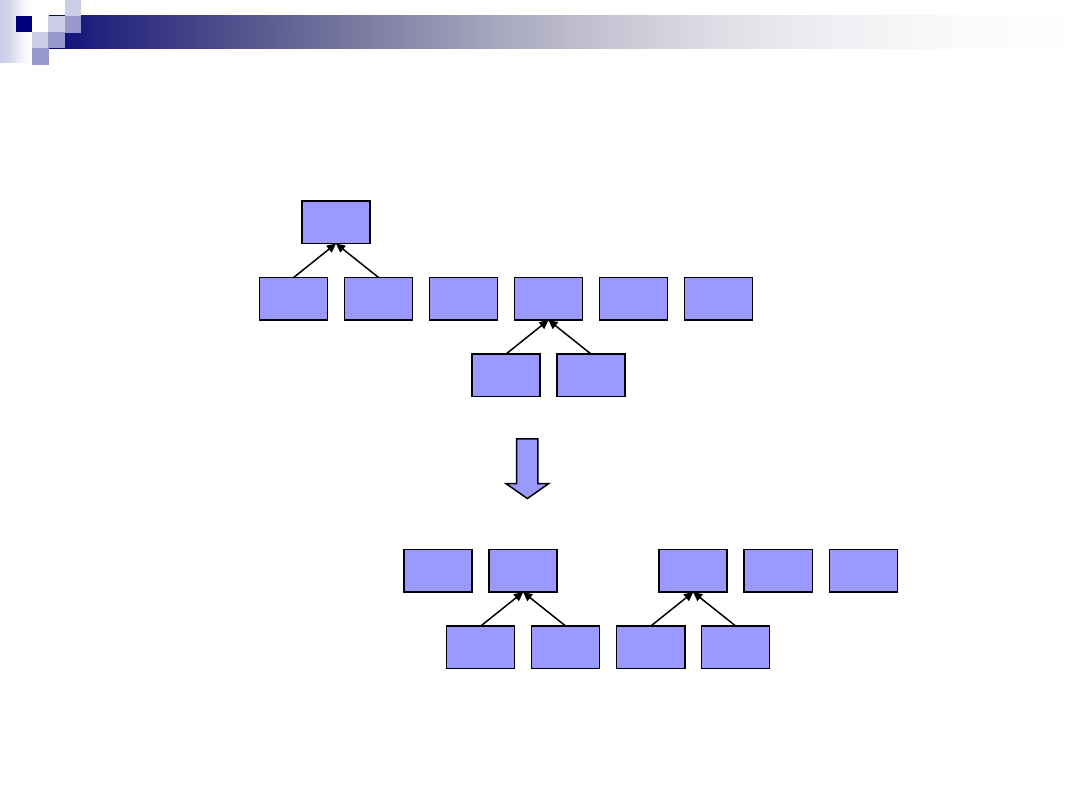
Kodowanie Huffmana

O(2)

L(3)

R(1)

(2)

D(1)

H(1)

W(1)

(2)

E(1)

W(1)

(2)

E(1)

O(2)

L(3)

R(1)

(2)

D(1)

H(1)

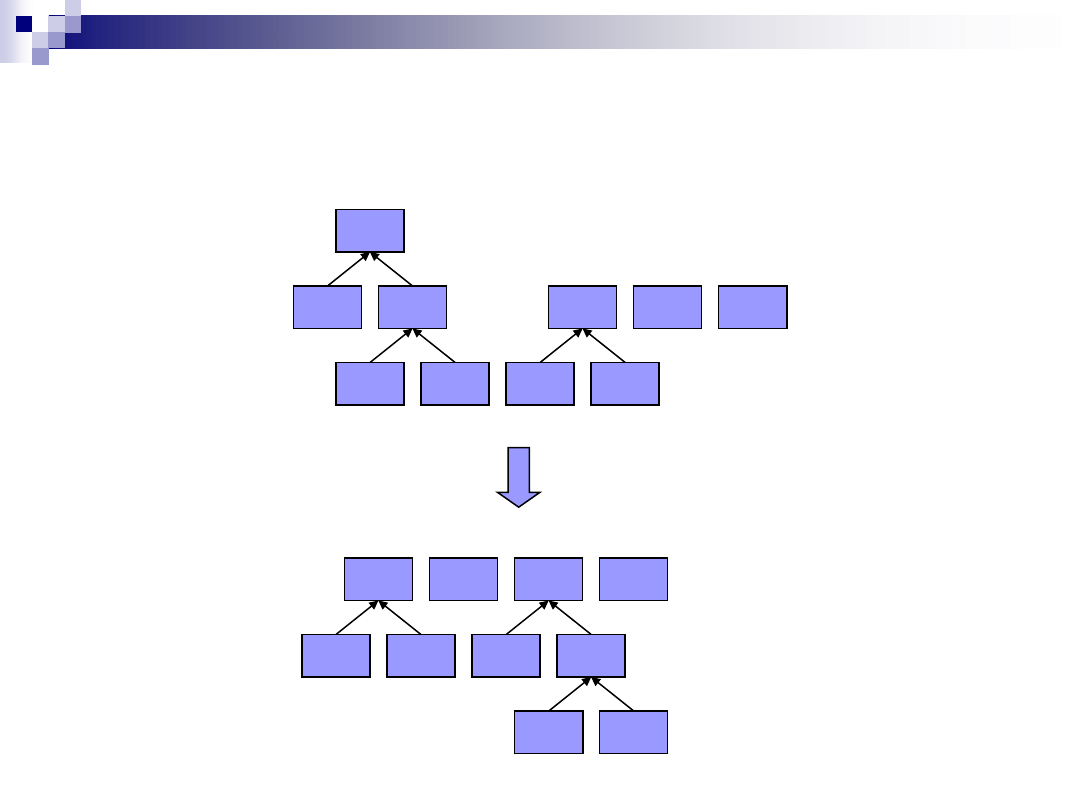
Kodowanie Huffmana

W(1)

(2)

E(1)

O(2)

L(3)

R(1)

(2)

D(1)

(3)

H(1)

W(1)

(2)

E(1)

(3)

H(1)

O(2)

L(3)

R(1)

(2)

D(1)

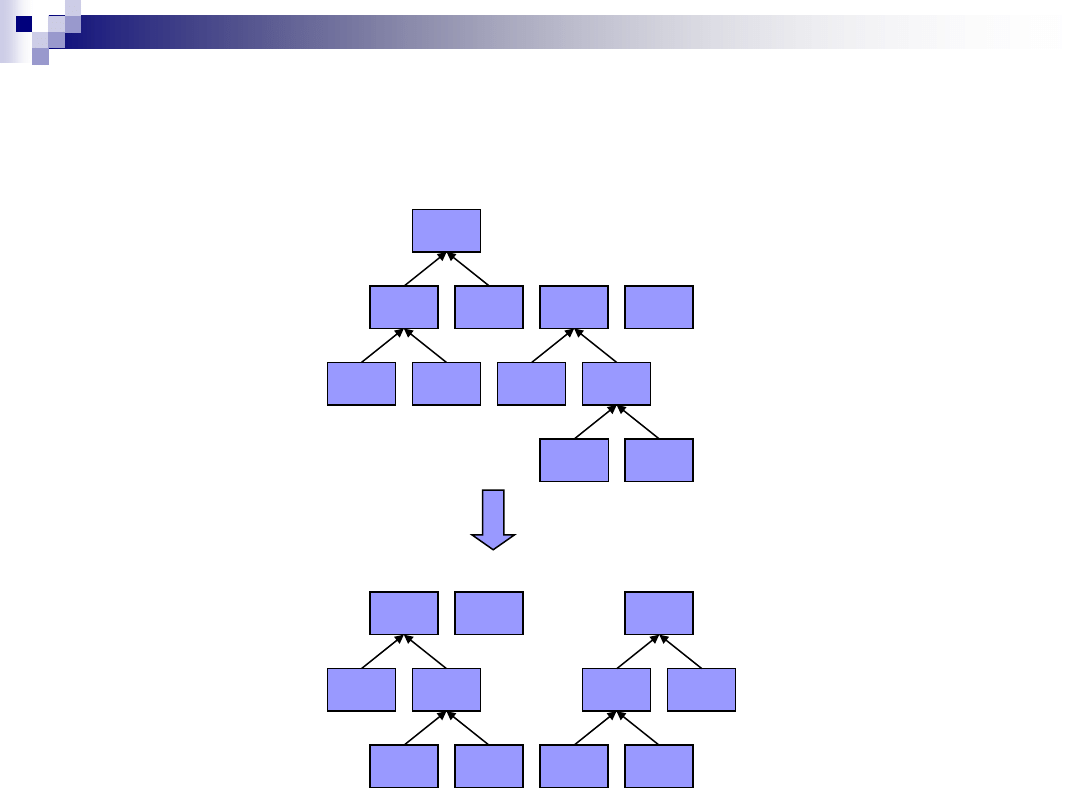
Kodowanie Huffmana

W(1)

(2)

E(1)

(3)

H(1)

O(2)

L(3)

R(1)

(2)

D(1)

(4)

O(2)

R(1)

(2)

D(1)

(4)

W(1)

(2)

E(1)

(3)

H(1)

L(3)

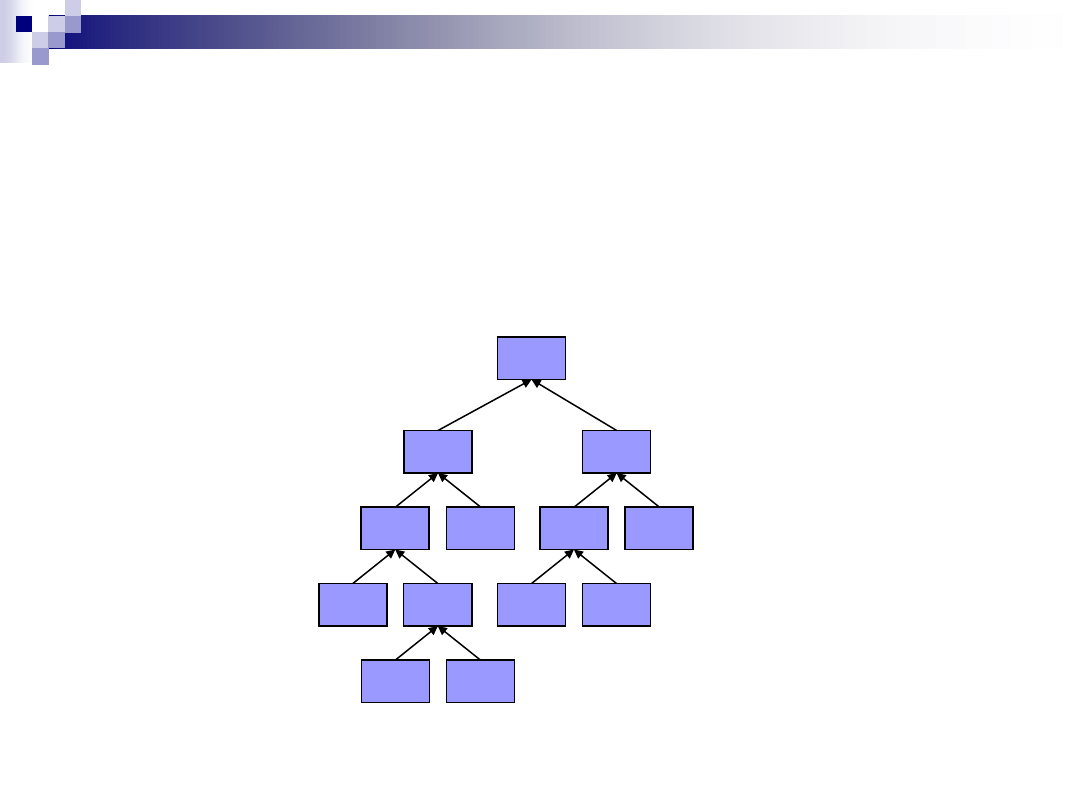
Kodowanie Huffmana



Zbudowane drzewo Huffmana dla „Hello World”

O(2)

R(1)

(2)

D(1)

(4)

W(1)

(2)

E(1)

(3)

H(1)

L(3)

(6)

(10)

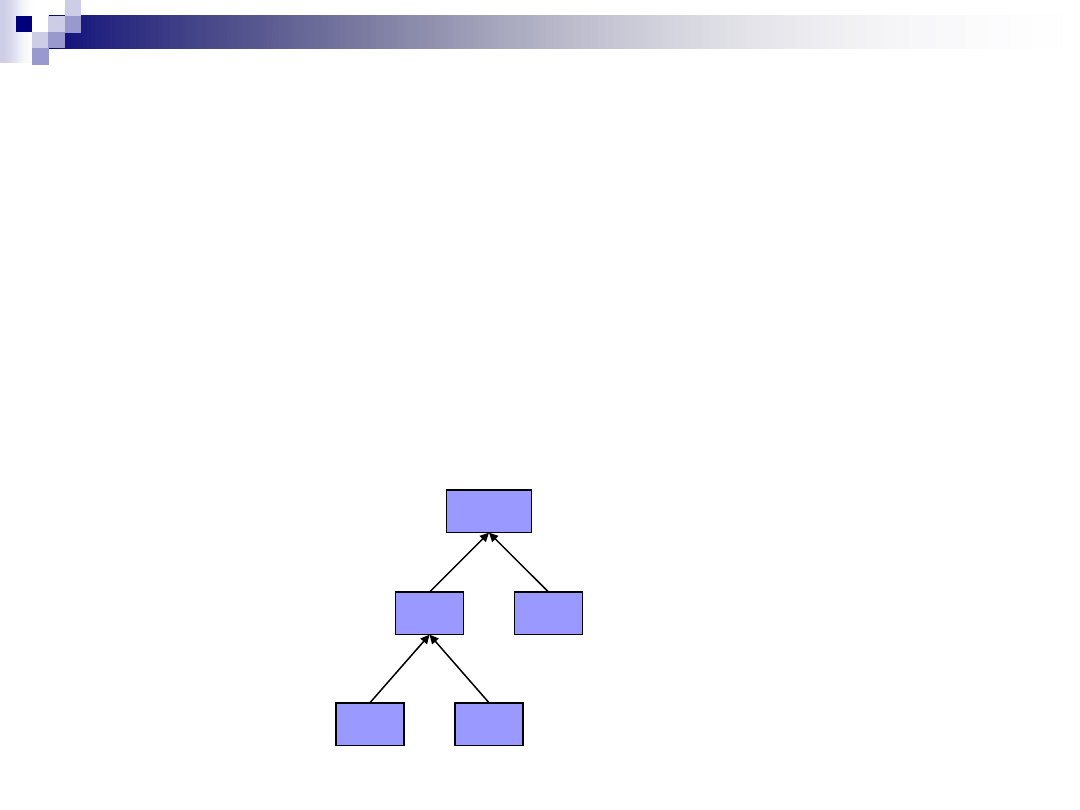
Kodowanie Huffmana



Etap 3:



Przypisanie gałęziom od rodzica do potomka cyfr 1 lub 0.



Gałąź lewa – 0, „idź w lewo”, gałąź prawa – 1, „idź w prawo”



Wtedy każda litera- liść może być jednoznacznie opisana
przez sekwencję zer i jedynek opisujących drogę od korzenia
do liścia.

A

B

(2)

(0)

C

0

1

0

1

Kod litery B: 01

Kod Huffmana - podsumowanie



Optymalny wśród kodów prefiksowych



Symbolom występującym najczęściej odpowiadają
najkrótsze słowa kodowe.



Kodowanie i dekodowanie w czasie liniowym

– więc

szybkie.



Konieczność przesłania informacji o drzewie znaków do
dekodera

– bez tego odczytanie jest niemożliwe.



Powszechnie stosowany jako samodzielny algorytm
kompresji bezstratnej, lub jako etap w bardziej
zaawansowanych metodach, stanowi element
standardów JPEG, MP3, gzip, arj.

Algorytmy słownikowe



Algorytmy słownikowe polegają na kolejnym czytaniu

danych wejściowych i przeglądaniu słownika w

poszukiwaniu dokładnie takiej samej sekwencji danych.

Słownik może być zadany lub budowany dynamicznie w

trakcie działania algorytmu.



Rodzina algorytmów o stałej długości słowa kodowego –

którym jest po prostu indeks pozycji danej grupy symboli

wejściowych w słowniku.



Efektywność algorytmów słownikowych dla danej

wiadomości zależy od częstości występowania w niej

takich samych grup symboli. Im dłuższa sekwencja w

słowniku, tym efektywniejsza kompresja.

Algorytmy słownikowe



Algorytm LZ77, opracowany przez pp. Jacoba Ziva i
Abrahama Lempela w 1977 roku. Podobnie jak
kodowanie Huffmana, jest wykorzystywany w szeregu

popularnych standardów kompresji, np. RAR, czy
formacie graficznym PNG.



W tej metodzie słownik budowany jest na bieżąco,

spośród pewnej liczby ostatnio przeanalizowanych

bajtów strumienia. Jeżeli jakaś grupa wystąpiła w
ostatnich n bajtach strumienia-

mamy ją w słowniku.



Słownik nie jest w tej metodzie stały!

Algorytm LZ77



Zasada działania:



Kompresor, czytając kolejne dane ze strumienia
sprawdza, czy nie natrafił ostatnio na podobny ciąg, a
jeżeli tak, to zamiast całego ciągu zapisuje tylko
długość powtórzonego ciągu i przesunięcie do tyłu.



Hej, 20 bajtów wcześniej widziałem taki sam ciąg o
długości 4 bajtów !



W praktycznych implementacjach śledzone „okno
słownikowe” jest dosyć duże – kilka, kilkanaście kB.

Algorytm LZ77



LZ77 - kodowanie



Przesuwanie okna wzdłuż czytanego strumienia danych

wejściowych.



Szukanie najdłuższego łańcucha danych w buforze „patrz w

przód”, który ma swój dokładny odpowiednik w słowniku.



Tworzenie sekwencji kodowej tego łańcucha (start, ile, następny
znak).



Przesuwanie okna o długość zakodowanej frazy.



Powtarzanie kroków 2, 3 i 4 aż do zakodowania ostatniego

symbolu z danych wejściowych.



Format słowa kodowego: [(o ile wstecz, jak długi ciąg)

następny znak]

Algorytm LZ77



Przykład:



Okno=(8-

słownik

,4-

Bufor „patrz w przód”

)



Wiadomość: ABRAKADABRA_CZARY_MARY



Tekst w oknie:

ABRAKADA

BRA_

CZARY_MARY



Zatem po zakodowaniu:

(0,0)A

(0,0)B

(0,0)R

(3,1)K

(2,1)D

(7,4)_

(0,0)C

(0,0)Z

(4,1)R

(0,0)Y

(6,1)M

(5,3)EOF

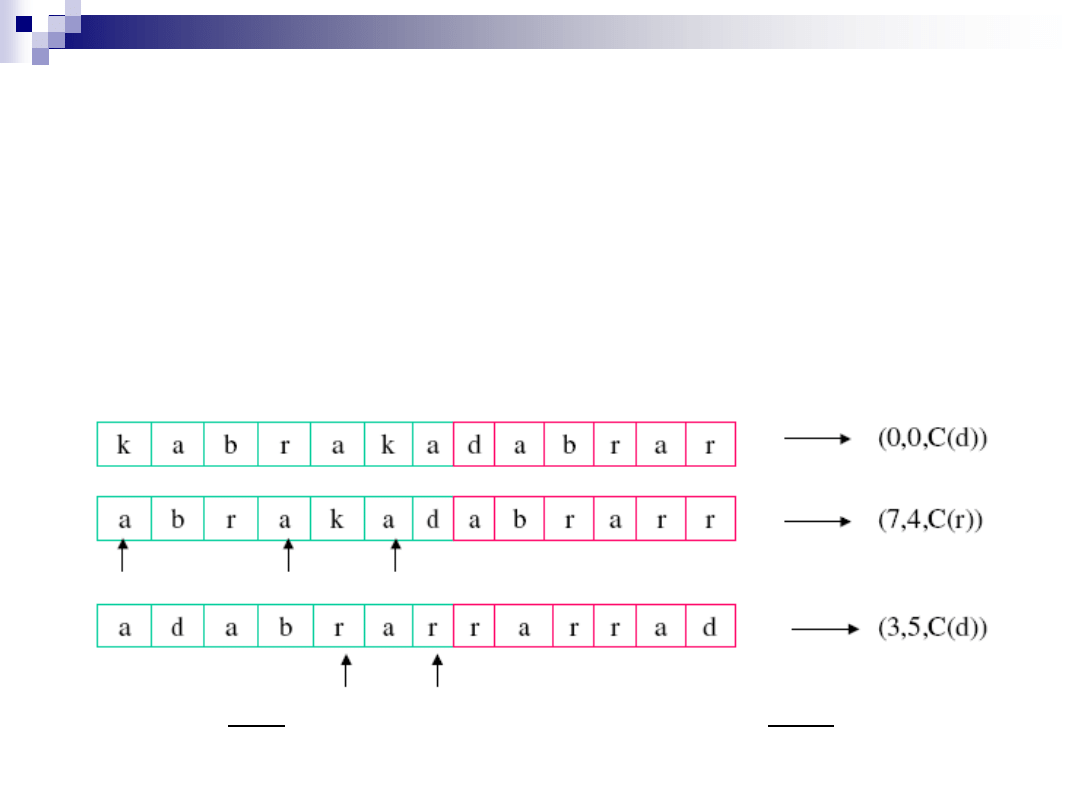
Inny przykład



Kodujemy ciąg zakładając długość słownika równą - 7.
długość bufora kodowania równą - 6



k a b r a k a d a b r a r r a r r a d



Zakładamy, że podciąg

k a b r a k a

jest już zakodowany

Dopasowanie musi

zaczynać się w buforze słownikowym a może kończyć się w

buforze kodowania

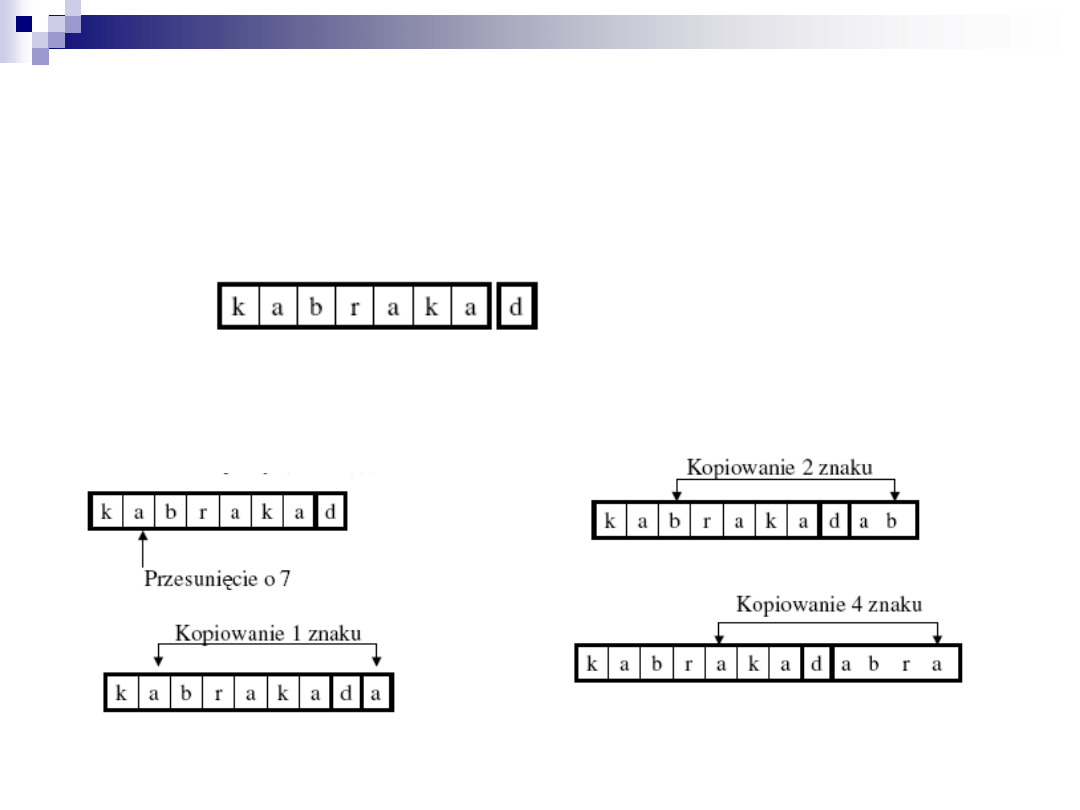
Dekodowanie algorytmu LZ77



Startujemy z odkodowanego podącigu

k a b r a k a



Odkodowujemy (0,0,C(d))

– czyli C(d)



Odkodowujemy (7,4,C(r)) tzn. przesuwamy o 7 i kopiujemy 4 kolejne
znaki słownika

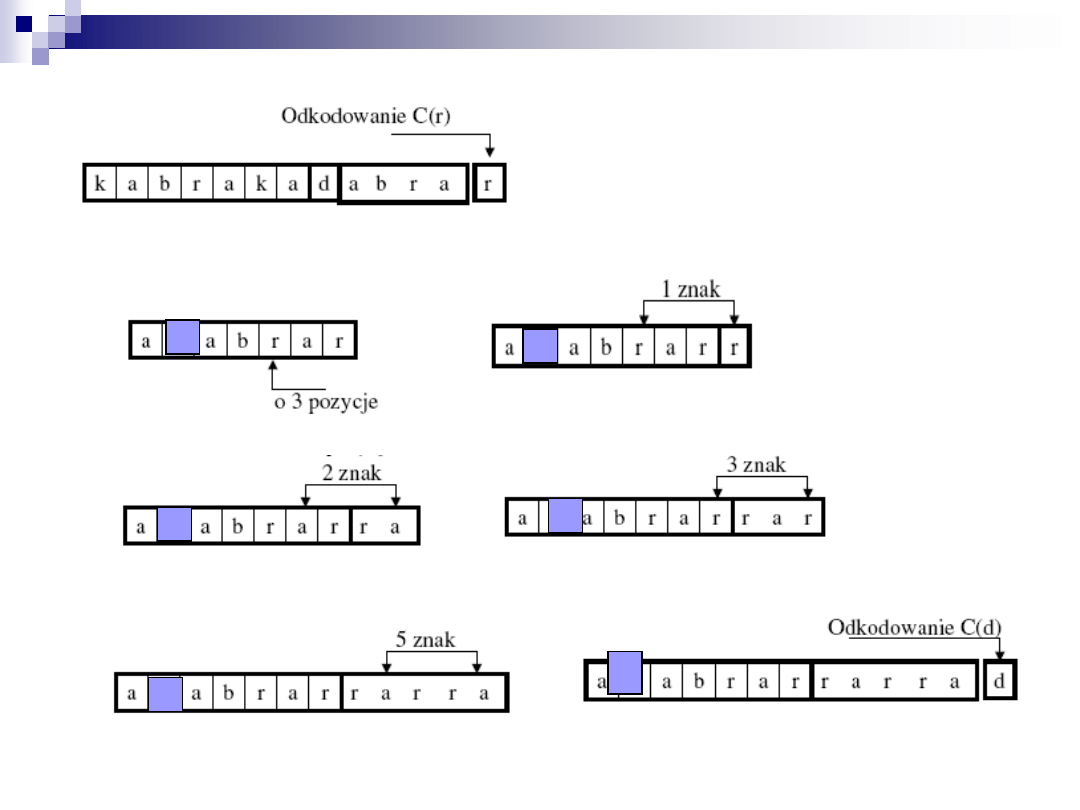
Odkodowanie trójki liczb (3,5,C(d))

d

d

d

d

d

d

Algorytm LZ77



LZ77 -

efektywność



Zależy silnie od długości fraz w słowniku – im
dłuższe, tym lepsze.



Skuteczna do kompresji tekstu języka naturalnego,
fotografii (ze względu na często występujące,
jednolite kolorystycznie regiony)



Szybki obliczeniowo