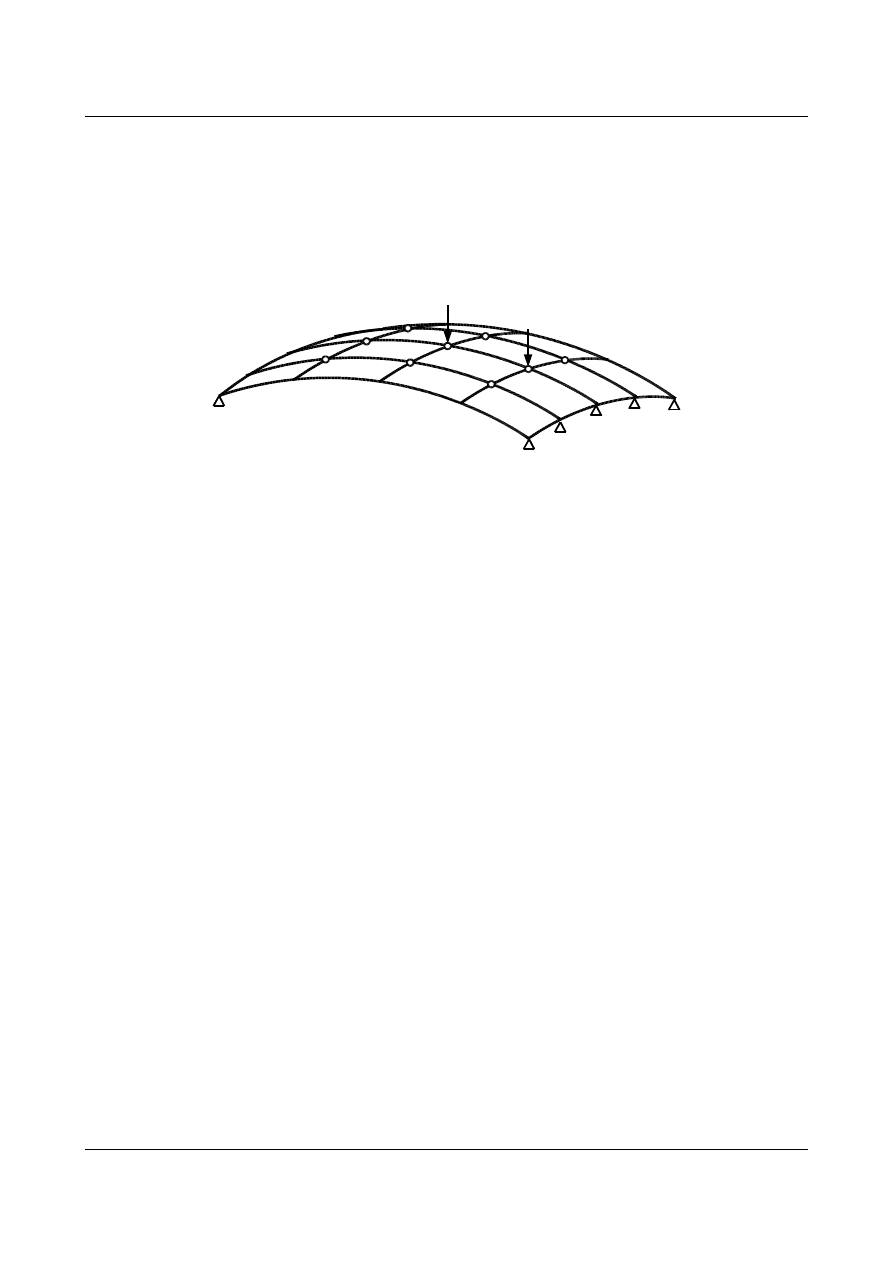
7. ELEMENTY PŁYTOWE

1

7.



7. ELEMENTY PŁYTOWE

Rys. 7.1. Element płytowy

Aby rozwiązać zadanie płytowe należy:

•

zdefiniować geometrię płyty,

•

dokonać podziału płyty na elementy,

•

zdefiniować węzły,

•

wprowadzić obciążenie,

•

ustalić więzy (warunki brzegowe),

•

wprowadzić odpowiednie funkcje kształtu

{u}=[ N ]⋅{d }

(7.1)

gdzie [N] oznacza przyjmowane funkcje kształtu,

•

zdefinować odkształcenia i naprężenia:

{}=[ B]{d }

{}=[ D]{B}{d }

(7.2)

•

zdefiniować macierz sztywności:

[ K

e

]=

∫

V

B

T

D B dv

(7.3)

(jest to macierz osobliwa),

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

7. ELEMENTY PŁYTOWE

2

•

dokonać transformacji macierzy sztywności (z układów lokalnych do układu globalnego)

[ K

e

G

]

[

K

e

]

(7.4)

•

zagragować macierz sztywności – zapewnia to nierozdzielność przemieszczeń węzłów:

A

 K

e

G



[

K

]

(7.5)

gdzie A oznacza operator,

•

postawić problem jako równanie:

[ K ]{D}={P}

(7.6)

[K] – macierz sztywności, będąca na tym etapie nadal osobliwą,

•

wprowadzić warunki brzegowe,

•

rozwiązać równanie:

{D}=[ K ]

−1

⋅{P}

(7.7)

w wyniku którego otrzymujemy szukane przemieszczenia,

•

przetransformować obliczone przemieszczenia do układów lokalnych,

•

odtworzyć interesujące nas stany odkształceń, naprężeń i przemieszczeń.

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

7. ELEMENTY PŁYTOWE

3

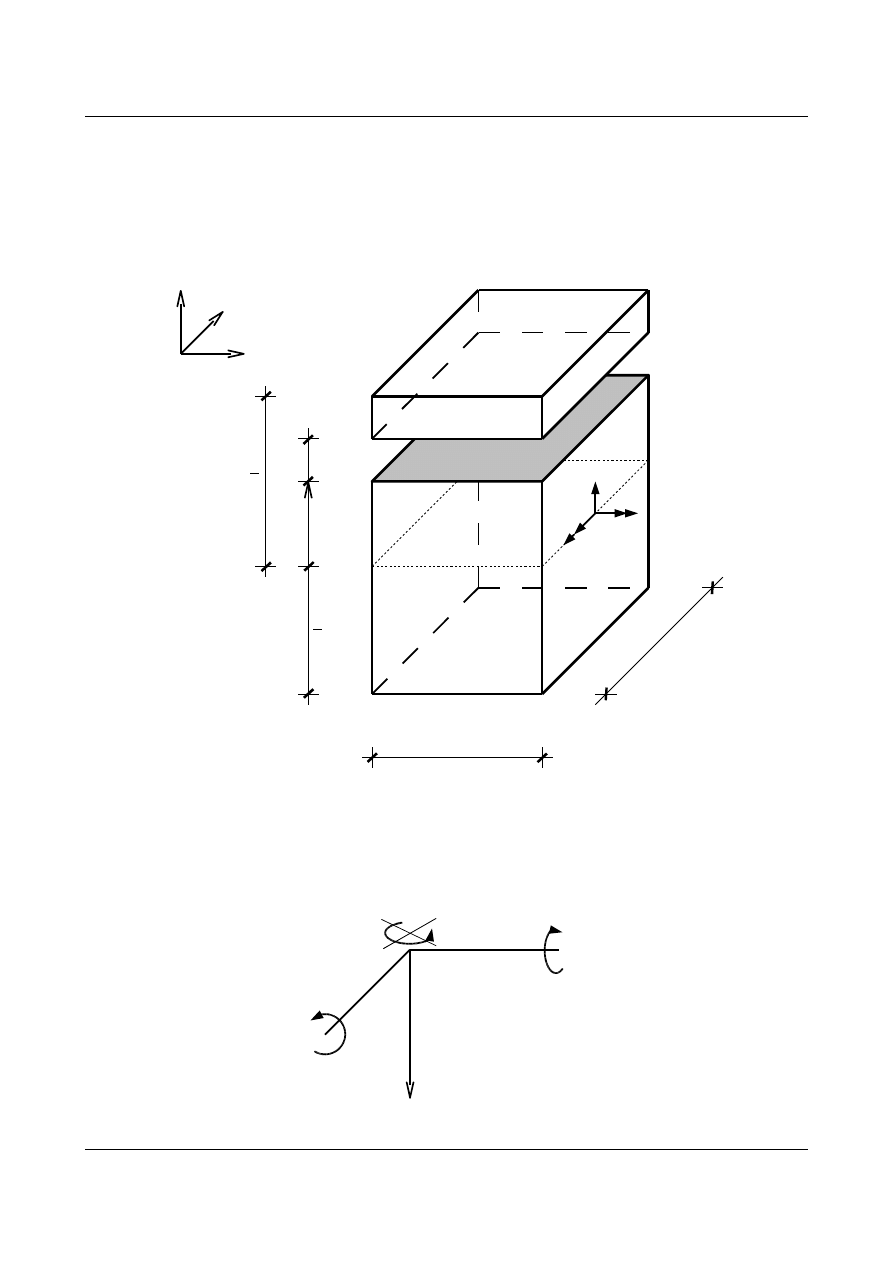
7.1. Płyty cienkie

Płyta cienka to obiekt dwuwymiarowy, w którym wymiary w kierunku osi x i y są wielokrotnie

większe niż jego grubość.

Rys. 7.1. Płyta cienka

Załóżmy, że ugięcia występują w jednym kierunku i mamy dwa kąty obrotu:

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

tego kąta obrotu nie

uwzględniamy

ugięcie (pionowo w dół)

po kierunku z

z

z,w

y,v

x,u

t

2

t

2

z

dz

dx

dy

Q

x

M

x

x

M

x

y

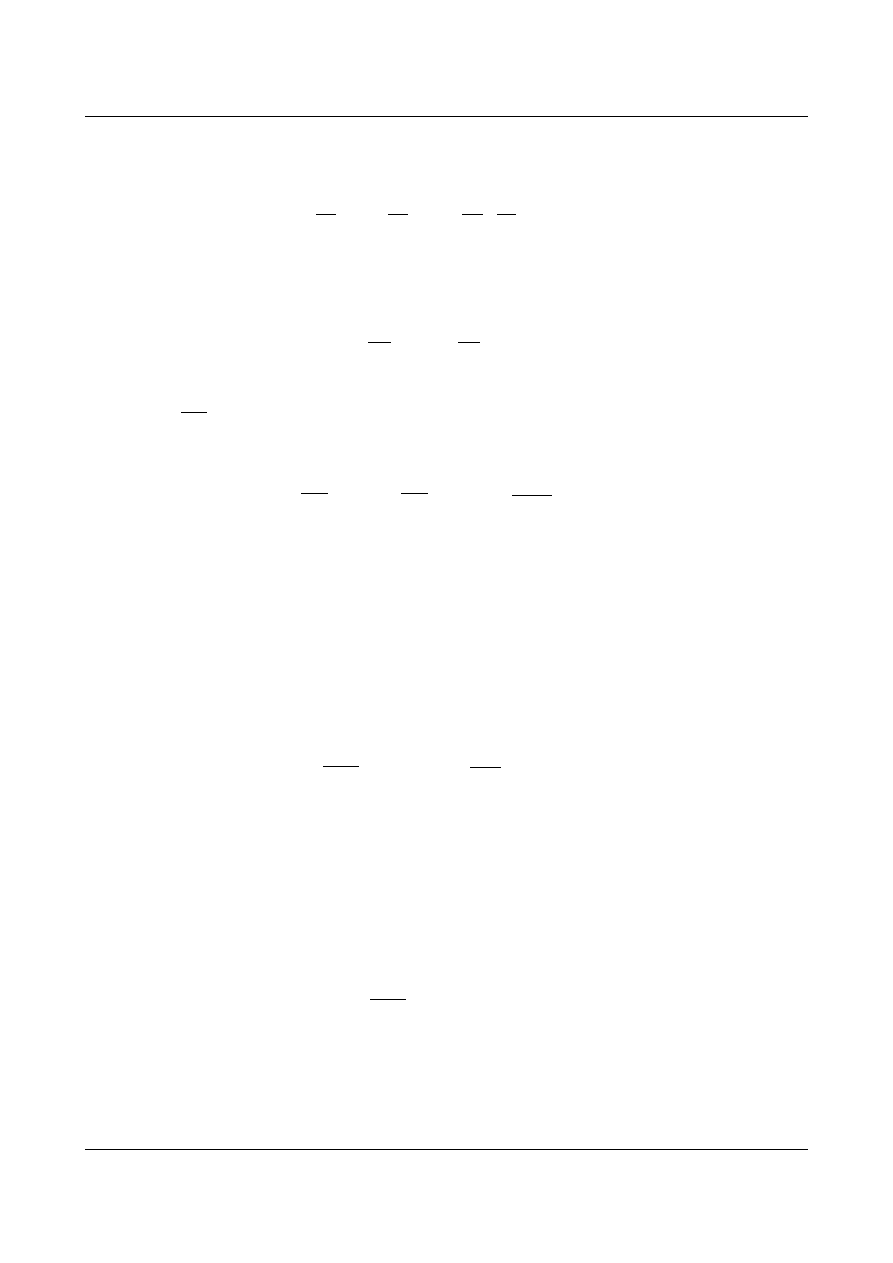
7. ELEMENTY PŁYTOWE

4

Odkształcenia w płaszczyźnie warstwy płyty opisane są wzorami:



x

= ∂

u

∂ x



y

= ∂

v

∂ y



x

= ∂

u

∂ y

 ∂

v

∂ x

(7.8)

Przemieszczenia dowolnego punktu:

u

=−z ∂

w

∂ x

v

=−z ∂

w

∂ y

(7.9)

gdzie ∂

w

∂ x

jest kątem obrotu. Po podstawieniu wzorów 7.9 do 7.8 otrzymujemy:



x

=−z ∂

2

w

∂ x

2



y

=−z ∂

2

w

∂ y

2



x

=−2 z ∂

2

w

∂ x ∂ y

(7.10)

Zależność między naprężeniami a odkształceniami dla warstwy płyty jest taka sama jak dla płaskiego

stanu naprężenia, mamy więc:

{}=[ D]{}

(7.11)

gdzie

D

=

E

1

−

2

[

1

 0

 1 0
0 1



]

,

=

1

−

2

(7.12)

Wektor naprężeń uogólnionych odpowiada wartościom momentów zginających:

[

M

]

=

[

M

xx

M

yy

M

xy

]

T

(7.13)

Jeśli



x

=

E

1

−

2



x



y



(7.14)

to uogólnione naprężenie M

xx

wynika z całkowania wyrażenia

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

7. ELEMENTY PŁYTOWE

5

M

xx

=−

∫

−

t

2

t

2



x

⋅z dz=

E

1

−

2

t

3

12

 ∂

2

w

∂ x

2

 ∂

2

w

∂ y

2



(7.15)

W podobny sposób uzyskujemy pozostałe składowe wektora uogólnionych naprężeń:

M

yy

=

E

1

−

2

t

3

12

 ∂

2

w

∂ y

2

 ∂

2

w

∂ x

2



(7.16)

M

xy

=

E t

3

12

1−

2



∂

2

w

∂ x ∂ y

(7.17)

Wektor uogólnionych odkształceń będzie postaci:

[



]

=

[



xx



yy



xy

]

T

=

[

W

, xx

W

, yy

2 W

, xy

]

T

(7.18)

Wówczas uogólniony operator D dla naprężeń i odkształceń wynosi:

D

=D

t

3

12

(7.19)

A zatem otrzymujemy relację:

[

M

]

=D

[



]

(7.20)

7.2. Rodzaje elementów płytowych

•

niedostosowany element prostokątny, zwany MZC (nie spełnia warunków ciągłości pochodnych na
brzegu elementu). Stopnie swobody są postaci:

[

d

i

]

=

[

w

i

∂ w

i

∂ y

−

∂ w

i

∂ x

]

T

(7.21)

Obciążenie węzłowe wynosi natomiast:

[

p

i

]

=

[

p

zi

M

xi

M

yi

]

T

, gdzie

i

=1, ... ,4

(7.22)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

7. ELEMENTY PŁYTOWE

6

Funkcja aproksymacyjna będzie postaci:

w

=c

1

c

2

c

3

c

4



2

c

5

c

6



2

c

7



3

c

8



2

c

9



2

c

10



3

c

11



3

c

12



3

(7.23)

Występujące 12 stałych to pełen zestaw z trójkąta Pascala (dla czterech pierwszych wierszy} wraz z

dodatkiem x

3

y oraz xy

3

. Macierz sztywności dla takiego elementu otrzymamy w następującej postaci:

[

K

e

]

=

E t

3

12

1−

2





[

K

1

]



[

K

2

]



[

K

3

]



[

K

4

]





macierz niezależna od przemieszczeńelementów

(7.24)

[K

e

] jest również macierzą niezależną od przemieszczeń elementów, co oznacza, że mamy zadanie

liniowe.

•

dostosowany element prostokątny, zwany BFS. Stopnie swobody są postaci:

[

d

i

]

=

[

[

d

i1

][

d

i2

][

d

i3

][

d

i4

]

]

T

=

[

w

i

∂ w

i

∂ y

−

∂ w

i

∂ x

∂

2

w

i

∂ x ∂ y

]

T

, gdzie

i

=1, ... , 4

(7.25)

Funkcję przemieszczeń opisuje równanie przedstawione poniżej:

przy czym dla czterech stopni swobody ograniczamy się do wyrazów rozwinięcia położonych

powyżej przekątnej.

Przykładowym elementem prostokątnym dostosowanym może być element czterowęzłowy (z węzłami

położonymi w narożnikach). Dla takiego przypadku odpowiednio dobieramy funkcje kształtu (tu z czterema
stopniami swobody). Jeśli stosujemy więcej punktów Gaussa, należy odpowiednio dobrać też funkcje
kształtu.

Z uwagi na długi czas potrzebny na całkowanie funkcji kształtu, korzystniej jest nam przyjąć większą

liczbę stopni swobody z odpowiadającymi prostymi funkcjami kształtu, niż mało punktów stopni swobody a
skomplikowane funkcje kształtu.

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater