Modelowanie efektów oświetlenia

1. Realizm obrazu, źródła światła, mechanizm transportu światła
2. Modele oświetlenia

- model światła otoczenia
- model empiryczny
- model Phonga
- Model Halla
- równanie renderingu

3. Metody modelowania oświetlenia
- śledzenie promieni (ray-tracing)
- metoda energetyczna bilansu promieniowania
4. Cieniowanie powierzchni
- stała intensywność oświetlenia
- metoda Gourauda
- metoda Phonga

Realizm obrazu – odwzorowanie w syntetycznym obrazie efektów
wizualnych obserwowanych w naturze.

Czynniki decydujące o realizmie obrazu:
1. Model geometryczny opisujący kształt i położenie w przestrzeni

wizualizowanych obiektów

2. Cechy powierzchni związane z jej kolorem oraz teksturą
3. Rozkład oświetlenia określony na podstawie definicji źródeł światła

oraz własności powierzchni związanych z rozproszeniem energii
ś

wietlnej (rozkład cieni i półcieni, odblask, przeźroczystość, załamanie

i odbicie światła)

Ź

ródła światła:

1. Punktowe pozycyjne (rozmiar znikomy w stosunku do wielkości

sceny) – promienie rozchodzą się równomiernie we wszystkich
kierunkach

2. Punktowe kierunkowe (źródło odpowiednio odległe) – promienie

dochodzą do oświetlanych powierzchni równoległe (kąt między
promieniem z tego żródła a wszystkimi powierzchniami mającymi tę
samą normalną jest stały)

3. Liniowe – kształt i położenie źródła mają istotny wpływ na

wyznaczanie intensywności oświetlenia powierzchni

4. Otaczające – pochodzące z różnych źródeł światła, wielokrotnie

odbijane od powierzchni i przenikające przez część z nich, dające w
pewnym otoczeniu jednorodne tło oświetleniowe. Dochodzi ze stałą
intensywnością do wszystkich powierzchni ze wszystkich kierunków.

Modele oświetlenia – definiują intensywność światła emitowanego i
odbijanego w kierunku obserwatora w danym punkcie powierzchni
obiektu na podstawie charakterystyki intensywności światła padającego i
właściwości optycznych powierzchni.
- modele lokalne – uwzględniają jedynie wpływ pierwotnych źródeł

ś

wiatła na oświetlenie powierzchni

- modele globalne

– uwzględniają pierwotne i wtórne źródła światła

modele lokalne
1. Model światła otoczenia
2. Podstawowy model empiryczny
3. Model Phonga

modele globalne
4. Model Halla
5. Równanie renderingu

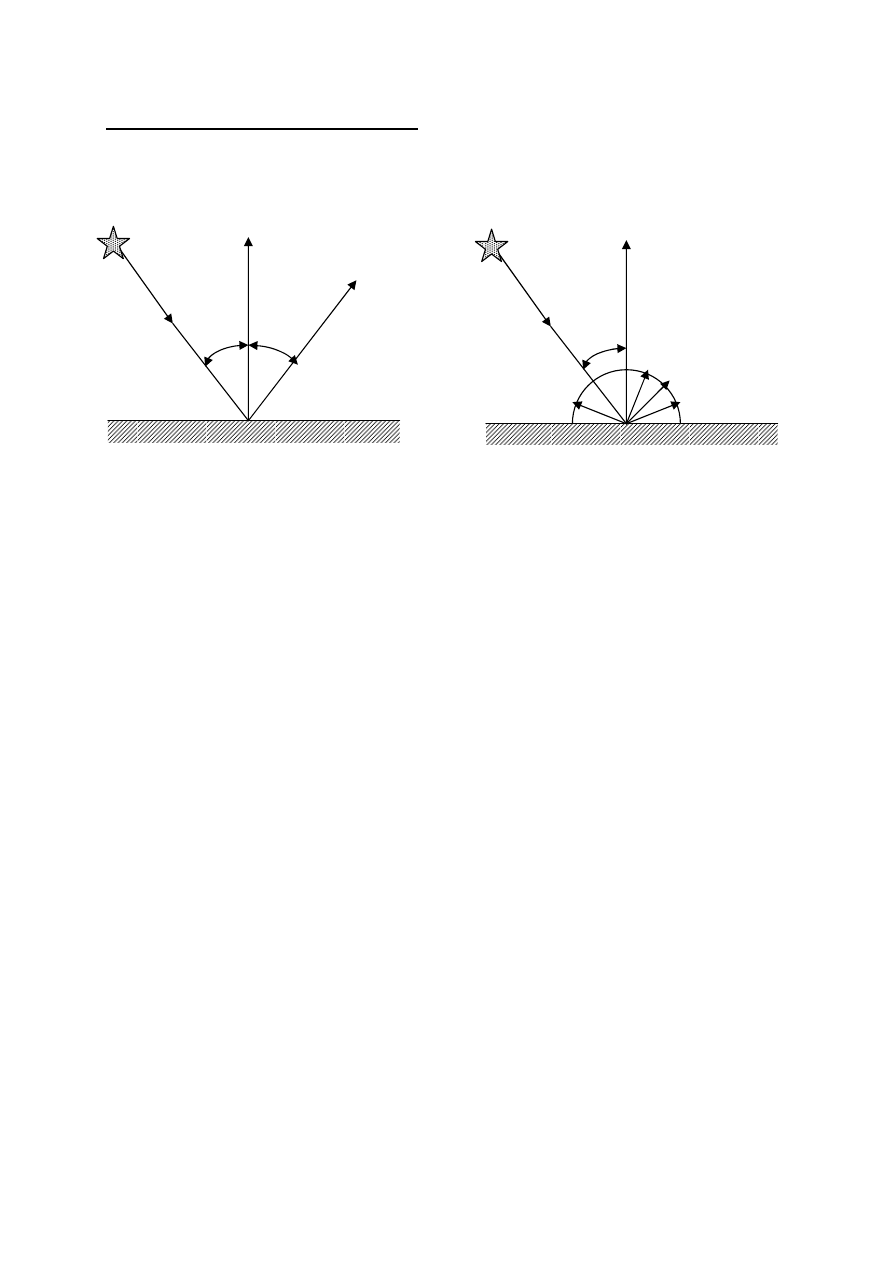
Mechanizmy transportu światła

a) odbicie kierunkowe

b) odbicie rozproszone

(lambertowskie)

powierzchnie lustrzane

powierzchnie matowe

bez połysku

N

α

1

α

2

α

1

= α

2

N

α

1

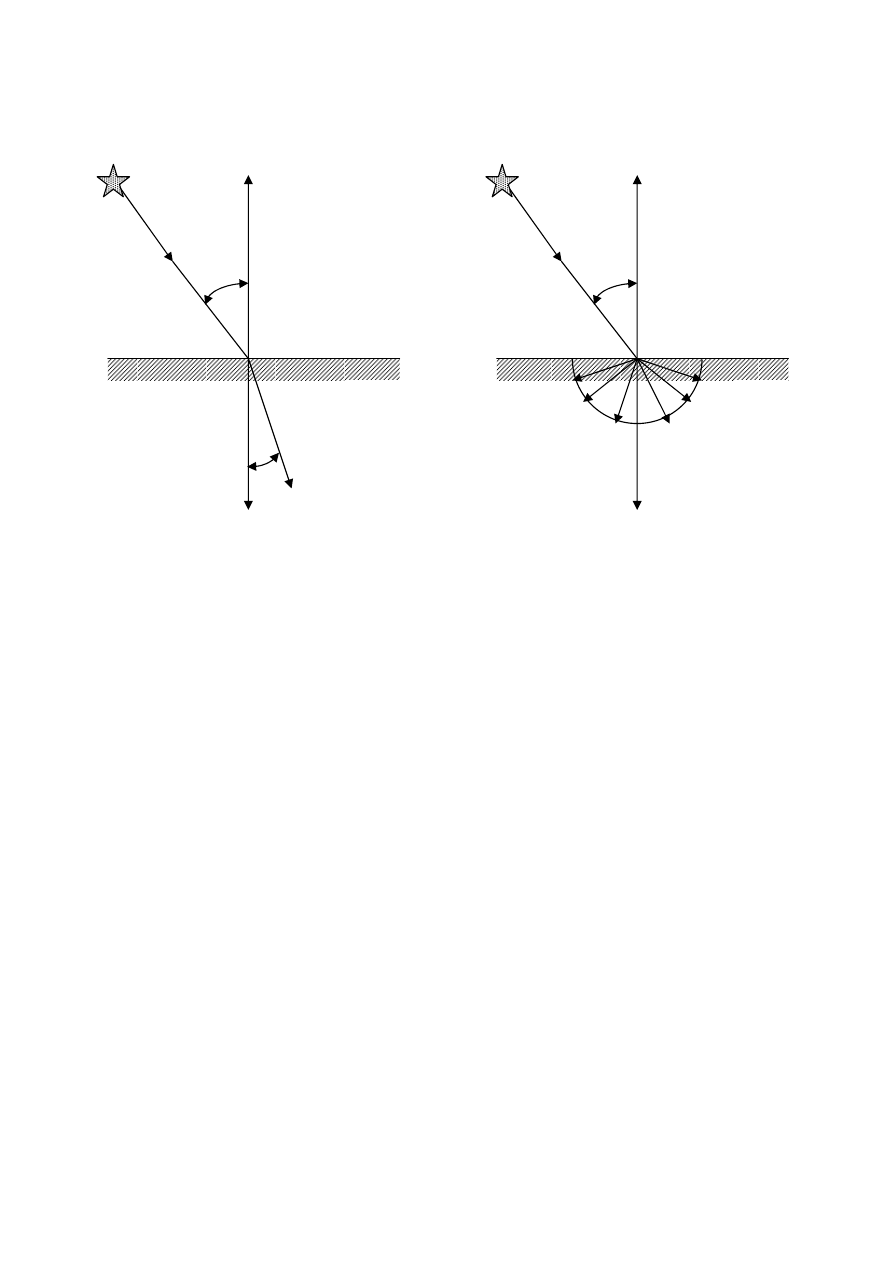
a) załamanie kierunkowe

b) załamanie rozproszone

η

– współczynnik załamania środowiska przeźroczystego względem

próżni

N

α

1

α

2

η

1

sinα

1

= η

2

sinα

2

-N

η

2

η

1

N

α

1

-N

η

2

η

1

Model światła otoczenia

Ś

wiatło pochodzi z różnych źródeł, jest wielokrotnie odbijane od

powierzchni i przenika przez część z nich, daje w pewnym otoczeniu
jednorodne tło oświetleniowe. Pada jednakowo na wszystkie
powierzchnie ze wszystkich kierunków.

Równanie oświetlenia

gdzie:
I – intensywność światła odbitego od powierzchni
I

α

– intensywność światła otoczenia

k

α

– współczynnik odbicia światła rozproszonego zależny od właściwości

optycznych powierzchni odbijającej, dobierany doświadczalnie z
przedziału [0 –1]

Kule cieniowane za pomocą modelu światła otoczenia.

Od lewej do prawej: k

a

= 0.8, 0.5, 0.3

α

α

k

I

I

=

Podstawowy model empiryczny

- uwzględnia pierwotne źródła światła
- wprowadza empiryczny stały współczynnik dla wtórnych źródeł

ś

wiatła

- zakłada lambertowską charakterystykę światła odbitego (odbicie

rozproszone)

L – wektor w kierunku źródła światła
N – wektor normalny do powierzchni

Właściwości powierzchni lambertowskich
- powierzchnie matowe bez połysku
- jednakowo jasne ze wszystkich kierunków obserwacji
- dla danej powierzchni jasność zależy tylko od kąta θ między

kierunkiem L do źródła światła i normalną do powierzchni N

N

θ

L

Równanie oświetlenia:

gdzie:
I – intensywność światła odbitego od powierzchni
I

α

– intensywność światła otoczenia

k

α

– współczynnik odbicia światła otoczenia zależny od właściwości

optycznych powierzchni odbijającej, dobierany doświadczalnie z
przedziału [0 –1]

I

p

– intensywność punktowego źródła światła

k

d

– współczynnik odbicia rozproszonego źródła światła pierwotnego

zależny od właściwości optycznych powierzchni odbijającej,
dobierany doświadczalnie z przedziału [0 –1]

θ

- kąt między kierunkiem do źródła światła i normalną do powierzchni

Kule

cieniowane

za

pomocą

modelu

odbicia

rozproszonego

z uwzględnienia światła otoczenia.
Dla wszystkich kul: I

a

= I

p

=1.0, k

a

= 0.3

Od lewej do prawej: k

d

= 0.3, 0.5, 0.8

θ

cos

d

p

a

a

k

I

k

I

I

+

=

Tłumienie źródła światła

Strumień światła z punktowego źródła światła maleje odwrotnie
proporcjonalnie do odległości d

L

źródła światła od powierzchni

gdzie:

f

α

tt

– współczynnik tłumienia źródła światła

d

L

– odległość źródła światła od powierzchni

c

1

, c

2

, c

3

– stałe określane empirycznie związane z właściwościami

ź

ródła światła

θ

cos

d

p

att

a

a

k

I

f

k

I

I

+

=













+

+

=

1

,

1

min

2

3

2

1

L

L

att

d

c

d

c

c

f

Ś

wiatła barwne i powierzchnie barwne

- definiowane przez oddzielne równania dla każdej składowej

podstawowe

- barwa odbicia rozproszonego od powierzchni reprezentowana przez

trzy współczynniki (O

dR

, O

dG

, O

dB

)

- składowe podstawowe I

pR

, I

pG

i I

pB

są odbijane odpowiednio w

proporcjach k

d

O

dR

, k

d

O

dG

i k

d

O

dB

Równanie oświetlenia w postaci układu 3 równań:

θ

cos

dR

d

pR

att

dR

a

aR

R

O

k

I

f

O

k

I

I

+

=

θ

cos

dG

d

pG

att

dG

a

aG

G

O

k

I

f

O

k

I

I

+

=

θ

cos

dB

d

pB

att

dB

a

aB

B

O

k

I

f

O

k

I

I

+

=

Założenie, że 3 składowe modelu RGB całościowo modelują
oddziaływanie światła z obiektami jest uproszczone. Równanie
oświetlenia powinno być przeliczane w sposób ciągły dla całego zakresu
widma światła widzialnego. Równanie oświetlenia przyjmie postać:

gdzie:

λ

- długość fali strumienia świetlnego w pełnym zakresie światła

widzialnego

θ

λ

λ

λ

λ

λ

cos

d

d

p

att

d

a

a

O

k

I

f

O

k

I

I

+

=

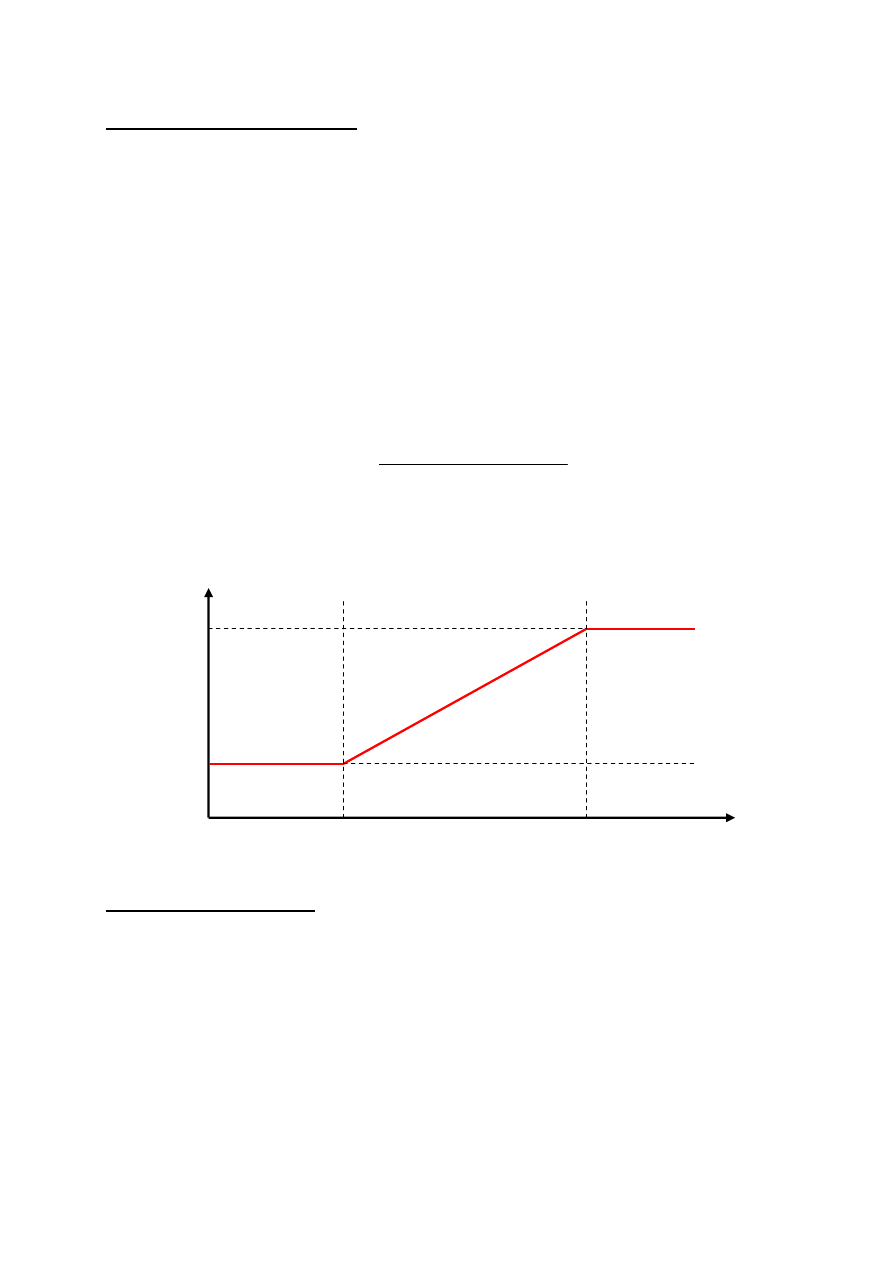
Tłumienie atmosferyczne

Zmiana intensywności oświetlenia w funkcji odległości obiektu od
obserwatora.

- definicja przedniej z

b

i tylnej z

f

płaszczyzny odniesienia

- wyznaczenie współczynników skalowania tłumienia atmosferycznego

s

b

i s

f

dla przedniej i tylnej płaszczyzny odniesienia

-

wyznaczenie współczynnika tłumienia s

0

dla płaszczyzny z

0

:

1) jeżeli z

0

jest przed z

f

to s

0

=s

f

2) jeżeli z

0

jest za z

b

to s

0

= s

b

3) jeżeli z

0

jest między z

f

i z

b

to:

Równanie oświetlenia:

gdzie:

I

λ

– intensywność światła dla przedniej płaszczyzny odniesienia

I

dcλ

– intensywność światła dla tylnej płaszczyzny odniesienia

I’

λ

– interpolowana intensywność światła dla płaszczyzny z

0

Odległość

Współczynnik

skalowania

λ

λ

λ

dc

I

s

I

s

I

)

1

(

'

0

0

−

+

=

1

s

b

s

f

1

z

b

z

f

b

f

b

f

b

b

z

z

s

s

z

z

s

s

−

−

−

+

=

)

)(

(

0

0

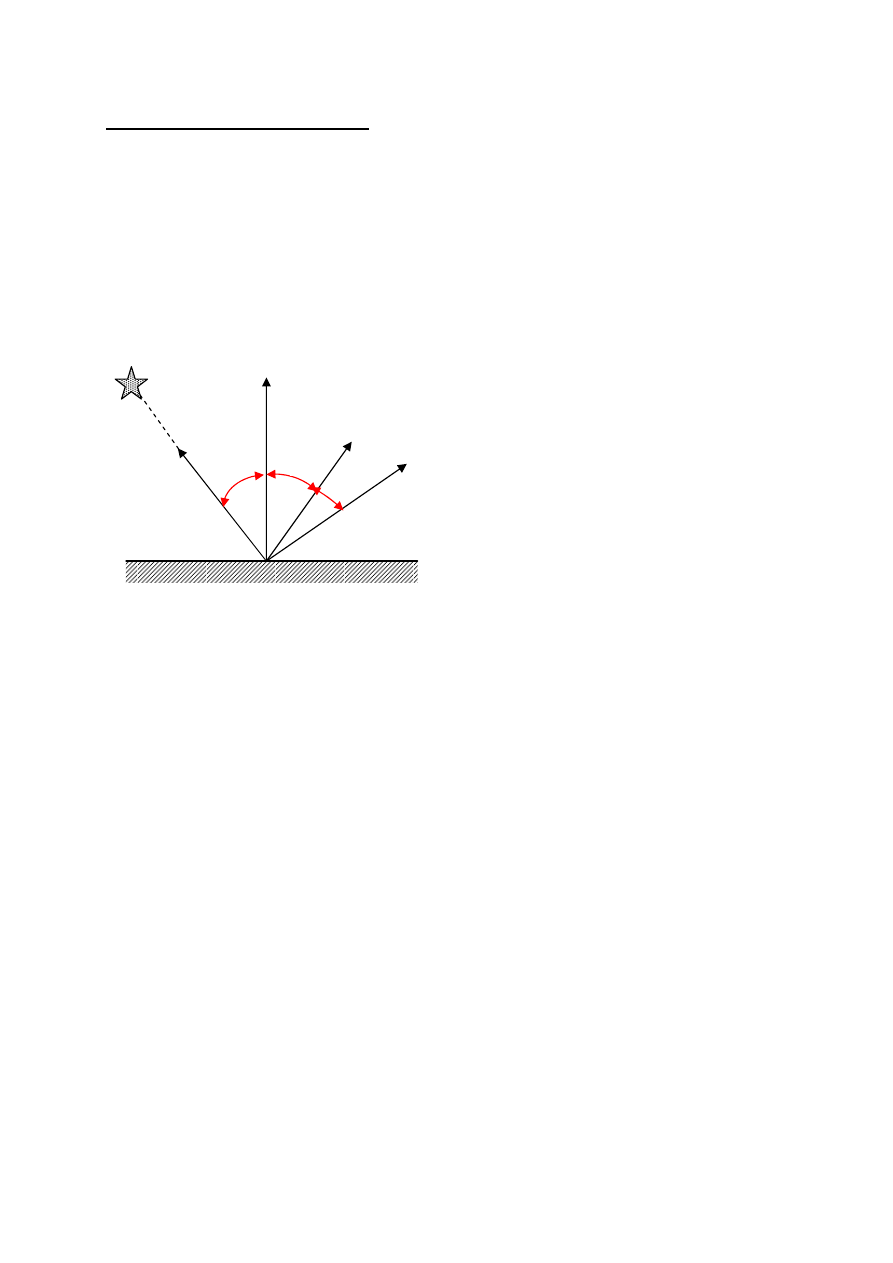
Model oświetlenia Phonga

- uwzględnia odbicie kierunkowe (zwierciadlane) światła
- powierzchnia odbijająca ma charakter lustrzany: powierzchnie gładkie

z połyskiem (światło odbijane w jednym kierunku)

- zapewnia złudzenie odblasku światła na powierzchni obiektów
- w miejscu rozświetlenia barwa zbliżona do barwy padającego światła
- efekty oświetlenia zależne od położenia obserwatora (kąta pomiędzy

kierunkiem światła odbitego a kierunkiem do obserwatora)

L – wektor w kierunku źródła światła
N – wektor normalny do powierzchni
V – wektor w kierunku obserwatora
R – wektor w kierunku światła

odbitego

N

θ

θ

L

R

V

α

Równanie oświetlenia:

gdzie:
k

s

– współczynnik odbicia kierunkowego zależny od właściwości

optycznych powierzchni odbijającej, dobierany doświadczalnie z
przedziału [0 –1]

O

sλ

– barwa światła odbitego

α

- kąt między kierunkiem światła odbitego a kierunkiem do obserwatora

n – współczynnik definiujący właściwości lustrzane powierzchni

odbijającej. Typowe wartości od 1 do kilkuset. Dla idealnego odbicia
kierunkowego n równe nieskończoność. Dla wartości 1 występuje
łagodny spadek jasności, dla wartości większych występują na
powierzchni ostre, ogniskowe rozświetlenia.

]

cos

cos

[

α

θ

λ

λ

λ

λ

λ

λ

n

s

s

d

d

p

att

d

a

a

O

k

O

k

I

f

O

k

I

I

+

+

=

Kule cieniowane za pomocą modelu oświetlenia Phonga

dla różnych wartości k

s

i n.

Dla wszystkich kul I

a

=I

p

=1.0, k

a

=0.2, k

d

=0.3.

Od góry do dołu: n = 5.0, 20.0, 100.0

Od lewej do prawej: k

s

= 0.2, 0.4, 0.6

Wiele źródeł światła

Przy wielu źródłach światła czynniki wpływające na oświetlenie
powierzchni sumują się

Równanie oświetlenia:

gdzie:
m

– liczba źródeł światła

]

cos

cos

[

1

∑

=

=

+

+

=

m

i

i

i

n

s

s

i

d

d

i

p

atti

d

a

a

O

k

O

k

I

f

O

k

I

I

α

θ

λ

λ

λ

λ

λ

λ

Scena generowana z uwzlędnieniem różnych modeli oświetlenia światła

Ś

wiatło otoczenia

Ś

wiatło otoczenia z odbiciem rozproszonym

Ś

wiatło otoczenia z odbiciem rozproszonym i kierunkowym

Model Halla

- globalny model oświetlenia: łączy elementy empiryczne i zjawiska

fizyczne związane z rozchodzeniem promieni świetlnych

- uwzględnia pierwotne źródła światła, światło otoczenia oraz światła

pośrednie z kierunków wyznaczonych przez promienie odbite i
załamane

- uwzględnia przeźroczystość oświetlanych obiektów

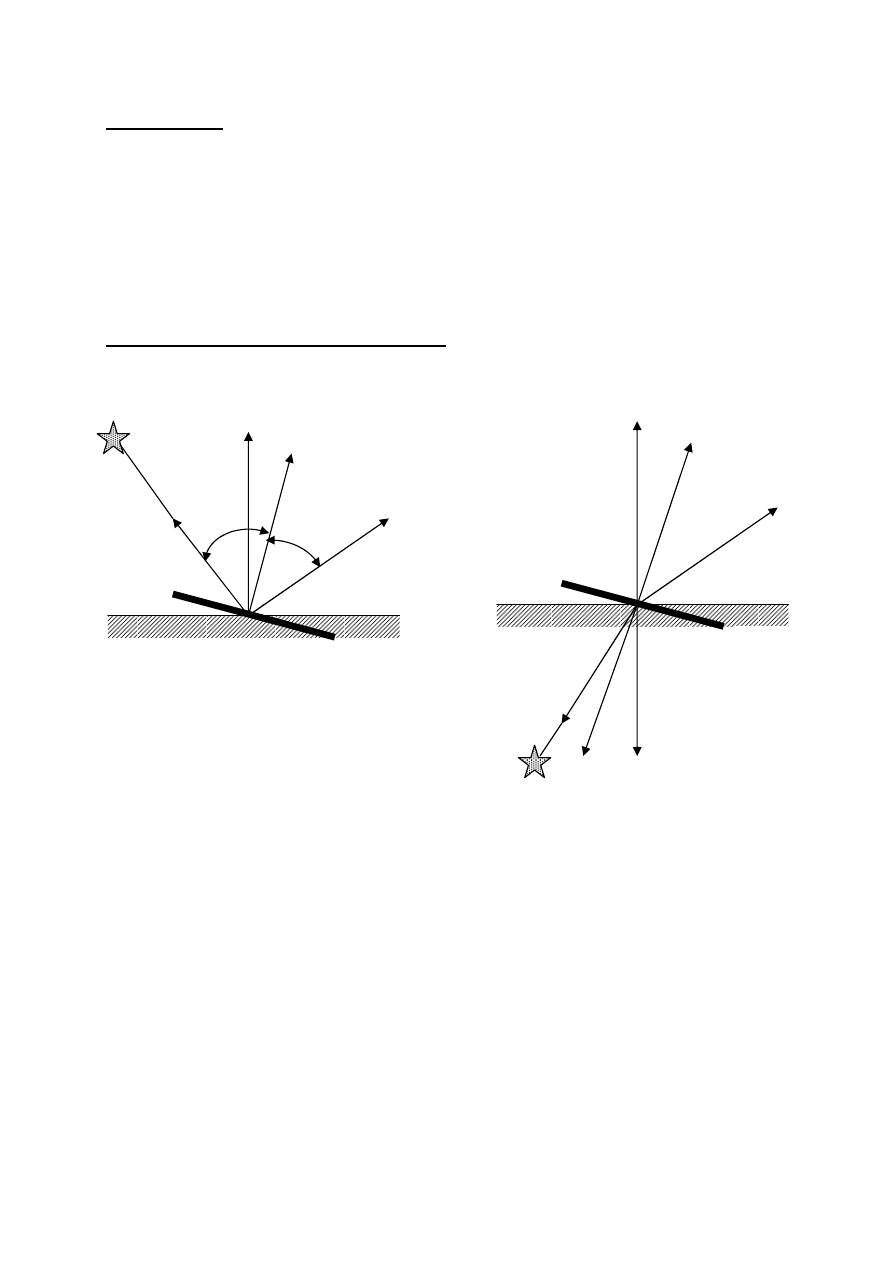
Oznaczenia przyjęte w modelu Halla

a

) obiekty nieprzeźroczyste

b) obiekty przeźroczyste

L – wektor w kierunku źródła światła
N – wektor normalny do powierzchni
V – wektor w kierunku obserwatora
H – wektor normalny do mikropowierzchni odbijającej wyznaczający kierunek

maksymalnego rozświetlenia

H’ – wektor normalny do mikropowierzchni załamującej wyznaczający kierunek

maksymalnego rozświetlenia

V

N

α

1

α

2

α

1

= α

2

N

-N

η

2

η

1

L

H

V

-H’

H’

L

V

L

V

L

H

r

r

r

r

r

+

+

=

n

H

N

)

(

r

r

⋅

Nowy czynnik odbicia zwierciadlanego w modelu Halla związany z wektorem H
wyznaczającym kierunek maksymalnego rozświetlenia




gdzie:

Wektor H jest w połowie między kierunkami do źródła światła i do obserwatora.
Gdyby normalna N byłaby w tym samym kierunku co H, wówczas obserwator
widziałby najjaśniejsze odbicie, ponieważ R i V wskazywałyby ten sam kierunek.

Równanie oświetlenia:

Składniki równania:

1. Oświetlenie wynikające z odbicia rozproszonego z m różnych źródeł

ś

wiatła

2. Oświetlenie wynikające z odbicia kierunkowego promieni świetlnych z

m różnych źródeł światła od powierzchni nieprzeźroczystych

3. Oświetlenie wynikające z załamania kierunkowego promieni

ś

wietlnych z m różnych źródeł światła przechodzących przez

powierzchnie przeźroczyste oświetlone z przeciwnej strony niż
obserwator

4. Oświetlenie pośrednie wynikające ze światła otoczenia
5. Oświetlenie pośrednie z kierunku wyznaczonego przez promień

odbity

6. Oświetlenie pośrednie z kierunku wyznaczonego przez promień

załamany

gtr

gspec

gdif

tr

spec

dif

I

I

I

I

I

I

I

λ

λ

λ

λ

λ

λ

λ

+

+

+

+

+

=

1. Oświetlenie wynikające z odbicia rozproszonego z m różnych źródeł

ś

wiatła

gdzie:
k

d

– współczynnik odbicia rozproszonego

O

dλ

– barwa światła odbitego

f

α

tti

– współczynnik tłumienia i-tego źródła światła

I

pλi

– intensywność i-tego punktowego źródła światła

N – wektor normalny do powierzchni
L

i

– wektor w kierunku i-tego źródła światła

)

(

1

i

i

p

m

i

atti

d

d

dif

L

N

I

f

O

k

I

r

r

⋅

=

∑

=

λ

λ

λ

2. Oświetlenie wynikające z odbicia kierunkowego promieni świetlnych z

m różnych źródeł światła od powierzchni nieprzeźroczystych

gdzie:
k

s

– współczynnik odbicia kierunkowego

F

sλ

– współczynnik Fresnela opisujący przenikalność światła na granicy

dwóch ośrodków

f

α

tti

– współczynnik tłumienia i-tego źródła światła

I

pλi

– intensywność i-tego punktowego źródła światła

N – wektor normalny do powierzchni
H

i

– wektor normalny do mikropowierzchni odbijającej wyznaczający

kierunek maksymalnego rozświetlenia z i-tego źródła światła

n – współczynnik określający właściwości lustrzane mikropowierzchni

odbijającej

n

i

i

p

m

i

atti

s

s

spec

H

N

I

f

F

k

I

)

(

1

r

r

⋅

=

∑

=

λ

λ

λ

3. Oświetlenie wynikające z załamania kierunkowego promieni

ś

wietlnych z m różnych źródeł światła przechodzących przez

powierzchnie przeźroczyste oświetlone z przeciwnej strony niż
obserwator

gdzie:
k

t

– współczynnik załamania kierunkowego

F

tλ

– współczynnik Fresnela opisujący przenikalność światła w materiale

przeźroczystym

f

α

tti

– współczynnik tłumienia i-tego źródła światła

I

pλi

– intensywność i-tego punktowego źródła światła

N – wektor normalny do powierzchni
H’

i

– wektor normalny do mikropowierzchni odbijającej wyznaczający

kierunek maksymalnego rozświetlenia z i-tego źródła światła

n’ – współczynnik określający rozpraszanie światła w materiale

przeźroczystym

'

1

)

'

(

n

i

i

p

m

i

atti

t

t

tr

H

N

I

f

F

k

I

r

r

⋅

=

∑

=

λ

λ

λ

4. Oświetlenie pośrednie wynikające ze światła otoczenia

gdzie:
k

a

– współczynnik odbicia światła otoczenia

O

dλ

– barwa światła odbitego

I

aλ

– intensywność światła otoczenia

λ

λ

λ

a

d

a

gdif

I

O

k

I

=

5. Oświetlenie pośrednie z kierunku wyznaczonego przez promień

odbity

gdzie:
k

s

– współczynnik odbicia kierunkowego

F

sλ

– współczynnik Fresnela opisujący przenikalność światła na granicy

dwóch ośrodków

I

sλ

– intensywność światła z kierunku promienia odbitego

T

s

– współczynnik transmisji ośrodka w którym porusza się promień

odbity

d

s

– odległość jaką przebył promień odbity w ośrodku

ds

s

s

s

s

gspec

T

I

F

k

I

λ

λ

λ

=

6. Oświetlenie pośrednie z kierunku wyznaczonego przez promień

załamany

gdzie:
k

t

– współczynnik załamania kierunkowego

F

tλ

– współczynnik Fresnela opisujący przenikalność światła w materiale

przeźroczystym

I

sλ

– intensywność światła z kierunku promienia załamanego

T

t

– współczynnik transmisji ośrodka w którym porusza się promień

załamany

d

t

– odległość jaką przebył promień załamany w ośrodku

dt

t

t

t

t

gtr

T

I

F

k

I

λ

λ

λ

=

Równanie renderingu (Kajiya 1986)

- globalny model oświetlenia
- rozwiązuje problem propagacji energii świetlnej w środowisku, nie

zajmuje się interakcją światła z danym rodzajem powierzchni

- oparte na znanym w termodynamice zjawisku transferu ciepła drogą

promieniowania i zasadzie zachowania energii

- modelowanie oświetlenia poprzez wielokrotne rozwiązanie równania

renderingu dla każdego punktu lub powierzchni elementarnej
wizualizowanej sceny

Równanie oświetlenia: wyznacza intensywność oświetlenia punktu x
przez światło emitowane lub odbijane w punkcie x’ w kierunku punktu x

gdzie:

g(x,x’) – czynnik geometryczny określający położenie punktu x w

stosunku do punktu x’

- jeżeli x i x’ są dla siebie niewidoczne to: g(x,x’) = 0
- w pozostałych przypadkach: g(x,x’) = 1/r

2

gdzie r jest odległością

między x i x’

ε

(x,x’) – intensywność światła emitowanego z punktu x’ w kierunku

punktu x , różna od zera jedynie dla powierzchni aktywnych
oświetleniowo (pierwotne źródła światła)

I(x’,x”) – intensywność światła w punkcie x’ emitowanego lub

odbijanego w punkcie x” w kierunku punktu x’

ρ

(x,x’,x”) – współczynnik odbicia światła I(x’,x”) w kierunku punktu x

W celu wyznaczenia światła odbitego w punkcie x’ w kierunku punktu x
należy zsumować światło emitowane lub odbite w kierunku punktu x’
pochodzące ze wszystkich punktów x” powierzchni S.









+

=

∫

S

dx

x

x

I

x

x

x

x

x

x

x

g

x

x

I

"

)

"

,

'

(

)

"

,

'

,

(

)

'

,

(

)

'

,

(

)

'

,

(

ρ

ε