1
7. Obliczenia statyczne i wymiarowanie
7.1. Stalowy wiązar kratowy
Przedmiotem obliczeń statycznych oraz wymiarowania jest stalowa kratownica o podstawowych
danych wyjściowych:
•
rozpiętość
= 15,0
•
rozstaw
= 6,0
•
liczba wiązarów
= 6
•
stal
235 ( 3 )
Budynek znajduje się w Słupcy, która leży w I strefie obciążenia wiatrem oraz II strefie obciążenia
śniegiem. Obciążenia te są głównym obciążeniem pokrycia dachowego.
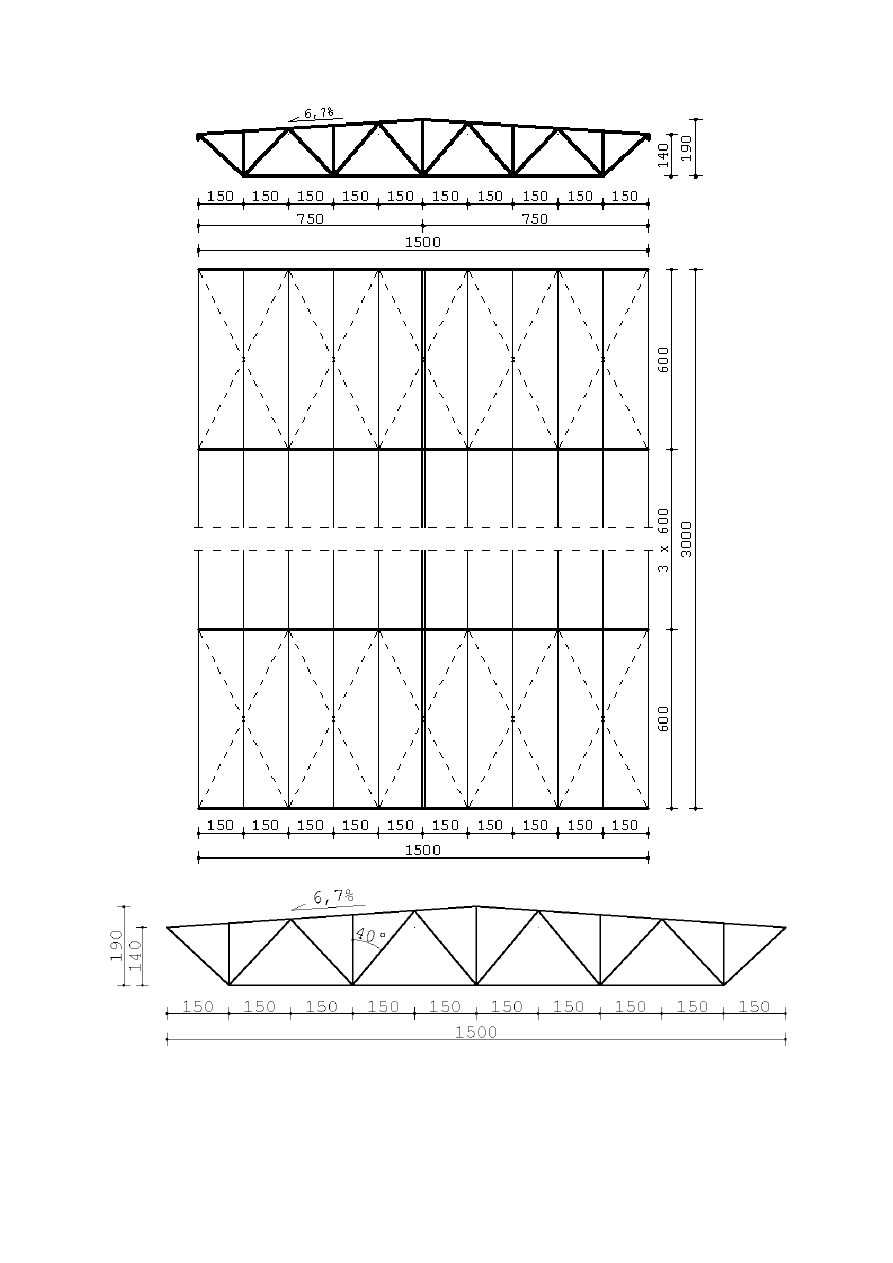
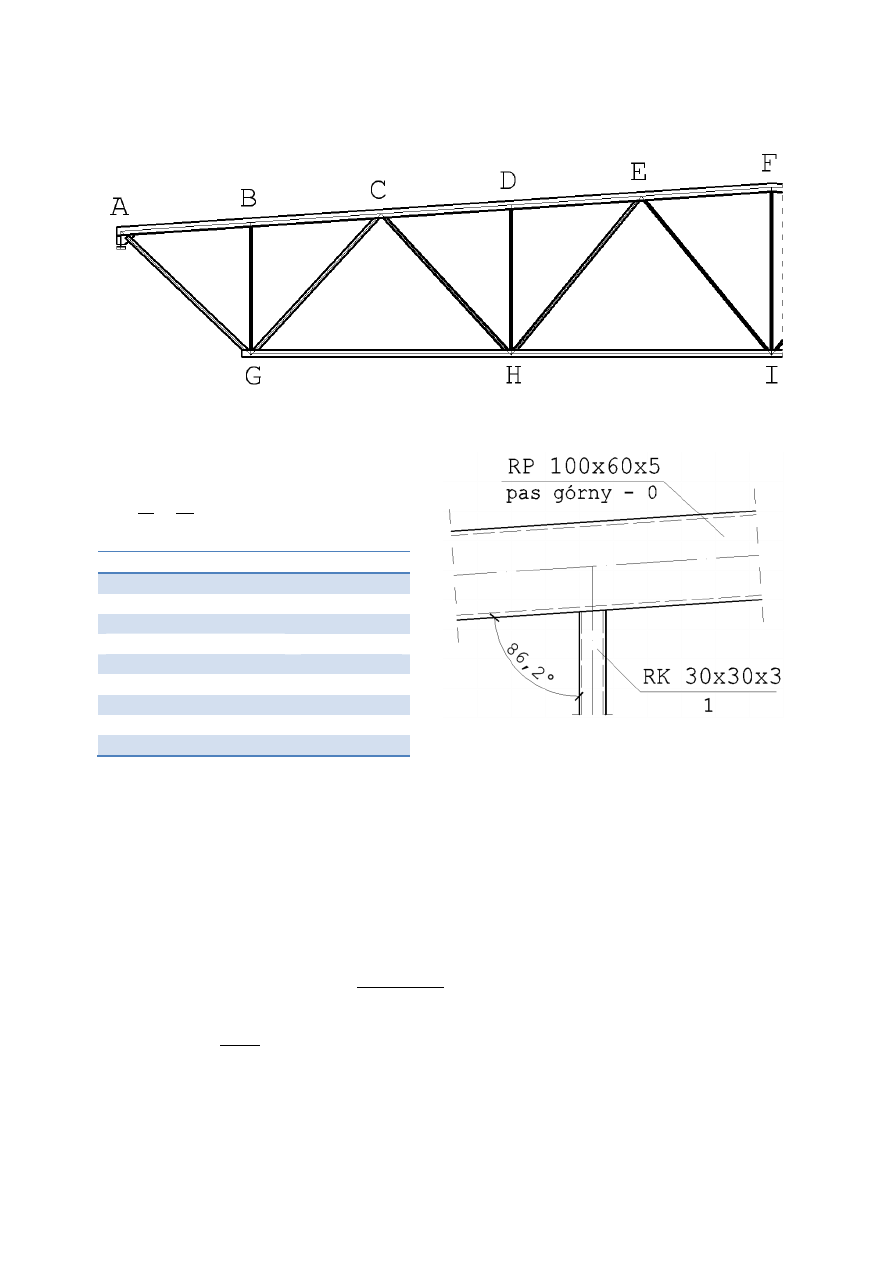
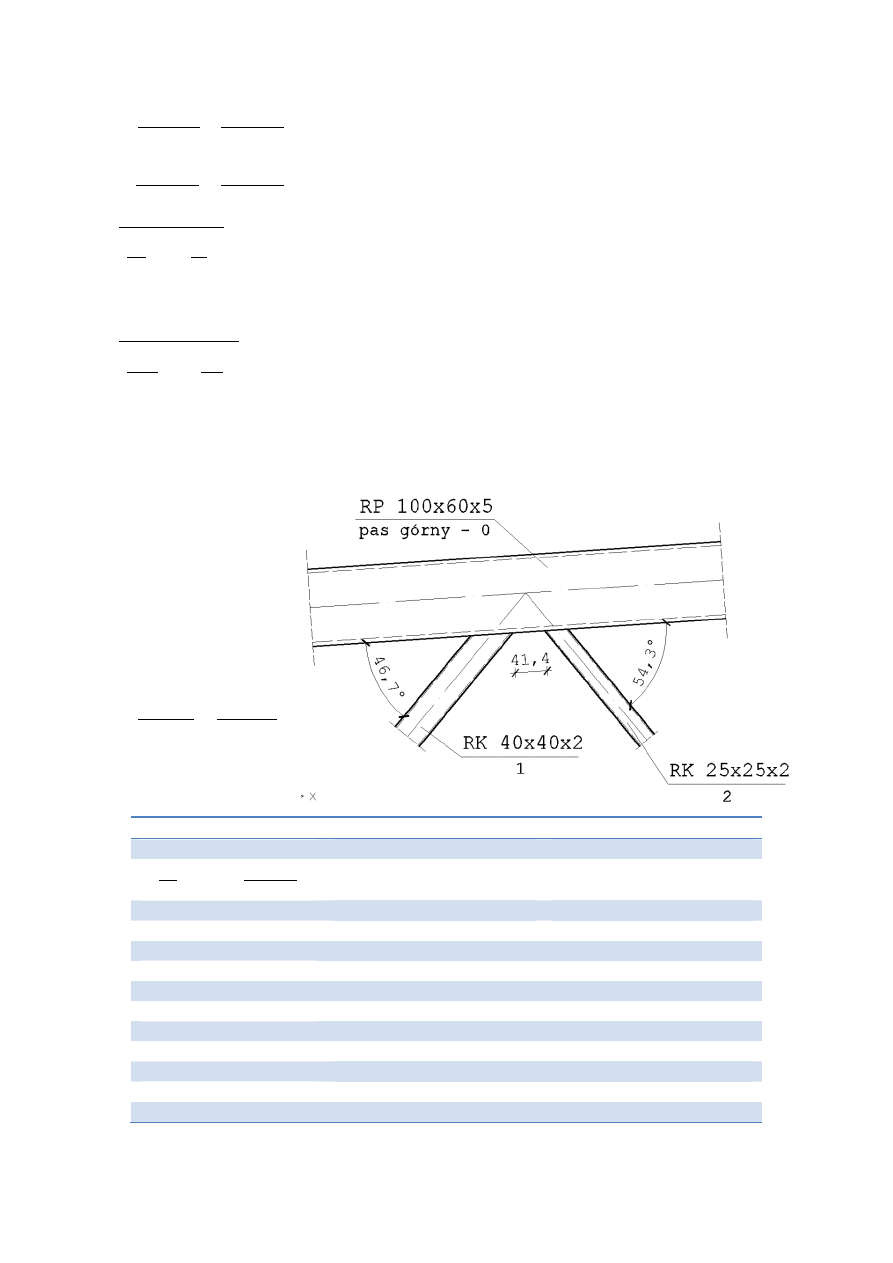
Pod względem geometrii wiązar to kratownica z obniżonym pasem dolnym oraz skratowaniem
trójkątnym ze słupkami. Schematycznie geometrię wiązara przedstawia poniższy rysunek.
7.1.1. Przyjęcie geometrii wiązara
Ze względu na minimum zużycia materiału ustala się optymalną wysokość wiązara w kalenicy:
≤ 21,0 → ℎ
=
1
7 ÷
1
8
→ ℎ
= (1,875 ÷ 2,143 )
- przyjęto -
ℎ
= ℎ
!"#
= 1,90
Wysokość na podporze nie powinna być mniejsza niż:
ℎ ≥
1
15 ÷
1
18
→ ℎ ≥ (0,83 ÷ 1,00 )
- przyjęto -
ℎ = 1,40
Zakłada się, że w węzłach pręty nie zbiegają się pod kątem mniejszym niż
30°.
Po wyrysowaniu geometrii z uwzględnieniem powyższych wartości, minimalny kąt wynosi
39,8°.
Spadek pokrycia dachowego a zarazem górnego pasa kratownicy wynosi
6,67% (3,81°).
Na kolejnej stronie przedstawiono układ skratowania wraz z wymiarami i minimalnym kątem.
Pokazano też układ całego dachu: wiązary zaznaczono pogrubioną linią, prostopadle do nich w
rozstawie 1,5 m rozmieszczone są płatwie (w kalenicy stosuje się podwojoną płatew), a
przerywanymi liniami zaznaczono założony układ stężeń połaciowych poprzecznych.
2
7.1.2. Pokrycie dachowe
Zgodnie z planami modernizacji, stare płyty warstwowe zastąpią nowe płyty z grubszym rdzeniem.
3
7.1.2.1. Zebranie obciążeń na pokrycie dachowe
Obiekt znajduje się w Słupcy, która według odpowiednich ilustracji w normach leży w:
- II strefie obciążenia śniegiem wg [N1]
- I strefie obciążenia wiatrem wg [N2]
Wartość charakterystyczna obciążenia śniegiem gruntu:
(
!
= 0,90
)*
+
Współczynnik kształtu dachu dwuspadowego o pochyleniu
3,81°:
, = ,
-
= ,
+
= 0,80
Obciążenie charakterystyczne dachu śniegiem:
!
= (
!
∙ , = 0,90 ∙ 0,80 = 0,72
)*
+
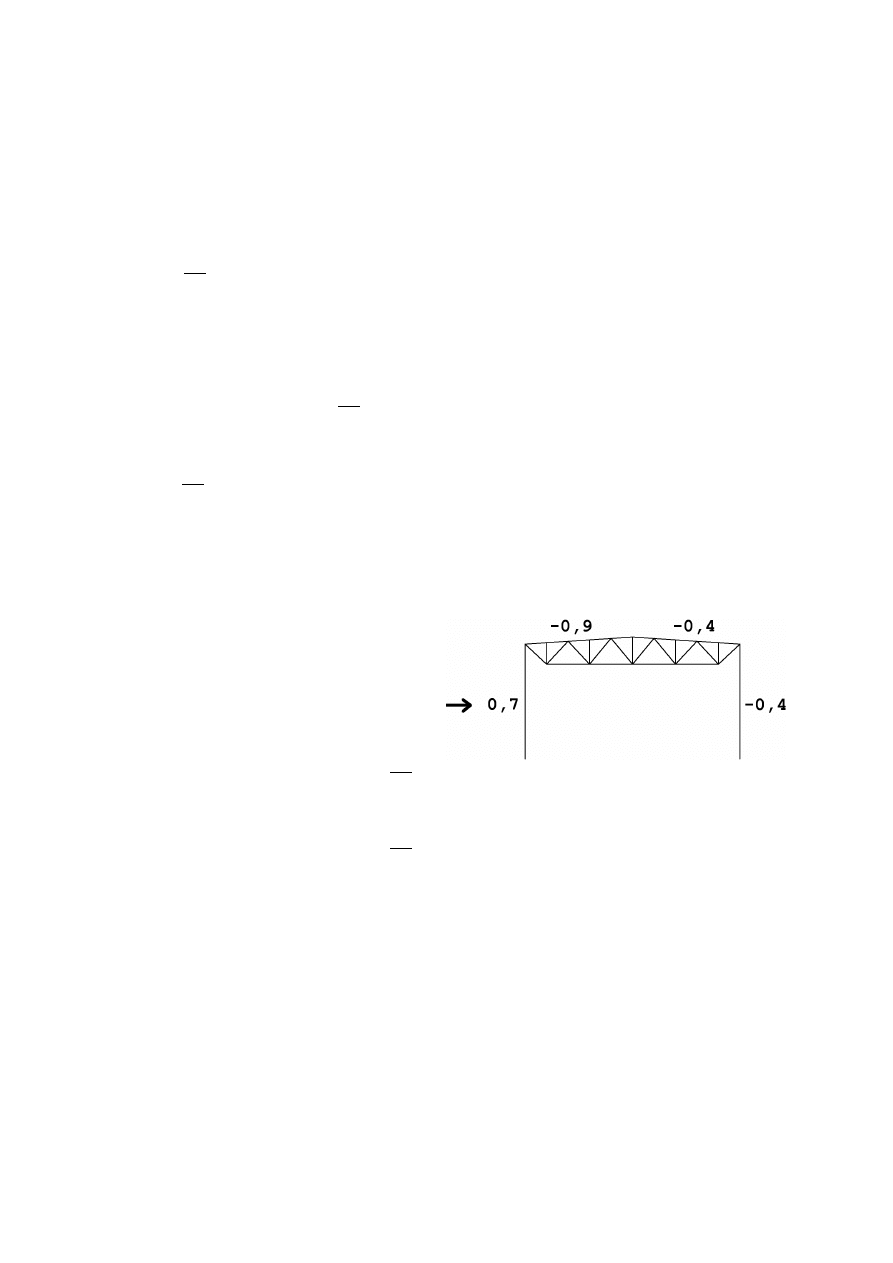
Charakterystyczne ciśnienie prędkości wiatru:
/
!
= 0,30
)*
+
Współczynnik ekspozycji (teren kategorii C):
,
0
= 0,60 (1 ≤ 10 )
Współczynnik działania porywów wiatru (budynek niepodatny):
2 = 1,8
Współczynnik ciśnienia zewnętrznego C (rysunek obok):
Obciążenie charakterystyczne dachu wiatrem:
3
!
= /
!
∙ ,
0
∙ , ∙ 2
- połać nawietrzna:
3
!
= 0,30 ∙ 0,60 ∙ (−0,9) ∙ 1,8 = −0,292
)*
+
- połać zawietrzna:
3
!
= 0,30 ∙ 0,60 ∙ (−0,4) ∙ 1,8 = −0,130
)*
+
7.1.2.2. Przyjęcie warstwowej płyty dachowej
Z uwagi na spełnienie wymogów cieplno-wilgotnościowych, zakłada się, aby współczynnik
przenikania ciepła płyty będzie na poziomie poniżej
0,30 W m
+
K
⁄
. W związku z tym przyjęto płytę
Ruukki SP2C PU 120/80.
Płyta z dużym zapasem spełnia warunek nośności i sztywności, głównie ze względu na mały rozstaw
płatwi (porównano z charakterystycznym obciążeniem śniegiem połaci dachu).
Ciężar płyty wynosi -
9
:
= 11,50 );
+
⁄
= 0,113 )*
+
⁄ .
Współczynnik przenikania ciepła płyty wynosi
< = 0,20 =
+
>
⁄
, a ponadto producent podaje, że
współczynnik zawiera wpływ liniowego mostka cieplnego, który występuje na styku płyt [nr].
4
Budowę płyty, dane na jej temat oraz charakterystyka styku płyt SP2C PU firmy Ruukki zawiera
dokument/PDF załączony do pracy.
7.1.3. Płatew dachowa
7.1.3.1. Zestawienie obciążeń
Dla dobranych płyt warstwowych minimalna szerokość podparcia pośredniego wynosi 60 mm.
wg [N nr], [N nr], [N nr]
Rodzaj obciążenia
Obciążenie
charakterystyczne
Współczynnik
obciążenia
?
@
Obciążenie
obliczeniowe
)*A
)*A
Płyta Ruukki SP2C PU 120/80
1,50 ∙ 0,113 )*
+
⁄
0,170
1,1
0,187
Płatew - I 140 PE
12,9 );⁄
0,127
1,1
0,140
razem
/
!
= 0,297
-
/
B
= 0,327
Obciążenie śniegiem
1,50 ∙ 0,72 )*
+
⁄
1,080
1,5
1,620
razem
C
D
= E, FGG DH I
⁄
-
C
J
= E, KLG DH I
⁄
W obliczeniach płatwi pomija się wpływ ssania wiatru, ponieważ obciążenie to redukuje jej
wytężenie. Do obciążeń dodano ciężar własny przyjętej płatwi I 140 PE.
Zapewniona jest odpowiednia szerokość podparcia płyt warstwowych (
b = 73 mm).
Zakłada się wykorzystanie dwóch 15-metrowych elementów I 140 PE lub trzech 10-metrowych
połączonych ze sobą i tworzących belkę ciągłą pięcioprzęsłową (sprawdzono długość handlową
dwuteownika, oba rozwiązania są możliwe).
7.1.3.2. Wyznaczenie sił wewnętrznych
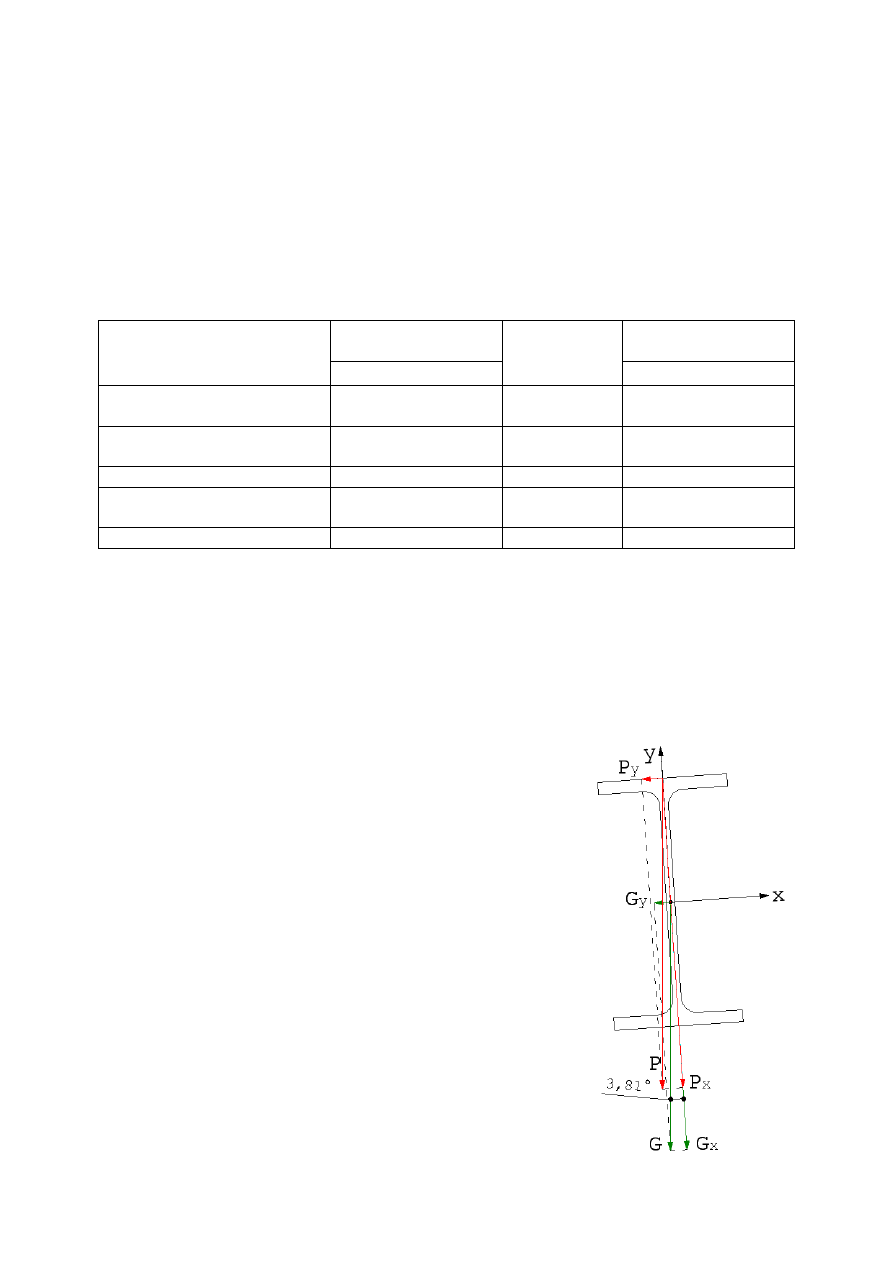
Całe obciążenie pionowe rozkłada się na kierunki równoległy i
prostopadły do płaszczyzny środka płatwi, zgodnie ze schematem
obliczeniowym na rysunku zamieszczonym obok.
Obciążenie zawieszone w środku ciężkości przekroju:
;
!N
= ;
!
∙ 9OPQ = 1,377 ∙ 0,9978 = 1,374 )*⁄
;
!R
= ;
!
∙ PS Q = 1,377 ∙ 0,0664 = 0,091 )*⁄
;
BN
= ;
B
∙ 9OPQ = 1,947 ∙ 0,9978 = 1,943 )*⁄
;
BR
= ;
B
∙ PS Q = 1,947 ∙ 0,0664 = 0,129 )*⁄
Przy dalszych obliczeniach zakłada się, że pokrycie dachowe nie
zabezpiecza płatwi przed zwichrzeniem.
Na podstawie tablic Winklera przyjęto odpowiednie współczynniki dla
belki czteroprzęsłowej równomiernie obciążonej.
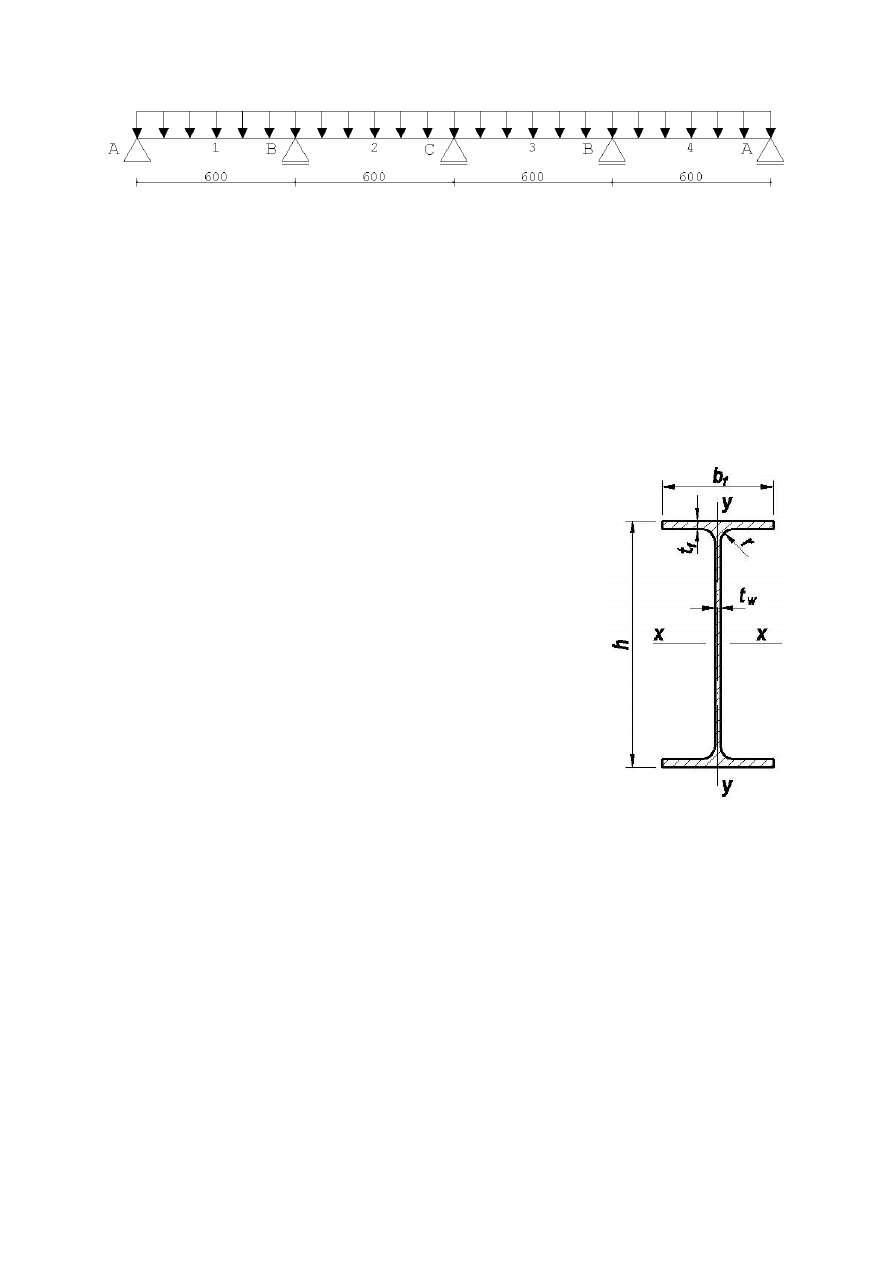
5
•
Momenty:
T
UV"N
(W)
= −0,107 ∙ 1,943 ∙ 6,0
+
= −7,484 )*
T
UV"N
(-)
= 0,077 ∙ 1,943 ∙ 6,0
+
= 5,386 )*
T
XV"N
(W)
= −0,107 ∙ 0,129 ∙ 6,0
+
= −0,497 )*
T
XV"N
(-)
= 0,077 ∙ 0,129 ∙ 6,0
+
= 0,358 )*
•
Siły tnące:
Y
UV"N
= Y
U#
(W)
= 0,607 ∙ 1,943 ∙ 6,0 = 7,076 )*
Y
XV"N
= Y
X#
(W)
= 0,607 ∙ 0,129 ∙ 6,0 = 0,470 )*
7.1.3.3. Projektowanie płatwi – I stan graniczny (SGN)
Informacje techniczne z tablic [nr] dla przekroju I 140 PE:
ℎ = 140
= 73
:
= 4,7
@
= 6,9
Z = 9,0
[ = 16,4 9
+
\ = 12,9 );⁄
Stal płatwi - S235JRG2 (St3SY)
Q =
ψ
= 1,0 (przekrój klasy nie większej niż 3)
Nośność na zginanie:
T
]N
= Q ∙ =
N
∙ ^
B
T
]N
= 1,0 ∙ 77,3 ∙ 21,5 = 1661,95 )*9
T
]R
= 1,0 ∙ 12,3 ∙ 21,5 = 264,45 )*9
Nośność na ściskanie:
*
]_
=
ψ
∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 16,4 ∙ 21,5 = 352,6 )*
Wyboczenie względem osi y-y:
•
Smukłość płatwi względem osi y-y
`
U
= 541 9
a
=
U
= 77,3 9
b
S
U
= 5,74 9
`
X
= 44,90 9
a
=
X
= 12,30 9
b
S
X
= 1,65 9
`
c
= 2,45 9
a
`
d
= 1980 9
e
=
d
= 81,50 9
a
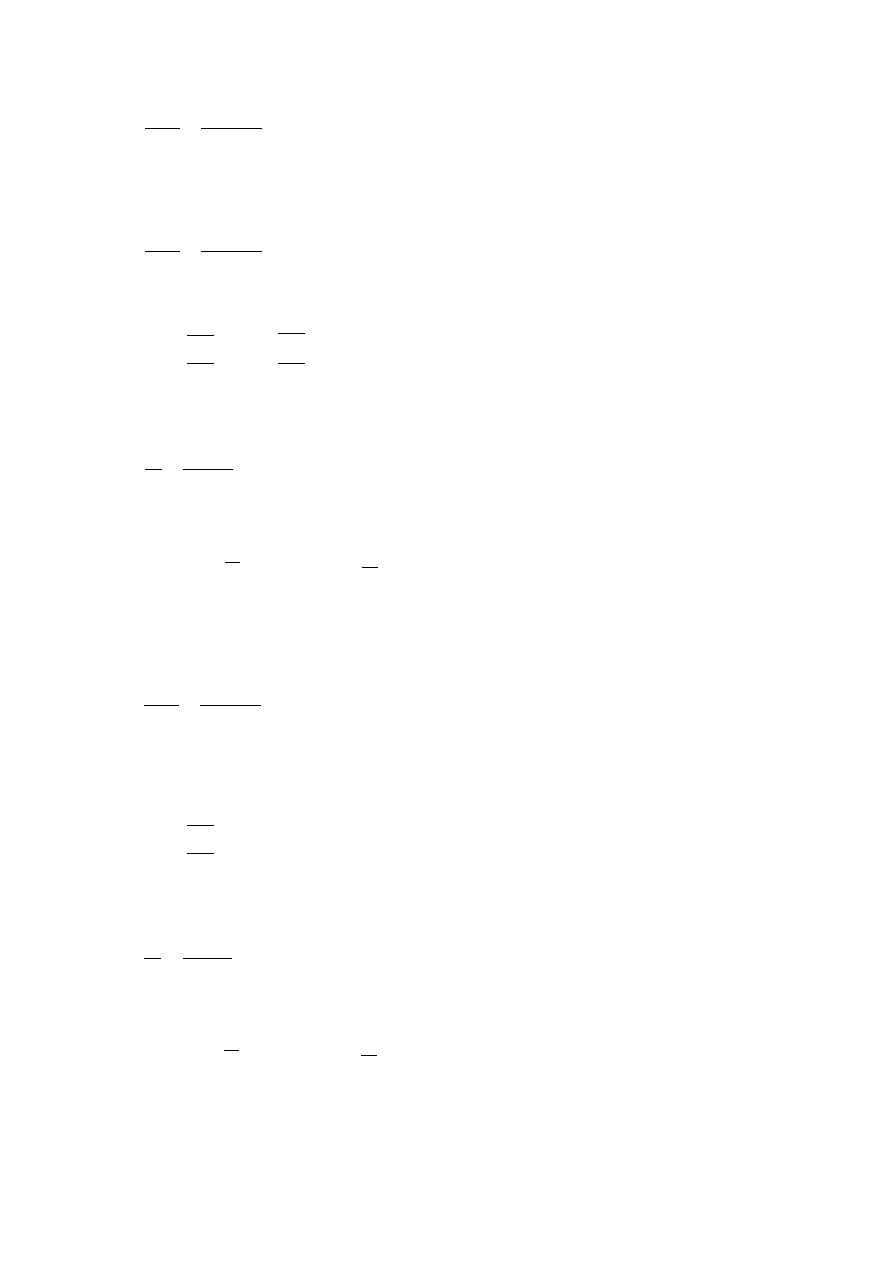
6
f
R
=
g
R
∙
S
R
=
1,0 ∙ 600
1,65 = 363,6 > 250
W celu zmniejszenia smukłości stosuje się pośrednie podparcie boczne, które zmniejszy o połowę
długość wyboczeniową płatwi:
f
R
=
g
R
∙
S
R
=
1,0 ∙ 300
1,65 = 181,82 < 250
•
Smukłość porównawcza
f = 84 ∙ j
215
^
B
= 84 ∙ j
215
215 = 84
•
Smukłość względna
f
R
kkk = f
R
f =
181,82
84 = 2,164
•
Współczynnik
l
R
względem krzywej b (n = 1,6)
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 2,164
b,+
)
q-
-,e
= 0,203
Wyboczenie względem osi x-x:
•
Smukłość płatwi względem osi x-x
f
N
=
g
N
∙
S
N
=
1,0 ∙ 600
5,74 = 104,53 < 250
f
N
< f
R
•
Smukłość porównawcza
f = 84 ∙ j
215
^
B
= 84
•
Smukłość względna
f
N
kkk = f
N
f =
104,53
84 = 1,244
•
Współczynnik
l
N
względem krzywej b (n = 1,6)
l
N
= m1 + f
N
kkk
+o
p
q-
o
= (1 + 1,244
b,+
)
q-
-,e
= 0,502
l
N
> l
R
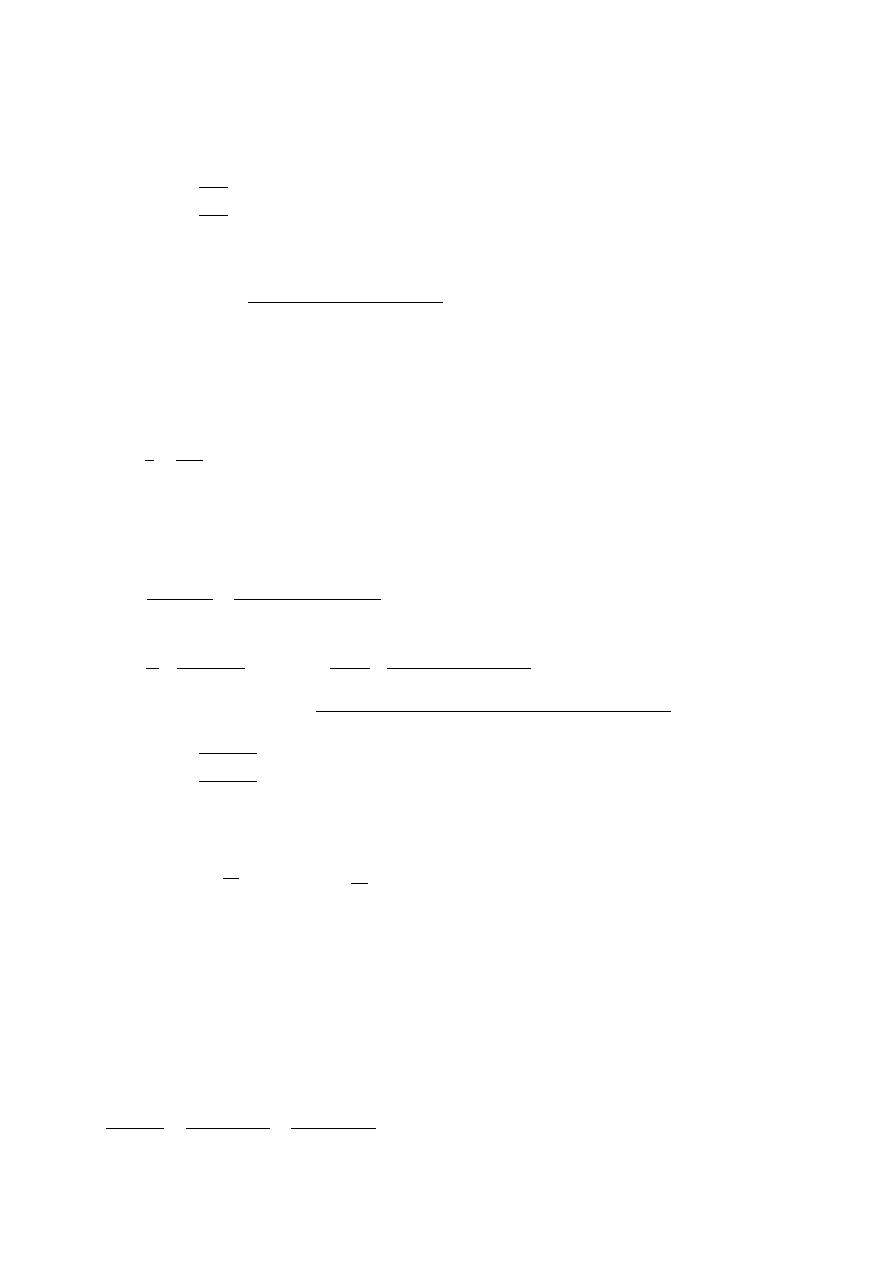
7
Określenie wpływu zwichrzenia:
•
Smukłość względna przy zwichrzeniu (wzór dokładny)
f̅
s
= 1,15 ∙ j
T
]N
T
_t
•
Wyznaczenie momentu krytycznego
T
_t
= ±[
v
∙ *
R
+ wx[
v
∙ *
R
y
+
+ z
+
∙ S
{
+
∙ *
R
∙ *
|
[
v
= [
-
∙
R
+ [
+
∙ }
{
[
-
= 0,61, [
+
= 0,53, g
R
= 1,0, g
d
= 1,0, z = 1,14
~
{
= 0, Z
N
= 0 ⟹
R
= 0
}
v
=
ℎ
2 =
140
2 = 70
= 7,0 9 ⟹ }
{
= ~
{
− }
v
= 0 − 7,0 = −7,0 9
S
{
+
= S
v
+
+ ~
{
+
S
v
+
= S
N
+
+ S
R
+
= 5,74
+
+ 1,65
+
= 35,67 9
+
S
{
+
= 35,67 + 0 = 35,67 9
+
[
v
= 0,61 ∙ 0 + 0,53 ∙ (−7,0) = −3,71 9
*
R
=
€
+
∙ • ∙ `
R
xg
R
∙ y
+
=
3,14
+
∙ 20500 ∙ 44,90
(1,0 ∙ 0,5 ∙ 600)
+
= 100,84 )*
*
|
=
1
S
{
+
∙ ‚
€
+
∙ • ∙ `
d
(g
d
∙ )
+
+ \ ∙ `
c
ƒ =
1
35,67 ∙ ‚
3,14
+
∙ 20500 ∙ 1980
(1,0 ∙ 600)
+
+ 8000 ∙ 2,45ƒ = 580,65 )*
T
_t
= +(−3,71) ∙ 100,84 + „(−3,71 ∙ 100,84)
+
+ 1,14
+
∙ 35,67 ∙ 100,84 ∙ 580,65 = 1315,34 )*
f̅
s
= 1,15 ∙ j
1661,95
1315,34 = 1,293
•
Współczynnik
l
s
względem krzywej a
0
(n = 2,5)
l
s
= m1 + f
s
kkk
+o
p
q-
o
= (1 + 1,293
…
)
q-
+,…
= 0,542
Nośność na dwukierunkowe zginanie ze ściskaniem:
•
Siła osiowa N pochodzi ze stężenia – założono wartość:
* = 10 )*
•
l
N
> l
R
, zatem:
l
†
= l
R
= 0,203
∆
†
= ∆
R
≤ 0,1
*
l
†
∙ *
]_
+
2
N
∙ T
N,V"N
l ∙ T
ˆ
+
2
R
∙ T
R,V"N
T
~
≤ 1 − ∆
†

8
•
wyznaczenie
2
N
∙ T
N,V"N
}ˆ ‰
T
N,V"N
-
= 5,386 )*
T
N,V"N
W
= 0,4 ∙ 7,484 = 2,994 )* Š
⟹
2
N
∙ T
N,V"N
= 5,386 )*
•
wyznaczenie
2
R
∙ T
R,V"N
}ˆ ‰
T
R,V"N
-
= 0,358 )*
T
R,V"N
W
= 0,4 ∙ 0,497 = 0,199 )* Š
⟹
2
R
∙ T
R,V"N
= 0,358 )*
10,0
0,203 ∙ 352,6 +
538,6
0,542 ∙ 1661,95 +
35,8
264,45 ≤ 1 − ∆
†
0,140 + 0,598 + 0,135 = 0,873 ≤ 1 − ∆
†
∆
†
= 1,25 ∙ l
†
∙
f
S
‹
2
∙
2
†
∙ T
†,V"N
T
S
∙
*
*
9
≤ 0,1
∆
R
= 1,25 ∙ 0,203 ∙ 2,164
+
∙
35,8
264,45 ∙
10
352,6 = 0,005 ≤ 0,1
Nośność na zginanie ze ścinaniem nad podporą oraz środnik w złożonym stanie naprężeń:
*
*
]
+
T
N
W
T
]N,Œ
+
T
R
W
T
]R,Œ
≤ 1,0
T
R
W
= 0,508 )*
•
Człon względem osi x-x
Y
],N
= 0,58 ∙ [
Œ
∙ ^
B
[
Œ
= (14 − 2 ∙ 0,69) ∙ 0,47 = 5,931 9
+
Y
],N
= 0,58 ∙ 5,931 ∙ 21,5 = 73,96 )*
Y
N,#
W
= 7,011 )* < 0,6 ∙ Y
],N
= 0,6 ∙ 73,96 = 44,38 )*
Zgodnie z punktem 4.5.2.d normy [nr] nie występuje redukcja nośności na zginanie ze względu na
ścinanie. Dalsze obliczenia
T
]N,Œ
nie są potrzebne.
T
]N,Œ
≡ T
]N
= 1661,95 )*9
•
Człon względem osi y-y
Y
],R
= 0,58 ∙ [
Œ
∙ ^
B
[
Œ
= 2 ∙ 14 ∙ 0,69 = 19,32 9
+
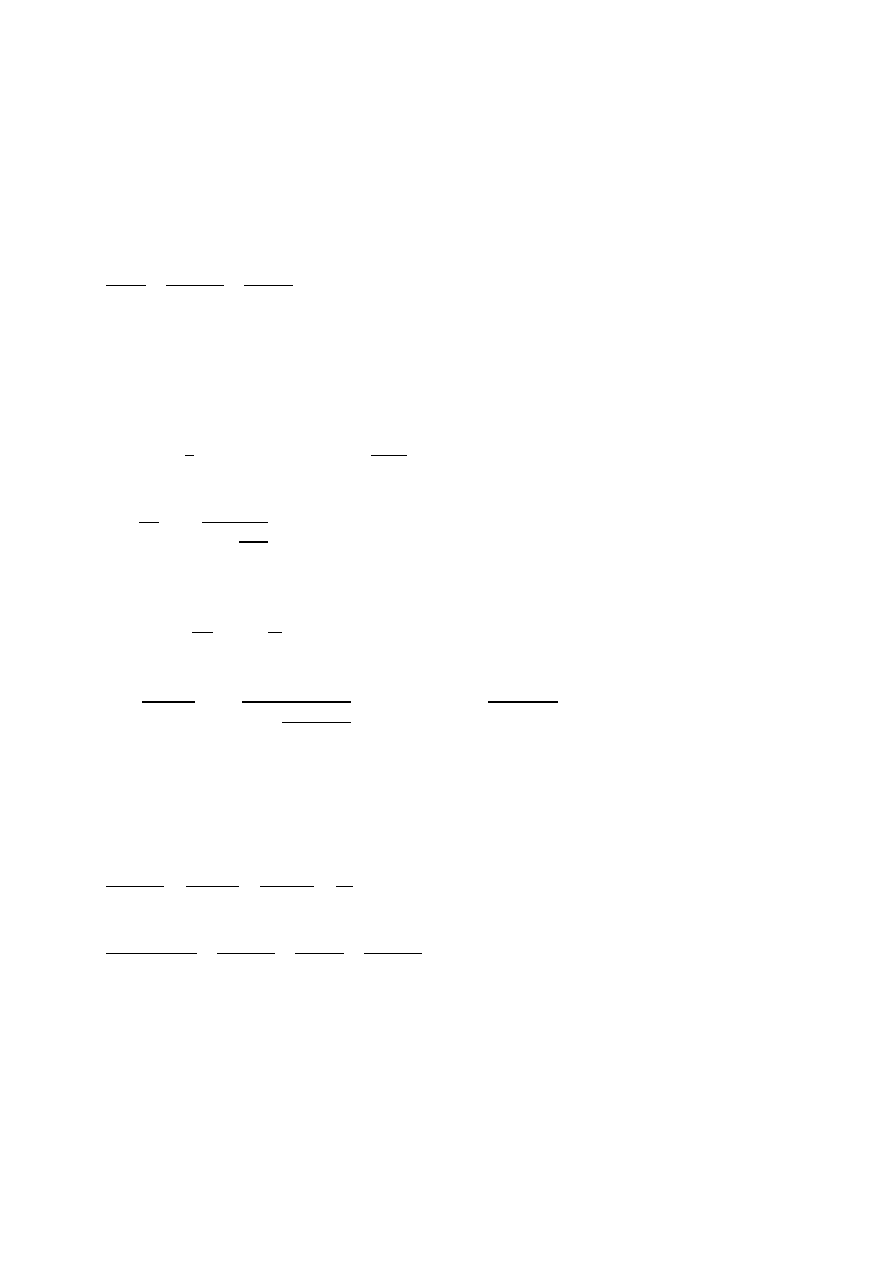
9
Y
],R
= 0,58 ∙ 19,32 ∙ 21,5 = 125,62 )*
Y
R,#
W
= 0,463 )* < 0,6 ∙ Y
],R
= 0,6 ∙ 125,62 = 75,37 )*
T
]R,Œ
≡ T
]R
= 264,45 )*9
•
Sprawdzenie nośności
10
352,6 +
748,4
1661,95 +
49,70
264,45 ≤ 1,0
0,028 + 0,450 + 0,188 ≤ 1,0
0,666 ≤ 1,0
Określenie wpływu skręcania:
{
= ;
BN
∙
ℎ
2 = 0,129 ∙ 0,07 = 0,0090
)*
z =
{
>
+
Ž1 −
1
9OPℎ > ∙2
•
Wartość K odczytano z tablic do projektowania konstrukcji metalowych [nr].
> = 0,0220
1
9 = 2,20
1
z =
0,0090
2,20
+
Ž1 −
1
9OPℎ 2,20 ∙ 6,0
2
• = 0,0018 1 −
1
9OPℎ6,60
z = 0,0018 ∙ 0,997 = 0,00179 )*
+
= 17,90 )*9
+
z
t
= =
d
∙ ^
B
= 81,5 ∙ 21,5 = 1752,25 )*9
+
Wartość
=
d
odczytano z tablic do projektowania konstrukcji metalowych [nr].
*
l
†
∙ *
]_
+
T
N,V"N
T
ˆ
+
T
R,V"N
T
~
+
z
z
Z
≤ 1,0
10,0
0,203 ∙ 352,6 +
538,6
1661,95 +
35,8
264,45 +
17,9
1752,25 ≤ 1,0
0,140 + 0,324 + 0,135 + 0,010 ≤ 1,0
0,609 ≤ 1,0
Wszystkie warunki dotyczące stanu granicznego nośności dla założonej płatwi są spełnione, dlatego
przyjęto ją do dalszych obliczeń.
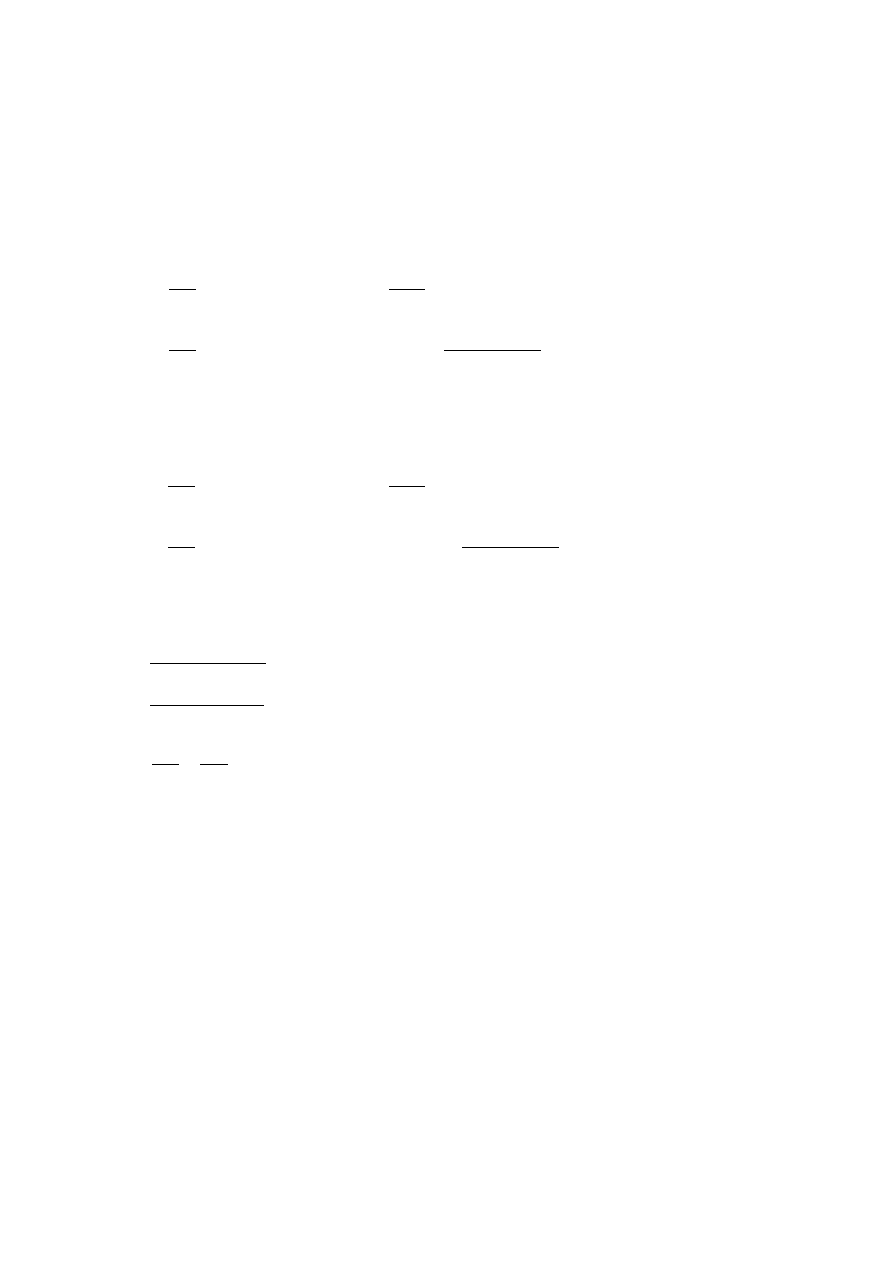
10
7.1.3.4. Projektowanie płatwi – II stan graniczny (SGU)
Dla stanu granicznego użytkowalności sprawdza się dopuszczalne ugięcie.
Sprawdzenie ugięcia metodą uproszczoną:
•
W płaszczyźnie y-z
ˆ
t|0_|
=
5
384 ∙ (0,5 ∙ /
!N
+ 0,75 ∙ /
|V,N
) ∙
a
`
U
∙ •
ˆ
t|0_|
=
5
384 ∙ (0,5 ∙ 0,00296 + 0,75 ∙ 0,01077) ∙
600
a
541,0 ∙ 20500
ˆ
t|0_|
= 0,0130 ∙ 0,0096 ∙ 11685,7 = 1,458 9
•
W płaszczyźnie x-z
~
t|0_|
=
5
384 ∙ (0,5 ∙ /
!R
+ 0,75 ∙ /
|V,R
) ∙
a
`
X
∙ •
~
t|0_|
=
5
384 ∙ (0,5 ∙ 0,000197 + 0,75 ∙ 0,000717) ∙
300
a
44,90 ∙ 20500
~
t|0_|
= 0,0130 ∙ 0,000636 ∙ 8800,0 = 0,073 9
•
Wypadkowe ugięcie
} = „ˆ
t|0_|+
+ ~
t|0_|+
} = „1,458
+
+ 0,073
+
= 1,460 9
}
•t
= 200 =
600
200 = 3,0 9
1,46 9 < 3,0 9
Ugięcie graniczne nie zostało przekroczone, stąd nie ma potrzeby sprawdzania ugięcia metodą
dokładną.
Warunek dotyczący stanu granicznego użytkowalności dla założonej płatwi jest spełniony.
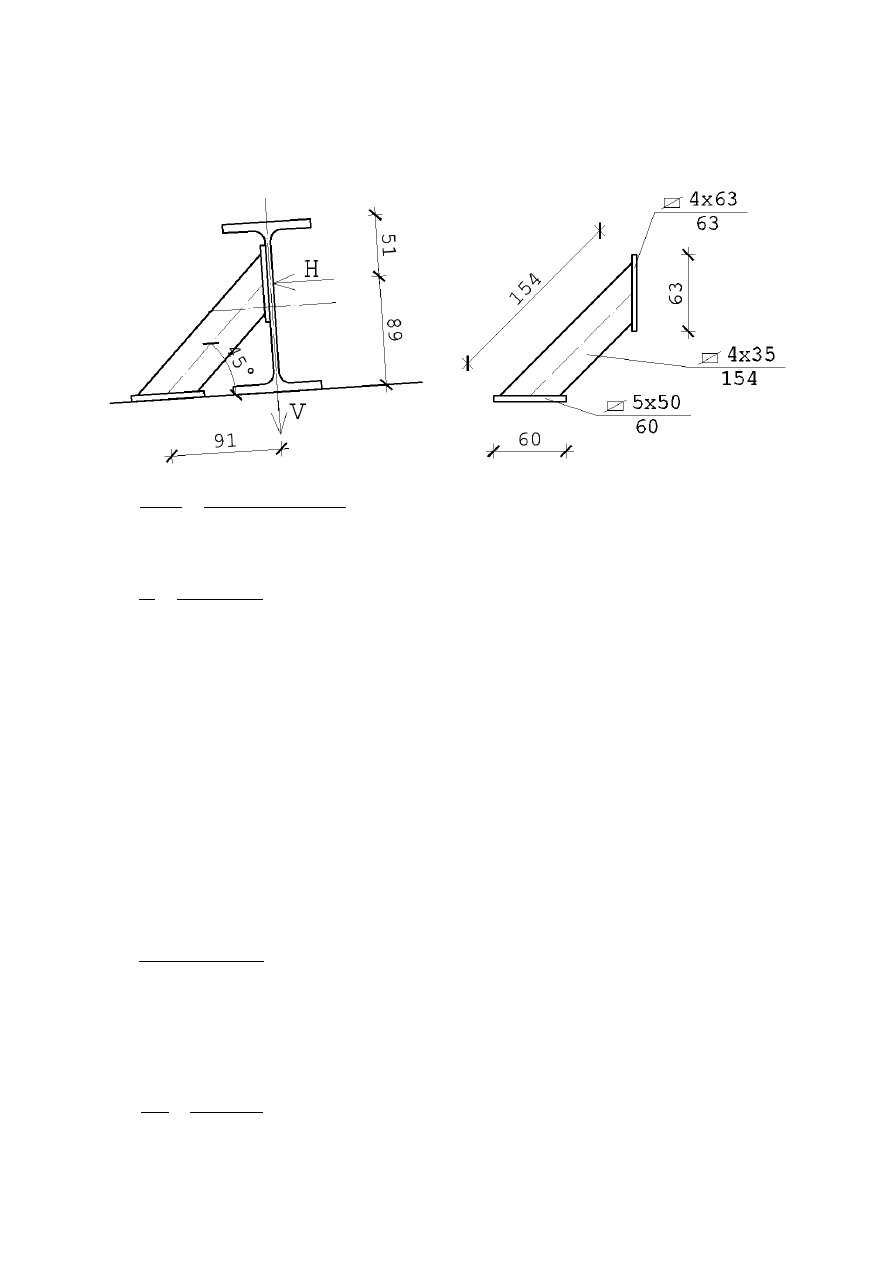
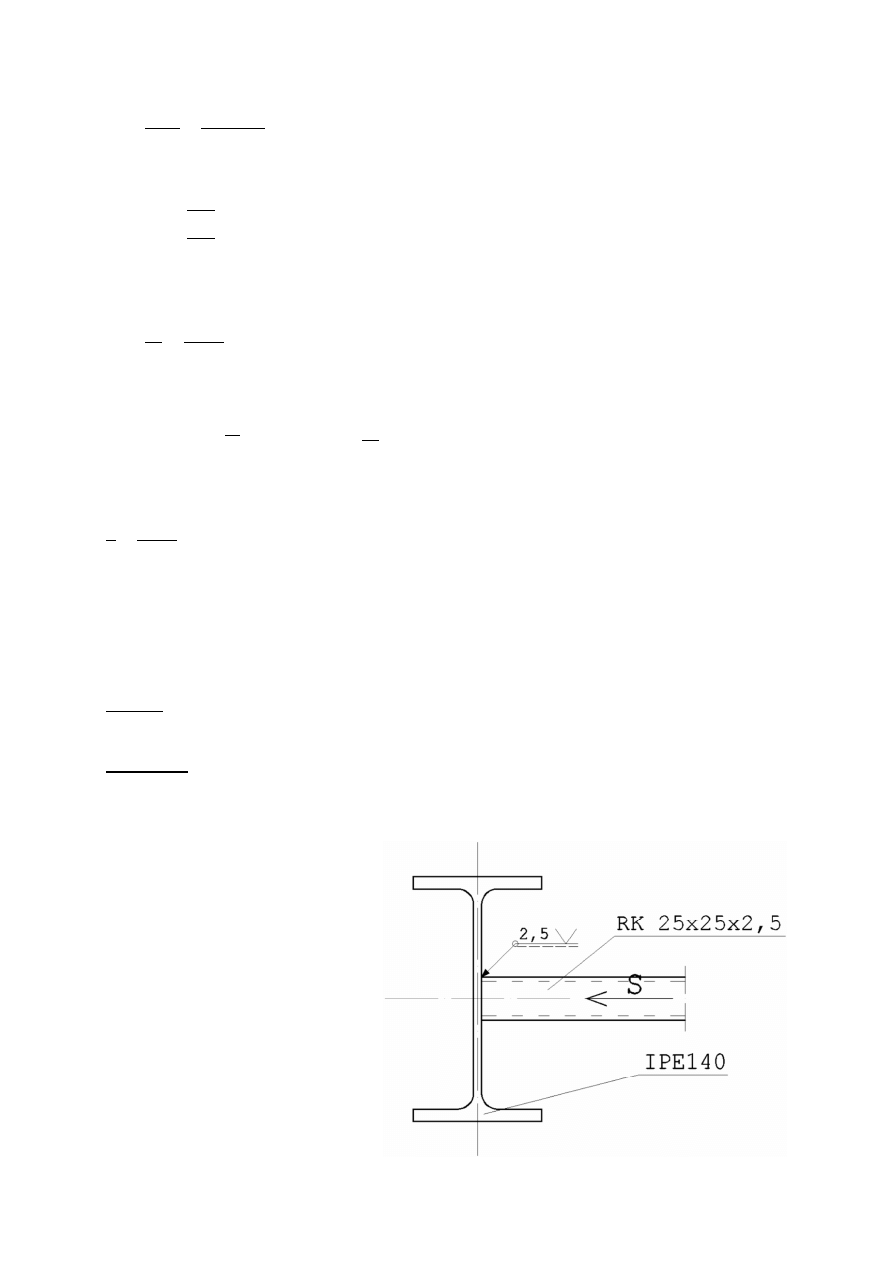
Dla płatwi przekroju I 140 PE oblicza się odpowiednie zamocowanie na podporze (do pasa górnego
kratownicy) oraz wcześniej założone podwieszenie.
11
7.1.3.5. Zamocowanie płatwi na podporze do pasa górnego kratownicy
Wyznaczenie sił działających w połączeniu:
1 =
/
BR
∙
2 =
0,129 )*⁄ ∙ 6,0
2
= 0,387 )*
T = 1 ∙ ‘
’
= 0,387 )* ∙ 8,9 9 = 3,444 kNc
Y =
T
‘
–
=
3,444 )*9
9,1 9
= 0,378 )*
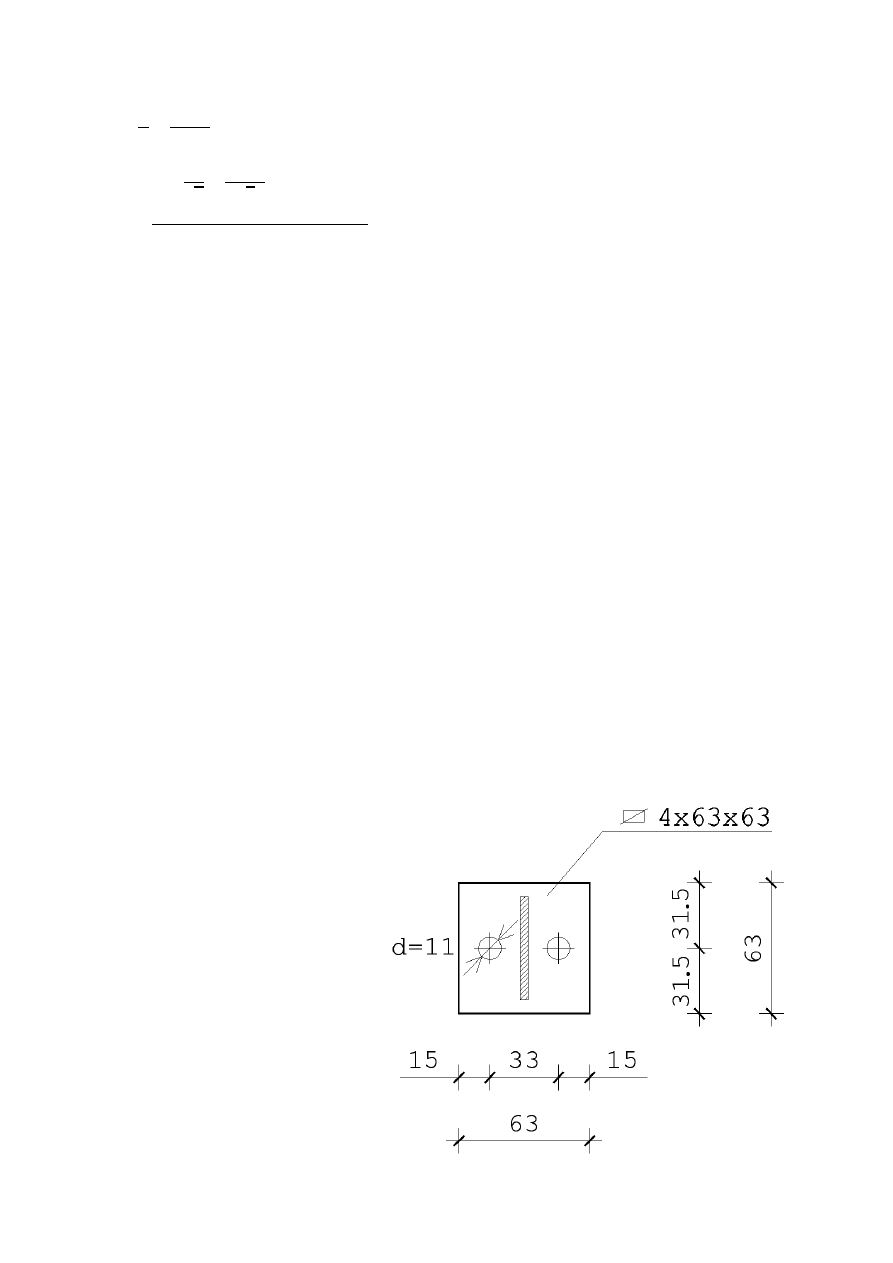
Połączenie podparcia z pasem górnym wiązara:
•
Grubość spoiny
0,2 ∙
V"N
2,5
— ≤ } ≤ ˜0,7 ∙
V†o
16
V"N
=
V†o
= 5
0,2 ∙ 5 ≤ } ≤ 0,7 ∙ 5
2,5 ≤ } ≤ 3,5
Przyjęto -
™ = š, › II
•
Nośność spoiny
œ ∙ w•
ž
+
+ 3 ∙ (Ÿ
∥
+
+ Ÿ
ž
+
) ≤ ^
B
= 5
< 16
→ ^
B
= 215 T¡}
0,V†o
= 235 T¡} ≤ 255 T¡} → œ = 0,7
Ÿ
∥
=
1
}
∙
=
0,387
2
∙
0,25
∙
6 = 0,129 )*/9
+
12
• =
Y
[ =
0,378
3 = 0,126 )*/9
+
•
ž
= Ÿ
ž
=
•
√2
=
0,126
√2
= 0,089 )*/9
+
0,7 ∙ „0,089
+
+ 3 ∙ (0,129
+
+ 0,089
+
) = 0,20 )*/9
+
≤ ^
B
= 21,5 )*/9
+
Warunek spełniono
Połączenie podparcia z płatwią na 2 śruby M10 kl. 4.8. (kategoria A):
•
Dane
]Œ
= 14,8 )*
V
= 420 T¡}
0
= 340 T¡}
Otwory okrągłe (średnio dokładne):
¤ = 10
; ∆= 1
; ¤
v
= ¤ + ∆= 11
•
Rozmieszczenie śrub (otworów)
1,5 ∙ ¤ ≤ }
-
, }
+
≤ S ¦
12 ∙
150
4 ∙ + 40
1,5 ∙ 10 ≤ }
-
, }
+
≤ S ¦
12 ∙ 4 = 48
150
4 ∙ 4 + 40 = 56
15
≤ }
-
, }
+
≤ 48
Przyjęto -
™
E
= FE, › II, ™
š
= E›, § II
2,5 ∙ ¤ ≤ }
b
≤ ˜ 14 ∙
200
2,5 ∙ 10 ≤ }
b
≤ ˜14 ∙ 4 = 56
200
25
≤ }
b
≤ 84
Przyjęto -
™
F
= FF II
Schemat rozmieszczenia śrub na
rysunku obok.
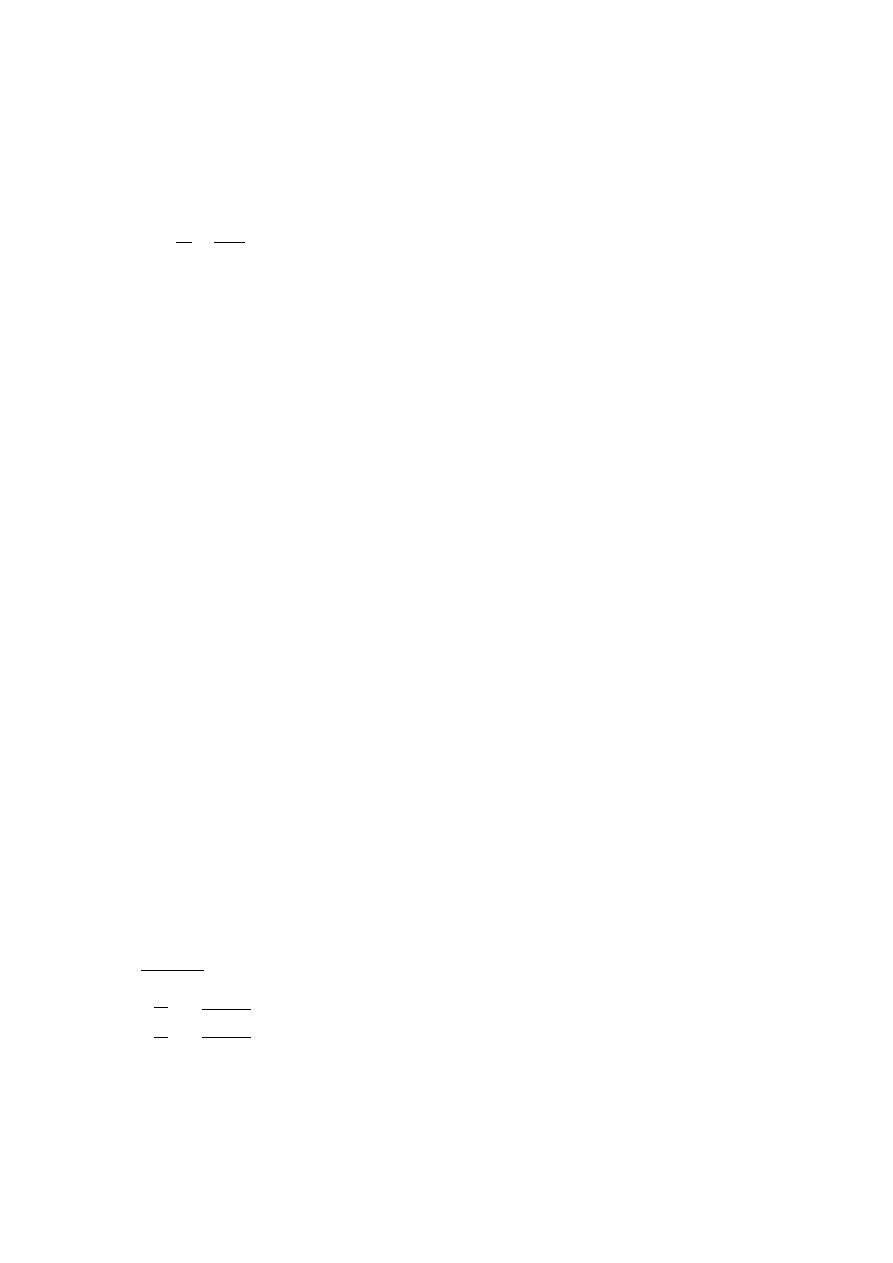
13
Sprawdzenie Stanu Granicznego Nośności łączników:
•
Nośność śrub ze względu na docisk
]¨
= Q ∙ Σ ∙ ^
B
∙ ¤
Q = S ª
}
-
¤ =
31,5
10 = 3,15 ≤ 2,5
Q = 2,5
Σ = 4
= 0,4 9
¤ = 10
= 1,0 9
]¨
= 2,5 ∙ 0,4 ∙ 21,5 ∙ 1,0 = 21,5 )*
•
Warunek nośności
* ≤ «
]¬
«
]¬
= ∙ - ∙
]
= 2 (dwie śruby)
- = 1,0 (nie trzeba stosować współczynnika redukcyjnego)
]
= S ª
]Œ
= 14,8 )*
]¨
= 21,5 )*
]
= 14,8 )*
«
]¬
= 2 ∙ 1,0 ∙ 14,8 = 29,6 )*
0,387 )* ≤ 29,6 )*
Warunek spełniono
Sprawdzenie nośności płaskownika połączenia:
•
Charakterystyka przekroju
[ = 0,4 ∙ 3,5 = 1,4 9
+
`
R
=
3,5 ∙ 0,4
b
12
= 0,0187 9
a
S
R
= j
`
R
[ = j
0,0187
1,4 = 0,116 9
•
Określenie wpływu wyboczenia
Smukłość względem osi y-y:
14
f
R
=
g
R
∙
S
R
1,0 ∙ 15,4
0,116
132,8 i 250
Smukłość porównawcza:
f
84
∙
j
215
^
B
84
Smukłość względna:
f
R
kkk f
R
f
132,8
84
1,581
Współczynnik
l
R
względem krzywej c (n = 1,2)
l
R
m1 n f
R
kkk
+o
p
q-
o
1 n 1,581
+,a
q-
-,+
0,315
•
Określenie klasy przekroju
8,427
0,4
21,08 i 33 ∙ ® 33 → ) }P} ` 3Z¯‘)ZO°±
•
Sprawdzenie nośności
*
]_
²
∙
[
∙
^
B
*
]_
1,0
∙
1,4
∙
21,5 30,1 )*
*
l
R
∙ *
]_
1,0
0,387
0,315 ∙ 30,1 0,05 1,0
Warunek spełniono
7.1.3.6. Podwieszenie płatwi
Podwieszenie oblicza się na siłę S,
którą wyraża wzór:
0,01 ∙ [ ∙ ^
B
[
[
:
:
∙
:
[
0,47 ∙ 10,8 5,076 9
+
0,01 ∙ 5,08 ∙ 21,5 1,091 )*
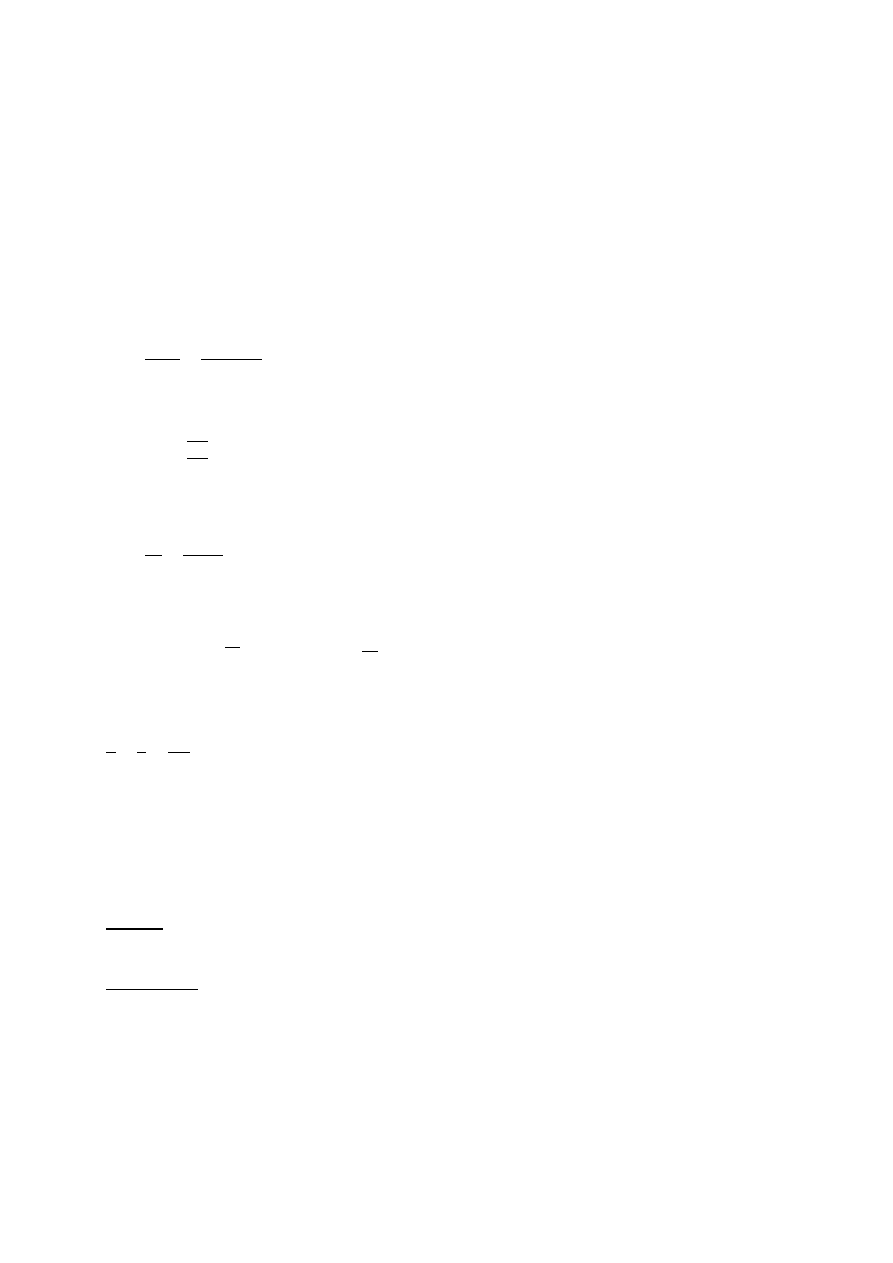
15
Wyznaczenie przekroju i obliczenie nośności:
•
Charakterystyka przekroju RK 25x25x2
[ 2,09 9
+
S
N
= S
R
= 0,899 9
•
Określenie wpływu wyboczenia
Smukłość względem osi y-y:
f
R
=
g
R
∙
S
R
=
1,0 ∙ 150
0,899 = 166,9 < 250
Smukłość porównawcza:
f = 84 ∙ w
+-…
@
³
= 84
Smukłość względna:
f
R
kkk = f
R
f =
166,9
84 = 1,987
Współczynnik
l
N
względem krzywej b (n = 1,6)
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,987
b,+
)
q-
-,e
= 0,237
•
Określenie klasy przekroju
ℎ
= =
25
2,5 = 10 < 23 × ® = 23 → ) }P} ` 3Z¯‘)ZO°±
•
Sprawdzenie nośności
*
]_
= ²
∙
[
∙
^
B
*
]_
= 1,0 ∙ 2,09 ∙ 21,5 = 44,94 )*
*
l
R
∙
*
]_
≤ 1,0
1,091
0,237
∙
44,94 = 0,10
0,10 ≤ 1,0
Warunek spełniono
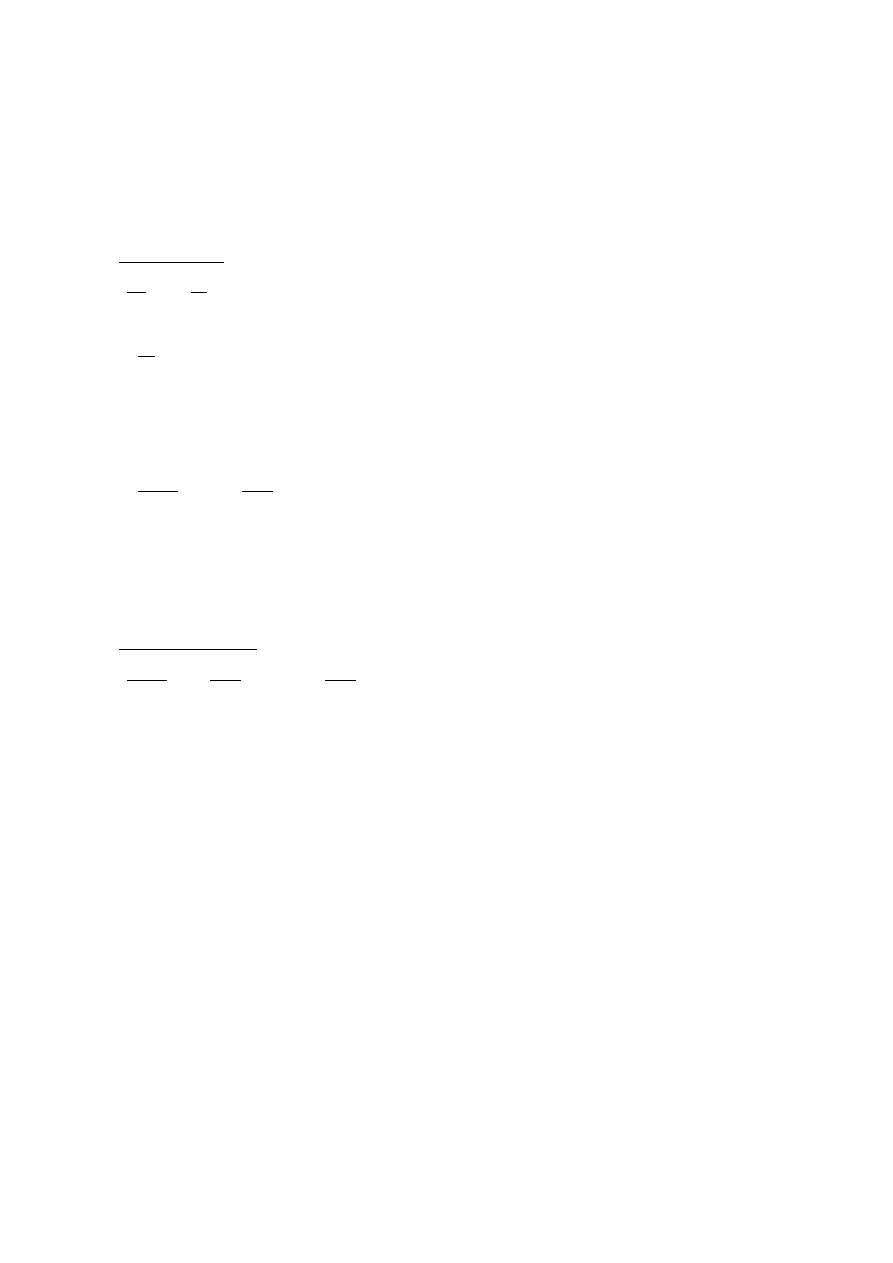
16
Zaprojektowanie spoiny łączącej podwieszenie z płatwią:
Grubość spoiny obwodowej:
™
V†o
š, › II
•
Naprężenia w spoinie:
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
• =
*
[
{
* = 1,091 )*
[
{
= 4 ∙ 0,25 ∙ 0,25 = 0,25 9
+
• =
1,091
0,25 = 4,364
)*
9
2
= 43,64 T¡}
Wartość współczynnika wytrzymałości spoiny, zgodnie tablicą 18 normy [N nr], należy zredukować,
gdyż jest to spoina pułapowa wykonywana na budowie.
Q
ž
= 0,70
Q
∥
= 0,42
j 4,364
0,70
+
+
0
0,42
+
= 6,234
)*
9
2
= 62,34 T¡} ≤ ^
B
= 215 T¡}
Warunek spełniono

17
7.1.4. Wiązar kratowy
7.1.4.1. Zestawienie obciążeń
Do obciążeń stałych dodany zostanie ciężar własny kratownicy według wzoru empirycznego
zawartego w normie [N nr].
,
·
¸
2,0
} + 0,12 ∙ x9
:
+
!
y¹ ∙ ∙ 10
q+
∙ Z ∙ }
= 15,0 ; Z = 1,50 ; } = 6,0
,
·
= ¸
2,0
6,0 + 0,12 ∙ (0,113 + 0,720)¹ ∙ 15,0 ∙ 0,01 ∙ 1,5 ∙ 6,0 = 0,585 )*
wg [N nr], [N nr], [N nr]
Rodzaj obciążenia
Obciążenie
charakterystyczne
Współczynnik
obciążenia
?
@
Obciążenie
obliczeniowe
)*
)*
Obciążenie stałe z płatwi
0,297 ∙ 6,0 ∙ (0,607 + 0,536)
2,037
1,1
2,241
Ciężar własny wiązara
,
·
= 0,585 )*
0,585
1,1
0,644
razem
2,622
-
2,885
Obciążenie śniegiem
0,72 ∙ 1,5 ∙ 6,0 ∙ 1,143
7,407
1,5
11,11
Obciążenie wiatrem
- połać nawietrzna
−0,292 ∙ 1,5 ∙ 6,0 ∙ 1,143
- połać zawietrzna
−0,130 ∙ 1,5 ∙ 6,0 ∙ 1,143
−3,004
−1,337
1,5
1,5
−4,506
−2,006
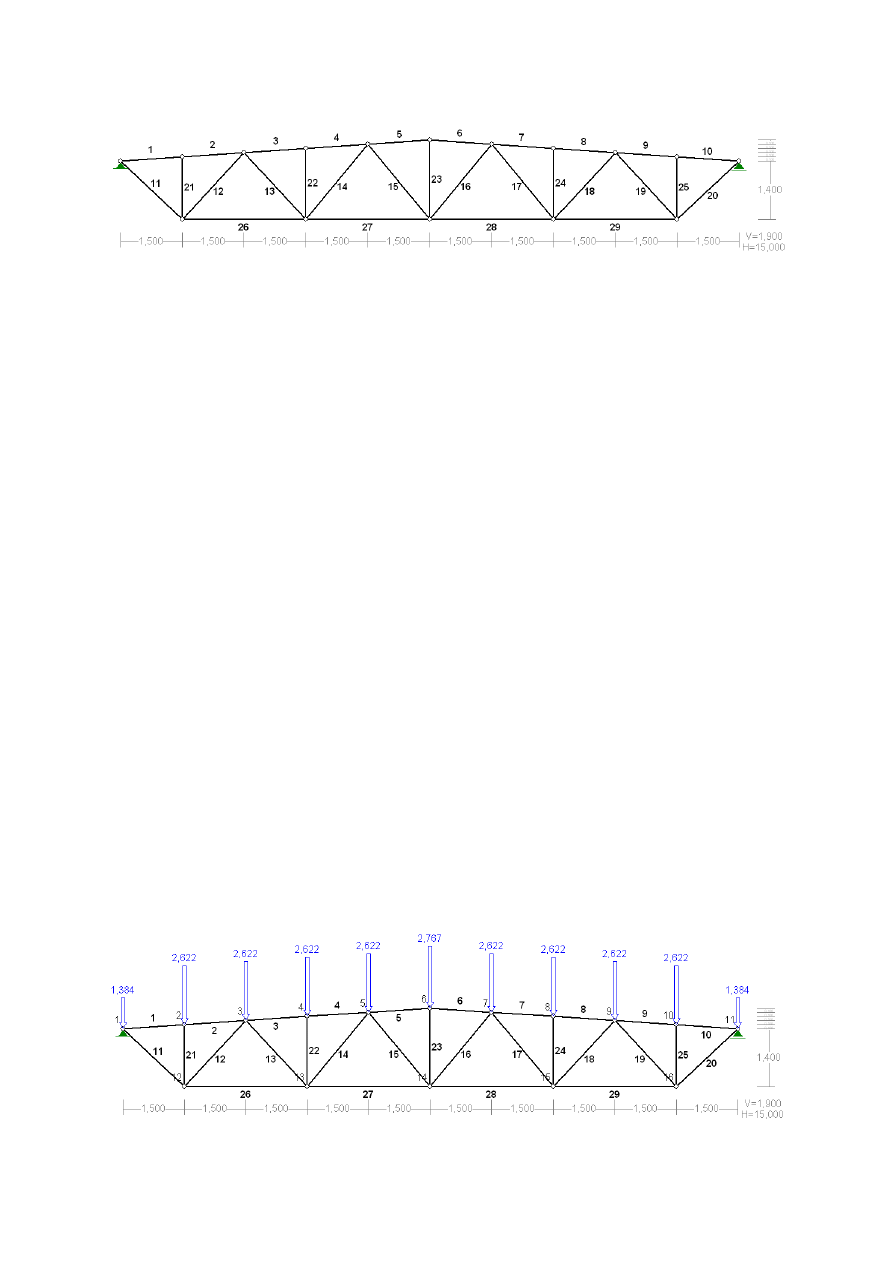
7.1.4.2. Wyznaczenie obciążeń na węzły wiązara
•
Reakcja od obciążenia ciężarem własnym płatwi
\
:!
= 0,127 ∙ 1,143 = 0,145 )*
•
Obciążenia stałe skupione w węzłach
¡
-!
= 0,5 ∙ (0,145 + 2,622) = 1,384 )*
¡
+!
= 2,622 )*
¡
b!
= 2,622 + 0,145 = 2,767 )*
W węźle okapowym do połowy obciążenia skupionego stałego na węzeł dodano połowę ciężaru
płatwi (
¡
-!
). W węźle kalenicowym do wyznaczonego obciążenia stałego dodano ciężar drugiej płatwi
znajdującej się w kalenicy (
¡
b!
).
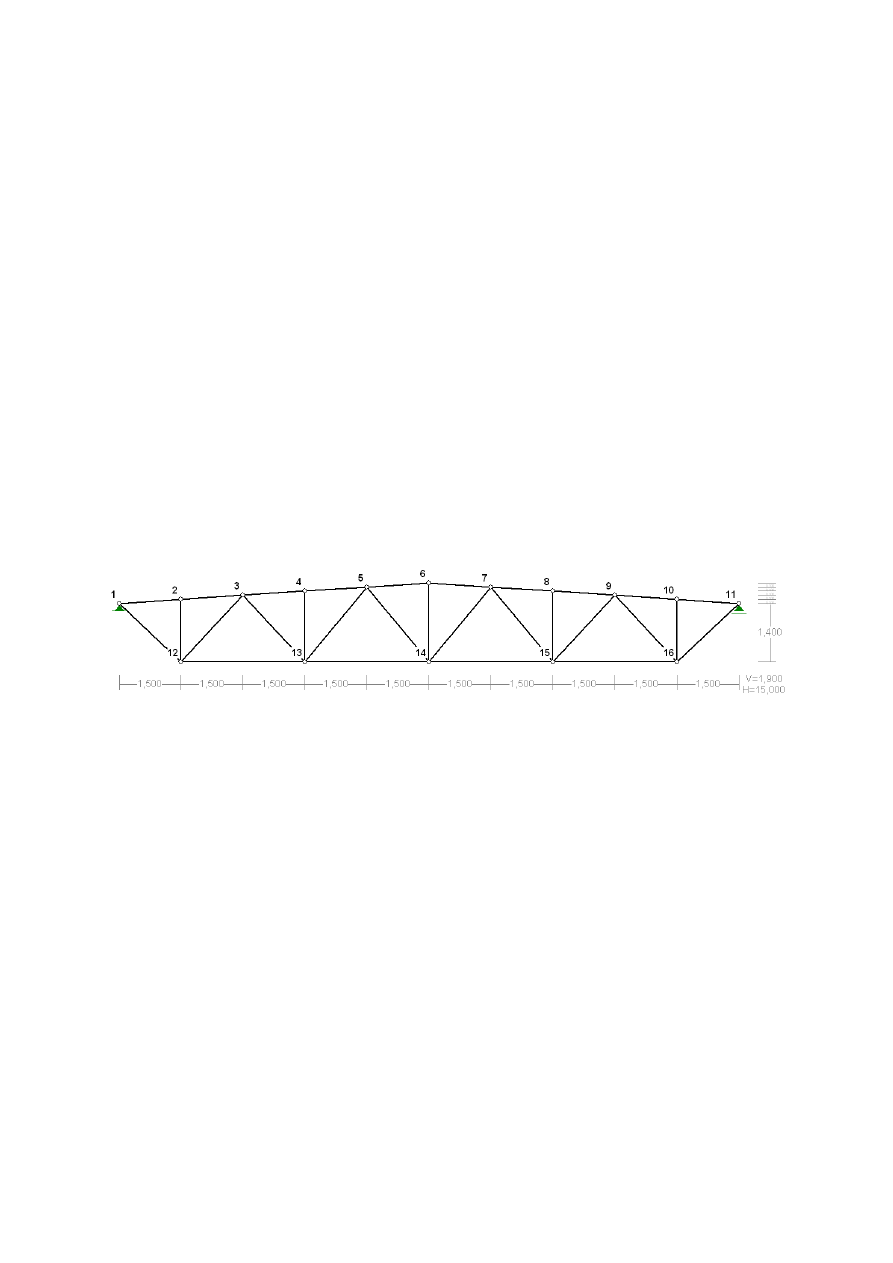
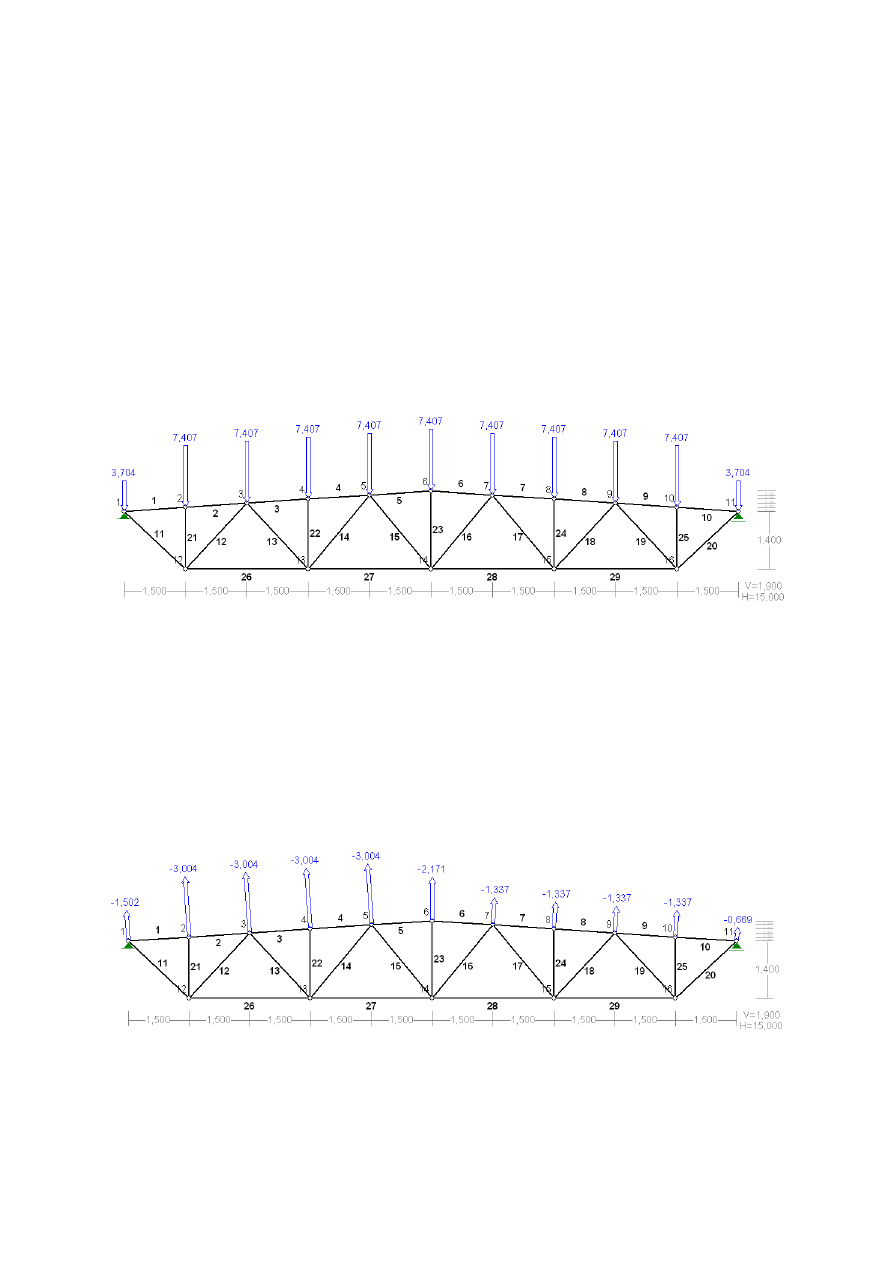
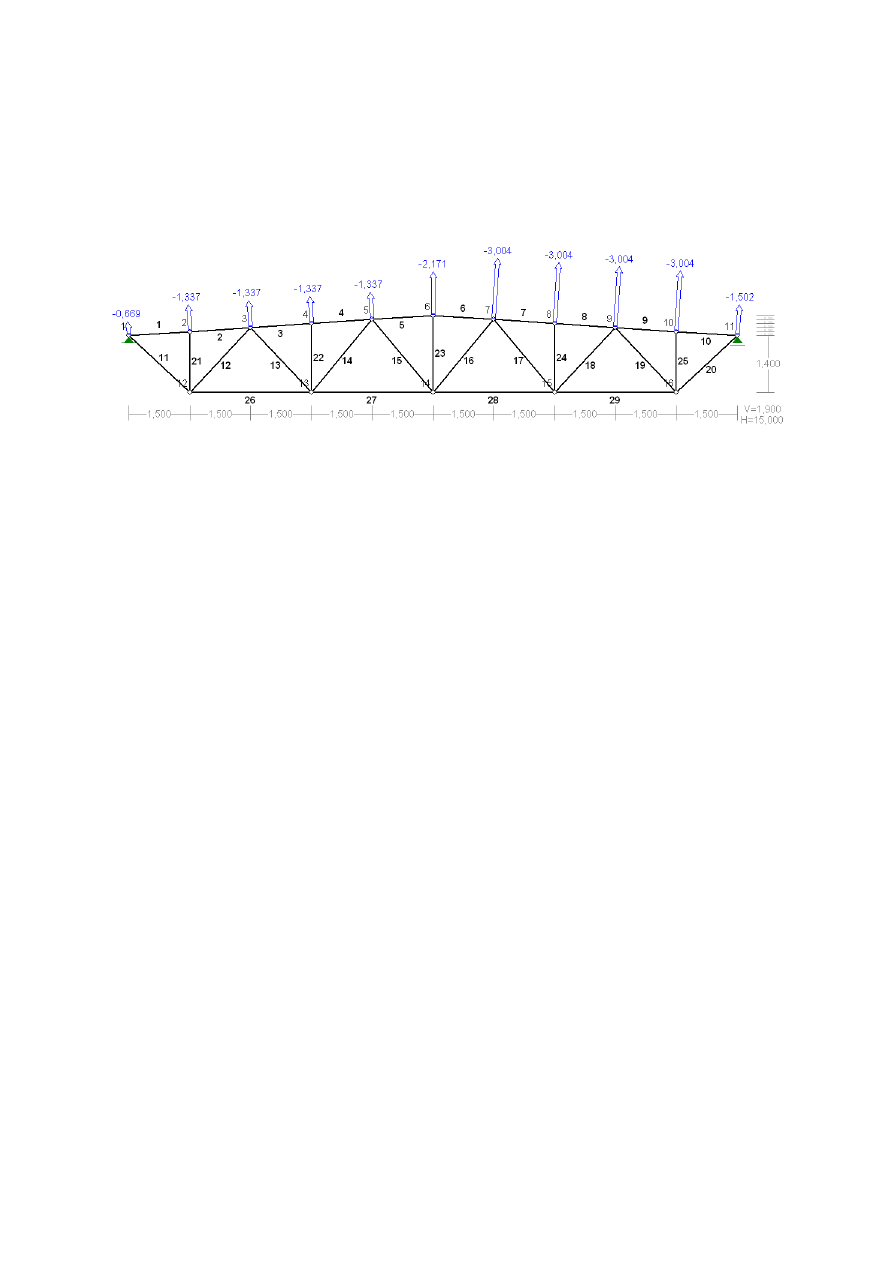
18
•
Obciążenia skupione od śniegu
-!
0,5 ∙ 7,407 = 3,704 )*
+!
= 7,407 )*
•
Obciążenia skupione od wiatru
=
-!
= −3,004 ∙ 0,5 = −1,502 )*
=
+!
= −3,004 )*
=
b!,o
= −3,004 ∙ 0,5 = −1,502 )*
=
b!,|
= −1,337 ∙ 0,5 = −0,669 )*
=
a!
= −1,337 )*
=
…!
= −1,337 ∙ 0,5 = −0,669 )*
7.1.4.3. Wyznaczenie (program RM-Win 4.21) i zestawienie sił w prętach
W
Ę
ZŁY
W
Ę
ZŁY:
------------------------------------------------------------------
Nr: X [m]: Y [m]: Nr: X [m]: Y [m]:
------------------------------------------------------------------
1 0,000 1,400 9 12,000 1,600
2 1,500 1,500 10 13,500 1,500
3 3,000 1,600 11 15,000 1,400
4 4,500 1,700 12 1,500 0,000
5 6,000 1,800 13 4,500 0,000
6 7,500 1,900 14 7,500 0,000
7 9,000 1,800 15 10,500 0,000
8 10,500 1,700 16 13,500 0,000
------------------------------------------------------------------
PODPORY: P o d a t n o
ś
c i
------------------------------------------------------------------
W
ę
zeł: Rodzaj: K
ą
t: Dx(Do*): Dy: DFi:
[ m / k N ] [rad/kNm]
------------------------------------------------------------------
1 stała 0,0 0,000E+00 0,000E+00
11 przesuwna 0,0 0,000E+00*
------------------------------------------------------------------
OSIADANIA:
B r a k O s i a d a
ń
19
PR
Ę
TY
PR
Ę
TY UKŁADU:
Typy pr
ę
tów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;
10 - przegub-sztyw.; 11 - przegub-przegub
22 - ci
ę
gno
------------------------------------------------------
Pr
ę
t: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ:
------------------------------------------------------
1 11 2 1 -1,500 -0,100 1,503 1,000
2 11 2 3 1,500 0,100 1,503 1,000
3 11 3 4 1,500 0,100 1,503 1,000
4 11 5 4 -1,500 -0,100 1,503 1,000
5 11 5 6 1,500 0,100 1,503 1,000
6 11 7 6 -1,500 0,100 1,503 1,000
7 11 8 7 -1,500 0,100 1,503 1,000
8 11 9 8 -1,500 0,100 1,503 1,000
9 11 10 9 -1,500 0,100 1,503 1,000
10 11 10 11 1,500 -0,100 1,503 1,000
11 11 12 1 -1,500 1,400 2,052 1,000
12 11 12 3 1,500 1,600 2,193 1,000
13 11 3 13 1,500 -1,600 2,193 1,000
14 11 13 5 1,500 1,800 2,343 1,000
15 11 5 14 1,500 -1,800 2,343 1,000
16 11 14 7 1,500 1,800 2,343 1,000
17 11 7 15 1,500 -1,800 2,343 1,000
18 11 15 9 1,500 1,600 2,193 1,000
19 11 9 16 1,500 -1,600 2,193 1,000
20 11 16 11 1,500 1,400 2,052 1,000
21 11 12 2 0,000 1,500 1,500 1,000
22 11 13 4 0,000 1,700 1,700 1,000
23 11 14 6 0,000 1,900 1,900 1,000
24 11 15 8 0,000 1,700 1,700 1,000
25 11 16 10 0,000 1,500 1,500 1,000
26 11 12 13 3,000 0,000 3,000 1,000
27 11 13 14 3,000 0,000 3,000 1,000
28 11 14 15 3,000 0,000 3,000 1,000
29 11 15 16 3,000 0,000 3,000 1,000
------------------------------------------------------
OBCI
ĄŻ
ENIA - A
20
OBCI
ĄŻ
ENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------
Pr
ę
t: Rodzaj: K
ą
t: P1(Tg): P2(Td): a[m]: b[m]:
------------------------------------------------------------------
Grupa: A "obci
ąż
enia stałe" Stałe
γ
f= 1,10
1 Skupione 0,0 1,384 1,50
2 Skupione 0,0 2,622 0,00
3 Skupione 0,0 2,622 0,00
4 Skupione 0,0 2,622 1,50
5 Skupione 0,0 2,622 0,00
6 Skupione 0,0 2,767 1,50
7 Skupione 0,0 2,622 1,50
8 Skupione 0,0 2,622 1,50
9 Skupione 0,0 2,622 1,50
10 Skupione 0,0 2,622 0,00
10 Skupione 0,0 1,384 1,50
OBCI
ĄŻ
ENIA - B
Grupa: B "
ś
nieg" Zmienne
γ
f= 1,50
1 Skupione 0,0 3,704 1,50
2 Skupione 0,0 7,407 0,00
3 Skupione 0,0 7,407 0,00
4 Skupione 0,0 7,407 1,50
5 Skupione 0,0 7,407 0,00
6 Skupione 0,0 7,407 1,50
7 Skupione 0,0 7,407 1,50
8 Skupione 0,0 7,407 1,50
9 Skupione 0,0 7,407 1,50
10 Skupione 0,0 7,407 0,00
10 Skupione 0,0 3,704 1,50
OBCI
ĄŻ
ENIA - C
Grupa: C "wiatr z lewej" Zmienne
γ
f= 1,50
1 Skupione 3,8 -1,502 1,50
2 Skupione 3,8 -3,004 0,00
3 Skupione 3,8 -3,004 0,00
4 Skupione 3,8 -3,004 1,50
5 Skupione 3,8 -3,004 0,00
21
6 Skupione 0,0 -2,171 1,50
7 Skupione -3,8 -1,337 1,50
8 Skupione -3,8 -1,337 1,50
9 Skupione -3,8 -1,337 1,50
10 Skupione -3,8 -1,337 0,00
10 Skupione -3,8 -0,669 1,50
OBCI
ĄŻ
ENIA - D
Grupa: D "wiatr z prawej" Zmienne
γ
f= 1,50
1 Skupione 3,8 -0,669 1,50
2 Skupione 3,8 -1,337 0,00
3 Skupione 3,8 -1,337 0,00
4 Skupione 3,8 -1,337 1,50
5 Skupione 3,8 -1,337 0,00
6 Skupione 0,0 -2,171 1,50
7 Skupione -3,8 -3,004 1,50
8 Skupione -3,8 -3,004 1,50
9 Skupione -3,8 -3,004 1,50
10 Skupione -3,8 -3,004 0,00
10 Skupione -3,8 -1,502 1,50
------------------------------------------------------------------
==================================================================
W Y N I K I
Teoria I-go rz
ę
du
Kombinatoryka obci
ąż
e
ń
==================================================================
OBCI
ĄŻ
ENIOWE WSPÓŁ. BEZPIECZ.:
------------------------------------------------------------------
Grupa: Znaczenie:
ψ
d:
γ
f:
------------------------------------------------------------------
A -"obci
ąż
enia stałe" Stałe 1,10
B -"
ś
nieg" Zmienne 1 1,00 1,50
C -"wiatr z lewej" Zmienne 1 1,00 1,50
D -"wiatr z prawej" Zmienne 1 1,00 1,50
------------------------------------------------------------------
RELACJE GRUP OBCI
ĄŻ
E
Ń
:
------------------------------------------------------------------
Grupa obc.: Relacje:
------------------------------------------------------------------
A -"obci
ąż
enia stałe" ZAWSZE
B -"
ś
nieg" EWENTUALNIE
C -"wiatr z lewej" EWENTUALNIE
Nie wyst
ę
puje z: D
D -"wiatr z prawej" EWENTUALNIE
Nie wyst
ę
puje z: C
------------------------------------------------------------------

22
KRYTERIA KOMBINACJI OBCI
ĄŻ
E
Ń
:
------------------------------------------------------------------
Nr: Specyfikacja:
------------------------------------------------------------------
1 ZAWSZE : A
EWENTUALNIE: B + C / D
------------------------------------------------------------------
SIŁY PRZEKROJOWE - WARTO
Ś
CI EKSTREMALNE:
T.I rz
ę
du
Obci
ąż
enia obl.: "Kombinacja obci
ąż
e
ń
"
------------------------------------------------------------------
Pr
ę
t: x[m]: M[kNm]: Q[kN]: N[kN]: Kombinacja obci
ąż
e
ń
:
------------------------------------------------------------------
1 0,000 0,000* -0,000 -63,196 AB
0,000 0,000* -0,000 -63,196 AB
0,000 0,000 -0,000* -63,196 AB
0,000 0,000 -0,000 3,497* AC
0,000 0,000 -0,000 -63,196* AB
2 0,000 0,000* 0,000 -63,196 AB
0,000 0,000* 0,000 -63,196 AB
0,000 0,000 0,000* -63,196 AB
0,000 0,000 0,000 3,797* AC
0,000 0,000 0,000 -63,196* AB
3 0,000 0,000* 0,000 -130,156 AB
0,000 0,000* 0,000 -130,156 AB
0,000 0,000 0,000* -130,156 AB
0,000 0,000 0,000 6,516* AC
0,000 0,000 0,000 -130,156* AB
4 0,000 0,000* 0,000 -130,156 AB
0,000 0,000* 0,000 -130,156 AB
0,000 0,000 0,000* -130,156 AB
0,000 0,000 0,000 6,816* AC
0,000 0,000 0,000 -130,156* AB
5 0,000 0,000* 0,000 -138,728 AB
0,000 0,000* 0,000 -138,728 AB
0,000 0,000 0,000* -138,728 AB
0,000 0,000 0,000 4,413* AD
0,000 0,000 0,000 -138,728* AB
6 0,000 0,000* 0,000 -138,728 AB
0,000 0,000* 0,000 -138,728 AB
0,000 0,000 0,000* -138,728 AB
0,000 0,000 0,000 4,413* AD
0,000 0,000 0,000 -138,728* AB
7 0,000 0,000* 0,000 -130,156 AB
0,000 0,000* 0,000 -130,156 AB
0,000 0,000 0,000* -130,156 AB
0,000 0,000 0,000 7,433* AD
0,000 0,000 0,000 -130,156* AB
8 0,000 0,000* 0,000 -130,156 AB
0,000 0,000* 0,000 -130,156 AB
0,000 0,000 0,000* -130,156 AB
0,000 0,000 0,000 7,133* AD
0,000 0,000 0,000 -130,156* AB

23
9 0,000 0,000* 0,000 -63,196 AB
0,000 0,000* 0,000 -63,196 AB
0,000 0,000 0,000* -63,196 AB
0,000 0,000 0,000 4,497* AD
0,000 0,000 0,000 -63,196* AB
10 0,000 0,000* 0,000 -63,196 AB
0,000 0,000* 0,000 -63,196 AB
0,000 0,000 0,000* -63,196 AB
0,000 0,000 0,000 4,197* AD
0,000 0,000 0,000 -63,196* AB
11 0,000 0,000* 0,000 86,253 AB
0,000 0,000* 0,000 86,253 AB
0,000 0,000 0,000* 86,253 AB
0,000 0,000 0,000 86,253* AB
0,000 0,000 0,000 -5,591* AC
12 0,000 0,000* 0,000 -61,488 AB
0,000 0,000* 0,000 -61,488 AB
0,000 0,000 0,000* -61,488 AB
0,000 0,000 0,000 2,993* AC
0,000 0,000 0,000 -61,488* AB
13 0,000 0,000* 0,000 36,199 AB
0,000 0,000* 0,000 36,199 AB
0,000 0,000 0,000* 36,199 AB
0,000 0,000 0,000 36,199* AB
0,000 0,000 0,000 -1,085* AD
14 0,000 0,000* 0,000 -16,159 AB
0,000 0,000* 0,000 -16,159 AB
0,000 0,000 0,000* -16,159 AB
0,000 0,000 0,000 2,169* AD
0,000 0,000 0,000 -16,159* AB
15 0,000 0,000* 0,000 -5,302 ABD
0,000 0,000* 0,000 -5,302 ABD
0,000 0,000 0,000* -5,302 ABD
0,000 0,000 0,000 3,458* AC
0,000 0,000 0,000 -5,302* ABD
16 0,000 0,000* 0,000 -5,350 ABC
0,000 0,000* 0,000 -5,350 ABC
0,000 0,000 0,000* -5,350 ABC
0,000 0,000 0,000 3,506* AD
0,000 0,000 0,000 -5,350* ABC
17 0,000 0,000* 0,000 -16,159 AB
0,000 0,000* 0,000 -16,159 AB
0,000 0,000 0,000* -16,159 AB
0,000 0,000 0,000 2,222* AC
0,000 0,000 0,000 -16,159* AB
18 0,000 0,000* 0,000 36,199 AB
0,000 0,000* 0,000 36,199 AB
0,000 0,000 0,000* 36,199 AB
0,000 0,000 0,000 36,199* AB
0,000 0,000 0,000 -1,142* AC
19 0,000 0,000* 0,000 -61,488 AB

24
0,000 0,000* 0,000 -61,488 AB
0,000 0,000 0,000* -61,488 AB
0,000 0,000 0,000 2,929* AD
0,000 0,000 0,000 -61,488* AB
20 0,000 0,000* 0,000 86,253 AB
0,000 0,000* 0,000 86,253 AB
0,000 0,000 0,000* 86,253 AB
0,000 0,000 0,000 86,253* AB
0,000 0,000 0,000 -5,523* AD
21 0,000 0,000* 0,000 -13,995 AB
0,000 0,000* 0,000 -13,995 AB
0,000 0,000 0,000* -13,995 AB
0,000 0,000 0,000 1,632* AC
0,000 0,000 0,000 -13,995* AB
22 0,000 0,000* 0,000 -13,995 AB
0,000 0,000* 0,000 -13,995 AB
0,000 0,000 0,000* -13,995 AB
0,000 0,000 0,000 1,632* AC
0,000 0,000 0,000 -13,995* AB
23 0,000 0,000* 0,000 4,302 AB
0,000 0,000* 0,000 4,302 AB
0,000 0,000 0,000* 4,302 AB
0,000 0,000 0,000 4,302* AB
0,000 0,000 0,000 -0,374* AD
24 0,000 0,000* 0,000 -13,995 AB
0,000 0,000* 0,000 -13,995 AB
0,000 0,000 0,000* -13,995 AB
0,000 0,000 0,000 1,632* AD
0,000 0,000 0,000 -13,995* AB
25 0,000 0,000* 0,000 -13,995 AB
0,000 0,000* 0,000 -13,995 AB
0,000 0,000 0,000* -13,995 AB
0,000 0,000 0,000 1,632* AD
0,000 0,000 0,000 -13,995* AB
26 0,000 0,000* 0,000 105,110 AB
0,000 0,000* 0,000 105,110 AB
0,000 0,000 0,000* 105,110 AB
0,000 0,000 0,000 105,110* AB
0,000 0,000 0,000 -6,134* AC
27 0,000 0,000* 0,000 140,213 AB
0,000 0,000* 0,000 140,213 AB
0,000 0,000 0,000* 140,213 AB
0,000 0,000 0,000 140,213* AB
0,000 0,000 0,000 -5,466* AC
28 0,000 0,000* 0,000 140,213 AB
0,000 0,000* 0,000 140,213 AB
0,000 0,000 0,000* 140,213 AB
0,000 0,000 0,000 140,213* AB
0,000 0,000 0,000 -5,300* AD
29 0,000 0,000* 0,000 105,110 AB
0,000 0,000* 0,000 105,110 AB

25
0,000 0,000 0,000* 105,110 AB
0,000 0,000 0,000 105,110* AB
0,000 0,000 0,000 -6,041* AD
------------------------------------------------------------------
* = Max/Min
REAKCJE - WARTO
Ś
CI EKSTREMALNE:
T.I rz
ę
du
Obci
ąż
enia obl.: "Kombinacja obci
ąż
e
ń
"
------------------------------------------------------------------
W
ę
zeł: H[kN]: V[kN]: R[kN]: M[kNm]: Kombinacja obci
ąż
e
ń
:
------------------------------------------------------------------
1 0,748* 50,780 50,785 ABC
0,748* -4,773 4,832 AC
-0,748* 56,994 56,999 ABD
-0,748* 1,441 1,624 AD
-0,000 70,134* 70,134 AB
0,748 -4,773* 4,832 AC
-0,000 70,134 70,134* AB
11 0,000* 70,134 70,134 AB
-0,000* -4,773 4,773 AD
0,000* 14,581 14,581 A
0,000 70,134* 70,134 AB
-0,000 -4,773* 4,773 AD
0,000 70,134 70,134* AB
------------------------------------------------------------------
* = Max/Min
PRZEMIESZCZENIA - WARTO
Ś
CI EKSTREMALNE:
T.I rz
ę
du
Obci
ąż
enia char.: "Kombinacja obci
ąż
e
ń
"
------------------------------------------------------------------
W
ę
zeł: Ux[m]: Uy[m]: Wypadkowe[m]: Kombinacja obci
ąż
e
ń
:
------------------------------------------------------------------
1 0,00000 ABD
0,00000 AB
0,00000
2 0,00000 AB
0,00053 AB
0,00053 AB
3 0,00000 ABC
0,00096 AB
0,00096 AB
4 0,00004 AB
0,00129 AB
0,00129 AB
5 0,00009 AB
0,00146 AB
0,00147 AB
6 0,00016 AB
0,00151 AB
0,00152 AB
7 0,00023 AB
0,00146 AB
0,00148 AB
8 0,00028 AB
0,00129 AB
0,00132 AB
26
9 0,00032 AB
0,00096 AB
0,00101 AB
10 0,00033 AB
0,00053 AB
0,00062 AB
11 0,00032 AB
0,00000 AB
0,00032 AB
12 0,00040 AB
0,00052 AB
0,00066 AB
13 0,00030 AB
0,00128 AB
0,00131 AB
14 0,00016 AB
0,00152 AB
0,00153 AB
15 0,00002 AB
0,00128 AB
0,00128 AB
16 0,00008 AB
0,00052 AB
0,00053 AB
------------------------------------------------------------------
W poniższej tablicy zestawiono maksymalne siły w poszczególnych prętach wiązara.
Nr pręta
Siły osiowe N [kN]
Długość [cm]
Przekroje –
obliczenia w
p. 7.1.4.5.
Uwagi
-
+
1 (10)
63,20
4,197
150,0
RP 100x60x5
Pas górny
2 (9)
63,20
4,497
150,0
3 (8)
130,2
7,133
150,0
4 (7)
130,2
7,433
150,0
5 (6)
138,7
4,413
150,0
26 (29)
6,134
105,1
300,0
RP 80x60x4
Pas dolny
27 (28)
5,466
140,2
300,0
11 (20)
5,591
86,25
205,2
RK 50x50x4
Krzyżulce
skratowania
12 (19)
61,49
2,993
219,3
13 (18)
1,142
36,20
219,3
RK 40x40x2
14 (17)
16,16
2,222
234,4
15 (16)
5,350
3,506
234,3
RK 25x25x2
21 (25)
14,00
1,632
150,0
RK 30x30x3
Słupki
skratowania
22 (24)
14,00
1,632
170,0
23
0,374
4,302
190,0
RK 25x25x2

27
7.1.4.4. Ugięcie wiązara (II stan graniczny)
Na podstawie wyników z programu obliczeniowego RM-Win 4.21 odczytano, że dla obciążeń
charakterystycznych największe jest przemieszczenie węzła nr 14, znajdującego się w geometrycznym
środku kratownicy. Wynosi ono:
~
V"N
-a
0,00153 = 0,153 9
Norma [N nr] podaje, że dla dźwigarów kratowych graniczne ugięcie wynosi:
^
•t
= 250 =
1500
250 = 6,0 9
6,0 9 > 0,153 9
Warunek stanu granicznego użytkowalności został zatem spełniony.
7.1.4.5. Wymiarowanie prętów kratownicy
7.1.4.5.1. Pas górny
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= *
_
= 138,7 )*; * = 7,433 )*
:N
=
:R
= 150,33 9
Sprawdzany przekrój – RP 100x60x5 (masa 11,30 kg/m)
•
Charakterystyki geometryczne
`
N
= 181 9
a
; `
R
= 80,8 9
a
S
N
= 3,55 9 ; S
R
= 2,37 9
=
N
= 36,2 9
b
; =
R
= 26,9 9
b
[ = 14,40 9
+
•
Określenie wpływu wyboczenia
Smukłość względem osi y-y:
f
R
=
g
R
∙
S
R
=
1,0 ∙ 150,3
2,37
= 63,42 < 250
Smukłość porównawcza:

28
f
84 ∙ j
215
^
B
= 84
Smukłość względna:
f
R
kkk = f
R
f =
63,42
84 = 0,755
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 0,755
b.+
)
qv,e+…
= 0,809
•
Określenie klasy przekroju
ℎ
=
100
5 = 20 < 23 ∙ ® = 23
= 60
5 = 12 <
23 ∙ ® =
23
» → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 14,40 ∙ 21,5 = 309,6 )*
*
l
R
∙ *
]_
≤ 1,0
138,7
0,809 ∙ 309,6 = §, ›› ≤ E, §
Warunek spełniono
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 14,40 ∙ 21,5 = 309,6 )*
*
*
]
≤ 1,0
7,433
309,6 = §, §š ≤ E, §
Warunek spełniono

29
7.1.4.5.2. Pas dolny
•
Dane
Stal S235JR (St3S) –
^
B
215 T¡}
*
V"N
= * = 140,2 )*; *
_
= 6,134 )*
:N
=
:R
= 300,0 9
Sprawdzany przekrój – RP 80x60x4 (masa 7,97 kg/m)
•
Charakterystyki geometryczne
`
N
= 87,9 9
a
; `
R
= 56,1 9
a
S
N
= 2,94 9 ; S
R
= 2,35 9
=
N
= 22,0 9
b
; =
R
= 18,7 9
b
[ = 10,10 9
+
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 10,10 ∙ 21,5 = 217,2 )*
*
*
]
≤ 1,0
140,2
217,2 = §, ¼› ≤ E, §
Warunek spełniono
•
Określenie wpływu wyboczenia
Smukłość względem osi y-y:
f
R
=
g
R
∙
S
R
=
1,0 ∙ 300
2,35 = 127,7 < 250
Smukłość porównawcza:
f = 84 ∙ j
215
^
B
= 84
Smukłość względna:
f
R
kkk = f
R
f =
127,7
84 = 1,520
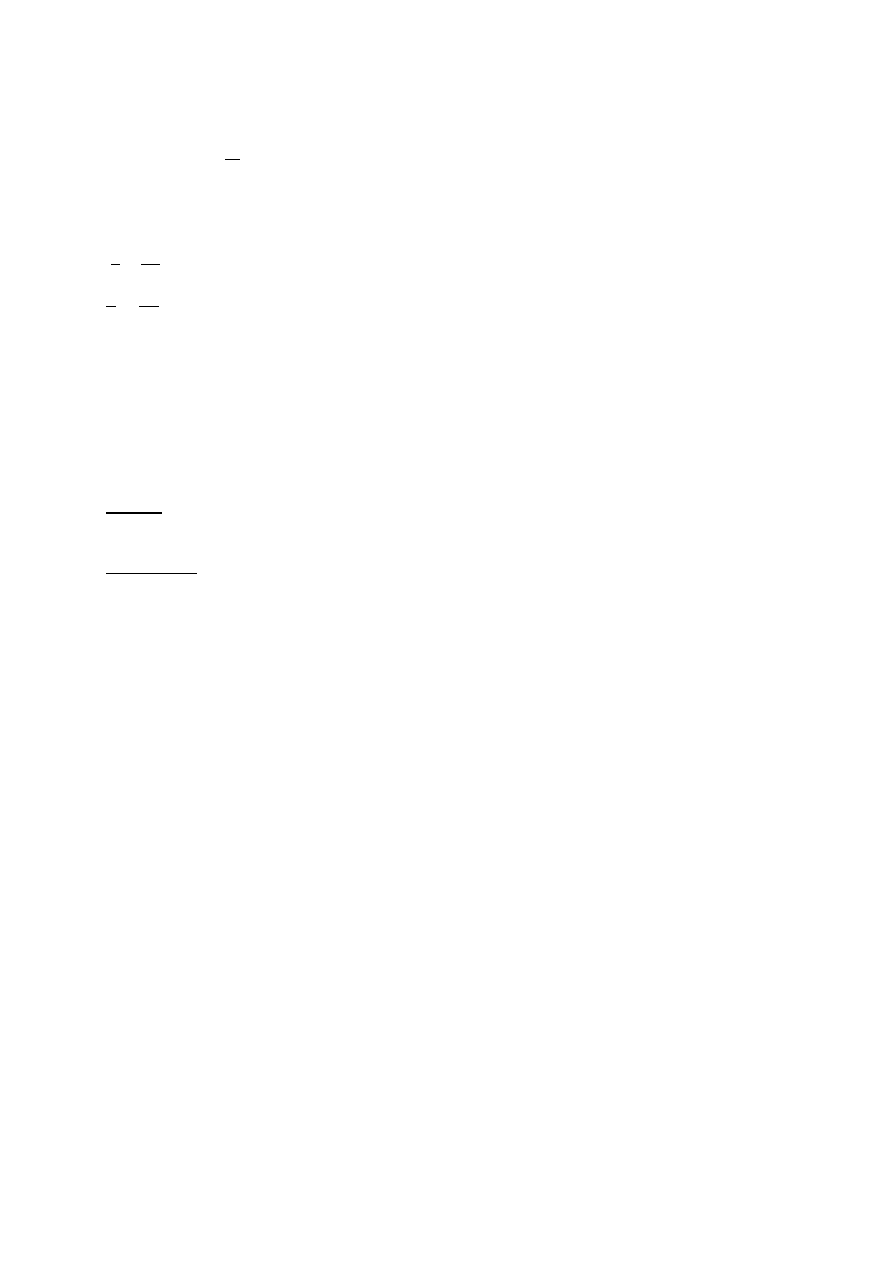
30
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,520
b.+
)
qv,e+…
= 0,374
•
Określenie klasy przekroju
ℎ
=
80
4 = 20 < 23 ∙ ® = 23
= 60
4 = 15 <
23 ∙ ® =
23
» → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 10,10 ∙ 21,5 = 217,2 )*
*
l
R
∙ *
]_
≤ 1,0
6,134
0,374 ∙ 217,2 = §, §½ ≤ E, §
Warunek spełniono
7.1.4.5.3. Krzyżulce
Krzyżulec nr 11 i 20:
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= * = 86,25 )*; *
_
= 5,591 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 205,2 9 = 164,1 9
Sprawdzany przekrój – RK 50x50x4 (masa 5,45 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 23,7 9
a
S
N
= S
R
= 1,85 9
=
N
= =
R
= 9,49 9
b
[ = 6,95 9
+
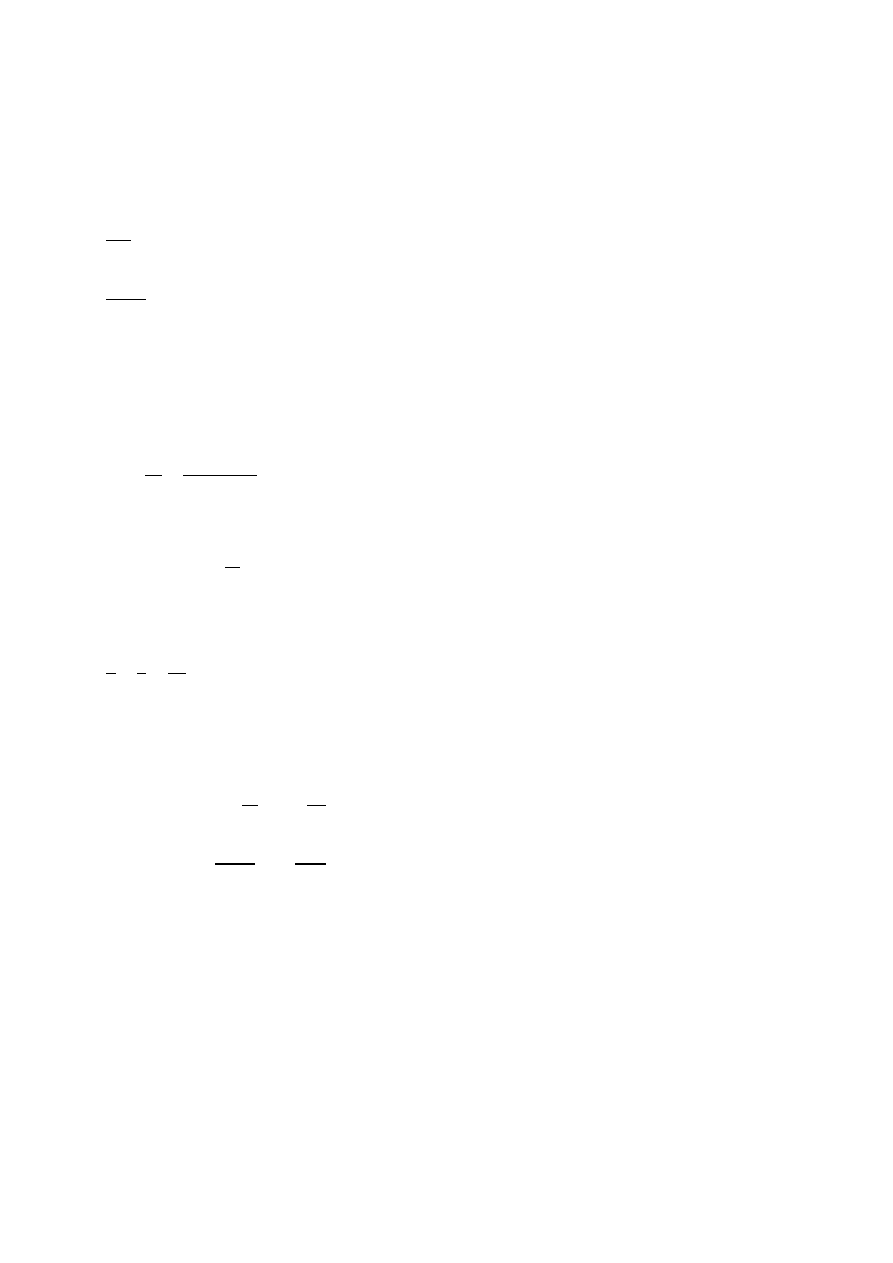
31
•
Sprawdzenie nośności na rozciąganie
*
]
[ ∙ ^
B
*
]
= 6,95 ∙ 21,5 = 149,4 )*
*
*
]
≤ 1,0
86,25
149,4 = §, ›½ ≤ E, §
Warunek spełniono
•
Określenie wpływu wyboczenia
Smukłość względna:
f
R
kkk = f
R
f =
1,0 ∙ 164,1
1,85 ∙ 84 = 1,056
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,056
b.+
)
qv,e+…
= 0,612
•
Określenie klasy przekroju
ℎ
= =
50
4 = 12,5 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 86,25 ∙
1
0,612 − 1
9,49
6,95 = 74,67 )*9
Nośność na zginanie pasa górnego:
T
]N, •
= Q ∙ =
N
∙ ^
B
= 1,0 ∙ 36,2 ∙ 21,5 = 778,3 )*9
T
]R, •
= Q ∙ =
R
∙ ^
B
= 1,0 ∙ 26,9 ∙ 21,5 = 578,4 )*9
Nośność na zginanie pasa dolnego:
T
]N, B
= Q
∙
=
N
∙
^
B
= 1,0 × 22,0 × 21,5 = 473,0 )*9
T
]R, B
= Q
∙
=
R
∙
^
B
= 1,0 × 18,7 × 21,5 = 402,1 )*9
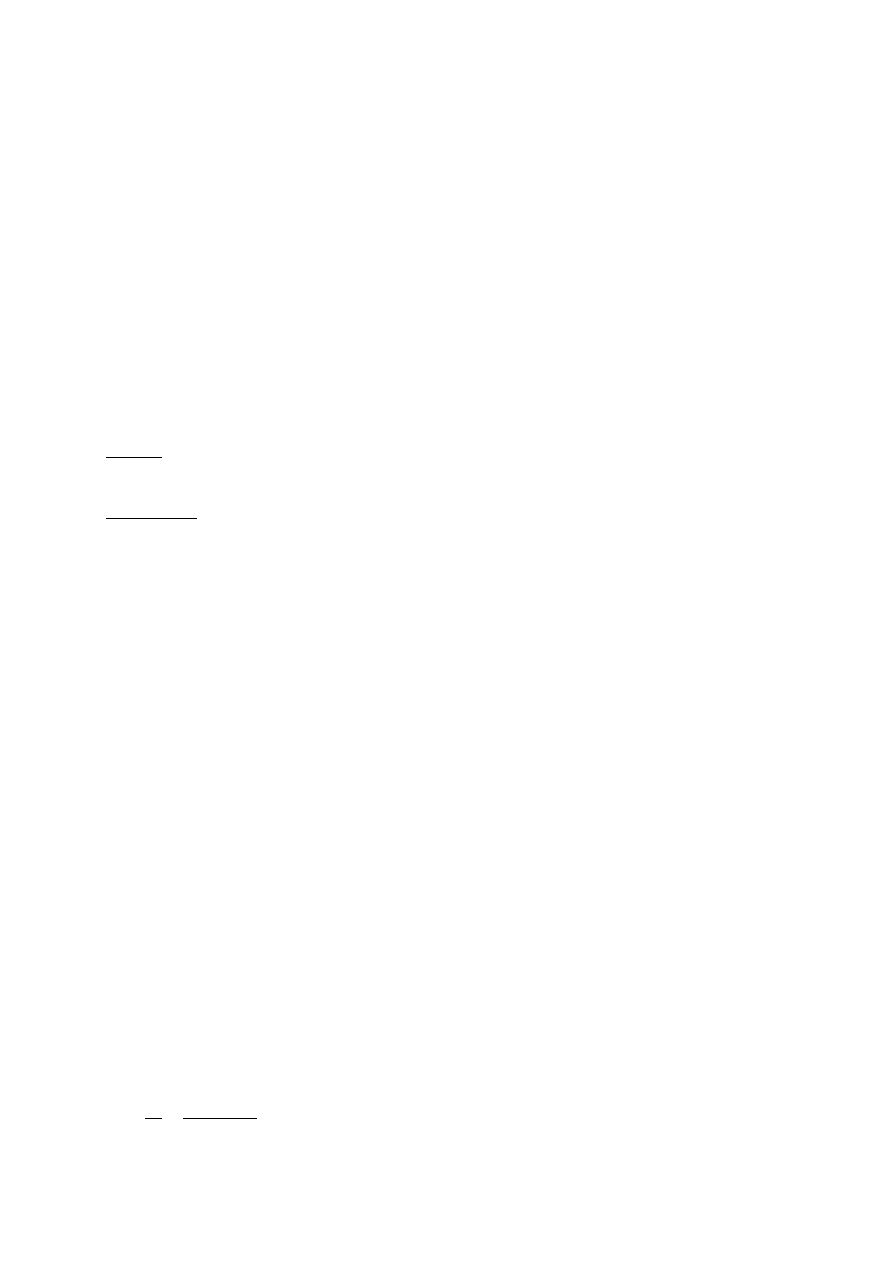
32
Przy wyboczeniu w płaszczyźnie oraz z płaszczyzny kratownicy otrzymujemy:
T
]N, •
= 778,3 )*9
T
]R, •
= 578,4 )*9
T
]N, B
= 473,0 )*9
T
]R, B
= 402,1 )*9 ¾¿
À
¿
Á
≥ ∆T
N
= ∆T
R
=
74,67 )*9
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 6,95 ∙ 21,5 = 149,4 )*
*
l
R
∙ *
]_
≤ 1,0
5,591
0,612 ∙ 149,4 = §, §¼ ≤ E, §
Warunek spełniono
Krzyżulec nr 12 i 19:
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= *
_
= 61,49 )*; * = 2,993 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 219,3 9 = 175,5 9
Sprawdzany przekrój – RK 50x50x4 (masa 5,45 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 23,7 9
a
S
N
= S
R
= 1,85 9
=
N
= =
R
= 9,49 9
b
[ = 6,95 9
+
•
Określenie wpływu wyboczenia
Smukłość względna:
f
R
kkk = f
R
f =
1,0 ∙ 175,5
1,85 ∙ 84 = 1,129
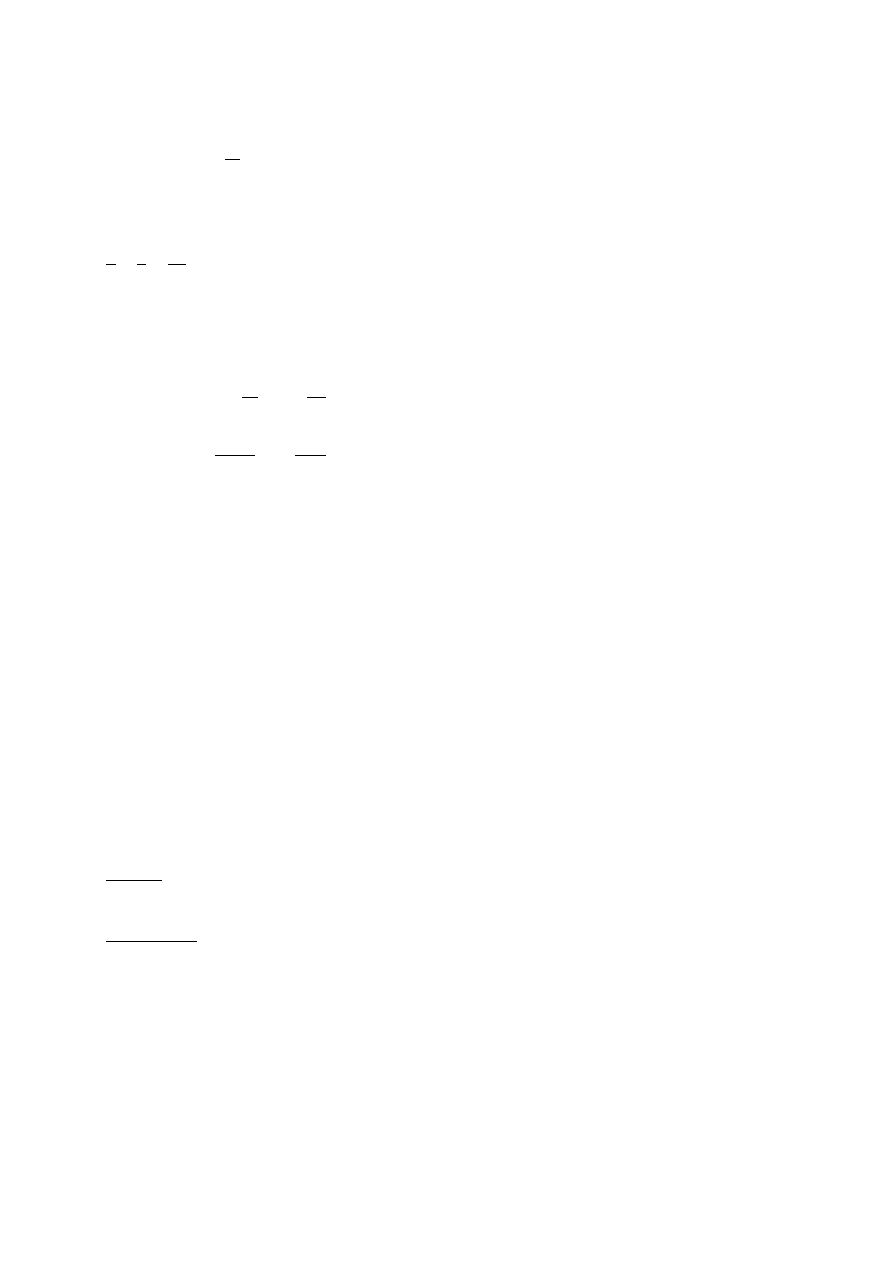
33
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,129
b.+
)
qv,e+…
= 0,568
•
Określenie klasy przekroju
ℎ
= =
50
4 = 12,5 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 61,49 ∙
1
0,568 − 1
9,49
6,95 = 63,86 )*9
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
Przy wyboczeniu w płaszczyźnie oraz z płaszczyzny kratownicy otrzymujemy:
T
]N, •
= 778,3 )*9
T
]R, •
= 578,4 )*9
T
]N, B
= 473,0 )*9
T
]R, B
= 402,1 )*9 ¾¿
À
¿
Á
≥ ∆T
N
= ∆T
R
=
63,86 )*9
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 6,95 ∙ 21,5 = 149,4 )*
*
l
R
∙ *
]_
≤ 1,0
61,49
0,617 ∙ 149,4 = §, GF ≤ E, §
Warunek spełniono
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 6,95 ∙ 21,5 = 149,4 )*

34
*
*
]
1,0
2,993
149,4 = §, §š ≤ E, §
Warunek spełniono
Krzyżulec nr 13 i 18:
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= * = 36,20 )*; *
_
= 1,142 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 219,3 9 = 175,5 9
Sprawdzany przekrój – RK 40x40x2 (masa 2,31 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 6,94 9
a
S
N
= S
R
= 1,54 9
=
N
= =
R
= 3,47 9
b
[ = 2,94 9
+
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 2,94 ∙ 21,5 = 63,21 )*
*
*
]
≤ 1,0
36,20
63,21 = §, ›G ≤ E, §
Warunek spełniono
•
Określenie wpływu wyboczenia
Smukłość względna:
f
R
kkk = f
R
f =
1,0 ∙ 175,5
1,54 ∙ 84 = 1,356
Współczynnik
l
R
względem krzywej b (n = 1,6):
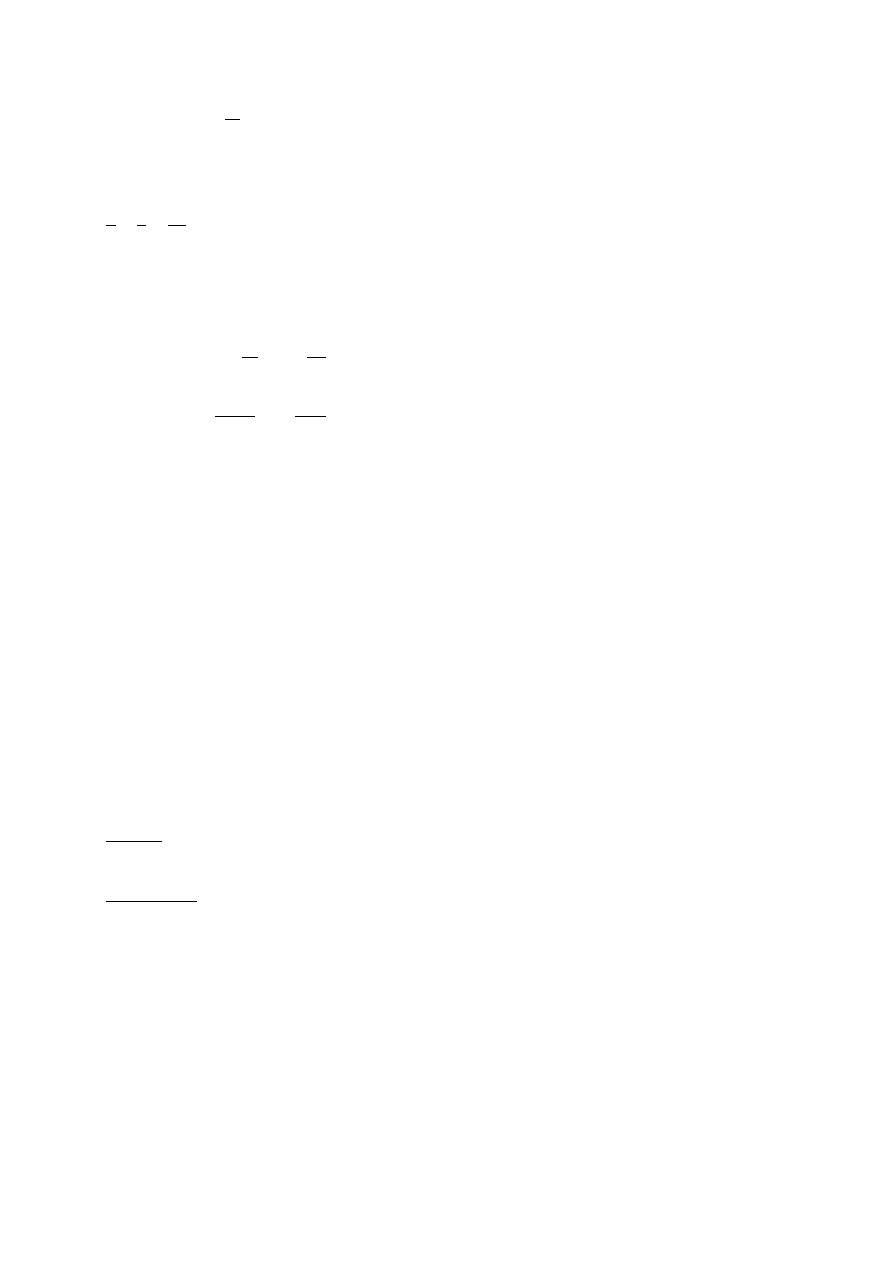
35
l
R
m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,356
b.+
)
qv,e+…
= 0,445
•
Określenie klasy przekroju
ℎ
= =
40
2 = 20 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 36,20 ∙
1
0,445 − 1
3,47
2,94 = 53,29 )*9
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
Przy wyboczeniu w płaszczyźnie oraz z płaszczyzny kratownicy otrzymujemy:
T
]N, •
= 778,3 )*9
T
]R, •
= 578,4 )*9
T
]N, B
= 473,0 )*9
T
]R, B
= 402,1 )*9 ¾¿
À
¿
Á
≥ ∆T
N
= ∆T
R
= 53,29
)*9
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 2,94 ∙ 21,5 = 63,21 )*
*
l
R
∙ *
]_
≤ 1,0
1,142
0,445 ∙ 63,21 = §, §L ≤ E, §
Warunek spełniono
Krzyżulec nr 14 i 17:
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= *
_
= 16,16 )*; * = 2,222 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 234,3 9 = 187,5 9
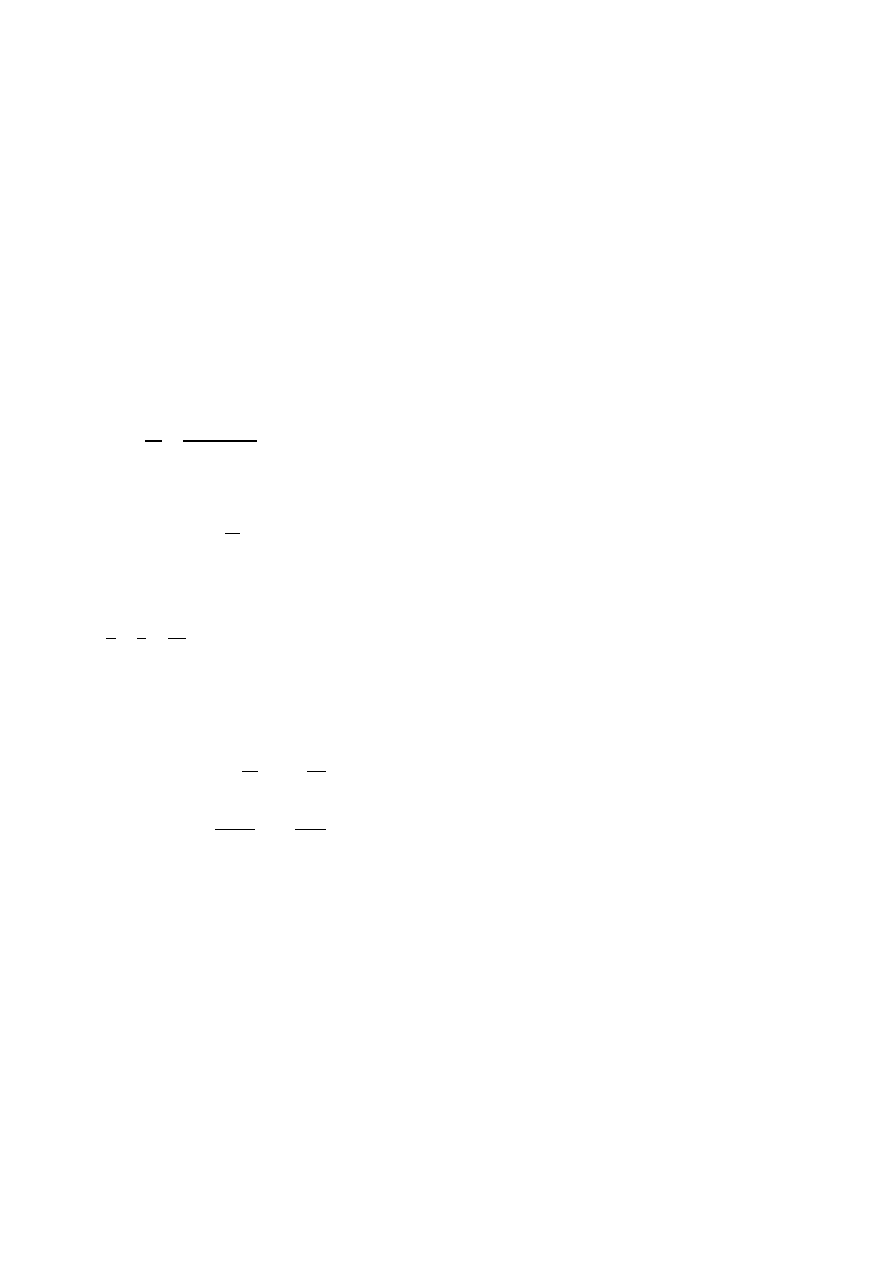
36
Sprawdzany przekrój – RK 40x40x2 (masa 2,31 kg/m)
•
Charakterystyki geometryczne
`
N
`
R
6,94 9
a
S
N
= S
R
= 1,54 9
=
N
= =
R
= 3,47 9
b
[ = 2,94 9
+
•
Określenie wpływu wyboczenia
Smukłość względna:
f
R
kkk = f
R
f =
1,0 ∙ 187,5
1,54 ∙ 84 = 1,449
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,449
b.+
)
qv,e+…
= 0,403
•
Określenie klasy przekroju
ℎ
= =
40
2 = 20 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 16,16 ∙
1
0,403 − 1
3,47
2,94 = 28,25 )*9
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
Przy wyboczeniu w płaszczyźnie oraz z płaszczyzny kratownicy otrzymujemy:
T
]N, •
= 778,3 )*9
T
]R, •
= 578,4 )*9
T
]N, B
= 473,0 )*9
T
]R, B
= 402,1 )*9 ¾¿
À
¿
Á
≥ ∆T
N
= ∆T
R
= 28,25
)*9
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.

37
•
Sprawdzenie nośności na ściskanie
*
]_
² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 2,94 ∙ 21,5 = 63,21 )*
*
l
R
∙ *
]_
≤ 1,0
16,16
0,403 ∙ 63,21 = §, ¼F ≤ E, §
Warunek spełniono
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 2,94 ∙ 21,5 = 63,21 )*
*
*
]
≤ 1,0
2,222
63,21 = §, §L ≤ E, §
Warunek spełniono
Krzyżulec nr 15 i 16:
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= *
_
= 5,350 )*; * = 3,506 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 234,3 9 = 187,5 9
Sprawdzany przekrój – RK 25x25x2 (masa 1,36 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 1,48 9
a
S
N
= S
R
= 0,924 9
=
N
= =
R
= 1,19 9
b
[ = 1,74 9
+
•
Określenie wpływu wyboczenia
Smukłość względna:
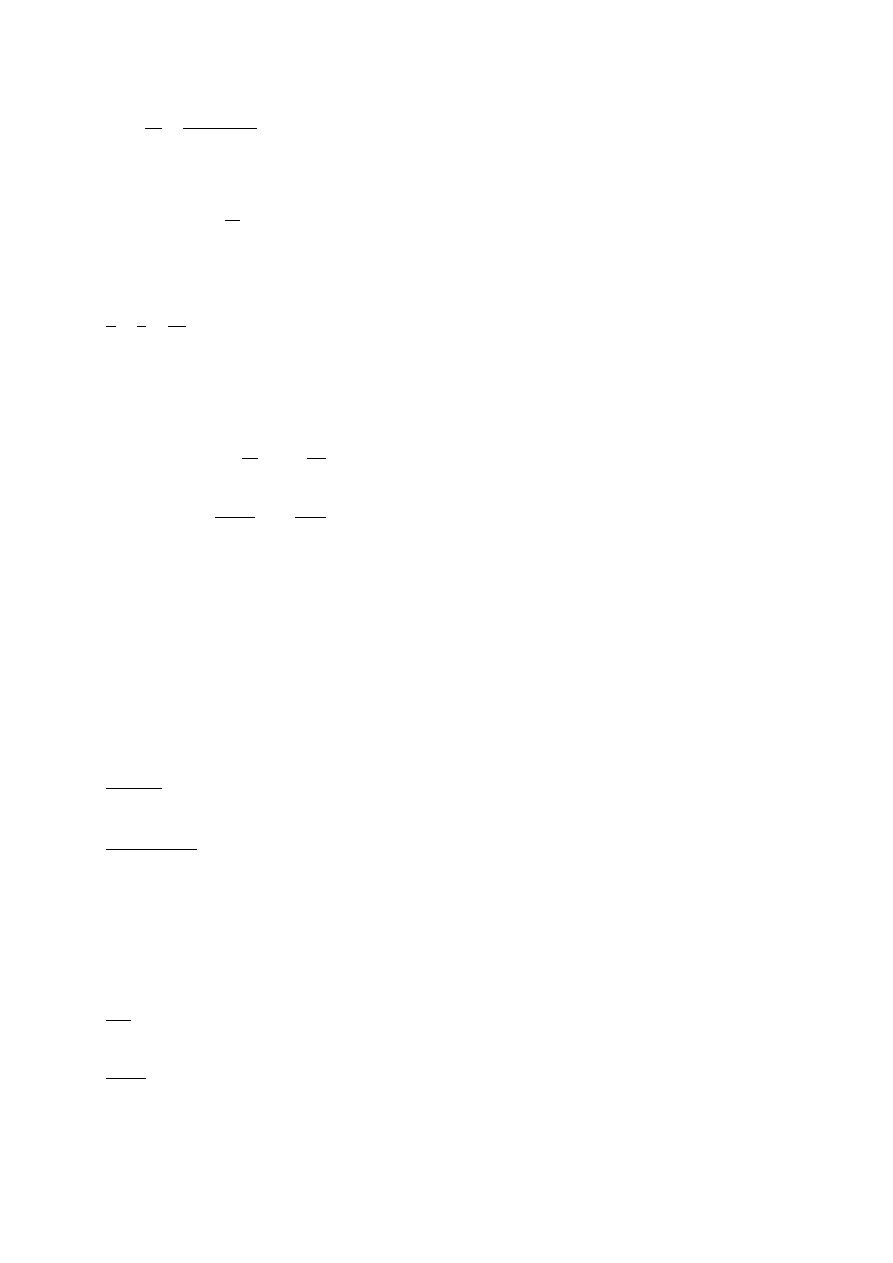
38
f
R
kkk f
R
f
1,0 ∙ 187,5
0,924 ∙ 84 = 2,415
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 2,415
b.+
)
qv,e+…
= 0,165
•
Określenie klasy przekroju
ℎ
= =
25
2 = 12,5 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 5,350 ∙
1
0,165 − 1
1,19
1,74 = 18,52 )*9 < T
]†
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 1,74 ∙ 21,5 = 37,41 )*
*
l
R
∙ *
]_
≤ 1,0
5,350
0,165 ∙ 37,41 = §, ½¼ ≤ E, §
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 2,94 ∙ 21,5 = 63,21 )*
*
*
]
≤ 1,0
3,506
37,41 = §, §K ≤ E, §
Warunki spełniono
39
7.1.4.5.4. Słupki
Słupek nr 21 i 25:
•
Dane
Stal S235JR (St3S) –
^
B
215 T¡}
*
V"N
= *
_
= 14,00 )*; * = 1,632 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 150,0 9 = 120,0 9
Sprawdzany przekrój – RK 30x30x3 (masa 2,36 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 3,50 9
a
S
N
= S
R
= 1,08 9
=
N
= =
R
= 2,34 9
b
[ = 3,01 9
+
•
Określenie wpływu wyboczenia
Smukłość względna:
f
R
kkk = f
R
f =
1,0 ∙ 120,0
1,08 ∙ 84 = 1,323
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,323
b.+
)
qv,e+…
= 0,461
•
Określenie klasy przekroju
ℎ
= =
30
3 = 10 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 14,00 ∙
1
0,461 − 1
2,34
3,01 = 12,73 )*9 < T
]†
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
40
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
:R
0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 3,01 ∙ 21,5 = 64,72 )*
*
l
R
∙ *
]_
≤ 1,0
14,00
0,461 ∙ 64,72 = §, LG ≤ E, §
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 3,01 ∙ 21,5 = 64,72 )*
*
*
]
≤ 1,0
1,632
64,72 = §, §F ≤ E, §
Warunki spełniono
Słupek nr 22 i 24:
•
Dane
Stal S235JR (St3S) –
^
B
= 215 T¡}
*
V"N
= *
_
= 14,00 )*; * = 1,632 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 170,0 9 = 136,0 9
Sprawdzany przekrój – RK 30x30x3 (masa 2,36 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 3,50 9
a
S
N
= S
R
= 1,08 9
=
N
= =
R
= 2,34 9
b
[ = 3,01 9
+
•
Określenie wpływu wyboczenia
Smukłość względna:
41
f
R
kkk f
R
f
1,0 ∙ 136,0
1,08 ∙ 84 = 1,499
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,499
b.+
)
qv,e+…
= 0,383
•
Określenie klasy przekroju
ℎ
= =
30
3 = 10 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
= * ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 14,00 ∙
1
0,383 − 1
2,34
3,01 = 17,53 )*9 < T
]†
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 3,01 ∙ 21,5 = 64,72 )*
*
l
R
∙ *
]_
≤ 1,0
14,00
0,383 ∙ 64,72 = §, ›G ≤ E, §
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 3,01 ∙ 21,5 = 64,72 )*
*
*
]
≤ 1,0
1,632
64,72 = §, §F ≤ E, §
Warunki spełniono
42
Słupek nr 23:
•
Dane
Stal S235JR (St3S) –
^
B
215 T¡}
*
V"N
= * = 4,302 )*; *
_
= 0,374 )*
:N
=
:R
= 0,8 ∙
v
= 0,8 ∙ 190,0 9 = 152,0 9
Sprawdzany przekrój – RK 25x25x2 (masa 5,45 kg/m)
•
Charakterystyki geometryczne
`
N
= `
R
= 1,48 9
a
S
N
= S
R
= 0,924 9
=
N
= =
R
= 1,19 9
b
[ = 1,74 9
+
•
Sprawdzenie nośności na rozciąganie
*
]
= [ ∙ ^
B
*
]
= 1,74 ∙ 21,5 = 37,41 )*
*
*
]
≤ 1,0
4,302
37,41 = §, EE ≤ E, §
Warunek spełniono
•
Określenie wpływu wyboczenia
Smukłość względna:
f
R
kkk = f
R
f =
1,0 ∙ 152,0
0,924 ∙ 84 = 1,958
Współczynnik
l
R
względem krzywej b (n = 1,6):
l
R
= m1 + f
R
kkk
+o
p
q-
o
= (1 + 1,958
b.+
)
qv,e+…
= 0,243
•
Określenie klasy przekroju
ℎ
= =
25
2 = 12,5 < 23 ∙ ® = 23 → ) }P} ` 3Z¯‘)ZO°±
Przekrój jest klasy 1.
43
•
Sprawdzenie sztywności zamocowania w pasach
T
]†
≥ ¸∆T
†
* ∙
1
l
†
− 1 ∙
=
†
[ ¹
∆T
†
= 4,302 ∙
1
0,243 − 1
1,19
1,74 = 9,166 )*9 < T
]†
Nośności na zginanie pasa górnego i dolnego obliczono wcześniej.
Połączenie z pasem górnym i dolnym jest wystarczająco sztywne i pozwala na przyjęcie zmniejszonej
długości wyboczeniowej
:N
=
:R
= 0,8 ∙
v
.
•
Sprawdzenie nośności na ściskanie
*
]_
= ² ∙ [ ∙ ^
B
*
]_
= 1,0 ∙ 1,74 ∙ 21,5 = 37,41 )*
*
l
R
∙ *
]_
≤ 1,0
0,374
0,243 ∙ 37,41 = §, §L ≤ E, §
Warunek spełniono
Ostateczne zestawienie danych dotyczących przekrojów prezentuje poniższa tabela.
Nr pręta
Siły osiowe N [kN]
:N
=
:R
[cm]
Przekrój
Nośność na
ściskanie
Nośność na
rozciąganie
-
+
1
10
63,20
4,197
150,3
RP
100x60x5
jak w 5(6)
0,55
jak w 5(6)
0,02
2
9
63,20
4,497
3
8
130,2
7,133
4
7
130,2
7,433
5
6
138,7
4,413
26
29
6,134
105,1
300,0
RP 80x60x4
jak w 27(28)
0,08
jak w 27(28)
0,65
27
28
5,466
140,2
11
20
5,591
86,25
164,1
RK 50x50x4
0,06
0,58
12
19
61,49
2,993
175,5
0,73
0,02
13
18
1,142
36,20
RK 40x40x2
0,04
0,57
14
17
16,16
2,222
187,5
0,63
0,04
15
16
5,350
3,506
RK 25x25x2
0,86
0,09
21
25
14,00
1,632
120,0
RK 30x30x3
0,47
0,03
22
24
14,00
1,632
136,0
0,57
0,03
23
0,374
4,302
152,0
RK 25x25x2
0,04
0,11
Średnie wytężenie pasów to 60%.
Średnie wytężenie skratowania to 56,5%.
44
7.1.4.6. Wymodelowanie i obliczenie połączeń węzłowych kratownicy
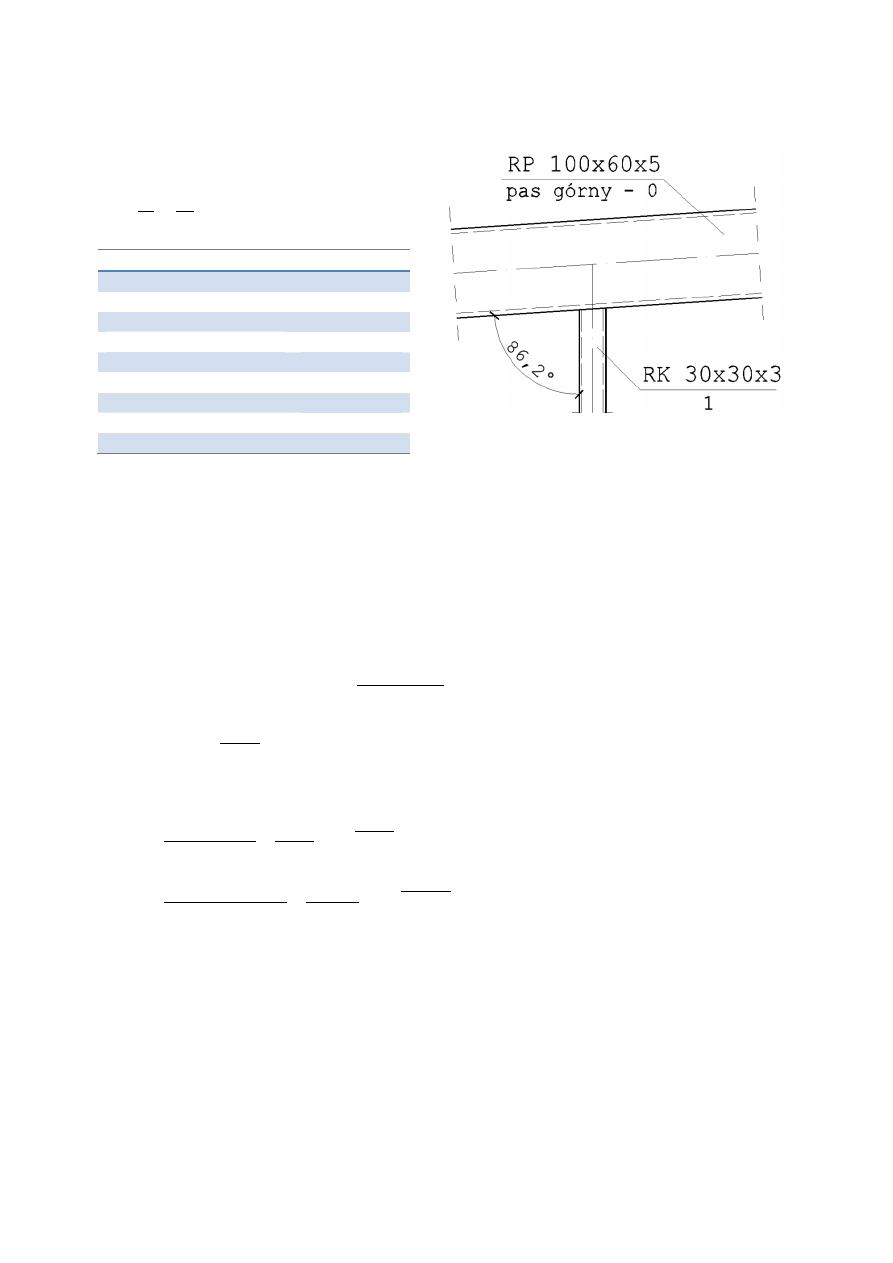
7.1.4.6.1. Węzeł B – węzeł typu Y
•
Warunki geometryczne wg [N nr]
2
-
v
30
60 = 0,5
Warunek
Wynik
Â
Ã
/Â
Ä
≥ §, š›
30 / 60 = 0,5
Â
Ã
/Å
Ã
≤ F›
30 / 3 = 10
Æ
Ã
/Å
Ã
≤ F›
30 / 3 = 10
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
100 / 60 = 1,67
§, › ≤ Æ
Ã
/Â
Ã
≤ š
30 / 30 = 1,0
Â
Ä
/Å
Ä
≤ F›
60 / 5 = 12
Æ
Ä
/Å
Ä
≤ F›
100 / 5 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
•
Dodatkowe warunki geometryczne
†
/ = 30/60 = 0,5 ≤ 0,85
/ = 60/5 = 12 ≥ 10
•
Zniszczenie przystykowe pasa
)
o
= 1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
63,20
(14,4 ∙ 23,5) = 0,187
)
o
= 1,3 − 0,4 ∙
0,187
0,5 = 1,15 → )
o
= 1,0
v
= 5
45
*
-,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
-
∙
22
PS Ð
-
+ 4„1 − 2
*
-,]B
=
1,0 ∙ 23,5 ∙ 0,5
+
(1 − 0,5)PS 86,2 ∙
2 ∙ 0,5
PS 86,2 + 4„1 − 0,5 = 45,11 )*
•
Sprawdzenie nośności
H
E,ÑJ
= L›, EE DH > H
E
= EL, §§ DH
•
Spoina obwodowa łącząca słupek 21 (25) z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= F II
*
-
∙ PS Q = 13,97 )*
*
-
∙ 9OPQ = 0,928 )*
• =
*
-
∙ PS Q
[
{
=
13,97
4 ∙ 3 ∙ 0,3 = 38,8 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
0,928
2 ∙ 3 ∙ 0,3 = 5,2 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1; Q
∥
= 0,6
j 38,8
1,0
+
+
5,2
0,6
+
= FK, ½ ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
Warunek spełniono
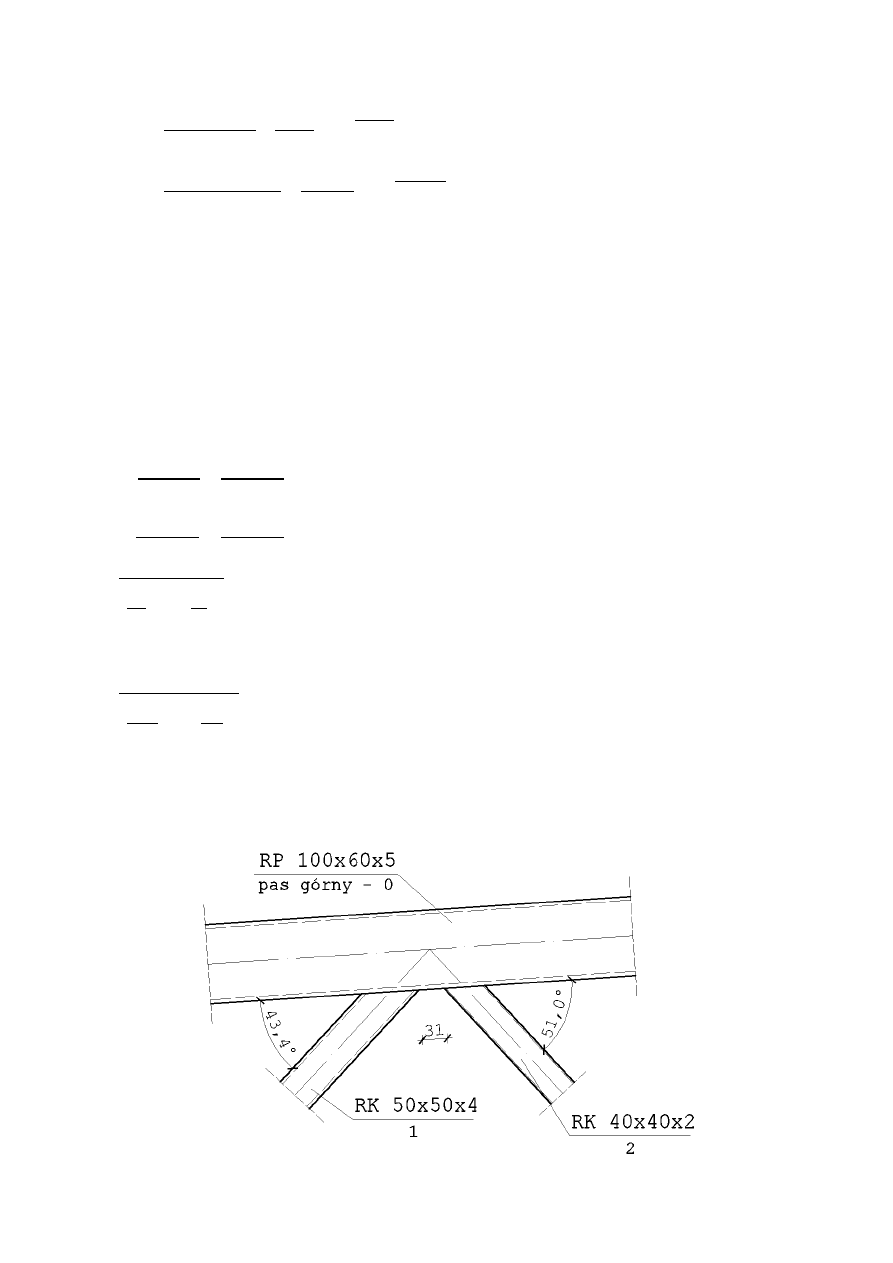
7.1.4.6.2. Węzeł C – węzeł typu K

46
•
Warunki geometryczne wg [N nr]
2
1
+
2
2
0
= 50 + 40
2 ∙ 60
= 0,75
; = 31
Warunek
RK 50x50x4 (1)
RK 40x40x2 (2)
Â
Ã
/Â
Ä
≥ §, F›
50 / 60 = 0,83
40 / 60 = 0,67
Â
Ã
Â
Ä
≥ §, E +
§, §EÂ
Ä
Å
Ä
0,83 > 0,1 + 0,01 x 60/5 = 0,23 0,67 > 0,1 + 0,01 x 60/5 = 0,23
Â
Ã
/Å
Ã
≤ F›
50 / 4 = 12,5
40 / 2 = 20
Æ
Ã
/Å
Ã
≤ F›
50 / 4 = 12,5
40 / 2 = 20
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
100 / 60 = 1,67
§, › ≤ Æ
Ã
/Â
Ã
≤ š
50 / 50 = 1
40 / 40 = 1
Â
Ä
/Å
Ä
≤ F›
60 / 5 = 12
Æ
Ä
/Å
Ä
≤ F›
100 / 5 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
C ≥ §, ›(E − Õ) ∙ Â
Ä
31 > 0,5 (1-0,75) x 60 = 7,5
C ≤ E, ›(E − Õ) ∙ Â
Ä
31 < 1,5 (1-0,75) x 60 = 22,5
C ≥ Å
E
+ Å
š
31 > 4 + 2 = 6
W związku z tym, że
; > 1,5(1 − 2) ∙ węzeł traktujemy jako dwa węzły typu Y (tab. 7.8. [N nr]).
•
Dodatkowe warunki geometryczne (jak dla węzła typu Y)
-
=
50
60 = 0,83 ≤ 0,85;
+
=
40
60 = 0,67 ≤ 0,85
/ = 60/5 = 12 ≥ 10
•
Zniszczenie przystykowe pasa
)
o-
= 1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
130,2
(14,4 ∙ 23,5) = 0,385
)
o-
= 1,3 − 0,4 ∙
0,385
0,75 = 1,09 → )
o-
= 1,0
)
o+
= 1,0 (rozciąganie)
v
= 5
*
Ö,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
Ö
∙
22
PS Ð
†
+ 4„1 − 2
*
-,]B
=
1,0 ∙ 23,5 ∙ 0,5
+
(1 − 0,833)PS 43,4 ∙
2 ∙ 0,833
PS 43,4 + 4„1 − 0,833 = 207,8 )*
47
*
+,]B
=
1,0 ∙ 23,5 ∙ 0,5
+
(1 − 0,667)PS 51,0 ∙
2 ∙ 0,667
PS 51,0 + 4„1 − 0,667 = 91,37 )*
•
Sprawdzenie nośności
H
E,ÑJ
= š§G, ½ DH > H
E
= ¼E, LK DH
H
š,ÑJ
= KE, FG DH > H
+
= F¼, š§ DH
•
Spoina obwodowa łącząca krzyżulec 12 (19) z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= L II
*
-
∙ PS Q = 61,49 ∙ PS 43,4 = 42,25 )*
*
-
∙ 9OPQ = 61,49 ∙ 9OP43,4 = 44,68 )*
• =
*
-
∙ PS Q
[
{
=
42,25
2 ∙ (5 + 7,28) ∙ 0,4 = 43,0 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
44,68
2 ∙ 7,28 ∙ 0,4 = 76,7 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1; Q
∥
= 0,6
j 43,0
1,0
+
+
76,7
0,6
+
= EFL, K ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Spoina obwodowa łącząca krzyżulec 13 (18) z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
+
∙ PS Q = 36,20 ∙ PS 51,0 = 28,13 )*
*
+
∙ 9OPQ = 36,20 ∙ 9OP51,0 = 22,78 )*
• =
*
+
∙ PS Q
[
{
=
28,13
2 ∙ (4 + 5,15) ∙ 0,2 = 76,9 T¡}
Ÿ =
*
+
∙ 9OPQ
[
Œ
=
22,78
2 ∙ 5,15 ∙ 0,2 = 110,6 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 0,85; Q
∥
= 0,6
j 76,9
0,85
+
+
110,6
0,6
+
= š§›, F ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
48
7.1.4.6.3. Węzeł D – węzeł typu Y
•
Warunki geometryczne wg [N nr]
2
-
v
30
60 = 0,5
Warunek
Wynik
Â
Ã
/Â
Ä
≥ §, š›
30 / 60 = 0,5
Â
Ã
/Å
Ã
≤ F›
30 / 3 = 10
Æ
Ã
/Å
Ã
≤ F›
30 / 3 = 10
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
100 / 60 = 1,67
§, › ≤ Æ
Ã
/Â
Ã
≤ š
30 / 30 = 1,0
Â
Ä
/Å
Ä
≤ F›
60 / 5 = 12
Æ
Ä
/Å
Ä
≤ F›
100 / 5 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
•
Dodatkowe warunki geometryczne
†
/ = 30/60 = 0,5 ≤ 0,85
/ = 60/5 = 12 ≥ 10
•
Zniszczenie przystykowe pasa
)
o
= 1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
130,2
(14,4 ∙ 23,5) = 0,385
)
o
= 1,3 − 0,4 ∙
0,385
0,5 = 0,992
v
= 5
*
-,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
-
∙
22
PS Ð
-
+ 4„1 − 2
*
-,]B
=
0,992 ∙ 23,5 ∙ 0,5
+
(1 − 0,5)PS 86,2 ∙
2 ∙ 0,5
PS 86,2 + 4„1 − 0,5 = 44,75 )*
•
Sprawdzenie nośności
H
E,ÑJ
= LL, G› DH > H
E
= EL, §§ DH
•
Spoina obwodowa łącząca słupek 22 (24) z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= F II
*
-
∙ PS Q = 13,97 )*
*
-
∙ 9OPQ = 0,928 )*
49
•
*
-
∙ PS Q
[
{
=
13,97
4 ∙ 3 ∙ 0,3 = 38,8 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
0,928
2 ∙ 3 ∙ 0,3 = 5,2 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1; Q
∥
= 0,6
j 38,8
1,0
+
+
5,2
0,6
+
= FK, ½ ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
Warunek spełniono
7.1.4.6.4. Węzeł E – węzeł typu K
•
Geometria wg [N nr]
2 =
1
+
2
2
0
= 40 + 25
2 ∙ 60
= 0,542
; = 41,4
Warunek
RK 40x40x2 (1)
RK 25x25x2 (2)
Â
Ã
/Â
Ä
≥ §, F›
40 / 60 = 0,67
25 / 60 = 0,42
Â
Ã
Â
Ä
≥ §, E +
§, §EÂ
Ä
Å
Ä
0,67 > 0,1 + 0,01 x 60/5 = 0,23 0,42 > 0,1 + 0,01 x 60/5 = 0,23
Â
Ã
/Å
Ã
≤ F›
40 / 2 = 20
25 / 2 = 12,5
Æ
Ã
/Å
Ã
≤ F›
40 / 2 = 20
25 / 2 = 12,5
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
100 / 60 = 1,67
§, › ≤ Æ
Ã
/Â
Ã
≤ š
40 / 40 = 1
25 / 25 = 1
Â
Ä
/Å
Ä
≤ F›
60 / 5 = 12
Æ
Ä
/Å
Ä
≤ F›
100 / 5 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
C ≥ §, ›(E − Õ) ∙ Â
Ä
41,4 > 0,5 (1-0,542) x 60 = 13,7
C ≤ E, ›(E − Õ) ∙ Â
Ä
41,4 < 1,5 (1-0,542) x 60 = 41,2
C ≥ Å
E
+ Å
š
41,4 > 4 + 2 = 6
50
W związku z tym, że
; > 1,5(1 − 2) ∙ węzeł traktujemy jako dwa węzły typu Y (tab. 7.8. [N nr]).
•
Dodatkowe warunki geometryczne (jak dla węzła typu Y)
-
=
40
60 = 0,67 ≤ 0,85;
+
=
25
60 = 0,42 ≤ 0,85
/ = 60/5 = 12 ≥ 10
•
Zniszczenie przystykowe pasa
)
o-
= 1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
138,7
(14,4 ∙ 23,5) = 0,410
)
o-
= 1,3 − 0,4 ∙
0,410
0,67 = 1,06 → )
o-
= 1,0
)
o+
= 1,3 − 0,4 ∙
0,410
0,417 = 0,907
v
= 5
*
Ö,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
Ö
∙
22
PS Ð
†
+ 4„1 − 2
*
-,]B
=
1,0 ∙ 23,5 ∙ 0,5
+
(1 − 0,67)PS 46,7 ∙
2 ∙ 0,67
PS 46,7 + 4„1 − 0,67 = 101,3 )*
*
+,]B
=
0,907 ∙ 23,5 ∙ 0,5
+
(1 − 0,42)PS 54,3 ∙
2 ∙ 0,42
PS 54,3 + 4„1 − 0,42 = 46,17 )*
•
Sprawdzenie nośności
H
E,ÑJ
= E§E, F DH > H
E
= E¼, E¼ DH
H
š,ÑJ
= L¼, EG DH > H
+
= ›, F›§ DH
•
Spoina obwodowa łącząca krzyżulec 14 (17) z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
-
∙ PS Q = 16,16 ∙ PS 46,7 = 11,76 )*
*
-
∙ 9OPQ = 16,16 ∙ 9OP46,7 = 11,08 )*
• =
*
-
∙ PS Q
[
{
=
11,76
2 ∙ (4 + 5,5) ∙ 0,2 = 38,0 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
11,08
2 ∙ 5,5 ∙ 0,2 = 50,4 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
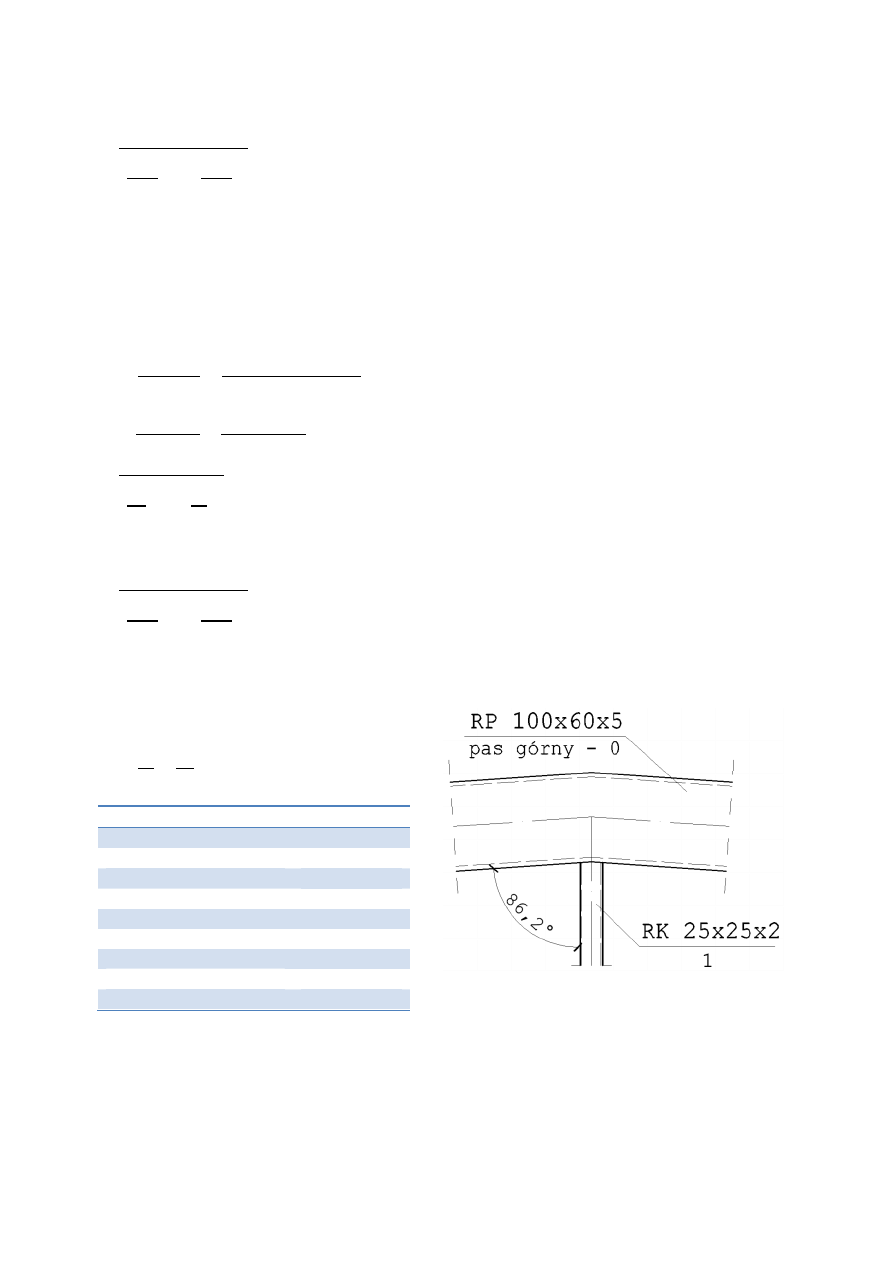
51
Q
ž
1; Q
∥
= 0,6
j 38,0
1,0
+
+
50,4
0,6
+
= Kš, š ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Spoina obwodowa łącząca krzyżulec 15 (16) z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
+
∙ PS Q = 5,350 ∙ PS 54,3 = 4,345 )*
*
+
∙ 9OPQ = 5,350 ∙ 9OP54,3 = 3,122 )*
• =
*
+
∙ PS Q
[
{
=
4,345
2 ∙ (2,5 + 3,08) ∙ 0,2 = 19,5 T¡}
Ÿ =
*
+
∙ 9OPQ
[
Œ
=
3,122
2 ∙ 3,08 ∙ 0,2 = 25,3 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1,0; Q
∥
= 0,6
j 19,5
1,0
+
+
25,3
0,6
+
= L¼, › ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
7.1.4.6.5. Węzeł F – węzeł typu Y
•
Warunki geometryczne wg [N nr]
2 =
-
v
=
25
60 = 0,417
Warunek
Wynik
Â
Ã
/Â
Ä
≥ §, š›
25 / 60 = 0,42
Â
Ã
/Å
Ã
≤ F›
25 / 2 = 12,5
Æ
Ã
/Å
Ã
≤ F›
25 / 2 = 12,5
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
100 / 60 = 1,67
§, › ≤ Æ
Ã
/Â
Ã
≤ š
25 / 25 = 1,0
Â
Ä
/Å
Ä
≤ F›
60 / 5 = 12
Æ
Ä
/Å
Ä
≤ F›
100 / 5 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
•
Dodatkowe warunki geometryczne
†
/ = 20/60 = 0,42 ≤ 0,85
/ = 60/5 = 12 ≥ 10
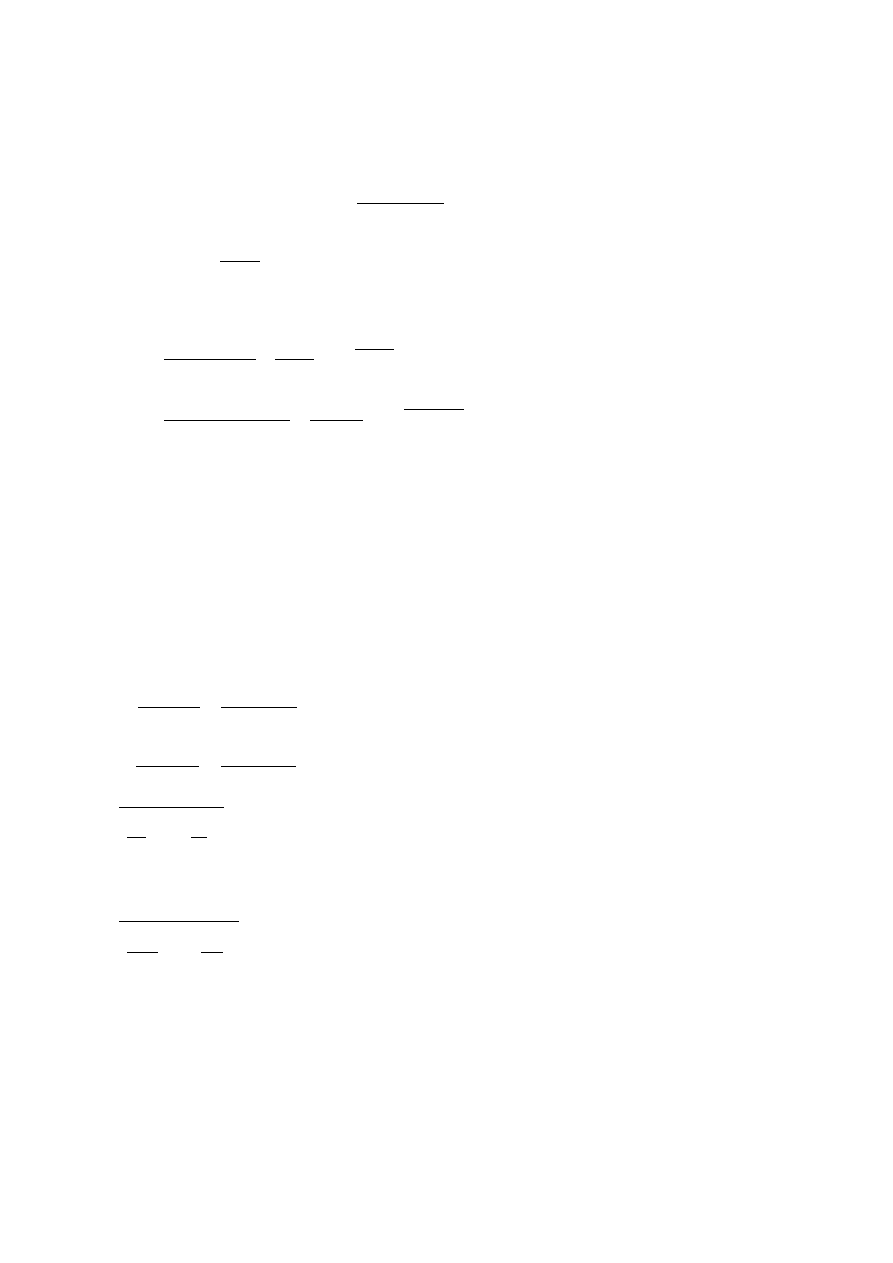
52
•
Zniszczenie przystykowe pasa
)
o
1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
138,7
(14,4 ∙ 23,5) = 0,410
)
o
= 1,3 − 0,4 ∙
0,410
0,417 = 0,907
v
= 5
*
-,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
-
∙
22
PS Ð
-
+ 4„1 − 2
*
-,]B
=
0,907 ∙ 23,5 ∙ 0,5
+
(1 − 0,42)PS 86,2 ∙
2 ∙ 0,42
PS 86,2 + 4„1 − 0,42 = 35,80 )*
•
Sprawdzenie nośności
H
E,ÑJ
= F›, ½§ DH > H
E
= L, Fš§ DH
•
Spoina obwodowa łącząca słupek 23 z pasem górnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
-
∙ PS Q = 4,311 )*
*
-
∙ 9OPQ = 0,286 )*
• =
*
-
∙ PS Q
[
{
=
4,311
4 ∙ 2,5 ∙ 0,3 = 14,8 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
0,286
2 ∙ 2,5 ∙ 0,3 = 1,9 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 0,85; Q
∥
= 0,6
j 14,8
0,85
+
+
1,9
0,6
+
= EG, G ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
Warunek spełniono
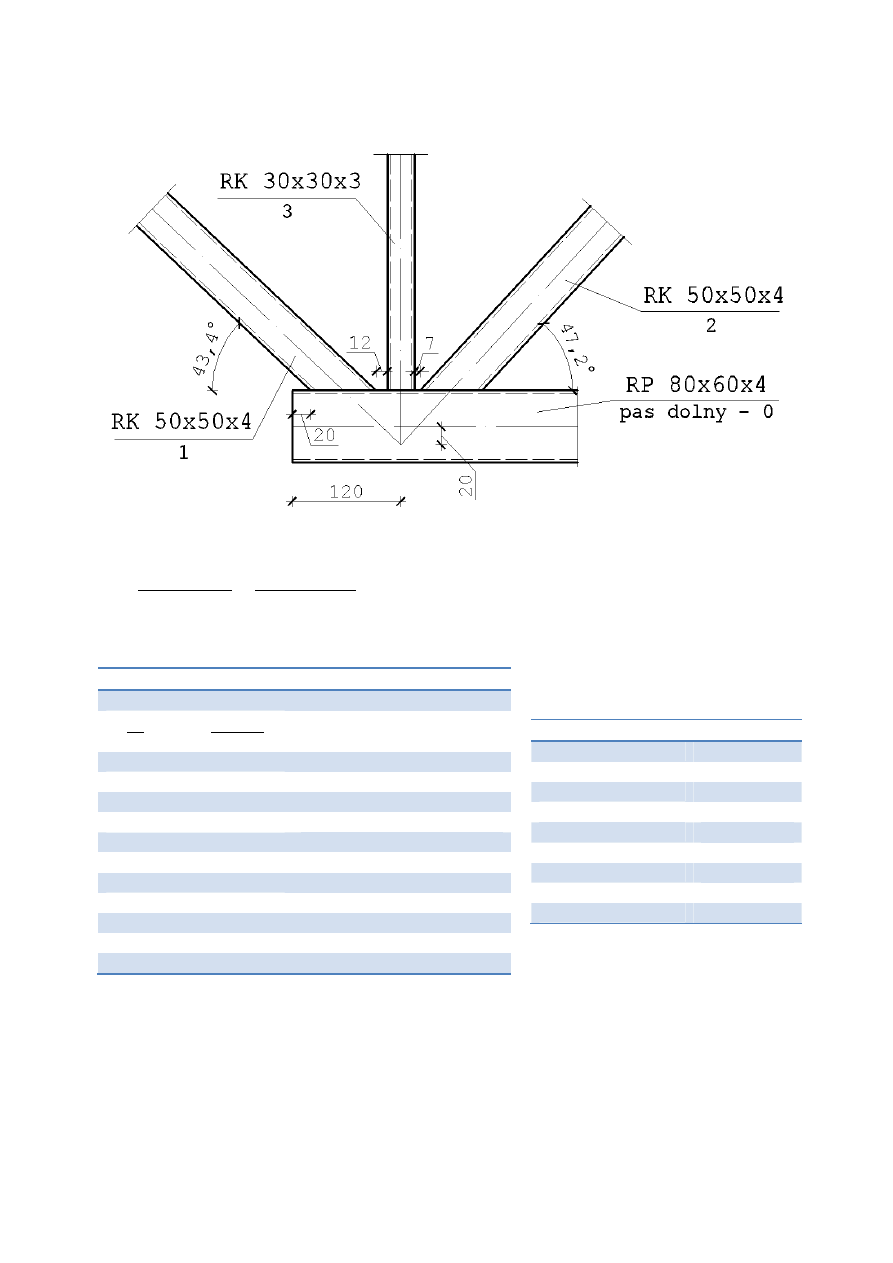
53
7.1.4.6.6. Węzeł G – węzeł typu KT
•
Warunki geometryczne wg [N nr]
2
1
+
2
+
3
3
0
= 50 + 50 + 30
3 ∙ 60
= 0,722
; = 12 + 7 = 19
Warunek – węzeł K
RK 50x50x4 (1, 2)
Â
Ã
/Â
Ä
≥ §, F›
50 / 60 = 0,83
Â
Ã
Â
Ä
≥ §, E +
§, §EÂ
Ä
Å
Ä
0,83 > 0,1 + 0,01 x 60/4 = 0,25
Â
Ã
/Å
Ã
≤ F›
50 / 4 = 12,5
Æ
Ã
/Å
Ã
≤ F›
50 / 4 = 12,5
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
80 / 60 = 1,33
§, › ≤ Æ
Ã
/Â
Ã
≤ š
50 / 50 = 1
Â
Ä
/Å
Ä
≤ F›
60 / 4 = 15
Æ
Ä
/Å
Ä
≤ F›
80 / 4 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
C ≥ §, ›(E − Õ) ∙ Â
Ä
19 > 0,5 (1-0,722) x 60 = 8,3
C ≤ E, ›(E − Õ) ∙ Â
Ä
19 < 1,5 (1-0,722) x 60 = 25,0
C ≥ Å
E
+ Å
š
19 > 4 + 4 = 8
•
Dopuszczalny mimośród wg [N nr]
−0,55 ∙ ℎ
v
≤ ‘ ≤ 0,25 ∙ ℎ
v
−0,55 ∙ 80 ≤ ‘ ≤ 0,25 ∙ 80
−44 ≤ ‘ ≤ 20
Warunek – węzeł T
Wynik
Â
Ã
/Â
Ä
≥ §, š›
30 / 60 = 0,5
Â
Ã
/Å
Ã
≤ F›
30 /3 = 10
Æ
Ã
/Å
Ã
≤ F›
30 / 3 = 10
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
80 / 60 = 1,33
§, › ≤ Æ
Ã
/Â
Ã
≤ š
30 / 30 = 1,0
Â
Ä
/Å
Ä
≤ F›
60 / 4 = 15
Æ
Ä
/Å
Ä
≤ F›
80 / 4 = 20
DÇ. ÈÉÊËD. șΙ ≤ š
klasa 1
54
•
Dodatkowe warunki geometryczne – węzeł T
†
/
30/60 = 0,50 ≤ 0,85
/ = 60/4 = 15 ≥ 10
•
Zniszczenie przystykowe pasa
)
o
= 1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
105,1
(10,1 ∙ 23,5) = 0,443
)
o
= 1,3 − 0,4 ∙
0,443
0,722 = 1,05 → )
o
= 1,0
v
= 4
*
b,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
-
∙
22
PS Ð
-
+ 4„1 − 2
*
b,]B
=
1,0 ∙ 23,5 ∙ 0,4
+
(1 − 0,722)PS 90 ∙
2 ∙ 0,722
PS 90 + 4„1 − 0,722 = 48,06 )*
•
Sprawdzenie nośności
H
F,ÑJ
= L½, §¼ DH > H
F
= EL, §§ DH
•
Spoina obwodowa łącząca słupek 21 (25) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= F II
*
-
∙ PS Q = 14,00 )*
• =
*
-
∙ PS Q
[
{
=
14,00
4 ∙ 3 ∙ 0,3 = 38,9 T¡}
j •
Q
ž
+
≤ ^
B
; Q
ž
= 1,0
j 38,9
1,0
+
= F½, K ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Dodatkowe warunki geometryczne – węzeł K
0,6 ≤ (
-
+
+
)/2
-
≤ 1,3
0,6 ≤ (50 + 50)/100 ≤ 1,3
0,6 ≤ 1,0 ≤ 1,3
/ = 60/4 = 15 ≥ 15
55
•
Zniszczenie przystykowe pasa
)
o-
1,0 (rozciąganie)
)
o+
= 1,3 − 0,4 /2 ≤ 1,0
)
o+
= 1,3 − 0,4 ∙
0,443
0,722 = 1,05 → )
o+
= 1,0
v
= 4
? =
v
/2
v
= 60/(2 ∙ 4) = 7,5
*
†,]B
=
8,9)
o
^
Rv
+
√?
PS Ð
†
∙ (2)
*
-,]B
=
8,9 ∙ 1,0 ∙ 23,5 ∙ 0,4
+
∙ „7,5
PS 43,4
∙ (0,722) = 96,30 )*
*
+,]B
=
8,9 ∙ 1,0 ∙ 23,5 ∙ 0,4
+
∙ „7,5
PS 47,2
∙ (0,722) = 90,18 )*
•
Ścięcie pasa
Q = ×
1
1 + 4;
+
3
+
= ×
1
1 + 4 ∙ 1,9
+
3 ∙ 0,4
+
= 0,179
[
Œ
= (2ℎ
v
+ Q
v
) ∙
v
= (2 ∙ 8 + 0,179 ∙ 6) ∙ 0,4 = 6,83 9
+
*
†,]B
=
^
Rv
∙ [
Œ
√3 ∙ PS Ð
†
*
-,]B
=
23,5 ∙ 6,83
√3 ∙ PS 43,4
= 134,9 )*
*
+,]B
=
23,5 ∙ 6,83
√3 ∙ PS 47,2
= 126,3 )*
*
v,]B
= [
v
∙ ^
Rv
= 10,1 ∙ 23,5 = 237,4 )*
•
Zniszczenie skratowania
*
†,]B
= ^
R† †
x2ℎ
†
− 4
†
+
†
+
0@@
y
0@@,†
=
10
v
/
v
∙
v
†
∙
†
≤
†
0@@,-
=
0@@,+
=
10
6/0,4 ∙
0,4
0,4 ∙ 5 = 3,33 9
*
-,]B
= *
+,]B
= 23,5 ∙ 0,4 ∙ (2 ∙ 5 − 4 ∙ 0,4 + 5 + 3,33) = 157,3 )*
56
•
Przebicie pasa
*
†,]B
=
^
Rv v
√3 ∙ PS Ð
†
µ
2ℎ
†
√3 ∙ PS Ð
†
+
†
+
0.
¶
0, ,-
=
10
v
∙
v
∙
†
≤
†
0, ,-
=
0, ,+
=
10
6 ∙ 0,4 ∙ 5 = 20,83 9 →
0,
= 5,0 9
*
-,]B
=
23,5 ∙ 0,4
√3 ∙ PS 43,4
∙
2 ∙ 5
PS 43,4 + 5 + 5 = 193,9 )*
*
-,]B
=
23,5 ∙ 0,4
√3 ∙ PS 47,2
∙
2 ∙ 5
PS 47,2 + 5 + 5 = 174,8 )*
•
Sprawdzenie nośności
H
E,ÑJ
= K¼, F§ DH > H
E
= ½¼, š› DH
H
š,ÑJ
= K§, E½ DH > H
+
= ¼E, LK DH
•
Spoina obwodowa łącząca krzyżulec 11 (20) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= L II
*
-
∙ PS Q = 59,26 )*
*
-
∙ 9OPQ = 62,67 )*
• =
*
-
∙ PS Q
[
{
=
59,26
2 ∙ (5 + 7,27) ∙ 0,4 = 60,4 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
62,67
2 ∙ 7,27 ∙ 0,4 = 107,8 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 0,85; Q
∥
= 0,6
j 60,4
0,85
+
+
107,8
0,6
+
= EKF, š ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Spoina obwodowa łącząca krzyżulec 12 (19) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= L II
*
-
∙ PS Q = 45,12 )*
*
-
∙ 9OPQ = 41,78 )*

57
•
*
-
∙ PS Q
[
{
=
45,12
2 ∙ (5 + 6,81) ∙ 0,4 = 47,8 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
41,78
2 ∙ 6,81 ∙ 0,4 = 76,7 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1,0; Q
∥
= 0,6
j 47,8
1,0
+
+
76,7
0,6
+
= EF¼, › ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
Warunki spełniono
7.1.4.6.7. Węzeł H – węzeł typu KT
•
Warunki geometryczne wg [N nr]
2 =
1
+
2
+
3
3
0
= 40 + 40 + 30
3 ∙ 60
= 0,611
; = 12 + 7 = 22
Warunek – węzeł K
RK 40x40x2 (1, 2)
Â
Ã
/Â
Ä
≥ §, F›
40 / 60 = 0,67
Â
Ã
Â
Ä
≥ §, E +
§, §EÂ
Ä
Å
Ä
0,67 > 0,1 + 0,01 x 60/4 = 0,25
Â
Ã
/Å
Ã
≤ F›
40 / 2 = 20
Æ
Ã
/Å
Ã
≤ F›
40 / 2 = 20
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
80 / 60 = 1,33
§, › ≤ Æ
Ã
/Â
Ã
≤ š
40 / 40 = 1
Â
Ä
/Å
Ä
≤ F›
60 / 4 = 15
Æ
Ä
/Å
Ä
≤ F›
80 / 4 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
C ≥ §, ›(E − Õ) ∙ Â
Ä
22 > 0,5 (1-0,611) x 60 = 11,7
C ≤ E, ›(E − Õ) ∙ Â
Ä
22 < 1,5 (1-0,611) x 60 = 35,0
C ≥ Å
E
+ Å
š
22 > 2 + 2 = 4
•
Dopuszczalny mimośród wg [N nr]
−0,55 ∙ ℎ
v
≤ ‘ ≤ 0,25 ∙ ℎ
v
−0,55 ∙ 80 ≤ ‘ ≤ 0,25 ∙ 80
−44 ≤ ‘ ≤ 20
Warunek – węzeł T
Wynik
Â
Ã
/Â
Ä
≥ §, š›
30 / 60 = 0,5
Â
Ã
/Å
Ã
≤ F›
30 /3 = 10
Æ
Ã
/Å
Ã
≤ F›
30 / 3 = 10
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
80 / 60 = 1,33
§, › ≤ Æ
Ã
/Â
Ã
≤ š
30 / 30 = 1,0
Â
Ä
/Å
Ä
≤ F›
60 / 4 = 15
Æ
Ä
/Å
Ä
≤ F›
80 / 4 = 20
DÇ. ÈÉÊËD. șΙ ≤ š
klasa 1
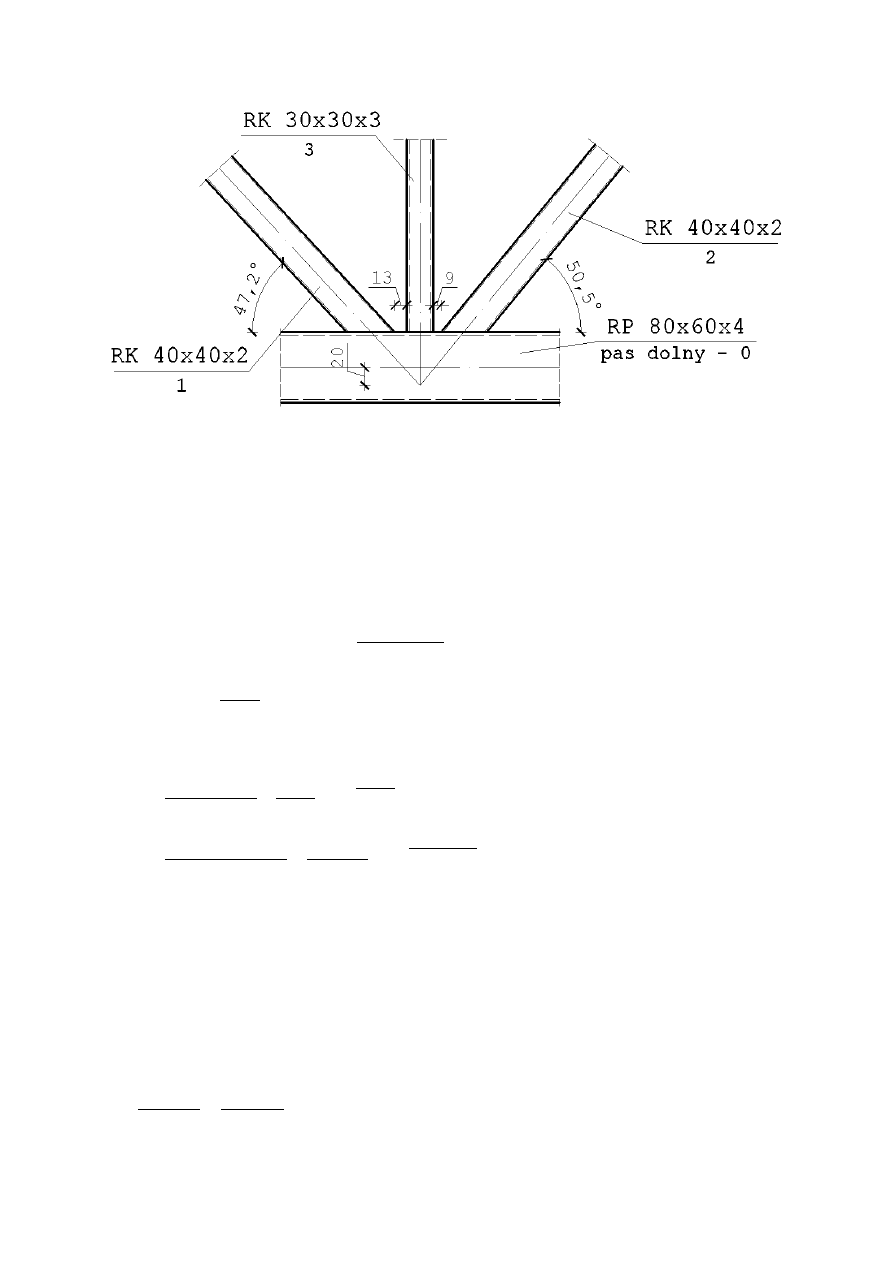
58
•
Dodatkowe warunki geometryczne – węzeł T
†
/
30/60 = 0,50 ≤ 0,85
/ = 60/4 = 15 ≥ 10
•
Zniszczenie przystykowe pasa
)
o
= 1,3 − 0,4 /2 ≤ 1,0
= •
v,ÏB
^
Rv
⁄
= *
v,ÏB
x[
v
∙ ^
Rv
y
⁄
=
140,2
(10,1 ∙ 23,5) = 0,591
)
o
= 1,3 − 0,4 ∙
0,591
0,611 = 0,913
v
= 4
*
b,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
b
∙
22
PS Ð
b
+ 4„1 − 2
*
b,]B
=
0,913 ∙ 23,5 ∙ 0,4
+
(1 − 0,611)PS 90 ∙
2 ∙ 0,611
PS 90 + 4„1 − 0,611 = 32,80 )*
•
Sprawdzenie nośności
H
F,ÑJ
= Fš, ½§ DH > H
F
= EL, §§ DH
•
Spoina obwodowa łącząca słupek 22 (24) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= F II
*
-
∙ PS Q = 14,00 )*
• =
*
-
∙ PS Q
[
{
=
14,00
4 ∙ 3 ∙ 0,3 = 38,9 T¡}
59
j •
Q
ž
+
^
B
; Q
ž
1,0
j 38,9
1,0
+
= F½, K ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Dodatkowe warunki geometryczne – węzeł K
0,6 ≤ (
-
+
+
)/2
-
≤ 1,3
0,6 ≤ (40 + 40)/80 ≤ 1,3
0,6 ≤ 1,0 ≤ 1,3
/ = 60/4 = 15 ≥ 15
•
Zniszczenie przystykowe pasa
)
o
= 1,3 − 0,4 /2 ≤ 1,0
)
o-
= )
o+
= 0,913
v
= 4
? =
v
/2
v
= 60/(2 ∙ 4) = 7,5
*
†,]B
=
8,9)
o
^
Rv
+
√?
PS Ð
†
∙ (2)
*
-,]B
=
8,9 ∙ 0,913 ∙ 23,5 ∙ 0,4
+
∙ „7,5
PS 47,2
∙ (0,611) = 69,68 )*
*
+,]B
=
8,9 ∙ 0,913 ∙ 23,5 ∙ 0,4
+
∙ „7,5
PS 50,5
∙ (0,611) = 66,25 )*
•
Ścięcie pasa
Q = ×
1
1 + 4;
+
3
+
= ×
1
1 + 4 ∙ 2,2
+
3 ∙ 0,4
+
= 0,155
[
Œ
= (2ℎ
v
+ Q
v
) ∙
v
= (2 ∙ 8 + 0,155 ∙ 6) ∙ 0,4 = 6,77 9
+
*
†,]B
=
^
Rv
∙ [
Œ
√3 ∙ PS Ð
†
*
-,]B
=
23,5 ∙ 6,77
√3 ∙ PS 47,2
= 125,2 )*

60
*
+,]B
=
23,5 ∙ 6,77
√3 ∙ PS 50,5
= 119,0 )*
*
v,]B
= [
v
∙ ^
Rv
= 10,1 ∙ 23,5 = 237,4 )*
•
Zniszczenie skratowania
*
†,]B
= ^
R† †
x2ℎ
†
− 4
†
+
†
+
0@@
y
0@@,†
=
10
v
/
v
∙
v
†
∙
†
≤
†
0@@,-
=
0@@,+
=
10
6/0,4 ∙
0,4
0,4 ∙ 4 = 2,67 9
*
-,]B
= *
+,]B
= 23,5 ∙ 0,4 ∙ (2 ∙ 4 − 4 ∙ 0,4 + 4 + 2,67) = 122,9 )*
•
Przebicie pasa
*
†,]B
=
^
Rv v
√3 ∙ PS Ð
†
µ
2ℎ
†
√3 ∙ PS Ð
†
+
†
+
0.
¶
0, ,-
=
10
v
∙
v
∙
†
≤
†
0, ,-
=
0, ,+
=
10
6 ∙ 0,4 ∙ 4 = 16,67 9 →
0,
= 4,0 9
*
-,]B
=
23,5 ∙ 0,4
√3 ∙ PS 47,2
∙
2 ∙ 4
PS 47,2 + 4 + 4 = 139,8 )*
*
+,]B
=
23,5 ∙ 0,4
√3 ∙ PS 50,5
∙
2 ∙ 4
PS 50,5 + 4 + 4 = 129,2 )*
•
Sprawdzenie nośności
H
E,ÑJ
= ¼K, ¼½ DH > H
E
= F¼, š§ DH
H
š,ÑJ
= ¼¼, š› DH > H
+
= E¼, E¼ DH
•
Spoina obwodowa łącząca krzyżulec 13 (18) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
-
∙ PS Q = 26,56 )*
*
-
∙ 9OPQ = 24,60 )*
• =
*
-
∙ PS Q
[
{
=
26,56
2 ∙ (4 + 5,45) ∙ 0,2 = 70,3 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
24,60
2 ∙ 5,45 ∙ 0,2 = 112,8 T¡}
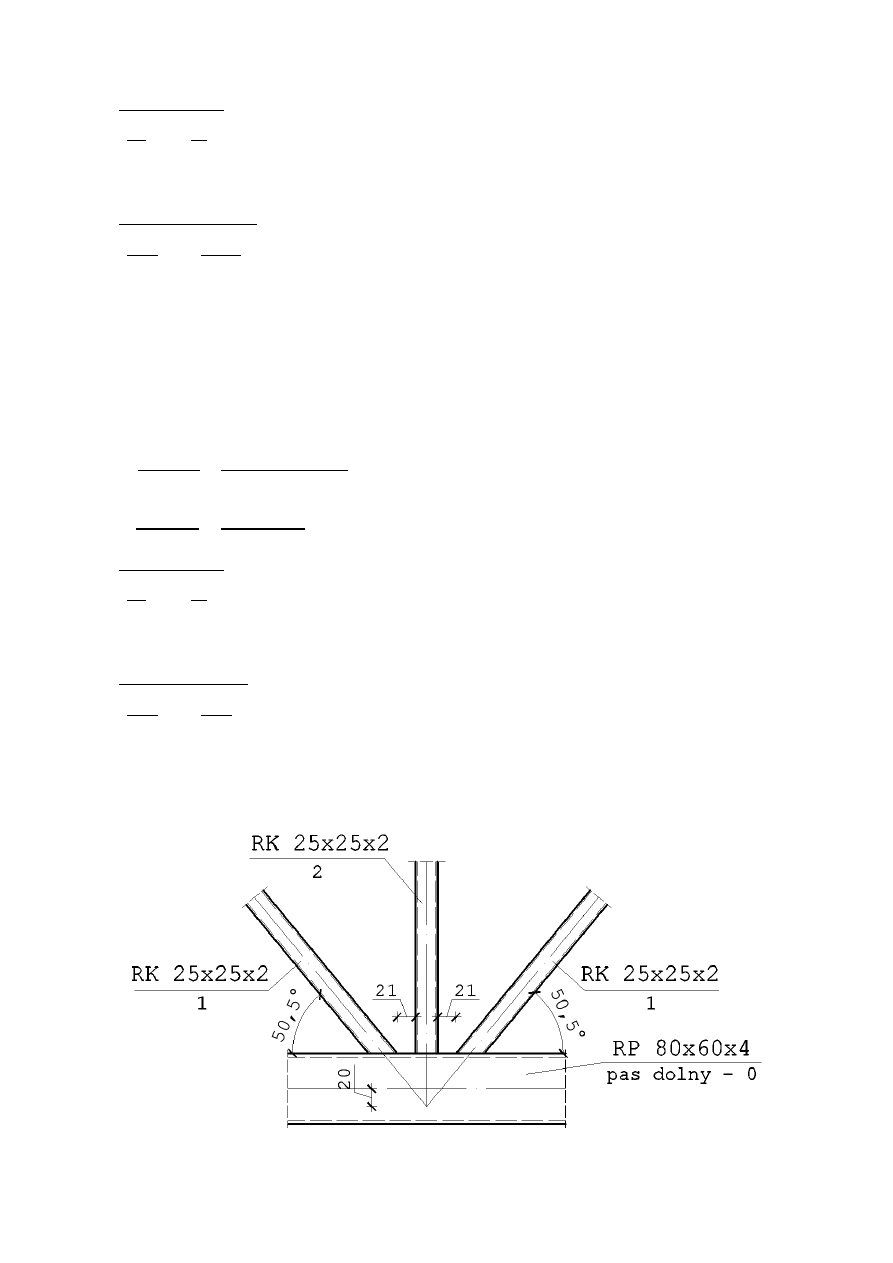
61
j •
Q
ž
+
n µ
Ÿ
Q
∥
¶
+
^
B
Q
ž
0,85; Q
∥
= 0,6
j 70,3
0,85
+
+
112,8
0,6
+
= š§›, L ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Spoina obwodowa łącząca krzyżulec 14 (17) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
-
∙ PS Q = 12,50 )*
*
-
∙ 9OPQ = 10,30 )*
• =
*
-
∙ PS Q
[
{
=
12,50
2 ∙ (4 + 5,18) ∙ 0,2 = 34,0 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
10,30
2 ∙ 5,18 ∙ 0,2 = 49,7 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1,0; Q
∥
= 0,6
j 34,0
1,0
+
+
49,7
0,6
+
= ½K, › ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
7.1.4.6.8. Węzeł I – węzeł typu KT

62
•
Warunki geometryczne wg [N nr]
2
1
+
2
+
3
3
0
= 25 + 25 + 25
3 ∙ 60
= 0,417
; = 21 + 21 = 42
Warunek – węzeł K
RK 25x25x2 (1)
Â
Ã
/Â
Ä
≥ §, F›
25 / 60 = 0,42
Â
Ã
Â
Ä
≥ §, E +
§, §EÂ
Ä
Å
Ä
0,42 > 0,1 + 0,01 x 60/4 = 0,25
Â
Ã
/Å
Ã
≤ F›
25 / 2 = 12,5
Æ
Ã
/Å
Ã
≤ F›
25 / 2 = 12,5
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
80 / 60 = 1,33
§, › ≤ Æ
Ã
/Â
Ã
≤ š
25 / 25 = 1
Â
Ä
/Å
Ä
≤ F›
60 / 4 = 15
Æ
Ä
/Å
Ä
≤ F›
80 / 4 = 20
DÇ. ÈÉÊËDÉÄÌÍ È™Î™ ≤ š
klasa 1
C ≥ §, ›(E − Õ) ∙ Â
Ä
42 > 0,5 (1-0,417) x 60 = 17,5
C ≤ E, ›(E − Õ) ∙ Â
Ä
42 < 1,5 (1-0,417) x 60 = 52,5
C ≥ Å
E
+ Å
š
42 > 2 + 2 = 4
•
Dopuszczalny mimośród wg [N nr]
−0,55 ∙ ℎ
v
≤ ‘ ≤ 0,25 ∙ ℎ
v
−0,55 ∙ 80 ≤ ‘ ≤ 0,25 ∙ 80
−44 ≤ ‘ ≤ 20
•
Dodatkowe warunki geometryczne – węzeł T
†
/ = 25/60 = 0,42 ≤ 0,85
/ = 60/4 = 15 ≥ 10
•
Zniszczenie przystykowe pasa
)
o
= 1,0 (rozciąganie)
v
= 4
*
Ö,]B
=
)
o
^
Rv v
+
(1 − 2)PS Ð
Ö
∙
22
PS Ð
†
+ 4„1 − 2
*
+,]B
=
1,0 ∙ 23,5 ∙ 0,4
+
(1 − 0,417)PS 90 ∙
2 ∙ 0,417
PS 90 + 4„1 − 0,417 = 25,08 )*
•
Sprawdzenie nośności
H
š,ÑJ
= š›, §½ DH > H
š
= L, F§š DH
Warunek – węzeł T
Wynik
Â
Ã
/Â
Ä
≥ §, š›
25 / 60 = 0,42
Â
Ã
/Å
Ã
≤ F›
25 / 2 = 10
Æ
Ã
/Å
Ã
≤ F›
25 / 2 = 10
DÇ. ÈÉÊËDÉÄÌÍ ≤ š
klasa 1
§, › ≤ Æ
Ä
/Â
Ä
≤ š
80 / 60 = 1,33
§, › ≤ Æ
Ã
/Â
Ã
≤ š
25 / 25 = 1,0
Â
Ä
/Å
Ä
≤ F›
60 / 4 = 15
Æ
Ä
/Å
Ä
≤ F›
80 / 4 = 20
DÇ. ÈÉÊËD. șΙ ≤ š
klasa 1

63
•
Spoina obwodowa łącząca słupek 23 z pasem dolnym
- spoina czołowa – grubość –
™
V†o
š II
*
-
∙ PS Q = 4,302 )*
• =
*
-
∙ PS Q
[
{
=
4,302
4 ∙ 2,5 ∙ 0,2 = 21,5 T¡}
j •
Q
ž
+
≤ ^
B
; Q
ž
= 0,85
j 21,5
0,85
+
= š›, F ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
•
Dodatkowe warunki geometryczne – węzeł K
0,6 ≤ (
-
+
-
)/2
-
≤ 1,3
0,6 ≤ (25 + 25)/50 ≤ 1,3
0,6 ≤ 1,0 ≤ 1,3
/ = 60/4 = 15 ≥ 15
•
Zniszczenie przystykowe pasa
)
o
= 1,3 − 0,4 /2 ≤ 1,0
)
o-
= 1,3 − 0,4 ∙ 0,591/0,417 = 0,733
v
= 4
? =
v
/2
v
= 60/(2 ∙ 4) = 7,5
*
†,]B
=
8,9)
o
^
Rv
+
√?
PS Ð
†
∙ (2)
*
-,]B
=
8,9 ∙ 0,733 ∙ 23,5 ∙ 0,4
+
∙ „7,5
PS 50,5
∙ (0,417) = 36,3 )*
•
Ścięcie pasa
Q = ×
1
1 + 4;
+
3
+
= ×
1
1 + 4 ∙ 4,2
+
3 ∙ 0,4
+
= 0,082
[
Œ
= (2ℎ
v
+ Q
v
) ∙
v
= (2 ∙ 8 + 0,082 ∙ 6) ∙ 0,4 = 6,60 9
+
*
†,]B
=
^
Rv
∙ [
Œ
√3 ∙ PS Ð
†

64
*
-,]B
=
23,5 ∙ 6,60
√3 ∙ PS 50,5
= 116,0 )*
•
Zniszczenie skratowania
*
†,]B
= ^
R† †
x2ℎ
†
− 4
†
+
†
+
0@@
y
0@@,-
=
10
6/0,4 ∙
0,4
0,2 ∙ 2,5 = 3,33 9 →
0@@,-
= 2,5 9
*
-,]B
= 23,5 ∙ 0,2 ∙ (2 ∙ 2,5 − 4 ∙ 0,2 + 2,5 + 2,5) = 43,24 )*
•
Przebicie pasa
*
†,]B
=
^
Rv v
√3 ∙ PS Ð
†
µ
2ℎ
†
√3 ∙ PS Ð
†
+
†
+
0.
¶
0, ,-
=
10
6 ∙ 0,4 ∙ 2,5 = 10,42 9 →
0,
= 2,5 9
*
-,]B
=
23,5 ∙ 0,4
√3 ∙ PS 50,5
∙
2 ∙ 2,5
PS 50,5 + 2,5 + 2,5 = 80,74 )*
•
Sprawdzenie nośności
H
E,ÑJ
= F¼, F§ DH > H
E
= ›, F›§ DH
•
Spoina obwodowa łącząca krzyżulec 15 (16) z pasem dolnym
- spoina czołowa – grubość –
™ =
V†o
= š II
*
-
∙ PS Q = 4,128 )*
*
-
∙ 9OPQ = 3,403 )*
• =
*
-
∙ PS Q
[
{
=
4,128
2 ∙ (2,5 + 3,24) ∙ 0,2 = 18,0 T¡}
Ÿ =
*
-
∙ 9OPQ
[
Œ
=
3,403
2 ∙ 3,24 ∙ 0,2 = 26,3 T¡}
j •
Q
ž
+
+ µ
Ÿ
Q
∥
¶
+
≤ ^
B
Q
ž
= 1,0; Q
∥
= 0,6
j 18,0
1,0
+
+
26,3
0,6
+
= LG, L ÒÓ™ ≤ Ô
J
= šE› ÒÓ™
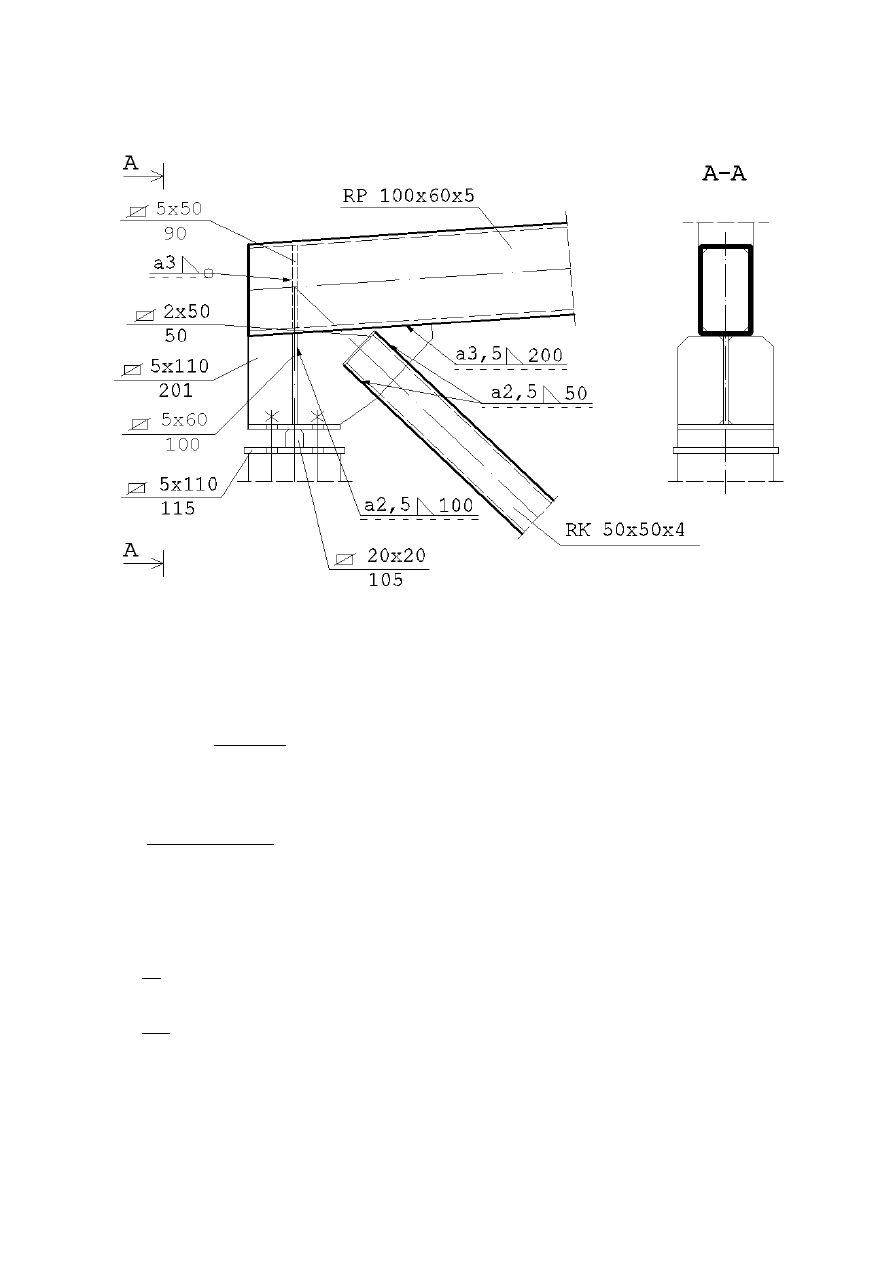
65
7.1.4.7. Zamocowanie wiązara na podporze (węzeł A)
Żeberko usztywniające:
•
Wysokość żeberka
Ø
70,13 )* (reakcja na podporze A)
ℎ
ż
≥
{
;
{
=
Ø
}
{
∙ Q ∙ ^
B
}
{
= š, › II
{
=
70,13
0,25 ∙ 2 ∙ 0,8 ∙ 21,5 = 8,155 9 → ℎ
ż
= 10 9
ℎ
ż
= E§§ II
•
Szerokość żeberka
ż
≥
ℎ
ż
30 + 40
;
ż
≥ 50
ż
≥
100
30 + 40 = 43,33;
ż
≥ 50
ż
= ݤ II
•
Grubość żeberka
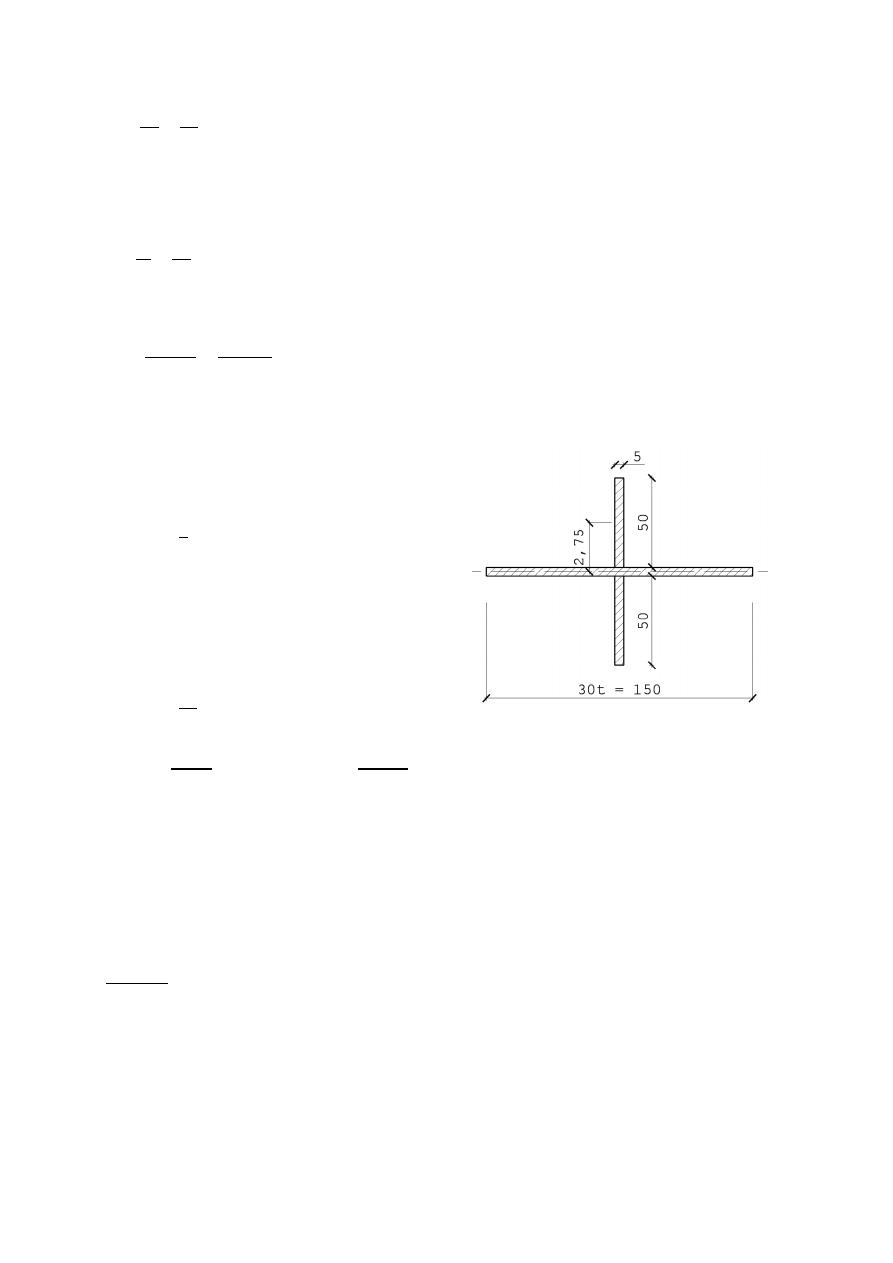
66
ż
≥
ż
15 =
50
15 = 3,33
ż
= › II
•
Klasa przekroju żeberka
f =
ż
ż
=
50
5 = 10,0 ≤ 10 ∙ ® = 10 → ) }P} 2 3Z¯‘)ZO°±
•
Warunek na docisk
•
B
=
0,5 ∙
Ø
ż
∙
ż
B
=
35,07
0,5 ∙ 4,5 = E›, ›K DH/ÚI
š
≤ ^
B¨
= 1,25 ∙ ^
B
= 26,88 )*/9
+
Warunek spełniony
•
Warunek sztywności
`
{
≥ ) ∙ ∙
b
) = 1,5 ∙ }
+
∩ ) ≥ 0,75
= ℎ
ż
= 100
= 10,0 9
} = 50
= 5 9
=
:
= 5
= 0,5 9
) = 1,5 ∙
10
5
+
= 6,0
`
{
=
2 ∙
‚
ż
∙
ż
3
12
+
ż
∙
ż
∙ }
2
ƒ
= 2 ∙
‚
0,5 ∙ 5
3
12
+ 0,5 ∙ 5 ∙ 2,75
2
ƒ = 48,23 9
a
`
{
= 48,23 9
a
≥ 6,0 ∙ 10 ∙ 0,5
b
48,23 9
a
≥ 7,50 9
a
Warunek spełniony
•
Warunek na ściskanie
*
l
ż
∙ *
]_,ż
≤ 1,0
* =
Ø
= 70,13 )*
*
]_,ż
= 1,0 ∙ [
¨t,ż
∙ ^
B
[
¨t,ż
= S ª[
ż
+
:
(
-
+
+
) = 0,5 ∙ 5,0 + 0,5 ∙ (5 + 5) = 7,5 9
+
[
ż
+ 30 ∙
:
+
= 0,5 ∙ 5,0 + 30 ∙ 0,5
+
= 10,0 9
+
—
67
[
¨t,ż
= 7,5 9
+
*
]_,ż
= 1,0 ∙ 7,5 ∙ 21,5 = 161,3 )*
`
ż
= `
{
= 48,23 9
a
S
ż
= j
`
ż
[
¨t,ż
= j
48,23
7,5 = 2,536 9
g
R
= 1,0
:
= g
R
∙ ℎ
ż
= 1,0 ∙ 10 = 10,0 9
f
ż
=
:
S
ż
=
10,0
2,536 = 3,943
f = 84
Współczynnik
l
ż
względem krzywej c (n = 1,2):
f
ż
‹ = f
ż
f =
3,943
84 = 0,0469 → l
ż
= (1 + f̅
+o
)
q-
o
= (1 + 0,0469
+,a
)
q…
e
= 0,9995
70,13
0,9995 × 161,3 = §, LL ≤ 1,0
Warunek spełniony
•
Spoina łącząca wewnętrzne żeberko z pasem górnym
0,2 ∙
V"N
≤ } ≤ 0,7 ∙
V†o
V"N
=
V†o
= 5
0,2 ∙ 5 ≤ } ≤ 0,7 ∙ 5
2,5 ≤ } ≤ 3,5 → 3Z¯~° ±°ę ™ = F II
= 90
Naprężenia w spoinie (na jedną spoinę działa 0,25 reakcji z podpory):
Ÿ
∥
=
0,25 ∙
Ø
} ∙
=
35,07
0,3 ∙ 9,0 = 12,99 )*/9
+
•
ž
= Ÿ
ž
= 0
Warunek na spoinę pachwinową:
œ ∙ √3 ∙ Ÿ
∥
≤ ^
B
Stal S235JR:
:
= 5
< 16
→ ^
B
= 215 T¡}
68
0,V†o
= 235 T¡} ≤ 255 T¡} → œ = 0,7
0,7 ∙ √3 ∙ 12,99 = E›, G› DH/ÚI
š
≤ 21,5 )*/9
+
Warunek spełniony
•
Spoina żeberko-blacha:
0,2 ∙
V"N
≤ } ≤ 0,7 ∙
V†o
V"N
=
V†o
= 5
2,5 ≤ } ≤ 3,5 → 3Z¯~° ±°ę ™ = š, › II
= 45
Naprężenia w spoinie:
Ÿ
∥
= 0
• =
0,25 ∙
Ø
} ∙
=
17,52
0,35 ∙ 4,5 = 11,12 )*/9
+
•
ž
= Ÿ
ž
=
•
√2
=
11,12
√2
= 78,6 T¡} ≤ ^
B
= 215 T¡}
Warunek na spoinę pachwinową:
œ ∙ „•
ž+
+ 3 ∙ Ÿ
ž+
≤ ^
B
Stal S235JR:
@
= 5
< 16
→ ^
B
= 215 T¡}
0,V†o
= 235 T¡} < 255 T¡} → œ = 0,7
0,7 ∙ „78,6
+
+ 3 ∙ 78,6
+
= EE§, L ÒÓ™ ≤ 215 T¡}
Warunek spełniony
Spoina łącząca blachę węzłową z pasem górnym
•
Długość spoiny
0,2 ∙
V"N
≤ } ≤ 0,7 ∙
V†o
V"N
=
V†o
= 5
2,5 ≤ } ≤ 3,5 → 3Z¯~° ±°ę ™ = F, › II
*
ÝÞ
= 138,7 )*
*
ÝÞ
} ∙ ß ≤ Q
∥
∙ ^
B
→ ß ≥
*
ÝÞ
} ∙ Q
∥
∙ ^
B
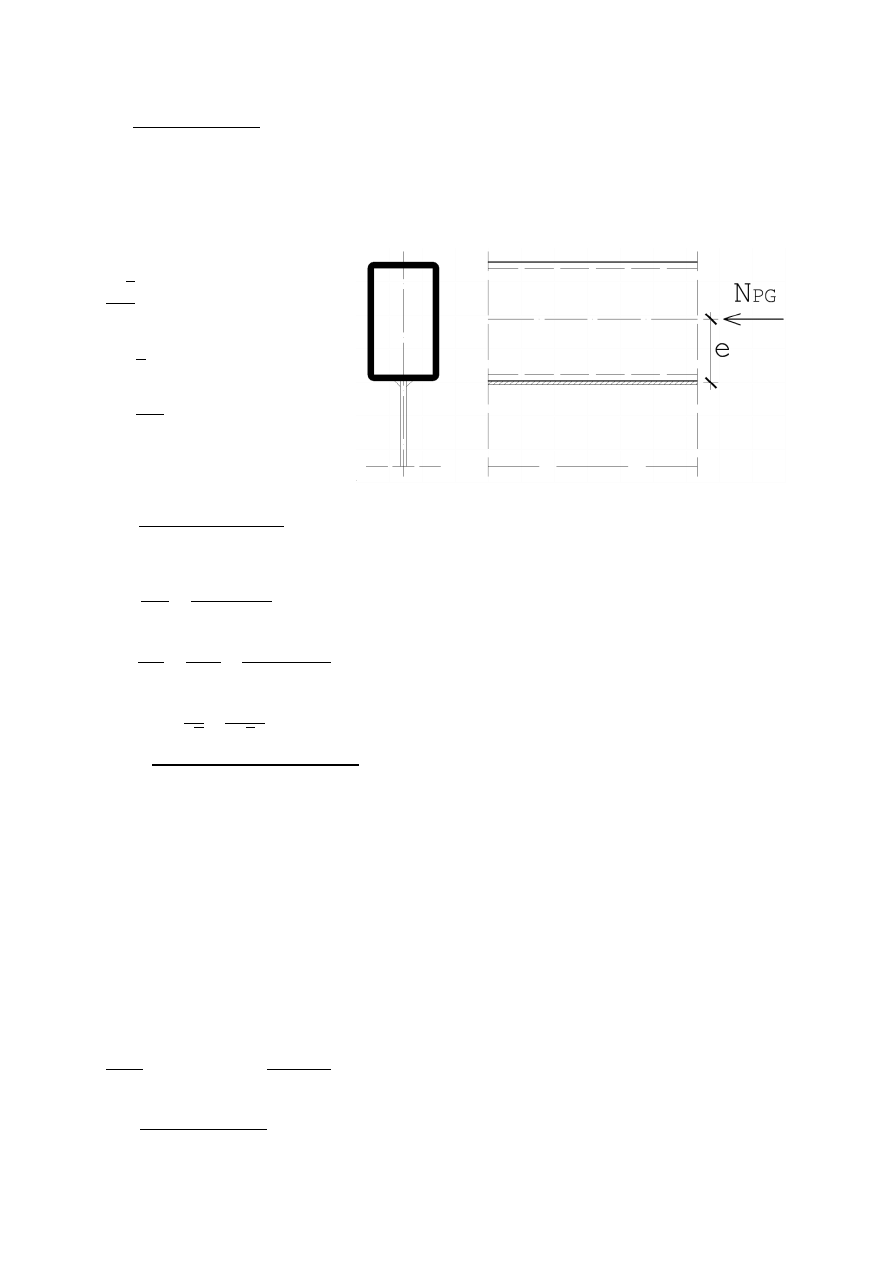
69
≥
138,7
2 ∙ 0,35 ∙ 0,8 ∙ 21,5 = 11,52 9
Przyjęto –
Ç = š§ ÚI = š§§ II (maksymalna długość wynikająca z konstrukcji węzła)
•
Uwzględnienie momentu powstałego na skutek mimośrodu
} = 3,5
2√2
3 } = 3,3
‘ =
ℎ
2 + 3,3
‘ =
100
2 + 3,3 = 53,3
T = *
ÝÞ
∙ ‘ = 138,7 )* ∙ 5,33
T = 739,3 )*9
œ ∙ w•
ž+
+ 3 ∙ (Ÿ
∥+
+ Ÿ
ž+
) ≤ ^
B
Ÿ
∥
=
*
ÝÞ
[
{
=
138,7
2 ∙ 0,35 ∙ 20 = 99,1 T¡}
• =
T
=
{
=
6 ∙ T
} ∙
+
=
6 ∙ 739,3
2 ∙ 0,35 ∙ 20
+
= 158,4 T¡}
•
ž
= Ÿ
ž
=
•
√2
=
158,4
√2
= 112,0 T¡} ≤ ^
B
= 215 T¡}
0,7 ∙ „112,0
+
+ 3 ∙ (99,1
+
+ 112,0
+
) = EKG, › ÒÓ™ ≤ 215 T¡}
Spoina łącząca blachę węzłową z krzyżulcem nr 11 (20)
•
Długość spoiny
0,2 ∙
V"N
≤ } ≤ 0,7 ∙
V†o
V"N
=
¨#
= 5
V†o
=
!--
= 4
2,5 ≤ } ≤ 2,8 → 3Z¯~° ±°ę ™ = š, › II
*
!--
= 86,25 )*
*
!--
} ∙ ß ≤ Q
∥
∙ ^
B
→ ß ≥
*
!--
} ∙ Q
∥
∙ ^
B
-
≥
86,25
4 ∙ 0,25 ∙ 0,8 ∙ 21,5 = 5,001 9
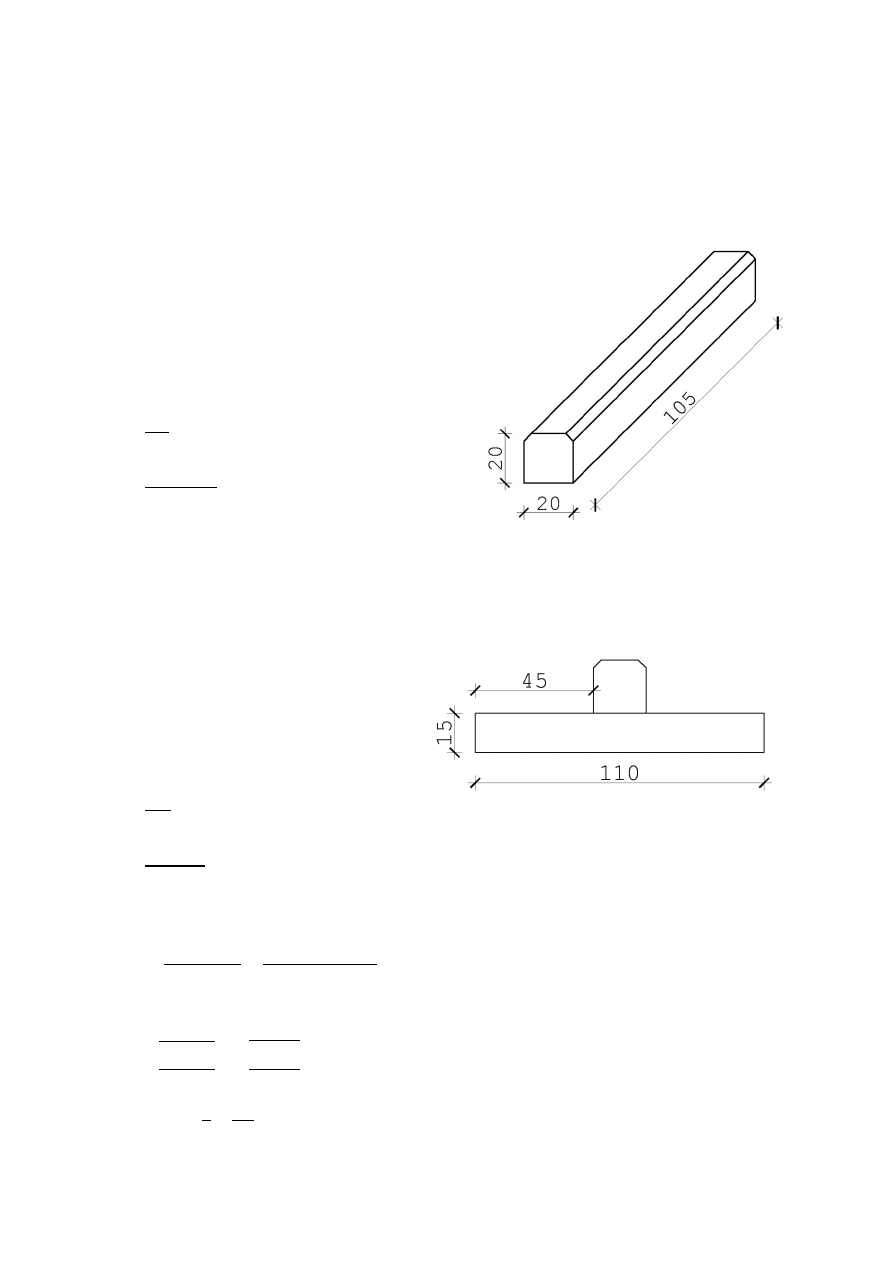
70
Przyjęto –
Ç › ÚI ›§ II (długość pojedynczej spoiny)
Blacha pozioma:
Przyjęto blachę o wymiarach – 5 x 100 x 105
Klocek centrujący:
•
Wymiarowanie klocka centrującego
!#
2 ∙
ż
+ →
!#
≤ 2 ∙ 50 + 5 = 105
Przyjęto wymiary klocka – 20 x 20 x 105 mm
Sprawdzenie docisku na klocku:
•
B
=
Ø
∙ ≤ ^
B¨
•
B
=
70,13
2,0 × 10,5 = FF, L T¡}
^
B¨
= 1,25 ∙ ^
B
= 1,25 × 21,5 = 268,8 T¡}
•
B
< ^
B¨
Krawędzie klocka należy sfrezować.
•
Wymiarowanie blachy pod klockiem
Wymiary blachy – 15 x 110 x 115
9 = 45
= 4,5 9
•
Sprawdzenie docisku na blasze dolnej
•
B
=
Ø
∙ ≤ ^
B¨
•
B
=
70,13
11 ∙ 11,5 = ›, ›L ÒÓ™ ≤ ^
B¨
= 268,8 T¡}
•
Wyznaczenie momentów zginających w przekroju 1-1 na 1cm szerokości
T
-q-
=
•
B
∙ 1,0 ∙ 9
+
2
=
0,554 ∙ 1,0 ∙ 4,5
+
2
= 5,61 )*9
Wymagana grubość blachy:
≥
à
¿
á
¿
âj6 ∙ T
-q-
^
B
= j
6 ∙ 5,61
21,5 = 1,25 9
9
3 =
4,5
3 = 1,5 9

71
Wyznaczono grubość blachy –
Å E, › ÚI = E› II
•
Zaprojektowanie spoiny łączącej klocek z blachą
Warunek dla spoiny blacha-klocek:
0,2 ∙
V"N
≤ } ≤ 0,7 ∙
V†o
V"N
=
!#
= 20
V†o
=
¨#
= 15
0,2 ∙ 20 ≤ } ≤ 0,7 ∙ 15
4 ≤ } ≤ 10,5
Przyjęto –
™ = L II
•
–
=
Ø
∑} ∙ =
70,13
2 ∙ 0,4 ∙ 10,5 = 83,5 T¡}
• = •
–
= 83,5 T¡}
•
ž
= Ÿ
ž
=
•
√2
=
83,5
√2
= 59,0 T¡} ≤ ^
B
= 215 T¡}
œ ∙ „•
ž+
+ 3 ∙ Ÿ
ž+
≤ ^
B
Stal S235JR:
!#
= 20
> 16
→ ^
B
= 205 T¡}
0,V†o
= 225 T¡} ≤ 255 T¡} → œ = 0,7
0,7 ∙ „59,0
+
+ 3 ∙ 59,0
+
= ½š, ¼ ÒÓ™ ≤ 205 T¡}
Warunek spełniony
Blacha dolna jest zarazem blachą poziomą głowicy słupa, na którym opiera się wiązar kratowy.
Wyszukiwarka
Podobne podstrony:
projekt wiazara ec algorytm
Projekt Inzynierski Obliczenia wiązara kratowego G3 mitek
Budownictwo I projekt, literatura, · Geometria wiązara
OBLICZENIE WIĄZARA PŁATWIOWO KLESZCZOWEGO, Projekt domku
Projekt Inzynierski Obliczenia wiązara kratowego P1 mitek
Projekt Inzynierski Obliczenia wiązara kratowego G3 mitek
projekt o narkomanii(1)
!!! ETAPY CYKLU PROJEKTU !!!id 455 ppt
Wykład 3 Dokumentacja projektowa i STWiOR
Projekt nr 1piątek
Projet metoda projektu
więcej podobnych podstron