Pomiar składowej poziomej pola magnetycznego 

ziemskiego metodą busoli stycznych 

Ćw.7 

 

Cel ćwiczenia 

Celem  ćwiczenia jest poznanie zjawiska występowania pola magnetycznego wokół przewodnika, w którym 

płynie prąd elektryczny, oraz wyznaczenie składowej poziomej magnetycznego pola ziemskiego. 

 

Zakres obowiązującego materiału teoretycznego 

Prawo Ampere’a. Prawo Biota-Savarta. Pole magnetyczne przewodnika prostoliniowego, kołowego i 

solenoidu. Strumień magnetyczny. Moment magnetyczny. Pole magnetyczne Ziemi. 

 

Przyrządy użyte w doświadczeniu 

Busola stycznych, zasilacz z amperomierzem, wyłącznik. 

 

Wprowadzenie 

W przestrzeni otaczającej przewodnik, przez który płynie prąd elektryczny 

, istnieje pole magnetyczne 

określane przez wektor indukcji pola magnetycznego 

(

)

(I

)

B

r

. Wektor indukcji pola magnetycznego (czyli wartość, 

kierunek i zwrot pola magnetycznego) powstałego na skutek przepływu prądu elektrycznego, zależy od 

długości i kształtu przewodnika oraz od natężenia prądu. Wektor indukcji pola magnetycznego w dowolnym 

punkcie przestrzeni można wyznaczyć korzystając z prawa Biota-Savarta:  

3

0

4

r

r

l

d

I

B

d

r

r

r

×

=

π

µ

 

 

(1) 

(

0

µ

 - oznacza przenikalność magnetyczna próżni 

) 

2

7

0

/

10

4

/

A

N

−

=

π

µ

Prawo to pozwala wyznaczyć wektor indukcji pola magnetycznego 

)

( B

d

r

 wytwarzany przez bardzo mały 

prostoliniowy element przewodnika 

)

( l

d

r

, w którym płynie prąd 

I

, w odległości 

)

(

rr

od początku wektora 

l

d

r

 

(rys. 1). Ponieważ każdy element 

na przewodniku powoduje powstanie pewnego składowego pola 

magnetycznego 

 w rozważanym punkcie przestrzeni, pole magnetyczne 

l

d

r

B

d

r

B

r

wytworzone przez cały 

przewodnik jest sumą wszystkich pól składowych 

B

d

r

. Kierunek wektora 

B

d

r

 jest określany przez wynik 

iloczynu wektorowego 

, czyli jest on prostopadły do płaszczyzny, w której leżą wektory 

r

l

d

r

r

×

l

d

r

 i 

rr

, a 

zwrot jest zgodny z ruchem postępowym  śruby prawoskrętnej obracanej od wektora 

 do wektora 

l

d

r

rr

 

przez mniejszy kąt.  

Jeżeli rozważany przewodnik, przez który płynie prąd 

I

, ma kształt okręgu o promieniu 

(

, to 

natężenie pola magnetycznego 

)

R

B

r

, które powstaje w środku okręgu, można wyznaczyć korzystając z wzoru 

Biota-Savarta. Każdy wycinek okręgu 

 wytwarza w środku tego okręgu pole (rys. 2), dla którego wartość 

l

d

r

 

1

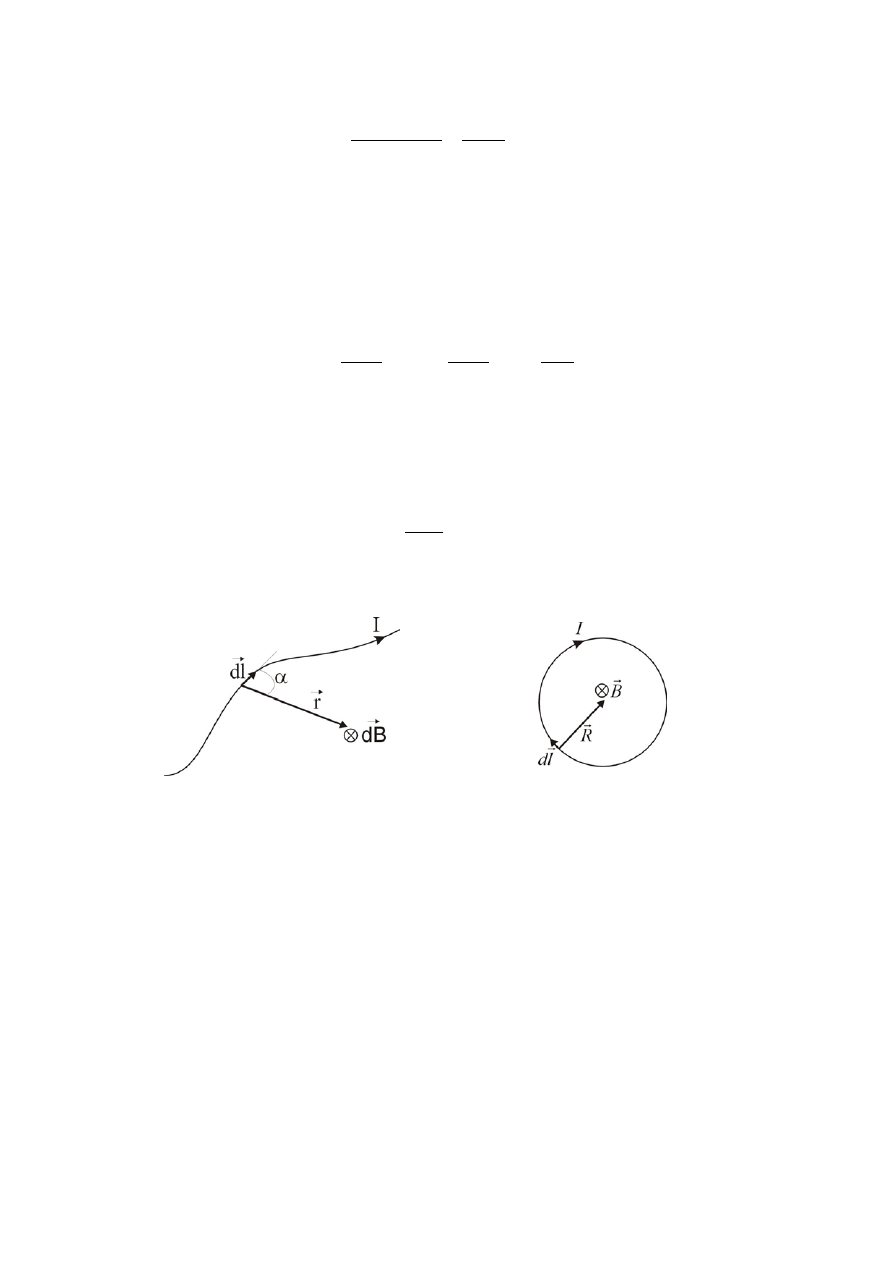
wektora indukcji 

 wyrażona jest następująco:  

dB

2

0

3

0

4

4

sin

R

Idl

R

IdlR

dB

π

µ

π

α

µ

=

=

 

 

(2) 

W tym przypadku 

sin

1

=

α

, ponieważ kąt między każdym elementarnym 

dl

r

i odcinkiem o długości 

 

łączącym początek wektora 

 z środkiem okręgu jest kątem prostym. Kierunek wektora 

 wytworzonego 

w środku okręgu przez jakikolwiek odcinek 

)

(

R

l

d

r

B

d

r

l

d

r

 jest zawsze prostopadły do płaszczyzny okręgu. Wobec tego 

można dodać do siebie algebraicznie wszystkie wartości indukcji magnetycznej 

. Suma długości wszystkich 

odcinków 

 wynosi 

dB

dl

R

π

2

, zatem całkowite natężenie pola w środku okręgu równa się: 

R

I

R

R

I

dl

R

I

dB

B

R

R

2

2

4

4

0

2

0

2

0

2

0

2

0

µ

π

π

µ

π

µ

π

π

=

=

=

=

∫

∫

 

 

(3) 

Jeżeli zamiast pojedynczego przewodnika kołowego rozpatruje się obwód złożony z 

 blisko siebie 

położonych identycznych przewodników kołowych, które praktycznie biorąc mają poprzeczne rozmiary 

(grubość drutów i izolacji) znikomo małe w stosunku do promienia koła, indukcja magnetyczna w środku okręgu 

wynosi: 

)

(

n

R

nI

B

2

0

µ

=

 

 

(4) 

gdy przez każdy z przewodników płynie prąd o natężeniu 

I

 (tzn. gdy są one połączone szeregowo, stanowiąc 

poszczególne zwoje wspólnego uzwojenia). 

 

 

Rys.1 Rys.2 

 

Obecność pola magnetycznego można wykazać za pomocą swobodnie zawieszonej igły magnetycznej, 

która ustawia się równolegle do kierunku pola. Jeżeli rozpatrywane poprzednio uzwojenie kołowe ustawione 

jest pionowo i w jego środku zawieszona jest igła magnetyczna, mająca swobodę obrotu w płaszczyźnie 

poziomej, to pod wpływem przepływu prądu przez uzwojenie igła ta ustawia się prostopadle do płaszczyzny 

uzwojenia, przy założeniu,  że na igłę magnetyczną działa w płaszczyźnie poziomej tylko pole magnetyczne 

wytworzone przez uzwojenie kołowe. Jeżeli jednocześnie igła magnetyczna poddana zostaje działaniu jeszcze 

jednego poziomego pola magnetycznego, które posiada kierunek odmienny od kierunku pola magnetycznego, 

wytworzonego przez uzwojenie, to igła ustawia się wzdłuż linii sil pola wypadkowego powstałego w miejscu, w 

którym się ona znajduje. 

Jeżeli oba pola są prostopadle do siebie tzn. pole ziemskie 

z

B

r

 jest równolegle do płaszczyzny 

wyznaczonej przez kołowy przewodnik, a pole indukowane przez prąd płynący w uzwojeniu 

 jest jak 

wiemy prostopadłe do płaszczyzny uzwojenia to igła ustawia się wzdłuż przekątnej prostokąta (rys. 3). Znając 

u

B

r

 

2

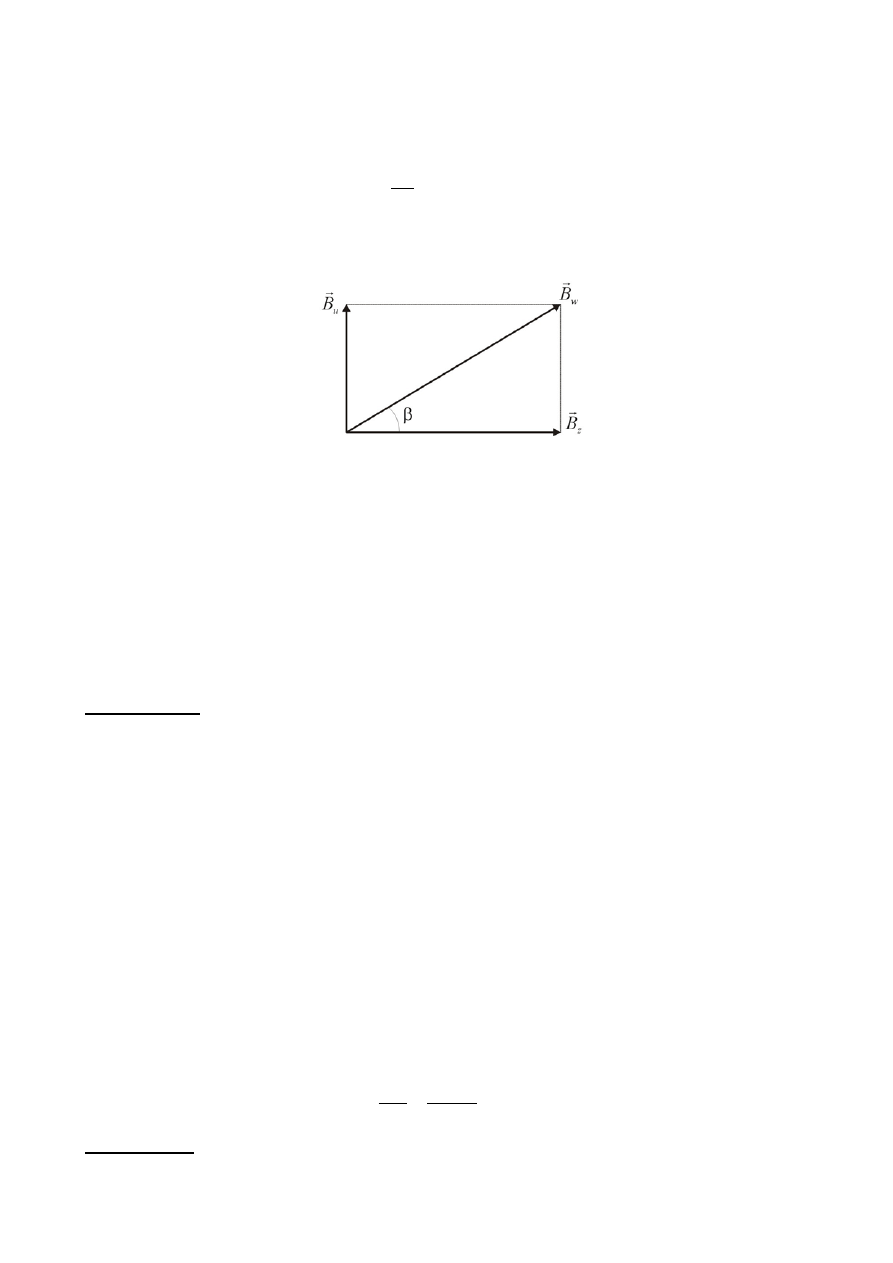
kierunek wypadkowej indukcji pola magnetycznego 

w

B

r

, a zarazem kąt 

β

, jaki tworzy igła z płaszczyzną, w 

której znajduje się uzwojenie, można wyznaczyć stosunek wartość wektorów indukcji 

z

B

r

 i 

: 

u

B

r

β

tg

µ

Rtg

2

0

B

B

z

u

=

 

 

(5) 

Przyrządem, który umożliwia porównywanie natężenia tych dwóch pól magnetycznych jest busola 

stycznych albo busola tangensów - nazwa jej pochodzi od nazwy funkcji, która wyznacza stosunek (

). 

z

u

B

B /

 

Rys.3 

 

Uwaga. Rozważanie dotyczące wartości 

 jest nieco uproszczone i obarczone jest pewnym niewielkim 

zresztą błędem. Wynika on stad, że w punktach, które zajmują bieguny igły magnetycznej po jej wychyleniu, 

wektor indukcji magnetycznej natężenia pola i jego kierunek są inne niż w punktach, które bieguny te 

zajmowały początkowo. Pole magnetyczne wytwarzane przez prądowy obwód kołowy nie jest jednorodne, w 

malej objętości zaś otaczającej środek obwodu jest ono jedynie w przybliżeniu jednorodne. Wspomniany błąd 

pomijamy (jest on zresztą znacznie mniejszy niż  błędy pomiarowe, jakimi obarczone są wyniki niniejszego 

ćwiczenia). 

z

u

B

B /

Zasada pomiaru 

Przedmiotem niniejszego ćwiczenia jest pomiar składowej poziomej pola ziemskiej indukcji magnetycznej 

. Pole magnetyczne ziemskie jest ukośne w stosunku do (poziomej) powierzchni Ziemi. Kąt, jaki tworzy jego 

kierunek z płaszczyzną poziomą, nie jest prosty, wartość tego kata nazywamy inklinacją magnetyczną w 

danym punkcie powierzchni kuli ziemskiej. Wektor indukcji magnetycznej pola ziemskiego można rozłożyć na 

dwa wektory składowe: poziomy i pionowy. (Znając wartość inklinacji można z takiego pomiaru obliczyć 

całkowitą indukcję pola magnetycznego ziemskiego i tak też postępuje się zazwyczaj). Jeżeli płaszczyzna 

uzwojenia busoli stycznych leży w płaszczyźnie południka magnetycznego ziemskiego, to kierunek pola 

magnetycznego wytworzonego przez prąd płynący w uzwojeniu jest prostopadły do kierunku pola 

magnetycznego ziemskiego. Spełnione są więc warunki podane poprzednio. Pomiar kąta wychylenia igły 

z

B

β

 

umożliwia wyznaczenie składowej poziomej indukcji magnetycznej pola ziemskiego. Oznaczamy przez 

 

indukcję magnetyczną pola ziemskiego, przez 

, indukcję magnetyczną pola wytworzonego przez uzwojenie, 

mamy więc 

z

B

u

B

β

β

nI

tg

B

B

u

z

=

=

 

 

(7) 

Opis przyrządu 

 

3

W płaszczyźnie pionowej nawiniętych jest kołowo i umieszczonych blisko siebie   = 5, 10 i 15 zwojów 

przewodnika, uzwojenia te mają średnicę 

n

R

2

 = 25 ± 0.5 cm. W środku uzwojenia znajduje się mała igła 

magnetyczna.  

 

Ustawienie przyrządu 

Uwaga. Przed przystąpieniem do pomiarów należy usunąć ze stołu i z kieszeni przedmioty żelazne 

(śrubokręty, scyzoryki, klucze itp.) 

1. Ustawić uzwojenie busoli w płaszczyźnie południka magnetycznego, tzn. w jednej płaszczyźnie z igłą 

magnetyczną. Najlepiej jest przyłożyć do uzwojenia tuż nad igłą poziomo linijkę i sprawdzić, czy oś igły 

jest równoległa do linijki. Obrócić stolik busoli tak, aby wskazówka znalazła się nad podziałką O

o

. 

2. Ustawić pokrętła napięcia zasilacza na najmniejszą wartość. Zamknąć obwód układu z uzwojeniem 15 

zwojów. 

3. Regulując napięciem na zasilaczu zwiększać natężenie prądu do uzyskania kąta wychylenia igły 

magnetycznej 45

o

. Zanotować wartość prądu 

I ′

. Zmienić kierunek prądu, sprawdzić czy wychylenie igły 

magnetycznej jest symetryczne. Jeżeli wychylenia igły nie są symetryczne, oznacza to, że uzwojenie nie 

było ustawione w płaszczyźnie południka ziemskiego. Należy poprawić ustawienie i powtórzyć pomiar. 

Zanotować wartość prądu 

I ′′

. 

Uwaga. Przy każdym pomiarze można lekko uderzyć zgiętym palcem w środek szybki stolika, zdarza się 

bowiem czasami, że igła magnetyczna nie ustawia się we właściwym położeniu na skutek tarcia. 

Punkty 1, 2, 3 powtórzyć siedem razy. 

4.  Pomiary jak w punkcie 1, 2, 3 powtórzyć dla liczby zwojów   = 5, 10, 15. 

n

5. Wyniki zapisać w następującej tabeli: 

 

 

n 

 

k 

 

I' 

 

I'' 

2

''

'

I

I

I

k

+

=

7

7

1

∑

=

=

k

k

śr

I

I

 

 

)

(

śr

z

I

B

 

[-] [-] [A] [A]  [A] 

[A] 

[T] 

1 

 

 

   

2 

 

 

   

3 

 

 

   

4 

 

 

   

5 

 

 

   

6 

 

 

   

5 

7 

 

 

   

1 

 

 

   

2 

 

 

   

3 

 

 

   

4 

 

 

   

5 

 

 

   

6 

 

 

   

10 

7 

 

 

   

1 

 

 

   

2 

 

 

   

3 

 

 

   

15 

4 

 

 

   

 

4

5 

 

 

   

6 

 

 

   

7 

 

 

   

 

 

6. Obliczyć wartość średnią 

 wspólną dla różnych liczb zwojów. 

z

B

7. Obliczyć metoda Studenta-Fishera błąd pomiaru wielkości 

. 

z

B

 

Przykład obliczenia błędu 

Obliczenia błędu dla wielkości 

x 

(x 

reprezentuje wielkość 

). Błąd pomiaru 

z

B

x

∆

 wielkości 

x

: 

1

−

=

∆

n

S

t

x

α

 

 
 

S

 - odchylenie standardowe wyrażone wzorem: 

(

)

n

x

x

S

n

i

i

∑

=

−

=

1

2

 

 
 

x

 - wartość średnia wielkości x wyliczona ze wzoru: 

n

x

x

n

i

i

∑

=

=

1

 

 
 

i

x

 - i-ty pomiar wielkości 

x

; 

n

 - liczba pomiarów; 

α

 - poziom istotności 

=

α

0,05; 

α

t

 - współczynnik Studenta odczytany z tablic (instrukcja Nr 17) dla r = n-1 stopni swobody; 

 

Wynik pomiaru wynosi: 

x

x

x

∆

±

=

 

 
 

 

Wyniki obliczeń i wnioski 

Na ostatniej stronie podać wynik obliczeń pola magnetycznego ziemskiego z uwzględnieniem błędu. Napisać 

wnioski. Wynik końcowy podać w postaci: 

x

x

x

∆

±

=

. Porównać uzyskaną wartość z wartością tablicową. 

 

5