TERMODYNAMIKA

TERMODYNAMIKA

Kinetyczna teoria gaz

Kinetyczna teoria gaz

ó

ó

w

w

→

1 cm

3

około 10

19

cz steczek

powietrza !

Jednostka ci nienia – 1 Torr

Jednostka ci nienia – 1 paskal

→

→

!

Prawo gaz

Prawo gaz

ó

ó

w doskona

w doskona

ł

ł

ych

ych

Gaz doskona

Gaz doskona

ł

ł

y

y

– zało enia modelu

:

• Obj to

cz steczek gazu jest o wiele mniejsza ni

obj to

zajmowana przez gaz (cz steczki gazu – punkty materialne)
• Zasi g sił działaj cych mi dzy dwiema cz stkami jest o wiele mniejszy

ni

rednia odległo

mi dzycz steczkowa

(oddziaływania mi dzycz steczkowe – pomijane)
• Zderzenia cz steczek s idealnie spr yste

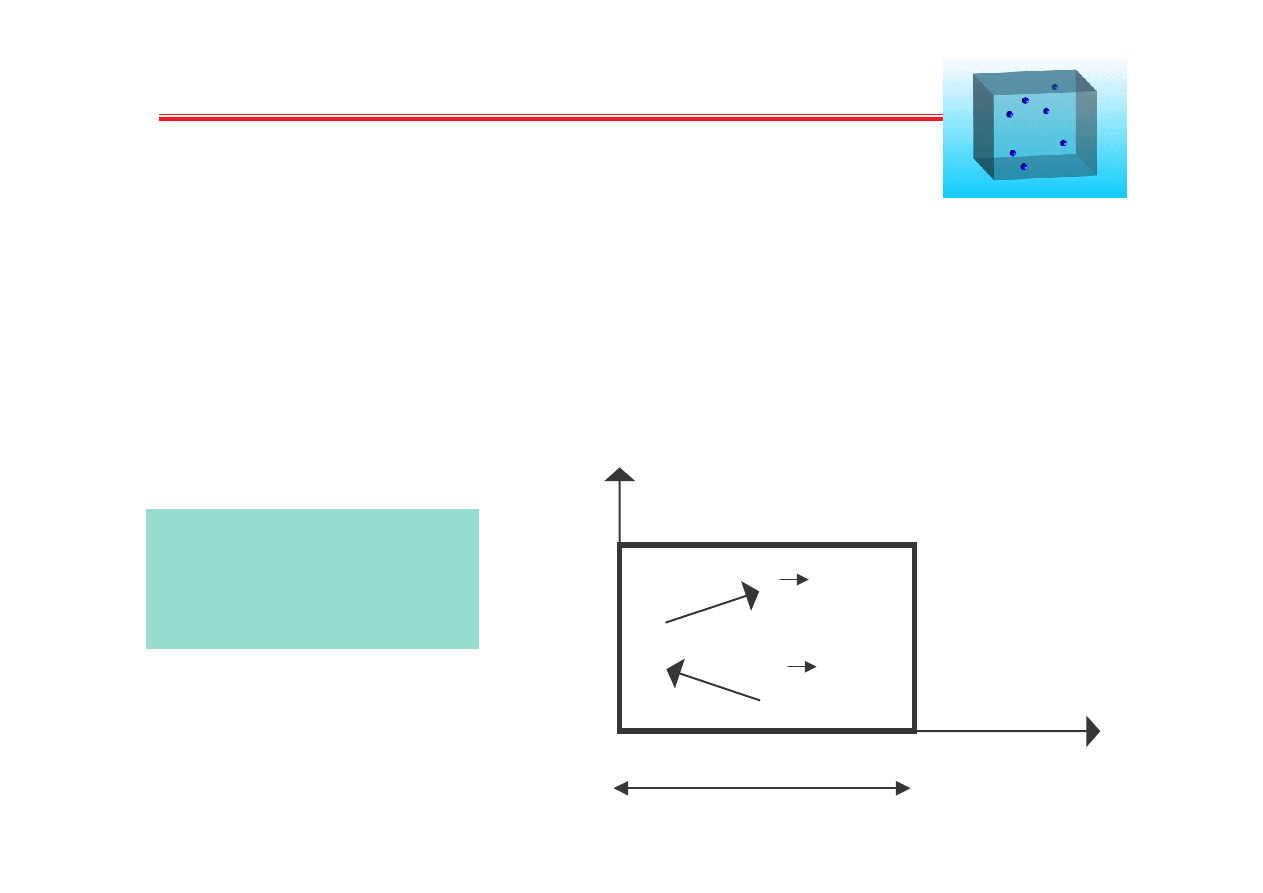
Rozwa amy 1 cz steczk

Cz steczki gazu:

N kulek w naczyniu

o obj to ci V

x

y

-v

x

v

x

l

v

1

v

2

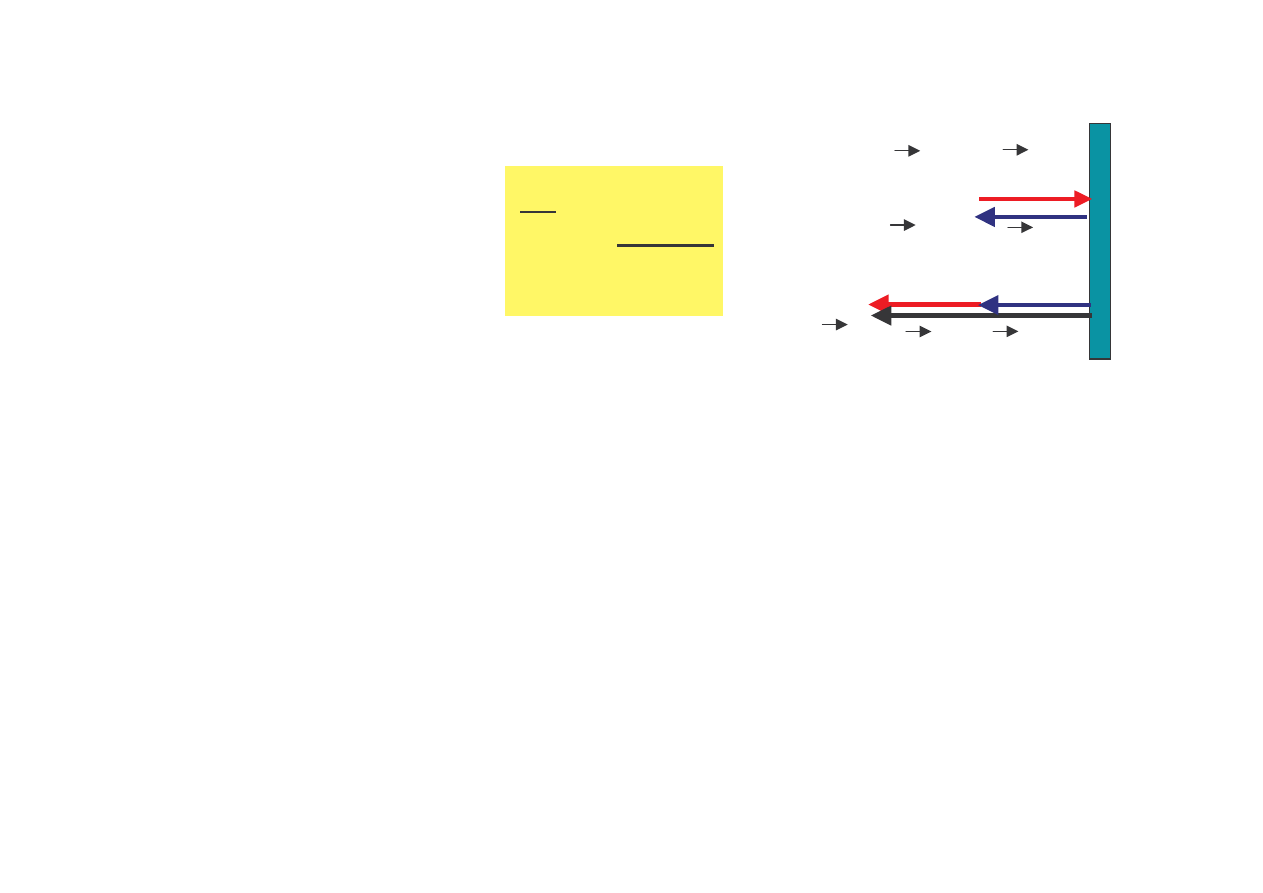
rednia siła

jak cz steczka wywiera na ciank w

czasie

∆∆∆∆

t wynosi

t

p

F

x

∆

∆

=

Zmiana p du

cz steczki:

∆∆∆∆p

x

= m

v

x

- ( - m

v

x

) = 2m

v

x

Czas

pomi dzy kolejnymi zderzeniami z t sam

ciank :

∆∆∆∆t = 2l/

v

x

gdzie

l

- odległo

mi dzy ciankami

Z II zasady

dynamiki:

1

1

v

m

p

=

2

2

v

m

p

=

1

2

p

p

p

−

=

∆

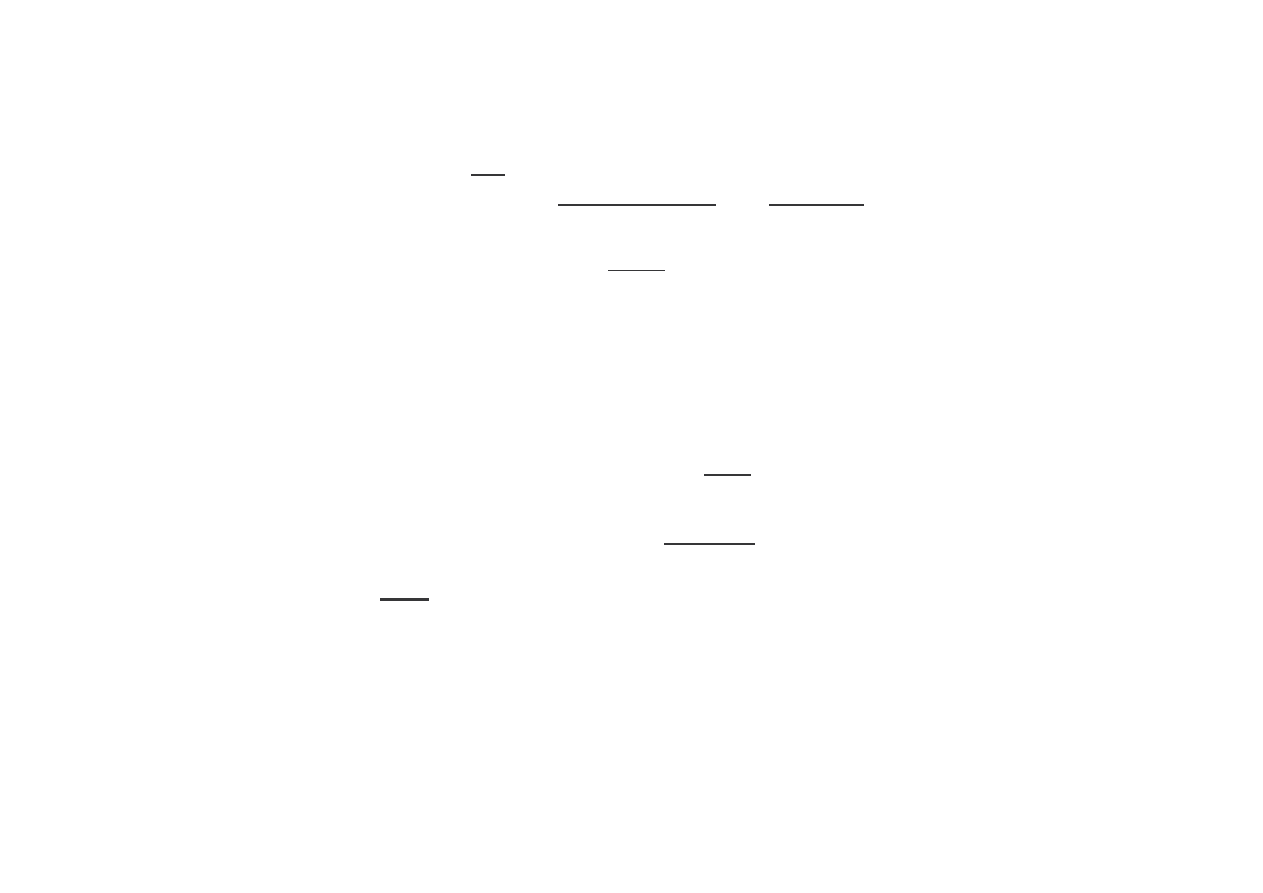
Całkowita siła działaj ca na ciank od

N cz steczek

:

l

m

N

F

2

x

v

=

gdzie

jest to

u rednione po wszystkich

cz steczkach ( rednia kwadratu pr dko ci).

2

v

x

2

v

x

l

m

l

m

F

x

x

x

2

v

v

2

)

v

2

(

=

=

St d:

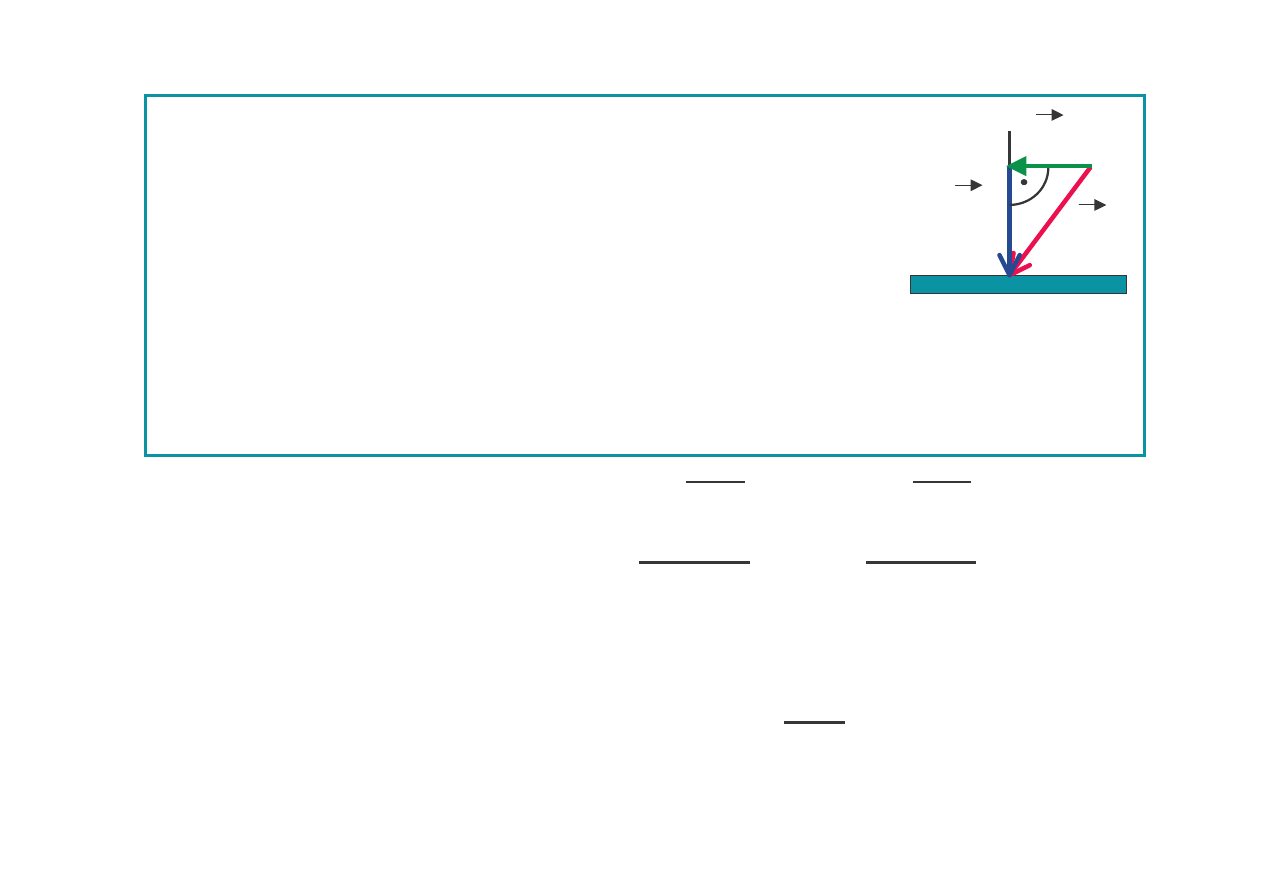
V

m

N

Sl

m

N

p

x

x

2

2

v

v =

=

Ci nienie

gdzie: S – pole powierzchni cianki

2

v

x

Nm

pV

=

lub:

Ci

Ci

nieniem

nieniem

p

p

nazywamy wielko

fizyczn

liczbowo równ sile działaj cej na powierzchni

ciała wzdłu normalnej do tej powierzchni:

p = dF

n

/ dS

normalna siły działaj cej na

ds

Jednostka: paskal 1 Pa = 1N / 1m

2

n

F

F

n

d

S

F

S

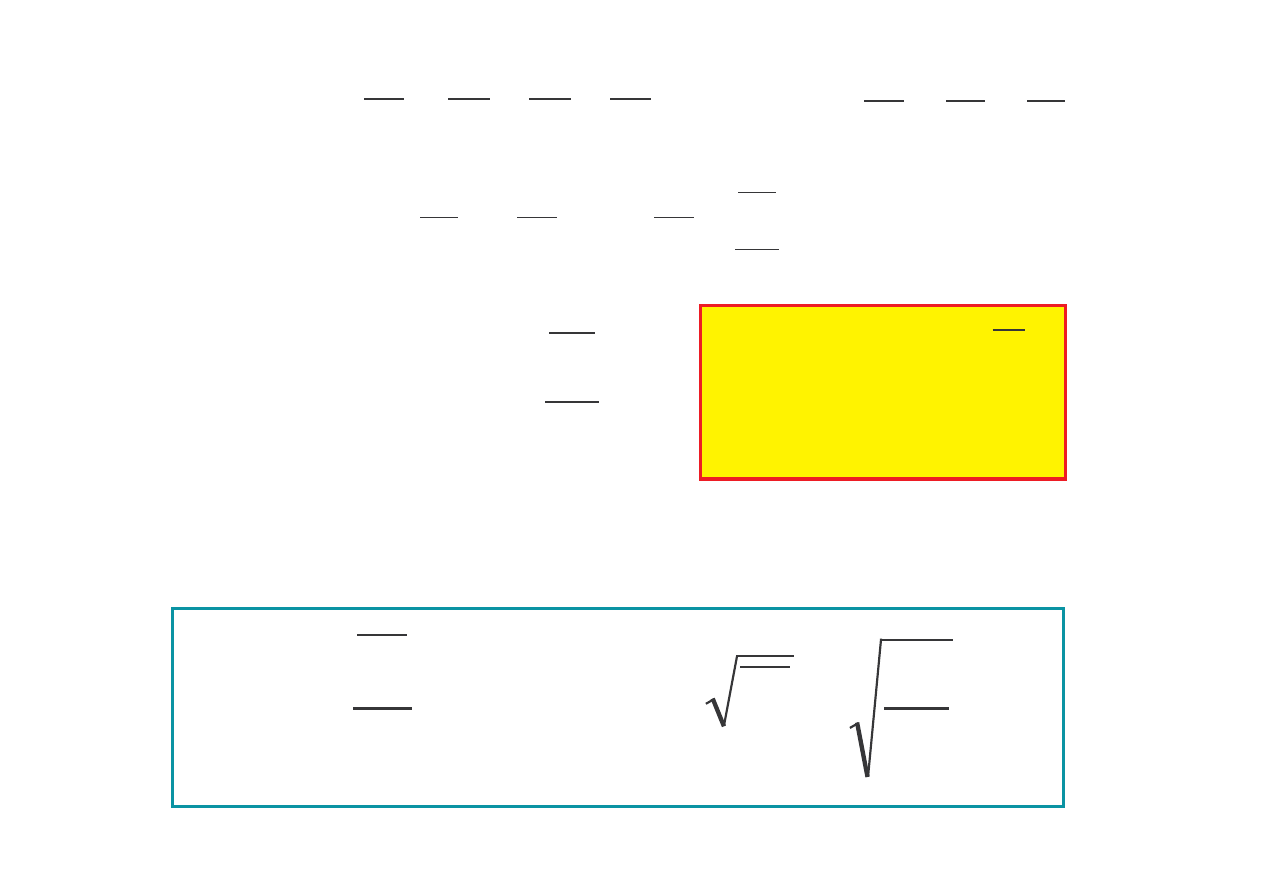
2

z

2

y

2

x

2

v

v

v

v

+

+

=

2

z

2

y

2

x

v

v

v

=

=

Poniewa

oraz

wi c:

3

v

v

czyli

,

v

3

v

2

2

x

2

x

2

=

=

oraz

3

v

Nm

pV

2

=

Poniewa N·m = M (masa gazu) oraz M/V =

ρρρρ

(g sto )

wi c:

ρ

ρ

p

p

kw

sr

3

v

v

,

3

v

2

.

.

2

=

=

=

czyli

p = (2/3)n

0

E

gdzie

n

0

= N/V

Temperatura

Temperatura

Temperatur

bezwzgl dn

definiujemy

jako

wielko

wprost proporcjonaln

do

redniej energii

kinetycznej cz steczek:

2

v

3

2

2

m

k

T

=

gdzie

k = 1.38·10

-23

J/K - stała Boltzmanna

Jednostka: kelvin (K)

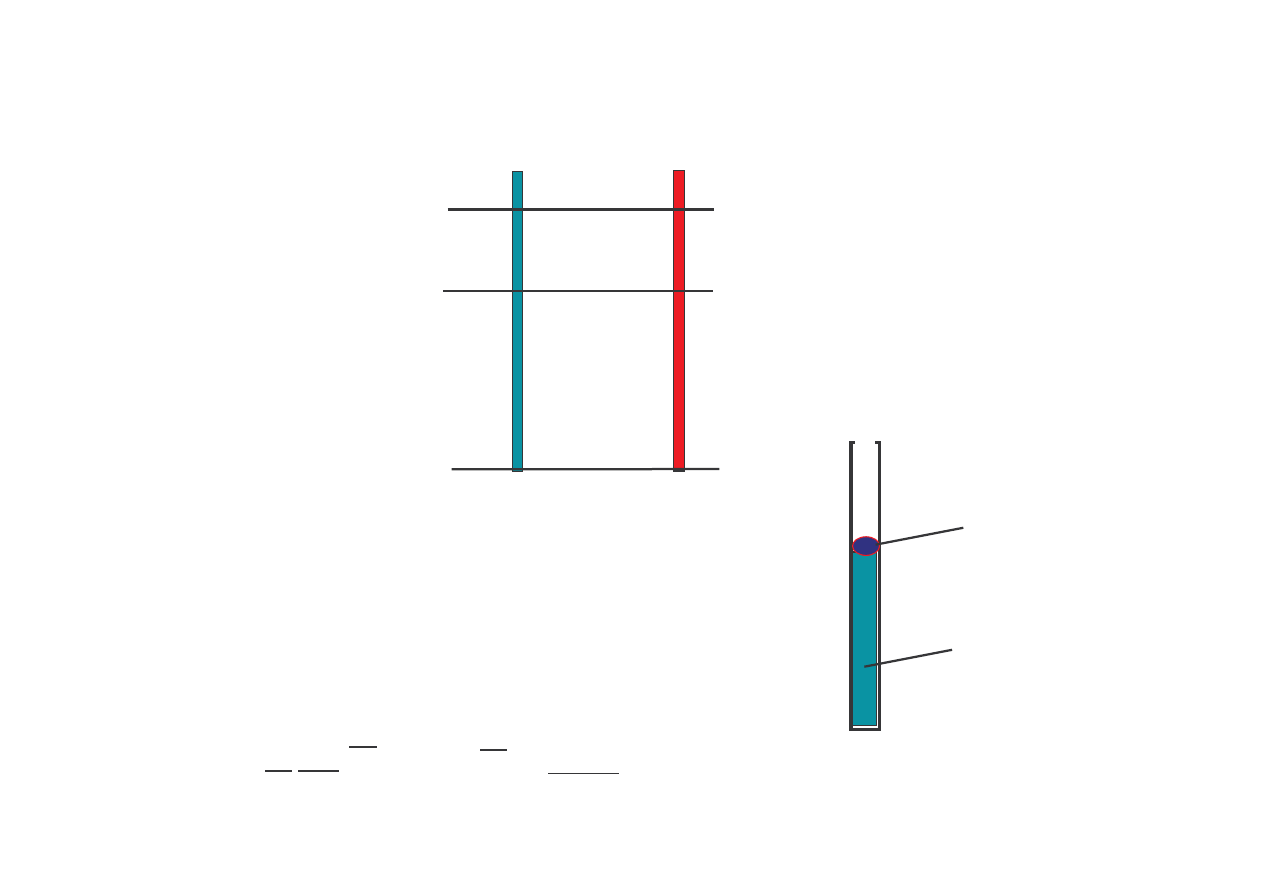
Skala bezwzgl dna T

– skala Kelvina

Punkt wrzenia H

2

O

Punkt zamarzania

H

2

O

Zero bezwzgl dne

Skala Celsjusza

0 K

273

- 273

0

0

C

100

Pomiar T – poprzez pomiar p i V

→

termometr

gaz doskonały

rt

V = N·kT/p

czyli

V

∼∼∼∼

T

E

V

N

p

3

2

=

oraz

2

3kT

E

=

Po przekształceniach:

pV = NkT = nN

A

kT

lub

pV = nRT

gdzie

n

- liczba moli gazu

R = 8.3145 J/(mol·K)

– stała gazowa

N

A

= 6.023·10

23

mol

-1

- stała (liczba) Avogadro

(liczba cz steczek w jednym molu)

R = k·N

A

równanie stanu gazu doskonałego

Clapeyron, XIX w.

W układzie SI:

Mol

jest jednostk liczno ci materii.

1 mol jest to liczno materii układu

zawieraj cego liczb cz stek (np. atomów,

cz steczek, jonów, elektronów itp.) równ liczbie

atomów w masie 12 gramów izotopu w gla

12

C.

W jednym molu znajduje si ok. 6,0221415(10)·10

23

cz stek (2002) – stała (liczb ) Avogadra.

Zerowa zasada termodynamiki

Zerowa zasada termodynamiki

Je eli ciała 1 i 2 s w równowadze termicznej i

ciała 2 i 3 s w równowadze termicznej, to

ciała 1 i 3 s

w tej samej równowadze

termicznej.

rednie energie kinetyczne ruchu post powego (na

cz steczk ) dla dwu kontaktuj cych si gazów s równe

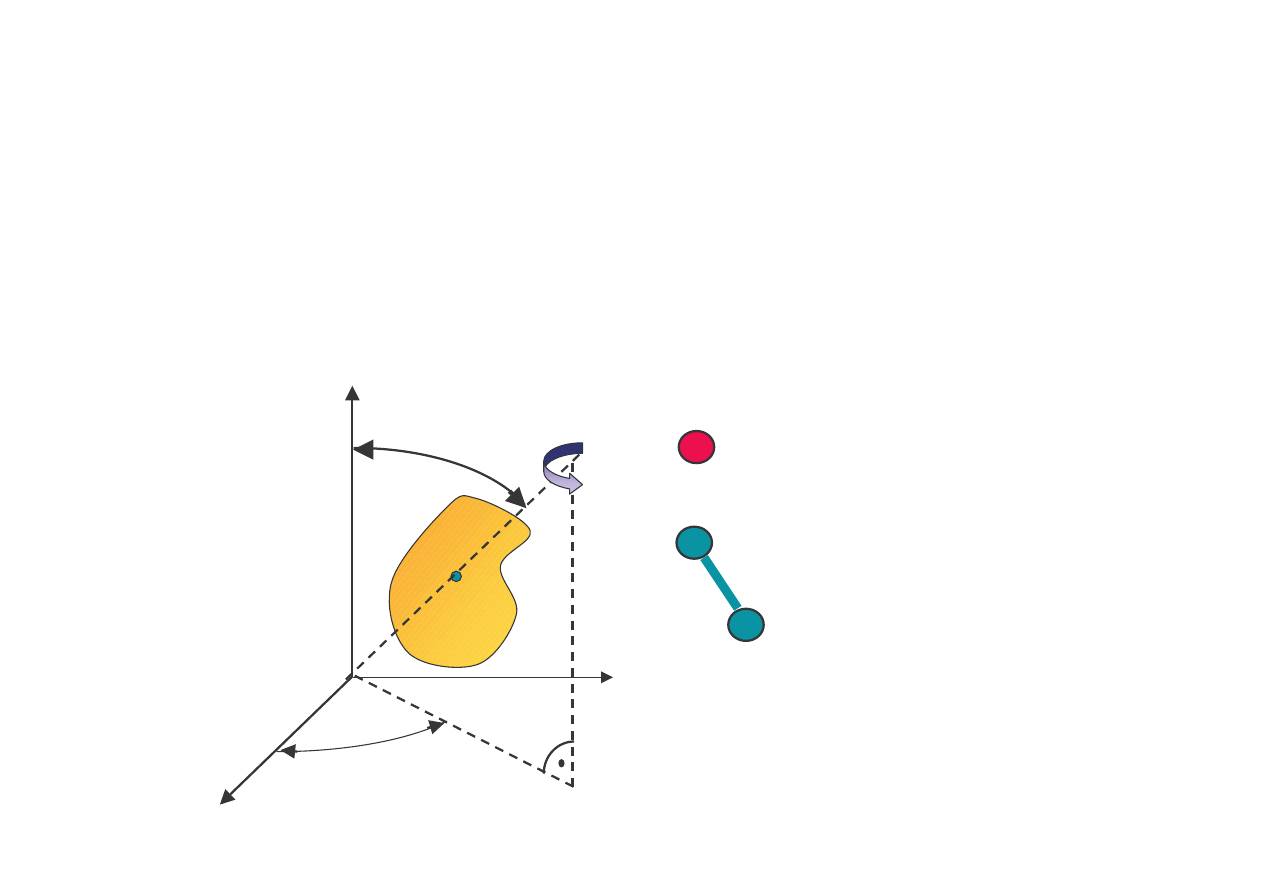
Sposoby absorpcji energii kinetycznej

przez cz steczki

wieloatomowe (bryły sztywne)

→

ruch post powy i obrotowy

→

stopnie swobody

- niezale ne współrz dne potrzebne

do okre lenia poło enia ciała w przestrzeni
liczba stopni swobody -

f

f

cz steczka jednoatomowa

f = 3

cz steczka dwuatomowa

f = 5

cz steczka wieloatomowa

f = 6

0 – rodek

masy

x

z

y

0

ϑϑϑϑ

φφφφ

Ψ

Ψ

Ψ

Ψ

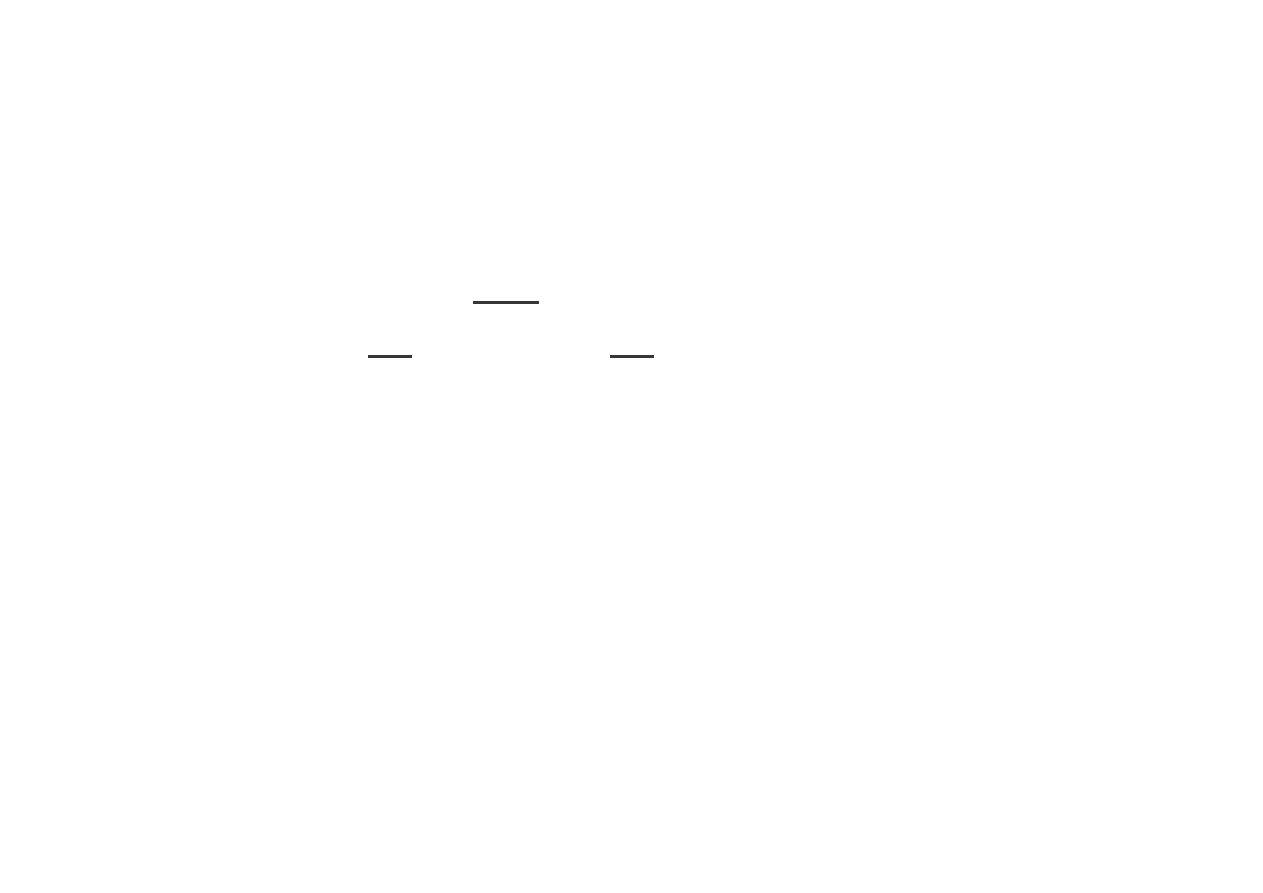
kT

m

2

3

v

2

1

2

=

rednia energia kinetyczna ruchu post powego –

3 stopnie swobody (współrz dne x, y, z):

St d

rednia energia na stopie swobody ruchu

post powego wynosi

E

f

=

kT/2

na cz steczk

(zale y tylko od T)

Zasada ekwipartycji energii

Zasada ekwipartycji energii

rednia energia kinetyczna na ka dy stopie

swobody jest taka sama dla wszystkich

cz steczek i wynosi

kT/2

.

kT

Nf

U

2

=

Dla układu N-cz stek – energia wewn trzna

kT

f

E

2

=

Całkowita energia kinetyczna cz steczki

traktowanej jako bryła sztywna wynosi

Pierwsza zasada termodynamiki

Pierwsza zasada termodynamiki

Zasada zachowania energii ciała - z rozdziałem na energi

• makroskopow (energia mechaniczna ruchu masy)

• mikroskopow (wewn trzna "ukryta" energia cz stek)

Gdy dwa układy (ciała) o ró nych temperaturach zetkniemy
ze sob , to

ciepło

∆∆∆∆

Q

przepływa z ciała cieplejszego do

chłodniejszego.

Ciepło

pobrane przez układ jest równe wzrostowi

energii wewn trznej

układu i

pracy

wykonanej przez

układ nad otoczeniem zewn trznym,

czyli

Umowa:

Q > 0 – dostarczone, W >0 – praca wykonana przez układ

∆∆∆∆Q = ∆∆∆∆U + ∆∆∆∆W

lub

dQ = dU + dW

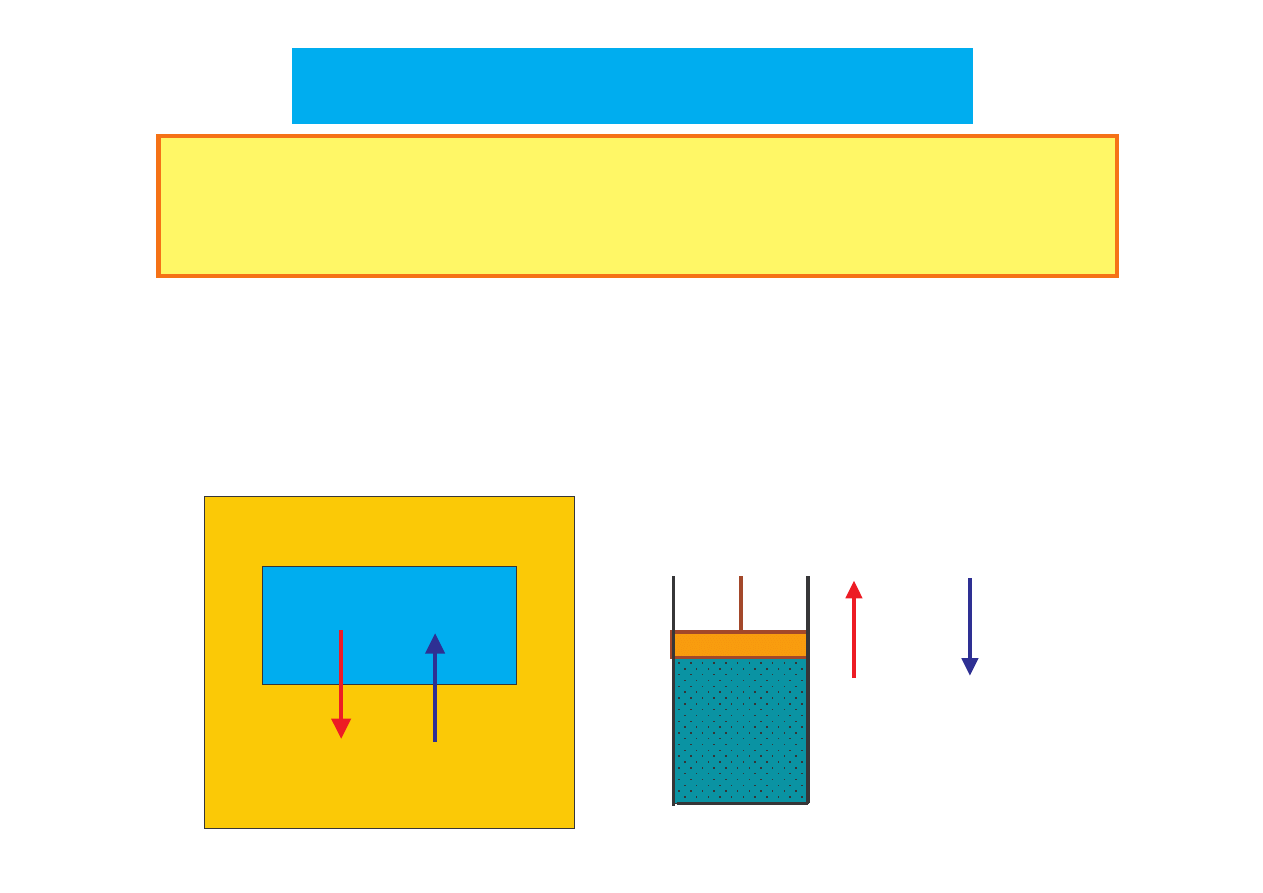
Przekazywanie

energii

– w postaci

ciepła Q

lub

pracy W

(za

po rednictwem siły działaj cej na układ).

Q

i

W

– nie s wła ciwo ciami układu (w przeciwie stwie do

T

,

p

i

V

).

układ

T

U

otoczenie

T

U

>>>>

T

O

T

O

Q

<<<<

0

Q

>>>>

0

T

U

<<<<

T

O

CIEPŁO

W

>>>>

0

W

<<<<

0

PRACA wykonana przez

układ

Ciepło Q

– energia przekazywana mi dzy układem a jego

otoczeniem na skutek istniej cej mi dzy nimi ró nicy

temperatur.

CIEPŁO i PRACA

Energia wewn trzna układu

U

- wzrasta, je eli układ pobiera energi w postaci ciepła

Q

- maleje, gdy układ wykonuje prac

W

.

Przemiana (proces) termodynamiczna:

stan pocz tkowy (p

p

, V

p

, T

p

)

→

stan ko cowy (p

k

, V

k

, T

k

)

ENERGIA WEWN TRZNA

Ró nica

∆∆∆∆

Q –

∆∆∆∆

W =

∆∆∆∆

U

jest dla wszystkich

procesów jednakowa !

P

K

U

– tzw.

funkcja stanu

, w

przeciwie stwie do

Q

i

W

Jednostka

U, Q, W: d ul 1(J)

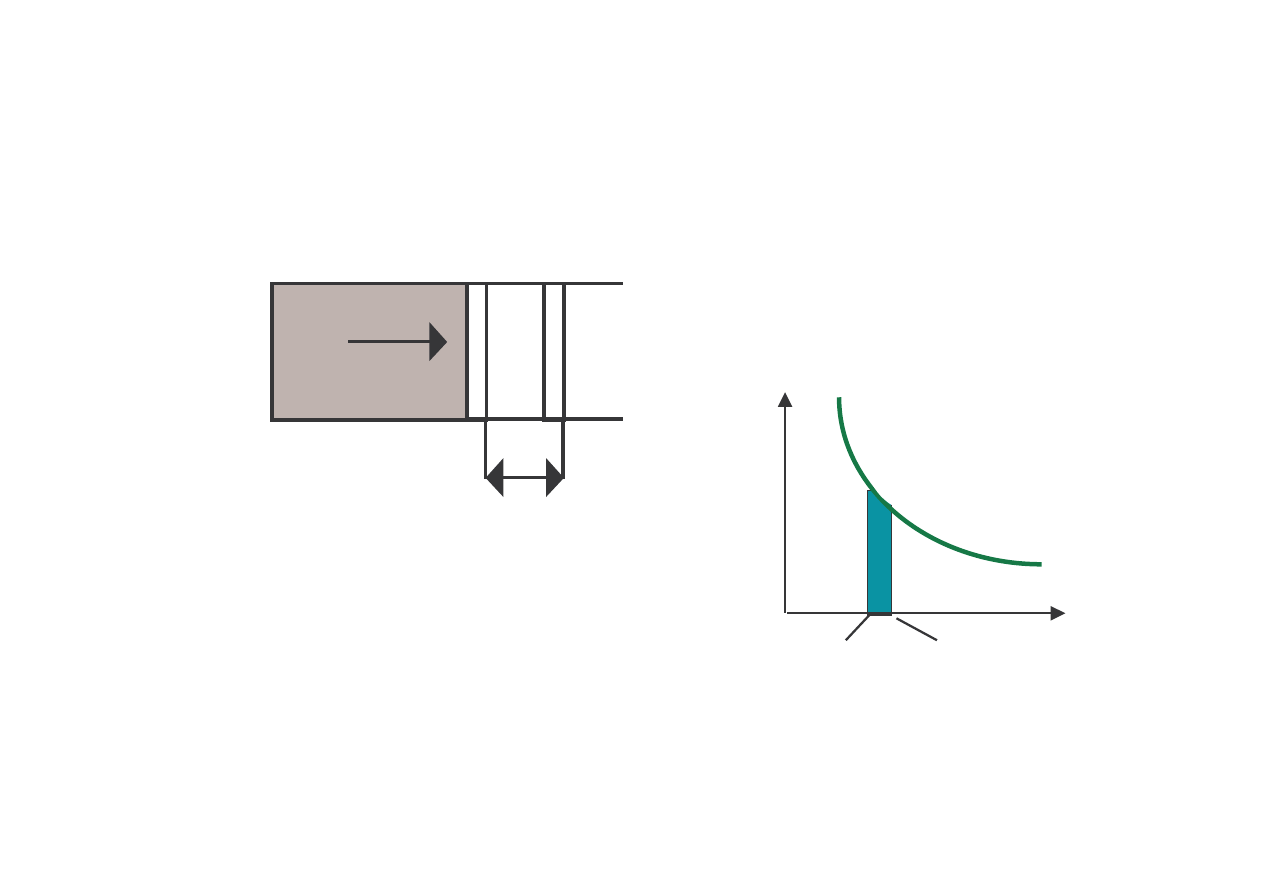
dW = Fdl = (F/S)(Sdl) = pdV

dU = dQ – pdV

F

V

dl

S

dU = dQ – dW

Mo na zwi kszy

energi wewn trzn

U

dostarczaj c ciepło oraz / lub ciskaj c gaz

∆∆∆∆

Q

i

∆∆∆∆

W

– zale od drogi przej cia

∆∆∆∆

U

–

nie zale y od drogi przej cia

V

p

V

V+

∆∆∆∆

V

dW=pdV

p(V)

Def.

Ciepłem wła ciwym

nazywamy wielko

fizyczn równ liczbowo ciepłu, które nale y dostarczy

do jednostki masy substancji, aby podwy szy jej

temperatur o jeden kelwin 1K (1

0

C)

dT

dQ

M

c

w

⋅

= 1

St d:

dQ = Mc

w

dT

Jednostka c

w

: J

·

kg

-1

·

K

-1

Ciepło molowe

- na 1 mol substancji

dT

dQ

M

dT

dQ

n

C

⋅

=

⋅

=

µ

1

gdzie

n=M/

µµµµ

- liczba moli gazu

M- masa gazu

µµµµ

- masa 1 mola

Jednostka C: J

·

mol

-1

·

K

-1

C=c

w

·

µµµµ

Ciep

Ciep

ł

ł

o

o

molowe

molowe

przy sta

przy sta

ł

ł

ej obj

ej obj

to

to

ci

ci

C

C

V

V

Przemiana izochoryczna

dV = 0

dU = dQ

st d:

C

V

= 1/n · dQ/dT = (

µµµµ

/M) · dU/dT

oraz

∆∆∆∆

U = (M/

µµµµ

)C

V

∆∆∆∆

T

Dla

1 mola

gazu

jednoatomowego

zatem

C

V

= (3/2)R

C

V

= (f/2)

R

Dla gazu

dwuatomowego

C

V

= (5/2)R

Dla gazu

wieloatomowego

C

V

= 3R

RT

kT

N

U

A

⋅

=

⋅

=

2

3

2

3

f

- liczba stopni

swobody

cz steczki

gazu

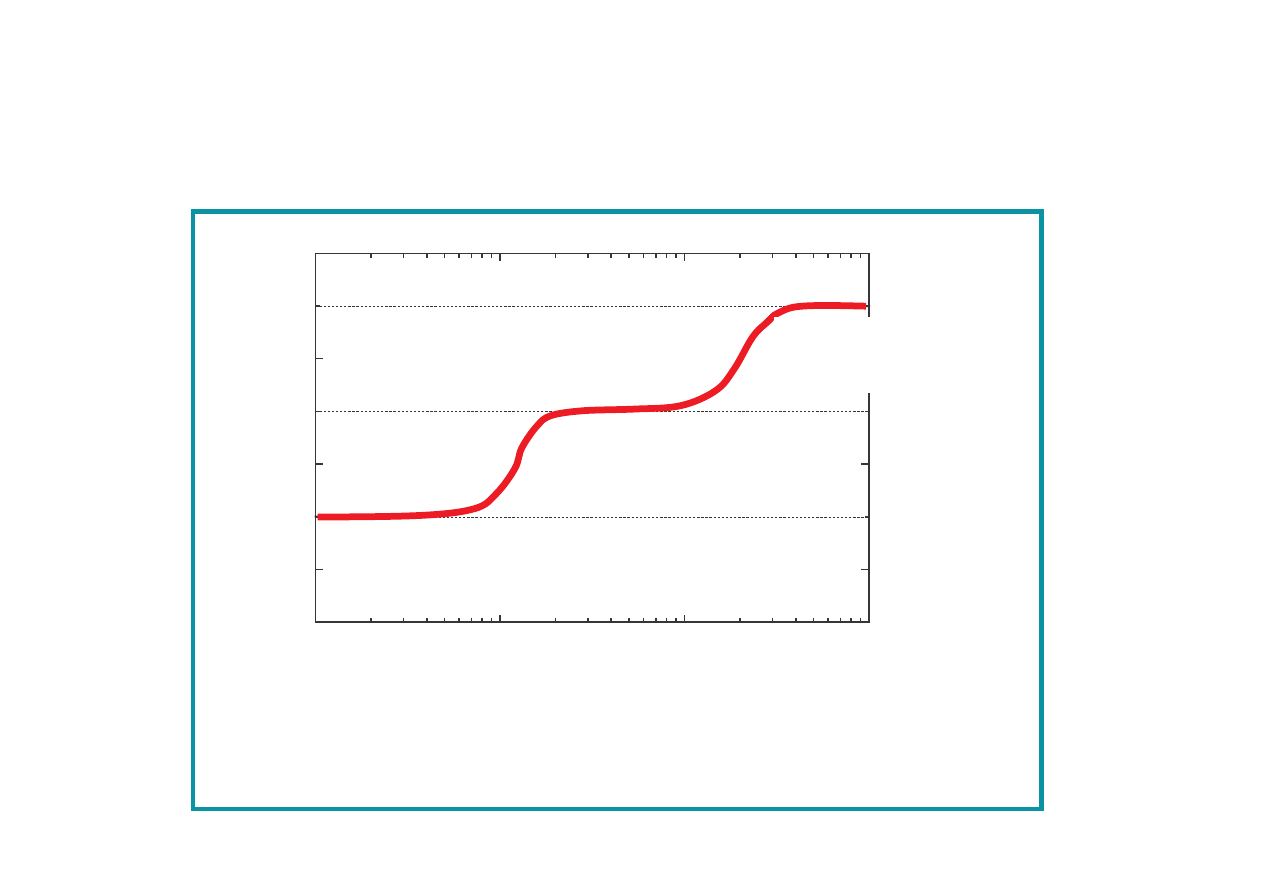
Brak zale no ci C

v

od T – sprzeczno

z eksperymentem !

C

V

dla wodoru (H

2

) w funkcji temperatury

10

100

1000

10000

2

4

6

8

(3/2) R

(5/2) R

(7/2) R

C

v

c

al

/m

ol

K

Temperatra (K)

C

V

/R

7/2

5/2

3/2

ruch post powy

ruch obrotowy

ruch

oscylacyjny

Dla T < 100 K,

C

V

= (3/2)R

brak rotacyjnych stopni

swobody

rednia energia wewn trzna na cz steczk wynosi

U = E

r,kin,post

+ E

r,kin,rot

+ E

r,kin,drg

+ E

r,pot,drg

U = (3/2)kT + (2/2)kT + (1/2)kT + (1/2)kT = (7/2)kT

Dla 1 mola
U = (7/2)RT wi c C

V

= (7/2)

R

Ciep

Ciep

ł

ł

o

o

molowe

molowe

przy sta

przy sta

łym

łym

ci nieniu

ci nieniu

C

C

p

p

Przemiana izobaryczna

Z I zasady termodynamiki:

dQ = dU + pdV

U zale y tylko od T

dla 1 mola gazu

dU = C

V

dT

wi c:

dQ = C

V

dT + pdV

C

p

= [(f+2)/2]

R

dV = RdT/p

dQ = C

V

dT + RdT

St d:

dQ/dT = C

V

+ R

Ostatecznie

C

p

= C

V

+ R

Typ gazu

c

v

c

p

c

p

/

c

v

Jednoatomowy

Dwuatomowy + rotacja

Dwuatomowy + rotacja +

drgania

Wieloatomowy + rotacja (bez

drga )

(3/2)R

(5/2)R

(7/2)R

(6/2)R

(5/2)R

(7/2)R

(9/2)R

(8/2)R

5/3

7/5

9/7

4/3

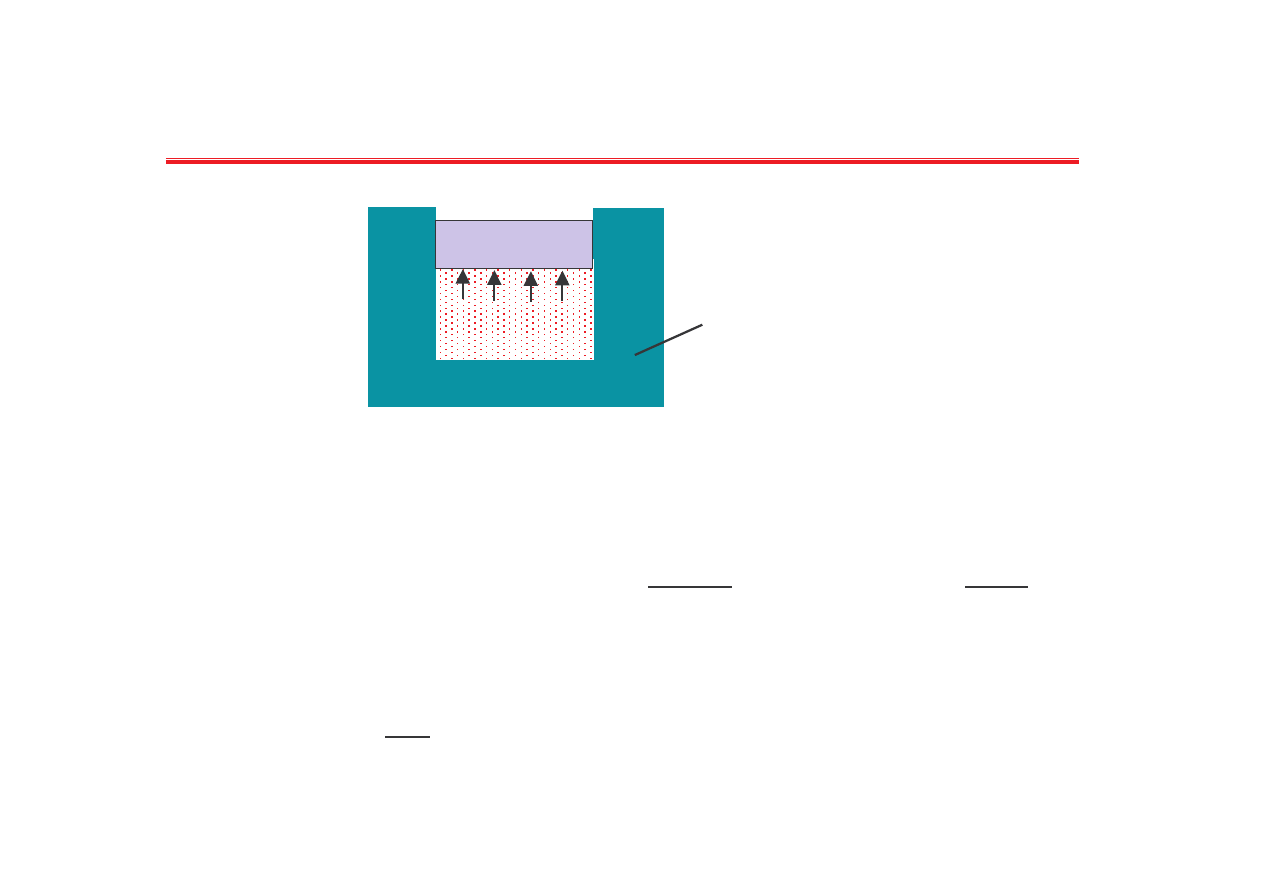
Rozpr

Rozpr

anie izotermiczne

anie izotermiczne

Poniewa

T = const. wi c dU = 0, a st d dQ = dW

=

=

=

=

=

∆

=

∆

1

2

1

ln

d

d

d

2

2

1

2

1

V

V

nRT

v V

V

nRT

V

V

nRT

V

p

W

Q

V

V

V

V

V

tłok

termostat

T = const.

V

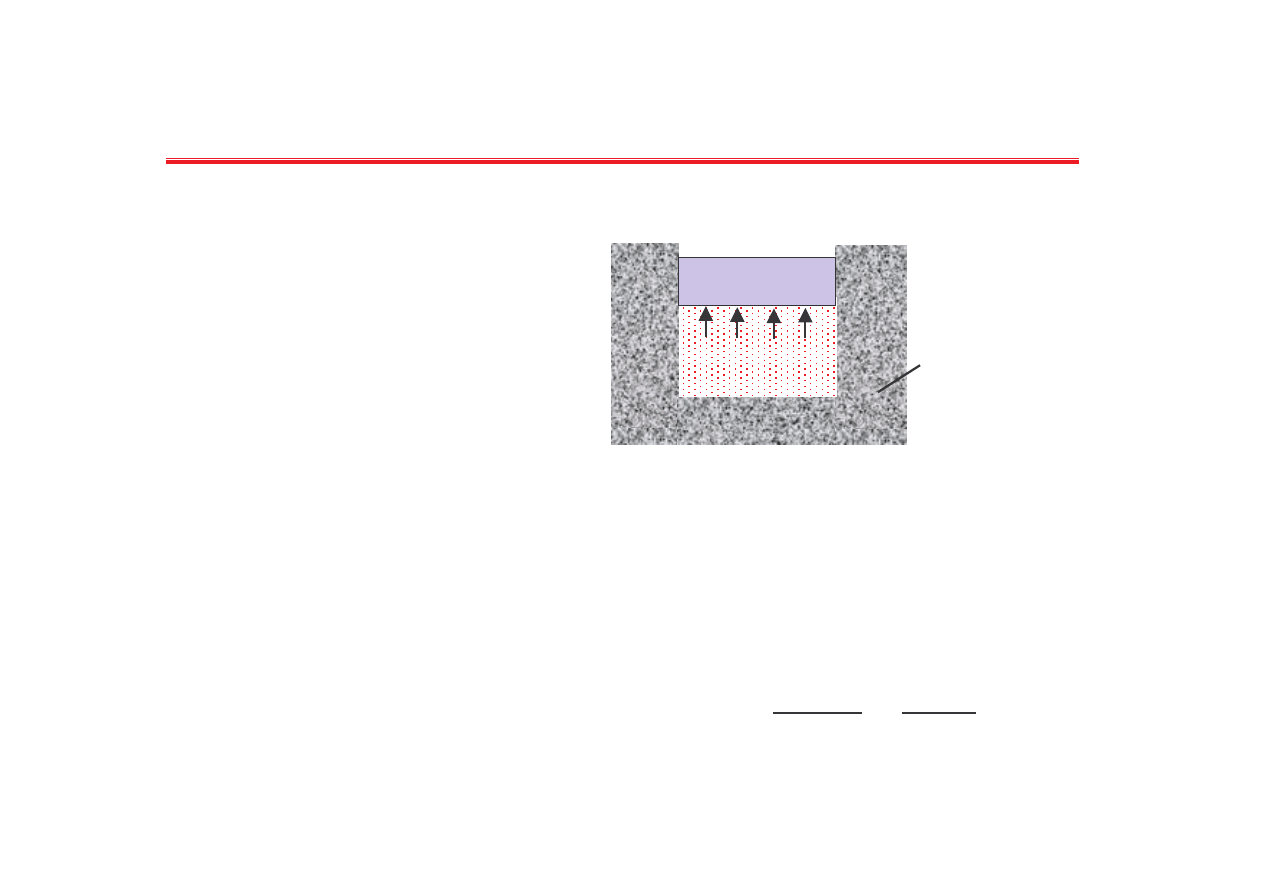
Rozpr

Rozpr

anie

anie

adiabatyczne

adiabatyczne

dQ = 0

dU + pdV = 0

lub na 1 mol:

c

v

dT + pdV = 0

tłok

V

izolacja

termiczna

Brak wymiany ciepła z otoczeniem

R

Vdp

R

pdV

dT

+

=

Vdp

pdV

RdT

+

=

Z równania stanu gazu doskonałego :

pV=RT

dT

0

d

d

0

1

R

c

pd

0

d

d

d

v

v

V

v

=

+

+

=

+

+

=

+

+

p

R

V

c

V

p

R

R

c

dp

R

V

c

V

V

p

R

p

V

R

V

p

c

V

0

=

+

p

dp

c

V

dV

c

V

p

0

=

+

Vdp

R

c

pdV

R

c

V

p

c

v

+ R = c

p

0

d

d

=

+

p

p

V

V

γ

gdzie

γγγγ

= c

p

/

c

v

.

const

ln

ln

0

d

d

=

+

=

+

p

V

p

p

V

V

γ

γ

Po scałkowaniu:

Mamy wi c

ln(pV

γγγγ

) = const.

czyli

pV

γγγγ

= const.

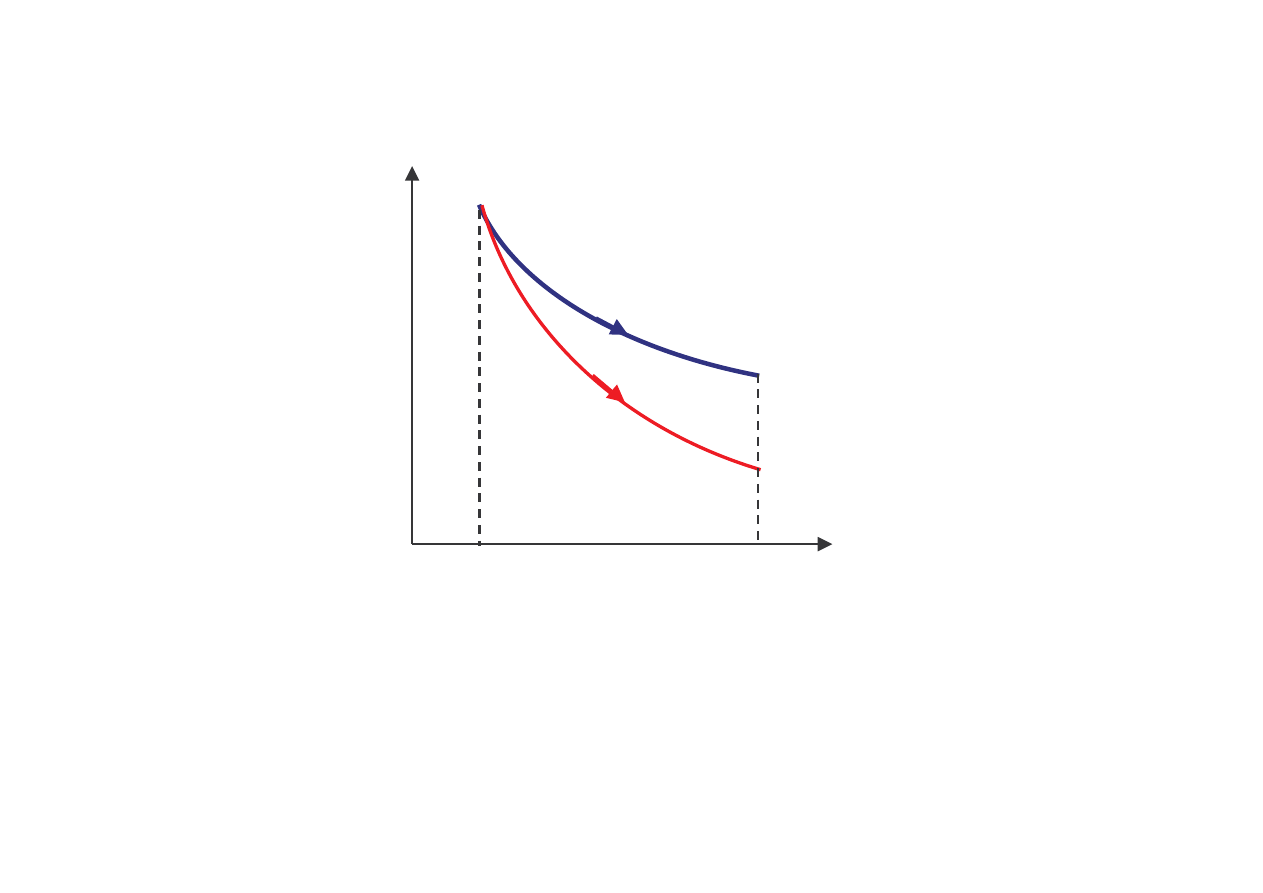
p

V

V

1

V

2

pV= const.

izoterma

pV

γγγγ

= const.

adiabata

Porównanie rozpr ania izotermicznego

i adiabatycznego