1
(etap IIIC przyjętego schematu modelowania ekonometrycznego)
1. Założenie liniowości - test serii
2. Założenie niezależności zakłóceń modelu
- autokorelacja składnika losowego - test Durbina - Watsona
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne. Test Harrisona-McCabe’a
4. Normalność rozkładu zakłóceń - test Jarque-Bera
Przykład
Sprawdzanie założeń przyjętych o modelu
Założenia do Metody Najmniejszych Kwadratów
- model jest liniowy
- zmienne objaśniająca jest deterministyczna
- wartość oczekiwana składnika losowego Z jest równa zero,
jego wariancja jest skończona.
Zatem dla każdej obserwacji momenty rozkładu zmiennej
losowej są stałe:
E(Z)=0, D
2
(Z)=
σ
2
< ¶
- Założenie dodatkowe: rozkład zakłóceń jest
normalny
Y =
β
1
X
1
+
β
2
X
2
+ ...+
β
k
X
k
+ Z
Sprawdzanie założeń przyjętych o modelu
(etap IIIC przyjętego schematu modelowania ekonometrycznego)
2
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
1. Założenie liniowości - test serii
Hipoteza zerowa:
oszacowany model ekonometryczny jest liniowy
Hipoteza alternatywna: oszacowany model ekonometryczny nie jest liniowy
Opis testu:
Szeregujemy reszty według wielkości zmiennej objaśniającej (czasu jeśli jest
to szereg czasowy)
Resztom dodatnim przypisujemy znak „+”, resztom ujemnym „
−”.
Reszty równe 0 odrzucamy!
Otrzymujemy w ten sposób ciąg typu:
− − + + + − + − + + − + + + − − − −
Obliczmy liczbę serii występujących w otrzymanym ciągu. Serią jest ciąg takich samych
znaków (także jednoelementowy)
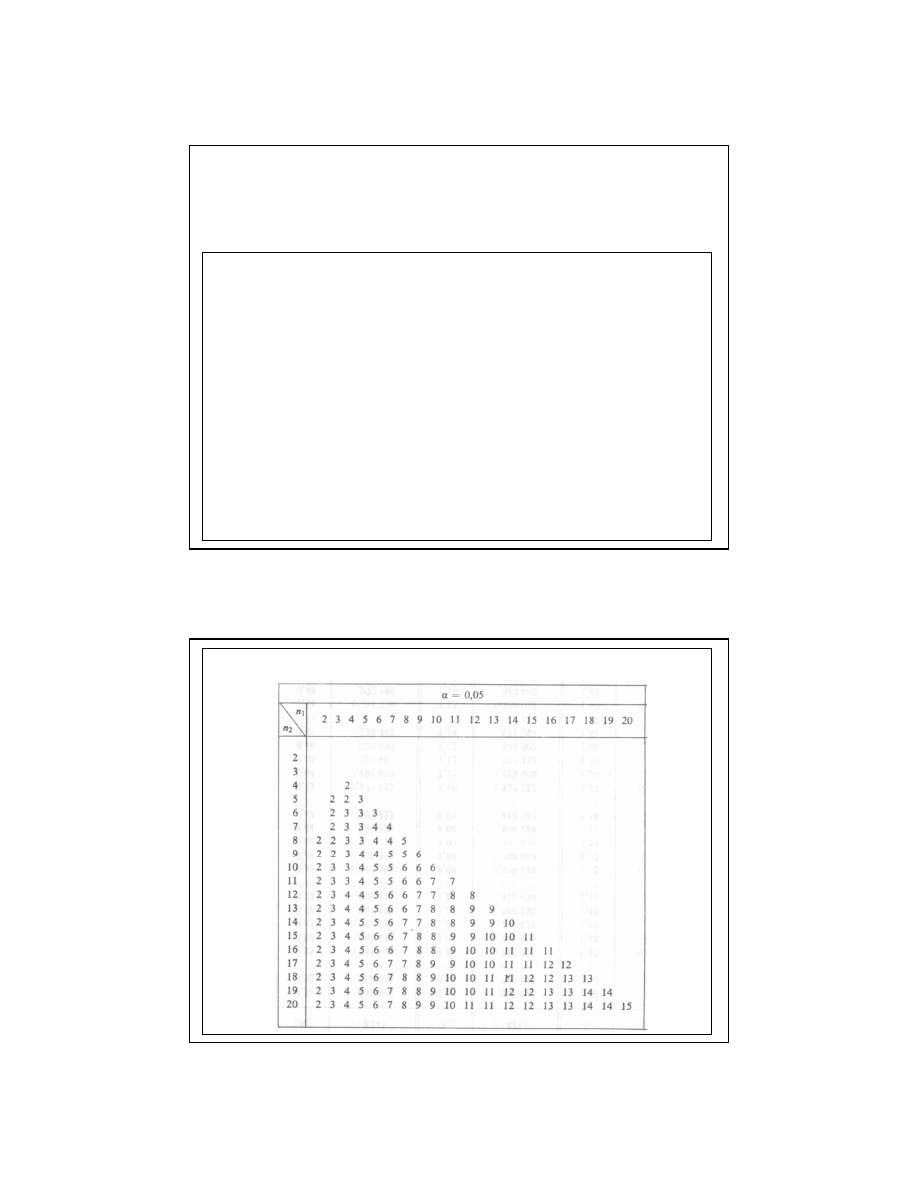
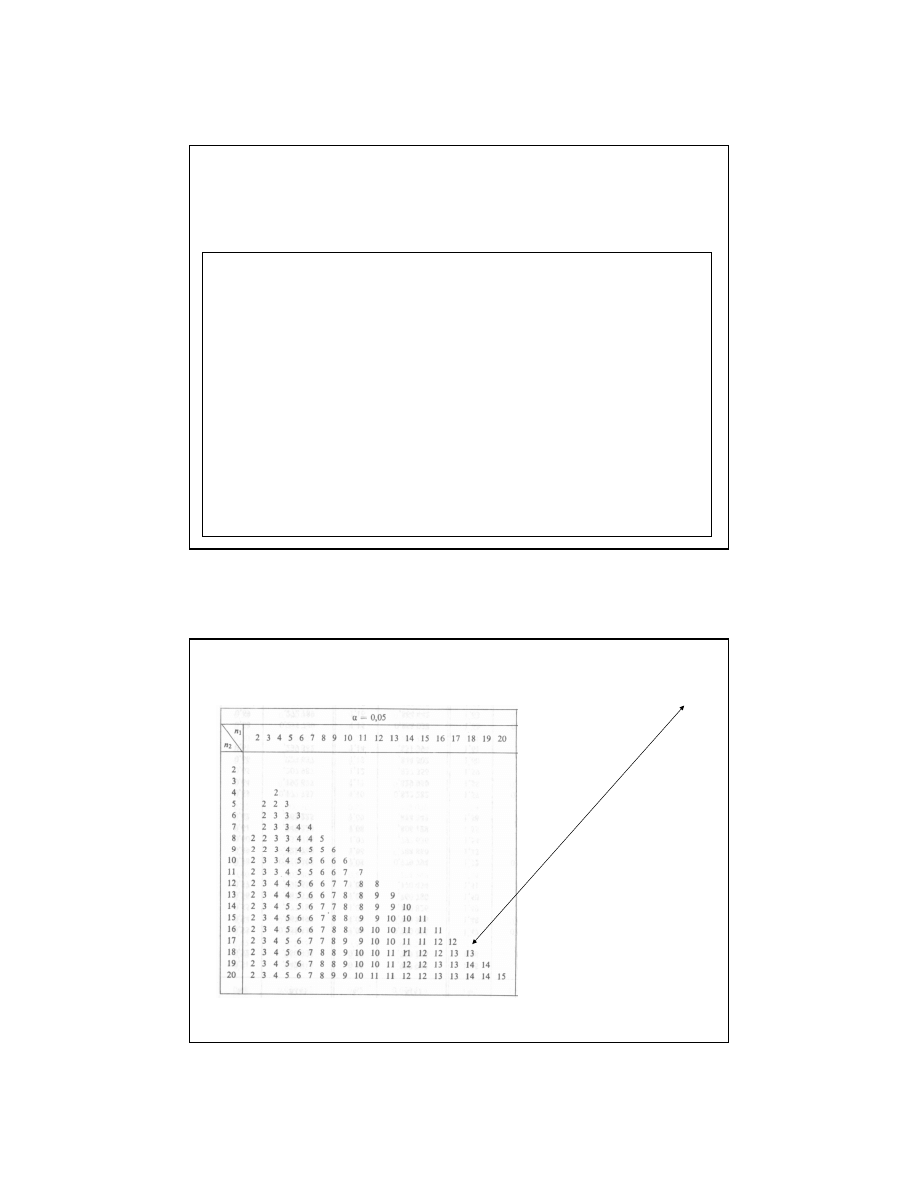
Odczytujemy z tablic dla testu serii i danego poziomu istotności wartość krytyczną N*
(zależy ona od liczby znaków „+” i liczby znaków „–” .
Hipotezę o liniowości modelu odrzucamy, jeśli liczba serii Ns jest mniejsza od N*.
Wartości kwantyli dla testu serii dla małych prób
3
3
2
1
2
2
1
2
1
1
1
4
1
2
+
+
+
=
n
n
n
n
u
n
n
n
k
α
α
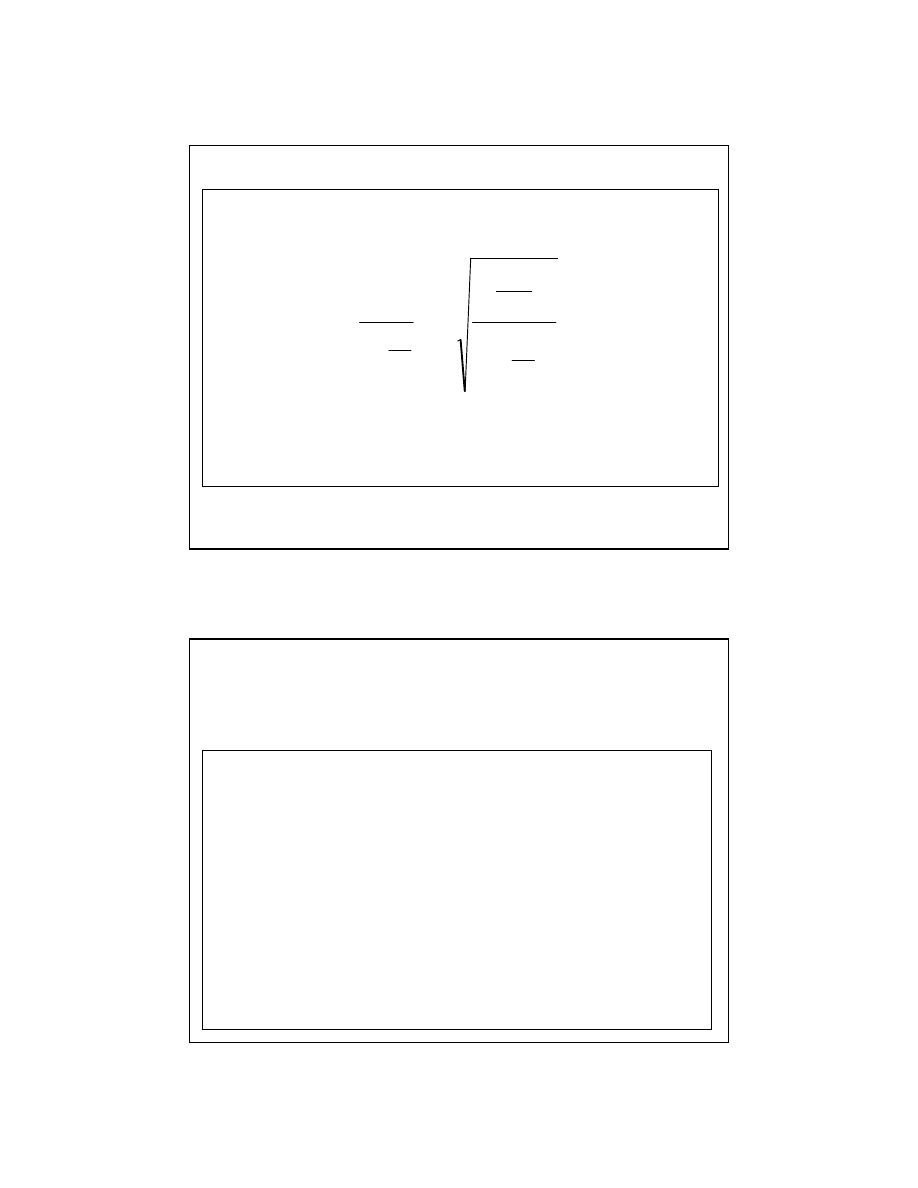
Przybliżone wartości kwantyli dla testu serii dla dużych prób można obliczyć z wzoru
Hipotezę o liniowości modelu odrzucamy, gdy liczba serii jest mniejsza od wartości
kwantyla k
α
gdzie
α jest poziomem istotności testu
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Y =
β
1
X
1
+
β
2
X
2
+ ...+
β
k
X
k
+Z
Model:
Autokorelacja zakłóceń (proces autokorelacji pierwszego rzędu):
Z
i+
1
=
ρ
Z
i
+ V, i=
1,2,....,n-1
ρ
-
współczynnik autokorelacji , |
ρ
|<
1
V -
zmienna losowa o średniej 0 i skończonej wariancji
Główne przyczyny autokorelacji zakłóceń:
- natura procesów gospodarczych
- niepoprawna postać modelu
- zbyt ubogi zestaw zmiennych objaśniających
Autokorelacja występuje często, gdy model szacujemy na podstawie szeregów czasowych
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
4
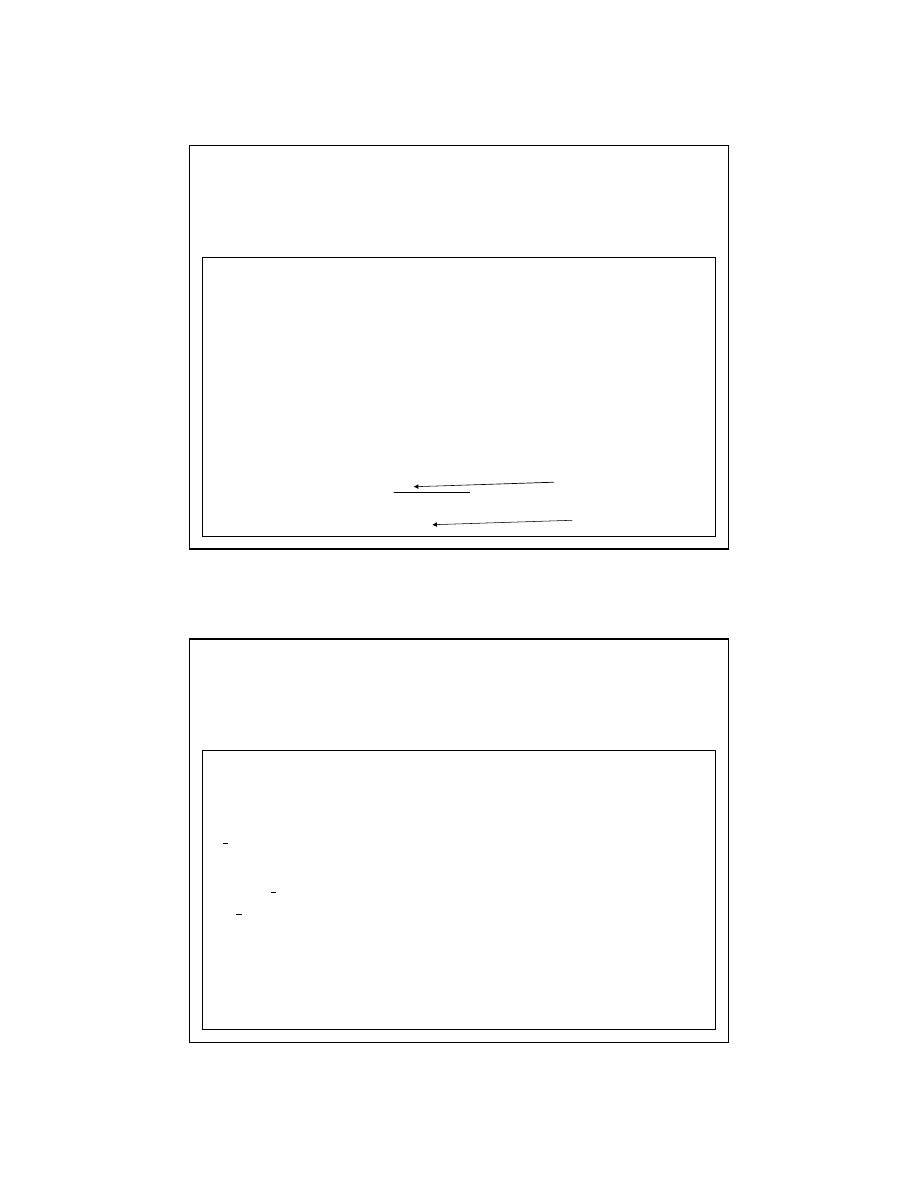
Hipoteza zerowa:
Hipoteza alternatywna:
ρ ∫
0
( autokorelacja występuje)
ρ =
0
( brak autokorelacji)
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
M
odel z wyrazem wolnym
: Y =
β
1
+
β
2
X
2
+ ...+
β
k
X
k
+ Z
Test Durbina - Watsona
∑
∑
=
=
−
−
=
n
i
i
n
i
i
i
e
e
e
d
1
2
2
2
1
)
(
Estymujemy parametry modelu.
Krok 1
Krok 2 Obliczmy reszty w oszacowanym modelu : e
1
,e
2
,...,e
n
Krok 3
Wyznaczamy wartość statystyki testowej
„
dwa”
„
jeden”
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Test Durbina - Watsona
Schemat podejmowania decyzji:
d § d
L
d
L
< d < d
U
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
4-d
U
§ d § 4-d
L
4-d
L
< d
Hipotezę zerową odrzucamy
brak decyzji
d
U
< d <
4 - d
U
d
L
oraz d
u
- wartości krytyczne wyznaczane z tablic
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
5
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Test Durbina - Watsona
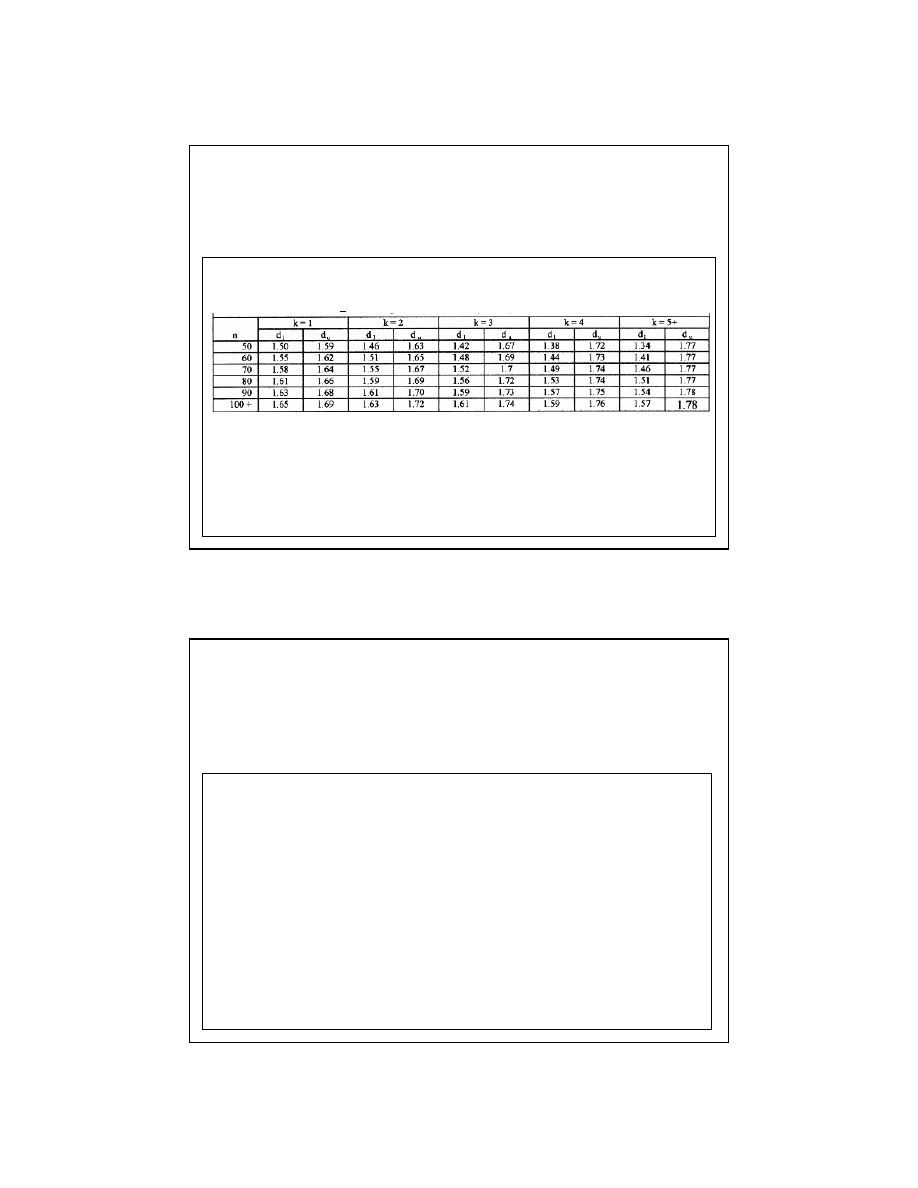
Wartości krytyczne d
L
oraz d
u
dla poziomu istotności
α = 0.05:
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
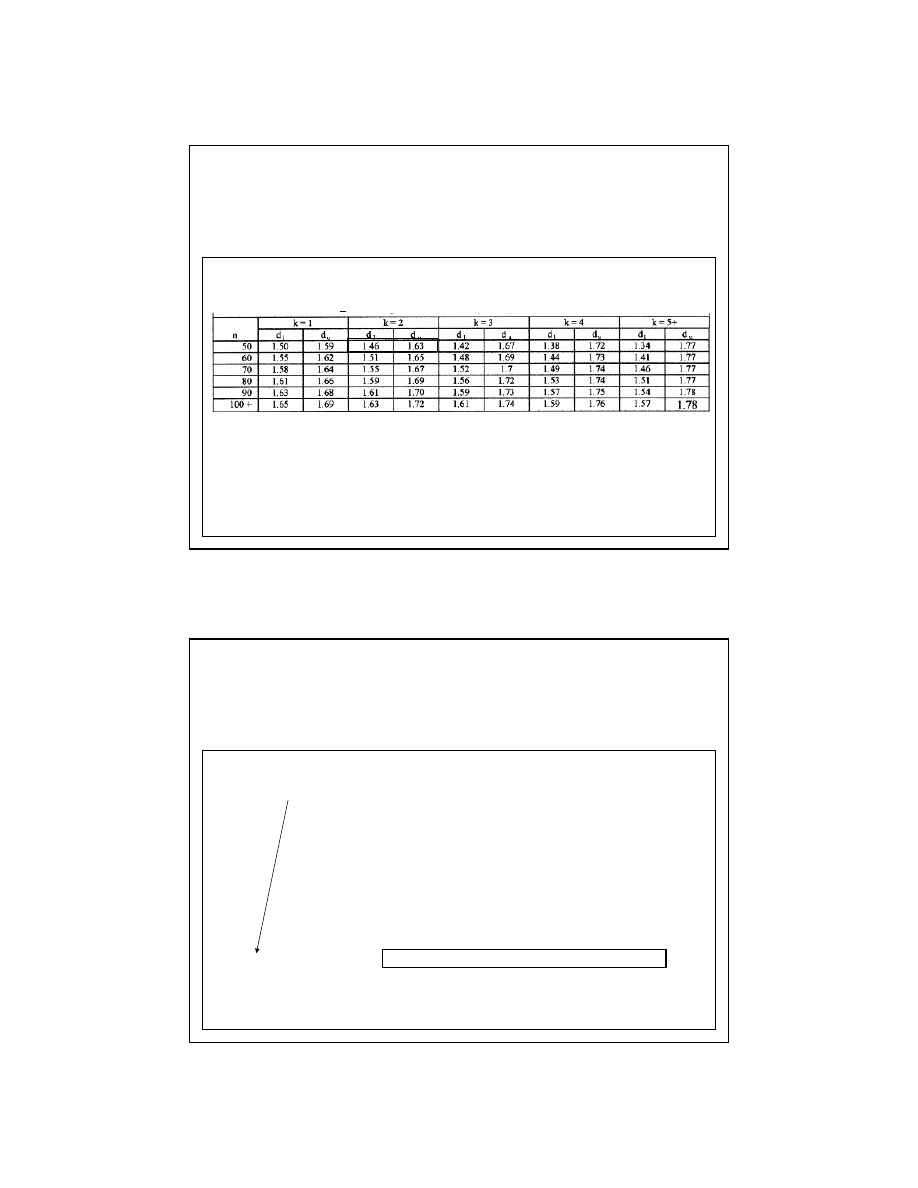
W tej tablicy k oznacza liczbę zmiennych objaśniających nie licząc wyrazy wolnego
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne. Test Harrisona-McCabe’a
Model nazywamy heteroskedastycznym, jeżeli składniki losowe dla
poszczególnych obserwacji mają różne wariancje. Jeśli wariancje są takie same
dla każdej obserwacji model nazywamy homoskedastycznym
Heteroskedastyczność składnika losowego pojawia sie czesto, gdy szacujemy
model na podstawie danych przekrojowych lub przekrojowo-czasowych
Hipoteza zerowa:
Hipoteza alternatywna:
σ
i
=
const
( model homoskedastyczny)
Formułujemy hipotezy.
( model heteroskedastyczny)
σ
i
∫
const
i=
1,2,....,n
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
6
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne.
Estymujemy parametry modelu : Y =
β
1
X
1
+
β
2
X
2
+ ...+
β
k
X
k
+ Z
Krok 1
Krok 2 Obliczamy reszty w oszacowanym modelu
i porządkujemy je od najmniejszej do największej : e
1
,e
2
,...,e
n
Krok 3
Wyznaczamy wartość statystyki testowej
Test Harrisona-McCabe’a
∑
∑
=
=
=
n
i
i
m
i
i
e
e
b
1
2
1
2
gdzie m jest środkowym numerem obserwacji (dla n parzystego przyjmujemy m=n/2)
Uwaga: musi być spełniony warunek: n>2k
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Krok 4
Schemat podejmowania decyzji:
Dla przyjętego poziomu istotności a odczytujemy z tablic rozkładu F-Snedecora
wartości:
F
1
dla stopni swobody (n-m) i (m-k ) oraz F
2
dla stopni swobody (n-m-k ) i m.
Krok 5
Wyznaczamy wartości krytyczne b
L
oraz d
U
dla poziomu istotności
α :
1
1
)
(
1
−
−
−
+
=
k
m
F
m
n
b
L
1
2
)
(
1
−
−
−
+
=
m
F
k
m
n
b
U
b § b
L
b
L
< b < d
U
d
U
§ b
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
Test Harrisona-McCabe’a
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne.
7
4. Normalność rozkładu zakłóceń
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Hipoteza zerowa:
Hipoteza alternatywna:
Składnik losowy Z ma rozkład normalny
Składnik losowy Z ma rozkład inny niż normalny
Estymujemy parametry modelu : Y =
β
1
X
1
+
β
2
X
2
+ ...+
β
k
X
k
+ Z
Krok 1
Krok 2 Obliczamy reszty w oszacowanym modelu : e
1
,e
2
,...,e
n
Krok 3
Test Jarque-Bera
∑
=
=
n
i
i
e
e
n
S
1
2
1
∑
=
=
n
i
e
i
S
e
n
B
1
3
3
3
1
∑
=
=
n
i
e
i
S
e
n
B
1
4
4
4
1
Obliczamy
−
+
=
2
4
2
3
)
3
(
24
1
6
1
B
B
n
JB
Statystyka testowa:
Zbiór krytyczny:
)
,
(
1
∞
χ
=
α
−
W
gdzie
χ
1-
α
jest kwantylem rzędu 1-
α z rozkładu χ
2
o dwóch stopniach swobody,
α jest przyjętym poziomem istotności testu
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Test Jarque-Bera
4. Normalność rozkładu zakłóceń
8
Model ceny wynajmu apartamentów (okręg Medison):
- cena na m
2
(CM),
- odległość od centrum w km (OC),
- powierzchnia oryginalnie w stopach kw, (przeliczone na metry) (PA),
- liczba apartamentów w budynku (LA),
Przykład 1 (cd)
Otrzymaliśmy już wcześniej model:
CM =
12.15
−
0.75OC
−
0.032PA
(0.68) (0.12) (0.009)
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Do wszystkich testów przyjmujemy poziom istotności
α=0.05
1. Założenie liniowości - test serii
Hipoteza zerowa:
oszacowany model ekonometryczny jest liniowy
Hipoteza alternatywna: oszacowany model ekonometryczny nie jest liniowy
1. Sortujemy dane wg. wybranej zmiennej objaśniającej -
9.74888
1
0.483
42
9.61673
1
0.483
45
8.774
1
0.322
46
8.6441
1
0.966
107
7.38086
1
0.644
114
2. Obliczamy reszty w modelu: CM =
12.15 − 0.75
OC
−0.032
PA
CM OC PA
Otrzymujemy:
9
Resztom dodatnim przypisujemy znak „+”, resztom ujemnym „
−”.
Otrzymujemy:
-0.699226, -0.735326, -1.66633, -0.235057, -0.522094, -1.42626, 1.97091, 0.685773, 0.314483,
1.66555, -0.647188, 0.538263, 0.520869, 0.169647, 0.530564, 0.73772, 0.465066, -0.945212,
-1.27833, 0.721934, -1.3712, 0.271387, -0.521057, 0.873627, -0.828638, 0.372159, 1.51762,
0.4892, 2.78054, -0.282807, -0.0400806, -1.14667, -0.388816, -1.88701, 0.637857, -0.641861
- - - - - - + + + + - + + + + + + - - + - + - + - + + + + - - - - - + -
Obliczamy :
N
+
=18, N
-
= 18, N
s
=15
.
-0.699226, -0.735326, -1.66633, -0.235057, -0.522094, -1.42626, 1.97091, 0.685773, 0.314483,
1.66555, -0.647188, 0.538263, 0.520869, 0.169647, 0.530564, 0.73772, 0.465066, -0.945212,
-1.27833, 0.721934, -1.3712, 0.271387, -0.521057, 0.873627, -0.828638, 0.372159, 1.51762,
0.4892, 2.78054, -0.282807, -0.0400806, -1.14667, -0.388816, -1.88701, 0.637857, -0.641861
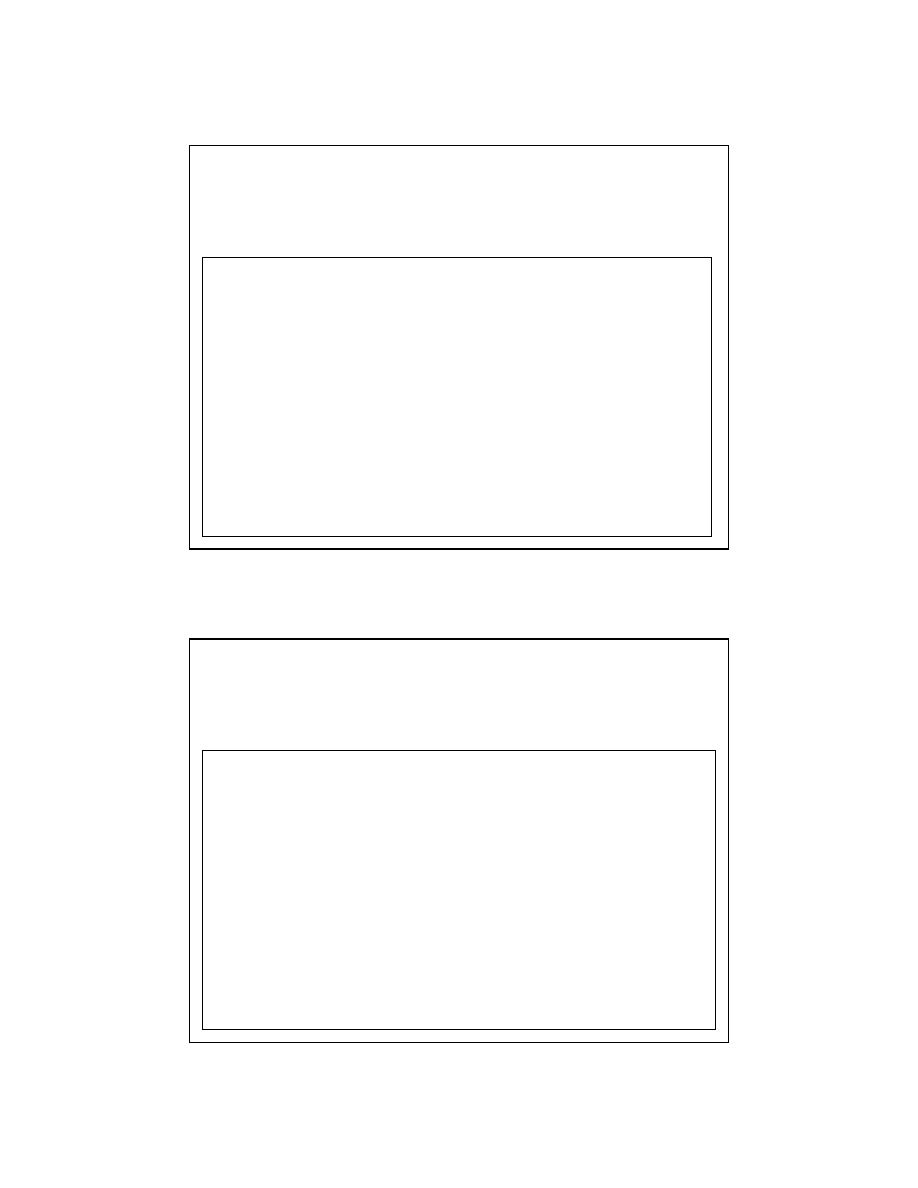
Odczytujemy z tablic dla testu serii i danego poziomu istotności wartość krytyczną N*=13
Ponieważ N
s
=15>13 wnioskujemy,
ż
e nie ma podstaw do odrzucenia
hipotezy o liniowości modelu
Obliczamy :
N
+
=18, N
-
= 18, N
s
=15
.
13
10
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Y =
β
1
X
1
+
β
2
X
2
+ ...+
β
k
X
k
+Z
Model:
Autokorelacja zakłóceń (proces autokorelacji pierwszego rzędu):
Z
i+
1
=
ρ
Z
i
+ V, i=
1,2,....,n-1
ρ
-
współczynnik autokorelacji , |
ρ
|<
1
V -
zmienna losowa o średniej 0 i skończonej wariancji
Główne przyczyny autokorelacji zakłóceń:
- natura procesów gospodarczych
- niepoprawna postać modelu
- zbyt ubogi zestaw zmiennych objaśniających
Autokorelacja występuje często, gdy model szacujemy na podstawie szeregów czasowych
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Hipoteza zerowa:
Hipoteza alternatywna:
ρ ∫
0
( autokorelacja występuje)
ρ =
0
( brak autokorelacji)
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
M
odel z wyrazem wolnym
: Y =
β
1
+
β
2
X
2
+ ...+
β
k
X
k
+ Z
Test Durbina - Watsona - dodatkowo założenie o normalności zakłóceń
Estymujemy parametry modelu - już zrobione.
Krok 1
Krok 2 Obliczmy reszty w oszacowanym modelu : e
1
,e
2
,...,e
n
- już zrobione:
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
-0.699226, -0.735326, -1.66633, -0.235057, -0.522094, -1.42626, 1.97091, 0.685773, 0.314483,
1.66555, -0.647188, 0.538263, 0.520869, 0.169647, 0.530564, 0.73772, 0.465066, -0.945212,
-1.27833, 0.721934, -1.3712, 0.271387, -0.521057, 0.873627, -0.828638, 0.372159, 1.51762,
0.4892, 2.78054, -0.282807, -0.0400806, -1.14667, -0.388816, -1.88701, 0.637857, -0.641861
11
∑
∑
=
=
−
−
=
n
i
i
n
i
i
i
e
e
e
d
1
2
2
2
1
)
(
Wyznaczamy wartość statystyki testowej
Krok 3
-0.699226, -0.735326, -1.66633, -0.235057, -0.522094, -1.42626, 1.97091, 0.685773, 0.314483,
1.66555, -0.647188, 0.538263, 0.520869, 0.169647, 0.530564, 0.73772, 0.465066, -0.945212,
-1.27833, 0.721934, -1.3712, 0.271387, -0.521057, 0.873627, -0.828638, 0.372159, 1.51762,
0.4892, 2.78054, -0.282807, -0.0400806, -1.14667, -0.388816, -1.88701, 0.637857, -0.641861
= 1.955
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Test Durbina - Watsona
Schemat podejmowania decyzji:
d § d
L
d
L
< d < d
U
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
4-d
U
§ d § 4-d
L
4-d
L
< d
Hipotezę zerową odrzucamy
brak decyzji
d
U
< d <
4 - d
U
d
L
oraz d
u
- wartości krytyczne wyznaczane z tablic
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
12
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Test Durbina - Watsona
Wartości krytyczne d
L
oraz d
u
dla poziomu istotności
α = 0.05:
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
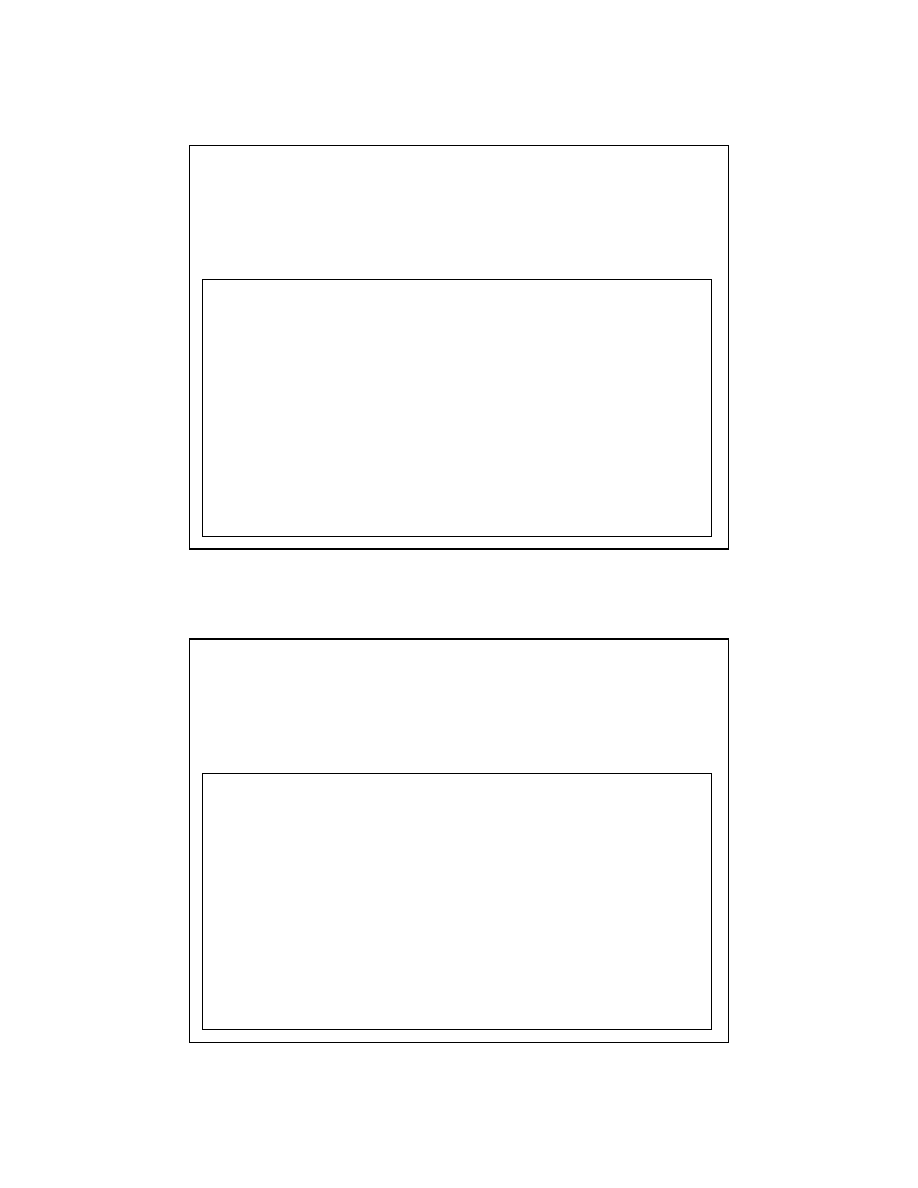
d §
1.46
1.46 < d < 1.63
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
2.37 § d § 2.54
2.54 < d
Hipotezę zerową odrzucamy
brak decyzji
1.63 < d < 4 - 1.63=2.37
2. Założenie niezależności zakłóceń modelu - autokorelacja zakłóceń
Test Durbina - Watsona
Ponieważ d=1.96 więc, nie ma podstaw do odrzucenia hipotezy mówiącej, że
autokorelacja nie występuje
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
Hipotezę zerową odrzucamy
brak decyzji
d §
1.46
1.46 < d < 1.63
2.37 § d § 2.54
2.54 < d
1.63 < d < 4 - 1.63=2.37
13
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne. Test Harrisona-McCabe’a
Model nazywamy heteroskedastycznym, jeżeli składniki losowe dla
poszczególnych obserwacji mają różne wariancje. Jeśli wariancje są takie same
dla każdej obserwacji model nazywamy homoskedastycznym
Heteroskedastyczność składnika losowego pojawia sie czesto, gdy szacujemy
model na podstawie danych przekrojowych lub przekrojowo-czasowych
Hipoteza zerowa:
Hipoteza alternatywna:
σ
i
=
const
( model homoskedastyczny)
Formułujemy hipotezy.
( model heteroskedastyczny)
σ
i
∫
const
i=
1,2,....,n
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne.
Estymujemy parametry modelu
Krok 1
Krok 2 Obliczamy reszty w oszacowanym modelu
i porządkujemy je od najmniejszej do największej :
Test Harrisona-McCabe’a
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
-1.88701, -1.66633, -1.42626, -1.3712, -1.27833, -1.14667,-0.945212,-0.828638, -0.735326, -0.699226, -
0.647188, -0.641861, -0.522094, -0.521057, -0.388816, -0.282807,-0.235057, -0.0400806, 0.169647, 0.271387,
0.314483, 0.372159, 0.465066, 0.4892, 0.520869, 0.530564, 0.538263, 0.637857, 0.685773, 0.721934, 0.73772,
0.873627, 1.51762, 1.66555, 1.97091, 2.78054
14
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne.
Krok 3
Wyznaczamy wartość statystyki testowej
Test Harrisona-McCabe’a
∑
∑
=
=
=
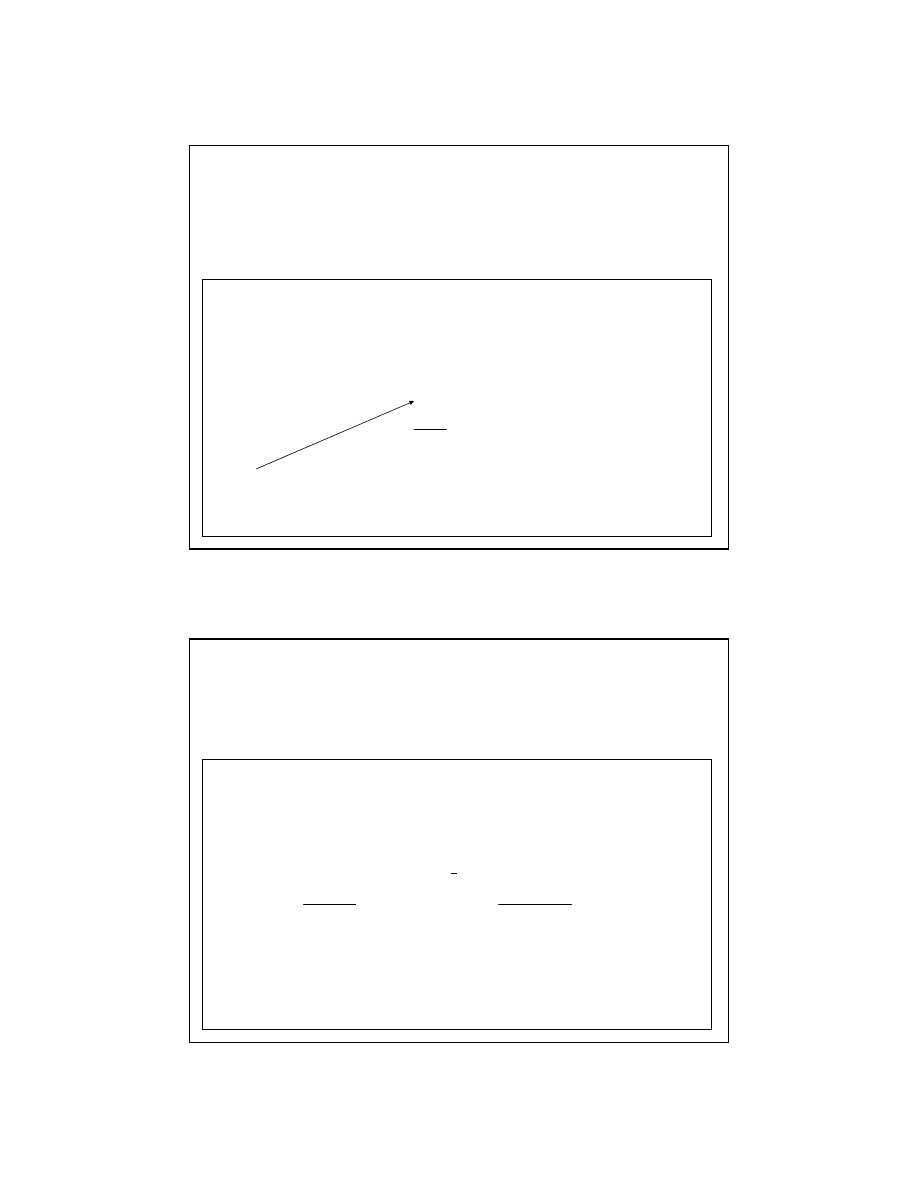
n
i
i
m
i
i
e
e
b
1
2
1
2
gdzie m=18 jest środkowym numerem obserwacji
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
-1.88701, -1.66633, -1.42626, -1.3712, -1.27833, -1.14667,-0.945212,-0.828638, -0.735326, -0.699226,
-0.647188, -0.641861, -0.522094, -0.521057, -0.388816, -0.282807,-0.235057, -0.0400806, 0.169647, 0.271387,
0.314483, 0.372159, 0.465066, 0.4892, 0.520869, 0.530564, 0.538263, 0.637857, 0.685773, 0.721934, 0.73772,
0.873627, 1.51762, 1.66555, 1.97091, 2.78054
= 0.45
Krok 4
Schemat podejmowania decyzji:
Dla przyjętego poziomu istotności
α=0.05 odczytujemy z tablic rozkładu
F-Snedecora wartości:
F
1
=
2.35 dla stopni swobody (n-m=18) i (m-k=15 ) oraz
F
2
=
2.27 dla stopni swobody (n-m-k =15) i m=18.
Krok 5
Wyznaczamy wartości krytyczne b
L
oraz d
U
dla poziomu istotności
α :
1
1
)
(
1
−
−
−
+
=
k
m
F
m
n
b
L
1
2
)
(
1
−
−
−
+
=
m
F
k
m
n
b
U
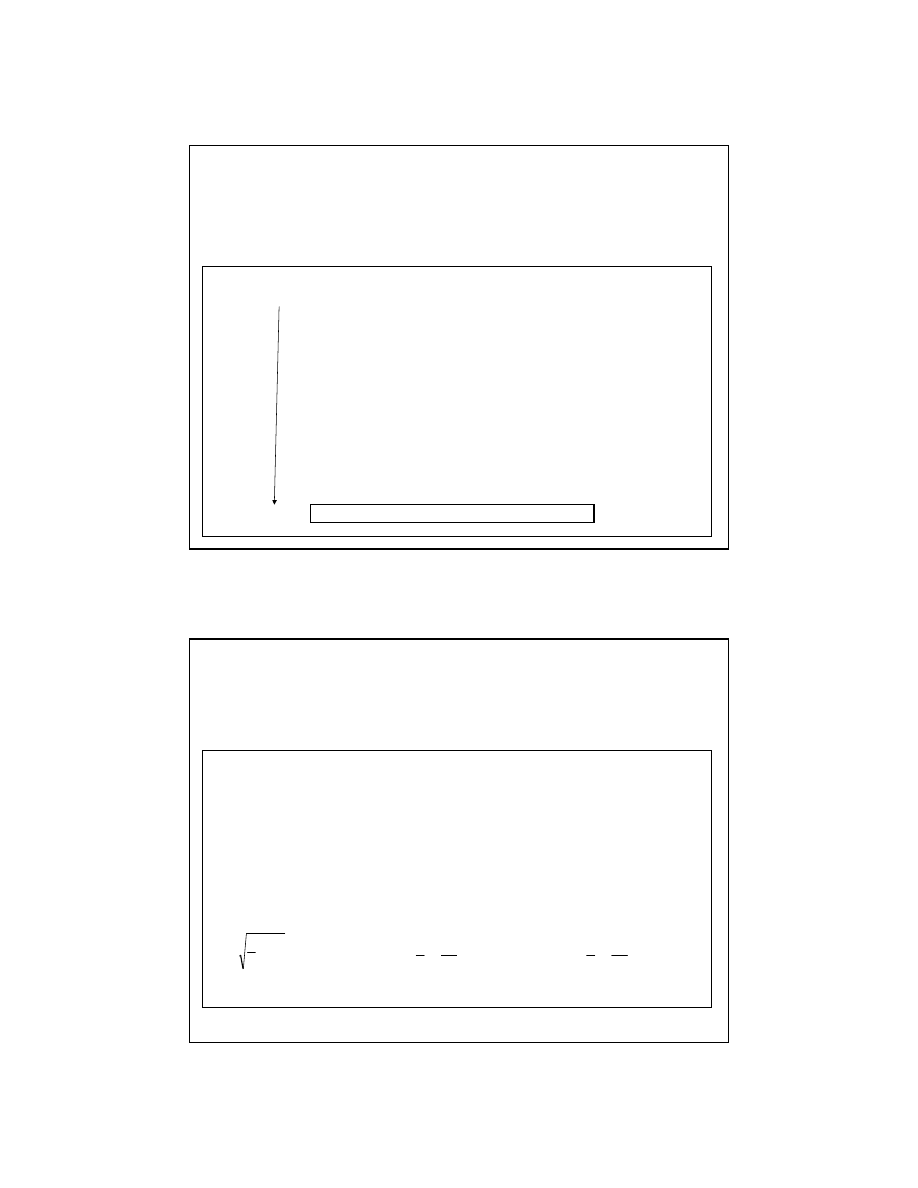
b § 0.26
0.26 < b < 0.35
0.35 § b
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
Test Harrisona-McCabe’a
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne.
= 0.26
= 0.35
15
Schemat podejmowania decyzji:
b § 0.26
0.26 < b < 0.35
0.35 § b
Hipotezę zerową odrzucamy
brak decyzji
Nie ma podstaw do odrzucenia hipotezy zerowej
Test Harrisona-McCabe’a
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
3. Założenie stałości momentów rozkładu zakłóceń modelu
- modele homo- i heteroskedastyczne.
Ponieważ b= 0.45 więc nie ma podstaw do odrzucenia hipotezy mówiącej, że
model jest homoskedastyczny
4. Normalność rozkładu zakłóceń
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Hipoteza zerowa:
Hipoteza alternatywna:
Składnik losowy Z ma rozkład normalny
Składnik losowy Z ma rozkład inny niż normalny
Estymujemy parametry modelu
Krok 1
Krok 2 Obliczamy reszty w oszacowanym modelu .
Krok 3
Test Jarque-Bera
∑
=
=
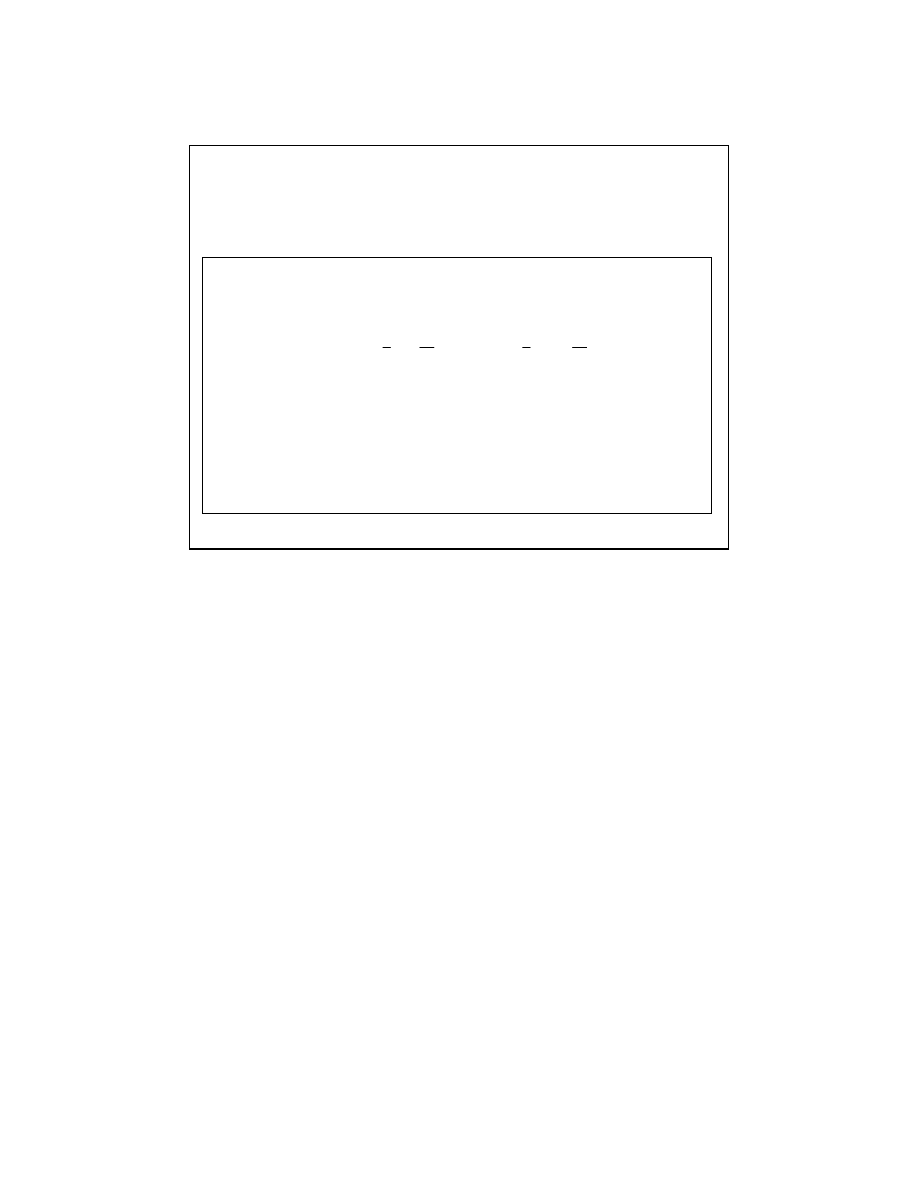
n
i
i
e
e
n
S
1
2
1
∑
=
=
n
i
e
i
S
e
n
B
1
3
3
3
1
∑
=
=
n
i
e
i
S
e
n
B
1
4
4
4
1
Obliczamy
= 0.98
= 0.32
= 3.29
16
−
+
=
2
4
2
3
)
3
(
24
1
6
1
B
B
n
JB
Statystyka testowa:
Zbiór krytyczny:
)
,
99
.
5
(
∞
=
W
gdzie
χ
0.95
=5.99 jest kwantylem rzędu 1-
α z rozkładu χ
2
o dwóch stopniach
swobody,
α=0.05 jest przyjętym poziomem istotności testu
Etap III C:
Sprawdzanie założeń przyjętych o modelu ekonometrycznym
Test Jarque-Bera
4. Normalność rozkładu zakłóceń
73
.
0
)
3
29
.
3
(
24
1
32
.
0
6
1
36
2
2
=
−
+
=
Ponieważ wartość statystyki nie należy do zbioru krytycznego, nie ma podstaw do
odrzucenia hipotezy zerowej. Możemy uznać, rozkład zakłóceń modelu jest normalny