1
Badanie istotności przyjętego układu zmiennych objaśniających
(etap IIIB przyjętego schematu modelowania ekonometrycznego)
1. Test Walda dla całego układu zmiennych objaśniających
2. Test Studenta dla poszczególnych zmiennych objaśniających
3. Uogólniony test Walda dla podukładu zmiennych objaśniających
4. Test mnożnika Lagrange’a dla podukładu zmiennych objaśniających
Przykład
2
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
1. Test Walda dla całego układu zmiennych objaśniających
(
model z wyrazem wolnym
)
Model:
Hipoteza zerowa:
Dla przeprowadzenia testu Walda przyjmujemy założenie dodatkowe:
zmienna losowa Z ma rozkład normalny
Y =
b
1
+
b
2
X
2
+ ...+
b
k
X
k
+ Z
b
2
=...=
b
k
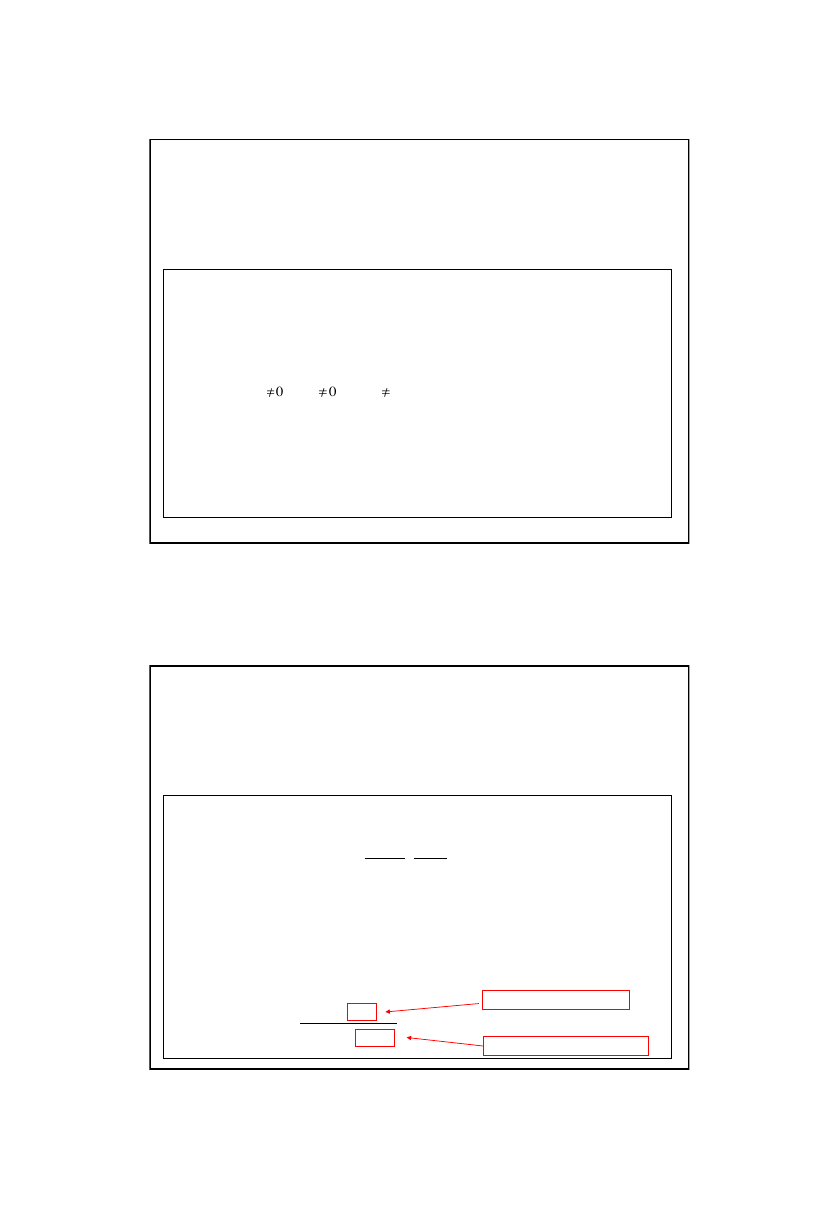
=0 (wszystkie zmienne są nieistotne)
Hipoteza alternatywna:
b
2
lub
b
3
...lub
b
k
0 (przynajmniej jedna zmienna jest istotna)
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
1. Test Walda dla całego układu zmiennych objaśniających
(
model z wyrazem wolnym
)
Statystyka testowa:
Zbiór krytyczny:
1
1
2
2
k
k
n
R
R
F
)
,
(
1
F
W
gdzie F
1-
jest kwantylem rzędu 1-
z rozkładu F-Snedecora o (k-1) oraz (n-k)
stopniach swobody,
jest przyjętym poziomem istotności testu.
)
/(
1
)
1
/(
2
2
k
n
R
k
R
F
Liczba stopni swobody licznika
Liczba stopni swobody mianownika

3
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
2. Test Studenta dla poszczególnych zmiennych objaśniających
Y =
b
1
X
1
+
b
2
X
2
+ ...+
b
k
X
k
+Z
Dla przeprowadzenia testu Studenta przyjmujemy założenie dodatkowe:
zmienna losowa Z ma rozkład normalny
Model:
Hipoteza zerowa:
Hipoteza alternatywna:
b
i
( i-ta zmienna jest istotna)
b
i
=
( i-ta zmienna jest nieistotna o ile wszystkie inne
pozostaną )

4
Statystyka testowa:
Zbiór krytyczny:
gdzie jest kwantylem rzędu 1 - z rozkładu Studenta o (n-k)
stopniach swobody,
jest przyjętym poziomem istotności testu
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
2. Test Studenta dla poszczególnych zmiennych objaśniających
)
,
(
)
,
(
2
1
2
1
t
t
W
2
1
t
i
b
i
S
b
t
ii
Z
b
S
S
i
A
1
)
(
X
X
A
T
2
gdzie
i
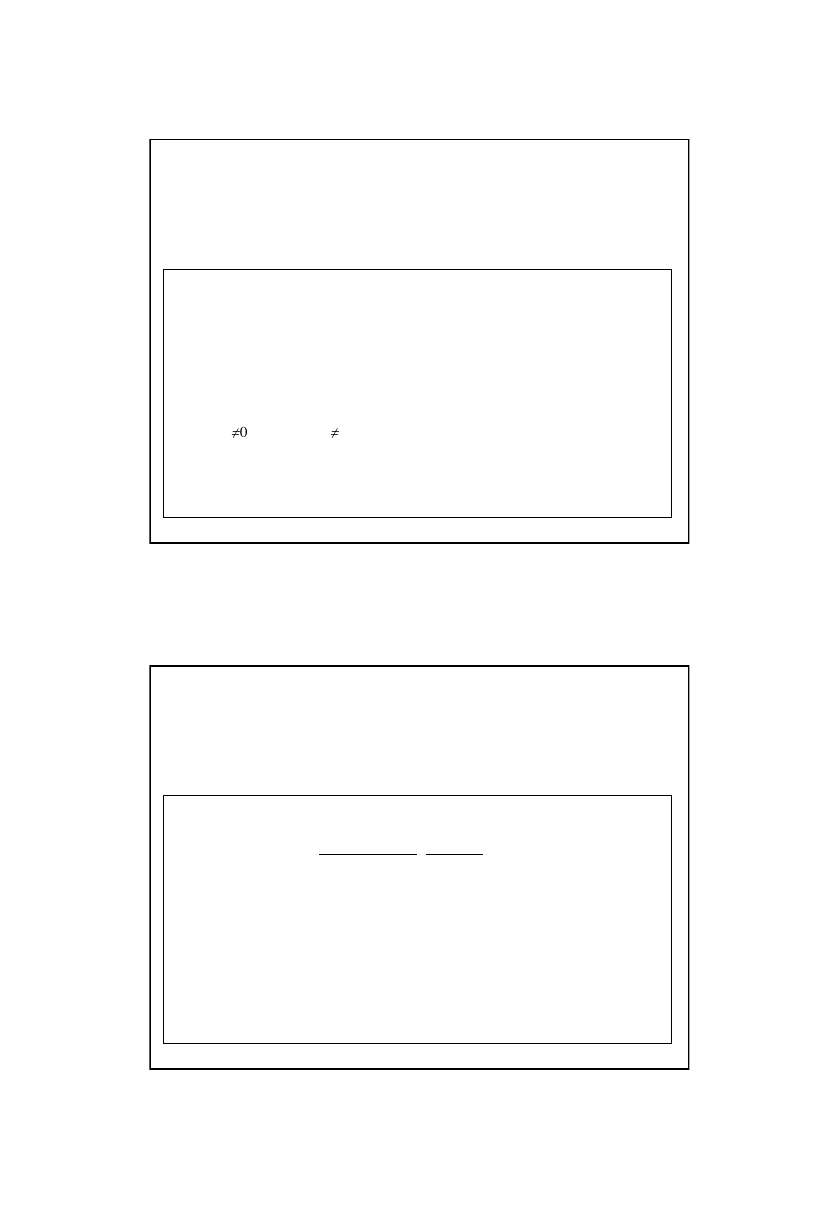
5
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
3. Uogólniony test Walda dla podukładu zmiennych objaśniających
Dla przeprowadzenia uogólnionego testu Walda przyjmujemy założenie dodatkowe:
zmienne losowe Z i V mają rozkłady normalne
Y =
b
1
X
1
+
b
2
X
2
+ ...+
b
k
X
k
+
b
k+1
X
k+1
+ ...+
b
k+m
X
k+m
+ Z
Hipoteza zerowa:
b
k+1
=...=
b
k+m
=0 (wszystkie zmienne od X
k+1
do X
k+m
są nieistotne)
Hipoteza alternatywna:
b
k+1
lub ... lub
b
k+m
0 (przynajmniej jedna z dodanych zmiennych jest istotna)
Model podstawowy:
Model rozszerzony:
Y =
b
1
X
1
+
b
2
X
2
+ ...+
b
k
X
k
+ V
Statystyka testowa:
Zbiór krytyczny:
)
,
(
1
F
W
gdzie F
1-
jest kwantylem rzędu 1-
z rozkładu F-Snedecora o m oraz (n-m-k)
stopniach swobody,
jest przyjętym poziomem istotności testu
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
3. Uogólniony test Walda dla podukładu zmiennych objaśniających
m
k
m
n
SKR
SKR
SKR
F
R
R
P
)
(
gdzie SKR
P
to suma kwadratów reszt w MNK dla modelu podstawowego,
a SKR
R
to suma kwadratów reszt w MNK dla modelu rozszerzonego
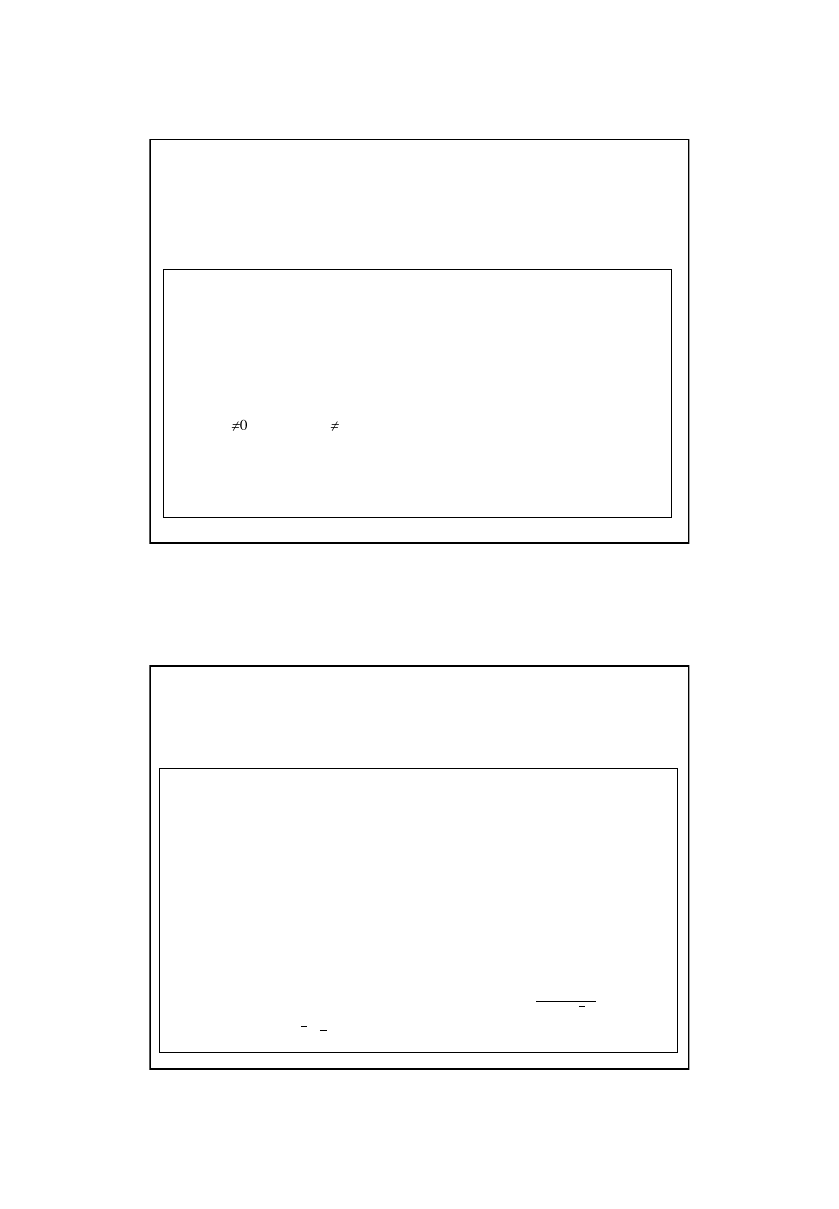
6
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
4. Test mnożnika Lagrange’a dla podukładu zmiennych objaśniających
Dla przeprowadzenia testu mnożnika Lagrange’a nie potrzebujemy założenia
o
normalności
rozkładu zmiennych losowych. Wymagana jest natomiast próba
dużego rozmiaru (n>30).
Y =
b
1
X
1
+
b
2
X
2
+ ...+
b
k
X
k
+
b
k+1
X
k+1
+ ...+
b
k+m
X
k+m
+ V
Hipoteza zerowa:
b
k+1
=...=
b
k+m
= 0 (wszystkie zmienne od X
k+1
do X
k+m
są nieistotne)
Hipoteza alternatywna:
b
k+1
lub ... lub
b
k+m
0 (przynajmniej jedna z dodanych zmiennych jest istotna)
Model podstawowy:
Model rozszerzony:
Y =
b
1
X
1
+
b
2
X
2
+ ...+
b
k
X
k
+ Z
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
4. Test mnożnika Lagrange’a dla podukładu zmiennych objaśniających
p
i
=
g
1
X
i1
+
g
2
X
i2
+ ..
.+
g
k+m
X
i,k+m
+ V
i
Estymujemy parametry modelu podstawowego: Y =
b
1
X
1
+
b
2
X
2
+ ...+
b
k
X
k
+ Z
Procedura obliczania statystyki testowej.
Krok 1
Krok 2 Obliczmy reszty w oszacowanym modelu podstawowym: p
1
,p
2
,...,p
n
Krok 3
Estymujemy parametry modelu pomocniczego:
p
X
X
X
T
R
R
T
R
g
1
)
(
Estymator MNK parametru
g
:
Krok 4 Obliczmy reszty w oszacowanym modelu pomocniczym: h
1
,h
2
,...,h
n
Np. reszta h
1
=p
1
- (g
1
X
11
+ g
2
X
12
+ ..
.+ g
k+m
X
1,k+m
)
Krok 5 Obliczmy sumę kwadratów reszt w modelu pomocniczym: SKR
H
=
2
2
2
2
1
...
n
h
h
h
oraz współczynnik determinacji dla tego modelu:
Oczywiście
i
i
H
H
p
p
SKR
R
2
2
)
(
1
i
i
p
n
p
1

7
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym
4. Test mnożnika Lagrange’a dla podukładu zmiennych objaśniających
Statystyka testowa:
Zbiór krytyczny:
gdzie
c
1-
jest kwantylem rzędu 1-
z rozkładu
c
2
o m stopniach swobody,
jest przyjętym poziomem istotności testu
2
H
nR
L
)
,
(
1
c
W
8
Model ceny wynajmu apartamentów (miasto Medison, USA):
- cena na m
2
w dolarach (CM),
- odległość od centrum w km (OC),
- powierzchnia oryginalnie w stopach kw, (przeliczone na metry) (PA),
-liczba apartamentów w budynku (LA),
-wiek budynku (WK),
-liczba miejsc parkingowych zarezerwowanych dla mieszkańców (MP)
Przykład 1
Model zapisywany na wykładzie jako
zapisujemy zwykle z użyciem symboli oddających sens zmiennych np.:
Y =
b
1
+
b
2
X
2
+
b
3
X
3
+
b
4
X
4
+
b
5
X
5
+
b
6
X
6
+ Z
CM =
b
1
+
b
2
OC+
b
3
PA+
b
4
LA +
b
5
PA+
b
6
LA + Z
Y x
2
x
3
x
4
x
4
x
5
CM
OC PA LA WK MP
974,9
0,48
42
32
1
13
961,7
0,48
45
24
2
13
877,4
0,32
46
24
3
8
1 014,1
0,32
48
176
2
47
979,0
0,32
50
16
1
16
1 007,0
0,97
51
23
2
25
750,6
3,06
51
104
3
107
1 042,1
0,97
53
9
4
15
854,2
2,9
55
120
5
128
1 001,2
0,48
55
28
4
33
742,8
3,06
56
68
3
72
1 038,6
0,64
57
39
21
80
684,8
5,31
58
41
2
44
1 010,6
0,48
58
18
3
23
1 004,2
0,97
60
29
2
31
1 008,9
0,97
65
25
1
26
968,8
0,97
69
14
2
17
655,4
3,06
74
216
3
220
927,9
0,64
74
23
4
29
995,3
0,48
80
27
5
36
794,9
0,32
81
150
6
161
576,6
5,31
84
80
10
99
665,8
3,06
84
104
4
112
630,4
5,31
86
68
5
77
637,4
2,9
87
210
8
226
919,5
0,64
89
39
7
51
810,8
1,45
90
51
4
57
900,8
0,97
91
39
3
42
767,0
0,97
93
18
4
24
850,1
0,48
94
25
5
33
825,4
0,97
98
28
3
33
643,0
2,9
99
72
2
74
709,9
3,06
99
68
4
73
798,9
0,32 102
16
4
24
864,4
0,97 107
14
1
6
738,1
0,64 114
22
1
7
9
... ... ... ... ... ...
CM
OC
PA LA WK MP
... ... ... ... … …
X =
Dane:
Estymator MNK
b = (X
T
X)
-1
X
T
Y = (X
T
X)
-1
X
T
CM
CM=
...
974,9
0,483
42
32
1
13
961,7
0,483
45
24
2
13
877,4
0,322
46
24
3
8
1 014,1
0,322
48
176
2
47
864,4
0,966 107
14
1
6
738,1
0,644 114
22
1
7
1
0,483
42
32
1
13
1
0,483
45
24
2
13
1
0,322
46
24
3
8
1
0,322
48
176
2
47
1
0,966 107
14
1
6
1
0,644 114
22
1
7
974,9
961,7
877,4
1 014,1
864,4
738,1
b = (X
T
X)
-1
X
T
CM =
CM = 1183.11 – 56.49 OC – 3.02 PA - 0.17 LA + 5.15WK – 0.55 MP
Model z oszacowanymi parametrami:
1183,11
-56,49
-3,02
-0,17
5,15
-0,55
10
Podstawowe wskaźniki jakości modelu:
5
.
58
k
n
SKR
S
Z
85
.
0
1
2
SKW
SKR
R
%
7
5
,
861
9
,
104
__
CM
S
V
Z
Etap III A
Test Walda dla całego układu zmiennych objaśniających (model z wyrazem wolnym)
Statystyka testowa:
Zbiór krytyczny:
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
- zakładamy normalny rozkład zmiennej losowej Z
5
.
34
1
6
6
36
68
.
0
1
68
.
0
1
1
2
2
k
k
n
R
R
F
)
,
53
.
2
(
)
,
(
1
F
W
Wniosek:
CM = 1183.11 – 56.49 OC – 3.02 PA - 0.17 LA + 5.15WK – 0.55 MP

11
A = (X
T
X)
-1
ii
Z
b
S
S
i
A
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Test Studenta dla poszczególnych zmiennych objaśniających
- zakładamy normalny rozkład zmiennej losowej Z
Obliczenia wstępne
Dla poprawnego przeprowadzenia obliczeń zalecamy korzystanie z arkusza
kalkulacyjnego lub ze specjalistycznych programów
i
b
i
S
b
t
CM = 1183.11 – 56.49 OC – 3.02 PA - 0.17 LA + 5.15WK – 0.55 MP

12
Hipoteza zerowa:
Hipoteza alternatywna:
b
2
0
( zmienna OC jest istotna)
b
2
= 0
(zmienna OC jest nieistotna o ile wszystkie
inne w modelu pozostaną )
Statystyka testowa:
Zbiór krytyczny:
327
.
7
2
2
b
S
b
t
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
)
,
042
.
2
(
)
042
.
2
,
(
)
,
(
)
,
(
975
.
0
975
.
0
t
t
W
)
,
(
)
,
(
2
1
2
1
t
t
W
Wniosek:
Test Studenta dla istotności zmiennej OC
- zakładamy normalny rozkład zmiennej losowej Z
CM = 1183.11 – 56.49
OC
– 3.02 PA - 0.17 LA + 5.15WK – 0.55 MP
13
Hipoteza zerowa:
Hipoteza alternatywna:
b
3
0
( zmienna PA jest istotna)
b
3
= 0
Statystyka testowa:
Zbiór krytyczny:
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
076
.
6
3
3
b
S
b
t
Test Studenta dla istotności zmiennej PA
- zakładamy normalny rozkład zmiennej losowej Z
Wniosek:
(zmienna PA jest nieistotna o ile wszystkie
inne w modelu pozostaną )
)
,
042
.
2
(
)
042
.
2
,
(
)
,
(
)
,
(
975
.
0
975
.
0
t
t
W
CM = 1183.11 – 56.49 OC – 3.02
PA
- 0.17 LA + 5.15WK – 0.55 MP
Hipoteza zerowa:
Hipoteza alternatywna:
b
4
0
( zmienna LA jest istotna)
b
4
= 0
Statystyka testowa:
Zbiór krytyczny:
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
360
.
0
4
4
b
S
b
t
Test Studenta dla istotności zmiennej LA
- zakładamy normalny rozkład zmiennej losowej Z
Wniosek:
(zmienna LA jest nieistotna o ile wszystkie
inne w modelu pozostaną )
)
,
042
.
2
(
)
042
.
2
,
(
)
,
(
)
,
(
975
.
0
975
.
0
t
t
W
CM = 1183.11 – 56.49 OC – 3.02 PA - 0.17
LA
+ 5.15WK – 0.55 MP
14
Hipoteza zerowa:
Hipoteza alternatywna:
b
5
0
( zmienna WK jest istotna)
b
5
= 0
Statystyka testowa:
Zbiór krytyczny:
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
553
.
1
5
5
b
S
b
t
Test Studenta dla istotności zmiennej LA
- zakładamy normalny rozkład zmiennej losowej Z
Wniosek:
(zmienna WK jest nieistotna o ile wszystkie
inne w modelu pozostaną )
)
,
042
.
2
(
)
042
.
2
,
(
)
,
(
)
,
(
975
.
0
975
.
0
t
t
W
CM = 1183.11 – 56.49 OC – 3.02 PA - 0.17 LA + 5.15
WK
– 0.55 MP
Hipoteza zerowa:
Hipoteza alternatywna:
b
6
0
( zmienna MP jest istotna)
b
6
= 0
Statystyka testowa:
Zbiór krytyczny:
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
034
.
1
6
6
b
S
b
t
Test Studenta dla istotności zmiennej LA
- zakładamy normalny rozkład zmiennej losowej Z
Wniosek:
(zmienna MP jest nieistotna o ile wszystkie
inne w modelu pozostaną )
)
,
042
.
2
(
)
042
.
2
,
(
)
,
(
)
,
(
975
.
0
975
.
0
t
t
W
CM = 1183.11 – 56.49 OC – 3.02 PA - 0.17 LA + 5.15WK – 0.55
MP

15
Uwaga: Testowanie hipotez „tradycyjne”, a testowanie z użyciem komputera.
Czy można nie umieć tradycyjnego sposobu?
Uogólniony test Walda dla istotności zmiennych „podejrzanych”: LA, WK, MP
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Dla przeprowadzenia uogólnionego testu Walda musi być spełnione założenie
dodatkowe: zmienne losowe Z i V mają rozkłady normalne
Hipoteza zerowa:
b
4
=
b
5
=
b
6
=0 (wskazane zmienne są nieistotne)
Hipoteza alternatywna:
Model podstawowy:
Model rozszerzony:
CM =
b
1
+
b
2
OC+
b
3
PA+ V
CM =
b
1
+
b
2
OC+
b
3
PA
+
b
4
LA +
b
5
WK+
b
6
MP
+ Z
CM =
b
1
+
b
2
OC+
b
3
PA+
b
4
LA +
b
5
WK+
b
6
MP
+ Z
b
4
≠0 lub
b
5
≠ 0 lub
b
6
≠ 0 (wśród wskazanych zmiennych jest
przynajmniej jedna istotna)
16
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Krok 1: budujemy model podstawowy i obliczamy sumę kwadratów reszt:
CM =
b
1
+
b
2
OC+
b
3
PA+ V
Po obliczeniach otrzymujemy: SKR
P
= 142123,8
Uogólniony test Walda dla istotności zmiennych „podejrzanych”: LA, WK, MP
CM =
b
1
+
b
2
OC+
b
3
PA+
b
4
LA +
b
5
WK+
b
6
MP
+ Z
Statystyka testowa:
Zbiór krytyczny:
m
k
m
n
SKR
SKR
SKR
F
R
R
P
)
(
)
,
(
1
F
W
U nas: n=36, m=3, k=3
Krok 2,3,4,5,6: budujemy model rozszerzony i obliczamy sumę kwadratów reszt
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Po obliczeniach otrzymujemy: SKR
R
= 102800,6
CM =
b
1
+
b
2
OC+
b
3
PA+
b
4
LA +
b
5
WK+
b
6
MP
+ Z
Uogólniony test Walda dla istotności zmiennych „podejrzanych”: LA, WK, MP
Podstawiamy do wzoru na statystykę testową (uwzględniając n=36, m=3, k=3)
m
k
m
n
SKR
SKR
SKR
F
R
R
P
)
(
Otrzymujemy:
F=3.83
Zbiór krytyczny:
gdzie F
0.95
=2.92 jest kwantylem rzędu 0.95 z rozkładu F-Snedecora o 3 (licznik)
oraz 30 (mianownik) stopniach swobody
Wniosek:
)
,
92
.
2
(
)
,
(
1
F
W
17
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Dla przeprowadzenia testu mnożnika Lagrange’a nie potrzebujemy założenia
o
normalności
rozkładu zmiennych losowych. Wymagana jest natomiast próba
dużego rozmiaru (n>30).
Hipoteza zerowa:
b
4
=
b
5
=
b
6
=0 (wskazane zmienne są nieistotne)
Hipoteza alternatywna:
Model podstawowy:
Model rozszerzony:
CM =
b
1
+
b
2
OC+
b
3
PA+ V
CM =
b
1
+
b
2
OC+
b
3
PA+
b
4
LA +
b
5
WK+
b
6
MP
+ Z
b
4
≠0 lub
b
5
≠ 0 lub
b
6
≠ 0 (wśród wskazanych zmiennych jest
przynajmniej jedna istotna)
Test mnożnika Lagrange’a dla istotności zmiennych „podejrzanych”: LA, WK, MP
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Procedura obliczania statystyki testowej w teście mnożnika Lagrange’a.
Krok 1 i 2
Obliczmy reszty w oszacowanym modelu podstawowym: p
1
,p
2
,...,p
36
Krok 3,4,5 Obliczamy współczynnik determinacji w modelu wyjaśniającym
zachowanie się reszt w zależności od wszystkich zmiennych objaśniających
występujących w modelu rozszerzonym
Test mnożnika Lagrange’a dla istotności zmiennych „podejrzanych”: LA, WK, MP
Krok 3,4,5 Otrzymujemy:
277
,
0
2
H
R

18
Etap III B:
Istotność zmiennych objaśniających w modelu ekonometrycznym (poziom istotności
=0.05)
Statystyka testowa:
Zbiór krytyczny:
gdzie
7.815
jest kwantylem rzędu 1-
0.95
z rozkładu
c
2
o m=3 stopniach
swobody
96
.
9
277
.
0
36
2
H
nR
L
)
,
815
.
7
(
)
,
(
)
,
(
95
.
0
1
c
c
W
Wniosek:
Test mnożnika Lagrange’a dla istotności zmiennych „podejrzanych”: LA, WK, MP
19
Co dalej ?
Podejście Hendry’ego (D. Hendry 1979)
Zalecany sposób upraszczania;
1. Stosujemy uogólniony test Walda i test mnożnika Lagrange’a (do wszystkich
podejrzanych na podstawie testu Studenta zmiennych naraz)
2. W razie wykrycia, że przynajmniej jedna zmienna jest istotna, usuwanie zmiennych
pojedynczo z modelu i przeprowadzanie kolejnych testów Studenta, aż zostaną
tylko zmienne istotne.
3. Ponowne zastosowanie uogólnionego testu Walda i testu mnożnika Lagrange’a (do
odrzuconych zmiennych naraz)
Intended overparametrization with data-based simplification
Zatem otrzymaliśmy propozycję modelu:
Czy taki model jest użyteczny ? Czy jest to już ostateczna jego postać?
O tym przekonamy się realizując kolejne etapy modelowania
Jego wskaźniki jakości są następujące:
84
.
0
2
R
%
7
V
23
.
7
2
b
S
49
.
0
3
b
S
34
.
38
1
b
S
Oszacowany model zapisujemy w postaci:
CM =
1207,13
–
58,97
OC
3.12
PA - 0.59 LA
20
.
0
4
b
S
CM =
1207,13
–
58,97
OC
3.12
PA - 0.59 LA
(38.34) (7.23) (0.49) (0.20)
Wyszukiwarka
Podobne podstrony:
Etap IIIC Testy założeń v11
Konkurs historyczny SP etap rejonowy
Etap rejonowy 2007 2008 klucz
Etap 3 9
Etap podstawowy XXV Olimpiady Wiedzy Ekologicznej ODPOWIEDZI
54 Olimpiada chemiczna Etap III
Konkurs historyczny GIM etap szkolny 2
gimnazjum etap szkolny 2013 angielski
Historia arkusz IIIb (czasy nowozytne do roku 1915) poziom rozszerzony wypracowanie6
Końcowy etap tworzenia pracy dyplomowej
historia 3 etap 2010 klucz
arkusz oceny 1 etap
46 Olimpiada chemiczna Etap I Zadania teoretyczne
Etap 8
chemia 3 etap 2010 klucz
Etap rejonowy 2006 2007 arkusz
52 Olimpiada chemiczna Etap III Zadania teoretyczne
więcej podobnych podstron