Ćwiczenie D5:

A

LGORYTMY

APROKSYMACJI

CAŁKI

PRZY

ZASTOSOWANIU

PROCESORÓW

SYGNAŁOWYCH

TMS320

SERII

28

XX

opracował:

mgr inż. Roman Niestrój

[e-mail]

Cele ćwiczenia:

–

poznanie wybranych algorytmów aproksymacyjnych

–

wykorzystanie sprzętowych możliwości obliczeniowych
procesora sygnałowego

–

doskonalenie umiejętności programowania w środowisku
Code Composer Studio

Metody aproksymacji całki w systemach cyfrowych

W procesie opracowywania programów dla cyfrowych systemów sterowania bardzo często zachodzi
konieczność aproksymowania operacji całkowania. Przy przekształcaniu równań analogowych
obiektów dynamicznych do postaci dyskretnej można posłużyć się jedną z następujących metod
aproksymacji całki:

•

wsteczną metodą prostokątów (wsteczna metoda Eulera);

•

postępującą metodą prostokątów (postępująca metoda Eulera);

•

metodą trapezów;

•

metodą Simpsona.

Metody te różnią się od siebie dokładnością uzyskanego wyniku a także ilością niezbędnych do
wykonania operacji matematycznych. W algorytmach aproksymacyjnych bazujących na
wymienionych metodach, występują operacje mnożenia i dodawania, które są sprzętowo
wykonywane przez procesory sygnałowe.

Wsteczna metoda prostokątów

Wsteczna metoda prostokątów pozwala na przybliżenie całki sumą iloczynów wartości kolejnych
próbek sygnału wejściowego cyfrowego układu całkującego i czasu próbkowania T, przy czym licząc
N-tą próbkę sygnału wyjściowego cyfrowego układu całkującego bierze się pod uwagę N próbek
sygnału wejściowego cyfrowego układu całkującego. Aproksymację całki wsteczną metodą
prostokątów dla przykładowego sygnału w przedstawiono na rysunku 1.
Aproksymację całki wsteczną metodą prostokątów można przedstawić następująco:

( )

( )

∑

∫

=

⋅

⋅

≅

N

i

T

N

i

w

T

dt

t

w

0

0

gdzie: w - wielkość całkowana; N - numer próbki (zmienna dyskretna).

Transmitancja operatorowa K(z) w dziedzinie zmiennej z dla aproksymacji całki wsteczną metodą
prostokątów wyraża się zależnością:

( ) ( )

1

−

=

z

T

z

K

gdzie: K – transmitancja operatorowa; z – operator.

Schemat blokowy cyfrowego układu całkującego wykorzystującego wsteczną metodę prostokątów
przedstawiono na rysunku 2.

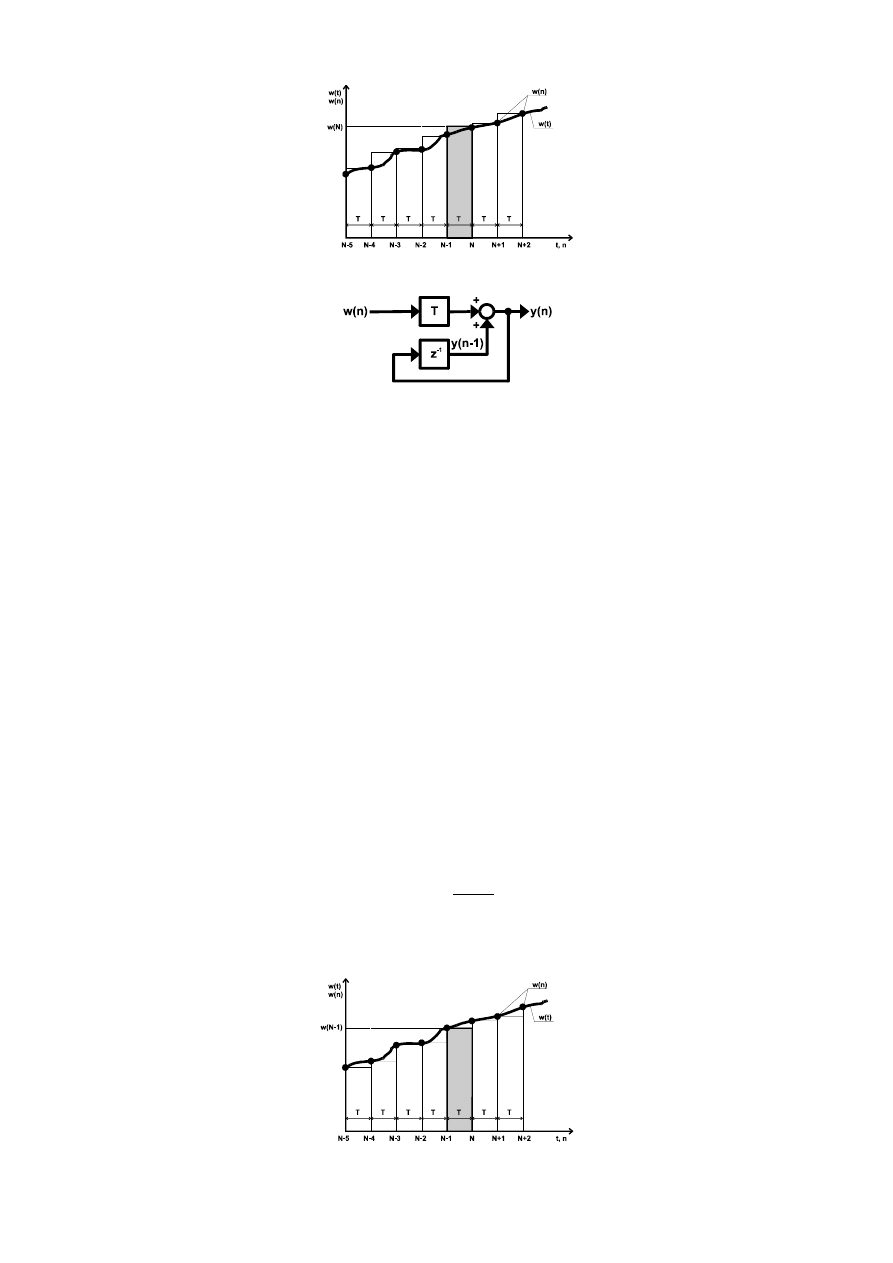
Rys. 1. Aproksymacja całki wsteczną metodą prostokątów.

Rys. 2. Schemat blokowy cyfrowego układu całkującego wykorzystującego aproksymację

całki wsteczną metodą prostokątów.

Przedstawiony na rysunku 2 cyfrowy układ całkujący realizuje równanie różnicowe wynikające
z transmitancji operatorowej K(z):

( ) (

)

( )

n

w

T

n

y

n

y

⋅

+

−

=

1

gdzie: y – wielkość wyjściowa z układu całkującego.

Wsteczna metoda prostokątów wymaga realizacji przez system cyfrowy jednej operacji mnożenia
i jednej operacji sumowania.

Postępująca metoda prostokątów

Postępująca metoda prostokątów pozwala na przybliżenie całki sumą iloczynów wartości kolejnych
próbek sygnału wejściowego cyfrowego układu całkującego i czasu próbkowania T, przy czym licząc
N-tą próbkę sygnału wyjściowego cyfrowego układu całkującego bierze się pod uwagę (N-1) próbek
sygnału wejściowego cyfrowego układu całkującego. Aproksymację całki postępującą metodą
prostokątów dla przykładowego sygnału w przedstawiono na rysunku 3.
Aproksymację całki postępującą metodą prostokątów można przedstawić następująco:

( )

( )

∑

∫

=

⋅

+

⋅

≅

N

i

T

N

i

w

T

dt

t

w

0

)

1

(

0

Transmitancja operatorowa K(z) w dziedzinie zmiennej z dla aproksymacji całki postępującą
metodą prostokątów wyraża się zależnością:

( ) ( )

1

z

Tz

z

K

−

=

Schemat blokowy cyfrowego układu całkującego wykorzystującego postępującą metodę prostokątów
przedstawiono na rysunku 4.

Rys. 3. Aproksymacja całki postępującą metodą prostokątów.

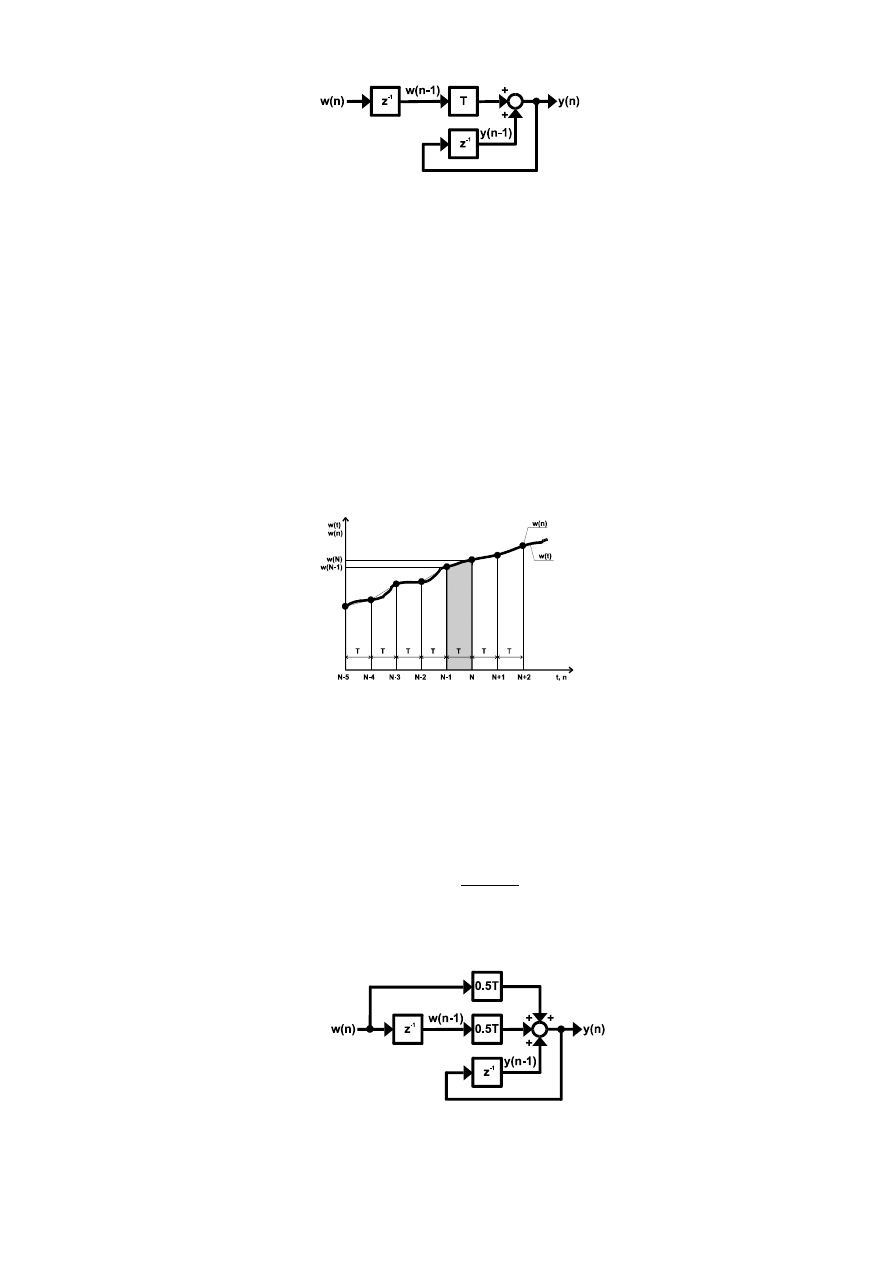
Rys. 4. Schemat blokowy cyfrowego układu całkującego wykorzystującego aproksymację

całki postępującą metodą prostokątów.

Przedstawiony na rysunku 4 cyfrowy układ całkujący realizuje równanie różnicowe wynikające
z transmitancji operatorowej K(z):

( ) (

)

(

)

1

1

−

⋅

+

−

=

n

w

T

n

y

n

y

Podobnie jak wsteczna metoda prostokątów, postępująca metoda prostokątów wymaga realizacji
przez system cyfrowy jednej operacji mnożenia i jednej operacji sumowania.

Metoda trapezów

Metoda trapezów pozwala na przybliżenie całki sumą iloczynów średniej arytmetycznej dwóch
kolejnych próbek sygnału wejściowego cyfrowego układu całkującego i czasu próbkowania T, przy
czym licząc N-tą próbkę sygnału wyjściowego cyfrowego układu całkującego bierze się pod uwagę
próbki sygnału wejściowego cyfrowego układu całkującego o numerach N i (N-1). Aproksymację
całki metodą trapezów dla przykładowego sygnału w przedstawiono na rysunku 5.

Rys. 5. Aproksymacja całki metodą trapezów.

Aproksymację całki metodą trapezów można przedstawić następująco:

( )

(

)

( )

[

]

0

)

1

(

,

1

5

,

0

0

0

=

−

+

−

⋅

⋅

≅

∑

∫

=

⋅

w

i

w

i

w

T

dt

t

w

N

i

T

N

Transmitancja operatorowa K(z) w dziedzinie zmiennej z dla aproksymacji całki metodą trapezów
wyraża się zależnością:

( )

(

)

(

)

1

2

1

−

⋅

+

⋅

=

z

z

T

z

K

Schemat blokowy cyfrowego układu całkującego wykorzystującego metodę trapezów przedstawiono
na rysunku 6.

Rys. 6. Schemat blokowy cyfrowego układu całkującego wykorzystującego aproksymację

całki metodą trapezów.

Przedstawiony na rysunku 6 cyfrowy układ całkujący realizuje równanie różnicowe wynikające
z transmitancji operatorowej K(z):

( ) (

)

(

)

( )

[

]

n

w

n

w

T

n

y

n

y

+

−

⋅

⋅

+

−

=

1

5

.

0

1

Metoda trapezów wymaga realizacji przez system cyfrowy dwóch operacji mnożenia i dwóch
operacji dodawania (w mikroprocesorach można dodawać tylko dwa składniki sumy jednocześnie).

Metoda Simpsona

Metoda Simpsona jest jedną z kwadratur interpolacyjnych Netwona-Cotesa, które powstają przez
scałkowanie wielomianu interpolacyjnego Lagrange'a, zbudowanego dla całkowanego ciągu próbek
sygnału w(n) i opartego na równoodległych węzłach (co przy stałej częstotliwości próbkowania jest
spełnione). Wyznaczając N-tą próbkę sygnału wyjściowego cyfrowego układu całkującego, metoda
Simpsona bierze pod uwagę próbki sygnału wejściowego cyfrowego układu całkującego o numerach
N, (N-1) i (N-2).

Aproksymację całki metodą Simpsona można przedstawić następująco:

∫

0

N⋅T

w



t



dt≈T⋅

∑

i=0

N

[

1
6

w



i





2
3

w



i−1





1
6

w



i−2



]

; w



−

1



=

0; w



−

2



=

0

Transmitancja operatorowa K(z) w dziedzinie zmiennej z dla aproksymacji całki metodą Simpsona
wyraża się zależnością:

K



z



=

T



z

2



4 z1



6 z



z −1



Schemat blokowy cyfrowego układu całkującego wykorzystującego metodę Simpsona przedstawiono
na rysunku 7.

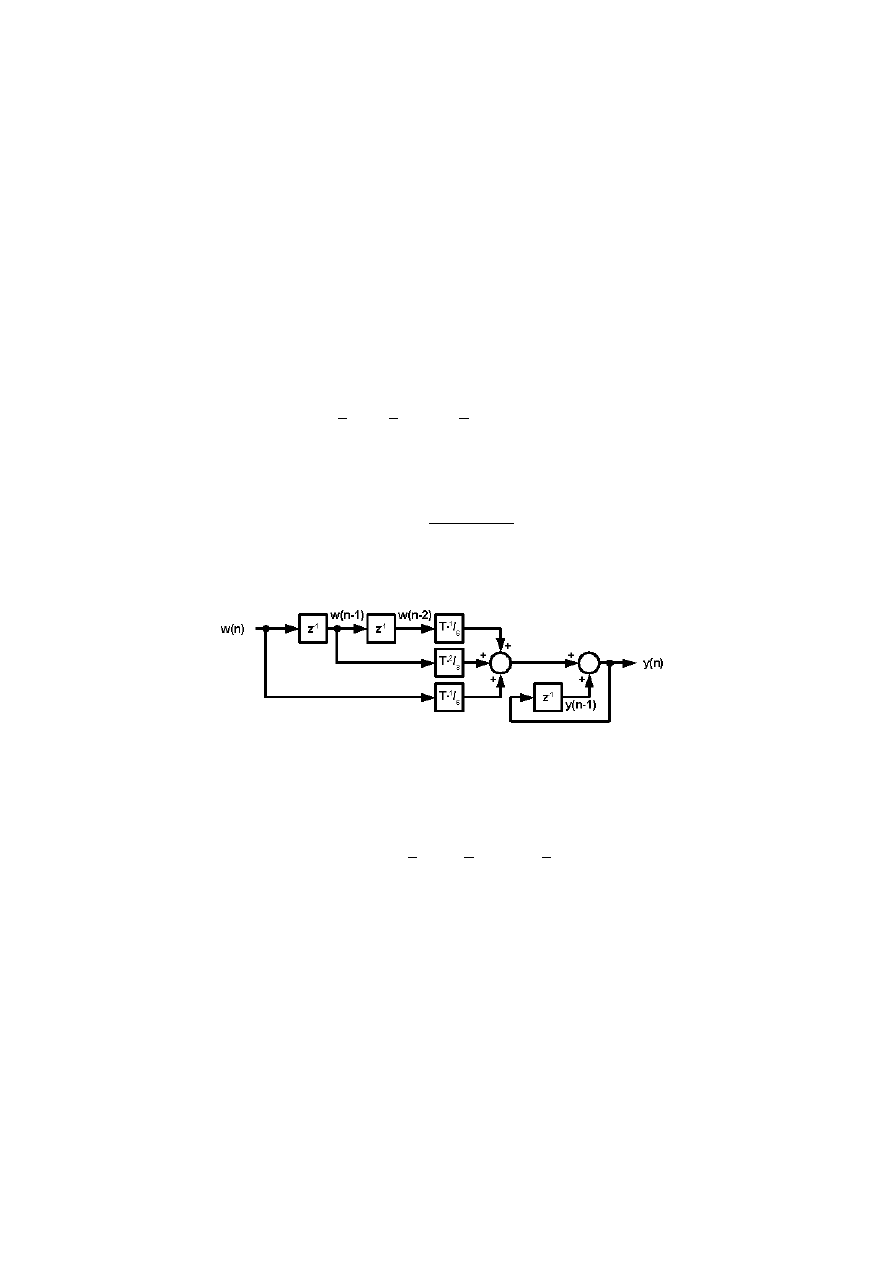
Rys. 7. Schemat blokowy cyfrowego układu całkującego wykorzystującego aproksymację

całki metodą Simpsona.

Przedstawiony na rysunku 7 cyfrowy układ całkujący realizuje równanie różnicowe wynikające
z transmitancji operatorowej K(z):

y



n



=

y



n−1





T⋅

[

1
6

⋅

w



n





2
3

⋅

w



n−1





1
6

⋅

w



n−2



]

Metoda trapezów wymaga realizacji przez system cyfrowy trzech operacji mnożenia i trzech operacji
dodawania (w mikroprocesorach można dodawać tylko dwa składniki sumy jednocześnie).

Uwagi końcowe

Dokładność przedstawionych metod aproksymacji całki zależy od wielu czynników, między innymi
od tego, czy częstotliwość próbkowania (i w związku z tym okres próbkowania T) jest przyjęta
prawidłowo. Następny czynnik, to sposób reprezentacji danych w systemie cyfrowym. Szczególnie
w systemach stałoprzecinkowych trzeba się liczyć z kumulacją błędów arytmetyki stałoprzecinkowej
przy stosowaniu metody Simpsona w sytuacji, gdy słowa bitowe, przeznaczone do przechowania
wartości współczynników występujących przy kolejnych próbkach sygnału wejściowego, będą zbyt
krótkie. Ta kumulacja błędów objawia się na wyjściu układu całkującego w postaci dryftu sygnału
całki. Dryft ten polega na tym, że na sygnał użyteczny nałożona jest pewna składowa narastająca
lub opadająca w czasie aż do nasycenia lub przepełnienia słowa bitowego przechowującego
obliczoną wartość całki. Podobne zjawisko wystąpi, gdy do wejścia układu całkującego dochodzi
składowa stała, zakłócająca wejściowy sygnał użyteczny (na przykład falę sinusoidalną). Dlatego
w układach sterowania maszyn elektrycznych często wykorzystuje się układy całkujące o specjalnej
strukturze, w których zjawisko dryftu nie występuje.

Zadanie 1.

Opracować program w środowisku CCS dla procesora sygnałowego TMS320F2812,

realizujący różne algorytmy aproksymacji całki.

Opracowany program będzie składał się z dwóch plików: nagłówkowego i źródłowego, w których
powinna znajdować się pełna definicja obiektu aproksymacji całki. Sprawdzenie działania tego
obiektu będzie możliwe w programie dostarczonym przez prowadzącego, zawierającym programowy
generator przebiegów: sinusoidalnego, piłokształtnego, prostokątnego i trapezowego. Do
sprawdzenia zostaną wykorzystane elementy Graph dostępne w CCS, działające w oparciu
o emulacje sprzętową.

Do wykonania ćwiczenia potrzebny jest komputer z CCS i zestaw uruchomieniowy eZdspF2812.

Wskazówki do wykonania zadania:

Opracowując program (obiekt) aproksymacji całki należy wykorzystać pliki definiujące
obiekt dla obsługi diody LED z ćwiczenia D2, kopiując je z innymi nazwami i dołączając do
projektu. Następnie należy w nich przeprowadzić niezbędne modyfikacje.

Obiekt realizujący aproksymację całki różnymi metodami powinien być zbudowany w oparciu
o następujące wskazówki (w razie wątpliwości należy skorzystać z instrukcji do ćwiczenia
D2):

Typ obiektu:

INTEGRALSUPPORT

Typ wskaźnikowy:

*INTEGRALSUPPORT_handle

Wartość domyślna (konstruktor obiektu):

INTEGRALSUPPORT_DEFAULTS (zbudowana w oparciu o wartości domyślne dla

pól danych)

Pola danych:

int16 In

- Wejście obiektu (domyślnie 0)

int16 Memory1

- Pamięć próbek 1 (domyślnie 0)

int16 Memory2

- Pamięć próbek 2 (domyślnie 0)

int16 Memory3

- Pamięć próbek 3 (domyślnie 0)

int16 Out

- Wyjście obiektu (domyślnie 0)

int16 Ki

- Stała całkowania (domyślnie 1)

Uint16 Scale

- Skala wyjścia

(domyślnie 8)

Pola metod:

tpcalc

- Wskaźnik funkcji obsługi
(wyliczenia całki metodą trapezów)

becalc

- Wskaźnik funkcji obsługi
(wyliczenia całki metodą wsteczną Eulera)

fecalc

- Wskaźnik funkcji obsługi
(wyliczenia całki metodą postępującą Eulera)

smcalc

- Wskaźnik funkcji obsługi
(wyliczenia całki metodą Simpsona)

reset

- Wskaźnik funkcji resetującej obiekt
(przywracającej we wszystkich polach wartości
domyślne)

Funkcje metod:

integral_tp_calc

- dla metody tpcalc

integral_be_calc

- dla metody becalc

integral_fe_calc

- dla metody fecalc

integral_sm_calc

- dla metody smcalc

integral_reset

- dla metody reset

Taka budowa obiektu jest wymuszona przez procedury obsługi obiektu, zamieszczone
w programie głównym dla ćwiczenia D5 (plik lab_d5.c).
Wszystkie elementy (między innymi okna Graph) potrzebne do sprawdzenia działania obiektu
zawarte są w pliku przestrzeni roboczej, właściwym dla ćwiczenia D5
(lab_d5_eZdspF2812_CCS3x.wks). Projekt dla ćwiczenia D5 zawiera dodatkowo pliki
z ćwiczenia D2, definiujące obiekt dla diody (led_eZdspF2812.h, led_eZdspF2812.c),w celu
ułatwienia ich wykorzystania do budowy obiektu dla układu całkującego).

Zadanie 2.

Zmierzyć czas wykonywania funkcji aproksymujących całkę w programie opracowanym

w zadaniu 1.

Pomiaru czasu wykonywania fragmentów programu dokonuje się przy pomocy Profilera zawartego
w CCS. Czas ten jest mierzony w cyklach maszynowych centralnej jednostki przetwarzającej
procesora sygnałowego. Wartości czasu zmierzone dla funkcji napisanych w języku C należy
porównać z czasem wykonywania funkcji o takim samym działaniu, napisanej w języku asembler
(przygotowanej przez prowadzącego). Ponadto należy przeanalizować sposób wywołania funkcji
napisanej w języku asembler z programu głównego napisanego w języku C (zwrócić uwagę na
wykorzystanie specyficznych trybów adresowania pośredniego). Do tego celu można wykorzystać
program funkcji realizującej aproksymację całki lub programy funkcji generatorów sygnałów (także
napisane są w języku asembler).

Do wykonania ćwiczenia potrzebny jest komputer z CCS i zestaw uruchomieniowy eZdspF2812.

Wskazówki do wykonania zadania:

Aby przyśpieszyć wykonanie zadania 2 można posłużyć się plikiem przestrzeni roboczej,
przygotowanym przez prowadzącego dla Profilera, zawartym w osobnym katalogu roboczym.
Plik ten zawiera wszystkie niezbędna okna i ustawienia potrzebne do wykonania zadania 2.
Podczas korzystania z Profilera należy WYŁĄCZYĆ tryb czasu rzeczywistego (Real-Time
Mode).

W czasie wykonywania ćwiczenia uczestnicy mogą korzystać z literatury dostarczanej przez
prowadzącego, dotyczącej wykorzystywanego procesora sygnałowego i środowiska
programistycznego.

Sprawozdanie z ćwiczenia

Sprawozdanie z ćwiczenia powinno zawierać kody napisanych w trakcie ćwiczenia programów wraz
z komentarzami opisującymi ich działanie.

Źródła literaturowe:

[1]. Dokumentacja procesora sygnałowego TMS320F2812. Texas Instruments.
[2]. Dokumentacja zestawu eZdsp i modułu DMC1500. Spectrum Digital.
[3]. C281x C/C++ Header Files and Peripheral Examples. Texas Instruments.

[5]. J. Klamka, Z. Ogonowski, M. Jamicki, M. Stasik: Metody numeryczne.

Wydawnictwo Politechniki Śląskiej, Gliwice 1998, skrypt 2068
[6]. J. Krupka, R.Z. Morawski, L.J. Opalski: Wstęp do metod numerycznych.

Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 1999

Żródła literaturowe [1, 2, 3] dostępne są na stronie internetowej firmy Texas Instruments
(

www.ti.com

).

opracowano dnia 30-10-2008, (v1.5)