
Instrukcja jest współfinansowana przez Unię Europejską
w ramach Europejskiego Funduszu Społecznego
w projekcie:
"Innowacyjna dydaktyka bez ograniczeń
- zintegrowany rozwój Politechniki Łódzkiej zarządzanie Uczelnią,
nowoczesna oferta edukacyjna
i wzmacniania zdolności do zatrudniania,
także osób niepełnosprawnych".
Ewa Dyka
Marek Mończyk
Instrukcja do laboratorium
Technologia informacyjna

Technologia informacyjna
1
Spis treści
1.
Opracowanie dokumentu .................................................................................................... 6
1.1
Ogólne zasady pisania tekstu....................................................................................... 6
1.1.1
Przejrzystość tekstu ............................................................................................. 6
1.1.2
Pisanie wzorów ................................................................................................. 11
1.1.3
Tabele ............................................................................................................... 12
1.1.4
Wykresy ............................................................................................................ 14
1.2
Formatowanie dokumentu przed wydrukiem ............................................................. 15
1.2.1
Podział i numeracja stron................................................................................... 15
1.2.2
Tworzenie spisu treści ....................................................................................... 16
2.
Pakiet biurowy Worda ...................................................................................................... 17
2.1
Szablony i formularze ............................................................................................... 17
2.2
Korespondencja seryjna ............................................................................................ 18
2.2.1
Listy seryjne...................................................................................................... 18
2.2.2
Etykiety adresowe ............................................................................................. 19
2.3
Makra ....................................................................................................................... 20
3.
Obliczenia w Excelu ......................................................................................................... 24
3.1
Pisanie formuł ........................................................................................................... 25
3.2
Makra ....................................................................................................................... 28
3.2.1
Projekt arkusza obliczeniowego......................................................................... 30
3.3
Rysowanie wykresów................................................................................................ 31
3.3.1
Wykresy o zwiększonej liczbie osi .................................................................... 31
3.3.2
Skala logarytmiczna .......................................................................................... 33
3.3.3
Linia trendu ....................................................................................................... 34
3.3.4
Wykresy powierzchniowe.................................................................................. 35
4.
Wybrane funkcje programu Excel ..................................................................................... 36
4.1
Funkcje inżynierskie – liczby zespolone.................................................................... 36
4.2
Funkcje matematyczne – rachunek macierzowy ........................................................ 38
4.3
Polecenie Szukaj wyniku............................................................................................ 39
4.4
Deklaracja własnej funkcji ........................................................................................ 41
4.5
Solver ....................................................................................................................... 42
5.
Pakiet biurowy Excela ...................................................................................................... 48
5.1
Formatowanie arkusza............................................................................................... 48
5.2
Prezentacja i przetwarzanie danych w arkuszu .......................................................... 50
5.2.1
Konsolidowanie danych .................................................................................... 50
5.2.2
Filtrowanie danych ............................................................................................ 51
5.2.3
Sumowanie danych............................................................................................ 52
5.2.4
Tworzenie konspektu......................................................................................... 53
5.2.5
Tabele przestawne ............................................................................................. 55
5.2.6
Wykresy przestawne.......................................................................................... 58
5.2.7
Scenariusze ....................................................................................................... 59
5.2.8
Kontrolki z okna dialogowego ........................................................................... 60
6.
Podstawowe wiadomości o środowisku Matlab................................................................. 63
6.1
Wiadomości wstępne ................................................................................................ 63
6.2
Pomocnicze polecenia okna Command Window ....................................................... 64
6.3
Skrypty i funkcje użytkownika .................................................................................. 67
6.4
Operacje na macierzach i tablicach wartości.............................................................. 69
6.5
Funkcje wspomagające generowanie macierzy.......................................................... 80
6.6
Liczby zespolone ...................................................................................................... 81

Technologia informacyjna
2
6.7
Funkcje matematyczne .............................................................................................. 82
6.8
Instrukcje języka skryptowego .................................................................................. 84
6.9
Instrukcje graficzne................................................................................................... 86
7.
Obliczenia w Matlabie ...................................................................................................... 89
7.1
Interpolacja ............................................................................................................... 89
7.2
Aproksymacja ........................................................................................................... 93
7.3
Miejsca zerowe wielomianów ................................................................................... 96
7.4
Miejsca zerowe funkcji ............................................................................................. 98
7.5
Algebra liniowa....................................................................................................... 100
7.5.1
Układy równań liniowych................................................................................ 100
7.5.2
Wykorzystanie pętli do deklaracji macierzy..................................................... 105
7.6
Całkowanie ............................................................................................................. 107
7.7
Różniczkowanie...................................................................................................... 110

Technologia informacyjna
3
Wstęp
Podstawowym celem ćwiczeń z przedmiotu Technologia informacyjna jest przygotowanie
studenta do wykonywania sprawozdań z zajęć laboratoryjnych. Zakres ćwiczeń obejmuje trzy
programy: Word, Excel i Matlab.
W ramach programu Word student zapoznaje się z zasadami poprawnego formatowania
tekstu łącznie z pisaniem wzorów, wstawianiem tabel, rysowaniem wykresów oraz tworzeniem
spisów treści, rysunków i tabel.
Z kolei Excel to przede wszystkim poprawne pisanie formuł, wykonywanie obliczeń
i rysowanie różnego rodzaju wykresów a ponadto praktyczne zastosowanie wybranych funkcji
matematycznych i inżynierskich dostępnych w programie oraz podstawy optymalizacji
w oparciu o dodatek Solver.
W zakresie Matlaba studentowi przedstawione zostają podstawowe metody obliczeń
numerycznych obejmujące przybliżanie funkcji (interpolację i aproksymację), wyznaczanie zer
funkcji i zer wielomianów, rozwiązywanie układów równań liniowych oraz całkowanie
i różniczkowanie funkcji.
Drugim celem tych ćwiczeń jest pokazanie możliwości pakietu Office w obszarze obsługi
biurowej firmy, czyli tworzenie dokumentów firmowych, korespondencji seryjnej, formularzy,
tabel
przestawnych,
konspektów,
scenariuszy,
przetwarzanie
danych
w
arkuszu
oraz usprawnienie pracy za pomocą makr.
W ramach zaliczenia przedmiotu student zobowiązany jest do wykonania projektu
na wybrany przez siebie temat z zakresu ogólnie pojętej elektryczności.

Technologia informacyjna
4
Projekt
1. Temat:
Dowolne zagadnienie związane z elektrycznością opisane funkcją dwóch zmiennych
2. Zawartość (max 10 stron):
część teoretyczna (opis zagadnienia: od 2 do 5 stron)
część obliczeniowa (od 2 do 4 stron)
wnioski (1 strona)
3. Obliczenia wykonane w Excelu:
wykorzystywane formuły
tabela z wynikami obliczeń
wykres
4. Obliczenia wykonane w Matlabie:
kod programu
wykres
5. Formatowanie projektu zgodnie z podanym wzorcem:
Formatowanie projektu.pdf, Wzór projektu.pdf

Technologia informacyjna - WORD
5
WORD
Technologia informacyjna - WORD
6
1. Opracowanie dokumentu
Rozmiar papieru A4 i orientacja pionowa są domyślnymi ustawieniami strony w programie
Word. Przed rozpoczęciem pisania tekstu należy ustalić marginesy strony (Plik – Ustawienie
strony – Marginesy) oraz jeżeli jest to wymagane zmienić odpowiednio rozmiar papieru
orientację strony. Domyślne parametry czcionki są następujące: Czcionka: Times New Roman,
Styl czcionki: Normalny, Rozmiar: 12. Jeżeli tekst ma być pisany inną czcionką, to należy przed
rozpoczęciem pisania dobrać odpowiedni jej typ (ćw. 1, ćw. 2, ćw. 3).
1.1 Ogólne zasady pisania tekstu
1.1.1 Przejrzystość tekstu
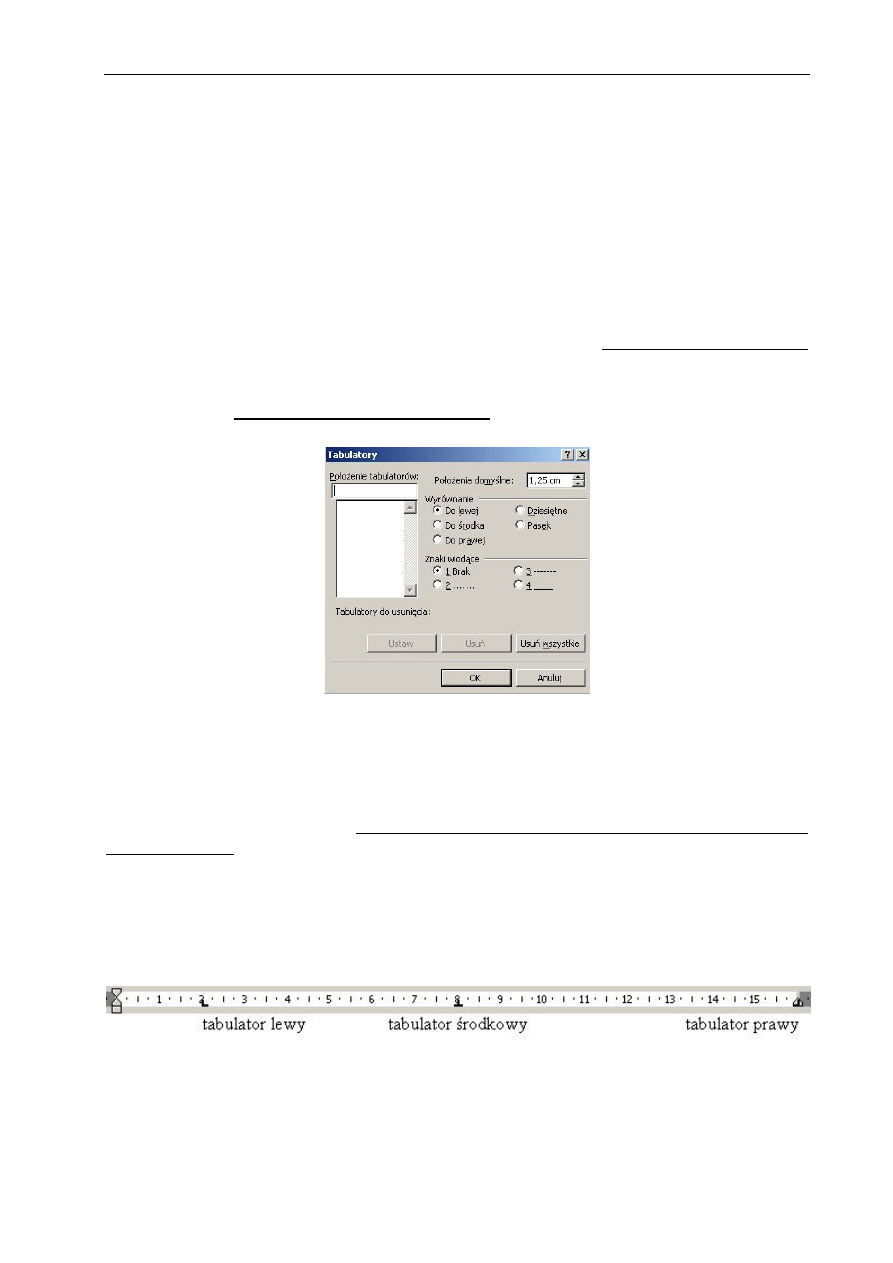
menu Format polecenie Akapit
Rys.1.1 Widok okna polecenia Akapit
Tekst powinien być podzielony na wyraźnie zaznaczone akapity; należy ustalić odstęp
przed i po akapicie (Wcięcia i odstępy - Odstępy: Przed (np. 6 pt), Po (np.6 pt)). Nie powinno się
używać pustych wierszy dla zwiększania odległości między akapitami.
Należy także w każdym akapicie zastosować wcięcie pierwszego wiersza Wcięcia
i odstępy - Specjalne: Pierwszy wiersz – Wielkość (np. 1 cm). Wiersz końcowy akapitu powinien
być krótszy od pozostałych, ale nie może być za krótki (co najmniej 7 znaków).
Podział tekstu na akapity zależy od treści w nim zawartej, każdy nowy wątek powinien być
umieszczony w nowym akapicie. Wciśnięcie klawisza Enter powoduje przejście do nowego
akapitu.
Pojedynczy wiersz akapitu nie powinien znajdować się ani na końcu strony (sierota)
ani na początku strony (wdowa). Można to wyeliminować dzięki opcjom dostępnym
w programie (Format – Akapit – Podział wiersza i strony – Kontroluj sieroty i wdowy).
Podobnie nie powinno się oddzielać rysunków, tabel, wykresów od ich podpisów a także
wzorów i ich oznaczeń. W tym przypadku należy korzystać z możliwości odpowiedniego
podziału strony (Wstaw – Podział: Typy podziałów: Podział strony). Nie powinno się używać
pustych wierszy w celu przejścia do następnej strony.
Technologia informacyjna - WORD
7
Przeważnie wyrównuje się tekst do prawej i lewej strony (justuje) (Wcięcia i odstępy –
Wyrównanie: Do lewej i prawej). Justowanie tekstu powoduje, że zmieniają się odstępy
pomiędzy poszczególnymi wyrazami w zależności od ilości wyrazów w wierszu i ich długości.
W pewnych przypadkach powinno się jednak zachować ustaloną odległość pomiędzy dwoma
kolejnymi wyrażeniami (np. między wartością a jej jednostką), wówczas między nimi należy
zastosować tzw. twardą spację (Ctr+Shift+Spacja).
Wyrazy złożone, których nie należy rozdzielać (np. biało-czerwony) powinny być
połączone łącznikiem nierozdzielającym (Ctr+Shift+-).
Na końcu żadnej linii tekstu nie powinien znajdować się spójnik, jednoliterowy przyimek
bądź też partykuła przecząca nie. Każdy taki element należy przenieść do nowego wiersza
naciskając klawisze (Shift+Enter). Przenoszenia należy dokonać po napisaniu i sprawdzeniu
całego tekstu.
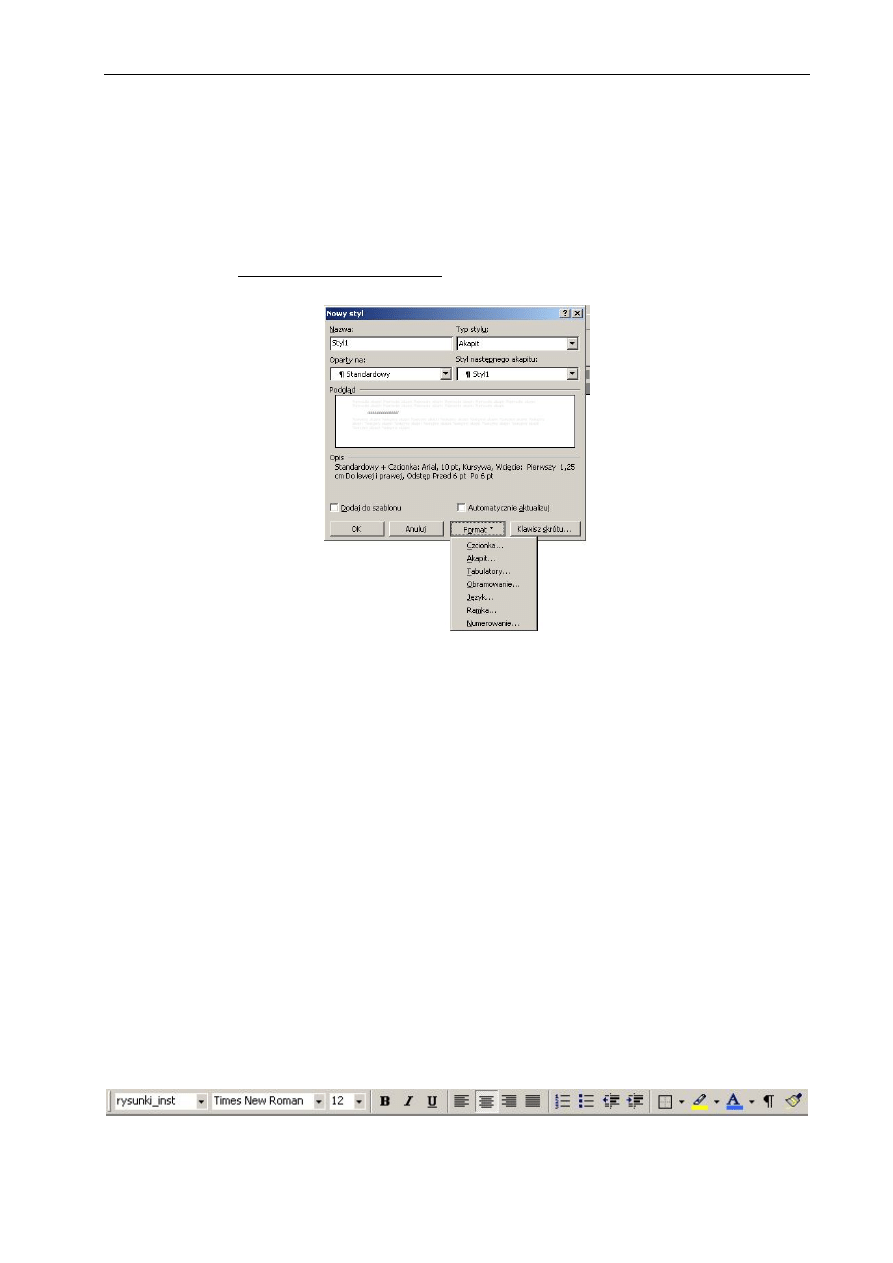
menu Format polecenie Tabulatory
Rys.1.2 Widok okna polecenia Tabulatory
Tabulatory to znaki rozmieszczone wzdłuż szerokości strony służące do wyrównywania
tekstu w wierszach. Jeżeli w danym wierszu ma znaleźć się kilka słów w określonych
odległościach od siebie, to najlepiej do tego celu wykorzystać tabulatory, które należy
odpowiednio ustawić, natomiast nie wolno nigdy stosować spacji do zwiększania odległości
między wyrazami. Do obsługi znaków tabulacji służy klawisz Tab; po jego wciśnięciu kursor
przesuwa się o zadeklarowaną odległość. Położenie domyślne tabulatora umożliwia zmianę
położenia kursora o stałą wartość wzdłuż całej szerokości strony. Znaki tabulacji pomagają także
w ustawieniu odpowiedniego wyrównania tekstu. Poniżej pokazany został przykład ustawienia
tabulatora lewego (tekst wyrównany do lewej), prawego (tekst wyrównany do prawej)
oraz wyrównującego tekst do środka.
Rys. 1.3 Widok linijki poziomej z ustawionymi tabulatorami
Dodanie do tabulatora znaku wiodącego pozwala na narysowanie jednej z trzech
wybranych linii o określonej długości i położeniu, które zależą od ustawienia tabulatora.
Technologia informacyjna - WORD
8
Tabulatory dziesiętne służą do oddzielania części dziesiętnych w przypadku liczb
umieszczonych w tabeli, natomiast tabulator pasek pozwala na narysowanie pionowej linii
w określonym miejscu wiersza..
Po wciśnięciu klawisza Enter automatycznie przenoszone jest ustawienie tabulatorów
do następnego wiersza, dlatego należy pamiętać o usunięciu dodatkowych tabulatorów
w wierszach w których nie są one potrzebne.
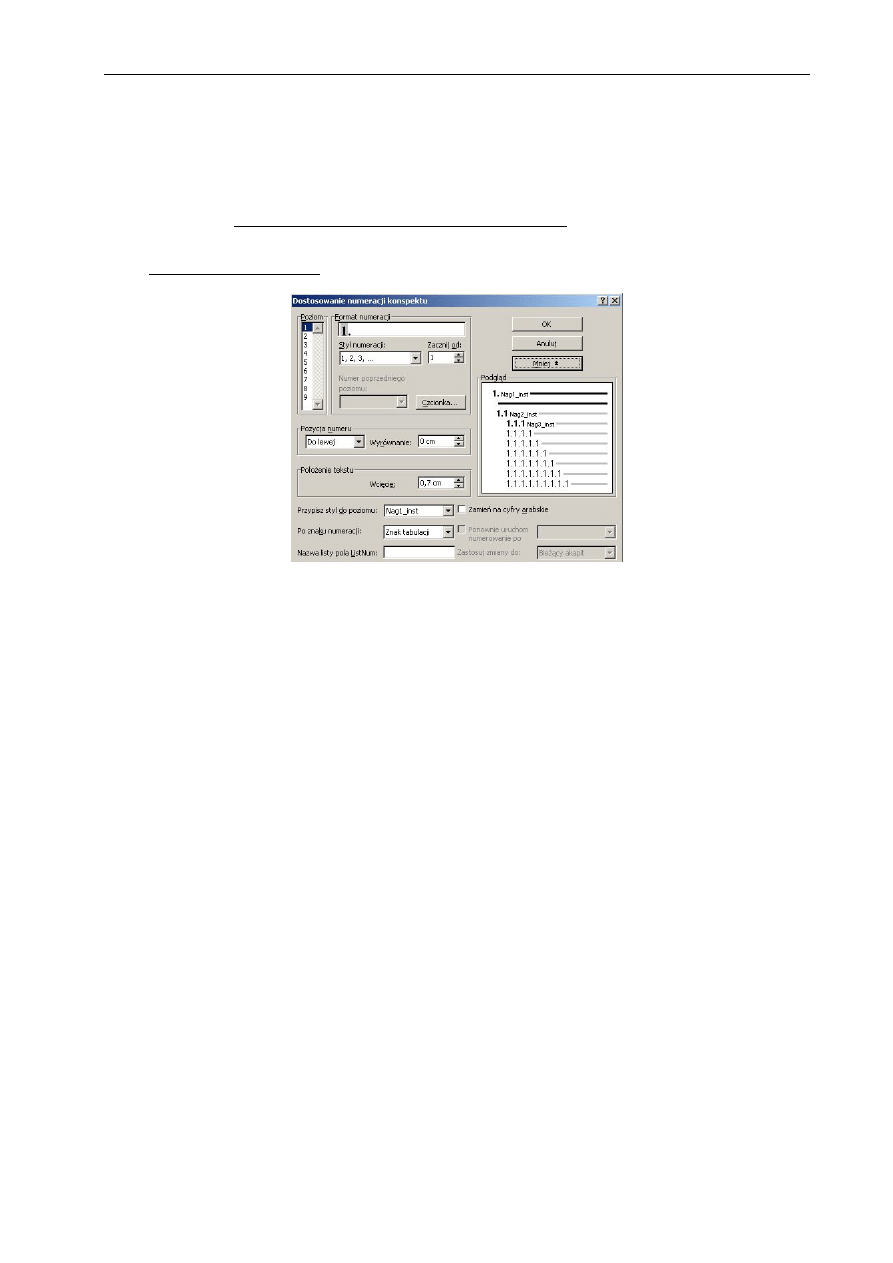
menu Format polecenie Styl
Rys. 1.4 Widok okna Nowy styl
Gdy zostaną już ustalone, wymienione wyżej, podstawowe parametry formatowania
określonego fragmentu tekstu można je zapisać w postaci własnego stylu (Format – Styl – Nowy
styl). Należy tylko nadać nazwę nowemu stylowi, natomiast wszystkie aktualne ustawienia
poleceń z menu format (widoczne na rys. 1.4) zostaną automatycznie do niego dopisane.
W trakcie pisania można modyfikować każde z ustawień własnego stylu; spowoduje
to automatyczną modyfikację tych fragmentów tekstu, które mają ten styl przypisany.
Można również na początku pracy z dokumentem zdefiniować wszystkie potrzebne style
i w trakcie pisania przypisywać je do kolejnych fragmentów tekstu. Nie trzeba zaznaczać tekstu,
aby przypisać styl, ponieważ jest on przypisywany akapitami. Wystarczy ustawić kursor
w dowolnym miejscu wybranego akapitu i z listy rozwijanej wybrać odpowiedni styl,
albo wykorzystać Malarza formatów do skopiowania stylu z wcześniejszego akapitu.
Podczas pisania tekstu bardzo przydatne są pokazane niżej ikony paska Formatowanie.
Pierwsza to Styl (lista rozwijana zdefiniowanych stylów), natomiast ostatnia z nich to Malarz
formatów. Na tym pasku została dodatkowo umieszczona ikona z paska Widok: Pokaż wszystko
(przedostatnia na rys. 1.5). Po wciśnięciu tej ikony zostają wyświetlone wszystkie znaki
niedrukowane, dzięki czemu zostaje uwidoczniona większość błędów formatowania (dodatkowe
spacje, puste wiersze itp.)
Rys. 1.5 Widok paska Formatowanie
Technologia informacyjna - WORD
9
W programie Word istnieje zarówno możliwość dodania lub usunięcia dostępnych pasków
narzędzi (prawy klawisz na menu) jak i dodania lub usunięcia poleceń z wybranego paska
(prawy klawisz na menu Dostosuj - Polecenia). Będąc w trybie Dostosuj można przeciągnąć
ikonę wybranego polecenia na dany pasek lub usunąć z paska dowolne polecenie.
menu Format polecenie Punktory i numeracja
Konspekty numerowane
Rys. 1.6 Widok okna Dostosowywanie numeracji konspektu
W przypadku pisania tekstów wymagających stworzenia spisu treści koniecznym staje się
odpowiednie zdefiniowanie kolejnych nagłówków. Rozpoczyna się od ustalenia stylu nagłówka
pierwszego, który jest nagłówkiem głównym dokumentu. W tym celu należy:
dodać nowy styl i nadać mu nazwę (Format – Styl – Nowy styl)
ustalić właściwości czcionki (Format – Styl – Nowy styl – Format –
Czcionka)
ustalić wyrównanie i odstępy w akapicie (Format – Styl – Nowy styl –
Format – Akapit – Wyrównanie; Odstępy: Przed, Po)
dodać numerację nagłówków (Format – Styl – Nowy styl – Format –
Numerowanie – Konspekty numerowane – Dostosuj (rys. 1.6)) w sposób
następujący:
określić Format i Styl numeracji
ustalić wcięcie numeru nagłówka (Pozycja numeru – Wyrównanie),
wartość ta jest automatycznie przepisywana do pozycji Wcięcie
w poleceniu Akapit (Akapit – Wcięcia: Od lewej)
ustalić wcięcie tekstu nagłówka (Położenie tekstu – Wcięcie), wartość ta
jest automatycznie przepisywana do pozycji Położenie tabulatorów
w poleceniu Tabulatory natomiast do pozycji Wcięcie w poleceniu Akapit
(Akapit – Wcięcia – Specjalne: Wysunięcie) wpisywana jest różnica
pomiędzy wcięciem numeru nagłówka a wcięciem tekstu nagłówka
(wysunięcie liczone jest od pozycji numeru).

Technologia informacyjna - WORD
10
przypisać stworzony styl do zdefiniowanego nagłówka Przypisz styl
do poziomu (należy odszukać na liście rozwijanej właściwy styl)
Po określeniu stylu należy przyporządkować zdefiniowany nagłówek do odpowiednich
fragmentów tekstu w dokumencie.
W taki sam sposób należy stworzyć kolejno style dla pozostałych nagłówków, które są
nagłówkami podrzędnymi dokumentu. Podgląd prawidłowo zdefiniowanych nagłówków
pokazany jest na rys. 1.16.
W dokumentach Worda są także dostępne wbudowane style standardowych nagłówków
z których można korzystać jeżeli nie istnieje potrzeba definiowania własnych.
Punktowane i Numerowane
Punktowanie i numerowanie wprowadza się w celu uporządkowania informacji
przedstawianych w postaci listy. Listy numerowane stosuje się, gdy ważna jest kolejność
przedstawianych informacji.
Można wybrać zarówno znak punktora jak i jego położenie w wierszu, które określa
Pozycja punktora: Wcięcie (rys. 1.7). Powyższa wartość jest automatycznie przenoszona
do Akapitu jako Wcięcia: Od lewej. Wcięcie tekstu określa się w pozycji Położenie tekstu:
Wcięcie. Wartość ta jednocześnie decyduje o położeniu tabulatora. Natomiast w Akapicie
Wcięcia specjalne: Wysunięcie: Wielkość to odległość między punktorem a tekstem.
W celu wyraźniejszego oddzielenia listy od pozostałych części tekstu czasami wprowadza
się również wcięcie od prawej strony (Akapit Wcięcia: Od prawej).
Rys. 1.7 Widok okna Akapit oraz Dostosowywanie listy wypunktowanej
Zasady numerowania są takie same jak punktowania, można również wybrać format i styl.
Przykładem specjalnego numerowania może być tworzenie spisu literatury, gdzie każdy
numer powinien być umieszczony w nawiasie kwadratowym.
Przykład:
[1] Autorzy: Tytuł, Wydawnictwo, Rok wydania
Jeżeli w dokumencie często występują listy numerowane lub punktowane można
dla każdej z nich stworzyć własny styl.
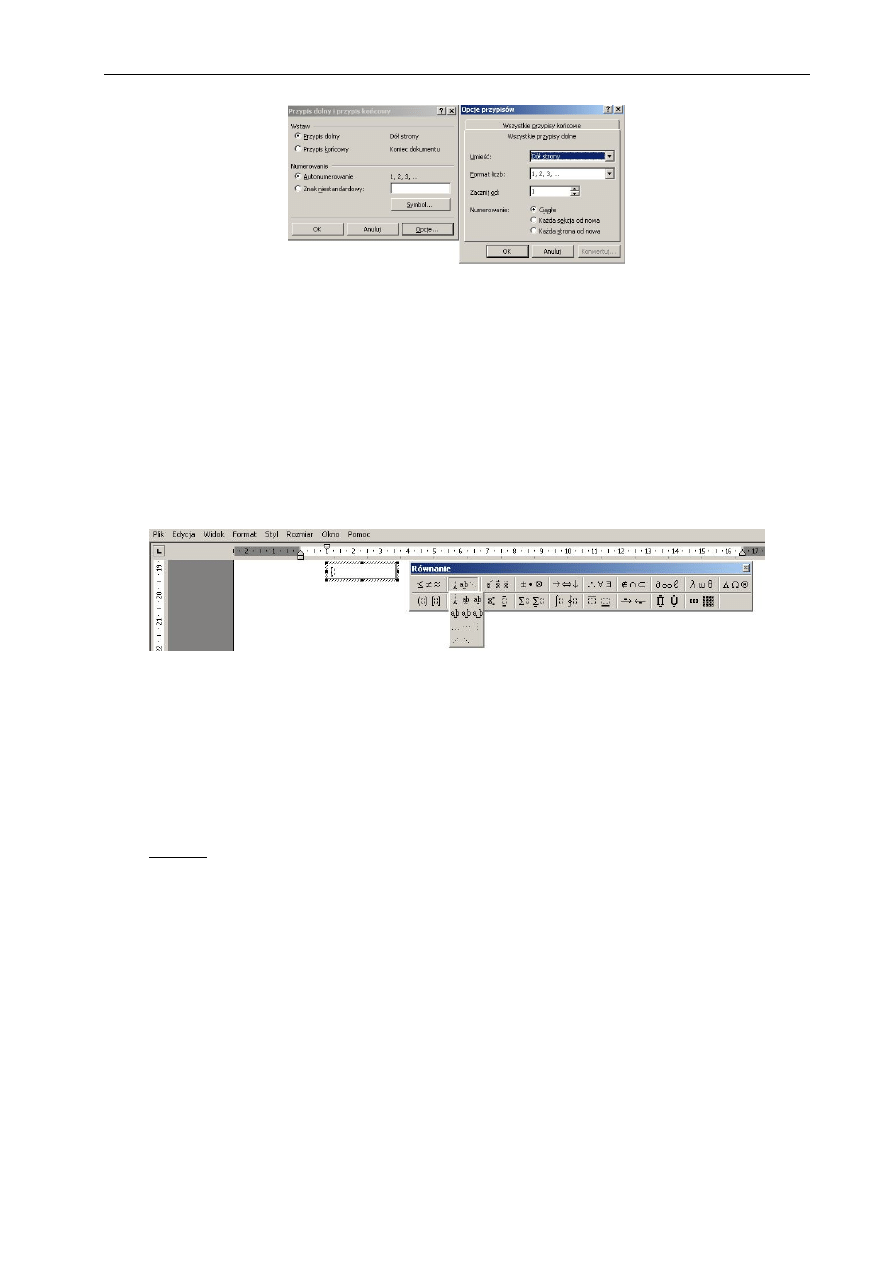
menu Wstaw polecenie Przypis
Przypis dolny lub końcowy służy do uzupełnienia informacji zawartych w tekście. Mogą to
być komentarze, wyjaśnienia albo odwołania do źródeł. Po umieszczeniu w wybranym miejscu
tekstu odnośnika przypisu dolnego (Wstaw – Odwołanie – Przypis dolny), na dole strony
pojawia się ten sam odnośnik po którym można wpisać tekst przypisu. W przypadku przypisu
końcowego odnośnik ten pojawia się na końcu dokumentu.
Technologia informacyjna - WORD
11
Rys. 1.8 Widok okna Przypis dolny i przypis końcowy oraz Opcje przypisów
1.1.2 Pisanie wzorów
W celu usprawnienia pracy z dokumentem można dołączyć do dowolnego paska narzędzi
ikony: Edytor równań, Wstaw symbol oraz Indeks górny i Indeks Dolny.
W edytorze równań dostępne są wszystkie znaki potrzebne do pisania wzorów
matematycznych a także istnieje możliwość wstawiania różnych odstępów między znakami.
Korzystając z menu edytora można również zmienić typ czcionki, jej format, styl i rozmiar.
Dokonane zmiany zostają zapisane w programie na stałe i podczas edycji równania jego styl jest
automatycznie zmieniany zgodnie z aktualnymi ustawieniami.
Rys. 1.9 Widok okna Edytora równań
Wszystkie wzory należy pisać w edytorze równań. Numeracja wzorów w dokumencie
powinna być zgodna z numeracją głównych nagłówków:
(numer_głównego_ nagłówka.numer_kolejny_wzoru)
Do ustalenia położenia numeru wzoru w wierszu należy wykorzystać prawy tabulator,
natomiast jako wartość położenia tabulatora można przyjąć szerokość strony bez marginesów.
Przykład
1
cos
sin
2
2
(3.11)
Można również zdefiniować styl umieszczania wzorów w dokumencie. Styl powinien
zawierać ustawienia z polecenia Akapit (Odstępy: Przed i Po) oraz z polecenia Tabulatory
(Położenie tabulatora - Wyrównanie: Do lewej (położenie wzoru); Do prawej (położenie
numeru wzoru)).
Do wzorów powinien być dołączony opis oznaczeń.
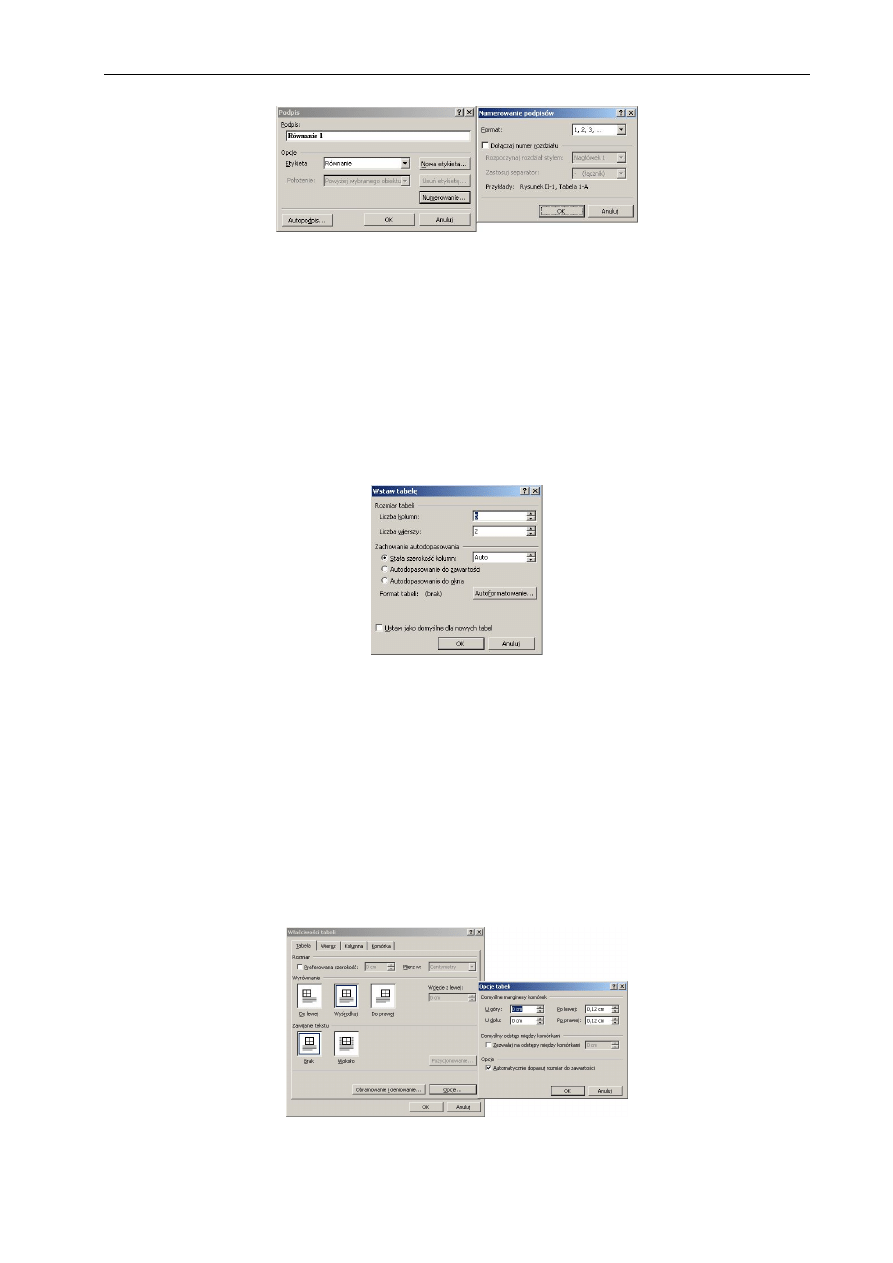
Można również umieścić w pracy spis wszystkich wymienionych w niej wzorów (tabel,
wykresów itp.). W tym celu należy każdy ze wzorów odpowiednio podpisać korzystając
ze standardowych podpisów dostępnych w programie Word (Wstaw – Odwołanie – Podpis).
Istnieje możliwość zamieszczenia własnej etykiety podpisu oraz dołączenia do numeru wzoru
numeru rozdziału.
Technologia informacyjna - WORD
12
Rys. 1.10 Widok okna Podpis i Numerowanie podpisów
Po podpisaniu wszystkich wzorów można wygenerować ich spis (Wstaw – Odwołanie –
Indeks i spisy – Spis ilustracji: Ogólne – Etykieta podpisu: wybrać odpowiednią etykietę).
1.1.3 Tabele
Tabela jest bardzo wygodną formą prezentacji danych umożliwiającą ich zwięzłe
i przejrzyste przedstawienie. Informacje umieszczane są w komórkach, których liczbę i sposób
rozmieszczenia można ustalić deklarując wymaganą ilość wierszy i kolumn tabeli (Tabela -
Wstaw – Tabela).
Rys. 1.11 Widok okna Wstaw tabelę
Wstawiona tabela jest automatycznie dopasowywana do szerokości strony co na wstępie
decyduje o szerokości kolumn. Z kolei początkowa wysokość wierszy we wstawionej tabeli
zależy od aktualnych ustawień w akapicie wiersza w którym tabela jest wstawiana (Akapit -
Odstępy: Przed i Po oraz Odstępy między wierszami).
Można zmieniać rozmiar tabeli dodając lub usuwając wiersze bądź kolumny (Tabela –
Wstaw: Kolumny w lewo, Kolumny do prawej, Wiersze powyżej, Wiersze poniżej) a także
zmieniać zarówno szerokość poszczególnych kolumn jak i wysokość wierszy (Tabela –
Właściwości tabeli: Wiersz, Kolumna). Wysokość i szerokość można także zmieniać
przesuwając odpowiednio myszą marginesy wierszy i kolumn.
Rys. 1.12 Widok okna Właściwości tabeli
Technologia informacyjna - WORD
13
W tabeli istnieje także możliwość scalania i dzielenia komórek (Tabela – Podziel komórki,
Scal komórki) a także podzielenia całej tabeli (Tabela – Podziel tabelę).
Można również ustalić położenie całej tabeli na stronie (Właściwości tabeli – Tabela:
Wyrównanie) i zmienić odpowiednio marginesy komórek (rys. 1.13).
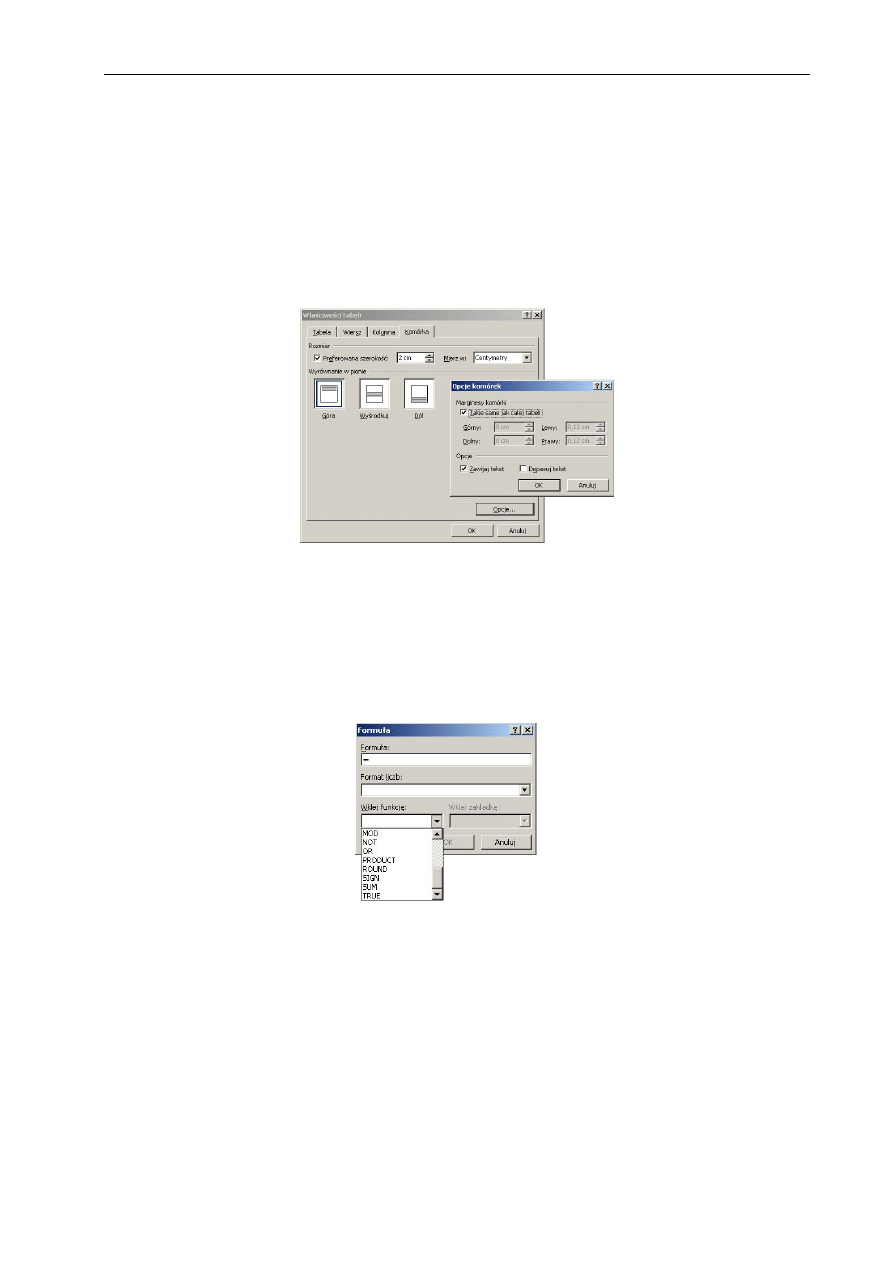
Ważną rzeczą jest także właściwe ustawienie i wyrównanie tekstu w poszczególnych
komórkach (Właściwości tabeli – Komórka: Wyrównanie w pionie). Istnieje możliwość
indywidualnego ustawienia wyrównania i marginesów dla pojedynczej komórki lub grupy
komórek (Właściwości tabeli – Komórka - Opcje komórek).
Rys. 1.13 Widok okna Właściwości tabeli i Opcje komórek
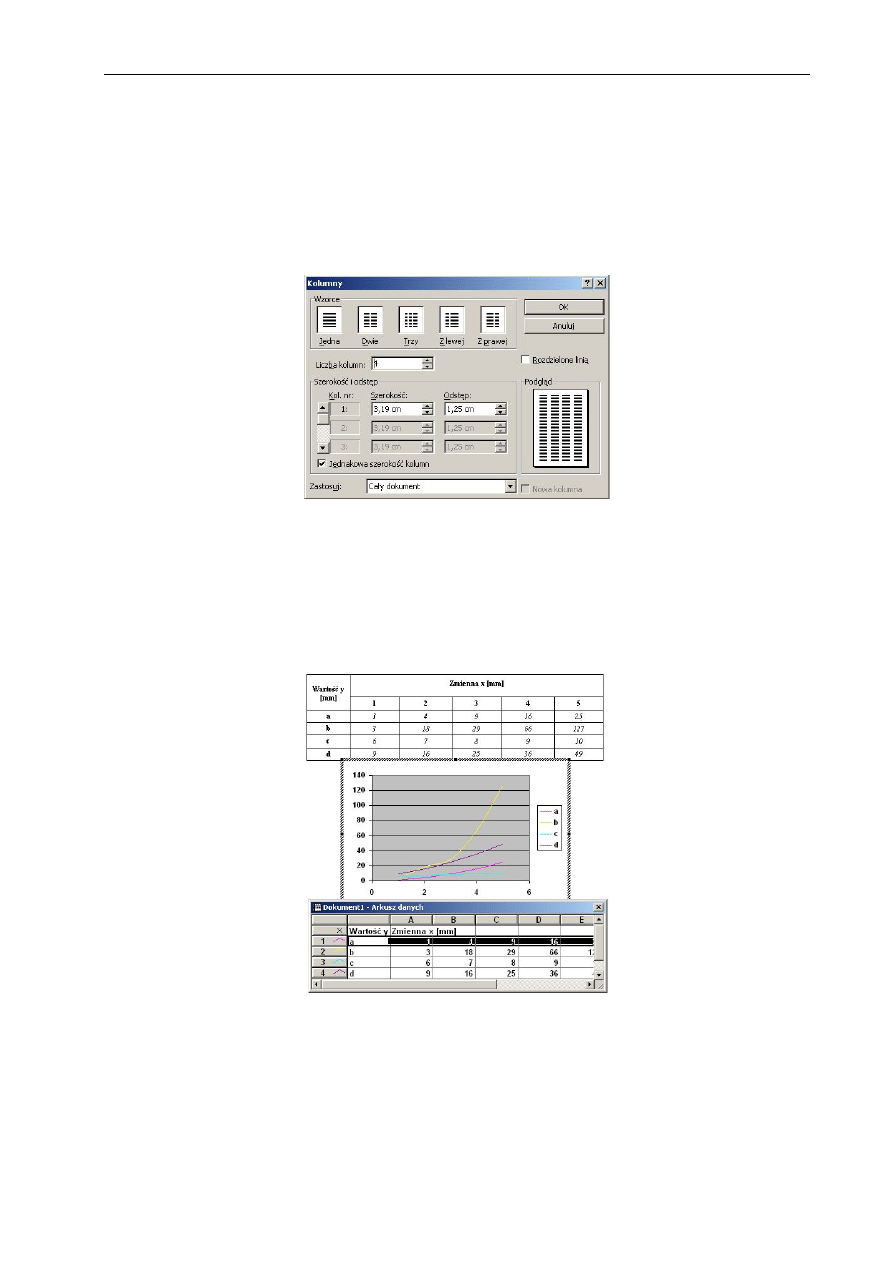
Tabulator dziesiętny, który określa położenie znaku oddzielającego część całkowitą
od części dziesiętnej, pozwala odpowiednio sformatować komórki zawierające dane w postaci
liczb rzeczywistych. Możliwe jest także wykonanie w tabeli podstawowych działań
matematycznych za pomocą funkcji dostępnych w oknie Formuła (Tabela – Formuła)
oraz odpowiednie posortowanie danych - okno Sortuj (Tabela – Sortuj).
Rys. 1.14 Widok okna Formuła
Dodanie odpowiedniego obramowania jest następnym elementem poprawiającym wygląd
tabeli a tym samym przejrzystość zawartych w niej danych..
Dane, które pooddzielane są jednakowymi separatorami można umieścić w tabeli (Tabela
– Konwertuj: Przekształć tekst na tabelę) a dane z tabeli daje się zamienić na tekst (Tabela –
Konwertuj: Przekształć tabelę na tekst).
Przeważnie w dokumencie tabele maja taki sam format, więc celowe jest zdefiniowanie
stylu dla tabel.
Technologia informacyjna - WORD
14
Numeracja tabel (tak jak równań, rysunków itp.) powinna być również zgodna
z numeracją głównego nagłówka. Podpis może być umieszczany pod albo nad tabelą.
numer_głównego_ nagłówka.numer_kolejny_tabeli Podpis tabeli
W Wordzie istnieje również możliwość stworzenia tekstu wielokolumnowego (Format –
Kolumny). Należy określić jedynie ilość kolumn i tekst zostanie automatycznie podzielony
na kolumny, które formatuje się tak samo jak tekst jednokolumnowy.
Rys. 1.15 Widok okna Kolumny
1.1.4 Wykresy
Do rysowania wykresów służy moduł Microsoft Graph (Wstaw – Obraz – Wykres).
Należy najpierw zaznaczyć tabelę z danymi na podstawie których ma być rysowany wykres
a następnie uruchomić rysowanie wykresu. Przykładowy wykres został pokazany poniżej.
Rys. 1.16 Widok przykładowego wykresu z tabelą danych
Można dowolnie modyfikować dane (znajdujące się w tabeli Arkusza danych) poprzez:
wpisanie innych wartości, zamianę osi na wykresie (wybierając z menu Dane inną kolejność
danych (Serie w wierszach, Serie w kolumnach)), dodanie ewentualnie usunięcie serii danych
Technologia informacyjna - WORD
15
(Dołącz wiersz/kolumnę, Odłącz wiersz/kolumnę). Również można dowolnie modyfikować sam
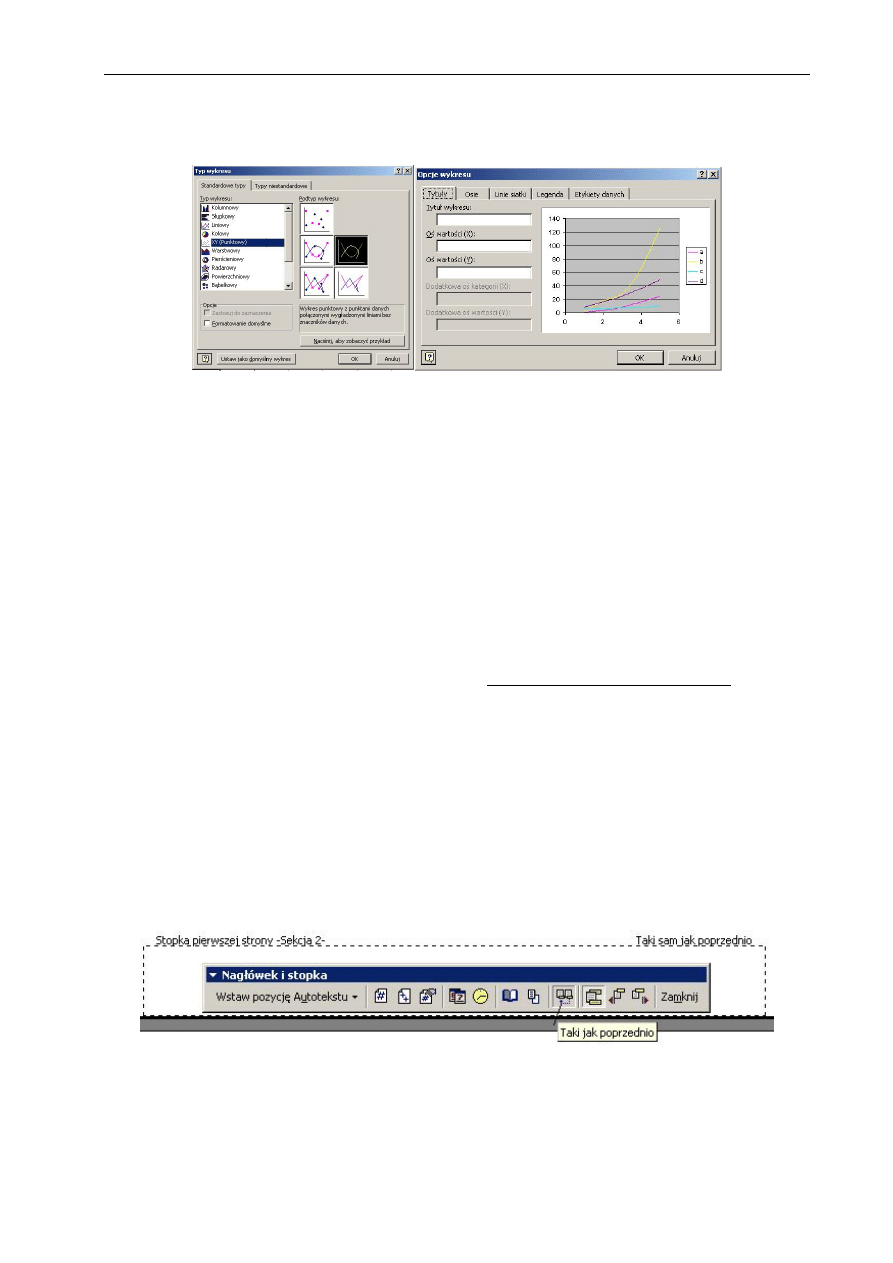
wykres tzn. np. jego typ, opcje (rys. 1.16), skalę, styl linii itp..
Rys. 1.17 Widok okna Typ wykresu oraz Opcje wykresu
W dużym dokumencie przydatne jest zdefiniowanie stylu podpisów pod rysunkami
i tabelami: Czcionka: Rozmiar, Akapit (Wyrównanie: i Odstępy: Przed i Po) a także stylu
rysunków: Akapit (Wyrównanie: i Odstępy: Przed i Po). Numeracja rysunków musi być zgodna
z numeracją głównego nagłówka a podpis powinien być umieszczany pod rysunkiem.
numer_głównego_ nagłówka.numer_kolejny_rysunku Podpis rysunku
1.2 Formatowanie dokumentu przed wydrukiem
1.2.1 Podział i numeracja stron
Każdy nagłówek główny powinien być umieszczony na nowej stronie. Aby dokonać
prawidłowo podziału strony należy ustawić kursor na początku nagłówka głównego i wstawić
znak podziału strony (Wstaw – Podział – Typy podziałów: Podział strony).
Jeżeli w dokumencie jedna strona lub kilka stron będzie miało inny format niż pozostałe
(np. marginesy lub orientację strony) to wówczas należy dokonać podziału dokumentu na sekcje
(Wstaw – Podział – Typy podziałów sekcji: Następna strona).
Podział sekcji należy wstawić również w przypadku, gdy strony będą różniły się
wyglądem nagłówka lub stopki. Aby móc dokonać zmian w wyglądzie nagłówka (stopki) trzeba
(po podziale na sekcje) odłączyć połączenie między sekcjami na stronie rozpoczynającej nową
sekcję. W tym celu należy przełączyć się do widoku nagłówka i stopki (Widok – Nagłówek
i stopka) i kliknąć wciśniętą ikonę Taki jak poprzednio (rys. 1.18). Powinien wówczas zniknąć
napis ”Taki sam jak poprzednio”, który jest widoczny na górze nagłówka oraz stopki.
Rys. 1.18 Widok okna Nagłówek i stopka oraz stopki strony
Numerację stron można wstawić korzystając z menu Wstaw – Numery stron. Wówczas
istnieje możliwość ustalenia położenia numeru, wyrównania, formatu liczb. (rys. 1.19).

Technologia informacyjna - WORD
16
Rys. 1.19 Widok okna Numery stron oraz Format numeru strony
Pasek Nagłówek i stopka pojawiający się w widoku Nagłówka i stopki umożliwia również
wstawianie numeracji stron (rys. 1.18 – pierwsza ikona od lewej strony). Będąc w tym widoku
można także dowolnie formatować czcionkę numeru oraz dodawać do niego dodatkowe
elementy (np. myślniki : –1–).
1.2.2 Tworzenie spisu treści
Spis treści przeważnie umieszczany jest na początku dokumentu. Należy wstawić nową
stronę, napisać tekst „Spis treści” i ustawić kursor w wierszu poniżej a następnie skorzystać
z menu Wstaw (Wstaw – Odwołanie – Indeks i spisy: Spis treści) W Wordzie spis treści jest
tworzony automatycznie na podstawie zdefiniowanych nagłówków, dlatego należy w oknie
Opcje spisu treści przypisać własne nagłówki do odpowiednich poziomów spisu treści
(nagłówek główny dokumentu – poziom 1). Pozostałe wybory należy wyczyścić (rys. 1.20).
Rys. 1.20 Widok okna Indeksy i spisy oraz Opcje spisu treści
Po stworzeniu spisu treści istnieje możliwość modyfikacji zarówno jego zawartości jak
i wyglądu. Treść modyfikowana jest automatycznie poprzez aktualizację całego spisu lub tylko
numeracji stron (okno Aktualizowanie spisu treści), natomiast zmiana wyglądu (przesuwanie
tekstu, zmiana czcionki itp.) może być wykonana w dowolnym miejscu ręcznie po wciśnięciu
klawisza Ctr.

Technologia informacyjna - WORD
17
2. Pakiet biurowy Worda
2.1 Szablony i formularze
Szablony (ćw. 4)
Szablon to szczególny typ dokumentu Worda (z rozszerzeniem „.dot”), który w momencie
otwierania tworzy własną kopię. W postaci szablonu zapisywane są pliki wymagające
zachowania specyficznych ustawień struktury i stylu. Przykładem takiego dokumentu może być
np. papier firmowy wykorzystywany w przedsiębiorstwie do korespondencji z klientami.
Rys. 2.1 Przykładowy papier firmowy
Wszystkie stałe elementy tekstowe papieru firmowego powinny być umieszczane
w nagłówku lub w stopce. Dodatkowe elementy graficzne (tak jak na rys.2.1) mogą zostać
dołączone poza marginesami bocznymi dokumentu. Przeważnie w nagłówku znajduje się logo
firmy i jej nazwa, natomiast w stopce dane kontaktowe: adres, telefon, fax, email.
Aby uatrakcyjnić wygląd papieru można dodać obramowanie strony, cieniowanie, wstawić znak
wodny itp..
Po zaprojektowaniu papieru firmowego należy go zapisać jako szablon (Word – szablon
dokumentu (*.dot)).
Formularze (ćw. 5)
Formularz jest typem dokumentu który można edytować tylko w określony sposób
i w określonych miejscach. Umieszcza się w nim specjalne pola z paska narzędzi Formularze
(Lista rozwijana, Pole wyboru, Pole tekstowe), w których użytkownik może dokonywać
odpowiednich zmian. Formularze są przeważnie wykorzystywane do przeprowadzania ankiet.
Najpierw należy na papierze firmowym zaprojektować cały formularz a następnie
uaktywnić pasek narzędzi Formularze i powstawiać odpowiednie pola w odpowiednie miejsca.
Dostępne pola:
Pole tekstowe – służy do wpisywania określonego rodzaju tekstu:
Tekst zwykły: dowolna kombinacja znaków z klawiatury
Liczba: tylko wartości liczbowe (można określić format)
Data: tylko data (można określić format)

Technologia informacyjna - WORD
18
Bieżąca data: aktualna data podana przez system komputera
Bieżąca godzina: aktualny czas systemowy komputera
Obliczenia: wykonuje obliczenia na podstawie podanych formuł
Pole wyboru – umożliwia odpowiedź poprzez zaznaczenie elementu lub nie
Lista rozwijana - umożliwia odpowiedź poprzez wybór z dostępnej listy
Po wstawieniu pola formularza należy odpowiednio zmienić jego właściwości (prawy
klawisz myszy albo dwukrotne kliknięcie na wybranym polu - Właściwości). Pojawi się
wówczas jedno z trzech widocznych poniżej okien.
Rys. 2.2 Okna opcji pól formularza
W Polu tekstowym należy wybrać odpowiedni typ i format pola oraz wpisać domyślną
wartość (np. Typ: Data, Format: yyyy-MM-dd, Domyślny tekst: 12-10-2011). W Polu wyboru
można zmienić rozmiar pola (np. 12 pt), natomiast do Listy rozwijanej należy dodać (za pomocą
dostępnych przycisków) odpowiedni tekst w postaci elementów, które mają być wybierane.
Na dole formularza można wstawić Pole tekstowe z ramką (zaznaczyć Pole tekstowe i wstawić
ramkę (Wstaw ramkę)) a następnie dodać ograniczenie długości tekstu (np. Długość
maksymalna: 100). Pole to będzie służyło do wpisywania uwag.
W skończonym formularzu należy wyłączyć cieniowanie pól (Cieniowanie pola
formularza) a następnie włączyć ochronę formularza (Chroń formularz). Formularz w takiej
postaci jest już gotowy do wypełnienia. Można go również wysłać drogą elektroniczną.
2.2 Korespondencja seryjna
2.2.1 Listy seryjne
Przygotować tabelę z danymi adresowymi zawierającą 10 rekordów.
L.p.
Tytuł
Imię
Nazwisko
Adres
Kod
Miasto
Kraj
Uwagi
1
Pani
Anna
Kowalska
ul. Mickiewicza 5 m. 12
73-241
Gdynia
Polska
K
...
10
Tab. 2.1 Dane adresowe
Na papierze firmowym napisać list do klienta i odpowiednio go sformatować. Jak wygląda
list profesjonalny można zobaczyć w szablonach Worda (Listy i faksy). Na górze dokumentu
zostawić jeden wiersz na dołączenie danych klienta (tytuł, imię, nazwisko). Dane klienta będą
wpisywane po lewej stronie. Napisać treść listu i zapisać go jako szablon.
Otworzyć kopię listu, będzie ona stanowiła dokument główny korespondencji seryjnej.

Technologia informacyjna - WORD
19
Tworzenie listów seryjnych:
wybrać polecenie Korespondencja seryjna (Narzędzia – Listy i dokumenty
wysyłkowe – Korespondencja seryjna)
krok 1: z okienka Korespondencja seryjna wybrać opcję Listy
krok 2: Dokument początkowy – Użyj bieżącego dokumentu
krok 3: Wybierz adresatów – Użyj istniejącej listy - Wybierz inną listę (odszukać
plik z danymi adresowymi)
pojawi się okno Adresaci korespondencji seryjnej z pełną listą adresatów, którą
można odpowiednio filtrować i sortować
po wybraniu adresatów zamknąć okno
krok 4: Napisz list - kliknąć polecenie Więcej elementów, pojawi się okno
Wstawianie pola korespondencji seryjnej
wstawić do listu następujące pola: Tytuł, Imię, Nazwisko; oddzielić je spacjami
i odpowiednio sformatować czcionkę
krok 5: Przejrzyj listy – następuje scalanie dokumentu głównego z wybranymi
rekordami źródła danych – pojawi się list do pierwszego adresata (można przejrzeć
kolejne listy)
krok 6: Ukończ scalanie, w sekcji Scal zaznaczyć Edytuj poszczególne listy –
pojawia się okno Scalanie z nowym dokumentem zaznaczyć Wszystko
zostaje stworzony nowy dokument złożony ze wszystkich listów
2.2.2 Etykiety adresowe
Etykiety adresowe umieszczane są na kopertach. Jest to etykieta odbiorcy oraz etykieta
nadawcy. Można skorzystać ze standardowych etykiet Worda lub zaprojektować własną etykietę
a następnie w podobny sposób jak w przypadku listów dołączyć adresatów korzystając ze źródła
danych adresowych.
Tworzenie etykiet odbiorcy:
otworzyć nowy dokument i wybrać polecenie Korespondencja seryjna (Narzędzia –
Listy i dokumenty wysyłkowe – Korespondencja seryjna)
krok 1: z okienka Korespondencja seryjna wybrać opcję Etykiety
krok 2: Dokument początkowy – wybrać Opcje etykiet: Nowa etykieta
(zaprojektować etykiety na papierze A4 o ilości 2x7)
nadać nazwę etykiecie i ustalić parametry:
(Margines górny: 0,2), (Margines boczny: 0), (Odstęp w pionie: 4,2),
(Odstęp w poziomie: 10,5), (Wysokość: 4,2), (Szerokość: 10,5),
(Liczba w poziomie: 2), (Liczba w pionie: 7)
krok 3: Wybierz adresatów – Użyj istniejącej listy - Wybierz inną listę (odszukać
plik z danymi adresowymi)
pojawi się okno Adresaci korespondencji seryjnej z pełną listą adresatów, którą
można odpowiednio filtrować i sortować

Technologia informacyjna - WORD
20
po wybraniu adresatów zamknąć okno
krok 4: Rozmieść dane na etykietach - kliknąć polecenie Więcej elementów, pojawi
się okno Wstawianie pola korespondencji seryjnej
wstawić do etykiety następujące pola rozdzielając je spacjami:
pierwszy wiersz: Tytuł, Imię, Nazwisko;
drugi wiersz : Adres
trzeci wiersz: Kod, Miasto
odpowiednio sformatować czcionkę i ustalić odstępy w akapicie
w grupie Etykiety zreplikowane kliknąć Aktualizuj wszystkie etykiety
(wstawione pola zostaną przekopiowane do pozostałych etykiet)
krok 5: Przejrzyj etykiety (pokazane zostaną gotowe etykiety)
krok 6: Ukończ scalanie (stworzony zostaje dokument gotowy do wydruku)
Tworzenie etykiet nadawcy:
otworzyć nowy dokument i wybrać polecenie Koperty i etykiety (Narzędzia – Listy
i dokumenty wysyłkowe – Koperty i etykiety) – Etykiety adresowe
w okienku Adres wpisać adres nadawcy i odpowiednio go sformatować
wcisnąć klawisz Opcje i w oknie Opcje etykiet wybrać zaprojektowaną
poprzednio etykietę
wcisnąć klawisz Nowy dokument - zostaje utworzona cała strona etykiet
adresowych nadawcy, które można wydrukować
2.3 Makra
Makra w Wordzie służą do usprawnienia obsługi dokumentu. Można nagrać czynności,
które trzeba wykonać np. podczas tworzenia specjalnie sformatowanej tabeli albo listów
seryjnych. Domyślnie makra zapisywane są pliku normal.dot dlatego w każdym dokumencie
Worda można je w razie potrzeby uruchomić korzystając z menu (Narzędzia – Makro – Makra)
lub z własnego paska narzędzi (opis tworzenia paska w p.3.2).
Przykład 1:
Uproszczone makro zmieniające kolor czcionki na niebieski oraz wygląd na pogrubiony (B),
kursywę (I), z podkreśleniem (U).
Makra dotyczące tekstu działają tylko na zaznaczonym fragmencie, podczas nagrywania takiego
makra również należy zaznaczyć dowolny fragment tekstu
.
Sub
czcionka()
With
Selection.Font
.Bold = True
.Italic = True
.Underline = wdUnderlineSingle
.Color = wdColorBlue
End With
End Sub
Przykład 2:
Uproszczone makro wstawiające tabelę (o określonej liczbie wierszy i kolumn) z odpowiednim
obramowaniem i formatowaniem czcionki.

Technologia informacyjna - WORD
21
Sub
tabela()
ActiveDocument.Tables.Add Range:=Selection.Range, _
NumRows:=InputBox("podaj liczbę _ wierszy"), _
‘pojawia się okienko dialogowe
NumColumns:=InputBox("podaj liczbę kolumn"), _
‘pojawia się okienko dialogowe
DefaultTableBehavior:=wdWord9TableBehavior, AutoFitBehavior:=FitFixed
Selection.Tables(1).Select
With
Selection.Tables(1)
With
.Borders(wdBorderLeft)
.LineWidth = wdLineWidth150pt
'szerokość lewej krawędzi obramowania
End With
With
.Borders(wdBorderRight)
.LineWidth = wdLineWidth150pt
'szerokość prawej krawędzi obramowania
End With
With
.Borders(wdBorderTop)
.LineWidth = wdLineWidth150pt
'szerokość górnej krawędzi obramowania
End With
With
.Borders(wdBorderBottom)
.LineWidth = wdLineWidth150pt
'szerokość dolnej krawędzi obramowania
End With
With
.Borders(wdBorderHorizontal)
.LineWidth = wdLineWidth075pt
'szerokość poziomych linii siatki
End With
With
.Borders(wdBorderVertical)
.LineWidth = wdLineWidth075pt
'szerokość pionowych linii siatki
End With
End With
Selection.Move Unit:=wdRow, Count:=-1
Selection.SelectRow
'zaznaczenie wiersza nagłówka tabeli
With
Selection.Cells
With
.Borders(wdBorderBottom)
.LineWidth = wdLineWidth150pt
'szerokość dolnej krawędzi nagłówka tabeli
End With
End With
Selection.Font.Bold = wdToggle
Selection.Tables(1).Select
'zaznaczenie tabeli
Selection.Rows.Height = CentimetersToPoints(0.8)
'wysokość wierszy w tabeli
Selection.Cells.VerticalAlignment = wdCellAlignVerticalCenter
'wyrównanie tekstu
With
Selection.Cells(1)
.WordWrap = True
'zawijanie tekstu w tabeli
End With
End Sub
Przykład 3:
Uproszczone makro tworzące listy seryjne do wszystkich adresatów zawartych w pliku źródłowym.
Sub
List_seryjny()
ActiveDocument.MailMerge.MainDocumentType = wdFormLetters
ActiveDocument.MailMerge.OpenDataSource Name:= _
"H:\Student\baza.doc"
‘wpisać ścieżkę do źródła danych
ActiveDocument.MailMerge.Fields.Add Range:=Selection.Range, Name:="Tytuł"
Selection.TypeText Text:=" "
‘spacja między wyrazami
ActiveDocument.MailMerge.Fields.Add Range:=Selection.Range, Name:="Imię_"
Selection.TypeText Text:=" "
‘spacja między wyrazami
ActiveDocument.MailMerge.Fields.Add Range:=Selection.Range, Name:="Nazwisko"
With
ActiveDocument.MailMerge
.Destination = wdSendToNewDocument
.SuppressBlankLines = True
.Execute Pause:=True
End With
End Sub

Technologia informacyjna - WORD
22
Ćwiczenia
1. Przepisać tekst odpowiednio go formatując (tekst.pdf).
2. Stworzyć stronę tytułową do laboratorium (strona.pdf).
3. Sformatować odpowiednio tekst (tekst1_format.doc, tekst2_format.pdf) [1].
4. Zaprojektować własny papier firmowy (papier_firmowy.pdf).
5. Stworzyć na papierze firmowym ankietę w formie formularza (ankieta.pdf).

Technologia informacyjna - EXCEL
23
EXCEL

Technologia informacyjna - EXCEL
24
3. Obliczenia w Excelu
Excel jest arkuszem kalkulacyjnym. Działania wykonywane są na wartościach zapisanych
w poszczególnych komórkach, dlatego bardzo ważne jest adresowanie komórek.
Format adresu zależy od ustawionego stylu odwołania (Narzędzia – Opcje - Ogólne).
Są dwa style odwołania:
W1K1 (wiersz kolumna) – adres komórki złożony jest z odpowiedniego numeru
wiersza i odpowiedniego numeru kolumny liczonych od lewego górnego rogu
arkusza
A1B1 – adres komórki złożony jest z literowego oznaczenia kolumny
i liczbowego oznaczenia wiersza
Niezależnie od wybranego stylu odwołania dostępne są trzy typy adresowania:
względne - A1, B1 (adres komórki zmienia się podczas dodawania lub usuwania
wierszy, kolumn, pojedynczych komórek lub grup komórek znajdujących się
na lewo bądź w górę od rozpatrywanej komórki)
bezwzględne - $A$1, $B$1 (adres komórki nie zmienia się nigdy)
mieszane - $A1, A$1, $B1, B$1 (zmienia się ta część adresu komórki, przed którą
nie ma znaku $)
Dodatkową możliwością adresowania jest nadawanie nazw poszczególnym komórkom
lub zakresom komórek.
Różnice w adresowaniu komórek
Przykład
1. Do komórki B2 wpisać 3 i wypełnić serią danych z krokiem 1 zakres komórek B2-B12
2. Do komórki C2 wpisać 2 i wypełnić serią danych z krokiem 2 zakres komórek C2-C12
3. Grupom komórek B2-B12 i C2-C12 nadać odpowiednio nazwy kol_B i kol_C
raz korzystając z polecenia paska narzędzi (Wstaw – Nazwę - Definiuj) i raz korzystając
z Pola Nazwy.
-
w Polu Nazwy można tylko nadawać nazwę, natomiast wszelkich zmian związanych
z nazwą należy dokonywać poprzez polecenie Wstaw – Nazwę – Definiuj
-
w nazwie mogą występować jedynie litery lub cyfry (bez spacji) bądź znak podkreślenia,
nazwa nie może rozpoczynać się od cyfry, nie może być pojedynczą literą K lub W bądź
też adresem np. D4
4. Grupy komórek D2-D12, E2-E12, F2-F12, G2-G12, H2-H12, I2-I12 wypełnić
następującymi formułami i przeanalizować otrzymane wyniki:
D2:
= B2
E2:
= $B$2
F2:
= $B2
G2: = B$2
H2: = B2*C2
I2:
= kol_B*kol_C
Wstawienie znaku $ przed nazwą kolumny lub numerem wiersza powoduje ustalenie tej
części adresu przed którą znak $ jest wstawiony, dzięki czemu nie zmienia się ona zarówno
podczas przeciągania formuły jak i kopiowania i wklejania jej w inne miejsce.
Technologia informacyjna - EXCEL
25
3.1 Pisanie formuł
Dużym ułatwieniem podczas pisania formuł, szczególnie w arkuszach zawierających dużo
obliczeń, jest stosowanie nazw zarówno w odniesieniu do pojedynczych komórek jak i grup
komórek arkusza. Dzięki wprowadzonym nazwom można o wiele szybciej zorientować się, jakie
operacje wykonywane są w poszczególnych częściach arkusza, można również łatwo odszukać
grupy komórek do których odwołują się formuły, ponadto arkusz staje się bardziej przejrzysty
i prostszy w obsłudze.
Kolejność wykonywania działań i operatory matematyczne:
1. potęgowanie
^
2. mnożenie
*
3. dzielenie
/
4. dodawanie
+
5. odejmowanie -
Składnia funkcji:
NAZWA_FUNKCJI(argument1; argument2; ....)
Argumentami mogą być:
dowolne adresy komórek zawierających odpowiednie dane:
np.: ŚREDNIA(A1;$B2;C$5;$D$7; E1:F8;zmienna;)
A1, $B2, C$5, $D$7, E1:F8, zmienna - adresy komórek
E1:F8 – grupa komórek
zmienna – nazwa komórki lub grupy komórek
liczby
np.: ŚREDNIA (12;15;7)
funkcje
np.: ŚREDNIA (SIN(15);COS(A7))
Podstawowe typy funkcji:
funkcje bazy danych – służą do analizy informacji zawartych w bazach danych
np. BD.POLE(baza;pole;kryteria) –
wydziela z bazy danych pole spełniające określone kryteria
funkcje daty i czasu - służą do wykonywania obliczeń na danych typu data,
godzina itp.
np. DZIŚ() –
podaje aktualną datę,
NETWORKDAYS(data_począt;data_końc.;święta) –
podaje ilość dni roboczych między
dwiema datami
Technologia informacyjna - EXCEL
26
funkcje inżynierskie – służą do obliczeń na liczbach zespolonych, konwersji liczb
między systemami, zamiany jednostek oraz umożliwiają obliczenia za pomocą
funkcji Bessela i Delta
np. DEC2BIN(liczba;miejsca)
–
zamienia liczbę dziesiętną na liczbę w kodzie dwójkowym
funkcje finansowe – służą do obliczania i analizy danych finansowych: odsetek,
amortyzacji, rat, itp.
np. PMT(stopa;liczba_rat;wa;wp;typ) –
oblicza wartość raty przy spłacaniu pożyczki przy stałych
ratach i stałym oprocentowaniu
funkcje logiczne – służą do konstruowania wyrażeń logicznych
np. JEŻELI (ORAZ(x>=-5;0;x<=5);x^2;25) –
przypisuje danym z przedziału <-5;5> wartości
x^2, natomiast danym spoza tego przedziału wartość 25
funkcje wyszukiwania i adresu – służą do wyszukiwania danych w tabelach
na podstawie adresu, uzyskiwania adresów określonych danych, tworzenia
odwołań, zamiany wierszy i kolumn tabeli ...
np. TRANSPONUJ(tablica) –
dokonuje zamiany wierszy i kolumn tabeli
funkcje matematyczne – służą do wykonywania obliczeń za pomocą
wbudowanych funkcji matematycznych (trygonometrycznych, logarytmicznych,
wykładniczych....)
np. EXP(liczba) –
oblicza wartość e ^liczba
MACIERZ.ILOCZYN(tablica1;tablicz2) –
wyznacza iloczyn dwóch macierzy
funkcje statystyczne – służą do wyznaczania wielkości statystycznych (średnich,
odchyleń standardowych, wariancji) oraz prawdopodobieństw i jego rozkładów
np. ODCH.KWADRATOWE(liczba1;liczba2;...)
– wyznacza sumę kwadratów odchyleń
punktów od średniej arytmetycznej z próbki
funkcje tekstowe – służą do manipulowania tekstem oraz zamiany danych
liczbowych na dane tekstowe
np. OCZYŚC(tekst) -
usuwa z tekstu wszystkie znaki, które nie mogą być drukowane
Przykłady
Każdy z przykładów należy rozwiązać w osobnym arkuszu
Przykład 1
Obliczyć długość przeciwprostokątnej i wielkość jednego z kątów trójkąta prostokątnego
o danych przyprostokątnych. Wprowadzić ograniczenie wynikające z faktu, że długość odcinka
nie może być zerem ani liczbą ujemną; w takim przypadku powinien pojawiać się komunikat
o treści „błąd”. Wykonać obliczenia (z krokiem równym 1) dla przyprostokątnych a i b
o długościach a <1; 10> i b <15; 25>

Technologia informacyjna - EXCEL
27
Rozwiązanie:
- do komórki A1 wpisać: a
- do komórki B1 wpisać: b
- do komórki C1 wpisać: c
- do komórki D1 wpisać: d
- zakres komórek A2-A11 wypełnić serią danych od 1 do 10 z krokiem 1:
(do komórki A2 wpisać 1, do komórki A3 wpisać 2, zaznaczyć komórki od A2
do A3 i przeciągnąć myszą po prawym marginesie do komórki A11)
- zakres komórek B2-B11 wypełnić serią danych od 15 do 25 z krokiem 1
- zaznaczyć cały obszar z danymi (Ctr+Shift+*)
- wstawić nazwy utworzone z górnego wiersza Wstaw – Nazwę – Utwórz - Górny
wiersz
- do komórki C2 wpisać formułę „=(a^2+b^2)^0,5” i przeciągnąć ją do komórek
z zakresu C3-C11; wyniki zaokrąglić do 4 miejsc po przecinku
- do
komórki
D2
wpisać
formułę
„=JEŻELI(LUB(a<=0;b<=0);"błąd";c)”
i przeciągnąć ją do komórek z zakresu C3-C11, wyniki zaokrąglić do 3 miejsc
po przecinku
Przykład 2
Wykorzystując formuły narysować wykres funkcji sinus w przedziale <0; 180
0
>. Wartości
kąta wprowadzić z krokiem równym 10
0
.
Rozwiązanie:
- do komórki A1 wpisać: alfa
- do komórki B1 wpisać: sinus
- do komórki A2 wpisać 0 i wypełnić serią danych odpowiedni zakres komórek
Edycja - Wypełnij - Serie Danych (Serie Kolumny, Typ Arytmetyczny, Wartość
kroku: 10, Wartość końcowa: 180)
- zaznaczyć cały obszar z danymi (Ctr+Shift+*)
- wstawić nazwy utworzone z górnego wiersza Wstaw – Nazwę – Utwórz - Górny
wiersz
- do komórki B2 wpisać formułę „=SIN(alfa*PI()/180)” i przeciągnąć ją
do pozostałych komórek
- zaznaczyć cały obszar z danymi (Ctr+Shift+*) i za pomocą Kreatora wykresów
narysować wykres punktowy
-
sformatować odpowiednio wykres
y = sin()
0
0,2
0,4
0,6
0,8
1
1,2
0
30
60
90
120
150
180
210
y
Rys. 3.1 Wykres funkcji sinus
Technologia informacyjna - EXCEL
28
Przykład 3
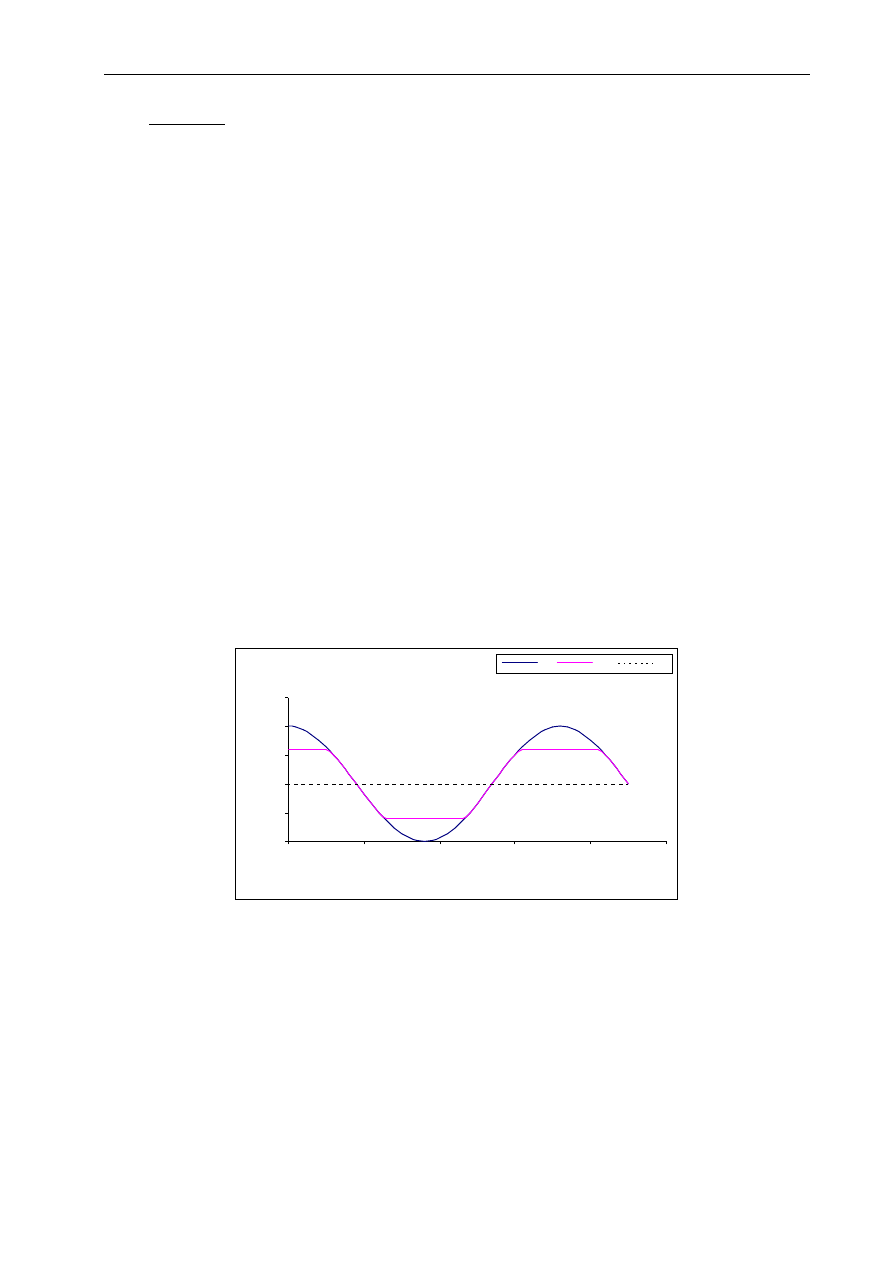
Narysować wykres funkcji y = cos + 1 w przedziale <0; 450
0
> z następującym
ograniczeniem: y <0,4; 1,6> . Wartości kąta wprowadzić z krokiem równym 10
0
.
Rozwiązanie:
- do komórki A1 wpisać: beta
- do komórki B1 wpisać: y
- do komórki C1 wpisać: y1
- do komórki A2 wpisać 0 i wypełnić serią danych odpowiedni zakres komórek
- zaznaczyć cały obszar z danymi (Ctr+Shift+*)
- wstawić nazwy utworzone z górnego wiersza Wstaw – Nazwę – Utwórz - Górny
wiersz
- do komórki B2 wpisać formułę „=COS(beta*PI()/180)+1” i przeciągnąć ją
do pozostałych komórek
- do komórki C2 wpisać formułę:
„=JEŻELI(ORAZ(y>0,4;y<1,6);y;JEŻELI(y<0,4;0,4;1,6))”
i
przeciągnąć
ją
do pozostałych komórek
- do komórki D1 wpisać: oś
- zakres komórek D2-D47 wypełnić wartością 1 (seria danych dla sztucznej osi)
- zaznaczyć cały obszar z danymi (Ctr+Shift+*) i za pomocą Kreatora wykresów
narysować wykres punktowy
- sformatować odpowiednio wykres
w yk res funkcji y = cos (beta)+1
0
0,5
1
1,5
2
2,5
0
100
200
300
400
500
be ta
y, y1
y
y1
oś
Rys. 3.2 Wykres funkcji cos+1
3.2 Makra
Makra służą do automatyzacji pracy z dokumentami Microsoft Office. Można nagrać
powtarzające się czynności, które są niezbędne do obsługi np. skoroszytu Excela. Zarejestrowane
makro zapisywane jest w języku VBA i umieszczane w module, który dostępny jest w oknie
Microsoft Visual Basic. Okno to można otworzyć za pomocą ikony Edytor Visual Basic,
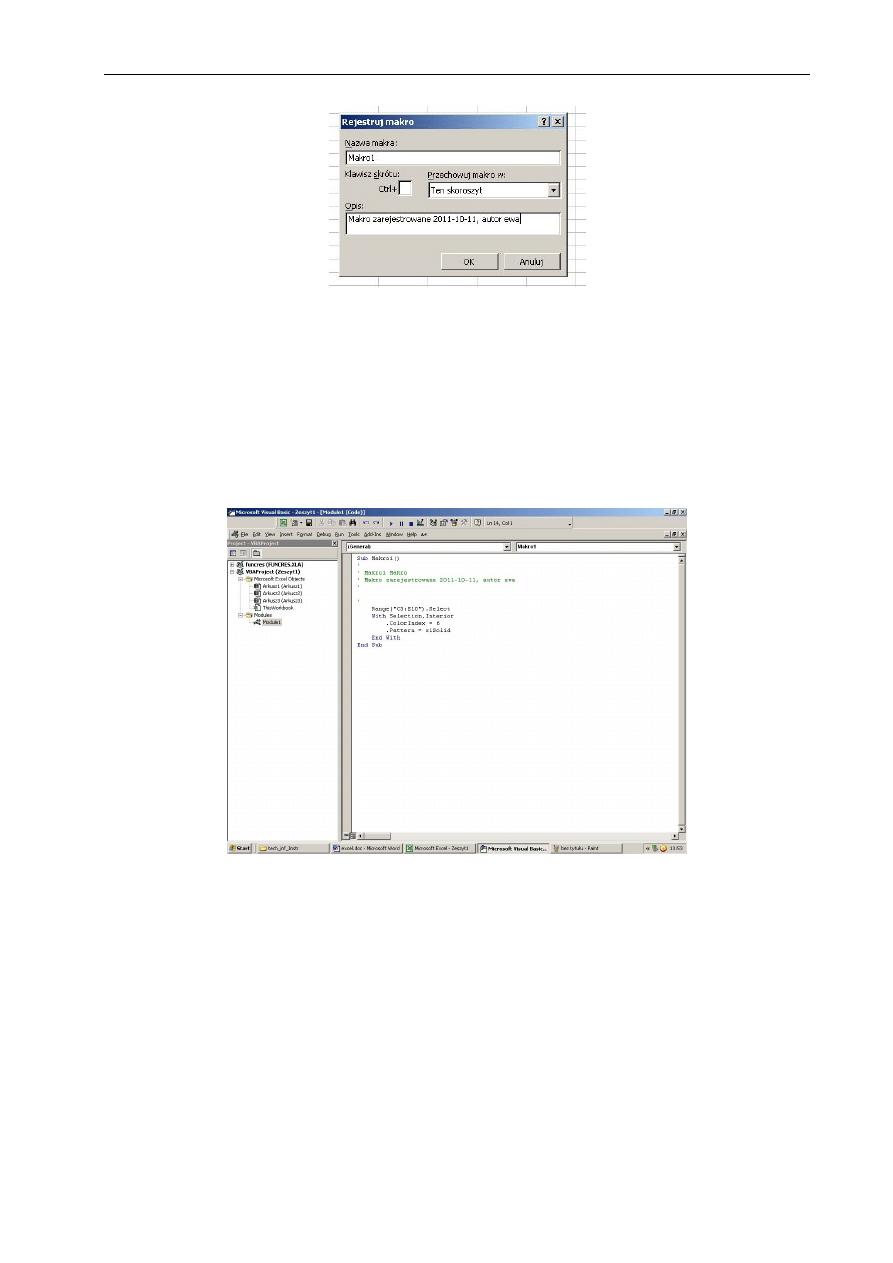
dostępnej na pasku narzędzi Visual Basic. Rejestracja makra rozpoczyna się po wciśnięciu ikony
Zarejestruj makro, pojawia się wówczas następujące okno:
Technologia informacyjna - EXCEL
29
Rys. 3.3 Okno Rejestruj makro
Można zmienić nazwę makra (w nazwie nie może być spacji), dodać klawisz skrótu
za pomocą którego będzie można go uruchamiać (Ctr+Shift+dowolny znak z klawiatury),
zmienić miejsce przechowywania. W większości przypadków makra przechowywane są
w aktualnym skoroszycie (Ten skoroszyt).
Po zarejestrowaniu makra można go dostosować do własnych potrzeb modyfikując
odpowiednio jego kod. Okno Microsoft Visual Basic z zarejestrowanym makrem zmieniającym
na żółty kolor wypełnienia komórek z zakresu C3:E10 wygląda następująco:
Rys. 3.4 Okno Microsoft Visual Basic
Sub Nazwa_makra() i End Sub są to słowa kluczowe pomiędzy którymi znajduje się
zapisany kod makra. Po apostrofach można dodawać dowolne komentarze, w tym przypadku są
to nagrane w czasie rejestracji informacje na temat makra. W module można również
dokonywać wszelkich zmian w kodzie makra. Pokazane powyżej makro można zmodyfikować
następująco:
Sub
kolor_wypełnienia()
'zmienia na żółty kolor wypełnienia dowolnej zaznaczonej grupy komórek
With
Selection.Interior
.ColorIndex = 6
End With
End Sub

Technologia informacyjna - EXCEL
30
W nazwie makra można używać polskich liter, jednak w ogólnym przypadku nie jest to
zalecane.
Zarejestrowane makro można uruchomić na kilka sposobów:
korzystając z paska narzędzi Visual Basic – ikona Uruchom makro
korzystając z menu Narzędzia – Makro – Makra – Uruchom
dodając własny pasek narzędzi oraz ikonę do uruchamiania makra;
- dodawanie i usuwanie pasków narzędzi i przycisków oraz ich edycja dokonywane są
w trybie Dostosuj (prawy klawisz myszy na menu Dostosuj):
dodawanie nowego paska narzędzi: Paski narzędzi - Nowy – Nowy pasek
narzędzi (zmienić nazwę na swoją i przeciągnąć pasek do menu);
dodawanie przycisku do paska narzędzi: Polecenia – Makra – Przycisk
niestandardowy (przeciągnąć przycisk do stworzonego paska narzędzi);
przypisać makro do przycisku, zmienić nazwę i obraz przycisku (prawy klawisz:
Przypisz makro, Obraz i tekst, Zmień obraz przycisku, Edytuj obraz przycisku)
dodając do arkusza dowolny Autokształt i przypisując do niego makro (prawy klawisz:
Przypisz makro),
po przypisaniu makra do Autokształtu można go edytować wciskając przycisk Ctr
Pasek narzędzi wraz z ikoną służącą do uruchamiania makra oraz Autokształt
z przypisanym makrem mogą wyglądać następująco:
zmiana koloru
wypełnienia
Rys. 3.5 Uruchamianie makra – pasek narzędzi z przyciskiem i Autokształt
3.2.1 Projekt arkusza obliczeniowego
Zaprojektować poniższy arkusz wraz z następującymi obliczeniami:
1. Rozwiązanie równania kwadratowego:
-
nazwać komórki: A2 jako a, B2 jako b, C2 jako c, A5 jako delta, B5 jako pierw1,
C5 jako pierw2, F2 jako start i zakresy komórek A9:A34 jako x, B9:B34 jako y
-
wstawić kolejno komentarze do komórek A2; B2; C2 (Podaj wartość
współczynnika a; Podaj wartość współczynnika b, ....)
-
wstawić komentarz do komórki F2 (Podaj początek przedziału dla zmiennej x)
-
wpisać odpowiednie formuły do komórek:
A5: „=JEŻELI(a<>0;b^2-4*a*c;"")”
B5: „=JEŻELI(a=0;JEŻELI(b=0;JEŻELI(c=0;"równanie tożsamościowe";
"równanie sprzeczne");-c/b);JEŻELI(delta>=0;(-b-delta^1/2)/(2*a);"brak
rozwiązania"))”,
C5 – analogicznie jak B5
-
zmieniając wartości a, b, c zaobserwować wyniki: delta, pierw1 i pierw2
-
wypełnić serią danych zakres komórek A9:A34
-
do komórek B9:C34 wpisać formułę: „=a*x^2+b*x+c”

Technologia informacyjna - EXCEL
31
Rys. 3.6 Widok arkusza obliczeniowego
2. Rysowanie wykresu na podstawie danych z tabeli
-
zaznaczyć obszar B9:B34 i narysować wykres punktowy
3. Nagranie i uproszczenie makra:
-
uaktywnić pasek narzędzi Visual Basic
-
zarejestrować nowe makro, które wypełnia kolumnę x serią danych z krokiem 1
zmienić nazwę makra na seria_danych, umieścić makro w aktualnym
skoroszycie, ustalić klawisz skrótu
-
uprościć następująco zarejestrowane makro:
Sub
seria_danych()
Range("x").DataSeries Rowcol:=xlColumns, Type:=xlLinear, _
Step:=InputBox("podaj krok")
End Sub
-
umieścić w arkuszu dowolny Autokształt (naciskając prawy klawisz myszy
odpowiednio go sformatować i dodać tekst) a następnie przypisać do niego makro
(prawy klawisz: Przypisz makro)
-
wkleić łącze pomiędzy komórką F2 i komórką A9
-
wpisać nową wartość do komórki F2 i uruchomić makro
3.3 Rysowanie wykresów
3.3.1 Wykresy o zwiększonej liczbie osi
W przypadku konieczności umieszczenia na jednym wykresie kilku serii danych
o znacznie różniących się wartościach istnieje możliwość dodania do wykresu jednej dodatkowej
osi a także można stworzyć własną oś. Przykładowe rozwiązanie zostało przedstawione poniżej.
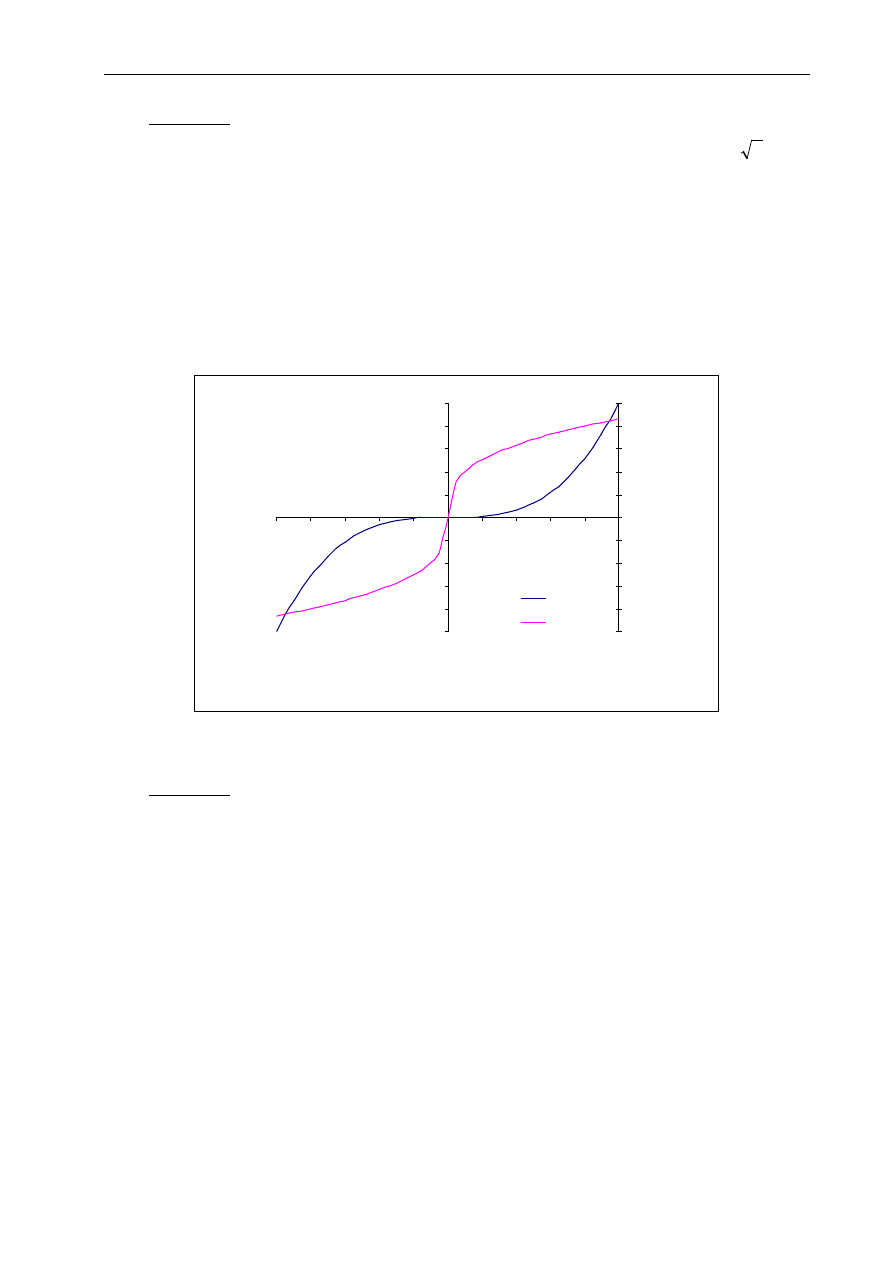
Technologia informacyjna - EXCEL
32
Przykład 1:
W jednym układzie współrzędnych zamieścić wykresy funkcji
3
1
x
y
i
3
2
x
01
,
0
y
dla
10
;
10
x
z krokiem 0,5.
Rozwiązanie:
-
wypełnić serią danych (z przedziału <-10; 10>, z krokiem 0,5) wybrany zakres
komórek i nazwać go jako x
-
w kolumnach obok wpisać odpowiednie formuły dla y
1
= f(x) i y
2
= f(x)
-
zaznaczyć cały obszar z danymi (Ctr+Shift+*) i za pomocą Kreatora wykresów
narysować wykres punktowy
-
dodać dodatkową oś y (Wykres - Opcje wykresu - Osie - Oś wartości (y))
Wykresy funkcji y
1
=x^3 i y
2
=0,01x^1/3
-1000
-800
-600
-400
-200
0
200
400
600
800
1000
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
y
1
-0,025
-0,02
-0,015
-0,01
-0,005
0
0,005
0,01
0,015
0,02
0,025
y
2
y1
y2
Rys. 3.7 Wykresy funkcji y
1
i y
2
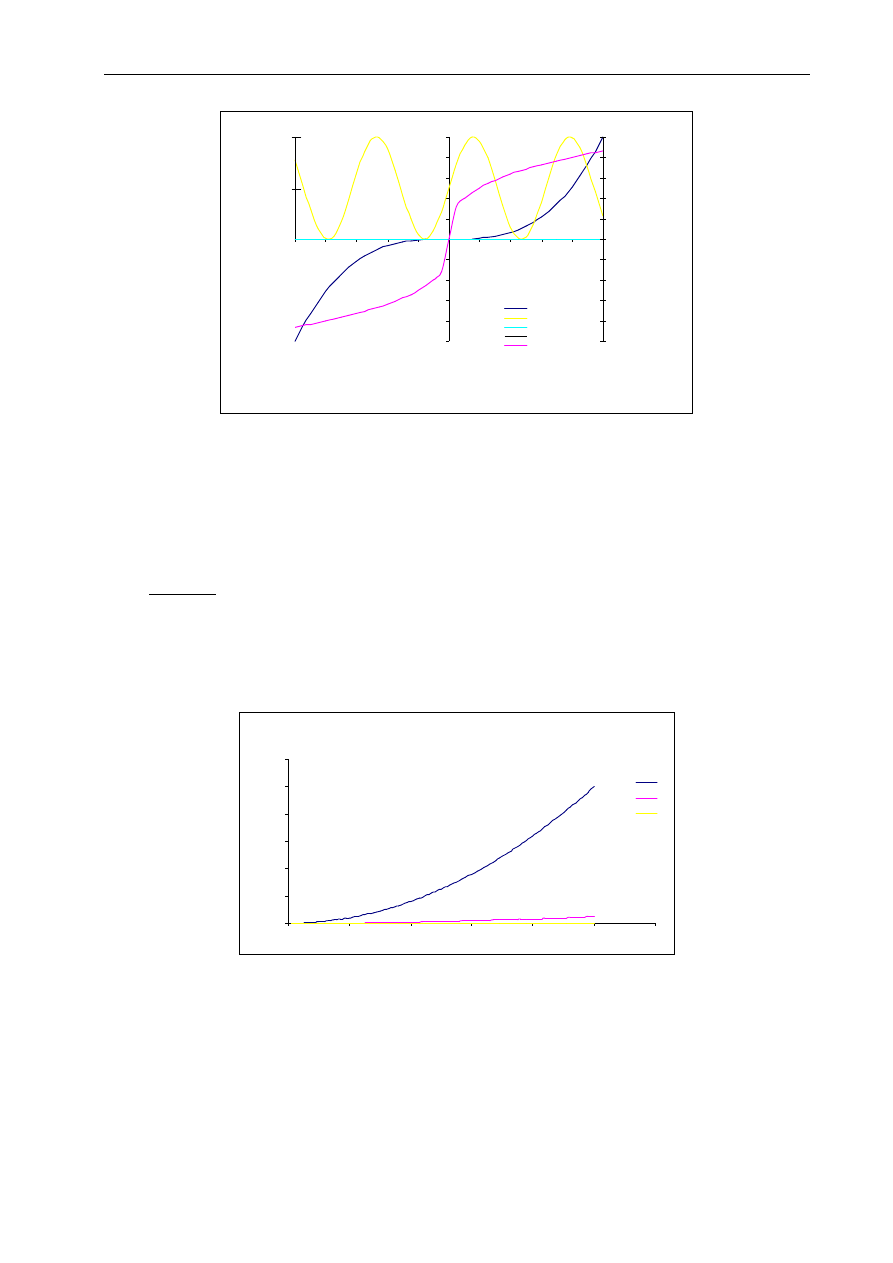
Przykład 2:
Na powyższym wykresie zamieścić dodatkowo wykres funkcji y
3
= sin(x) +1
Rozwiązanie:
-
stworzyć serię danych dla wartości y
3
-
przeskalować y
3
mnożąc przez odpowiednią liczbę taką, aby nowe wartości były
rzędu liczb na osi y
1
(np. przez 500), czyli dodać nową serię danych dla funkcji y
3
:
y
3
* 500
-
stworzyć sztuczną oś podając współrzędne dwóch jej punktów krańcowych
(-10, 0) i (-10, 1000)
-
dołączyć do wykresu serie danych y
3
i y
3
*500 oraz oś (Dane źródłowe – Serie –
Dodaj: Nazwa (np. y3), Wartości X (zaznaczyć odpowiedni zakres danych),
Wartości Y (zaznaczyć odpowiedni zakres danych))
-
dodać pola tekstowe zawierające opis sztucznej osi i jej skalę oraz dwie poziome
kreski oznaczające podziałkę skali na nowej osi
Technologia informacyjna - EXCEL
33
Wykresy funkcji y
1
=x^3, y
2
=0,01x^1/3 i y
3
=sin(x)+1
-1000
-800
-600
-400
-200
0
200
400
600
800
1000
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
y
1
-0,025
-0,02
-0,015
-0,01
-0,005
0
0,005
0,01
0,015
0,02
0,025
y
2
y1
y3*500
y3
oś
y2
2
y
3
1
0
Rys. 3.8 Wykresy funkcji y
1,
y
2
i y
3
3.3.2 Skala logarytmiczna
Skalę logarytmiczną stosuje się w przypadku, gdy występują znaczne różnice pomiędzy
wartościami serii danych, które mają zostać umieszczone na wspólnym wykresie.
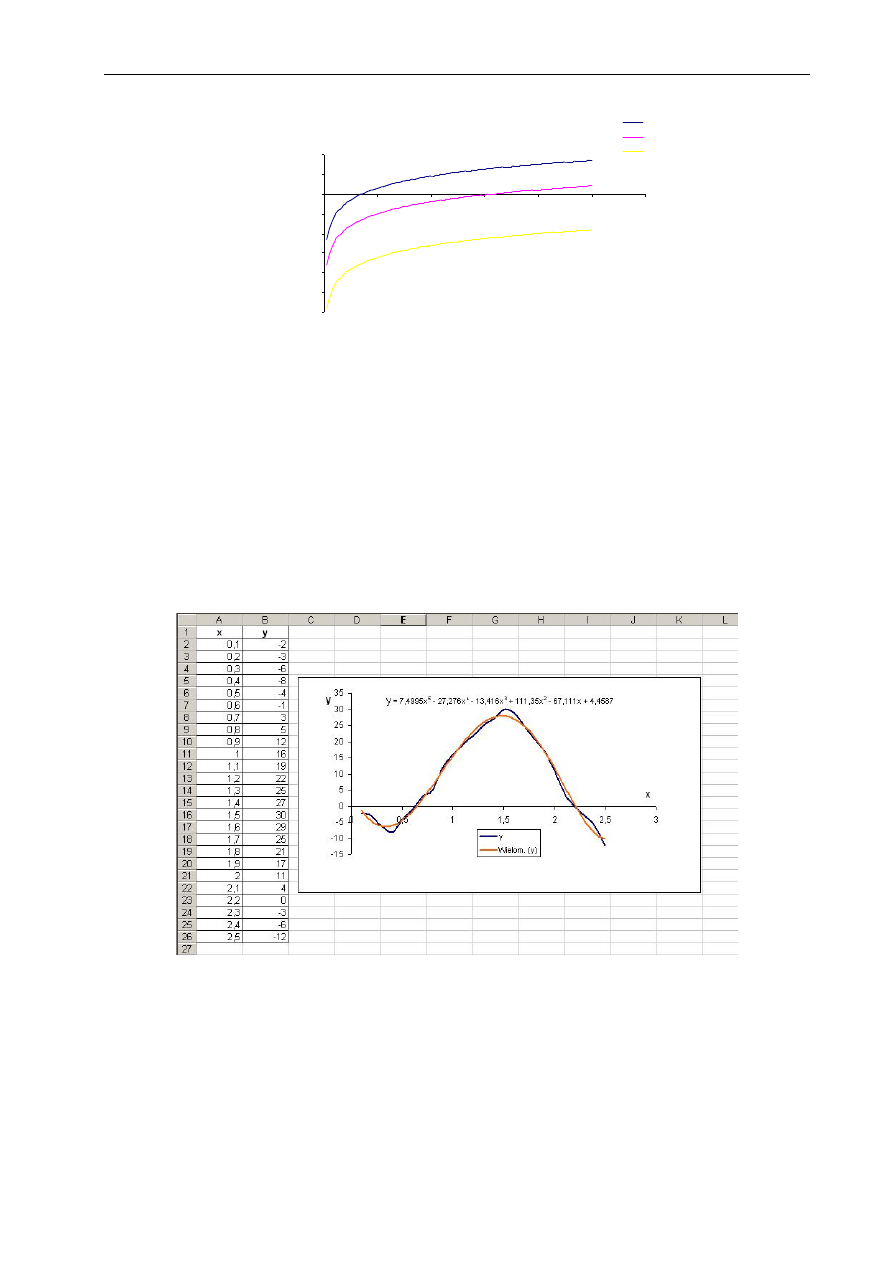
Przykład:
Narysować wykresy następujących funkcji:
2
3
2
2
2
1
t
00015
,
0
s
,
t
025
,
0
s
,
t
5
,
0
s
w przedziale
10
;
1
,
0
t
z krokiem 0,1.
Rozwiązanie:
Wykres funkcji s=f(t)
0
10
20
30
40
50
60
0
2
4
6
8
10
12
t
s
s1
s2
s3
Rys. 3.9 Wykresy funkcji s = f(t)
Ponieważ krzywe s
2
i s
3
są słabo widoczne na wykresie, należy zastosować skalę
logarytmiczną na osi s. Zmiana rodzaju skali powoduje zmianę charakteru przebiegu krzywych,
dlatego stosuje się ją w przypadku, gdy wyłącznie zależy nam na uwidocznieniu różnic
w wartościach poszczególnych krzywych.
Technologia informacyjna - EXCEL
34
Wykres funkcji s=f(t)
0,000001
0,00001
0,0001
0,001
0,01
0,1
1
10
100
0
2
4
6
8
10
12
t
s
s1
s2
s3
Rys. 3.10 Wykresy funkcji s = f(t) w skali logarytmicznej na osi s
3.3.3 Linia trendu
W przypadku, gdy mamy do czynienia np. z wynikami pomiarów, które należy oszacować
przybliżając je za pomocą znanych funkcji matematycznych, można wykorzystać dostępną
w arkuszu linię trendu (Wykres – Dodaj linię trendu). Linia trendu, która oparta jest
na metodach interpolacji i aproksymacji, umożliwia przybliżenie danego przebiegu
za pomocą: wielomianu określonego stopnia, funkcji liniowej, logarytmicznej, wykładniczej,
potęgowej oraz średniej ruchomej. W poniższym przykładzie dokonano przybliżenia serii
danych widocznych w tabeli wielomianem 5-go stopnia, którego wzór został wyświetlony
na wykresie (Wykres – Dodaj linię trendu – Opcje – Wyświetl równanie na wykresie).
Rys. 3.11 Wykres funkcji z linią trendu
Technologia informacyjna - EXCEL
35
3.3.4 Wykresy powierzchniowe
Aby narysować wykres powierzchniowy funkcji dwóch zmiennych z = f(x, y)
dla argumentów z przedziałów
2
1
2
1
y
,
y
y
,
x
,
x
x
należy stworzyć tablicę wartości.
W pierwszej kolumnie tablicy w kolejnych wierszach umieścić serię danych dla zmiennej x,
natomiast w pierwszym wierszu w kolejnych kolumnach serię danych dla zmiennej y. Wewnątrz
utworzonego obszaru tablicy należy wprowadzić formułę określającą funkcję.
Przykład:
Narysować wykres powierzchniowy dla funkcji
6
u
v
sin
u
v
,
u
f
2
,
1
;
4
,
4
v
1
,
1
;
3
,
0
u
Rozwiązanie:
-
zakres komórek A3:A43 wypełnić serią danych z przedziału <0,3; 1,1> z krokiem
0,02 i nazwać jako u
-
zakres komórek B2:AD2 wypełnić serią danych z przedziału <-4,4; 1,2>
z krokiem 0,2 i nazwać jako v
-
zakres komórek B3:AD43 wypełnić formułą: „=u^(1/2)*SIN(v/u-PI()/6)”
-
zaznaczyć cały obszar (Ctr+Shift+*) i narysować wykres powierzchniowy
0,3
0,44
0,58
0,72
0,86
1
-4
,4
-3
,4
-2
,4
-1
,4
-0
,4
0
,6
-1,5
-1
-0,5
0
0,5
1
1,5
f(u,v)
u
v
Rys. 3.12 Wykres funkcji f(u,v)
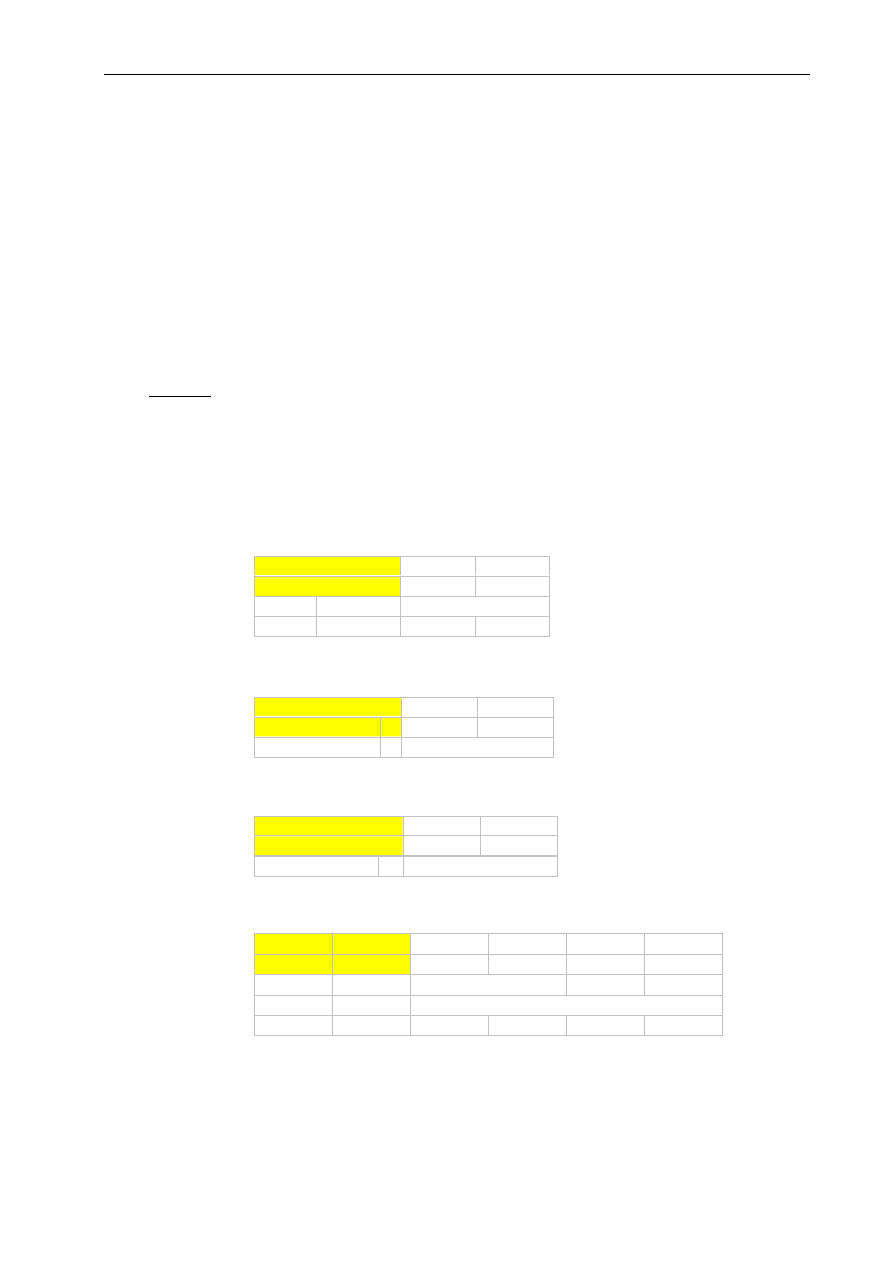
Technologia informacyjna - EXCEL
36
4. Wybrane funkcje programu Excel
4.1 Funkcje inżynierskie – liczby zespolone
Jedną z grup funkcji inżynierskich dostępnych w programie Excel stanowią funkcje
umożliwiające wykonywanie działań na liczbach zespolonych. Liczbę zespoloną deklaruje się
za pomocą funkcji COMPLEX, której argumentami są: część rzeczywista i część urojona liczby.
Wszystkie funkcje dotyczące wykonywania działań na liczbach zespolonych mają w nazwie
przedrostek IM (np. IMABS, IMSUM, IMDIV ..).
W poniższym przykładzie zostały przedstawione podstawowe funkcje dotyczące liczb
zespolonych zawarte w Excelu. W celu udostępnienia użytkownikowi funkcji inżynierskich
należy zainstalować dodatek Analysis ToolPak (Narzędzia – Dodatki).
Przykład
Zadeklarować dwie liczby zespolone a oraz b (a = 2+3i, b = 4-7i) i wykonać na nich
podstawowe działania matematyczne wykorzystując funkcje Excela i wzory matematyczne.
Rozwiązanie:
-
deklaracja liczby zespolonej (nazwać komórki w których wyznaczane są liczby
zespolone jako a i b)
-
część rzeczywista liczby zespolonej (nazwać wynikową komórkę jako Re_a)
-
część urojona liczby zespolonej (nazwać wynikową komórkę jako Im_a)
-
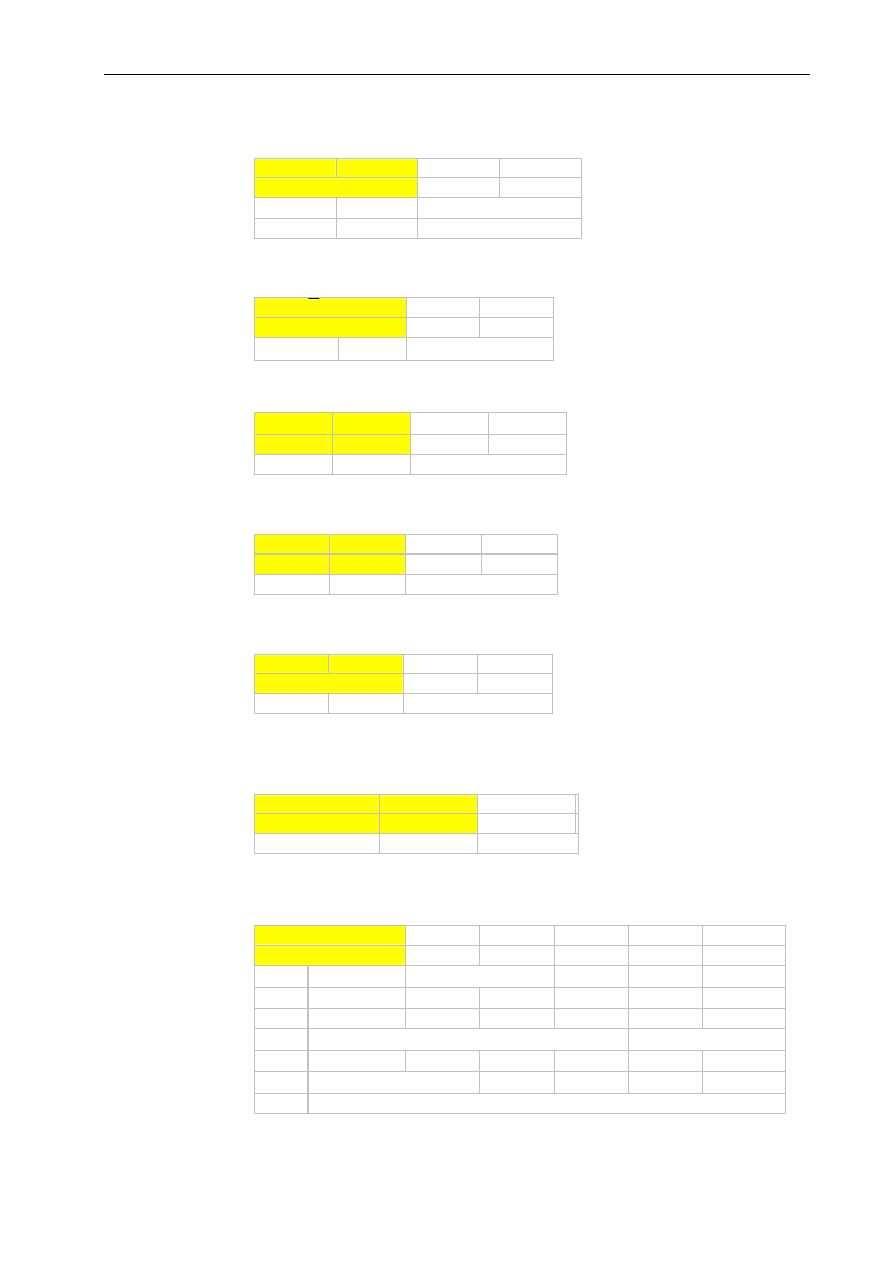
moduł liczby zespolonej
liczba zespolona
COMPLEX
a = 2+3i
=COMPLEX(2;3)
b = 4-7i
część rzeczywista
IMREAL
Re(a) =2 =IMREAL(a)
część urojona
IMAGINARY
Im(a) =3 =IMAGINARY(a)
moduł
IMABS
|a| =
3,605551 =IMABS(a)
|a| =
3,605551 =PIERWIASTEK(Re_a^2+Im_a^2)
|b| =
8,062258
Technologia informacyjna - EXCEL
37
-
argument liczby zespolonej
-
liczba sprzężona
-
suma
-
różnica
-
iloczyn
-
iloraz
-
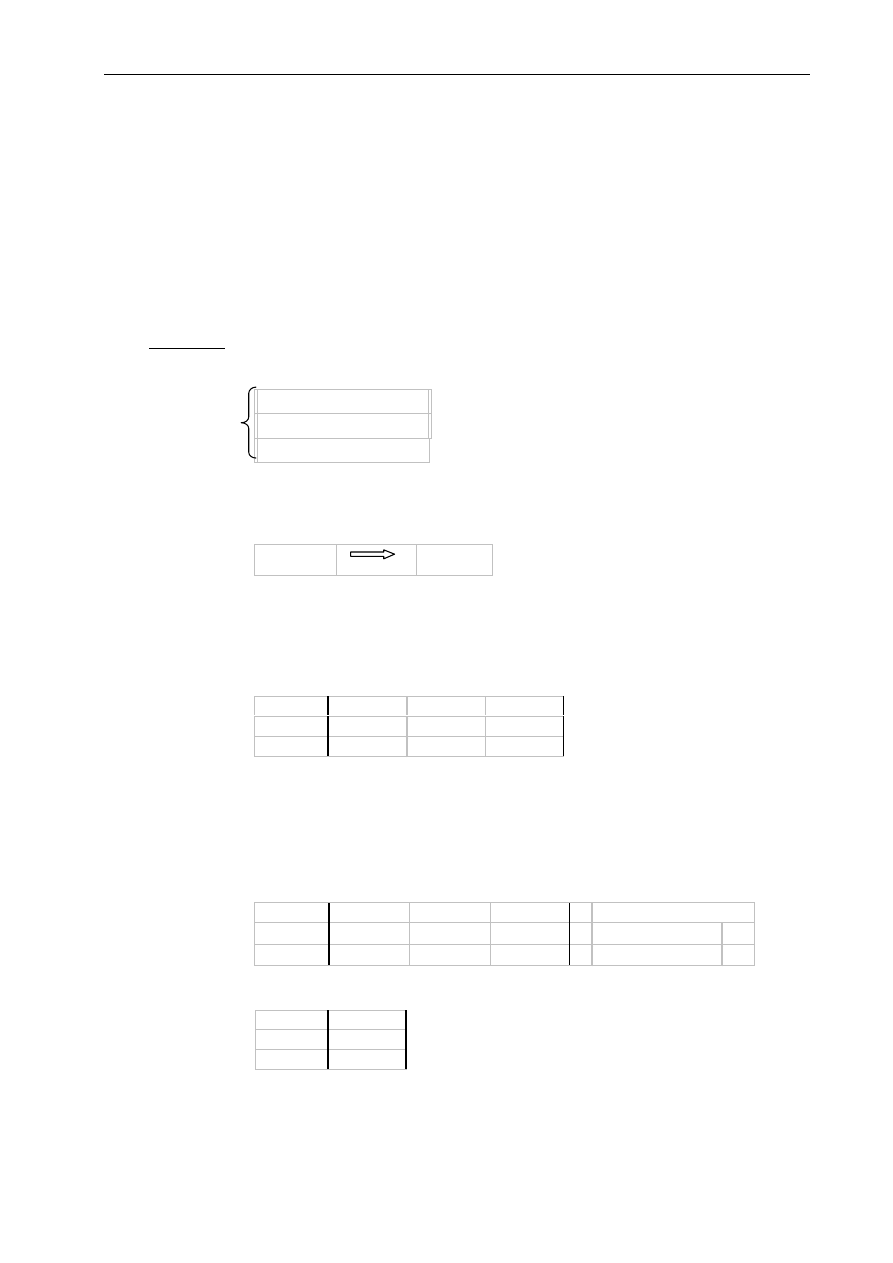
potęgowanie (nazwać komórkę w której obliczana jest wartość b^(1/3) jako b_n)
argument
IMARGUMENT
Arg(a) =
0,982794 =IMARGUMENT(a)
Arg(a) =
0,982794 =ATAN(Im_a/Re_a)
liczba sprzężona
IMCONJUGATE
a =
2-3i
=IMCONJUGATE(a)
suma
IMSUM
a+b = 6-4i
=IMSUM(a;b)
różnica
IMSUB
a-b = -2+10i
=IMSUB(a;b)
iloczyn
IMPRODUCT
a*b = 29-2i
=IMPRODUCT(a;b)
iloraz
IMDIV
a/b = -0,2+0,4i
=IMDIV(a;b)
potęgowanie
IMPOWER
b
n
= -5+12i
=IMPOWER(b;2)
n = 2
b
n
= 1,88322794290822-0,688606036597656i
=IMPOWER(b;1/3)
n = 1/3
b
n
= 1,8832-0,6886i
=COMPLEX(ZAOKR(IMREAL(b_n);4);ZAOKR(IMAGINARY(b_n);4))
Technologia informacyjna - EXCEL
38
Aby zaokrąglić liczbę zespoloną (do określonej liczby cyfr po przecinku) należy najpierw
oddzielnie zaokrąglić jej część rzeczywistą i część urojoną a następnie za pomocą funkcji
COMPLEX przedstawić zaokrąglone części w postaci liczby zespolonej. W powyższym
przykładzie liczba zespolona b
n
została zaokrąglona do 4 miejsc po przecinku.
4.2 Funkcje matematyczne – rachunek macierzowy
W arkuszu Excela można również wykonywać obliczenia na macierzach. W poniższym
przykładzie rachunek macierzowy zostanie wykorzystany do rozwiązania układu równań
liniowych.
Przykład 1
Stosując rachunek macierzowy rozwiązać następujący układ równań:
Rozwiązanie:
Powyższy układ równań można zapisać w postaci macierzowej:
M - macierz współczynników
n – wektor prawych stron
y – wektor rozwiązania
a.) deklaracja macierzy M (nazwać odpowiedni zakres komórek 3 x 3 jako M)
b.) wyznaczenie macierzy odwrotnej M
-1
(należy wprowadzić formułę tablicową):
- zaznaczyć dowolny zakres komórek 3 x 3 i nazwać jako M_o
- do pierwszej komórki zakresu wpisać formułę „ =MACIERZ.ODW(M) ”
- nacisnąć
(Ctr+Shift+Enter)
w
celu
wprowadzenia
formuły
tablicowej
(formuły zostają umieszczone w nawiasach klamrowych)
c.) deklaracja wektora prawych stron n (nazwać odpowiedni zakres komórek 3 x 1 jako n)
d.) wyznaczenie rozwiązania
- zaznaczyć dowolny zakres komórek 3 x 1
4*y
1
+ 5*y
2
+ 7*y
3
= 5
9*y
1
+ 8*y
2
+ 5*y
3
= 8
11*y
1
+ 3*y
2
+ 2*y
3
= 9
M*y = n
y = M
-1
*n
4
5
7
M =
9
8
5
11
3
2
-0,004202 -0,046218 0,1302521
{=MACIERZ.ODW(M)}
M
-1
= -0,155462
0,289916 -0,180672
0,2563025 -0,180672 0,0546218
5
n =
8
9
Technologia informacyjna - EXCEL
39
- do pierwszej komórki zakresu wpisać formułę „=MACIERZ.ILOCZYN(M_o;n) ”
- nacisnąć (Ctr+Shift+Enter) w celu wprowadzenia formuły tablicowej
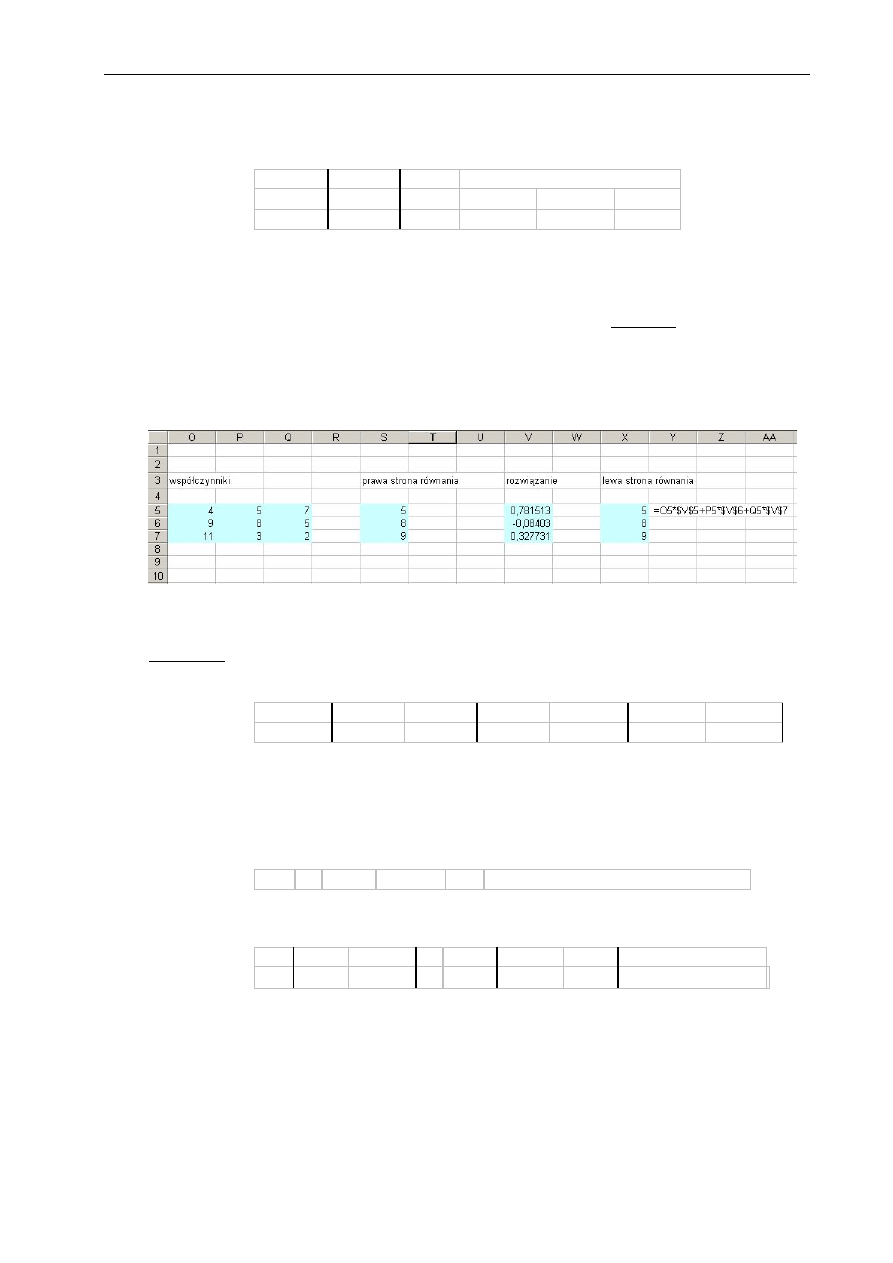
e.) sprawdzenie rozwiązania
- umieścić w dowolnym obszarze arkusza skopiowane wartości: współczynników,
prawej strony równania oraz rozwiązania otrzymanego powyżej
- w miejscu lewej strony równania wpisać odpowiednie formuły wynikające
z mnożenia macierzy współczynników przez wektor prawych stron
- porównać otrzymane wyniki (prawa strona równania i lewa strona równania)
Rys. 4.1 Widok arkusza ze sprawdzeniem rozwiązania
Przykład 2
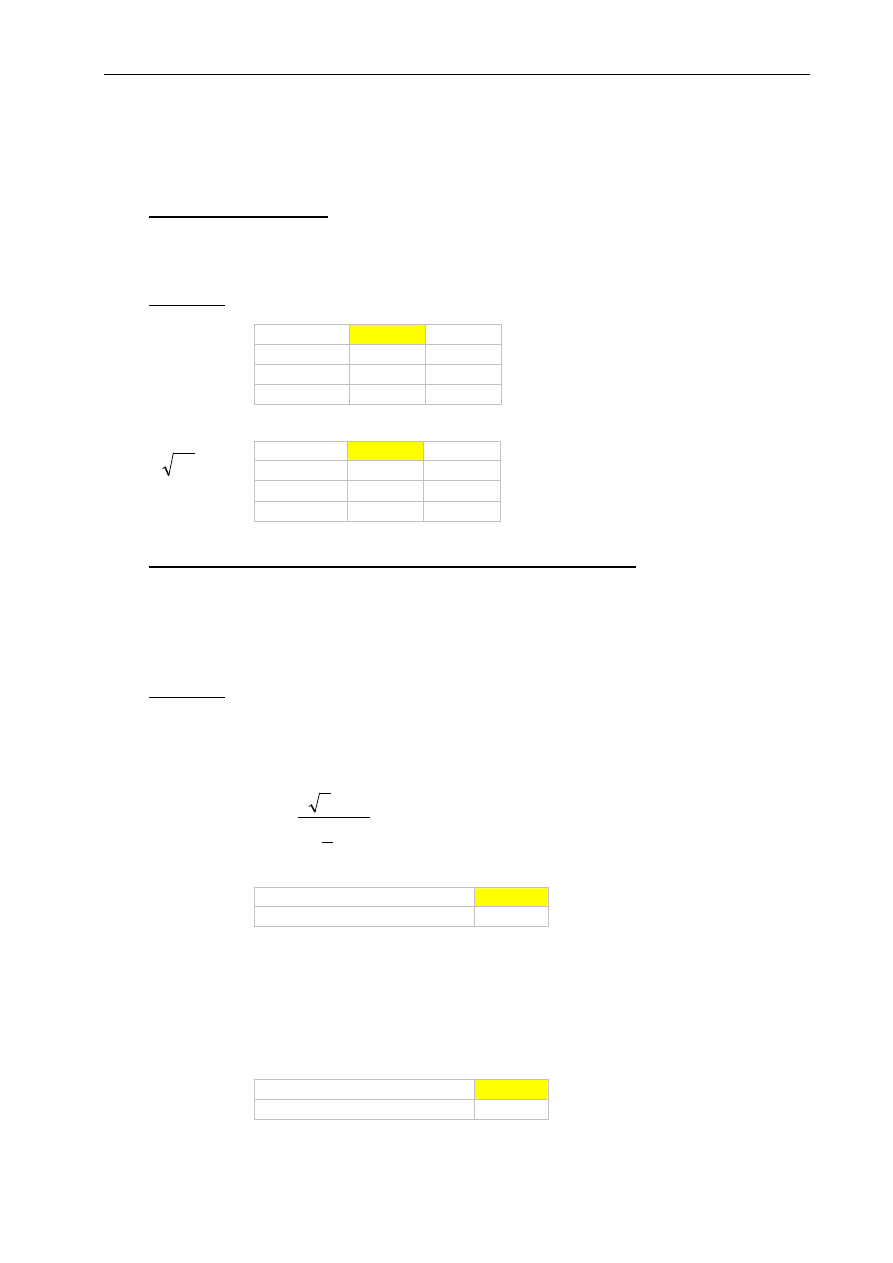
Obliczyć wyznaczniki macierzy P i Q oraz dokonać ich transpozycji.
Rozwiązanie:
Nazwać macierze jako p i q
- wyznaczniki macierzy
- transpozycja macierzy (należy wprowadzić formułę tablicową)
4.3 Polecenie Szukaj wyniku
Polecenie Szukaj wyniku pozwala na znalezienie argumentu funkcji jednej zmiennej
na podstawie znanej wartości funkcji. Polecenie to można wykorzystać np. do wyznaczania
miejsc zerowych funkcji. Otrzymany wynik zależy od podanej na wstępie wartości argumentu,
0,781513
{=MACIERZ.ILOCZYN(M_o;n)}
y = -0,08403
0,327731
3
7
-4
9
P =
2
5
Q =
23
15
|P| =
1
|Q| = -267
=WYZNACZNIK.MACIERZY(q)
3
2
-4
23
{=TRANSPONUJ(q)}
P
T
=
7
5
Q
T
=
9
15
Technologia informacyjna - EXCEL
40
ponieważ poszukiwany jest on w otoczeniu wartości początkowej. Przykładowo, aby w danym
przedziale znaleźć wszystkie miejsca zerowe jakiejś funkcji, należy przed każdym
uruchomieniem polecenia Szukaj wyniku odpowiednio zmieniać wartość początkową argumentu
(Przykład 3).
Zapis wzorów w Excelu
Podczas pisania formuł należy zwrócić szczególną uwagę na kolejność wykonywania
działań oraz na znaki stojące przed poszczególnymi składnikami.
Przykład 1
2
x
3
2
x
Znajdowanie argumentu x funkcji y = f(x) dla znanej wartości y
- nazwać komórkę arkusza zawierającą argument funkcji (np. x)
- nazwać sąsiednią komórkę (np. y) i wpisać wzór funkcji (np. =x^2)
- uruchomić polecenie Szukaj wyniku (Narzędzia – Szukaj wyniku: Ustaw
komórkę: y, Wartość: (np. 0) , Zmieniając komórkę: x )
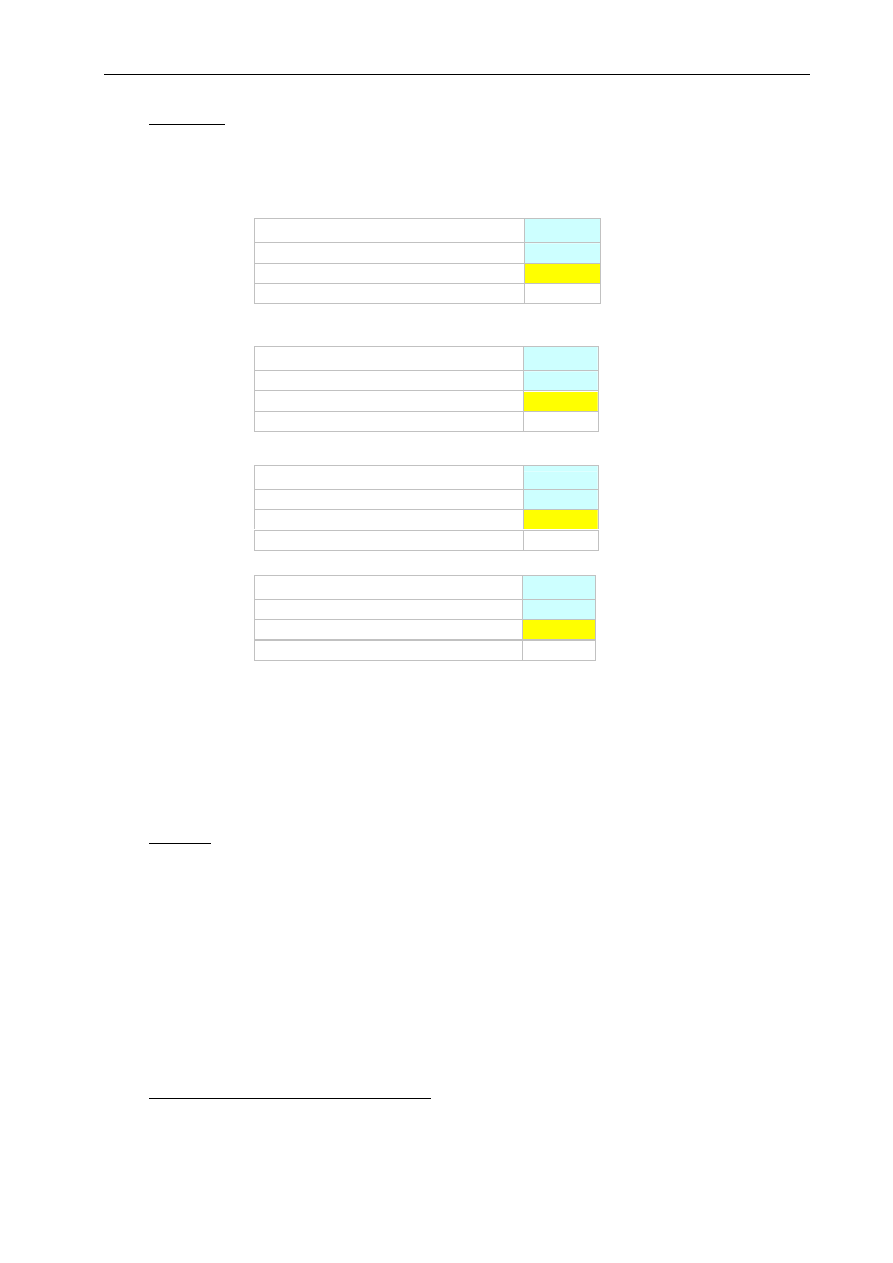
Przykład 2
Znaleźć argumenty poniższych funkcji:
1. Dla y = 2
2
3
x
ln
e
x
y
2
x
3
2. Dla y = -1
5
e
4
x
ln
x
y
3
x
5
2
x =
-6
-x^2 =
36
błąd
-1*x^2 =
-36
-(x^2) =
-36
x =
-6
x^2/3 =
12
błąd
x^(2/3) = #LICZBA!
błąd
(x^2)^(1/3) = 3,301927
x =
0,75968
x^(1/3)*EXP(x^2)/LN(x/3+2)=
2,00031
x =
2,87341
-x^5-LN(x+4)+EXP(x^2-3)+5 =
-1,00001
Technologia informacyjna - EXCEL
41
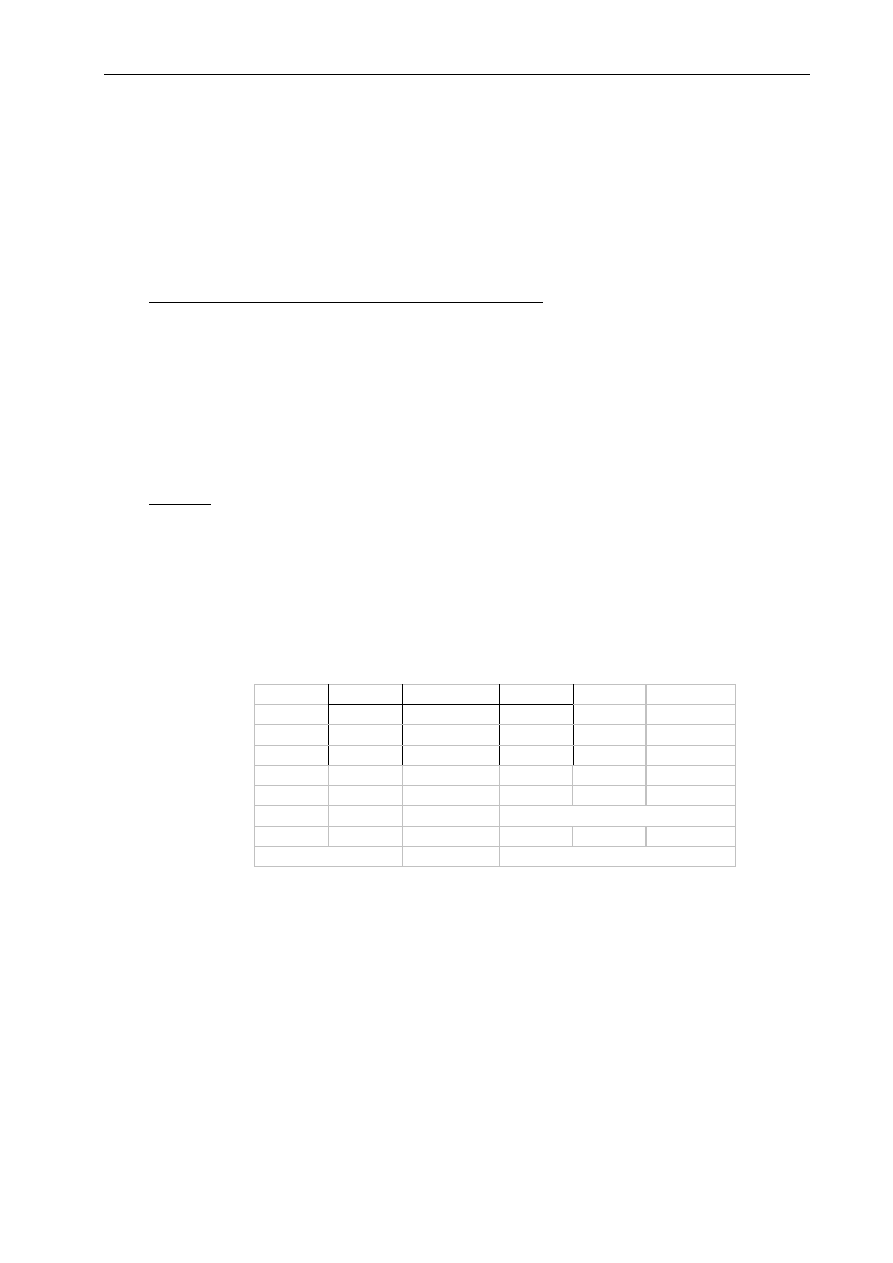
Przykład 3
W przedziale <-4; 3> wyznaczyć miejsca zerowe następującego wielomianu:
12
x
14
x
6
x
15
x
7
x
x
)
x
(
w
2
3
4
5
6
4.4 Deklaracja własnej funkcji
W skoroszycie Excela można stworzyć własną funkcję, która zostanie zapisana jako
funkcja użytkownika. Własne funkcje są dostępne jedynie w tych skoroszytach w których
zostały zapisane. Poniżej zostanie przedstawiona funkcja użytkownika obliczająca długość
wektora oraz funkcja wyznaczająca iloczyn skalarny wektorów.
Przykład:
Zaprojektować funkcję wyznaczającą długość wektora w przestrzeni trójwymiarowej
oraz funkcję obliczającą iloczyn skalarny dwóch wektorów.
Rozwiązanie:
Własną funkcję projektuje się w języku VBA i umieszcza się ją w module programu.
W tym celu należy wykonać następujące czynności:
-
uaktywnić pasek narzędzi Visual Basic
-
za pomocą ikony Edytor Visual Basic otworzyć okno Microsoft Visual Basic
-
wstawić nowy moduł Insert – Module i zadeklarować w nim funkcję
Funkcja wyznaczająca długość wektora dł_wekt = f(a, b, c)
dł_wekt - nazwa funkcji
a, b, c – argumenty funkcji (współrzędne wektora)
wartość początkowa x
p
=
-4
w(x
p
) =
2340
miejsce zerowe x =
-3
x^6-x^5-7*x^4+15*x^3-6*x^2-14*x+12 = 3,54E-06
wartość początkowa x
p
=
-0,5
w(x
p
) = 15,23438
miejsce zerowe x =
-1
x^6-x^5-7*x^4+15*x^3-6*x^2-14*x+12 =
4,24E-06
wartość początkowa x
p
=
0
w(x
p
) =
12
miejsce zerowe x =
1
x^6-x^5-7*x^4+15*x^3-6*x^2-14*x+12 =
3,1E-06
wartość początkowa x
p
=
3
w(x
p
) =
240
miejsce zerowe x = 2,000002
x^6-x^5-7*x^4+15*x^3-6*x^2-14*x+12 = 4,68E-05
Technologia informacyjna - EXCEL
42
Przy deklaracji funkcji należy podać jakiego typu są argumenty i wartości funkcji.
Double – zmienna rzeczywista z przedziału (-1,79*10
308
1,79*10
308
)
Sqr – pierwiastek kwadratowy (funkcja VBA)
Public Function
dł_wekt(a
As Double
, b
As Double
, c
As Double
)
As Double
dł_wekt = Sqr(a ^ 2 + b ^ 2 + c ^ 2)
End Function
Funkcja obliczająca iloczyn skalarny dwóch wektorów il_skal = f(a1 ,b1, c1, a2,b 2, c2)
Public Function
il_skal(a1
As Double
, b1
As Double
, c1
As Double
, a2
As Double
, _
b2
As Double
, c2
As Double
)
As Double
il_skal = a1 * a2 + b1 * b2 + c1 * c2
End Function
il_skal - nazwa funkcji
a1, b1, c1 – współrzędne pierwszego wektora
a2, b2, c2 – współrzędne drugiego wektora
Przykład:
Obliczyć długość i iloczyn skalarny wektorów
u
(u_x, u_y, u_v) i
v
(v_x, v_y, v_z)
o podanych współrzędnych:
Rozwiązanie:
Nazwać odpowiednie komórki zawierające współrzędne wektora
u
jako u_x, u_y, u_z
a wektora
v
jako v_x, v_y, v_z a następnie wstawić lub wpisać wymaganą funkcję.
4.5 Solver
Dodatek Solver umożliwia dokonanie obliczeń optymalizacyjnych z ograniczeniami.
Za jego pomocą można np. wyznaczyć ekstrema lokalne lub miejsca zerowe funkcji wielu
zmiennych bądź też znaleźć argumenty funkcji dla których przyjmuje ona założone wartości.
Rozwiązanie poszukiwane jest w otoczeniu punktu początkowego, dlatego aby zlokalizować
wszystkie
rozwiązania
spełniające
określone kryteria należy odpowiednio zmieniać
(w zależności od narzuconych ograniczeń) początkowe argumenty funkcji przed każdym
uruchomieniem Solvera.
W przypadku, gdy dodatek ten nie jest widoczny można go udostępnić następująco:
(Narzędzia – Dodatki – Solver).
u
v
x
1
-2
y
2
4
z
-3
5
Długość =
3,7417 =dł_wekt(u_x;u_y;u_z)
Iloczyn skalarny =
-9 =il_skal(u_x;u_y;u_z;v_x;v_y;v_z)
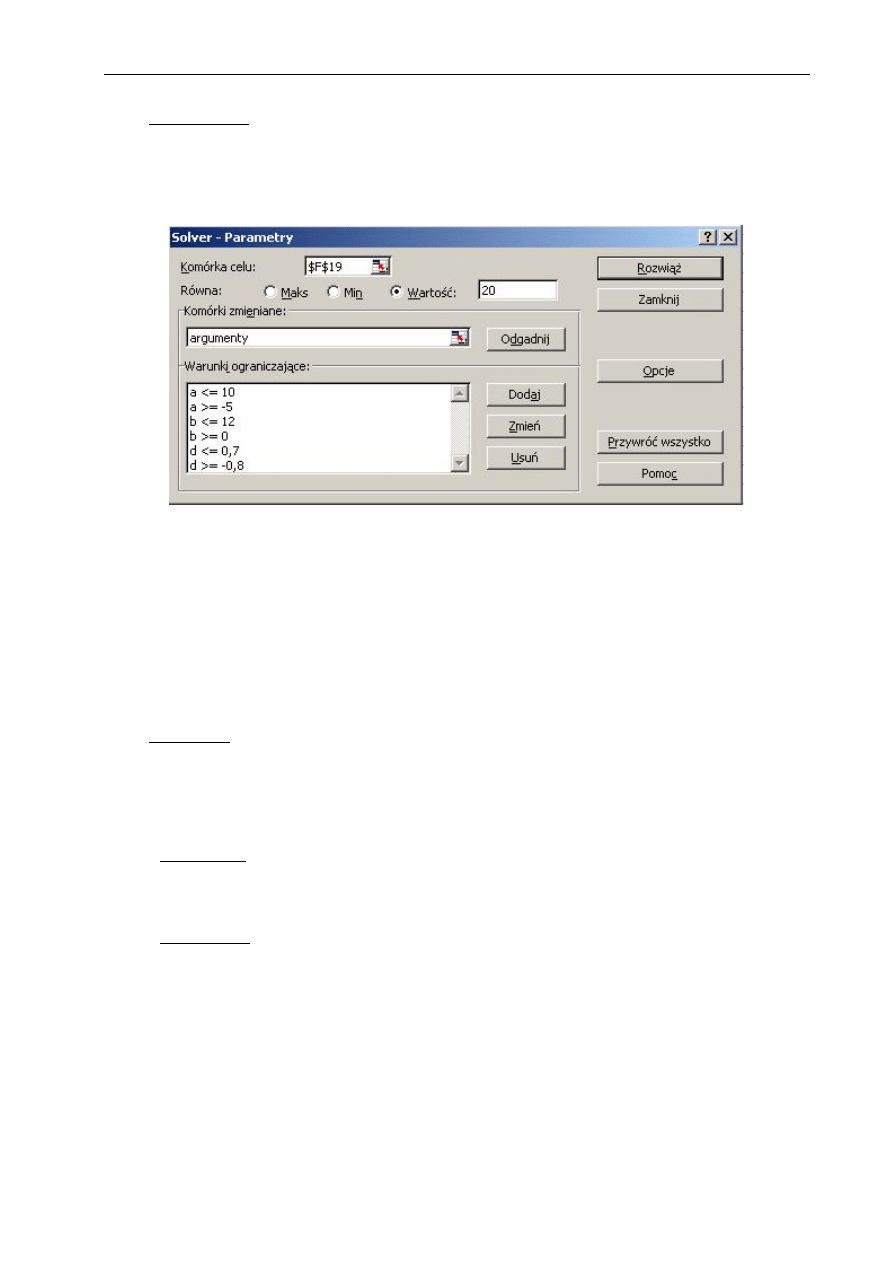
Technologia informacyjna - EXCEL
43
Opis działania
W arkuszu należy zdefiniować zakres komórek w którym będą przechowywane argumenty
funkcji a następnie do wybranej komórki wpisać formułę określająca badaną funkcję
i uruchomić Solvera.
Rys. 4.2 Okno Solvera
Komórka celu – komórka zawierająca wzór funkcji
Komórki zmieniane – komórki zawierające argumenty funkcji
Warunki ograniczające – założenia jakie powinny spełniać argumenty funkcji
Należy podać powyższe parametry a warunki ograniczające wprowadzić za pomocą
przycisku Dodaj. Rozwiązanie uzyskuje się po naciśnięciu przycisku Rozwiąż.
W poniższym przykładzie zostanie rozwiązane proste zagadnienie optymalizacyjne.
Przykład 1:
Należy tak dobrać wartości argumentów x
1
i x
2
, aby funkcja f(x
1,
x
2
) osiągnęła swoją
wartość maksymalną przy danych ograniczeniach.
Rozwiązanie:
funkcja celu:
2
1
2
1
x
23
x
15
x
,
x
f
ograniczenia:
0
x
0
x
60
x
2
x
2
40
x
8
x
4
2
1
2
1
2
1
Wykresem funkcji celu jest płaszczyzna pokazana na rysunku poniżej, tak więc wartość
funkcji f(x
1
, x
2
) rośnie wraz ze wzrostem argumentów x
1
i x
2
, dlatego też rozwiązaniem będą
największe dopuszczalne wartości x
1
i x
2
.
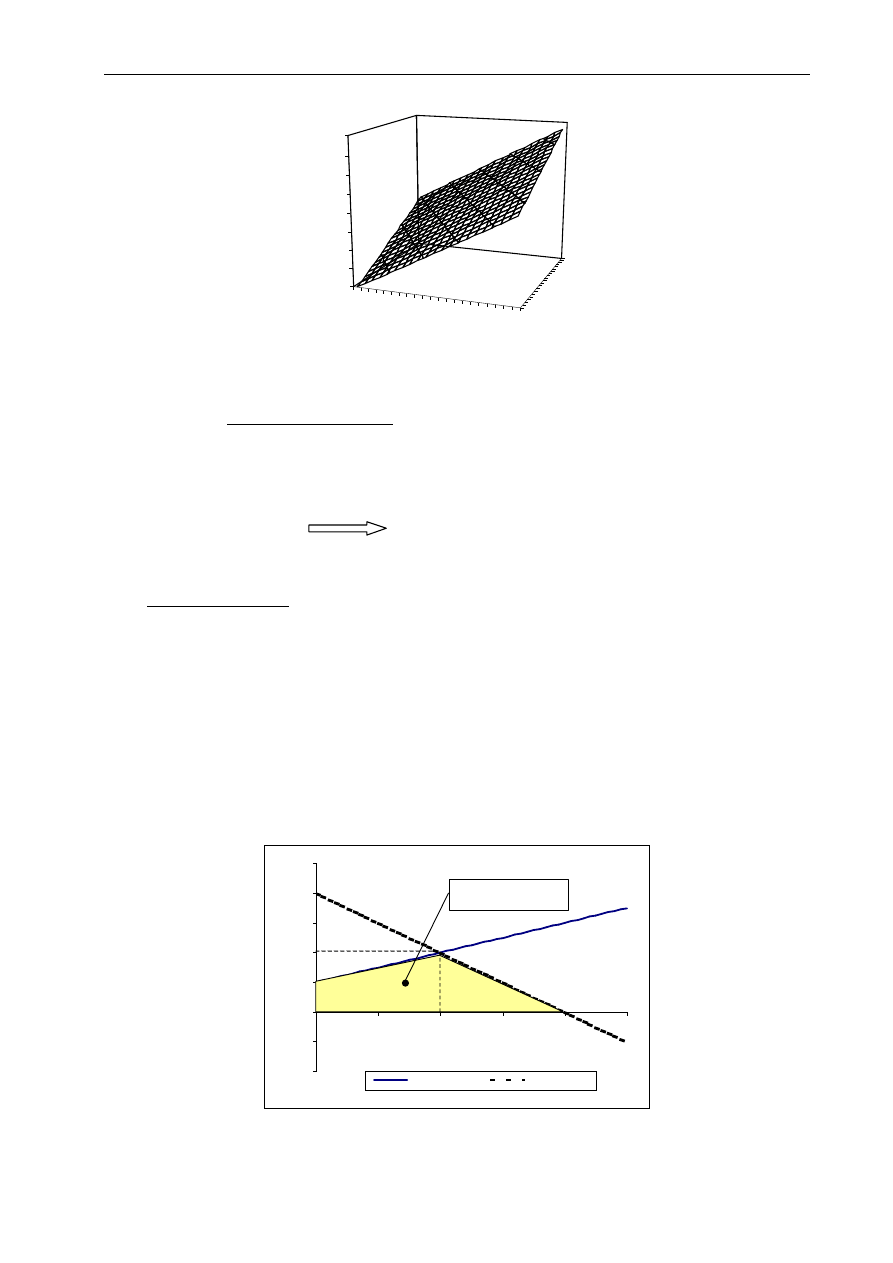
Technologia informacyjna - EXCEL
44
0
2
4
6
8
1
0
12
14
16
18
2
0
0
6
12
18
0
100
200
300
400
500
600
700
800
f(x
1
, x
2
)
x
1
x
2
Rys. 4.3 Wykres funkcji celu
Rozwiązanie graficzne:
W celu określenia dopuszczalnego obszaru do którego może należeć rozwiązanie zostanie
narysowany wykres ograniczeń (wykresami ograniczeń będą półpłaszczyzny wraz z brzegami):
1
2
2
1
1
2
x
f
x
x
f
x
20
x
x
5
x
5
,
0
x
1
2
1
2
Wykres ograniczeń:
- do komórek A1, B1, C1 wpisać kolejno tekst: x1, f1(x1), f2(x1)
- do komórek z zakresu A2:A52 wprowadzić serię danych z przedziału <0, 25>
z krokiem 0,5 i nazwać powyższe komórki jako x_1
- do komórek z zakresu B2:B52 wprowadzić formułę określającą pierwsze
ograniczenie
- do komórek z zakresu C2:C52 wprowadzić formułę określającą drugie
ograniczenie
- narysować wykresy funkcji x
2
= f
1
(x
1
) i x
2
= f
2
(x
1
) we wspólnym układzie
współrzędnych
-10
-5
0
5
10
15
20
25
0
5
10
15
20
25
x
1
x
2
ograniczenie 1
ograniczenie 2
Obszar dopuszczalnych
rozw iązań
f
1
(x
1
)
f
2
(x
1
)
P(10,10)
Rys. 4.4 Wykresy funkcji ograniczających

Technologia informacyjna - EXCEL
45
Aby umieścić na wykresie dopuszczalny obszar rozwiązań należy:
- zaznaczyć wykres
- z paska narzędzi Rysowanie wybrać Dowolny kształt i zaznaczyć kolejno
wierzchołki obszaru a następnie wypełnić obszar dowolnym kolorem
- dodać pola tekstowe, strzałkę i linie określające współrzędne punktu P (również
przy zaznaczonym wykresie)
Rozwiązanie na podstawie wykresu:
- rozwiązaniem jest punkt o współrzędnych P(10, 10), maksymalna wartość
funkcji: f(10
,
10) = 380
x1_opt = 10, x2_opt = 10, f(x1_opt, x2_opt) = 380
Optymalizacja za pomocą Solvera:
Rys. 4.5 Widok fragmentu arkusza z parametrami optymalizacji
- do komórek L1, L2, L3 wpisać odpowiedni tekst
- komórki M1 i M2 odpowiednio nazwać (x1_opt i x2_opt)
- do
komórki
M3
wpisać
formułę
określającą
funkcję
celu:
„=15*x_1opt+23*x_2opt” i nazwać ją: funkcja_celu
- zakres komórek M1:M2 nazwać: argumenty_funkcji_celu
- do
komórek
M6
i
M7
wpisać
formuły
określające
ograniczenia
„=-4*x_1opt+8*x_2opt”, „=2*x_1opt+2*x_2opt” i nazwać je odpowiednio:
ograniczenie_1 i ograniczenie_2
- do komórek N6 i N7 wpisać wartości ograniczeń (40, 40) i nazwać je
odpowiednio: granica_1 i granica_2
- parametry Solvera:
Komórka celu: funkcja_celu
Równa: Max
Komórki zmieniane: argumenty_funkcji_celu
Warunki ograniczające:
ograniczenie_1 <= granica_1
ograniczenie_2 <= granica_2
x1_opt >= 0
x2_opt >= 0
- zmienić warunki początkowe dla argumentów x
1
_opt i x
2
_opt i rozwiązać
zagadnienie.
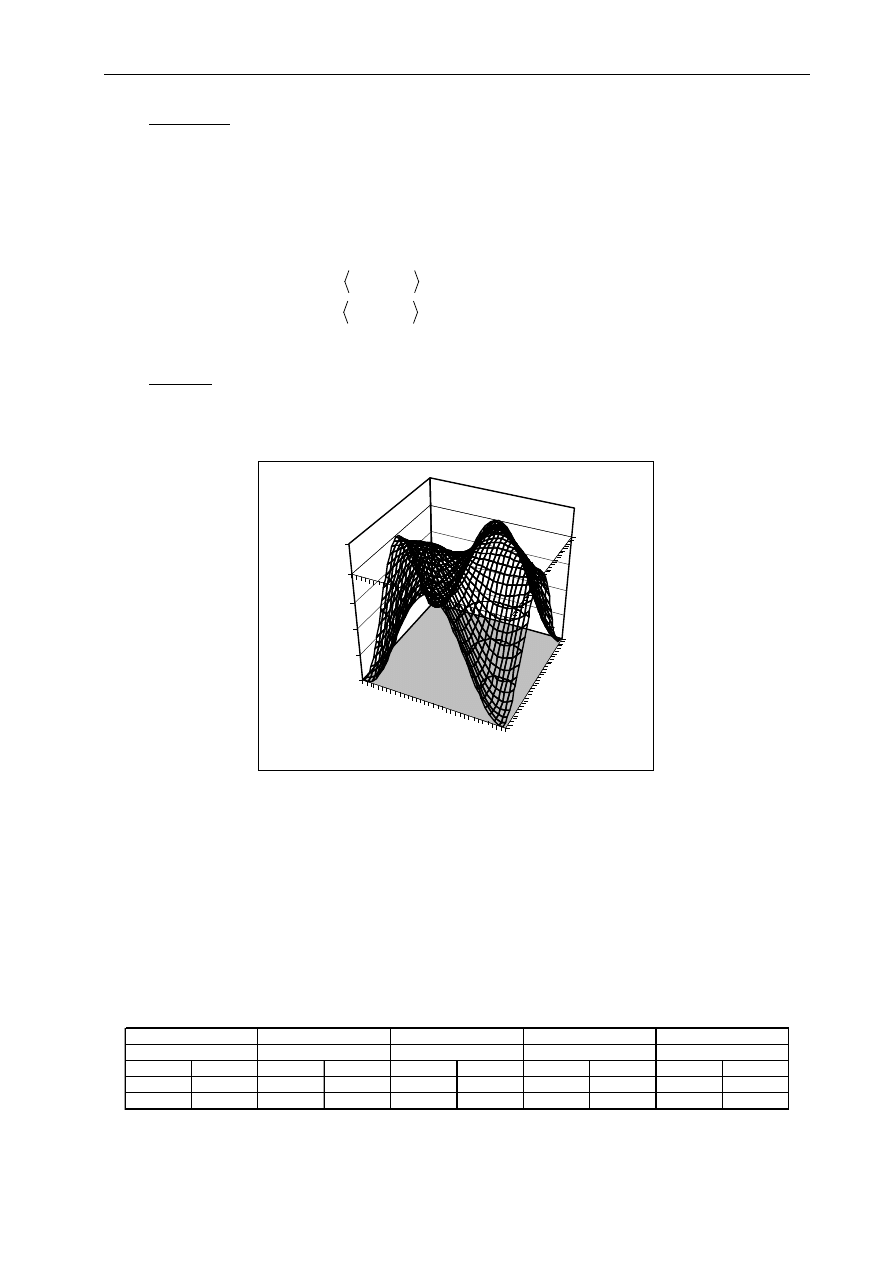
Technologia informacyjna - EXCEL
46
Przykład 2:
Dla funkcji t = f(u,v) narysować wykres powierzchniowy oraz wykresy punktowe v = f(u)
(ograniczeń) i t = f(u) (przekrój płaszczyzną prostopadłą do płaszczyzny uv przecinającą ją
wzdłuż przekątnej prostokąta ograniczeń). Przy podanych ograniczeniach, wyznaczyć minimum,
maksimum i miejsca zerowe w pobliżu punktu (1; -1):
funkcja celu:
2
2
2
v
sin
u
sin
v
u
sin
v
,
u
f
ograniczenia:
1
,
3
v
1
,
3
u
Rozwiązanie:
Wykresy
Sposób tworzenia wykresu powierzchniowego t = f(u,v) został opisany w podrozdziale
Wykresy powierzchniowe.
-1
,6
-0
,9
-0
,2
0
,5
1
,2
-1,6
-0,5
0,6
-2
-1,5
-1
-0,5
0
0,5
u
v
t
Rys. 4.6 Wykres funkcji t = f(u,v)
Wykresem ograniczeń będzie prostokąt, którego wierzchołki w układzie współrzędnych uv
mają następujące współrzędne (-3; -3), (-3; -1), (-1; -3), (-1; -1). Aby narysować wykres
powyższego prostokąta wystarczy podać te współrzędne jako kolejne serie podczas rysowania
wykresu. Na wykresie zamieszczona została również przekątna prostokąta wzdłuż której będzie
przebiegało przecięcie płaszczyzny prostopadłej do płaszczyzny uv z płaszczyzną uv. Łatwo
sprawdzić, że wszystkie punkty leżące na tej płaszczyźnie będą miały współrzędną v = u, tak
więc wzór funkcji t = f(u) będzie wyglądał następująco:
2
2
u
sin
2
u
2
sin
t
.
X
Y
X
Y
X
Y
X
Y
X
Y
-3
-1
-1
-1
-3
-1
-3
-3
-4
-4
-3
-3
-1
-3
-1
-1
-1
-3
1
1
przekątna
Serie1
Serie2
Serie3
Serie4
Serie5
prawy bok prostokąta
lewy bok prostokąta
górny bok prostokąta dolny bok prostokąta
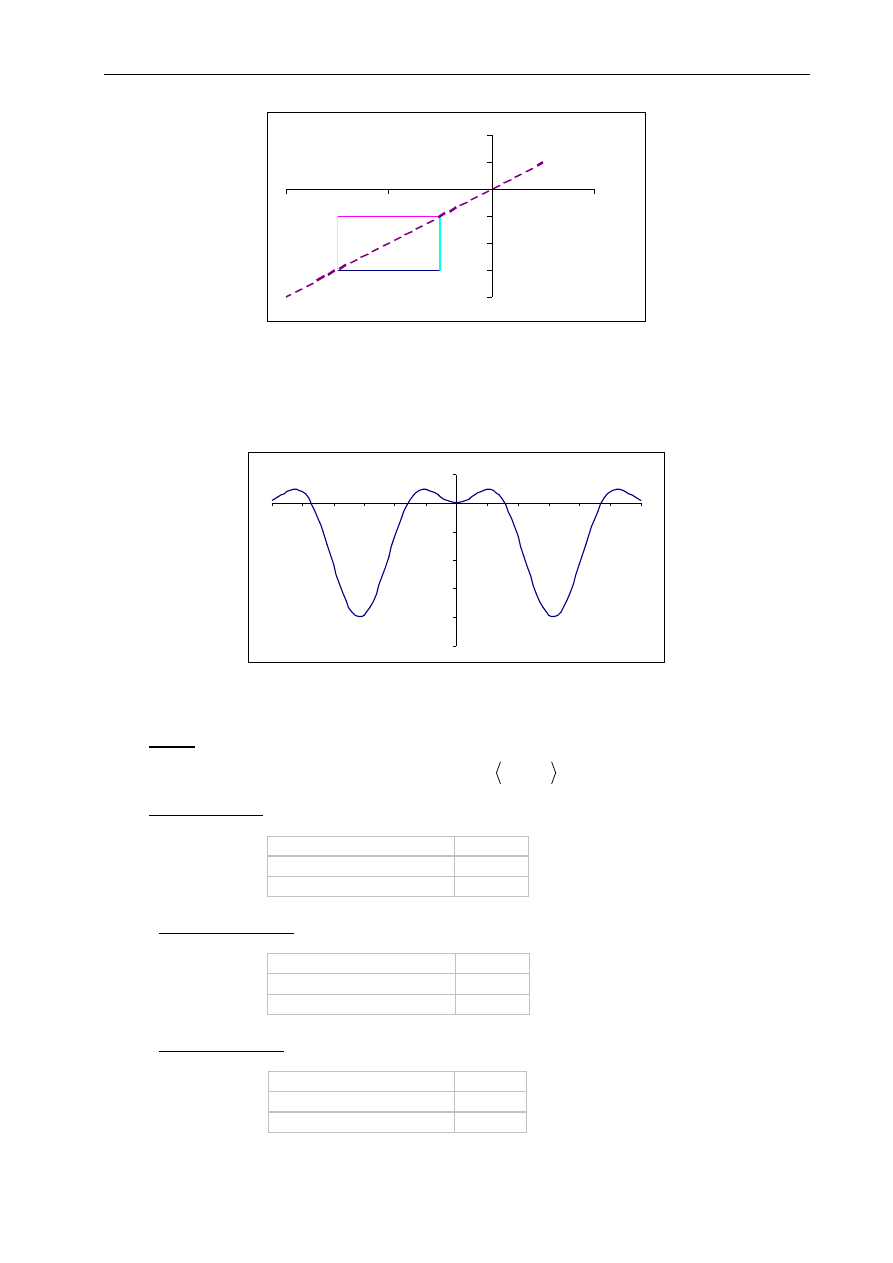
Technologia informacyjna - EXCEL
47
-4
-3
-2
-1
0
1
2
-4
-2
0
2
u
v
Rys. 4.7 Wykres ograniczeń
Wykres t = f(u) zostanie narysowany w celu zobrazowania położenia ekstremów funkcji
f(u,v) oraz jej miejsc zerowych..
-2,5
-2
-1,5
-1
-0,5
0
0,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
t
u
Rys. 4.8 Wykres funkcji t = f(u)
Solver
Wyniki otrzymane za pomocą Solvera dla
1
,
3
v
,
u
są następujące:
miejsce zerowe:
u_opt_0
-2,35619
v_opt_0
-2,35619
t = f(u_opt_0,v_opt_0)
9,8E-07
maksimum funkcji:
u_opt_max
-2,61799
v_opt_max
-2,61799
t = f(u_opt_max,v_opt_max)
0,25
minimum funkcji:
u_opt_min
-1,5708
v_opt_min
-1,5708
t = f(u_opt_min,v_opt_min)
-2

Technologia informacyjna - EXCEL
48
5. Pakiet biurowy Excela
5.1 Formatowanie arkusza
Program Excel jest wyposażony w szereg funkcji, które umożliwiają zarówno odpowiednią
zmianę wyglądu arkusza jak i sprawdzenie poprawności wprowadzanych danych, powiązanie
formatu komórki z aktualną wartością, zablokowanie wybranych komórek przed edycją a także
ochronę poszczególnych arkuszy i całego skoroszytu wraz z możliwością zapisywania z kopią
zapasową w celu zabezpieczenia przed utratą danych.
W poniższym przykładzie projektu faktury wykorzystane zostały wymienione wyżej
możliwości Excela.
Przykład:
Zaprojektować fakturę własnej firmy; może ona mieć wygląd następujący:
Rys. 5.1 Widok wypełnionego arkusza z zaprojektowaną fakturą
- nadać nazwę Faktura nowemu skoroszytowi i arkuszowi w tym skoroszycie
(pozostałe arkusze usunąć)
- ustawić marginesy: P, L –1 cm; G, D – 2,5 cm oraz szerokość kolumn: A – 5,
B –13, C – 32, D – 13, E – 17, F – 8, G –12 i wysokości kolejnych wierszy: 60,
24, 70, 30, 15, 15, 15, 40, 30 (pozostałe wiersze mają wysokość standardową)
- w obszarze A1 – B2 umieścić logo firmy

Technologia informacyjna - EXCEL
49
- komórki E1–F1: scalić komórki, 12, B, Arial, Wyrównanie tekstu - Poziomo:
Lewe (wcięcie): 2, wpisać tekst: „FAKTURA VAT NR”
- komórka G1: 12, B, Arial; wstawić komentarz: „Proszę wpisać numer faktury”
- komórki E2–F2: scalić komórki, Wyrównanie tekstu - Poziomo: Lewe (wcięcie):
5, wpisać tekst: „Data wystawienia”
- komórka G2: B, wpisać formułę „=DZIŚ()” (będzie wyświetlana aktualna data)
- komórki D3–F3: scalić komórki, I, Wyśrodkuj, wpisać tekst: „Dane klienta”
- komórki D4–F4: scalić komórki, 12, B, Arial,
- komórki D5–F5: użyć Malarza formatów do skopiowania formatu z komórek
powyżej
- komórka D6: 12, B, Arial, Format specjalne – kod pocztowy
- komórki E6-F6: scalić komórki, 12, B, Arial
- komórki D7-F7: scalić komórki, 12, B, Arial, Format specjalne – numer NIP
- komórki D4-F7: dodać obramowanie
- komórka A9: zdefiniować styl Nagłówek_tabeli (Format – Styl): 11, Arial, B, I,
Wyrównanie - Poziomo: Środek, Pionowo: Środek, Zawijaj tekst
- komórki B9–G9: zaznaczyć i przypisać styl Nagłówek_ tabeli
- komórki A9-G14: dodać obramowanie
- komórki E10-G17: kolor wypełnienia – jasnożółty
- komórki D10-D14: Dane - Sprawdzanie Poprawności - Ustawienia Dozwolone;
Pełna liczba, Większe lub równe 10, Ostrzeżenie o błędzie Tytuł: Błędne dane;
Komunikat błędu: Liczba godzin nie może być mniejsza od 10
- komórki E10-E14: formatowanie Niestandardowe Typ 0 (wpisać) zł”za godzinę”
- komórki F10-F14: formatowanie Procentowe
- komórki G10-G14: formatowanie Walutowe, Miejsca Dziesiętne 0 ; Format –
Formatowanie Warunkowe – Warunek1 wartość komórki jest mniejsza niż 2000
formatuj kolor czcionki na niebiesko Warunek2 wartość komórki jest większa niż
50000 formatuj kolor czcionki na czerwono
- komórki D9-G14: nadać nazwy Wstaw – Nazwa – Utwórz - Górny Wiersz
- komórki G10-G14: wpisać formułę: „=Ilość_godzin*Stawka_godzinowa”
- komórki F15-F17: 12, B, Arial, Wyrównanie do prawej, kolor czcionki –
jasnozielony, wpisać kolejno tekst: „Suma”, „Podatek”, „Do zapłaty”
- komórki F15-G17: nadać nazwy Wstaw – Nazwa – Utwórz – Lewa Kolumna
- komórki
G15-G17:
wpisać
kolejno
formuły:
„=SUMA(Wartość)”,
„=SUMA.ILOCZYNÓW(VAT;Wartość)”, „=Suma+Podatek”
- komórki A21-G21: scalić komórki, kolor czcionki – ciemnozielony, wpisać
formułę: „=JEŻELI(Do_zapłaty>50000;"Dla należności większych od 50 000 zł
udzielane jest 3% rabatu przy płatności w terminie do 30 dni";"")”
- komórki A27-G27: scalić komórki, wpisać hasło reklamowe, 14, Impact, B, I,
kolor czcionki – fioletowy Wyrównanie – Poziomo: Środek, Pionowo: Środek
- nagłówek i stopka strony: dodać nazwę firmy do nagłówka: Widok - Nagłówki
i stopki - Nagłówek niestandardowy - Środkowa sekcja 12, Arial, B (wpisać
nazwę firmy); umieścić numer strony w stopce: Stopka niestandardowa –
Środkowa sekcja - &[Strona]; 10, Arial
- ustawienie wydruku: Plik – Ustawienie strony – Marginesy - Wyśrodkuj
na stronie – W poziomie; obejrzeć podgląd wydruku
- komórki G1, D4-F7, A10-F14: zaznaczyć komórki, Format – Komórki –
Ochrona – Zablokuj (odznaczyć), Narzędzia – Ochrona – Chroń arkusz wpisać
hasło (udostępnione do edycji pozostaną jedynie komórki odblokowane,
w pozostałych nie będzie możliwości dokonywania zmian)
Technologia informacyjna - EXCEL
50
- zapisać jako szablon pod nazwą Faktura i zamknąć
- otworzyć kopię szablonu: Plik – Nowy (wybrać Faktura), wypełnić dowolnymi
danymi i zapisać z kopią zapasową oraz z hasłem ochrony przed otwarciem
i przed zmianami Plik – Zapisz jako – Narzędzia – Opcje ogólne
Rys. 5.2 Podgląd wydruku faktury
5.2 Prezentacja i przetwarzanie danych w arkuszu
5.2.1 Konsolidowanie danych
Można konsolidować dane ze skoroszytów do arkusza, bądź z arkuszy do skoroszytu,
dzięki czemu możliwe jest np. zsumowanie odpowiadających sobie danych umieszczonych
w różnych miejscach różnych arkuszy i skoroszytów. W przykładzie poniżej zostaną
skonsolidowane (za pomocą sumowania) wydatki trzech pracowników (zapisywane w trzech
różnych skoroszytach) ponoszone w tym samym czasie oraz nastąpi konsolidacja całkowitych
wydatków tych pracowników ponoszonych w różnych okresach czasowych.
Przykład:
Konsolidowanie danych z różnych skoroszytów.
Skoroszyty pracownik1, pracownik2, pracownik3 zawierają dane dotyczące wydatków
ponoszonych przez poszczególnych pracowników w ciągu jednego miesiąca. W odrębnym
skoroszycie o nazwie zestawienie należy stworzyć podsumowanie tych wydatków wykorzystując
konsolidację danych dostępną w arkuszu.
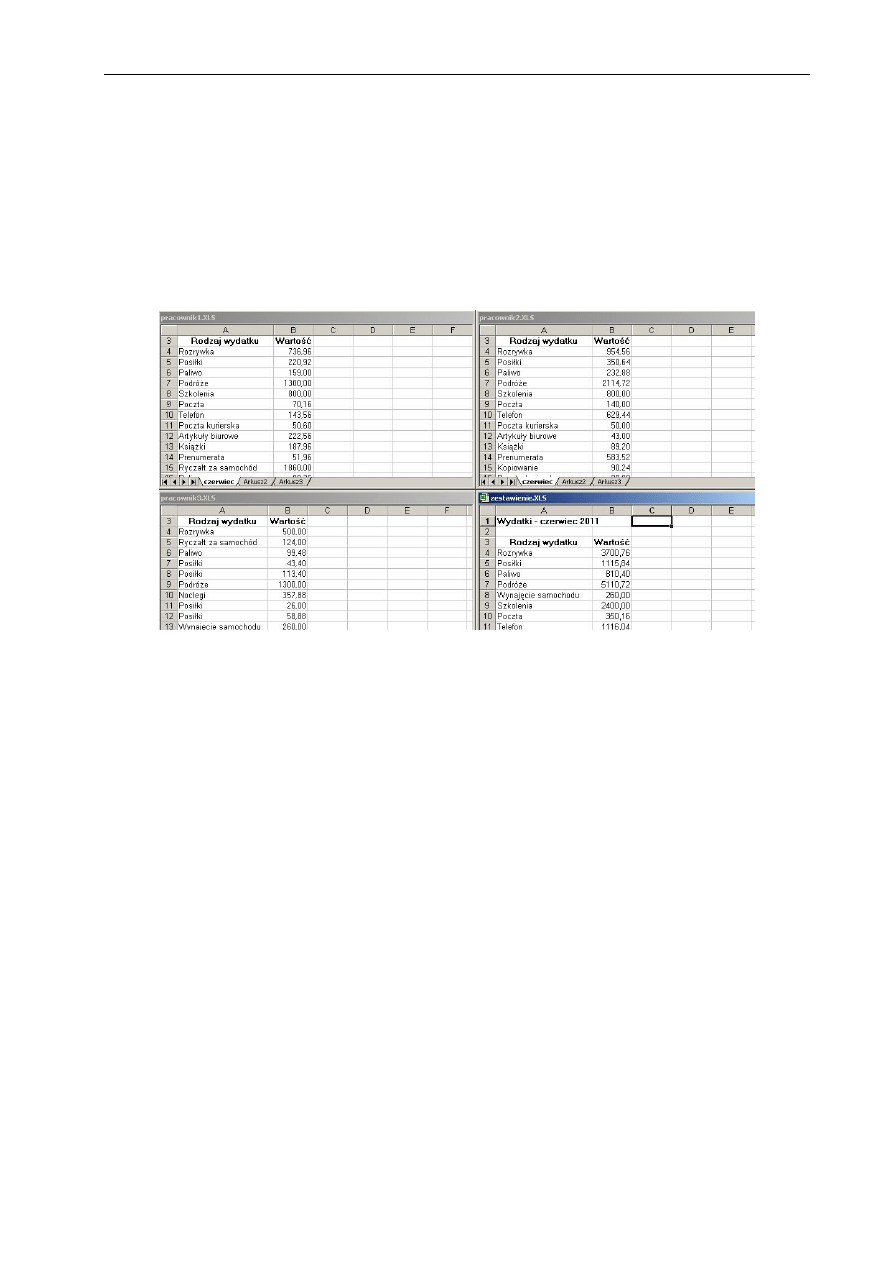
Technologia informacyjna - EXCEL
51
otworzyć skoroszyty: pracownik1, pracownik2, pracownik3, zestawienie
(4 okna sąsiadująco).
w skoroszycie zestawienie dodać nowy arkusz czerwiec
- w komórce A1 tego arkusza umieścić tekst: Wydatki – czerwiec 2011
- zaznaczyć komórkę A3 a następnie użyć polecenia Dane – Konsoliduj (Funkcja –
Suma)
- w skoroszycie pracownik1 zaznaczyć komórki A3 – B23 i kliknąć Dodaj
- powtórzyć to dla skoroszytów pracownik2 i pracownik3
- zaznaczyć Użyj etykiet w: górny wiersz, lewa kolumna
Rys. 5.3 Konsolidowanie danych z różnych skoroszytów
Konsolidowanie danych z różnych arkuszy tego samego skoroszytu
W poszczególnych arkuszach skoroszytu zestawienie znajdują się, zsumowane
w kolejnych miesiącach, dane ze skoroszytów pracowników. W nowym arkuszu tego skoroszytu
należy stworzyć podsumowanie wszystkich dotychczasowych wydatków.
do skoroszytu zestawienie dodać nowy arkusz Podsumowanie1
- w komórce A1 napisać: Podsumowanie I półrocza 2011
- zaznaczyć komórkę A3 a następnie użyć polecenia Dane – Konsoliduj (Funkcja –
Suma)
- w arkuszu styczeń zaznaczyć komórki A3 – B18 i kliknąć Dodaj
- powtórzyć to dla pozostałych arkuszy tego skoroszytu
5.2.2 Filtrowanie danych
Filtrowanie danych, zawartych w tabelach umieszczonych w arkuszu Excela, polega
na ukrywaniu wierszy nie spełniających założonego kryterium. Dane można filtrować za pomocą
Autofiltru (wówczas lista filtrowana jest w miejscu) lub Filtru zaawansowanego (można listę
filtrować w miejscu, bądź przenieść przefiltrowaną listę w inny obszar arkusza).
W skoroszycie pracownik1_klienci zamieszczone są informacje dotyczące dochodów
pracownika uzyskanych z różnych form działalności.
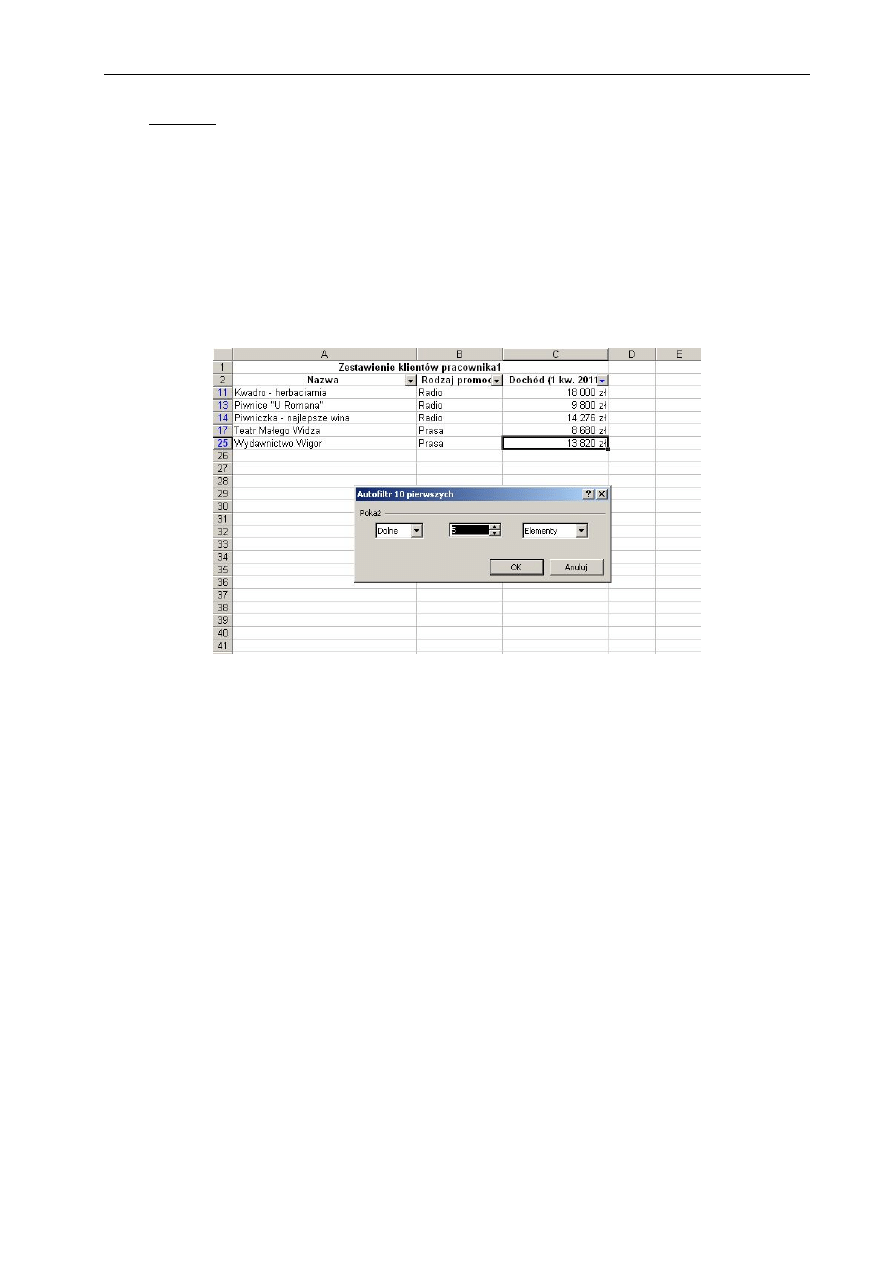
Technologia informacyjna - EXCEL
52
Przykład:
Autofiltr
otworzyć skoroszyt pracownik1_klienci
- zaznaczyć komórkę B2 a następnie polecenie Dane – Filtr – Autofiltr
- zaznaczyć Radio w Autofiltrze kolumny Rodzaj promocji a następnie przywrócić
pełną listę zaznaczając w Autofiltrze Wszystkie
zaznaczyć 10 pierwszych w Autofiltrze kolumny Dochód(1 kw. 2011) (Pokaż Dolne 5
Elementy) a następnie przywrócić pełną listę (rys. 5.4)
zaznaczyć Inne w Autofiltrze kolumny Dochód(1 kw. 2011) (Autofiltr niestandardowy
jest większe lub równe 100 000) a następnie przywrócić pełną listę
Rys. 5.4 Filtrowanie danych zużyciem Autofiltru
Filtr zaawansowany
- skopiować wiersze A2 – C3 i wkleić je do E2 – G3
- usunąć tekst z komórek E3 i G3
zaznaczyć komórkę B2 a następnie polecenie Dane – Filtr –Filtr Zaawansowany (Filtruj
listę na miejscu, zakres listy A2- C25 zakres kryteriów E2 – G3)
zaznaczyć komórkę B2 a następnie polecenie Dane – Filtr –Filtr Zaawansowany (Kopiuj
w inne miejsce, Zakres listy A2- C25 Zakres kryteriów E2 – G3 Kopiuj do A27)
-
usunąć kryteria i przekopiowaną listę
5.2.3 Sumowanie danych
W arkuszu istnieje możliwość automatycznego sumowania (wyznaczania średniej,
iloczynu, max, min itp.) wybranych rekordów. Można w tym celu wykorzystać Pole
automatycznego obliczania , które znajduje się na Pasku stanu (Narzędzia – Opcje – Widok –
Pasek stanu) lub funkcję SUMY.POŚREDNIE.
Pole automatycznego obliczania
- kliknąć prawym klawiszem Pole automatycznego obliczania (NUM) i zaznaczyć
opcję Suma
- zaznaczyć komórki C2, C4, C7, C16, C18 (na pasku Pola automatycznego
obliczania pojawiła się wartość sumy)

Technologia informacyjna - EXCEL
53
- powtórzyć to samo dla średniej
Sumy pośrednie
- włączyć Autofiltr i wybrać Rodzaj promocji: Prasa
- zaznaczyć komórki od C17 do C25 i kliknąć przycisk Autosumowanie (
)
- kliknąć komórkę C26 (SUMY.POŚREDNIE(9,C17:C25)
- zmienić Rodzaj promocji na Telewizja
- argumenty funkcji SUMY.POŚREDNIE mogą być następujące: 1=ŚREDNIA,
2=ILE.LICZB,
3=ILE.NIEPUSTYCH,
4=MAX,
5=MIN,
6=ILOCZYN,
7=ODCH.STANDARDOWE
8=ODCH.STANDARDOWE.POPUL,
9=SUMA,
10=WARIANCJA, 11==WARIANCJA.POPUL
- obliczyć SUMY.POŚREDNIE dla średniej
Rys. 5.5 Sumowanie wybranych danych
5.2.4 Tworzenie konspektu
Po odpowiednim do potrzeb posortowaniu danych można je przedstawić w postaci
konspektu .Funkcja SUMY.POŚREDNIE (wykorzystywana w konspekcie) umożliwia uzyskanie
wymaganych podsumowań. Kolejne poziomy konspektu pozwalają na wyświetlenie danych
z różnym stopniem szczegółowości.
Przykład:
Plik I_kwartał zawiera dane na temat dochodów pracowników pewnej firmy uzyskanych
z różnych źródeł. Należy wykonać zestawienie dochodów (łączne z podsumowaniami)
poszczególnych pracowników z podziałem na kolejne miesiące. W tym celu najpierw sortuje się
tabelę względem pracowników a następnie względem miesięcy a później tworzy się konspekt.
otworzyć plik I_kwartał
- posortować tabelę: Dane – Sortuj – Sortuj według Reprezentant – rosnąco, Miesiąc
– rosnąco, Dochody_Suma– malejąco
- zablokować komórkę A3 ( w celu umożliwienia przewijania arkusza bez nagłówka
tabeli): ustawić się w komórce A3 i wybrać polecenie: Okno – Zablokuj okienka
- ukryć kolumnę C
pierwszy poziom konspektu
- kliknąć dowolną komórkę w tabeli
- polecenie Dane – Sumy Pośrednie – Dla każdej zmiany w polu Reprezentant, Użyj
funkcji: Suma, Dodaj sumę pośrednią do: Dochody Prasa, Dochody Radio/TV,
Dochody Internet, Dochody Suma; zaznaczyć Zamień bieżące sumy pośrednie
i Podsumowanie poniżej danych
drugi poziom konspektu
- kliknąć dowolną komórkę w tabeli
- polecenie Dane – Sumy Pośrednie – Dla każdej zmiany w polu: Miesiąc, Użyj
funkcji: Suma, Dodaj sumę pośrednią do: Dochody Suma; odznaczyć Zamień
bieżące sumy pośrednie
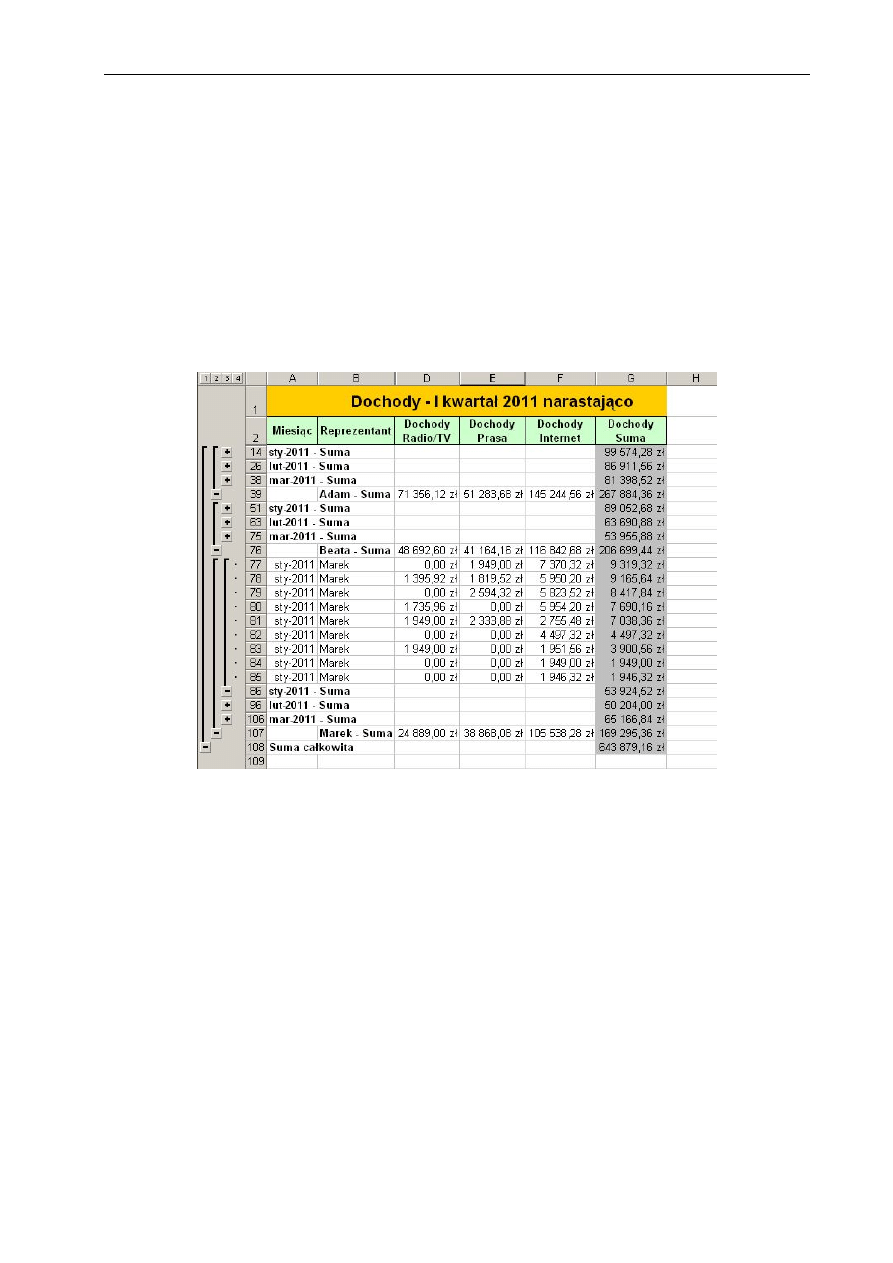
Technologia informacyjna - EXCEL
54
korzystanie z konspektu
- kliknąć poziom 3 (ukryte zostają wszystkie szczegóły poza sumami)
- kliknąć poziom 2 i usunąć wiersz 109
tworzenie rysunku z konspektu arkusza
- kliknąć poziom 3 konspektu
- zaznaczyć obszar A2 – G108
- nacisnąć Shift i wybrać Edycja – Kopiuj Rysunek – Tak jak na ekranie - Obraz
- otworzyć program Word a następnie plik Dochody i wkleić rysunek
- zmienić wielkość rysunku
wstawić do skoroszytu Dochody kilka kopii arkusza Dochody a następnie nagrać makro
służące do sortowania danych (sortuj) i makro do tworzenia sum pośrednich (sumy)
- stworzyć makro konspekt i je przetestować
Rys.5.6 Widok konspektu
Kod nagranego makra sortuj i makra sumy oraz makro konspekt przedstawione są poniżej:
Sub
sortuj()
Selection.Sort Key1:=Range("B3"), Order1:=xlAscending, Key2:=Range("A3") _
, Order2:=xlAscending, Key3:=Range("G3"), Order3:=xlDescending, Header _
:=xlGuess, OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom
End Sub
Sub
sumy()
Selection.Subtotal GroupBy:=2, Function:=xlSum, TotalList:=Array(4, 5, 6, 7)
_
, Replace:=True, PageBreaks:=False, SummaryBelowData:=True
Selection.Subtotal GroupBy:=1, Function:=xlSum, TotalList:=Array(7), _
Replace:=False, PageBreaks:=False, SummaryBelowData:=True
End Sub
Sub
konspekt()
sortuj
sumy
End Sub
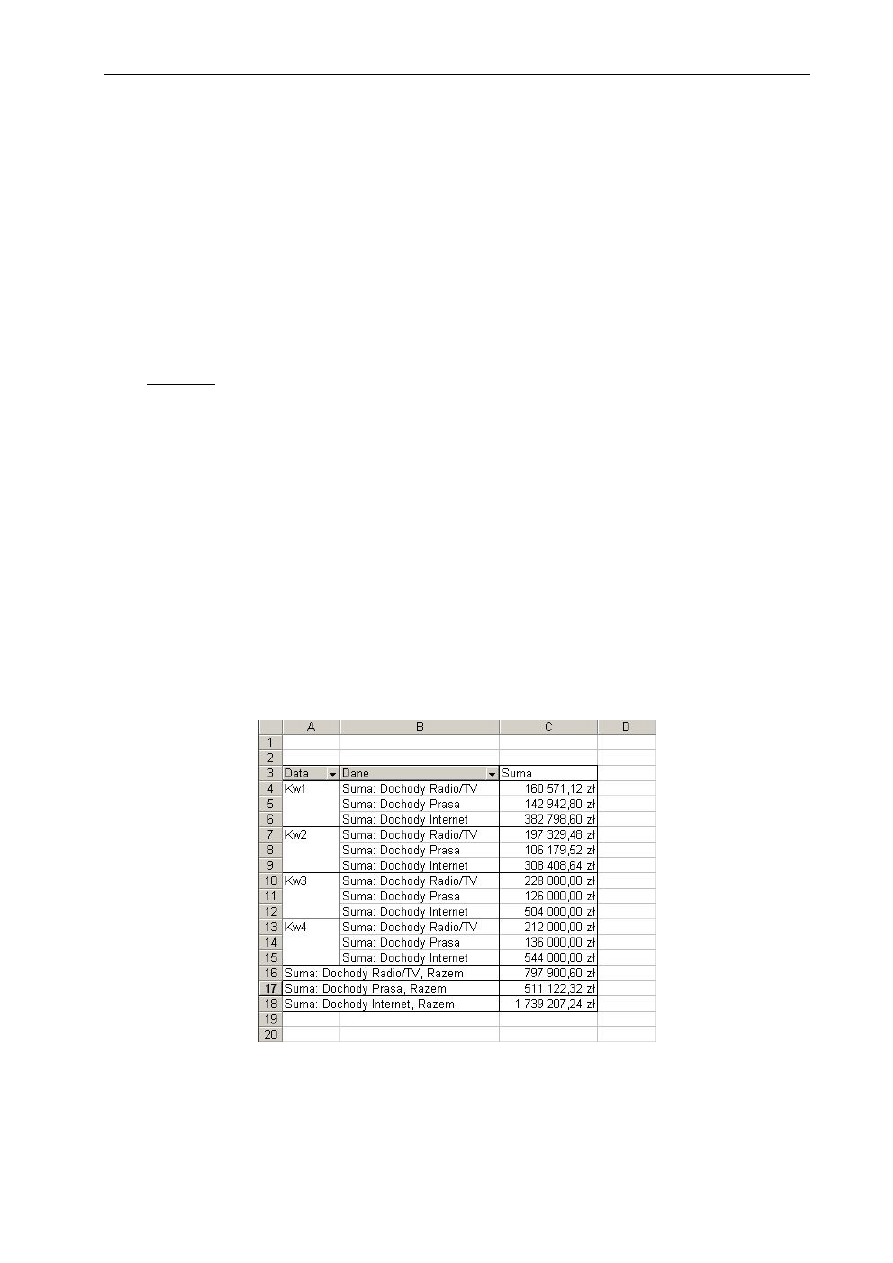
Technologia informacyjna - EXCEL
55
5.2.5 Tabele przestawne
Tabele przestawne pozwalają na modyfikację prezentacji danych zawartych w zwykłej
tabeli dzięki możliwości przenoszenia kolumn. W kreatorze tabel przestawnych dostępne są
następujące 4 pola w których można umieszczać kolumny danej tabeli: KOLUMNA, WIERSZ,
STRONA i DANE. W polu DANE mogą znajdować się jedynie kolumny zawierające wartości
liczbowe lub logiczne, ponieważ jest to pole obliczeniowe. Przesunięcie wybranej kolumny
do pola WIERSZ zmienia orientację danych na poziomą, natomiast umieszczenie jej w polu
STRONA pozwala na wyświetlenie danych w kolejnych arkuszach skoroszytu.
W poniższym przykładzie zostanie utworzonych kilka różnych tabel przestawnych
na podstawie danych zawartych w arkuszu Excela (tabela.xls) oraz w pliku tekstowym
(dane.txt).
Przykład:
tabela przestawna na podstawie danych z arkusza
tabela przestawna1 – sumaryczne dochody według kwartałów:
- ustawić się w dowolnej komórce tabeli arkusza Dochody (tabela.xls) i uruchomić
kreator tabeli przestawnej: Dane – Raport tabeli przestawnej
- w obszarze WIERSZ umieścić pole Data a w obszarze DANE pola: Dochody Internet,
Dochody Radio/TV, Dochody Prasa
- umieścić tabelę przestawną w nowym arkuszu i pogrupować dane według
kwartałów:
ustawić się w kolumnie Data, prawy klawisz: Grupy i konspekt – Grupuj
(według Kwartały)
- sformatować dane w kolumnie Suma jako walutowe:
ustawić się w dowolnej komórce kolumny Suma zawierającej dane liczbowe,
prawy klawisz: Ustawienia pola – Liczby – Walutowe; powtórzyć formatowanie
dla pozostałych pól
Rys. 5.7 Widok tabeli przestawnej 1

Technologia informacyjna - EXCEL
56
tabela przestawna 2 – modyfikacje tabeli przestawnej 1
- dodać pole Reprezentant do tabeli:
prawy klawisz – Kreator – do obszaru WIERSZ dodać pole Reprezentant
i umieścić tabelę przestawną w nowym arkuszu
ukryć wszystkich reprezentantów oprócz Beaty (kliknąć strzałkę listy rozwijanej
Reprezentant i ukryć odpowiednie pola)
Rys. 5.8 Widok tabeli przestawnej 2 dla wybranego pracownika
- zmienić orientację danych:
odsłonić ukryte pola
pole Data przenieść do KOLUMNY
w obszarze DANE umieścić pole Dochody Suma; pozostałe pola usunąć z tabeli
Rys. 5.9 Tabela przestawna 2 – zmiana orientacji danych
- zmienić prezentację danych:
przenieść pole Reprezentant z WIERSZA na STRONĘ
z obszaru DANE usunąć pole Dochody Suma; natomiast dodać pola: Dochody
Radio/TV, Dochody Prasa, Dochody Internet
obejrzeć strony dla poszczególnych reprezentantów
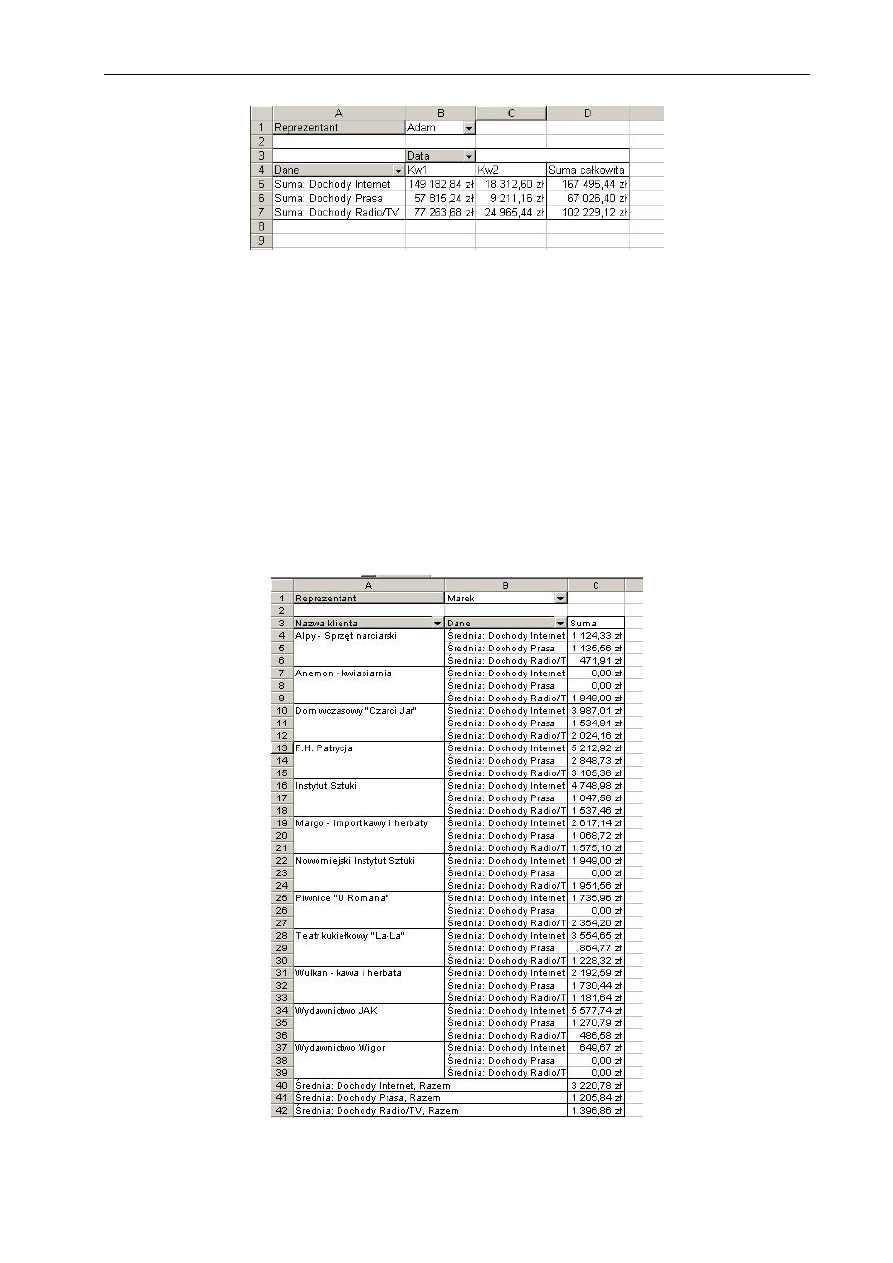
Technologia informacyjna - EXCEL
57
Rys. 5.10 Tabela przestawna 2 – zmiana prezentacji danych
- zmienić funkcję podsumowującą:
usunąć pole Reprezentant
pole Nazwa Klienta umieścić w WIERSZU
pole Data usunąć z KOLUMNY
zmienić funkcję podsumowującą: prawy klawisz: Pole – Średnia
- wyświetlić dane szczegółowe:
kliknąć dwukrotnie na dowolnej komórce pola Nazwa Klienta i wybrać
odpowiedni filtr
usunąć dodane pola
- stworzyć raport stronicowy
dodać pole Reprezentant do STRONY
prawy klawisz Pokaż strony
Rys. 5.11 Tabela przestawna 2 – raport stronicowy dla wybranego pracownika
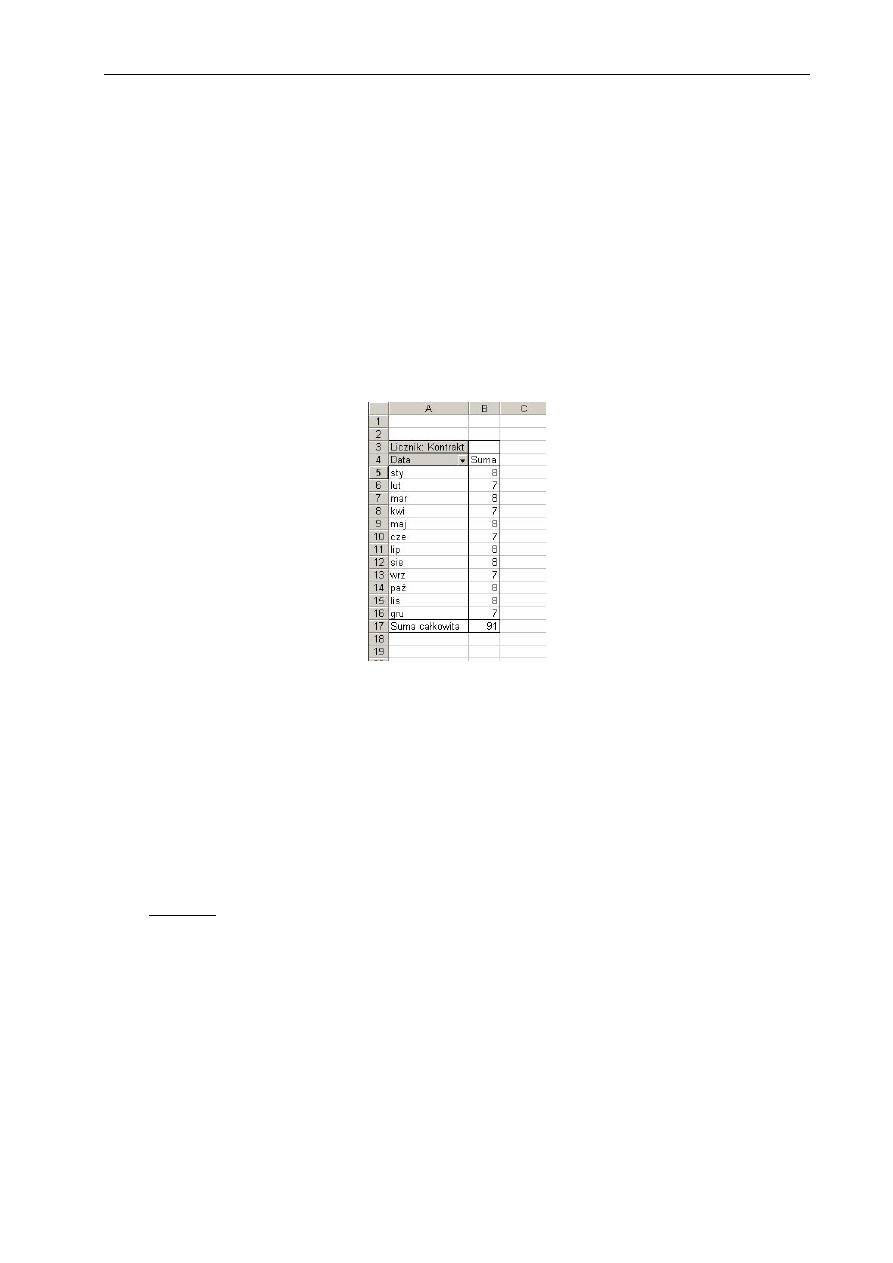
Technologia informacyjna - EXCEL
58
tabela przestawna na podstawie danych z pliku tekstowego
- import pliku tekstowego:
ustawić się w dowolnej komórce arkusza Dochody, Plik – Otwórz - Dane.txt;
pojawia się Kreator importu tekstu:
krok 1: zacznij import od wiersza 1; z separatorami
krok 2: separatory – tabulator
krok 3: format danych w kolumnie Data – RMD
- uruchomić kreator tabeli przestawnej: Dane – Raport tabeli przestawnej
- w obszarze WIERSZ umieścić pole Data a w obszarze KOLUMNA umieścić pole
Kontrakt w obszarze DANE pole Oferty
- umieścić tabelę przestawną w nowym arkuszu i pogrupować dane według miesięcy:
ustawić się w kolumnie Data, prawy klawisz: Grupy i konspekt – Grupuj
(według: Miesiące)
Rys. 5.12 Widok tabeli przestawnej z pliku tekstowego
5.2.6 Wykresy przestawne
Na podstawie tabeli przestawnej można w prosty sposób utworzyć wykres przestawny.
Wykres przestawny jest powiązany z tabelą a tabela z wykresem. Wszystkie listy rozwijane
z tabeli są dostępne na wykresie, więc można za ich pomocą modyfikując wykres jednocześnie
modyfikować tabelę.
W poniższym przykładzie została zaprojektowana tabela przestawna i wykres przestawny
na podstawie danych zawartych w pliku dane.xls.
Przykład:
Zaprojektować wykres przestawny zawierający prognozę spodziewanych dochodów
z trzech rodzajów reklam.
Rozwiązanie:
stworzyć tabelę przestawną o następująco rozmieszczonych polach:
- STRONA: pole Reprezentant, WIERSZ: pole Kwartał, KOLUMNA: pole Rodzaj
reklamy, DANE: pole Dochody
- wybrać Reprezentanta (Marek)
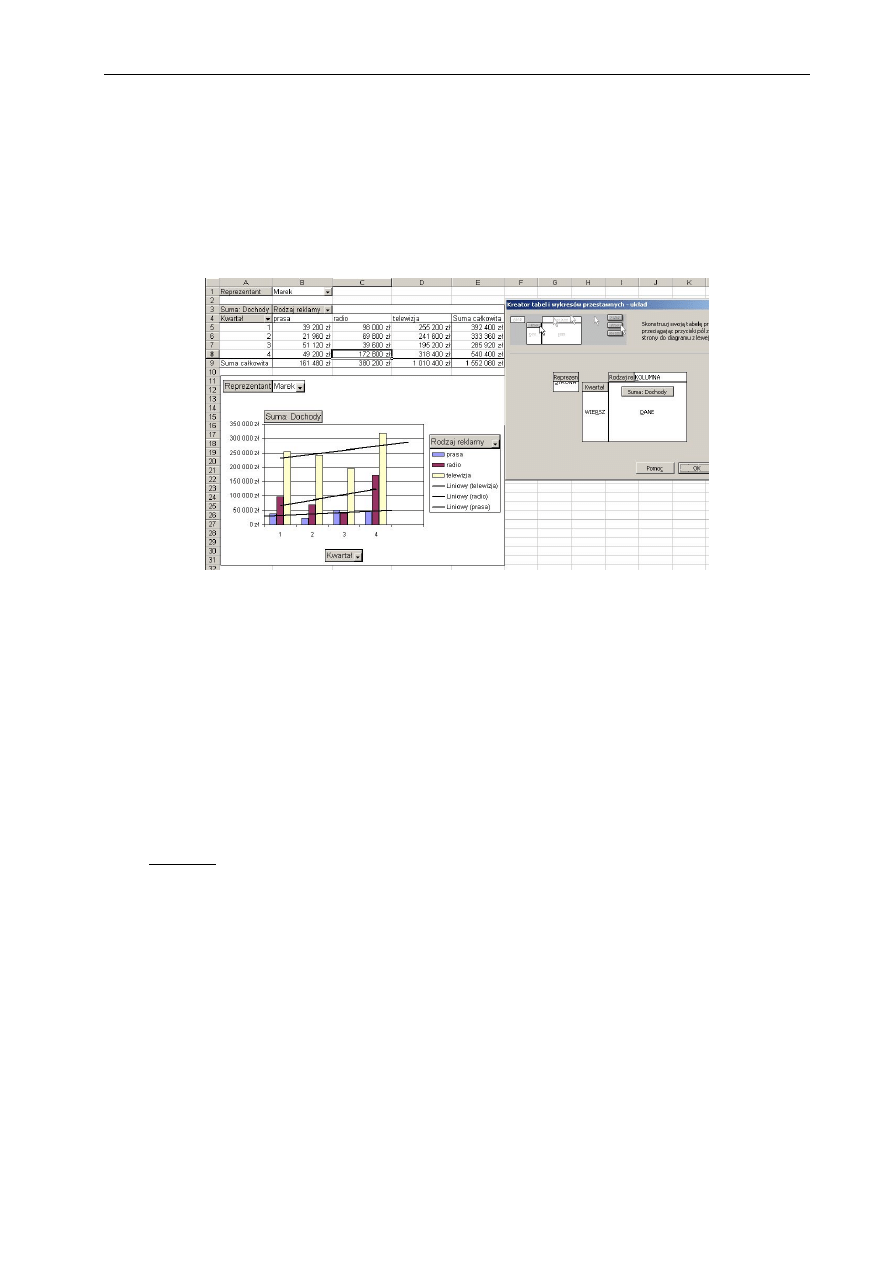
Technologia informacyjna - EXCEL
59
narysować wykres kolumnowy grupowany na podstawie danych z tabeli:
- dodać linię trendu z prognozą (prawy klawisz na określonym wykresie Dodaj linię
trendu - Typ liniowy, Opcje – Prognoza – Do przodu (podać ilość okresów))
Rodzaj reklamy: telewizja (Do przodu 1 okres), prasa (Do przodu 0,5 okresu,
Do tyłu 0,5 okresu)
-
wybierając różne dane z dostępnych list rozwijanych zaobserwować jak zmienia się
wykres i tabela przestawna
Rys. 5.13 Wykres przestawny dla wybranego pracownika
5.2.7 Scenariusze
Za pomocą Menadżera scenariuszy można stworzyć różne warianty tych samych obliczeń
umożliwiające analizę wpływu poszczególnych argumentów funkcji wielu zmiennych na jej
wartość końcową.
W przykładzie rozpatrywanym poniżej przedstawiony jest budżet pewnej firmy (plik
budżet.xls). Należy najpierw obliczyć (wykorzystując procedurę Szukaj wyniku) o ile muszą
wzrosnąć dochody z pracy, aby zysk operacyjny wzrósł o 40% a następnie stworzyć
odpowiednie scenariusze umożliwiające analizę wpływu wzrostu poszczególnych dochodów
na wzrost zysku operacyjnego.
Przykład:
Komórka B20 zawiera funkcję określoną formułą „=Dochody_suma-Wydatki_suma”.
Argumenty tej funkcji („Praca”, „Materiały”, „Produkcja”, „Podróże”), które zapisane są
w komórkach B3-B6, nazwane zostały jako „Dochody”.
Rozwiązanie:
zaznaczyć komórki A3–B6 oraz A9-B18 i wstawić nazwy (Wstaw – Nazwę – Utwórz –
Lewa kolumna)
Zastosowanie procedury Szukaj wyniku:
obliczyć jaką wartość powinny mieć dochody z pracy, aby zysk operacyjny wzrósł o 40%
- zaznaczyć komórkę B20: Narzędzia - Szukaj wyniku: Wartość – 70000, Zmieniając
komórkę - B3
- anulować zmiany i zapamiętać wartość
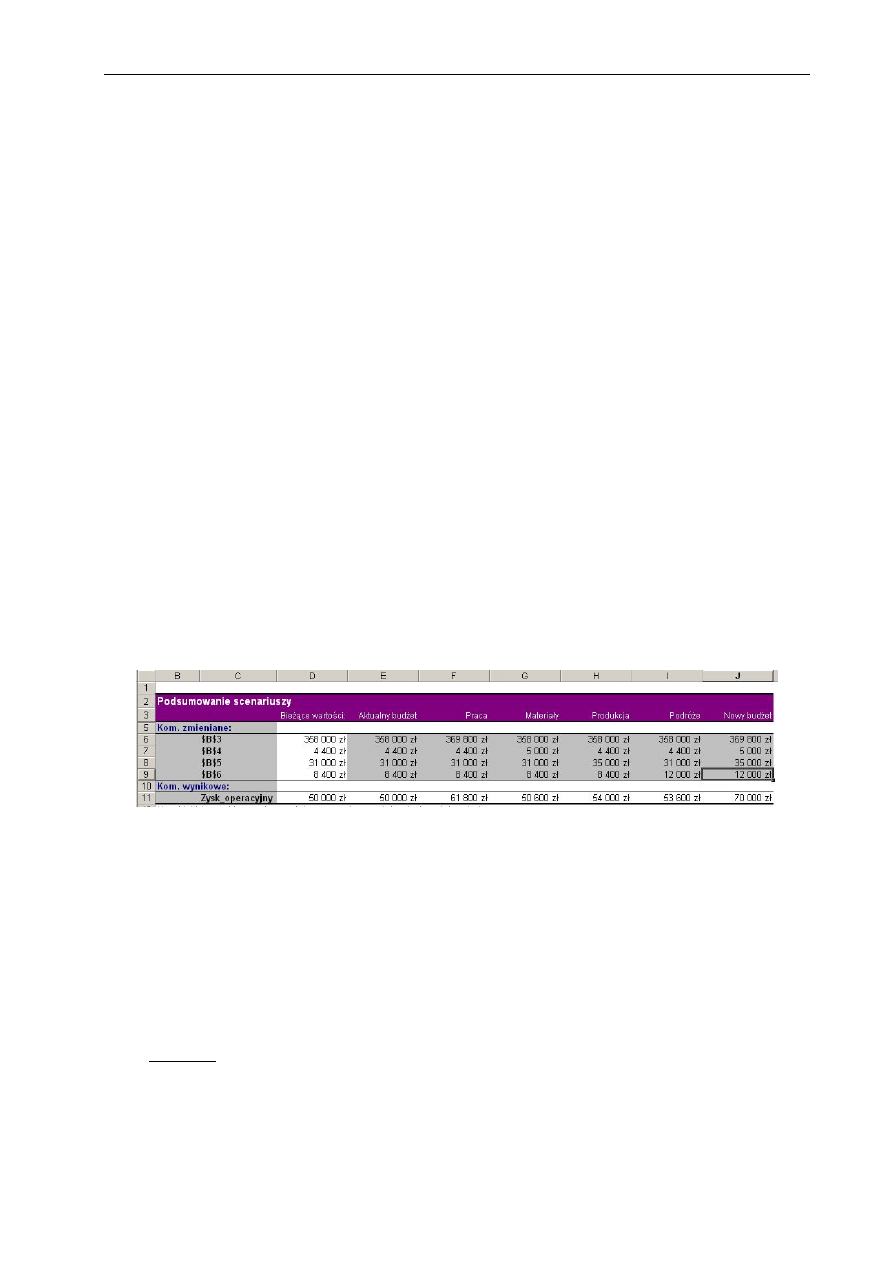
Technologia informacyjna - EXCEL
60
Tworzenie scenariuszy:
stworzyć 6 scenariuszy obejmujących kolejno aktualny budżet a następnie wzrost
dochodów (wynikający z dodania marży) z pracy, materiałów, produkcji i podróży
oraz nowy budżet uwzględniający wszystkie powyższe zmiany:
- Narzędzia – Menedżer scenariuszy – Dodaj: Nazwa scenariusza: Aktualny budżet,
Komórki zmieniane: B3-B6
- Narzędzia – Menedżer scenariuszy – Dodaj: Nazwa scenariusza: Praca, Komórki
zmieniane: B3-B6, Wartości scenariusza – Praca: 378 000
- Narzędzia – Menedżer scenariuszy – Dodaj: Nazwa scenariusza: Materiały,
Komórki zmieniane: B3-B6, Wartości scenariusza – Materiały: 5 000
- Narzędzia – Menedżer scenariuszy – Dodaj: Nazwa scenariusza: Produkcja,
Komórki zmieniane: B3-B6, Wartości scenariusza – Produkcja: 35 000
- Narzędzia – Menedżer scenariuszy – Dodaj: Nazwa scenariusza: Podróże,
Komórki zmieniane: B3-B6, Wartości scenariusza – Podróże: 12 000
-
Narzędzia – Menedżer scenariuszy – Dodaj: Nazwa scenariusza: Nowy budżet,
Komórki zmieniane: B3-B6, Wartości scenariusza – Praca: 378 000, Materiały:
5 000, Produkcja: 35 000, Podróże: 12 000
przeglądanie scenariuszy: Narzędzia – Menedżer scenariuszy – Pokaż (obejrzeć kolejne
scenariusze)
tworzenie podsumowania: Narzędzia – Menedżer scenariuszy – Podsumowanie
dokonywanie zmian w scenariuszach:
- usunąć arkusz Podsumowanie scenariuszy
-
Narzędzia – Menedżer scenariuszy: zaznaczyć scenariusz Nowy budżet – Edytuj
(zmienić: Podróże: 9 200, Produkcja: 36 800 ); odznaczyć: Chroń przed zmianami
Rys. 5.14 Widok Podsumowania scenariuszy
5.2.8 Kontrolki z okna dialogowego
W arkuszu Excela istnieje możliwość korzystania z kontrolek ActiveX, które są obiektami
graficznymi stanowiącymi interfejs użytkownika ułatwiający obsługę arkusza. Wszystkie te
kontrolki dostępne są na pasku Visual Basic w Przyborniku formantów. Są to m.in. Przycisk
polecenia, Przycisk pokrętła, Pasek przewijania, Pole kombi.
Jako
przykład
przedstawione
zostanie
wykorzystanie
powyższych
kontrolek
do zaprojektowania kalkulatora rat.
Przykład:
Zaprojektować kalkulator rat obliczający wysokość miesięcznej raty przy spłacie kredytu
na zakup domu. Oprocentowanie kredytu: (0 – 20% z krokiem 0,25%), Rabat przy zakupie:
(0 – 40% z krokiem 1%), Lata spłaty kredytu: (5 – 30 lat).

Technologia informacyjna - EXCEL
61
Rozwiązanie:
- komórki
B2-B7:
wpisać
kolejno
tekst:
„Cena”,
„Rabat”,
„Zapłata”,
„Oprocentowanie”, „Lata”, „Raty”
- komórki C2-C7: nadać nazwy (zaznaczyć B2-C7: Wstaw – Nazwę – Utwórz – Lewa
kolumna), wstawić obramowanie
- komórka C2: format walutowy całkowity, wpisać dowolną wartość
- komórka C3: format procentowy całkowity, wpisać dowolną wartość
- komórka C4: format walutowy całkowity, wpisać formułę: „= Cena*(1 - Rabat)”
- komórka C5: format procentowy (dwa miejsca po przecinku), wpisać dowolną
wartość
- komórka C6: wpisać dowolną dodatnią wartość całkowitą
- komórka C7: wpisać formułę: „=PMT(Oprocentowanie/12; Lata*12; Zapłata)”
funkcja PMT(oblicza wysokość raty) - zwraca liczbę okresów dla inwestycji
polegającej na stałych okresowych wpłatach przy stałym oprocentowaniu
PMT(stopa; liczba_rat; wa); wa - wartość do zapłacenia
- kolumna E: szerokość 23, wiersze od 1 do 8 wysokość 21
- komórka E6: wstawić Przycisk pokrętła; (w celu dopasowania wielkości formantu do
wielkości komórki kliknąć na formant a następnie wcisnąć klawisz Alt i przeciągnąć
wskaźnik myszy od lewego górnego rogu komórki E6 do jej prawego dolnego rogu)
zmienić właściwości formantu (prawy klawisz: Właściwości): LinkedCell
(komórka docelowa) – C6, Max: 30, Min: 5
- komórka E3: wstawić Przycisk pokrętła (analogicznie jak poprzednio)
właściwości formantu: LinkedCell – H3 (H3 - komórka pośrednia wprowadzana
w przypadku zmian o liczbę ułamkową, ponieważ we właściwościach formantu
dozwolone jest wpisywanie jedynie liczb całkowitych), Max: 40, Min: 0,
SmallChange: 1,
komórka C3: wpisać formułę: ”=H3/100” w celu zamiany liczby całkowitej
na wartość procentową
- komórka E5: wstawić Pasek przewijania (analogicznie jak poprzednio)
właściwości formantu: LinkedCell – H5, Max: 2000, Min: 100, LargeChange
(zmiana przy kliknięciu na pasku formantu)): 100, SmallChange (zmiana przy
kliknięciu na strzałkę formantu): 25,
komórka C5: wpisać formułę: ”=H5/10000”
- komórki J2 - L8: nadać nazwę Lista_domów, wpisać dane i dodać obramowanie
- komórka E2: wstawić Pole kombi
właściwości
formantu:
LinkedCell:
C2,
ListFillRange:
Lista_domów,
ColumnCount (ilość kolumn z danymi): 3, BoundColumn (numer kolumny
z której pobierane są dane): 3, Style (styl listy): 2-frmStyleDropDownList (2-lista
rozwijana; 0-lista rozwijana z edycją), Font (czcionka): 8, ColumnWidth
(szerokość kolumn z danymi wyświetlanymi w formancie): 36;36;36
Rys. 5.15 Widok arkusza z kalkulatorem rat

Technologia informacyjna - MATLAB
62
MATLAB
Technologia informacyjna - MATLAB
63
6. Podstawowe wiadomości o środowisku Matlab
6.1 Wiadomości wstępne
Pakiet Matlab jest szeroko stosowanym narzędziem wspomagającym rozwiązywanie
wszelkiego rodzaju problemów inżynierskich.
Pakiet składa się z interpretera języka symbolicznego, pakietu standardowych bibliotek,
pakietu bibliotek dodatkowych służących do rozwiązywania szczegółowych problemów
z wybranych dziedzin nauki (Toolbox) oraz nakładki Simulink wraz z własnymi bibliotekami
(tzw. „blockset”).
Program Matlab pozwala na pracę w dwóch trybach:
interaktywnym,
skryptowym
Tryb interaktywny polega na kolejnym pisaniu i wykonywaniu na bieżąco poszczególnych
komend w oknie poleceń (Command Window). Jest to wygodny sposób w przypadku bardzo
prostych zadań jak np. wykonywanie obliczeń arytmetycznych lub znajdowanie wartości funkcji
elementarnych.
Tryb skryptowy jest zasadniczym trybem pracy w środowisku Matlab. Polega on
na kolejnym wykonywaniu, linijka po linijce, poszczególnych komend przez wbudowany
interpreter języka programowania. Komendy te umieszcza się w pliku typu M-File. Pliki tego
rodzaju posiadają rozszerzenie m (nazwa_pliku .m).
Bezpośrednio po uruchomieniu programu pojawia się okno główne i można rozpocząć
pracę w trybie interaktywnym.
Rys. 6.1. Widok okna głównego Matlaba
W lewej części okna głównego widoczne są dwa okna pomocnicze wyświetlające
odpowiednio:
Launch Pad
załadowane biblioteki
Workspace
zestaw przechowywanych w pamięci zmiennych
Command history
listę wcześniej wykonanych komend
Current directory
zawartość bieżącego katalogu
W prawej części okna głównego znajduje się okno poleceń (Command Window) w którym
wykonywane są polecenia oraz wyświetlane są wyniki obliczeń i komunikaty o błędach.
Technologia informacyjna - MATLAB
64
6.2 Pomocnicze polecenia okna Command Window
cd
Polecenie cd z parametrami służy do zmiany bieżącego katalogu, natomiast bez
parametrów do wyświetlania aktualnego katalogu.
Składnia polecenia cd ma postać:
cd ścieżka
cd
Przykład:
zmiana katalogu
» cd c:/test/katalog1
przejście do nadrzędnego katalogu
» cd..
wyświetlenie bieżącego katalogu
» cd
clear
Polecenie clear powoduje usunięcie z obszaru roboczego (Workspace) znajdujących się
tam zmiennych. Polecenie clear może posiadać następujące składnie:
Clear nazwa_zmiennej
Clear functions
Clear all
Polecenie clear all powoduje usunięcie wszystkich zmiennych, funkcji oraz łącz
ze zbiorami MEX z obszaru roboczego.
clc
Polecenie clc czyści okno poleceń Matlaba (Command Window).
dir
Polecenie dir wyświetla zawartość bieżącego katalogu. Jest to polecenie analogiczne
do polecenia wykorzystywanego w DOS–ie.
disp
Polecenie disp służy do wyświetlania określonej zmiennej w oknie poleceń (Command
Window).
Przykład:
>> A=[1 2 3;4 5 6]
A =
1 2 3
4 5 6

Technologia informacyjna - MATLAB
65
>> disp(A)
1 2 3
4 5 6
format
Polecenie format umożliwia określenie formatu liczb wyświetlanych na ekranie.
W Matlabie domyślnym formatem jest format short, który pozwala na wyświetlenie czterech
cyfr po przecinku. Wyświetlenie czternastu cyfr po przecinku zapewnia format long.
Przykład:
>> 1/7
ans =
0.1429
>> format long
>> 1/7
ans =
0.14285714285714
help
Polecenie help użyte bez parametrów wyświetla listę katalogów Matlaba zdefiniowanych
w ścieżkach przeszukiwań, natomiast polecenie help z parametrem powoduje wyświetlenie
pomocy dotyczącej wskazanego polecenia.
Polecenie help bez parametru:
Przykład:
» help
HELP topics:
MATLAB\general - General purpose commands.
MATLAB\ops - Operators and special characters.
MATLAB\lang - Programming language constructs.
MATLAB\elmat - Elementary matrices and matrix manipulation.
MATLAB\elfun - Elementary math functions.
For more help on directory/topic, type "help topic".
Polecenie help z parametrem:
Help nazwa_polecenia
Przykład:
» help sin
SIN Sine.
SIN(X) is the sine of the elements of X.
home
Polecenie home powoduje wyczyszczenie okna poleceń Matlaba oraz ustawienie kursora
w jego lewym górnym rogu.
Technologia informacyjna - MATLAB
66
matlabpath
Polecenie matlabpath wyświetla listę ścieżek przeszukiwań. Polecenie to nie posiada
argumentów wejściowych.
Przykład:
» matlabpath
MATLABPATH
D:\MATLAB\sn
D:\MATLAB\toolbox\MATLAB\general
D:\MATLAB\toolbox\MATLAB\ops
path
Polecenie path służy do wyświetlania i dodawania ścieżek przeszukiwań. Użycie polecenie
path bez parametrów ma działanie analogiczne jak polecenie matlabpath.
W przypadku, gdy chcemy dodać ścieżkę przeszukiwań należy zastosować składnię:
path(path,
’ścieżka_do_katalogu’
)
pwd
Polecenie pwd wyświetla zawartość bieżącego katalogu; jest ono analogiczne do polecenia
cd bez parametrów.
Przykład:
» pwd
ans =
D:\MATLAB\bin
ver
Polecenie ver wyświetla informacje o wykorzystywanej wersji Matlaba i zainstalowanych
bibliotekach dodatkowych.
Przykład:
>> ver
To get started, select "MATLAB Help" from the Help menu.
MATLAB Version 6.0.0.88 (R12) on PCWIN
MATLAB License Number: 191257
--------------------------------------------------
MATLAB Toolbox Version 6.0 (R12) 06-Oct-2000
Simulink Version 4.0 (R12) 16-Jun-2000
MATLAB Compiler Version 2.1 (R12) 26-Jul-2000
Control System Toolbox Version 5.0 (R12) 01-Sep-2000
DSP Blockset Version 4.0 (R12) 01-Sep-2000
who
Polecenie who wyświetla listę zmiennych przechowywanych w obszarze roboczym
(Workspace).
Technologia informacyjna - MATLAB
67
Przykład:
» who
Your variables are:
a b
whos
Działanie polecenia whos jest podobne do polecenia who, ale wyświetla rozszerzone
informacje o przechowywanych zmiennych.
Przykład:
» whos
Name Size Bytes Class
a 2x3 48 double array
b 2x3 48 double array
Grand total is 33 elements using 138 bytes
6.3 Skrypty i funkcje użytkownika
Skrypty
Skrypt jest plikiem typu M-File (o rozszerzeniu m), w którym umieszcza się program
obliczeniowy napisany zgodnie z regułami obowiązującymi w Matlabie.
Obliczenia można również przeprowadzać w trybie interaktywnym, jednakże jest on mało
efektywny i dlatego powinien być wykorzystywany jedynie do prostych działań.
Jeżeli skrypt zapisany został w katalogu roboczym Matlaba (katalog Work), wówczas
wykonanie obliczeń w nim zawartych (bez potrzeby jego otwierania) następuje po napisaniu
w oknie poleceń (Command Window) nazwy skryptu (bez rozszerzenia) i wciśnięciu klawisza
Enter. Otwarty skrypt można również uruchomić korzystając z poleceń paska narzędzi edytora
skryptów (Editor - Debug - Run).
W przypadku umieszczenia skryptu w innym katalogu niż roboczy, należy podać ścieżkę
do tego katalogu korzystając z polecenia path (np. path(path,’G:\katalog’)), lub po jej
zmapowaniu ustawić ją w oknie Command Window (File - Set Path...).
Przykład prostego skryptu zostanie przedstawiony poniżej.
Przykład:
Rysowanie funkcji sinus w przedziale < 1; 2 > z krokiem 0,01.
x=1:0.01:2;
y=sin(x);
plot(x,y)
Należy zwrócić uwagę na zastosowanie znaku średnika. Znak średnika umieszczony
na końcu wiersza powoduje, że w oknie poleceń (Command Window) nie są wyświetlane
zarówno pośrednie obliczenia jak i wynik końcowy. Aby wyświetlić określoną zmienną
lub jedną z jej wartości należy skorzystać z polecenia disp.

Technologia informacyjna - MATLAB
68
Komentarze
Znak „%” na początku wiersza oznacza, że wiersz ten jest komentarzem lub, że polecenia
w nim zawarte mają zostać pominięte podczas wykonywania programu.
Komentarz zamieszczony na początku skryptu (do momentu pojawienia się pierwszego
pustego wiersza lub wiersza bez znaku komentarza) traktowany jest jako tekst pomocy danego
skryptu.
Przykład:
kod skryptu plik.m:
%komentarz 1
%komentarz 2
%x=2
y=5
help skryptu plik.m:
>> help plik
komentarz 1
komentarz 2
wykonanie skryptu plik.m:
>> plik
y =
5
Funkcje
W Matlabie istnieje możliwość zadeklarowania własnej funkcji. Definicję własnej funkcji
umieszcza się w skrypcie, którego nazwa powinna być taka sama jak nazwa funkcji.
Składnia polecenia jest następująca:
function zmienna = nazwa_funkcji(argument_1,..., argument_n)
instrukcje
Przykład:
deklaracja funkcji obliczającej sumę trzech liczb (skrypt o nazwie suma.m):
function
y=suma(a,b,c)
y=a+b+c;
kod skryptu o nazwie dodawanie.m wykorzystującego deklarowaną funkcję
:
a=2;
b=3;
c=4;
wynik=suma(a,b,c)
wykonanie skryptu:
>>dodawanie
wynik =
9
Zmienne deklarowane w funkcji są zmiennymi lokalnymi, czyli po zakończeniu działania
funkcji usuwane są z pamięci, co powoduje, że nie można się już do nich odwołać.

Technologia informacyjna - MATLAB
69
Zadeklarowanie zmiennych jako globalnych spowoduje, że po zakończeniu działania
funkcji zmienne te będą ciągle dostępne.
Zmienne deklarowane są jako globalne przy pomocy instrukcji global:
global zmienna_1 zmienna_2 ... zmienna_N
Należy zadeklarować wykorzystywane w funkcji zmienne globalne również w skrypcie.
input
Polecenie input wykorzystywane jest do wprowadzania z klawiatury wartości zmiennych.
Składnia polecenia input jest następująca:
zmienna = input(
‘tekst_zachęty’
)
Przykład:
obliczanie sumy dwóch liczb a i b wprowadzanych z klawiatury (skrypt o nazwie plik.m):
a=input(
'Podaj wartość liczby a = '
);
b=input(
'Podaj wartość liczby b = '
);
wynik=a+b
wykonanie skryptu plik.m następuje po podaniu wartości a i b:
>> plik
Podaj wartość liczby a = 2
Podaj wartość liczby b = 5
wynik =
7
6.4 Operacje na macierzach i tablicach wartości
W Matlabie podstawowym typem danych są macierze. Wielkości skalarne można
traktować jako macierze o wymiarach 1 x 1, a po umieszczeniu ich w tablicach wartości można
wykonywać na nich dowolne operacje matematyczne.
Zastosowanie rachunku macierzowego pozwala na prostsze rozwiązywanie różnorodnych
problemów matematycznych, np. rozwiązywanie układu n równań.
Operatory matematyczne
Postać ogólną macierzy można zapisać w następujący sposób:
n
m
mn
1
m
n
1
11
a
...
a
...
...
...
a
...
a
A
m n jest wymiarem macierzy A
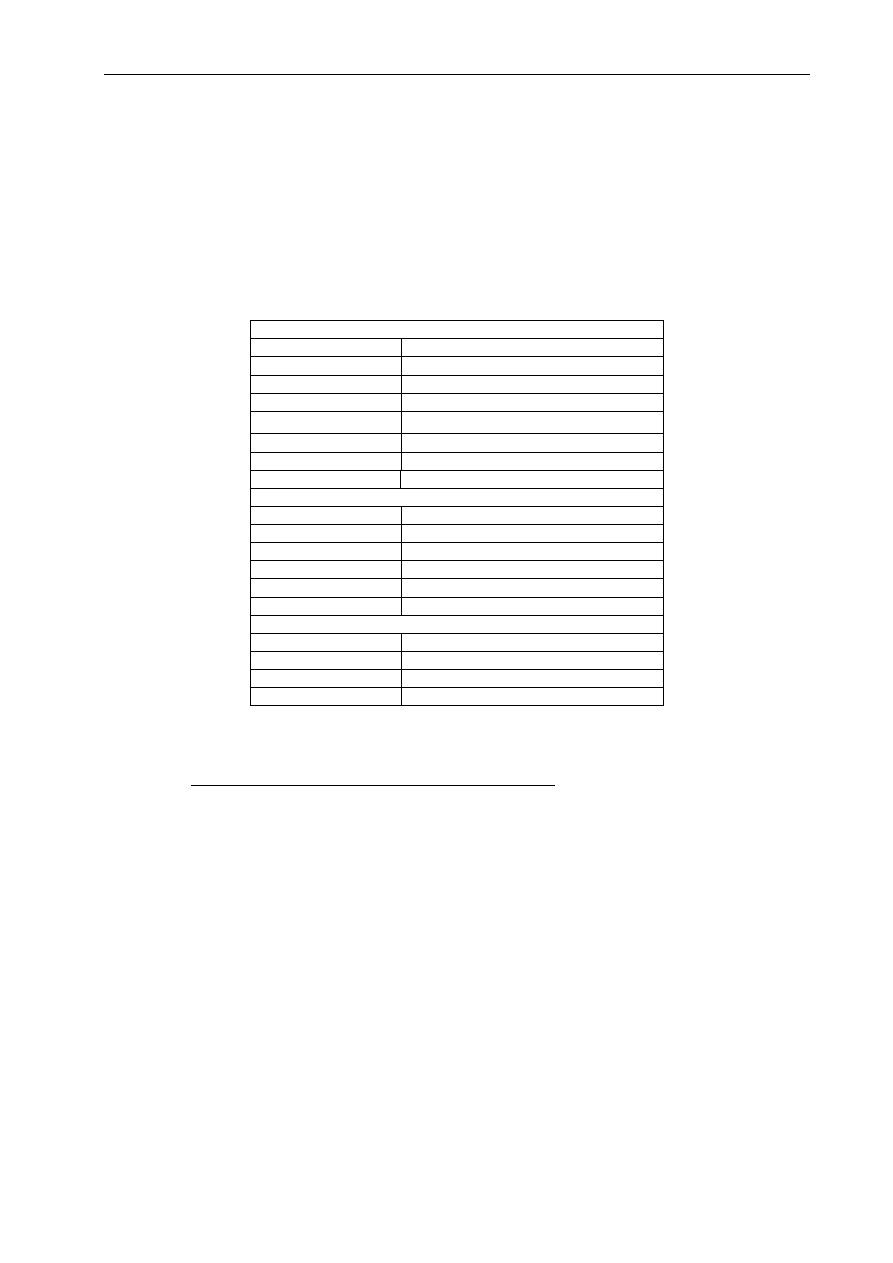
Technologia informacyjna - MATLAB
70
Działania na macierzach lub tablicach wartości sprowadzają się do odpowiednich działań
na poszczególnych elementach macierzy lub tablicy wartości. Zastosowanie wszystkich
operatorów matematycznych w obydwu przypadkach jest identyczne za wyjątkiem mnożenia,
dzielenia i potęgowania.
Wykorzystanie operatorów porównania i operatorów logicznych powoduje przypisanie
każdemu niezerowemu elementowi danej macierzy wartości logicznej 1 i każdemu elementowi
zerowemu wartości logicznej 0. W wyniku otrzymuje się, zgodnie z wymaganym działaniem,
odpowiednią macierz o elementach zerojedynkowych.
Operatory arytmetyczne
+, -
dodawanie, odejmowanie
mnożenie
/
dzielenie (dzielenie prawostronne)
\
dzielenie (dzielenie lewostronne)
^
potęgowanie
transpozycja macierzy (tablicy)
=
znak równości
.
operator tablicowy
Operatory porównania
==
równe tożsamościowo
~=
różne
<
mniejsze
>
większe
<=
mniejsze równe
>=
większe równe
Operatory logiczne
|
alternatywa
&
koniunkcja
xor( )
różnica symetryczna
-
negacja
Tab. 6.1 Operatory matematyczne
Wprowadzanie formuł i wartości liczbowych
Matlab umożliwia także dokonywanie operacji arytmetycznych dla poszczególnych
elementów macierzy, przy wykorzystaniu tzw. operatorów tablicowych. W celu odróżnienia
działań dokonywanych na macierzach od działań dokonywanych na tablicach wartości,
w przypadku tablic wartości należy zawsze po zmiennej umieścić kropkę przed znakiem
mnożenia dzielenia i potęgowania (np. 3*x.^2 – x.*sin(x) + x./cos(x)). W przypadku dzielenia
kropkę stosuje się również przed znakiem dzielenia (np. 2./x).
Elementy macierzy lub tablicy wartości umieszcza się zawsze w nawiasach kwadratowych,
natomiast nawiasy zwykłe są zarezerwowane dla argumentów poleceń lub funkcji Matlaba.
Poszczególne argumenty oddzielane są przecinkami i jeżeli nie stanowią zmiennej lub liczby
umieszczane są w apostrofach (np. plot(x, y,’r*’)).
W Matlabie macierze należy oznaczać dużymi literami, natomiast wektory bądź tablice
wartości mogą być oznaczane małymi lub dużymi literami. Tę samą zmienną zapisaną raz małą
a raz dużą literą program traktuje jak dwie różne zmienne.

Technologia informacyjna - MATLAB
71
Deklaracje macierzy
Macierz można zadeklarować w sposób następujący: podać elementy macierzy,
wygenerować elementy macierzy, zdefiniować macierz wykorzystując zależności określające jej
elementy lub skorzystać z biblioteki Matlaba.
Tworzenie macierzy przez podanie jej elementów
Macierz tworzy się poprzez umieszczenie jej poszczególnych elementów, oddzielonych
spacjami, w nawiasach kwadratowych.
22
21
12
11
a
a
;
a
a
A
Przykład
:
» A=[1 1;2 2]
A =
1 1
2 2
Znak średnika (;) lub wciśnięcie klawisza Enter oznacza początek następnego wiersza
macierzy.
W przypadku, gdy liczba elementów macierzy jest duża (lub polecenie nie mieści się
w jednej linii) należy wykorzystać znak ..., który powoduje, że tekst znajdujący się
w następnej linii jest częścią tekstu poprzedniej linii.
Przykład:
» A=[1 1;...
2 2]
A =
1 1
2
2
Deklaracja pustej macierzy:
» A=[]
A =
[]
Definiowanie macierzy poprzez generowanie jej elementów
Definiowanie
macierzy
poprzez
generowanie
jej
elementów
realizowane
jest
w następujący sposób:
A = wartość_początkowa : krok : wartość_końcowa
Przykład:
» A=1:1:10
A =
1 2 3 4 5 6 7 8 9 10
Powyższe polecenie powoduje utworzenie 10-elementowej macierzy wierszowej.

Technologia informacyjna - MATLAB
72
Wykorzystując elementy tablicy wartości x można wygenerować tablicę wartości y, której
elementy określone są w sposób następujący: y
ij
= f(x
ij
).
Przykład:
>> x=1:1:5
x =
1
2
3
4
5
>> y=x.^2
y =
1
4
9
16
25
Generowanie macierzy na podstawie zależności określającej jej elementy
Przykład:
Elementy macierzy Hilberta zdefiniowane są za pomocą zależności: A(i,j) = 1/(i+j-1).
Elementy te można wygenerować wykorzystując dwie pętle for. Dla stopnia macierzy n = 5
program obliczeniowy jest następujący:
>> n=5
for
i=1:n
for
j=1:n
A(i,j)=1/(i+j-1);
end
end
disp(A)
Rozwiązanie:
A =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
Średnik na końcu linii powoduje pominięcie wyświetlania pośrednich obliczeń
wykonywanych w danej linii. Polecenie disp(A) wyświetla wynik.
Macierz Hilberta można także pobrać z biblioteki Matlaba pisząc polecenie hilb(n), gdzie
n jest stopniem macierzy.
Wyznacznik macierzy
Wyznacznik macierzy kwadratowej (|macierz|) obliczany jest przy pomocy funkcji
det(macierz).
Dla macierzy stopnia drugiego zależności są następujące:
22
21
12
11
b
b
b
b
B
21
12
22
11
b
b
b
b
B

Technologia informacyjna - MATLAB
73
Przykład:
>> B=[1 2; 3 4]
B =
1 2
3 4
>> det(B)
ans =
-2
Wymiar macierzy
Polecenie size(macierz) służy do określania wymiaru macierzy.
[w, k] = size (A
)
wyświetla ilość wierszy w i kolumn k macierzy A
w= size (A,1)
wyświetla ilość wierszy w macierzy A
k= size (A,2)
wyświetla kolumn k macierzy A
Przykład:
» A=[ 1 4 6;2 3 4; 4 8 10]
A =
1 4 6
2 3 4
4 8 10
» size(A)
ans =
3 3
length
Polecenie length(wektor) podaje wymiar wektora. W przypadku, gdy argumentem
wejściowym jest macierz wyświetlany jest większy z wymiarów macierzy.
Przykład:
wymiar wektora
>> A=[1 2 3 4 5 6 7]
A =
1 2 3 4 5 6 7
>> length(A)
ans =
7
wymiar macierzy
» A=[1 2 3 4 5;1 3 4 5 6]

Technologia informacyjna - MATLAB
74
A =
1 2 3 4 5
1 3 4 5 6
» length(A)
ans =
5
Odwołania do dowolnego elementu macierzy
Aby odwołać się do danego elementu A(i,j) macierzy A należy podać jego współrzędne;
tzn. numer wiersza i oraz kolumny j na przecięciu których znajduje się ten element.
Przykład:
» A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15]
A =
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
» A(2,3)
ans =
8
Transpozycja macierzy
Transpozycja macierzy, czyli zamiana wierszy i kolumn, realizowana jest przy pomocy
operatora ‘ .
23
22
21
13
12
11
a
a
a
a
a
a
A
23
13
22
12
21
11
'
a
a
a
a
a
a
A
Przykład:
>> A=[1 2 3; 4 5 6]
A =
1 2 3
4 5 6
>> A'
ans =
1 4
2 5
3 6
Odwracanie macierzy
Odwracanie macierzy (macierz
-1
) realizowane jest zgodnie z poniższym zależnościami
(przedstawionymi dla macierzy stopnia drugiego), przy pomocy funkcji inv(macierz).
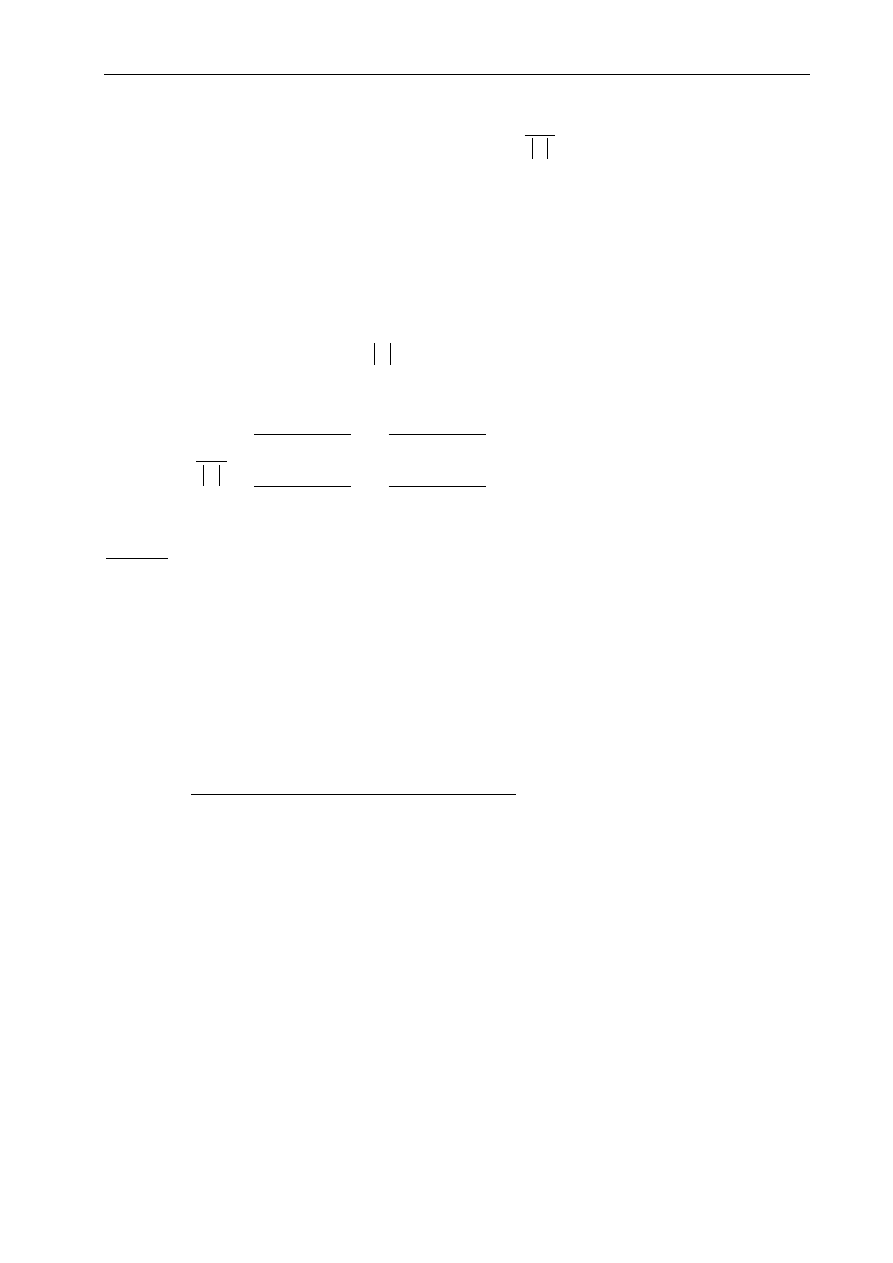
Technologia informacyjna - MATLAB
75
22
21
12
11
b
b
b
b
B
B
B
B
*
D
1
11
4
*
22
12
3
*
21
21
3
*
12
22
2
*
11
T
*
22
*
21
*
12
*
11
*
D
b
1
b
1
b
1
b
1
B
B
B
B
B
B
B
B
B
11
21
12
22
*
D
b
b
b
b
B
21
12
22
11
b
b
b
b
B
21
12
22
11
11
21
12
22
11
21
21
12
22
11
12
21
12
22
11
22
*
D
1
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
B
B
B
Przykład:
>> A=[1 2;3 4]
A =
1 2
3 4
>> inv(A)
ans =
-2.0000 1.0000
1.5000 -0.5000
Dodawanie oraz odejmowanie macierzy
Dodawanie oraz odejmowanie macierzy lub tablic wartości o jednakowych wymiarach
dokonywane jest zgodnie z zależnościami:
22
21
12
11
a
a
a
a
A
22
21
12
11
b
b
b
b
B
22
22
21
21
12
12
11
11
b
a
b
a
b
a
b
a
B
A
Dodawanie dowolnej stałej s do macierzy realizowane jest w sposób następujący:
s
a
s
a
s
a
s
a
s
22
21
12
11
A
Technologia informacyjna - MATLAB
76
W przypadku, gdy wymiary macierzy A i B są różne wyświetlony zostanie komunikat o błędzie:
Matrix dimensions must agree. (Wymiary macierzy muszą się zgadzać)
Mnożenie macierzy
Działanie mnożenia macierzy wykonywane jest przy pomocy operatora *. Macierz
można pomnożyć zarówno przez inną macierz jak i przez skalar. W przypadku mnożenia
macierzy musi być spełniony następujący warunek: liczba kolumn pierwszej macierzy jest równa
liczbie wierszy drugiej macierzy.
W przypadku mnożenia tablic wartości ich wymiary muszą być identyczne, a ponadto
należy przed znakiem mnożenia postawić kropkę (tzw. operator tablicowy).
Zasady mnożenia macierzy i tablic wartości dla macierzy kwadratowych stopnia drugiego
zostały przedstawione poniżej:
22
21
12
11
a
a
a
a
A
22
21
12
11
b
b
b
b
B
mnożenie macierzy
22
22
12
21
21
22
11
21
22
12
12
11
21
12
11
11
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
* B
A
mnożenie tablic wartości
22
22
21
21
12
12
11
11
b
a
b
a
b
a
b
a
B
*
.
A
potęgowanie macierzy
A^3 = A*A*A
potęgowanie tablic wartości
3
22
3
21
3
12
3
11
a
a
a
a
3
.^
A
Przykłady:
>> A=[1 2;3 4]
A =
1 2
3 4
>> B=[5 6;7 8]
B =
5 6
7 8
Technologia informacyjna - MATLAB
77
mnożenie macierzy
>> A*B
ans =
19 22
43 50
mnożenie tablic wartości
>> A.*B
ans =
5 12
21 32
Dzielenie macierzy
Działanie dzielenia macierzy wykonywane jest za pomocą operatora / (dzielenie
prawostronne) lub operatora \ (dzielenie lewostronne).
22
21
12
11
a
a
a
a
A
22
21
12
11
b
b
b
b
B
dzielenie macierzy (dzielenie prawostronne)
B
B
A
B
A
B
A
*
D
1
*
*
/
21
12
22
11
11
22
12
21
21
12
22
11
21
22
22
21
21
12
22
11
11
12
12
11
21
12
22
11
21
12
22
11
1
b
b
b
b
b
a
b
a
b
b
b
b
b
a
b
a
b
b
b
b
b
a
b
a
b
b
b
b
b
a
b
a
* B
A
dzielenie tablic wartości
22
22
21
21
12
12
11
11
b
a
b
a
b
a
b
a
B
/
.
A
dzielenie lewostronne macierzy
Dzielenie lewostronne macierzy wykorzystywane jest przy rozwiązywaniu układów
równań liniowych metodą eliminacji Gaussa z częściowym wyborem elementu głównego.
Rozwiązanie układu dwóch równań liniowych realizowane jest w sposób pokazany poniżej.

Technologia informacyjna - MATLAB
78
b
\
x
lub
b
x
to
b
x
x
x
x
b
b
b
a
a
a
a
b
x
a
x
a
b
x
a
x
a
1
2
1
2
1
22
21
12
11
2
2
22
1
21
1
2
12
1
11
A
A
A
A
x = A \ b
rozwiązanie układu równań liniowych metodą eliminacji Gaussa
z częściowym wyborem elementu głównego (dzielenie lewostronne)
x = A
-1
b
rozwiązanie układu równań metodą odwracania macierzy
dzielenie lewostronne tablic wartości
A
/
.
B
a
b
a
b
a
b
a
b
B
.\
A
22
22
21
21
12
12
11
11
Zapis A.\B równoznaczny jest z zapisem B./A
Przykłady:
W przykładach wykorzystane zostały dane macierze A i B.
>> A=[1 2;3 4]
A =
1 2
3 4
>> B=[5 6;7 8]
B =
5 6
7 8
dzielenie macierzy (dzielenie prawostronne)
>> A/B
ans =
3.0000 -2.0000
2.0000 -1.0000
dzielenie tablic wartości
>> A./B
ans =
0.2000 0.3333
0.4286 0.5000

Technologia informacyjna - MATLAB
79
dzielenie stałej przez tablicę wartości
>> 2./B
ans =
0.4000 0.3333
0.2857 0.2500
W przypadku dzielenia stałej przez tablicę wartości również należy wykorzystać operator
dzielenia tablicowego ./ , w przeciwnym wypadku pojawi się komunikat o błędzie.
>> 2/B
??? Error using ==> mrdivide
Matrix dimensions must agree.
dzielenie lewostronne macierzy
Dany układ równań zostanie rozwiązany metodą eliminacji Gaussa z częściowym
wyborem elementu głównego i metodą odwracania macierzy.
7
x
3
x
2
4
x
2
x
2
1
2
1
>> A=[1 2;2 3]
A =
1 2
2 3
>> b=[4;7]
b =
4
7
>> x=A\b
x =
2
1
>> x=inv(A)*b
x =
2
1
dzielenie lewostronne tablic wartości
A.\B=B./A
>> A.\B
ans =
5.0000 3.0000
2.3333 2.0000
>> B./A
ans =
5.0000 3.0000
2.3333 2.0000
Technologia informacyjna - MATLAB
80
6.5 Funkcje wspomagające generowanie macierzy
Zestawienie funkcji wspomagających generowanie macierzy dostępnych w Matlabie
zawiera tabela 6.2.
Nazwa
Opis
Eye(n)
Eye(m,n)
Eye([m n])
Tworzy macierz zawierającą jedynki na głównej przekątnej.
Ones(n)
Ones([m n])
Generuje macierz o danych wymiarach, której elementami są
jedynki.
Zeros(n)
Zeros([m n])
Generuje macierz o danych wymiarach, której elementami są
zera
Rand(n)
Rand([m n])
Tworzy macierz stopnia n o elementach pseudolosowych i
rozkładzie jednostajnym z przedziału <0, 1>
Randn(n)
Randn([m n])
Tworzy macierz o danych wymiarach zawierającą elementy
pseudolosowe o rozkładzie normalnym, wartościach średnich 0 i
wariancji 1
Linspace(a1,a2,N)
Tworzy wektor o N elementach rozmieszczonych równomiernie
w przedziale <a1, a2>
Logspace(a1,a2,N)
Tworzy N-elementowy wektor o elementach równomiernie
rozmieszczonych w skali logarytmicznej pomiędzy wartościami
10
a1
i 10
a2
Tab. 6.2 Funkcje wspomagające generowanie macierzy
Przykłady:
» eye(2)
ans =
1 0
0 1
» ones(2)
ans =
1 1
1 1
» zeros([3 2])
ans =
0 0
0 0
0 0
» rand(2)
ans =
0.8913 0.4565
0.7621 0.0185
» randn(2)
ans =
-1.1465 1.1892
1.1909 -0.0376

Technologia informacyjna - MATLAB
81
» linspace(0,100,10)
ans =
Columns 1 through 7
0 11.1111 22.2222 33.3333 44.4444 55.5556 66.6667
Columns 8 through 10
77.7778 88.8889 100.0000
» logspace(0,1,10)
ans =
Columns 1 through 7
1.0000 1.2915 1.6681 2.1544 2.7826 3.5938 4.6416
Columns 8 through 10
5.9948 7.7426 10.0000
6.6 Liczby zespolone
Operacje na liczbach zespolonych wymagają wykorzystania jednostki urojonej oznaczanej
w matematyce symbolem i, j lub
1
. W Matlabie jedność urojoną można zadeklarować
w następujący sposób:
>> i
ans =
0 + 1.0000i
>> j
ans =
0 + 1.0000i
>> sqrt(-1)
ans =
0 + 1.0000i
Matlab umożliwia również wykonywanie działań na macierzach, których elementami są
liczby zespolone. Deklaracja liczby zespolonej o dowolnej części rzeczywistej a i dowolnej
części urojonej b jest następująca:
Przykład:
>> a=2
a =
2
>> b=3
b =
3
>> z=a+b*i
z =
2.0000 + 3.0000i
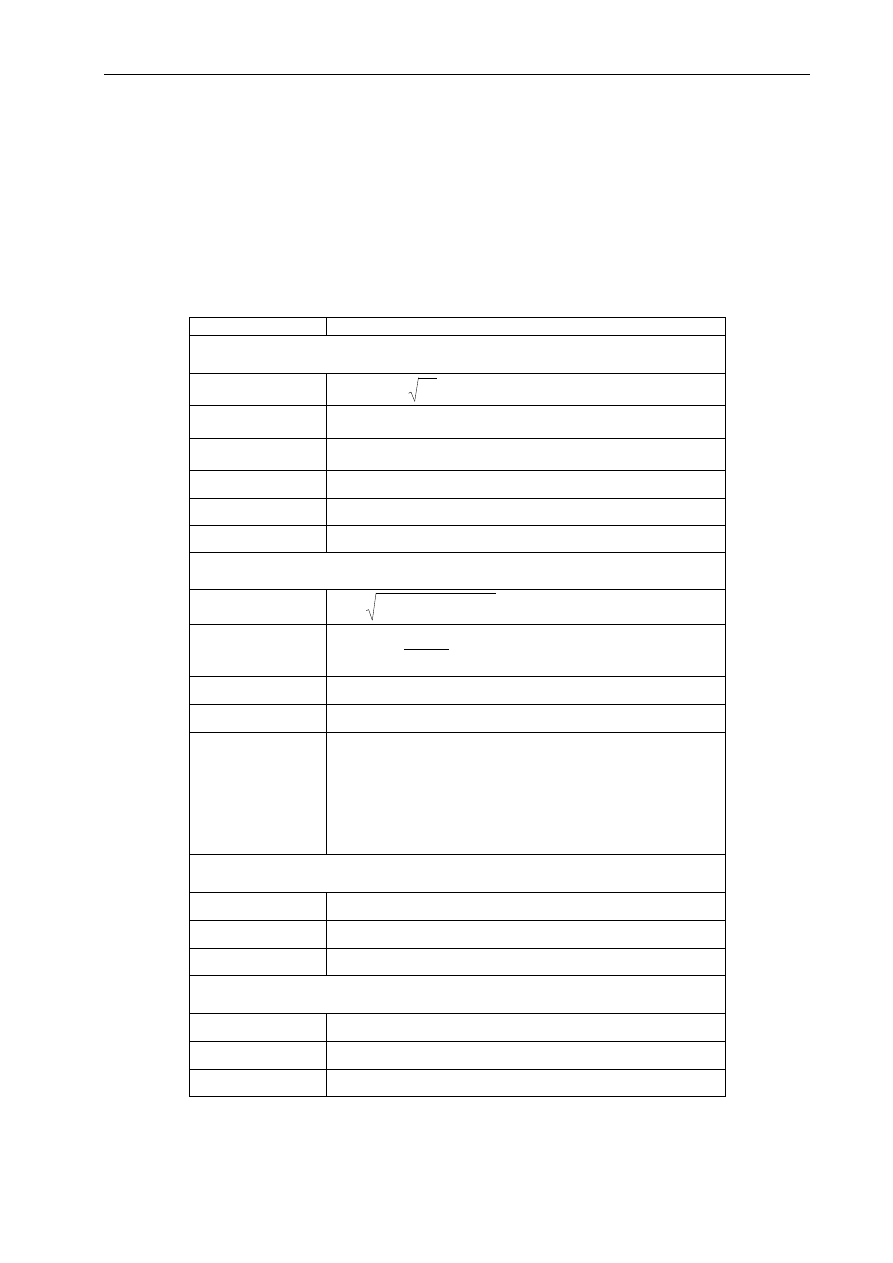
Technologia informacyjna - MATLAB
82
6.7 Funkcje matematyczne
W zależności od wersji i zainstalowanego pakietu ToolBox Matlab zawiera szereg funkcji
matematycznych, graficznych, optymalizacyjnych oraz wiele innych.
Poniżej zostały przedstawione wybrane funkcje matematyczne, które odpowiednio
przekształcają każdy z elementów macierzy.
Przykładowa macierz A, której elementy a
ij
mogą być liczbami rzeczywistymi lub zespolonymi
m
n
ij
a
A
przekształcana jest do macierzy
m
n
ij
b
B
zgodnie z odpowiednią funkcją matematyczną.
Funkcja
Opis
Funkcje potęgowe, logarytmiczne i wykładnicze
sqrt(A)
ij
ij
a
b
exp(A)
ij
a
ij
e
b
pow2(A)
ij
a
ij
2
b
log(A)
ij
ij
a
ln
b
.
log2(A)
ij
2
ij
a
log
b
.
log10(A)
ij
ij
a
log
b
Funkcje liczb zespolonych
abs(A)
2
ij
2
ij
ij
a
Im
a
Re
b
angle(A)
ij
ij
ij
a
Re
a
Im
arctg
b
real(A)
ij
ij
a
Re
b
imag(A)
ij
ij
a
Im
b
conj(A)
Oblicza macierz, której elementami są sprzężone liczby
zespolone odpowiednich elementów macierzy
A.
ij
ij
a
b
ij
ij
a
Re
b
Re
ij
ij
a
Im
b
Im
Funkcje trygonometryczne
sin(A)
ij
ij
a
sin
b
cos(A)
ij
ij
a
cos
b
tan(A)
ij
ij
a
tg
b
Funkcje cyklometryczne
asin(A)
ij
ij
a
sin
arc
b
acos(A)
ij
ij
a
cos
arc
b
.
atan(A)
ij
ij
a
arctg
b
.

Technologia informacyjna - MATLAB
83
Funkcje hiperboliczne
sinh(A)
ij
ij
a
h
sin
b
cosh(A)
ij
ij
a
h
cos
b
.
tanh(A)
ij
ij
a
h
tg
b
Funkcje odwrotne do hiperbolicznych
asinh(A)
ij
ij
a
h
sin
arc
b
.
acosh(A)
ij
ij
a
h
cos
arc
b
.
atanh(A)
ij
ij
a
h
arctg
b
.
Funkcje znaku, zaokrągleń i reszty z dzielenia
ceil(A)
Zaokrągla wartości elementów macierzy A w górę. W
przypadku liczb zespolonych zaokrąglane są zarówno część
rzeczywista i urojona.
floor(A)
Zaokrągla wartości elementów macierzy A w dół. W przypadku
liczb zespolonych zaokrąglane są zarówno część rzeczywista i
urojona.
fix(A)
Zaokrągla wartości elementów macierzy A: elementy dodatnie
w dół a ujemne w górę. W przypadku liczb zespolonych
zaokrąglane są odpowiednio część rzeczywista i urojona.
round(A)
Zaokrągla elementy macierzy A do najbliższej liczby
całkowitej. W przypadku liczb zespolonych zaokrąglane są
odpowiednio część rzeczywista i urojona.
sign(A)
Tworzy macierz o wymiarach równych macierzy A i
elementach zależnych od znaku:
1
b
0
a
0
b
0
a
1
b
0
a
ij
ij
ij
ij
ij
ij
rem(A, C)
Oblicza resztę z dzielenia odpowiadających sobie elementów
macierzy A i C.
ij
ij
ij
c
a
b
.
gcd(x,y)
Oblicza największy wspólny dzielnik liczb x i y.
lcm(x, y)
Oblicza najmniejsza wspólną wielokrotność liczb x i y.
Tab. 6.3 Funkcje matematyczne
Przykłady:
wyznaczenie wartości funkcji sinus:
>> sin(pi/4)
ans =
0.7071
obliczanie modułu liczby zespolonej:
» z=1+2*i
z =
1.0000 + 2.0000i

Technologia informacyjna - MATLAB
84
» abs(z)
ans =
2.2361
zastosowanie funkcji sign:
» A=[-10 20 0; 10 -20 0]
A =
-10 20 0
10 -20 0
» sign(A)
ans =
-1 1 0
1 -1 0
6.8
Instrukcje języka skryptowego
Instrukcja pętli „for”
Instrukcja
for
służy
do
określenia
indeksu
wybranego
elementu
macierzy
i wykorzystywana jest wówczas, gdy należy przeprowadzić operacje na poszczególnych jej
elementach.
Składnia instrukcji for jest następująca:
for
zmienna=macierz_indeksów
instrukcje
end
Szczególnym zastosowaniem pętli for jest generowanie macierzy, gdzie macierz_indeksów
jest macierzą wierszową służącą do indeksowania elementów generowanej macierzy
znajdujących się w kolejnych wierszach.
Przykład:
Wygenerować macierz A o wymiarach n x m (n = 3, m = 5), której elementy określone są
następująco:
A(i,j)= i/j
n=3;
m=5;
for
i=1:n
for
j=1:m
A(i,j)=i/j;
end
end
disp(A)
W oknie poleceń wyświetlona zostanie wygenerowana macierz A.
A=
1.0000 0.5000 0.3333 0.2500 0.2000
2.0000 1.0000 0.6667 0.5000 0.4000
3.0000 1.5000 1.0000 0.7500 0.6000

Technologia informacyjna - MATLAB
85
Wyrażenia 1:n i 1:m tworzą wektory o elementach odpowiednio [1, 2, ..., n] (numery
wierszy) i [1, 2, ..., m] (numery kolumn), które są indeksami elementów generowanej macierzy.
Instrukcja pętli „while”
Instrukcja while („dopóki”) wykorzystywana jest wówczas, gdy wykonanie ciągu
instrukcji uzależnione jest od spełnienia odpowiedniego warunku.
Składnia instrukcji while jest następująca:
while
warunek
instrukcje
end
Działanie instrukcji ilustruje poniższy przykład.
Przykład:
x = 0
while
x~=10
x = x + 1
end
W przypadku pętli while, w odniesieniu do liczb, bezpieczniej jest stosować zamiast
warunku równości (==) warunek (~=), ponieważ zapis zmiennoprzecinkowy liczb
rzeczywistych wprowadza pewne błędy, które często uniemożliwiają spełnienie warunku
równości.
Instrukcja warunkowa „if”
Instrukcja if jest typową instrukcją warunkową wykorzystywaną w większości używanych
języków programowania.
Składnia instrukcji if ma postać:
if
warunek_1
instrukcje
elseif
warunek_2
instrukcje
elseif
warunek_N
instrukcje
else
instrukcje
end
Przykład:
x=-100
if
x<0
disp(abs(x))
else
disp(x)
end
Instrukcja „break”
Użycie instrukcji break spowoduje przerwanie wykonywania jednego poziomu pętli.
Technologia informacyjna - MATLAB
86
Instrukcja „return”
Użycie instrukcji return powoduje opuszczenie bieżącej funkcji lub skryptu i przejście
do miejsca wywołania danej funkcji lub skryptu.
6.9 Instrukcje graficzne
W tym rozdziale przedstawione zostaną wybrane instrukcje graficzne służące do tworzenia
i formatowania wykresów na płaszczyźnie (2-D).
figure
Polecenie figure otwiera nowe okno o nazwie Figure. W oknie Figure zamieszczane są
przede wszystkim wykresy, ale można również w nim umieścić inne elementy np. przyciski.
plot
Podstawowym zastosowaniem instrukcji plot jest rysowanie wykresów funkcji jednej
zmiennej. Instrukcja plot dla funkcji y = f(x) ma następującą składnię:
plot(x,y,
’format’
)
Jeżeli nie zostanie określony styl linii wykres rysowany jest linią ciągłą a kolor linii
dobierany jest automatyczne ( plot(x,y) ). Można określić styl i kolor znaczników punktów
wykresu korzystając z zamieszczonej niżej tabeli.
Opcja
Opis
Kolor linii
y
żółty
m
magenta
c
cyjan
r
czerwony
g
zielony
b
niebieski
w
biały
k
czarny
Styl linii (znaczniki linii)
.
punktowa
-
ciągła
:
kropkowana
-.
kreska – kropka
--
przerywana
O
kółka
X
znak x
+
znak +
*
znak *
S
znak kwadratu
D
znak diamentu
V
znak trójkąta (w dół)
^
znak trójkąta (w górę)
<
znak trójkąta (w lewo)
>
znaj trójkąta (w prawo)
P
znak pentagramu (gwiazdy pięcioramiennej)
H
znak gwiazdy sześcioramiennej
Tab. 6.4. Parametry stylu linii
Technologia informacyjna - MATLAB
87
Aby narysować wykresy kilku funkcji np.: y
1
=f(x), y
2
=f(x), y
3
=f(x) ... , w jednym układzie
współrzędnych należy użyć polecenia plot w następującej postaci: plot( x, y1, x, y2, x, y3, ... ) -
wykresy kreślone linią ciągłą, lub plot( x, y1,’ format’, x, y2, ’ format’, x, y3, ’ format’ ... ) –
wykresy kreślone wybranym znacznikiem i kolorem.
subplot
Polecenie subplot dzieli obszar okna graficznego Figure na n
m obszarów, w których
wyświetlane są odpowiednie wykresy.
Składnia polecenia jest następująca:
subplot(n, m, p)
Parametr n oznacza liczbę okien w pionie, m liczbę okien w poziomie
a p jest numerem okna liczonym od lewego górnego rogu obiektu Figure.
Przykład:
subplot(2,3,1)
plot(x,y)
Okno zostało podzielone na dwa obszary w pionie, trzy obszary w poziomie, wykres
y=f(x) został umieszczony w pierwszym oknie (licząc od lewej górnej krawędzi okna
graficznego Figure).
xlabel
Polecenie xlabel służy do opisu osi x. Składnia polecenia xlabel ma postać:
xlabel(
‘opis osi x’
)
Opis osi pojawia się pod osią odciętych.
ylabel
Polecenie ylabel służy do opisu osi y. Składnia polecenia ylabel ma postać:
ylabel(
‘opis osi y’
)
Opis osi pojawia się obok osi rzędnych.
title
Polecenie title służy wstawienia nazwy wykresu. Składnia polecenia title ma postać:
title(
‘opis wykresu’
)
legend
Polecenie legend wstawia legendę dla bieżącego wykresu. Składnia polecenia legend ma
postać:
legend(
‘1_seria_danych’
,...,
‘N_seria_danych’
)

Technologia informacyjna - MATLAB
88
grid
Polecenie grid służy do włączania lub wyłączania siatki na wykresie.
% siatka włączona
grid on
% siatka wyłączona
grid off
axis
Polecenie axis służy do formatowania osi wykresu. Polecenie axis posiada wiele
możliwych wariantów składni, które zarazem powodują odmienne działanie tego polecenia.
Poniżej przedstawione zostaną wybrane funkcje polecenia axis.
axis([x
min
x
max
y
min
y
max
])
skalowanie osi wykresu
(zakresy osi podane są w macierzy)
axis auto
automatyczne skalowanie osi
axis off
wyłączanie osi wykresu
axis on
włączanie osi wykresu
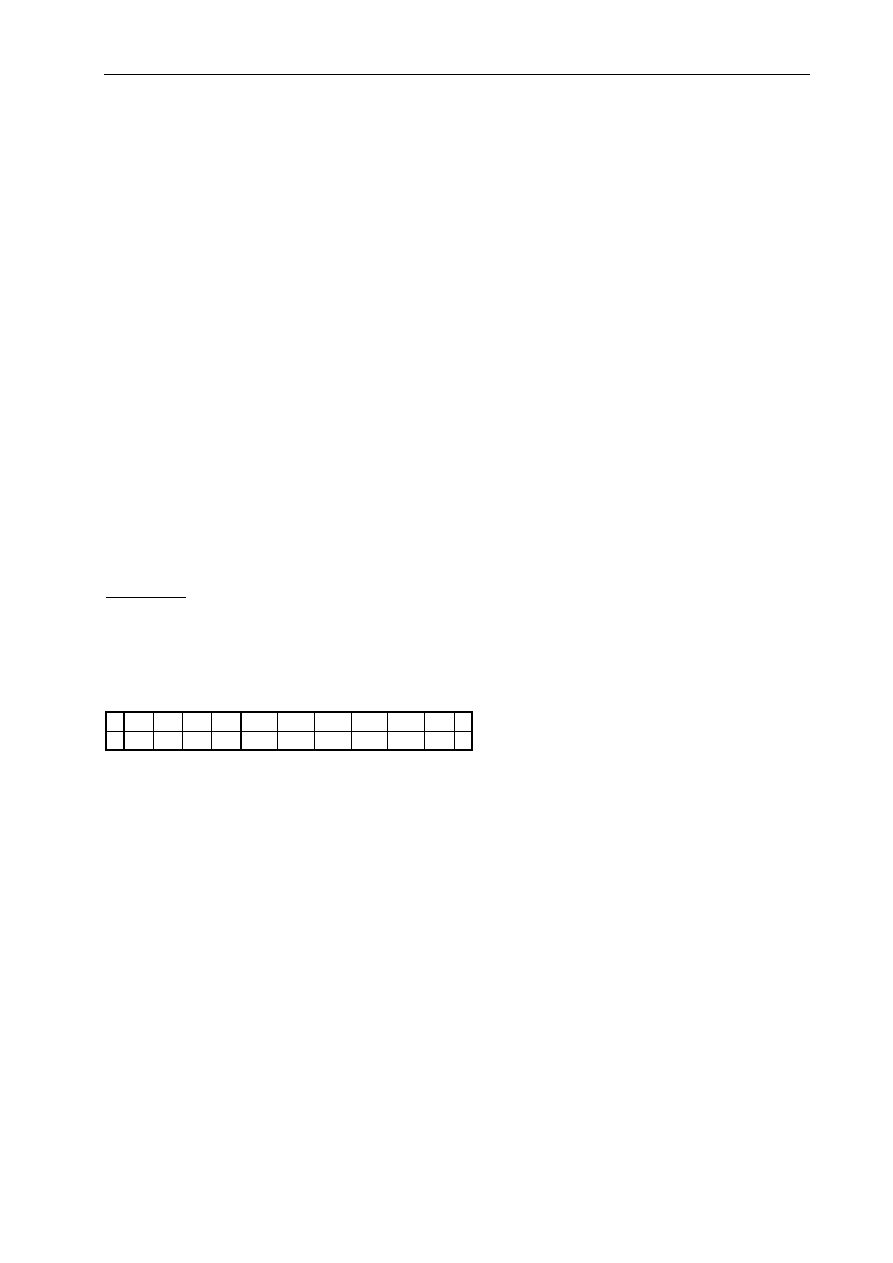
Technologia informacyjna - MATLAB
89
7. Obliczenia w Matlabie
7.1 Interpolacja
Program Matlab, dzięki swojej funkcji bibliotecznej interp1, umożliwia dokonanie
interpolacji funkcji jednej zmiennej y = f(x) w punktach xi nie będących węzłami. Składnia tej
funkcji ma postać:
yi = interp1(xw, yw, xi, ’metoda’)
(7.1)
%(xw, yw) - węzły interpolacji
Funkcja interp1 umożliwia obliczenia za pomocą następujących metod:
nearest
interpolacja metodą „najbliższego sąsiada” (przybliżenie stanowi funkcja schodkowa
przyjmująca wartości z najbliższego węzła interpolacji)
linear
interpolacja liniowa
spline
interpolacja funkcjami sklejanymi trzeciego stopnia
cubic
interpolacja wielomianami trzeciego rzędu
We wszystkich przypadkach elementy wektora xw muszą stanowić ciąg rosnący, natomiast
trzecią metodę należy stosować tylko dla węzłów równoodległych. W składni polecenia można
pominąć nazwę metody; wówczas metodą domyślną jest interpolacja liniowa.
Przykład 1:
W poniższej tabeli zamieszczone zostały wyniki pomiarów; należy je przybliżyć (z krokiem 0,1)
za pomocą wszystkich wymienionych wyżej metod interpolacji. Najpierw umieścić wszystkie krzywe
na wspólnym wykresie a następnie podzielić okno i narysować każdy wykres w oddzielnym układzie
współrzędnych (wartości z tabeli zaznaczyć na wykresie *).
x -5 -4 -3 -2
-1
0
1
2
3
4 5
y 1,2 3,1 4,5 6,7 12,4 17,9 25,8 19,8 10,3 4,2 0
skrypt1.m
%%interpolacja funkcji jednej zmiennej
%(xw,yw) - współrzędne węzłów interpolacji
xw=-5:1:5;
yw=[9.5 10.1 11.3 12.5 13.7 15.1 16.7 18.4 20.7 22.5 25.8];
%(xi,yi1,xi,yi2,xi,yi3,xi,yi4)– współrzędne punktów,
% w których dokonywana jest interpolacja
xi=-5:0.1:5;
yi1=interp1(xw,yw,xi,
'linear'
);
yi2=interp1(xw,yw,xi,
'spline'
);
yi3=interp1(xw,yw,xi,
'cubic'
);
yi4=interp1(xw,yw,xi,
'nearest
');
%wszystkie krzywe na jednym wykresie
plot(xw,yw,
'*'
,xi,yi1,xi,yi2,xi,yi3,xi,yi4);
grid on;
title(
'interpolacja funkcji jednej zmiennej'
);
xlabel(
'zmienna x'
);
ylabel(
'zmienna y'
);
text(-3.5,1,
'* - wezly interpolacji'
);
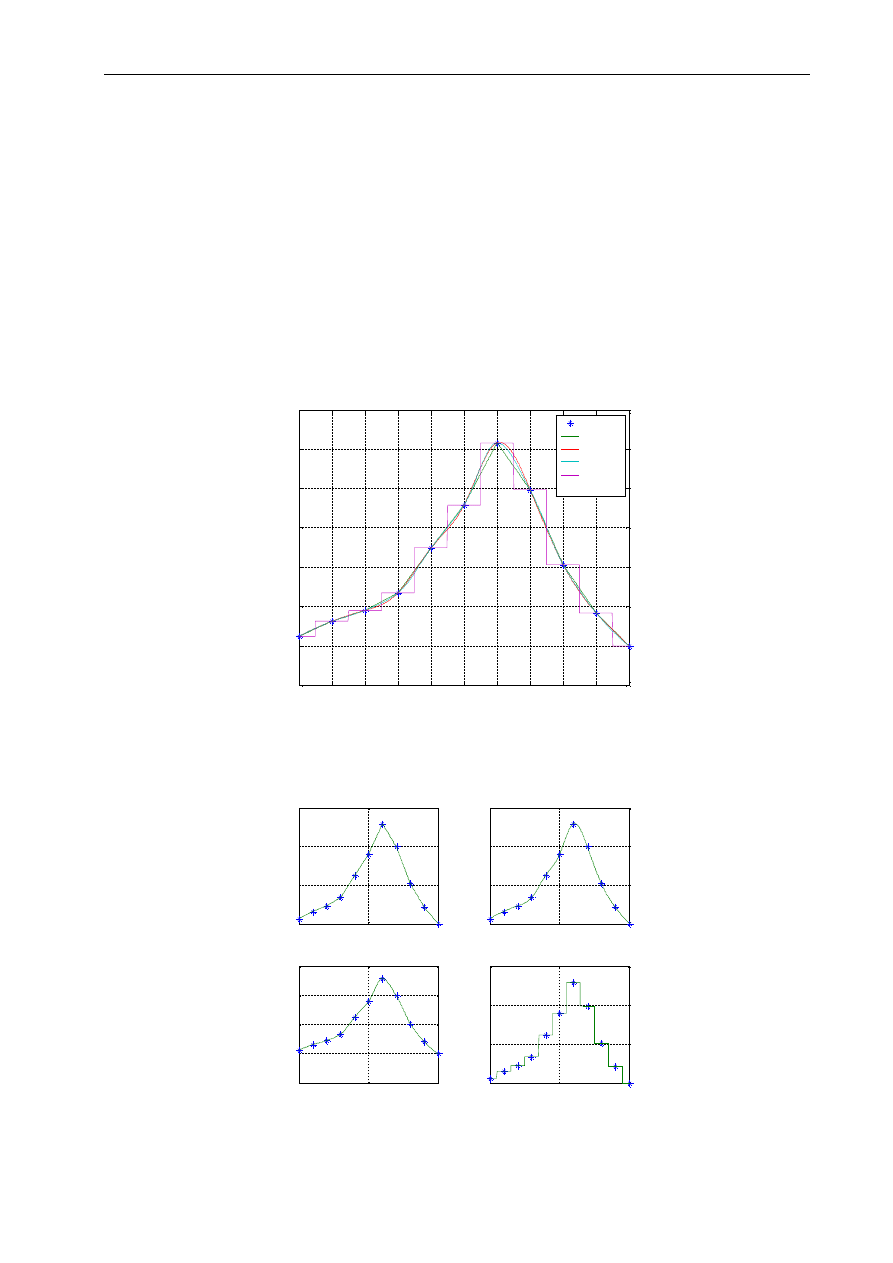
Technologia informacyjna - MATLAB
90
%każda krzywa w oddzielnym układzie współrzędnych
%subplot(2,2,1)
%plot(xw,yw,'*',xi,yi1)
%title('interpolacja liniowa')
%grid on
%subplot(2,2,2)
%plot(xw,yw,'*',xi,yi2)
%title('interpolacja funkcjami sklejanymi')
%grid on
%subplot(2,2,3)
%plot(xw,yw,'*',xi,yi3)
%title('interpolacja wielomianem 3-go stopnia')
%grid on
%subplot(2,2,4)
%plot(xw,yw,'*',xi,yi4)
%title('interpolacja funkcja schodkowa')
%
grid on
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
0
5
10
15
20
25
30
interpolacja funkcji jednej zmiennej
zmiena x
z
m
ie
n
n
a
y
* - wezly interpolacji
wezly
linear
spline
cubic
nearest
Rys. 7.1 Porównanie metod interpolacji 1
-5
0
5
0
10
20
30
interpolacja liniowa
-5
0
5
0
10
20
30
interpolacja funkcjami sklejanymi
-5
0
5
-10
0
10
20
30
interpolacja wielomianem 3-go stopnia
-5
0
5
0
10
20
30
interpolacja funkcja schodkowa
Rys. 7.2 Porównanie metod interpolacji 2
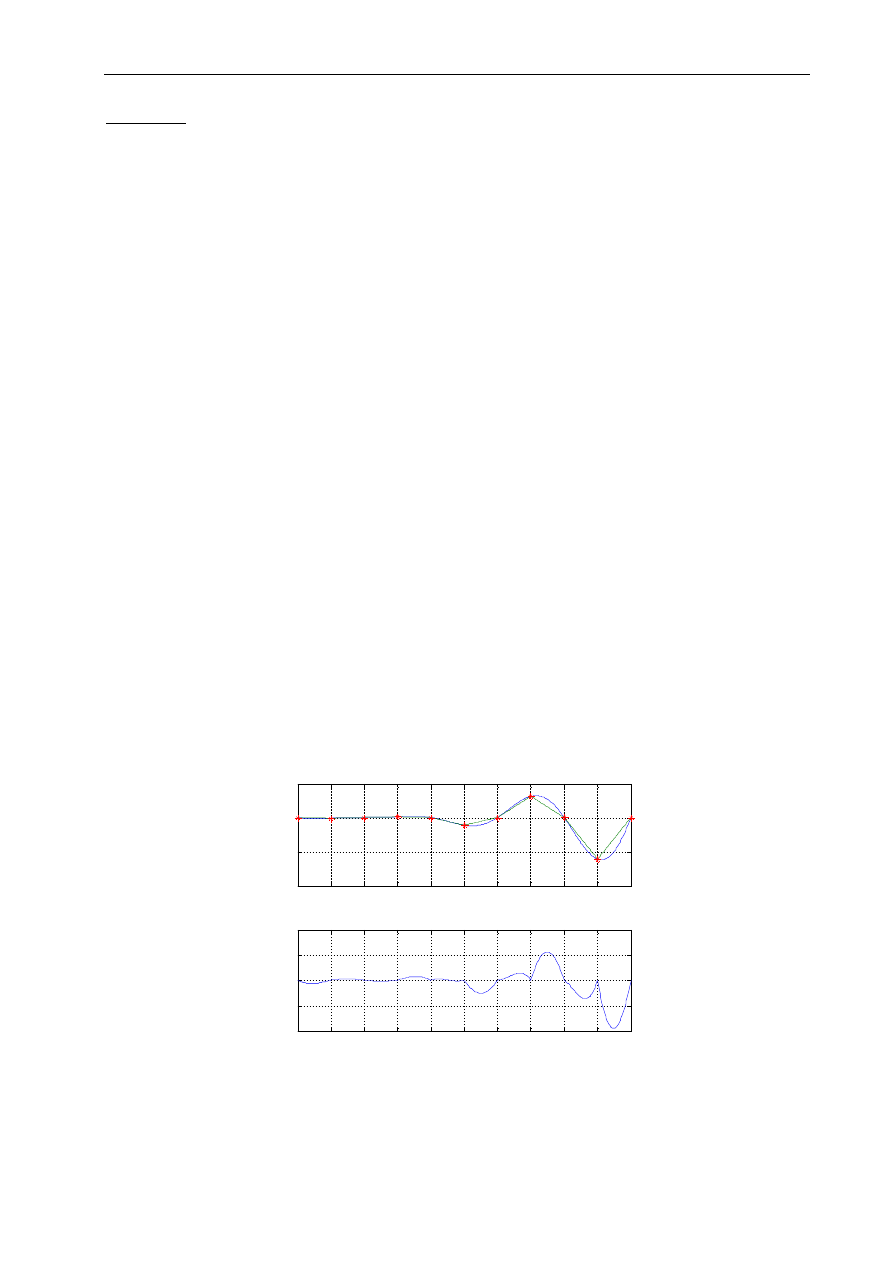
Technologia informacyjna - MATLAB
91
Przykład 2:
Dokonać interpolacji liniowej funkcji
x
sin
x
y
2
w przedziale <-1;4> z krokiem 0,5.
Narysować wykres danej funkcji i funkcji przybliżającej w jednym układzie współrzędnych, natomiast
wykres błędu interpolacji w drugim; węzły interpolacji zaznaczyć *. Wyznaczyć maksymalną wartość
bezwzględnego błędu interpolacji w rozpatrywanym przedziale.
skrypt2.m
%%interpolacja funkcji jednej zmiennej
x=-1:0.01:4;
y=(x.^2).*sin(pi*x);
%(xw,yw) - współrzędne węzłów interpolacji
xw=-1:0.5:4;
yw=(xw.^2).*sin(pi*xw);
%yi - wartości funkcji przybliżającej
% w punktach xi przedziału interpolacji
xi=-1:0.01:4;
yi=interp1(xw,yw,xi);
bl=y-yi;
%błąd interpolacji
blm=max(abs(bl));
%max wartość błędu interpolacji
subplot(2,1,1);
plot(x,y,xi,yi,xw,yw,
'*'
);
grid on;
title(
'wykres danej funkcji i jej przyblizenia'
);
xlabel(
'zmienna x'
);
ylabel(
'zmienna y'
);
text(1.7,-12.5,
'* - wezly interpolacji'
);
subplot(2,1,2);
plot(x,bl);
grid on;
title(
'wykres bledu'
);
xlabel(
'zmienna x'
);
ylabel(
'zmienna y'
);
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
-20
-10
0
10
wykres danej funkcji i jej przyblizenia
zmienna x
z
m
ie
n
n
a
y
* - wezly interpolacji
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
-4
-2
0
2
4
wykres bledu
zmienna x
z
m
ie
n
n
a
y
Rys. 7.3 Przykład interpolacji liniowej funkcji jednej zmiennej
Maksymalna wartość błędu interpolacji w rozpatrywanym przedziale wynosi: blm = 3,8265.
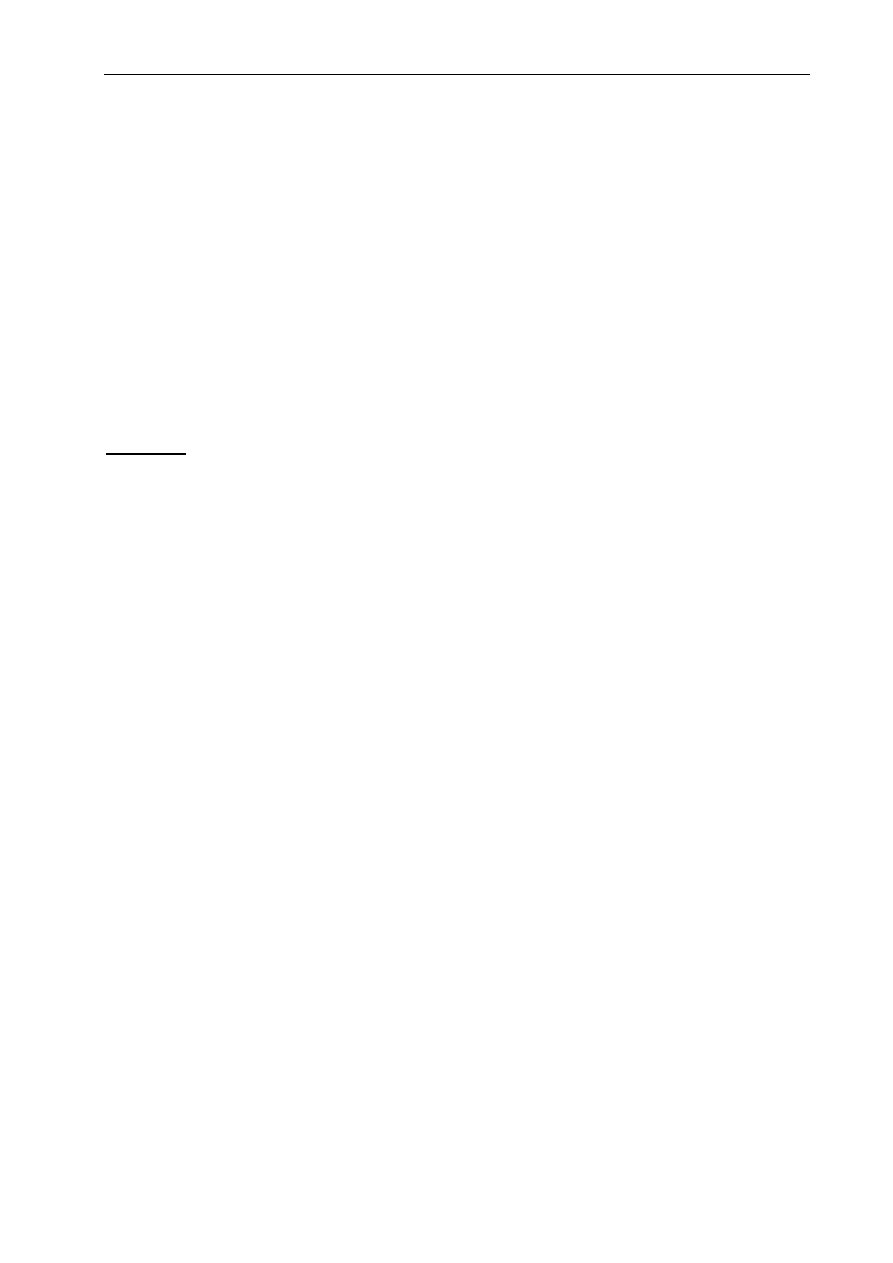
Technologia informacyjna - MATLAB
92
W bibliotece Matlaba dostępne są również procedury interp2, interp3 i interpn
umożliwiające dokonywanie interpolacji funkcji odpowiednio: dwóch, trzech i n-zmiennych
niezależnych.
W przypadku funkcji interp2 wymiary wektorów X i Y muszą być identyczne a ich
elementy powinny stanowić ciągi monotoniczne, ponieważ funkcja Matlaba meshgrid
wykorzystuje je do stworzenia siatki. W węzłach tej siatki umieszczane są wartości funkcji
Z = F(X, Y).
ZI = interp2(X,Y,Z,XI,YI,
’
metoda
’
)
(7.2)
Wektory X, Y, Z zawierają współrzędne węzłów interpolacji (Z = F(X, Y)), natomiast ZI
jest wektorem wartości funkcji interpolującej w punktach o współrzędnych (XI, YI). Dla funkcji
dwóch zmiennych niezależnych nazwy metod interpolacji są takie same jak w przypadku funkcji
jednej zmiennej.
Przykład 3:
Dokonać
interpolacji
liniowej
funkcji
dwóch
zmiennych
niezależnych
Z = - X
2
- X.*Y+5*Y
2
w przedziale <-5;3> z krokiem 1. Narysować wykres danej funkcji i jej
przybliżenia.
skrypt3.m
%% interpolacja funkcji dwóch zmiennych niezależnych
%ustalenie węzłów siatki
% dla danej funkcji w przedziale interpolacji
[X,Y]=meshgrid(-5:.2:3);
Z=-X.^2-X.*Y+5*Y.^2;
%ustalenie węzłów interpolacji
[Xw,Yw]=meshgrid(-5:1:3);
Zw=-Xw.^2-Xw.*Yw+5*Yw.^2;
%ustalenie węzłów siatki dla funkcji interpolującej
[Xi,Yi]=meshgrid(-5:.2:3);
%wyznaczenie wartości funkcji interpolującej
V=interp2(Xw,Yw,Zw,Xi,Yi);
%wyznaczenie błędu interpolacji
B=Z-V;
%wykreślenie wykresów danej funkcji
% i jej przybliżenia przesuniętych wzajemnie
%o 100 jednostek w celu zachowania przejrzystości rysunku
mesh(Xw,Yw,Zw),hold, mesh(Xi,Yi,V+100);
%włączenie czyszczenia okna graficznego
hold off;
title(
'Wykres danej funkcji i jej przyblizenia'
);
xlabel(
'zmienna X'
);
text(-4,5,200,
'Wykres funkcji interpolujacej'
);
text(0,0,-50,
'Wykres funkcji interpolowanej'
);
ylabel(
'zmienna Y'
);
zlabel(
'zmienna Z'
);
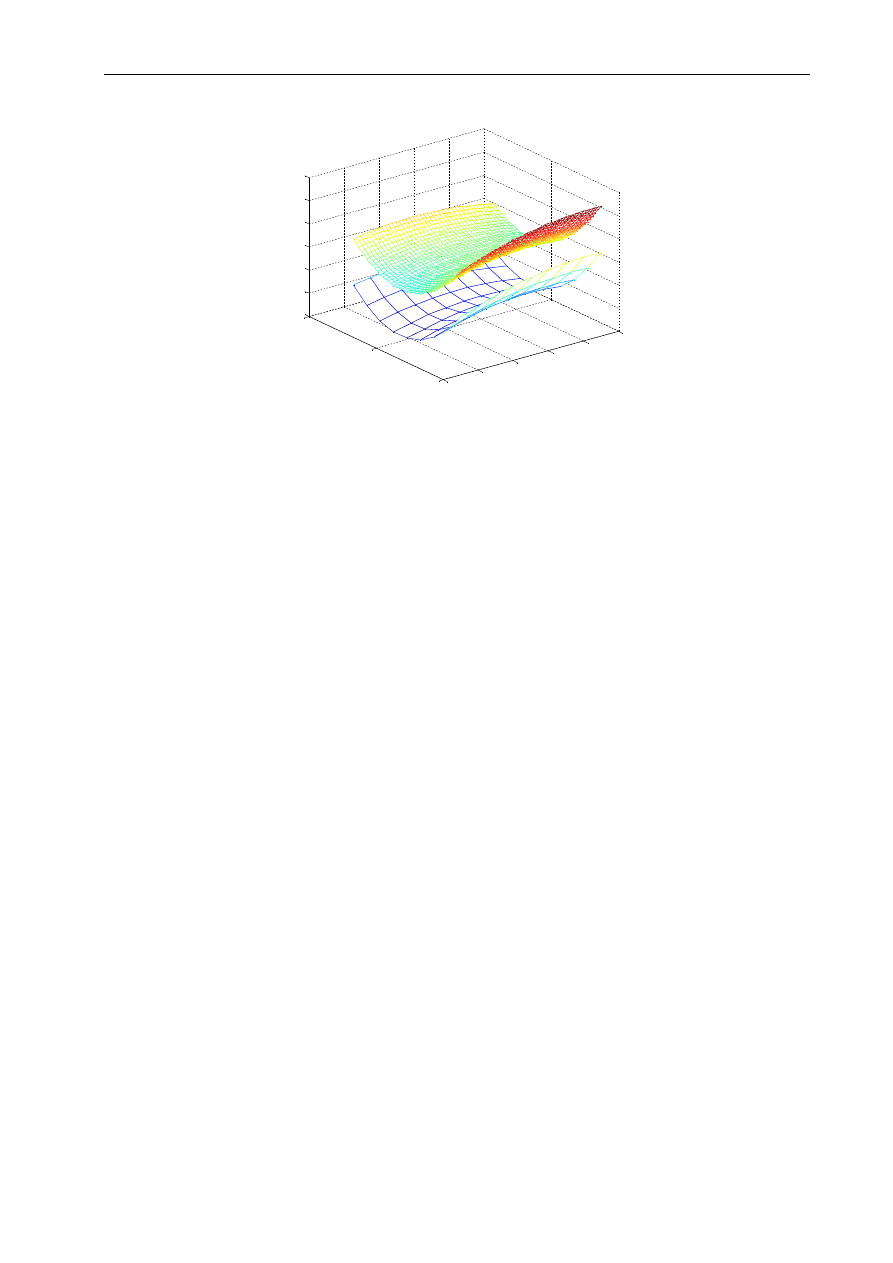
Technologia informacyjna - MATLAB
93
-6
-4
-2
0
2
4
-5
0
5
-50
0
50
100
150
200
250
zmienna X
Wykres funkcji interpolowanej
Wykres danej funkcji i jej przyblizenia
zmienna Y
Wykres funkcji interpolujacej
z
m
ie
n
n
a
Z
Rys. 7.4 Przykład interpolacji liniowej funkcji dwóch zmiennych
7.2 Aproksymacja
Aproksymację średniokwadratową funkcji jednej zmiennej y = f(x) przy pomocy
wielomianu stopnia r realizuje funkcja Matlaba polyfit:
a = polyfit(x, y, r)
(7.3)
r - stopień wielomianu
0
1
...
a
a
a
a
r
r
(7.4)
a jest wektorem współczynników wielomianu W(x) opisanego wzorem (7.5)
0
1
1
r
1
r
r
r
a
x
a
...
x
a
x
a
)
x
(
W
(7.5)
Funkcja polyfit dla danych wektorów x i y znajduje wektor współczynników a wielomianu
stopnia r. Współczynniki te dobierane są pod kątem zminimalizowania średniokwadratowego
odchylenia pomiędzy daną funkcją y = f(x) a wielomianem przybliżającym W(x).
Dla r = 1 otrzymuje się najprostszą metodę aproksymacji średniokwadratowej,
tzn. aproksymację za pomocą funkcji liniowej nazywaną także regresją liniową.
W celu wyznaczenia wartości wielomianu przybliżającego W(x) należy posłużyć się
funkcją Matlaba polyval:
p = polyval(a, x)
(7.6)
Funkcja ta wyznacza wartości wielomianu o współczynnikach określonych wektorem a
dla wszystkich elementów wektora x (macierzy X lub liczby); otrzymane wartości umieszcza
w wektorze p lub macierzy P.
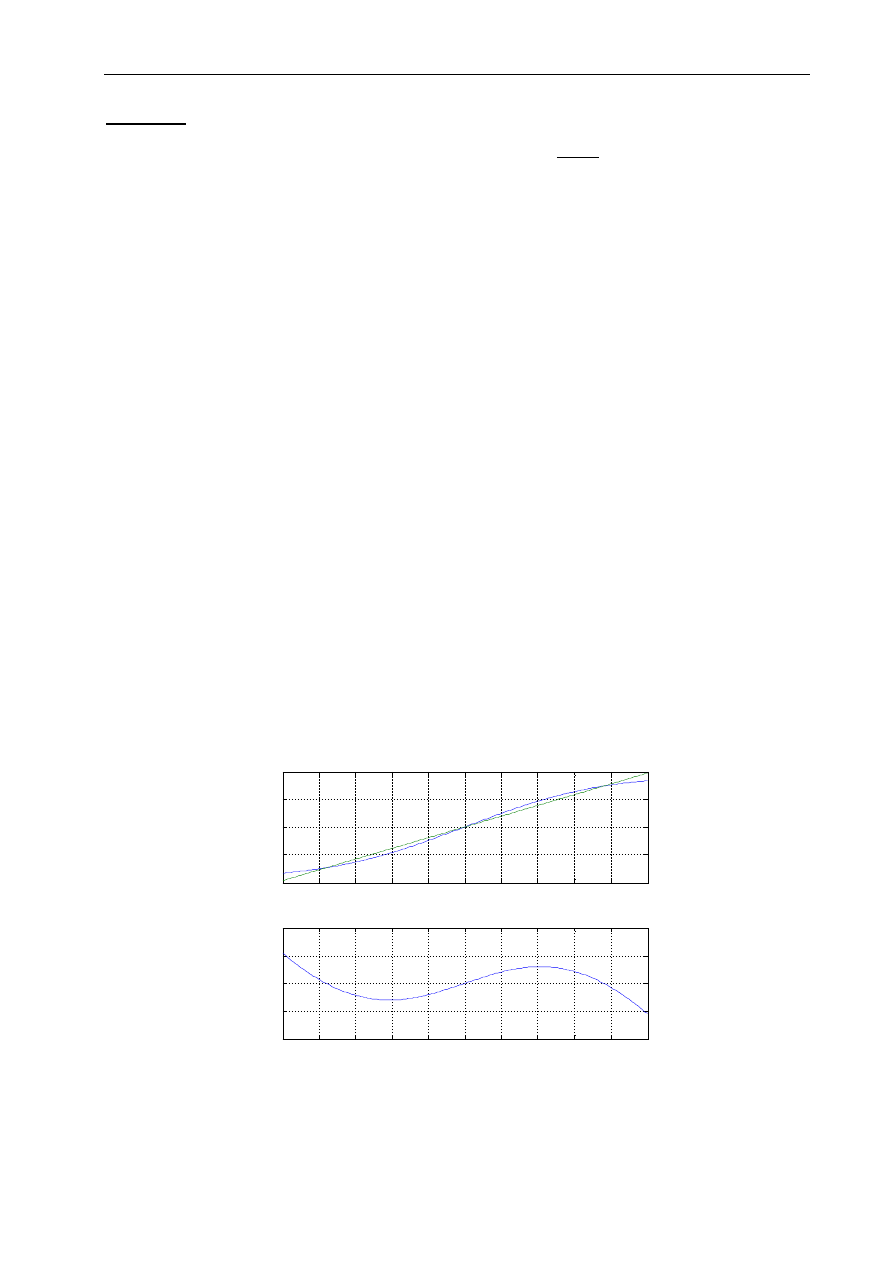
Technologia informacyjna - MATLAB
94
Przykład 1:
Dokonać aproksymacji średniokwadratowej funkcji
2
x
x
y
2
wielomianem 2-go stopnia
w przedziale <-1;1> z krokiem 0,01. Narysować wykres danej funkcji i funkcji przybliżającej w jednym
układzie współrzędnych natomiast wykres błędu aproksymacji w drugim. Wyznaczyć maksymalną
wartość bezwzględnego błędu aproksymacji w rozpatrywanym przedziale.
skrypt4.m
%%aproksymacja funkcji jednej zmiennej
x=-1:0.01:1;
y=x./(x.^2+2);
%stopień wielomianu przybliżającego
r=2;
%wektor współczynników wielomianu przybliżającego
a=polyfit(x,y,r);
%wektor wartości wielomianu przybliżającego
p=polyval(a,x);
bl=y-p;
%błąd aproksymacji
blm=max(abs(bl));
%max wartość błędu aproksymacji
subplot(2,1,1);
plot(x,y,x,p);
grid on;
title(
'aproksymacja funkcji jednej zmiennej'
);
text(0.35,0.1,
'wykres wielomianu'
);
text(-0.5,-0.25,
'wykres danej funkcji'
);
xlabel(
'zmienna niezalezna'
);
ylabel(
'zmienna zalezna'
);
subplot(2,1,2);
plot(x,bl);
grid on;
text(-0.5,0.07,
'wykres bledu aproksymacji'
);
xlabel(
'zmienna niezalezna'
);
ylabel(
'zmienna zalezna'
);
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-0.4
-0.2
0
0.2
0.4
aprok symac ja funkc ji jednej zmiennej
wykres wielomianu
wyk res danej funk cji
zmienna niezalez na
z
m
ie
n
n
a
z
a
le
z
n
a
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-0.1
-0.05
0
0.05
0.1
wyk res bledu aproks ymacji
zmienna niezalez na
z
m
ie
n
n
a
z
a
le
z
n
a
Rys. 7.5 Przykład aproksymacji średniokwadratowej funkcji jednej zmiennej
Maksymalna wartość błędu aproksymacji w rozpatrywanym przedziale wynosi: blm = 0,0546.
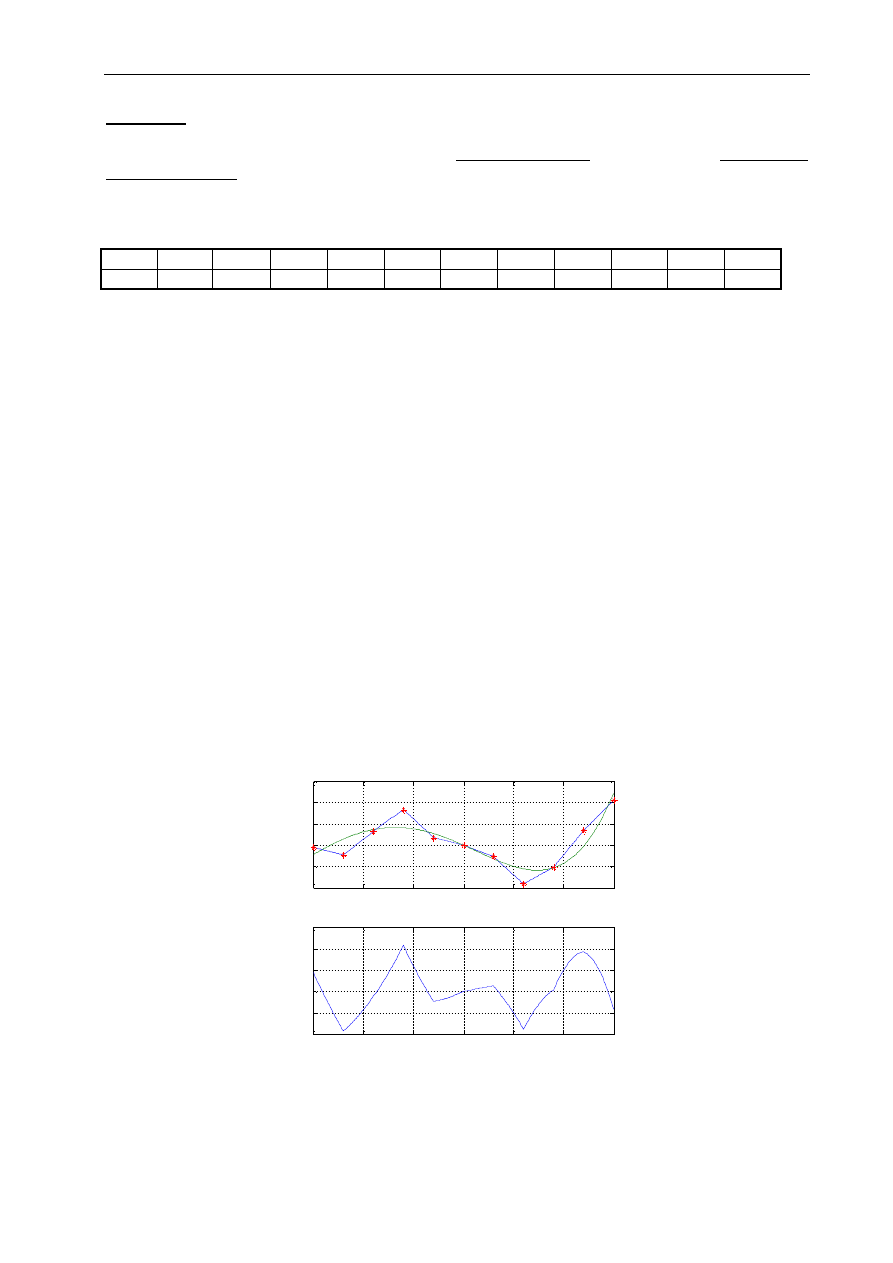
Technologia informacyjna - MATLAB
95
Przykład 2:
Dla wartości zapisanych w tabeli dokonać interpolacji liniowej z krokiem 0,1 i aproksymacji
średniokwadratowej wielomianem czwartego stopnia oraz narysować wykresy dla aproksymacji
i interpolacji (w jednym oknie), przy czym wartości z tabeli zaznaczyć na wykresie *. Wyznaczyć różnicę
pomiędzy przybliżeniami dokonanymi obydwoma metodami i narysować jej wykres w drugim oknie
.
x
-15
-12
-9
-6
-3
0
3
6
9
12
15
y
-0,5
-2,3
-3,2
-8,4
1,8
0
-2,7
-9,1
-5,2
3,4
10,5
skrypt5.m
%%porównanie interpolacji i aproksymacji funkcji jednej zmiennej
x=-15:0.1:15;
xw=-15:3:15;
yw=[-0.5 -2.3 3.2 8.4 1.8 0 -2.7 -9.1 -5.2 3.4 10.5];
yi=interp1(xw,yw,x);
r=4;
a=polyfit(xw,yw,r);
ya=polyval(a,x);
bl=yi-ya;
blm=max(abs(bl
))
subplot(2,1,1)
plot(x,yi,x,ya,xw,yw,'*')
grid on
title(
'interpolacja i aproksymacja funkcji jednej zmiennej')
xlabel(
'x'
)
ylabel(
'y')
subplot(2,1,2)
plot(x,bl)
grid on
title(
'roznica miedzy przyblizeniami')
xlabel(
'x'
)
ylabel(
'yi - ya')
-15
-10
-5
0
5
10
15
-10
-5
0
5
10
15
interpolacja i aproksymacja funkcji jednej zmiennej
x
y
-15
-10
-5
0
5
10
15
-4
-2
0
2
4
6
roznica miedzy przyblizeniami
x
y
i
-
y
a
Rys. 7.6 Porównanie interpolacji liniowej i aproksymacji średniokwadratowej
Maksymalna różnica między przybliżeniami wynosi 4,2977
.
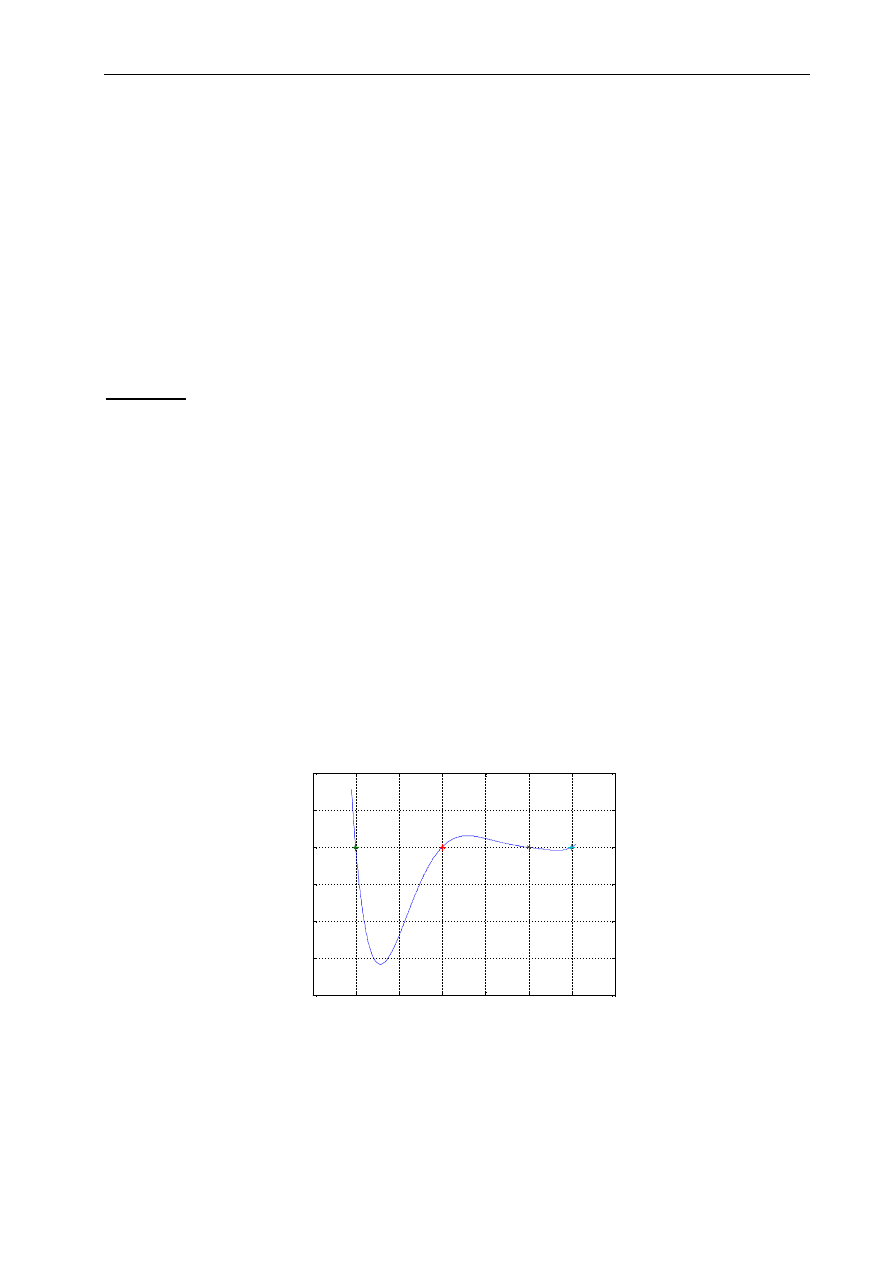
Technologia informacyjna - MATLAB
96
7.3 Miejsca zerowe wielomianów
W programie Matlab dostępna jest także funkcja roots(a), gdzie a jest macierzą wierszową
zawierającą współczynniki wielomianu, dzięki której można wyznaczyć wektor z zawierający
miejsca zerowe (zarówno rzeczywiste jak i zespolone) danego wielomianu W(x) o znanych
współczynnikach: a
0
, a
1
, ......,a
n-1
, a
n
.
n
1
n
2
n
2
1
n
1
n
0
a
x
a
....
x
a
x
a
x
a
)
x
(
W
(7.7)
a = [a
0
a
1
......
a
n-1
a
n
]
(7.8)
z = roots(a)
(7.9)
Przykład 1:
Wyznaczyć wszystkie miejsca zerowe wielomianu
12
x
14
x
6
x
15
x
7
x
x
)
x
(
w
2
3
4
5
6
i narysować jego wykres (zera zaznaczyć *).
skrypt6.m
%%miejsca zerowe wielomianu
a=[1 -1 -7 15 -6 -14 12];
%wektor współczynników wielomianu
z=roots(a);
%wektor zawierający zera wielomianu
x=-3.1:0.01:2.1;
y=x.^6-x.^5-7*x.^4+15*x.^3-6*x.^2-14*x+12;
%real(z) - wektor zawierający części rzeczywiste wektora z
plot(x,y,real(z),0,
'*'
);
grid on;
title(
'wykres wielomianu'
);
xlabel(
'x'
);
ylabel(
'w(x)'
);
-4
-3
-2
-1
0
1
2
3
-200
-150
-100
-50
0
50
100
wy kres wielomianu
x
w
(x
)
Rys. 7.7 Zera wielomianu
12
x
14
x
6
x
15
x
7
x
x
)
x
(
w
2
3
4
5
6
Wartości zer rozpatrywanego wielomianu są następujące:
z = -3 -1 1 + i 1 - i 1 2
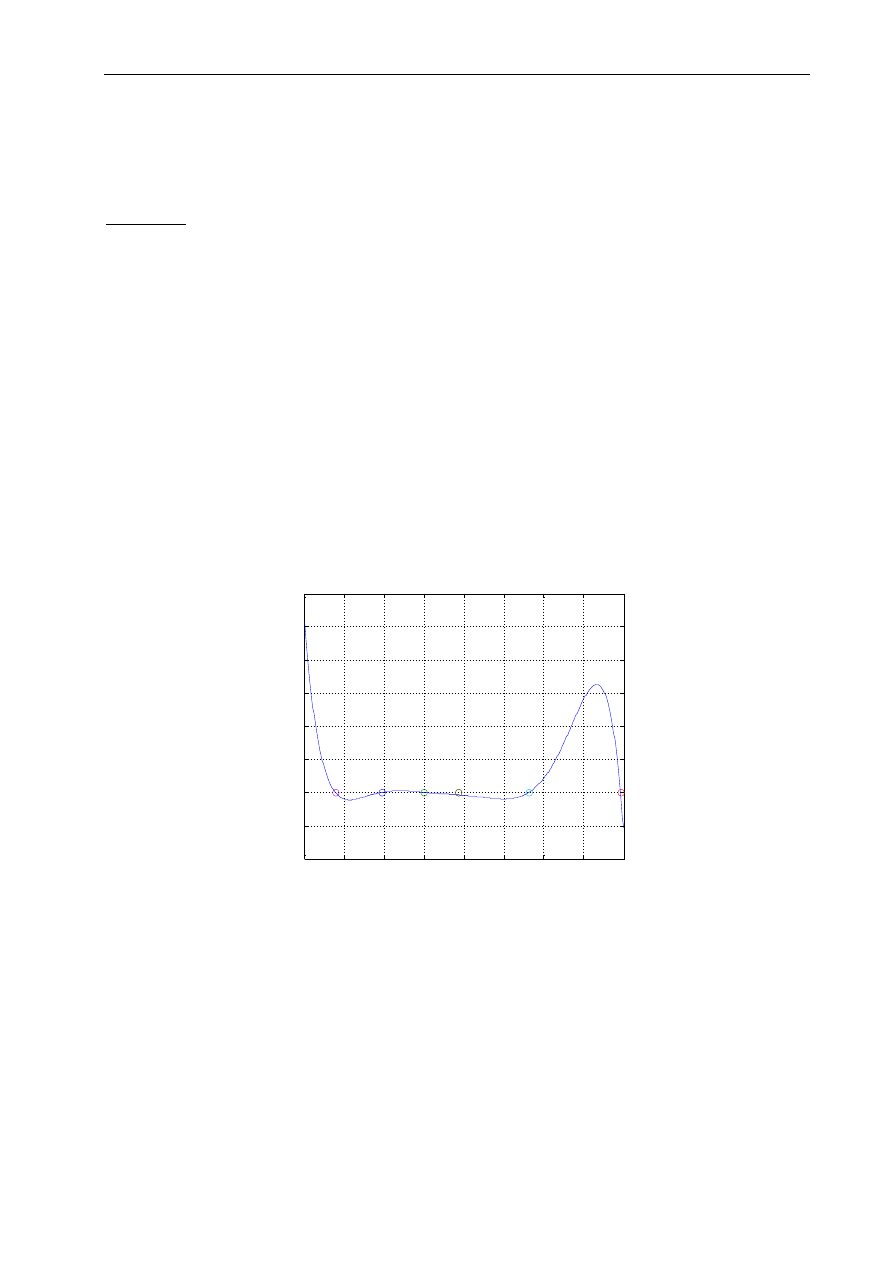
Technologia informacyjna - MATLAB
97
Każdy wielomian stopnia n – tego posiada dokładnie n+1 współczynników i n zer; jeżeli
wśród nich są zera zespolone to są to zawsze zera sprzężone. Wykres wielomianu rysowany jest
na płaszczyźnie zmiennej rzeczywistej, natomiast w wyniku można również otrzymać zera
urojone, dlatego na wykresie umieszcza się jedynie części rzeczywiste wyznaczonych zer.
Przykład 2:
Wyznaczyć wszystkie zera następującego wielomianu i narysować jego wykres; miejsca zerowe
zaznaczyć „o”:
x
x
2
x
4
x
3
x
)
x
(
w
3
4
6
7
skrypt7.m
%%miejsca zerowe wielomianu
x=-1.5:0.01:2.5;
y=-x.^7+3*x.^6-4*x.^4+2*x.^3-x;
z=roots([-1 3 0 -4 2 0 -1 0])
zr=real(z)
’czesci rzeczywiste zer
plot(x,y,zr,0,'o')
grid on
title('miejsca zerowe wielomianu')
xlabel('x');
ylabel('y')
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
-10
-5
0
5
10
15
20
25
30
miejsca zerowe wielomianu
x
y
Rys. 7.8 Zera wielomianu
x
x
2
x
4
x
3
x
)
x
(
w
3
4
6
7
Wartości otrzymanych zer (z) i umieszczonych na wykresie (zr):
z =
zr =
0
0
2,4637
2,4637
1,3170
1,3170
-1,1107
-1,1107
0,4288 + 0,5849i
0,4288
0,4288 - 0,5849i
0,4288
-0,5276
-0,5276

Technologia informacyjna - MATLAB
98
7.4 Miejsca zerowe funkcji
Rzeczywiste miejsca zerowe funkcji można wyznaczyć wykorzystując funkcję fzero.
W tym celu należy w skrypcie (np.: plik.m) zadeklarować rozpatrywaną funkcję y = f(x)
w sposób następujący:
function y = f(x)
(7.10)
y=
Następnie należy określić przybliżenie początkowe x0, czyli punkt, wokół którego będzie
poszukiwane zero. Podstawowa składnia polecenia fzero, które należy napisać w oknie
programu, lub umieścić w oddzielnym pliku, jest następująca:
z = fzero(‘plik’, x0)
(7.11)
Plik jest to nazwa skryptu (bez rozszerzenia) zawierającego rozpatrywaną funkcję,
natomiast x0 jest to przybliżenie początkowe. Obliczenia wykonywane są z dokładnością równą
eps (dokładność maszynowa w Matlabie), czyli 2,22*10
-16
.
Algorytm polecenia fzero oparty jest na kombinacji metod bisekcji, siecznych
i interpolacji.
Przykład 1:
W
przedziale
<-3,
3>
wyznaczyć
wszystkie
rzeczywiste
miejsca
zerowe
funkcji:
)
1
x
(
arctg
)
2
x
(
y
i narysować jej wykres w tym przedziale; miejsca zerowe zaznaczyć za pomocą
symbolu „o”.
zera.m
%%zera funkcji
function
y=f(x)
y=(x+2).*atan(x-1);
skrypt8.m
% ustalić punkty, w otoczeniu których poszukiwane będą zera
% (np. 3 i %-3)
z1=fzero(
'zera'
,-3);
%obliczenia z dokładnością 2,22*10
-16
z2=fzero(
'zera'
,3,1e-6,1);
%obliczenia np. z dokładnością 10
-6
%rysowanie wykresu:
x=-3:0.01:3;
y=(x+2).*atan(x-1);
plot(x,y,z1,0,
'ro'
,z2,0,
'ro'
);
grid on;
title(
'zera funkcji'
);
xlabel(
'x'
);
ylabel(
'y'
);
W przedziale < -3; 3> rozpatrywana funkcja posiada następujące zera rzeczywiste:
z1 = -2 z2 = 1
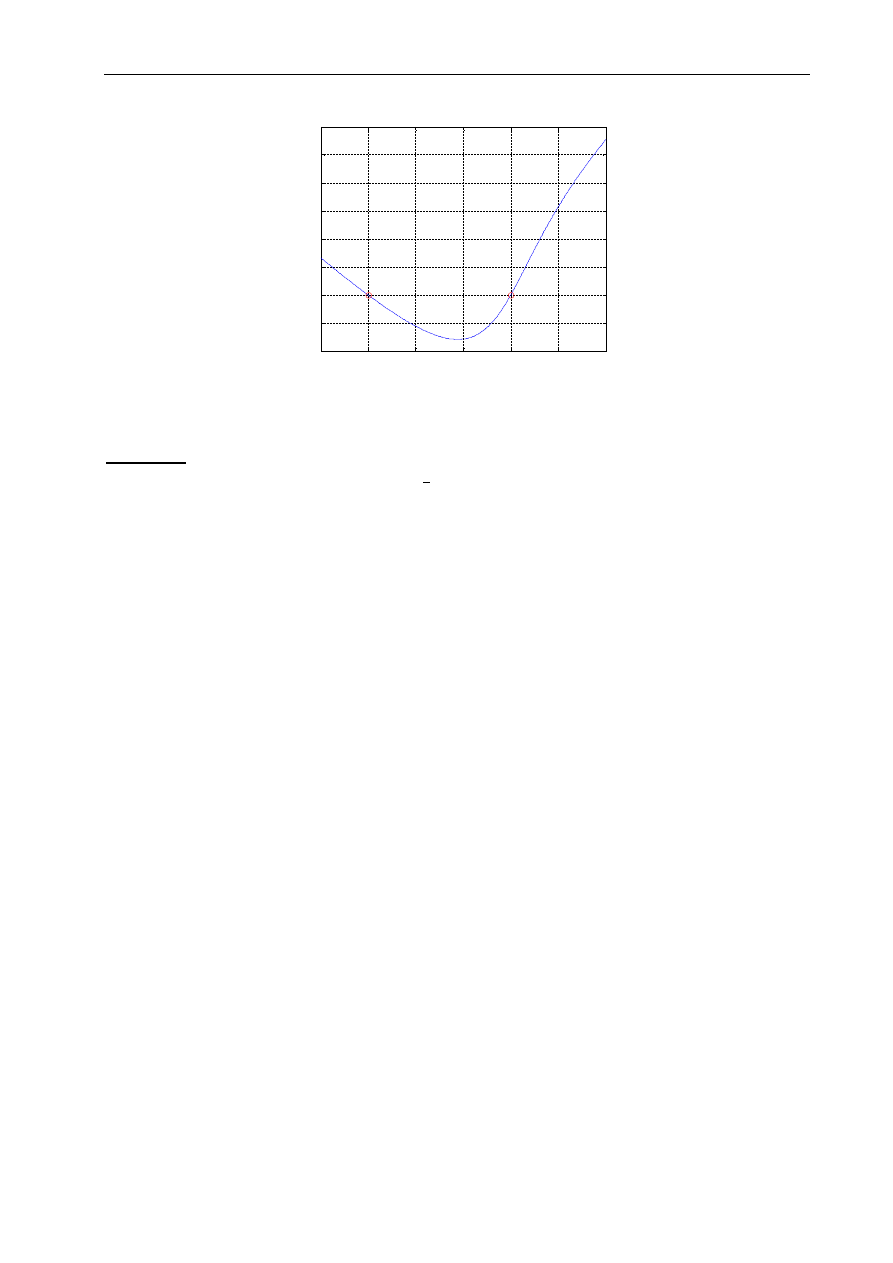
Technologia informacyjna - MATLAB
99
-3
-2
-1
0
1
2
3
-2
-1
0
1
2
3
4
5
6
zera funkcji
x
y
Rys. 7.9 Zera rzeczywiste funkcji
)
1
x
(
arctg
)
2
x
(
y
w przedziale <-3,3>
Przykład 2:
Wyznaczyć zera funkcji:
x
1
2
e
)
1
x
(
y
i narysować jej wykres w przedziale <-2; 2>. Krzywe
wykreślić zieloną linią a zera zaznaczyć niebieskimi gwiazdkami.
Funkcja jest nieciągła dla x = 0, dlatego w celu narysowania wykresu i lokalizacji zer należy
podzielić przedział na dwa podprzedziały x1 i x2.
zera1.m
function
y1=f(x1)
y1=(x1.^2-1).*exp(1./x1);
zera2.m
function
y2=f(x2)
y2=(x2.^2-1).*exp(1./x2);
skrypt9.m
% ustalić punkty, w otoczeniu których poszukiwane będą zera
% (np. 2 i -2)
% podzielić odpowiednio przedział na dwa podprzedziały x1 i x2
x1=-2:0.01:-0.01;
x2=0.3:0.01:2;
y1=(x1.^2-1).*exp(1./x1);
y2=(x2.^2-1).*exp(1./x2);
z1=fzero(
'zera1'
,-2)
z2=fzero(
'zera2
',2)
subplot(2,1,1)
plot(x1,y1,
'g',
z1,0,
'b*'
)
grid on
title(
'wykres funkcji w 1 przedziale'
)
xlabel(
'x1'
)
ylabel(
'y1'
)
subplot(2,1,2)
plot(x2,y2,
'g'
,z2,0,
'b*'
)
grid on
title(
'wykres funkcji w 2 przedziale'
)
xlabel(
'x2'
)
ylabel(
'y2'
)
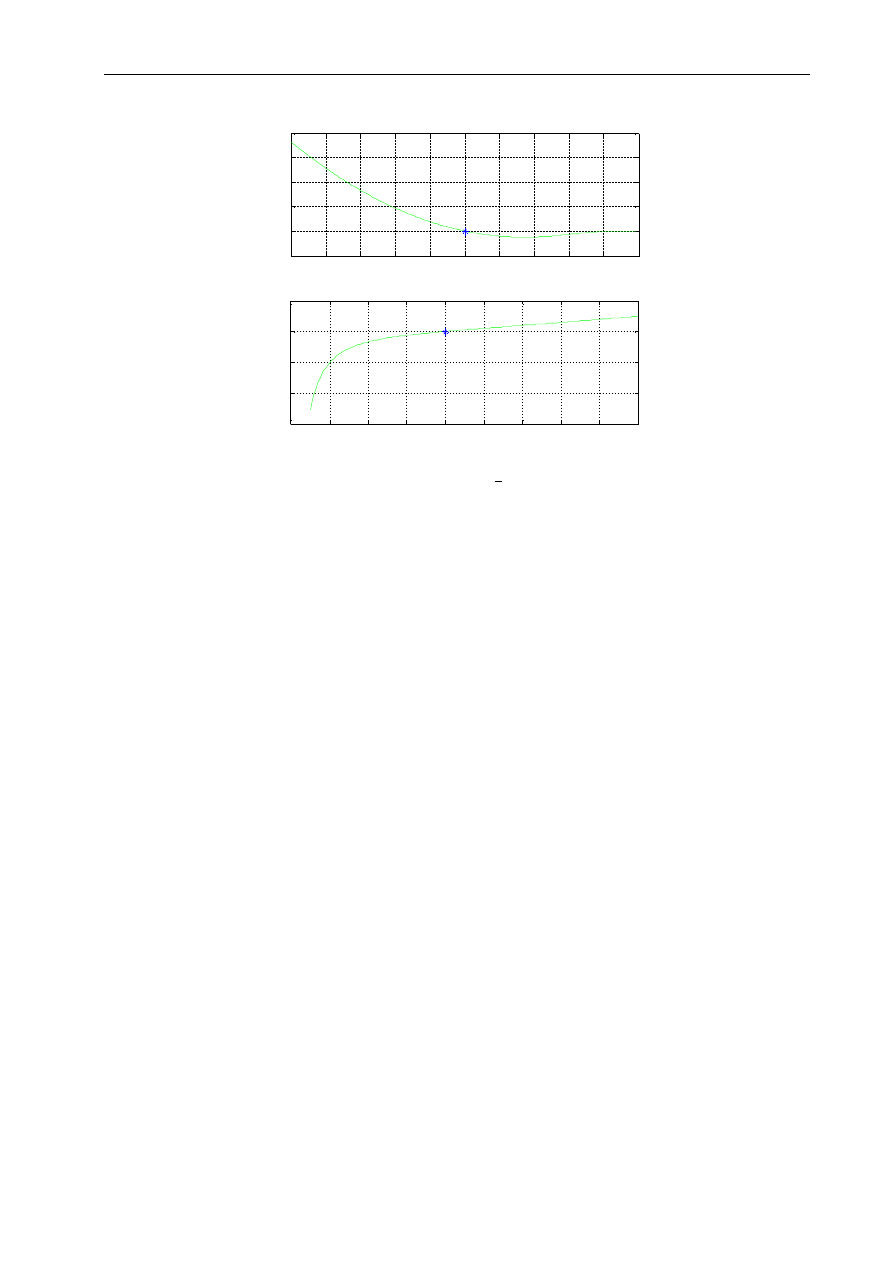
Technologia informacyjna - MATLAB
100
-2
-1.8
-1.6
-1.4
-1.2
-1
-0.8
-0.6
-0.4
-0.2
0
-0.5
0
0.5
1
1.5
2
wykres funkcji w 1 przedziale
x1
y1
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
-30
-20
-10
0
10
wykres funkcji w 2 przedziale
x2
y2
Rys. 7.10 Zera rzeczywiste funkcji
x
1
2
e
)
1
x
(
y
w przedziałach <-2,-0,01> i <0,3, 2>
7.5 Algebra liniowa
7.5.1 Układy równań liniowych
Następujący układ równań liniowych:
n
1
j
,
i
i
i
ij
b
x
a
i = 1, 2, .... n
(7.12)
można przedstawić w postaci macierzowej:
b
x
A
(7.13)
A = [a
ij
] - macierz układu
b = [b
1
, b
2
, ... b
n
]
T
- wektor prawych stron
x = [x
1
, x
2
, ... x
n
]
T
- wektor rozwiązania
Jeżeli macierz A jest macierzą nieosobliwą (det(A)
0), wówczas rozpatrywany układ
równań ma dokładnie jedno rozwiązanie:
b
x
1
A
(7.14)
A
-1
- macierz odwrotna do macierzy A
Korzystając z programu Matlab rozwiązanie powyższego układu równań można uzyskać
dwiema metodami:
eliminacja Gaussa z częściowym wyborem elementu głównego,
odwracanie macierzy
.
W programie Matlab dostępne są m.in. następujące funkcje dotyczące macierzy:
Technologia informacyjna - MATLAB
101
inv(A)
odwracanie macierzy
A\b
rozwiązanie układu równań liniowych metodą eliminacji Gaussa
z częściowym wyborem elementu głównego (A - macierz układu,
b - wektor prawych stron)
det(A)
wyznacznik macierzy
[L,U] = lu(A)
rozkład macierzy na macierz trójkątną dolną L i macierz trójkątną
górną U
[U,S,V] = svd(A)
rozkład SVD macierzy (A = USV
T
, U, V - macierze ortogonalne,
S - macierz diagonalna (przekątniowa) z wartościami
szczególnymi (osobliwymi)
i
na przekątnej
s = svd(A)
wektor wartości szczególnych (osobliwych)
c = cond(A)
wskaźnik uwarunkowania zadania rozwiązywania układów
równań liniowych równy iloczynowi największych wartości
szczególnych macierzy A i A
-1
eps
dokładność maszynowa
norm(x)
norma wektora równa pierwiastkowi z sumy kwadratów jego
współrzędnych
norm(A,’fro’)
norma Frobeniusa macierzy równa pierwiastkowi z sumy
kwadratów jej elementów
Tab. 7.1. Wybrane funkcje dotyczące macierzy.
Ponadto można obliczyć czas wyznaczania rozwiązania (tic - początek pomiaru czasu,
toc - koniec pomiaru czasu):
tic, x3=inv(A)*b, toc
tic, x2=A\b, toc
Warunki dla rozwiązań układów równań liniowych
Znając wartości wyznaczników W, W
x
i W
y
dla danego układu równań liniowych można
określić jakie będzie rozwiązanie tego układu. Warunki jakie muszą spełniać wyznaczniki W, W
x
i W
y
zostaną przedstawione na podstawie układu dwóch równań liniowych.
0
b
a
b
a
W
c
y
b
x
a
c
y
b
x
a
2
2
1
1
2
2
2
1
1
1
(7.15)
Wyznacznik główny W 0 – istnieje dokładnie jedno rozwiązanie układu równań
0
c
a
c
a
W
0
b
c
b
c
W
0
b
a
b
a
W
2
2
1
1
y
2
2
1
1
x
2
2
1
1
(7.16)
Wyznacznik główny W = 0, wyznaczniki W
x
0 i W
y
0 - układ równań sprzeczny
Technologia informacyjna - MATLAB
102
0
c
a
c
a
W
0
b
c
b
c
W
0
b
a
b
a
W
2
2
1
1
y
2
2
1
1
x
2
2
1
1
(7.17)
Wyznacznik główny W = 0, wyznaczniki W
x
= 0 i W
y
= 0 - układ równań tożsamościowy
lub sprzeczny
Rozwiązując układ równań liniowych należy najpierw obliczyć wyznacznik W.
W przypadku, gdy jest on różny od zera można wyznaczyć rozwiązanie. Natomiast jeżeli W jest
równy zero , to wówczas oblicza się wartości W
x
i W
y
i na ich podstawie określa rozwiązanie.
Przykład 1:
Wyznaczyć rozwiązania następujących trzech układów równań:
5
y
2
x
3
y
3
x
2
2
y
6
x
9
5
y
4
x
6
25
y
10
x
5
10
y
4
x
2
Powyższe układy równań można zapisać w postaci macierzowej:
5
3
c
2
1
3
2
c
x
2
5
d
6
9
4
6
d
y
25
10
f
10
5
4
2
f
z
skrypt10.m
%% układ 1: dokładnie jedno rozwiązanie
%macierz układu
A=[2 -3
1 2]
%wektor prawych stron
c=[3 5]'
%wyznacznik macierzy
W=det(A)
%rozwiązanie metodą eliminacji Gaussa
% z częściowym wyborem elementu głównego
x1=A\c
%rozwiązanie metodą odwracania macierzy
x2=inv(A)*c
Rozwiązanie:
W = 7
x1 =
1
3
x2 =
1
3

Technologia informacyjna - MATLAB
103
skrypt11.m
%% układ 2: sprzeczny
B=[6 -4
9 -6]
d=[5 2]'
W=det(B)
mWx=[5 -4
2 -6]
mWy=[6 5
9 2]
Wx=det(mWx)
Wy=det(mWy)
Rozwiązanie:
W = 0,
Wx = -22,
Wy = -33
Układ równań sprzeczny.
skrypt12.m
%%układ 3: tożsamościowy
E=[2 -4
5 -10]
f=[10 25]'
W=det(E)
mWx=[10 -4
25 -10]
mWy=[2 10
5 25]
Wx=det(mWx)
Wy=det(mWy
)
Rozwiązanie:
W = 0,
Wx = 0,
Wy = 0
Układ równań tożsamościowy.
Przykład 2:
Stosując metodę eliminacji Gaussa z częściowym wyborem elementu głównego i metodę
odwracania macierzy rozwiązać następujący układ równań liniowych:
4
u
3
z
3
y
x
3
1
u
z
2
y
x
5
3
u
2
z
y
x
2
10
u
z
5
y
2
x
skrypt13.m
%%układy równań liniowych
%macierz układu
A=[1 -2 5 1
2 1 -1 -2
5 1 2 -1
3 -1 3 -3]
Technologia informacyjna - MATLAB
104
%wektor prawych stron
b=[10 -3 1 4]'
%wyznacznik macierzy A
W=det(A)
%rozwiązanie metodą eliminacji Gaussa
% z częściowym wyborem elementu głównego
x1=A\b
%rozwiązanie metodą odwracania macierzy
x2=inv(A)*b
Rozwiązanie:
W = 2
Przykład 3:
Stosując metodę eliminacji Gaussa z częściowym wyborem elementu głównego i metodę
odwracania macierzy rozwiązać następujący układ równań liniowych:
24
t
4
y
x
13
t
z
4
y
2
x
6
20
t
z
2
x
3
44
z
5
y
6
x
skrypt14.m
A=[1 6 5 0
3 0 2 1
6 -2 4 -1
1 1 0 -4]
b=[44 20 13 -24]'
W=det(A)
x1=A\b
x2=inv(A)*b
Rozwiązanie:
W = 189
Przykład 4:
Stosując metodę eliminacji Gaussa z częściowym wyborem elementu głównego i metodę
odwracania macierzy rozwiązać następujący układ równań liniowych:
0
23
z
2
y
17
x
4
0
76
z
10
y
3
x
5
0
43
z
5
y
12
x
3
skrypt14.m
A=[3 12 5
5 -3 -10
4 -17 2]
b=[-43 -76 23]'
W=det(A)
x1=A\b
x2=inv(A)*b
x1 =
-10.0000
20.0000
13.0000
-5.0000
x2 =
-10.0000
20.0000
13.0000
-5.0000
x1 =
1.0000
3.0000
5.0000
7.0000
x2 =
1.0000
3.0000
5.0000
7.0000
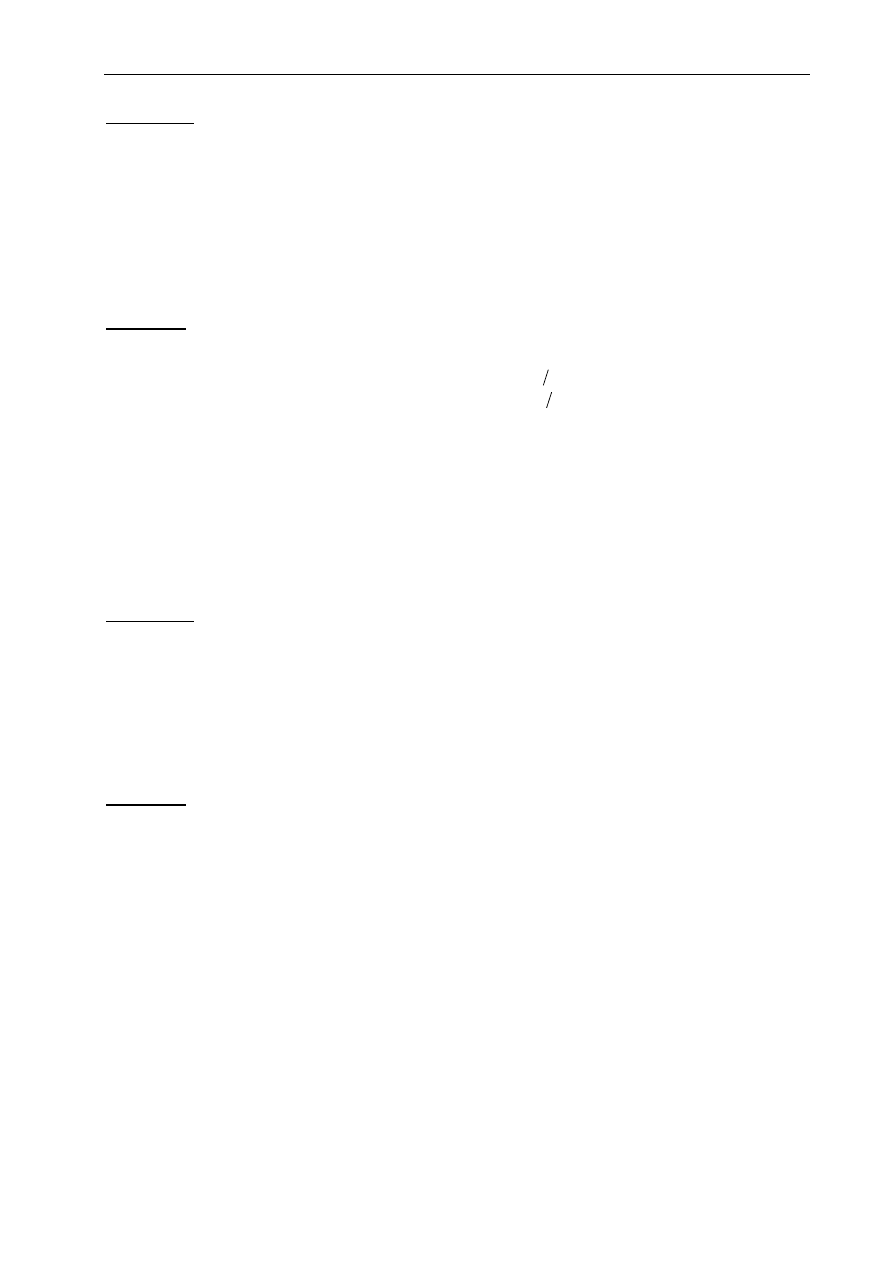
Technologia informacyjna - MATLAB
105
Rozwiązanie:
W = -1493
7.5.2 Wykorzystanie pętli do deklaracji macierzy
W tym podrozdziale zostanie przedstawionych kilka przykładów wykorzystania pętli For
i pętli If do deklaracji macierzy o współczynnikach określonych znaną zależnością.
Przykład 1:
Wygenerować macierz Lehmera stopnia 5 , której współczynniki są określone następująco:
j
i
dla
i
j
)
j
,
i
(
a
j
i
dla
j
i
)
j
,
i
(
a
skrypt15.m
n=5
for
i=1:n
for
j=1:n
if
i<j A(i,j)=i/j;
else
A(i,j)=j/i;
end
end
end
disp(A)
Rozwiązanie:
n = 5
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 1.0000 0.6667 0.5000 0.4000
0.3333 0.6667 1.0000 0.7500 0.6000
0.2500 0.5000 0.7500 1.0000 0.8000
0.2000 0.4000 0.6000 0.8000 1.0000
Przykład 2:
Wygenerować macierz Pei stopnia 5 , której współczynniki są określone następująco:
j
i
dla
1
)
j
,
i
(
a
j
i
dla
t
)
j
,
i
(
a
1
,
0
t
skrypt16.m
n=5
t=0.1
for
i=1:n
for
j=1:n
if
i==j A(i,j)=t;
else
A(i,j)=1;
end
end
end
disp(A)
x1 =
-9.0000
-3.0000
4.0000
x2 =
-9.0000
-3.0000
4.0000

Technologia informacyjna - MATLAB
106
Rozwiązanie:
n = 5
t = 0.1000
0.1000 1.0000 1.0000 1.0000 1.0000
1.0000 0.1000 1.0000 1.0000 1.0000
1.0000 1.0000 0.1000 1.0000 1.0000
1.0000 1.0000 1.0000 0.1000 1.0000
1.0000 1.0000 1.0000 1.0000 0.1000
Przykład 3:
Wygenerować macierz Wernera stopnia 5 , której współczynniki są określone następująco:
i
1
n
)
i
,
j
(
a
)
j
,
i
(
a
skrypt17.m
n=5
for
i=1:5
for
j=1:5
A(i,j)=n+1-i;
A(j,i)=n+1-i;
end
end
disp(A)
Rozwiązanie:
n = 5
5 4 3 2 1
4 4 3 2 1
3 3 3 2 1
2 2 2 2 1
1 1 1 1 1
Przykład 4:
Wygenerować macierz Goluba stopnia 5 , której współczynniki są określone następująco
j
i
dla
0
)
j
,
i
(
a
n
j
i
oraz
j
i
dla
1
)
j
,
i
(
a
1
n
,....,
2
,
1
i
dla
1
)
i
,
i
(
a
skrypt18.m
n=5
for
i=1:n
for
j=1:n
if
i>j | (i==n & j==n) A(i,j)=-1;
elseif
i~=n A(i,i)=1;
elseif
i<j A(i,j)=0;
end
end
end
disp(A)
Rozwiązanie:
n = 5
1 4 3 2 1
-1 1 3 2 1
-1 -1 1 2 1
-1 -1 -1 1 1
-1 -1 -1 -1 -1

Technologia informacyjna - MATLAB
107
7.6 Całkowanie
W bibliotece Matlaba istnieje wiele funkcji umożliwiających całkowanie numeryczne.
Funkcje te działają w oparciu o różne procedury. W poniższej tabeli przedstawione zostały trzy
podstawowe metody całkowania.
quad
adaptacyjna kwadratura oparta o regułę Simpsona stosowana dla funkcji
wolnozmiennych (interpolacja wielomianem drugiego stopnia)
quad8
adaptacyjna kwadratura ośmioprzedziałowa Newtona-Cotesa stosowana
dla funkcji szybkozmiennych (aproksymacja wielomianem ósmego stopnia)
quadl
adaptacyjna kwadratura Gauss-Lobatto
Tab. 7.2 Metody całkowania
Składnia powyższych poleceń które należy napisać w oknie programu, lub umieścić
w oddzielnym pliku, jest następująca:
Q = quad(‘plik’, a, b, tol, trace)
Q = quad8(‘plik’, a, b, tol, trace)
(7.18)
Q = quadl(‘plik’, a, b, tol, trace)
plik
nazwa pliku (bez rozszerzenia) w którym zadeklarowana jest funkcja podcałkowa
a, b
przedział całkowania
tol
wymagana tolerancja względna (domyślna 10
-3
)
trace
niezerowy parametr umożliwiający wyświetlenie wykresu funkcji podcałkowej
z zaznaczonymi węzłami kwadratury
Tab. 7.3 Parametry poleceń quad, quad8 i quadl
Funkcję podcałkową deklaruje się w skrypcie (np.: plik.m) w sposób następujący:
function y = f(x)
(7.19)
y =
Przykład 1:
Obliczyć wartość całki:
5
0
1
x
3
x
2
dx
i narysować wykres funkcji podcałkowej w przedziale
całkowania.
calk.m
function
y=f(x)
y=1./(2*x+sqrt(3*x+1));
skrypt19.m
%%całkowanie
Q=quad('calk',0,5);
%rysowanie wykresu:
x=0:0.01:5;
y=1./(2*x+sqrt(3*x+1));
plot(x,y);
grid on;
title(
'calkowanie'
);
text(1.2,0.25,
'wykres funkcji podcalkowej'
);
xlabel(
'x'
);
ylabel(
'y'
);
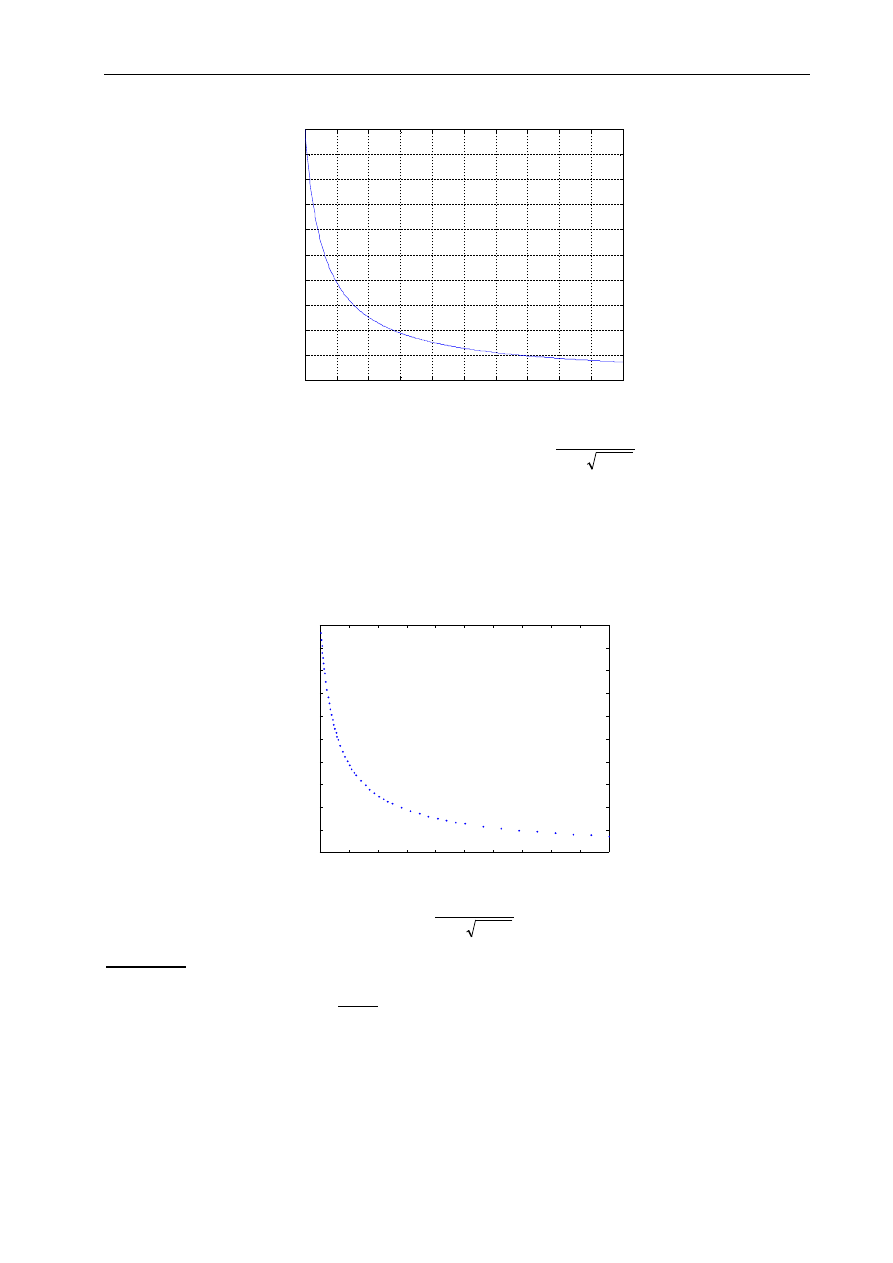
Technologia informacyjna - MATLAB
108
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
calkowanie
wykres funkcji podcalkowej
x
y
Rys. 7.11 Wykres funkcji podcałkowej
5
0
1
x
3
x
2
dx
Wartość całki wynosi: Q = 0.9437.
Wykres funkcji podcałkowej z zaznaczonymi węzłami kwadratury można również uzyskać
deklarując w poleceniach niezerową wartość parametru trace
:
Q=quad(
‘calk’
, 0,5, 1e-3, 1)
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Rys. 7.12 Wykres funkcji podcałkowej
5
0
1
x
3
x
2
dx
z zaznaczonymi węzłami kwadratury
Przykład 2:
Obliczyć wartość całki:
dx
1
e
x
e
5
,
0
x
i narysować wykres funkcji podcałkowej w przedziale
całkowania
calk1.m
function
y=f(x)
y=x./(exp(x)-1);
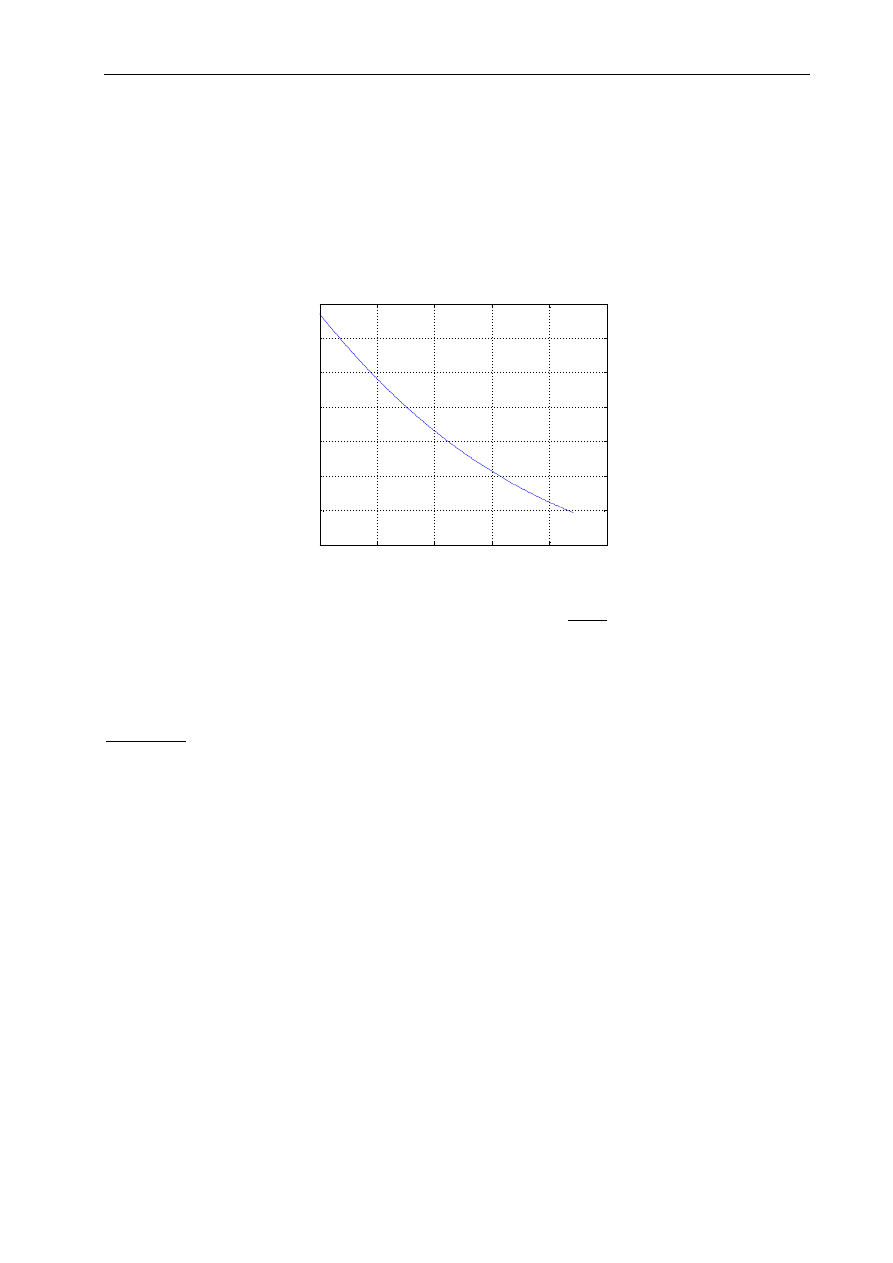
Technologia informacyjna - MATLAB
109
skrypt20.m
x=0.5:0.01:exp(1);
y=x./(exp(x)-1);
Q=quad(
'calk1'
,0.5,exp(1))
plot(x,y)
grid on
title(
'wykres funkcji podcalkowej'
)
xlabel(
'x'
)
ylabel(
'y'
)
0.5
1
1.5
2
2.5
3
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
wykres funkcji podcalkowej
x
y
Rys. 7.13 Wykres funkcji podcałkowej
dx
1
e
x
e
5
,
0
x
Wartość całki wynosi: Q = 0.9513.
Przykład 3:
Obliczyć wartość całki:
xdx
sin
xe
1
x
i narysować wykres funkcji podcałkowej w przedziale
całkowania.
calk2.m
function
y=f(x)
y=x.*exp(x).*sin(x);
skrypt20.m
x=1:0.01:pi;
y=x.*exp(x).*sin(x);
Q=quad(
'calk2'
,1,pi)
plot(x,y)
grid on
title(
'wykres funkcji podcalkowej'
)
xlabel(
'x'
)
ylabel(
'y'
)
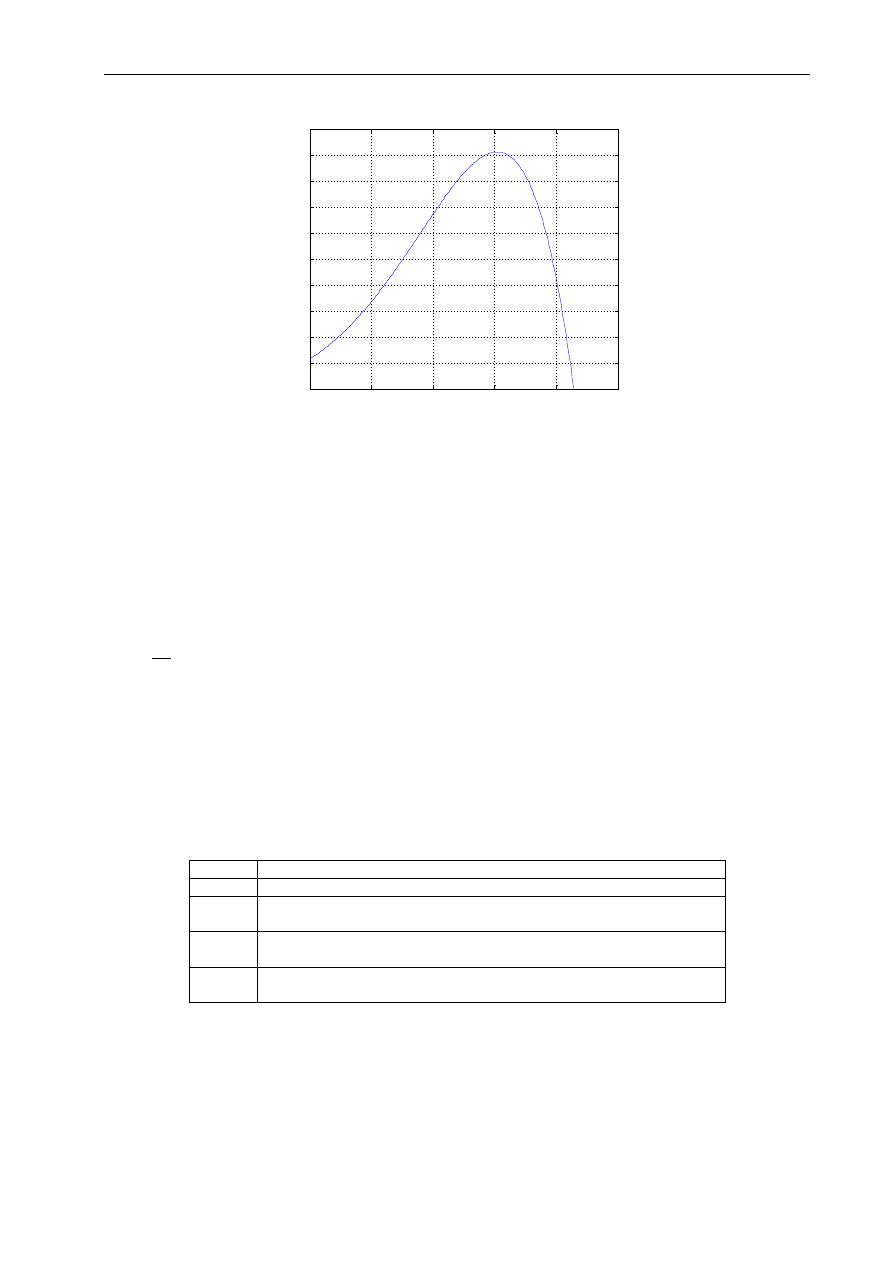
Technologia informacyjna - MATLAB
110
1
1.5
2
2.5
3
3.5
0
2
4
6
8
10
12
14
16
18
20
wykres funkcji podcalkowej
x
y
Rys. 7.14 Wykres funkcji podcałkowej
xdx
sin
xe
1
x
Wartość całki wynosi Q = 23,6353.
7.7 Różniczkowanie
W programie Matlab dostępnych jest kilka funkcji pozwalających na rozwiązanie
zagadnienia początkowego dla układów równań różniczkowych zwyczajnych postaci:
n
0
0
0
,
;
)
(
y
),
,
(
t
R
t
t
d
d
y
y
y
y
F
y
(7.20)
Przykładowo rozpatrzone zostaną dwie z nich (ode23 i ode45).
Każda z tych funkcji korzysta z pary metod Rungego-Kutty rzędu 2 i 3 (ode23) lub rzędu 4 i 5
(ode45).
[t, Y] = ode23(‘plik’, [t0 tk], [y0]’, tol, tr)
(7.21)
[t, Y] = ode45(‘plik’, [t0 tk], [y0]’, tol, tr)
plik
nazwa pliku (bez rozszerzenia) w którym zdefiniowana jest funkcja F(t, y)
t0, tk
przedział czasu w którym poszukiwane jest rozwiązanie
y0
warunek początkowy (wektor kolumnowy zawierający wartość rozwiązania
w chwili początkowej)
tol
parametr określający dokładność; domyślna wartość: 10
-3
dla ode23 i 10
-6
dla ode45
tr
parametr ten, jeżeli ma wartość niezerową umożliwia wypisanie na ekranie
kolejnych kroków metody
Tab. 7.4 Parametry poleceń ode23 i ode45
Aby wyznaczyć wartość rozwiązania należy, po zadeklarowaniu funkcji F(t, y), napisać
w oknie programu, lub w oddzielnym pliku, polecenie o postaci jak powyżej, zawierające nazwę
odpowiedniej funkcji ode.

Technologia informacyjna - MATLAB
111
Po wprowadzeniu oznaczenia dy = F(t, y), funkcję F(t, y) można zadeklarować w skrypcie
typu M-File w sposób następujący:
function dy = F(t, y)
(7.22)
dy =
W przypadku równania różniczkowego zwyczajnego wyższego rzędu należy,
wprowadzając dodatkowe zmienne, sprowadzić to równanie do układu równań rzędu pierwszego
i definiując funkcję F(t, Y) zamieścić wszystkie równania w macierzy.
Przykład 1:
W przedziale < 0; 3 >, stosując metodę ode23, znaleźć rozwiązanie następującego równania
różniczkowego:
2
t
1
1
dt
dy
, spełniającego warunek początkowy y(0) = 0. Wyznaczyć błąd w punkcie
końcowym i narysować wykres rozwiązania numerycznego i dokładnego w jednym układzie
współrzędnych a wykres błędu w drugim. Rozwiązanie dokładne określone jest zależnością: y = arctg(t).
rozn1.m
%%różniczkowanie
function
dy=F(t,y)
dy=1./(1+t.^2);
%dy=y’
skrypt10.m
[t,Y]=ode23(
'rozn1'
,[0 3],[0]);
%Y - rozwiązanie numeryczne
%wyznaczenia błędu różniczkowania
y=atan(t);
%y - rozwiązanie dokładne
bl=y-Y;
%błąd różniczkowania
%rysowanie wykresu
subplot(2,1,1);
plot(t,Y,t,y);
grid on;
title(
'rozniczkowanie'
)
text(1.2,0.7,
'rozwiazanie numeryczne i dokladne'
);
xlabel(
't'
);
ylabel(
'y'
);
subplot(2,1,2);
plot(t,bl);
grid on;
text(1.2,3e-5,
'wykres bledu'
);
xlabel(
't'
);
ylabel(
'y'
);
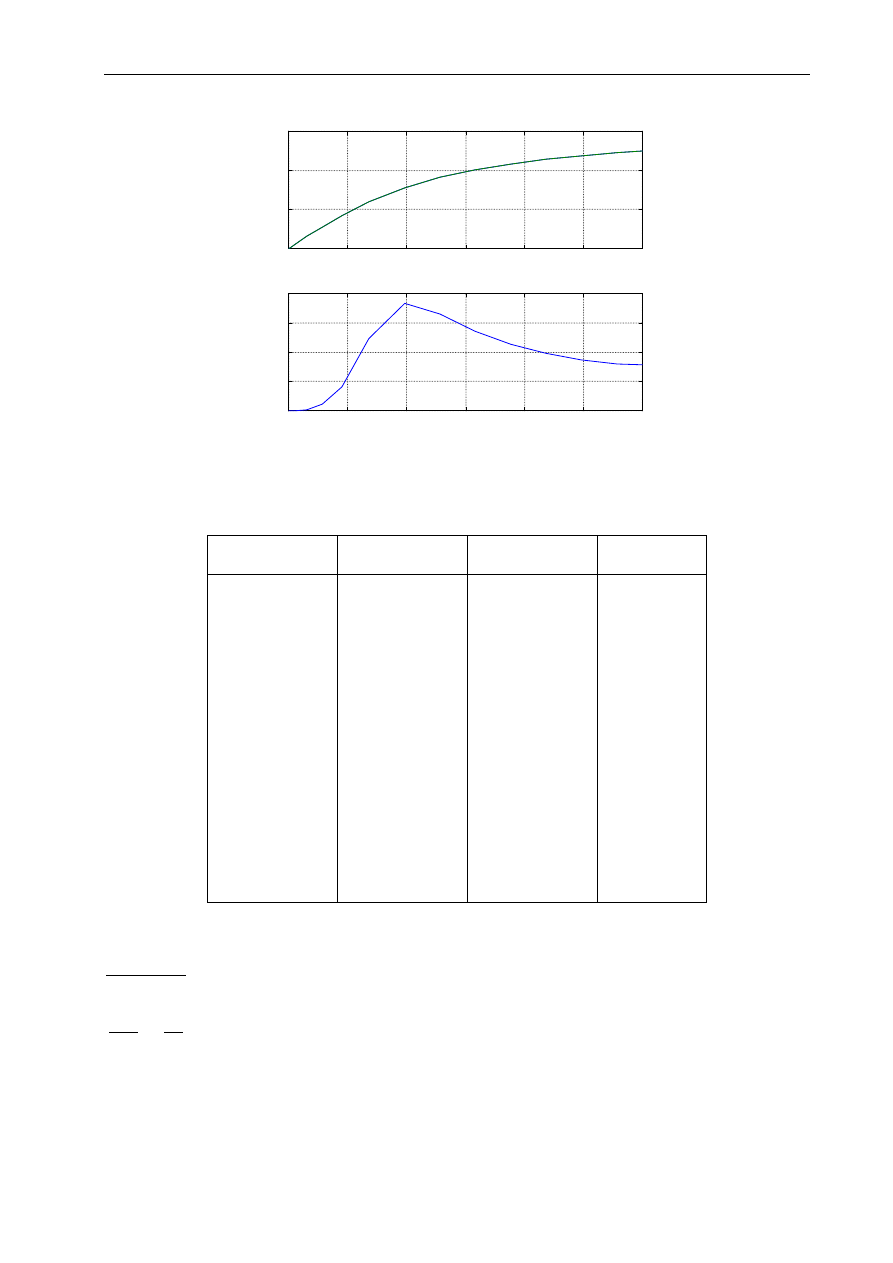
Technologia informacyjna - MATLAB
112
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
rozniczkowanie
rozwiazanie numeryczne i dokladne
t
y
0
0.5
1
1.5
2
2.5
3
0
2
4
6
8
x 10
-5
wykres bledu
t
y
Rys. 7.15. Rozwiązanie równania różniczkowego I-go rzędu metodą ode23
Rozwiązania uzyskane w Matlabie:
czas
rozwiązanie
numeryczne
rozwiązanie
dokładne
błąd
t =
0
0.0001
0.0005
0.0025
0.0125
0.0625
0.1543
0.2810
0.4472
0.6819
0.9819
1.2819
1.5819
1.8819
2.1819
2.4819
2.7819
3.0000
Y =
0
0.0001
0.0005
0.0025
0.0125
0.0624
0.1531
0.2740
0.4205
0.5984
0.7762
0.9082
1.0070
1.0823
1.1410
1.1877
1.2257
1.2490
y =
0
0.0001
0.0005
0.0025
0.0125
0.0624
0.1531
0.2740
0.4205
0.5985
0.7762
0.9083
1.0071
1.0824
1.1410
1.1878
1.2257
1.2490
bl =1.0e-004 *
0
0.0000
0.0000
0.0000
0.0000
0.0002
0.0061
0.0424
0.1640
0.4944
0.7331
0.6621
0.5453
0.4527
0.3896
0.3482
0.3210
0.3157
Wartość błędu w punkcie końcowym wynosi 0,3157*10
-4
.
Przykład 2:
Dla t <0;10> znaleźć rozwiązanie następującego równania różniczkowego II-rzędu
0
y
dt
dy
2
dt
y
d
2
2
o zadanym warunku brzegowym y(0) = [1 0].
Aby rozwiązać powyższe równanie należy sprowadzić je do układu dwóch równań I-rzędu
wprowadzając dodatkowe zmienne y
1
i y
2
:
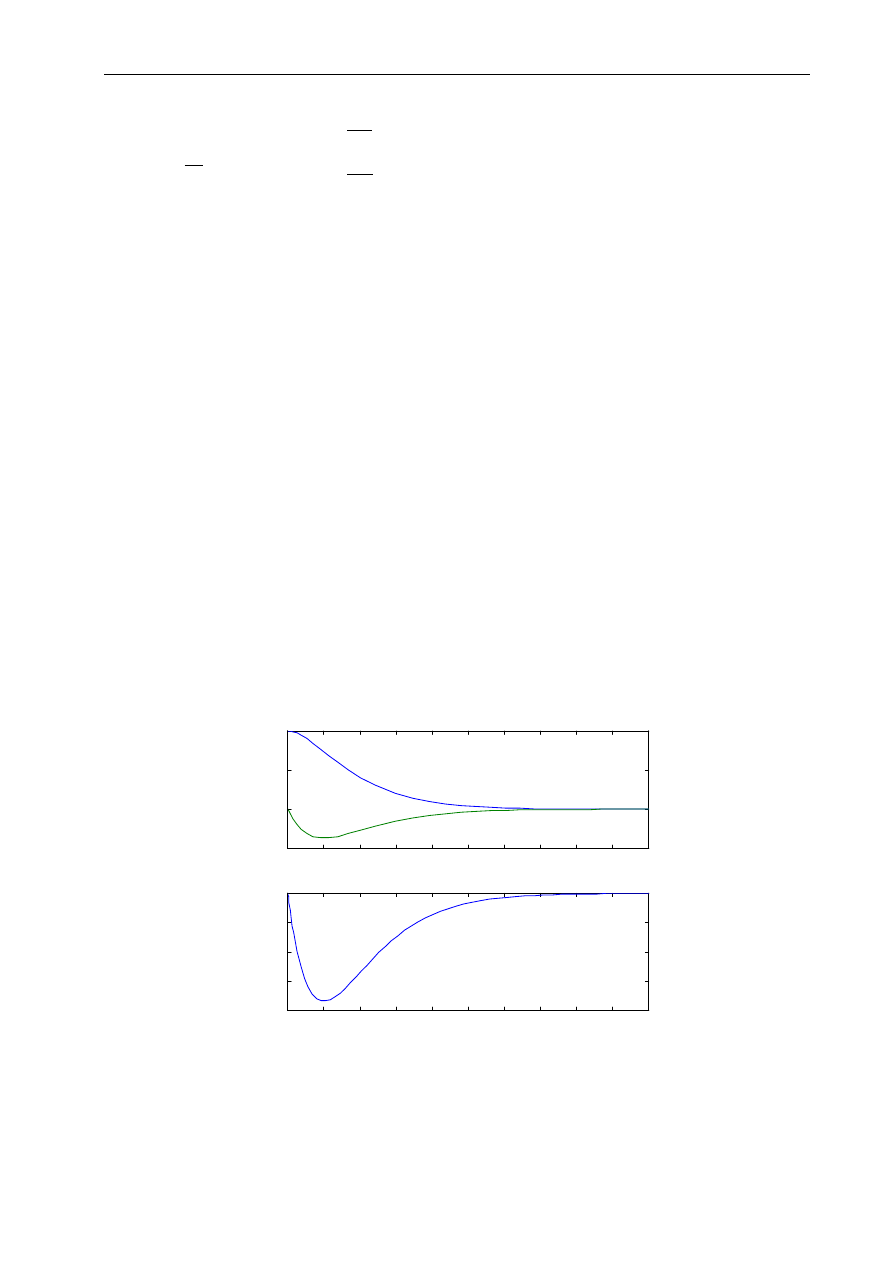
Technologia informacyjna - MATLAB
113
dt
dy
y
y
y
2
1
1
2
2
2
1
y
y
2
dt
dy
y
dt
dy
(7.23)
rozn2.m
%%równanie różniczkowe II-go rzędu
function
d2y=F(t,y)
%d2y=y''
d2y=[y(2);-y(1)-2*y(2)];
%y(1)=yy(2)=y’
skrypt11.m
%Y1 - rozwiązanie numeryczne metodą ode23
[t1,Y1]=ode23(
'rozn2'
,[0 10],[1 0]');
%Y2 - rozwiązanie numeryczne metodą ode45
[t2,Y2]=ode45(
'rozn2'
,[0 10],[1 0]');
%Y1 – pierwsze i drugie rozwiązanie metodą ode23
subplot(2,1,1);
plot(t1,Y1);
xlabel(
't'
);
title(
'rownanie rozniczkowe II-go rzedu'
);
ylabel(
'ode23'
)
text(3,0.4,
'rozwiazanie Y1[1]'
);
text(3,-0.25,
'rozwiazanie Y1[2]'
);
%Y2(:,2) - drugie rozwiązanie metodą ode45
subplot(2,1,2);
plot(t2,Y2(:,2));
xlabel(
't'
);
ylabel(
'ode45'
);
text(3,-0.2,
'rozwiazanie Y2[2]'
);
0
1
2
3
4
5
6
7
8
9
10
-0.5
0
0.5
1
t
rownanie rozniczkowe II-go rzedu
o
d
e
2
3
rozwiazanie Y1[1]
rozwiazanie Y1[2]
0
1
2
3
4
5
6
7
8
9
10
-0.4
-0.3
-0.2
-0.1
0
t
o
d
e
4
5
rozwiazanie Y2[2]
Rys. 7.16. Rozwiązania równania różniczkowego II-go rzędu metodami ode23 i ode45

Technologia informacyjna
114
Spis literatury
[1] Microsoft Office Word 2003 krok po kroku, Wydawnictwo RM, Łódź 2004
[2] Microsoft Office Excel 2003 krok po kroku, Wydawnictwo RM, Łódź 2004
[3] Jacobson R.: Microsoft Office Excel 2003 Visual Basic krok po kroku,
Wydawnictwo RM, Łódź 2004
[4] Bourg D.: Excel w nauce i technice receptury, Wydawnictwo Helion, Gliwice 2006
[5] Zalewski A., Cegieła R.: Matlab – obliczenia numeryczne i ich zastosowanie:
Wydawnictwo Naukowe PWN, Warszawa 1996
[6] Dyka E., Markiewicz P., Sikora R.: Modelowanie w elektrotechnice z wykorzystaniem
środowiska Matlab, Wydawnictwo PŁ 2006

Instrukcja jest współfinansowana przez Unię Europejską
w ramach Europejskiego Funduszu Społecznego
w projekcie:
"Innowacyjna dydaktyka bez ograniczeń
- zintegrowany rozwój Politechniki Łódzkiej zarządzanie Uczelnią,
nowoczesna oferta edukacyjna
i wzmacniania zdolności do zatrudniania,
także osób niepełnosprawnych".
Wyszukiwarka
Podobne podstrony:
tekst format, Politechnika, Pomoce dydaktyczne cz III, Pomoce, Dyka Mończyk - Informatyka, Dyka Mońc
Dyka Mończyk Podstawy informatyki
Konspekt Podstawy informatyki Dyka E , Mończyk M
Technologia informacji i komunikacji w nowoczesnej szkole
TECHNOLOGIE INFORMATYCZNE CRM
Technologia Informacyjna w moim życiu
Wykorzystanie technologii informacyjnych pokaz WTZ 4
test nr 7 wyrażenia regularne, STUDIA, LIC, TECHNOGIE INFORMACYJNE POLONISTYKA ZAOCZNE UW Uniwersyt
Technologia Informacyjna 22.11.2008, ściągnięte, IT, Technologia Informacyjna(5)
M3, WSFiZ Warszawa, Semestr II, Technologie informacyjne - ćwiczenia (e-learning) (Grzegorz Stanio)
2010 Grudzień 6, Rok I, Semestr I, Technologia Informacyjna
Zadania z, Studia, PK OŚ, technologia informacyjna, exel
Strona tytulowa referatu, Administracja, Semestr 1, Technologia informacyjna
Katalog Mediów Polskich, Informacja naukowa i bibliotekoznawstwo, Technologia informacyjna
KWERENDY dod 2, Szkoła, Semestr 1, Technologia informacyjna, Ćwiczenie 6
inf, SGGW, Niezbędnik Huberta, Leśnictwo, Semestr 1, Technologia Informacyjna, Egzamin
więcej podobnych podstron