1

Algorytmy i struktury danych

wykład 4

Algorytmy sortowania cz.2

2/38

Plan prezentacji



sortowanie metodą drzewa



sortowanie metodą kopcowania (Heapsort)



sortowanie metodą scalania



porównanie poznanych metod sortowania



wyszukiwanie wskazanego elementu tablicy

3/38

Poznane metody sortowania



przez wstawianie



przez wybieranie



bąbelkowe



przez wstrząsanie (shakesort)



szybkie (quicksort)

4/38

Sortowanie drzewiaste



buduje się drzewo wyboru, składające się elementów
sortowanej tablicy znajdujących się na najniższym
poziomie (gałęziach) drzewa



porównując wielokrotnie dwa elementy wyszukany
zostanie najmniejszy element (korzeń drzewa)



eliminuje się element z korzenia i ponownie metodą
porównań wyznacza najmniejszy, większy od
poprzedniego korzenia

5/38

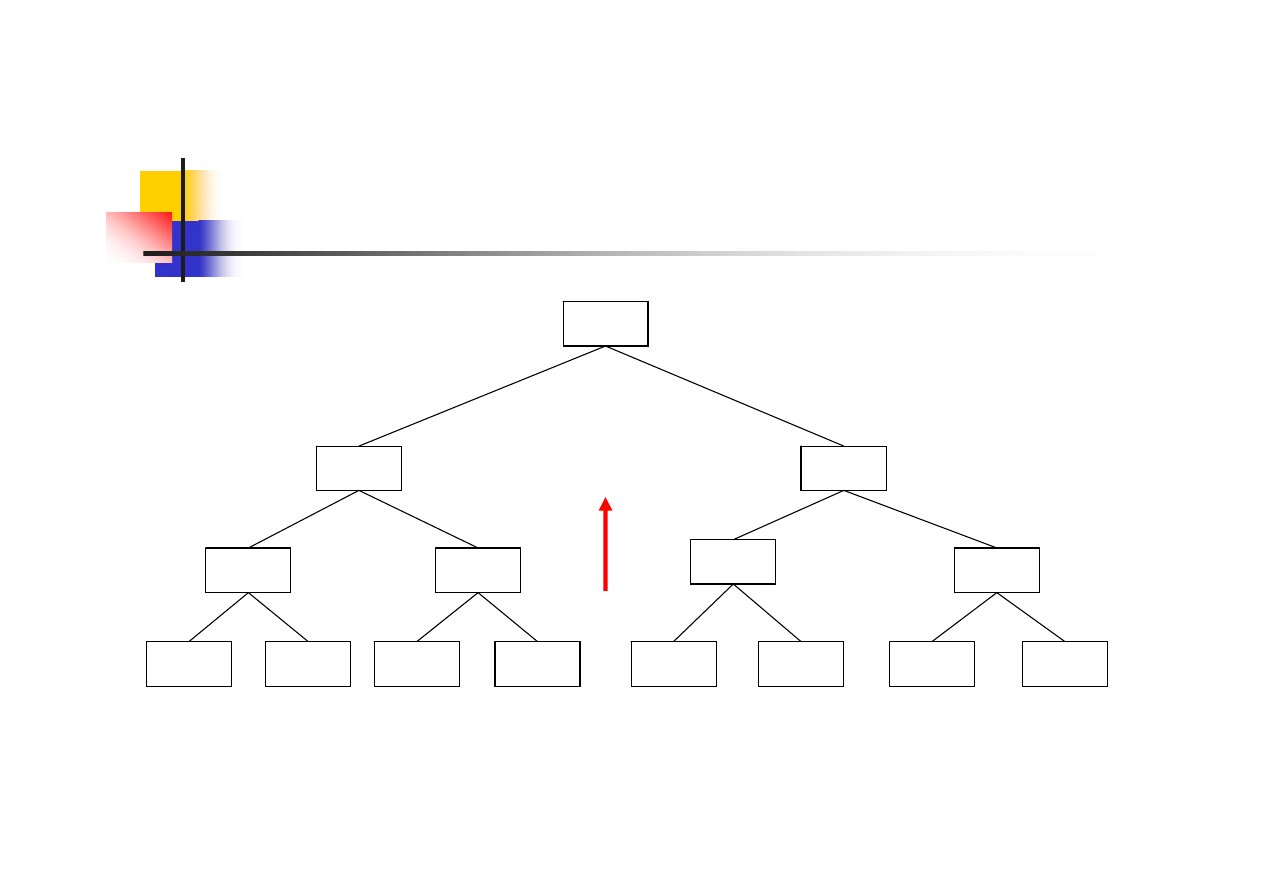
Sortowanie drzewiaste – budowa

drzewa

5

4

8

1

9

10

2

7

2

4

1

9

2

1

1

6/38

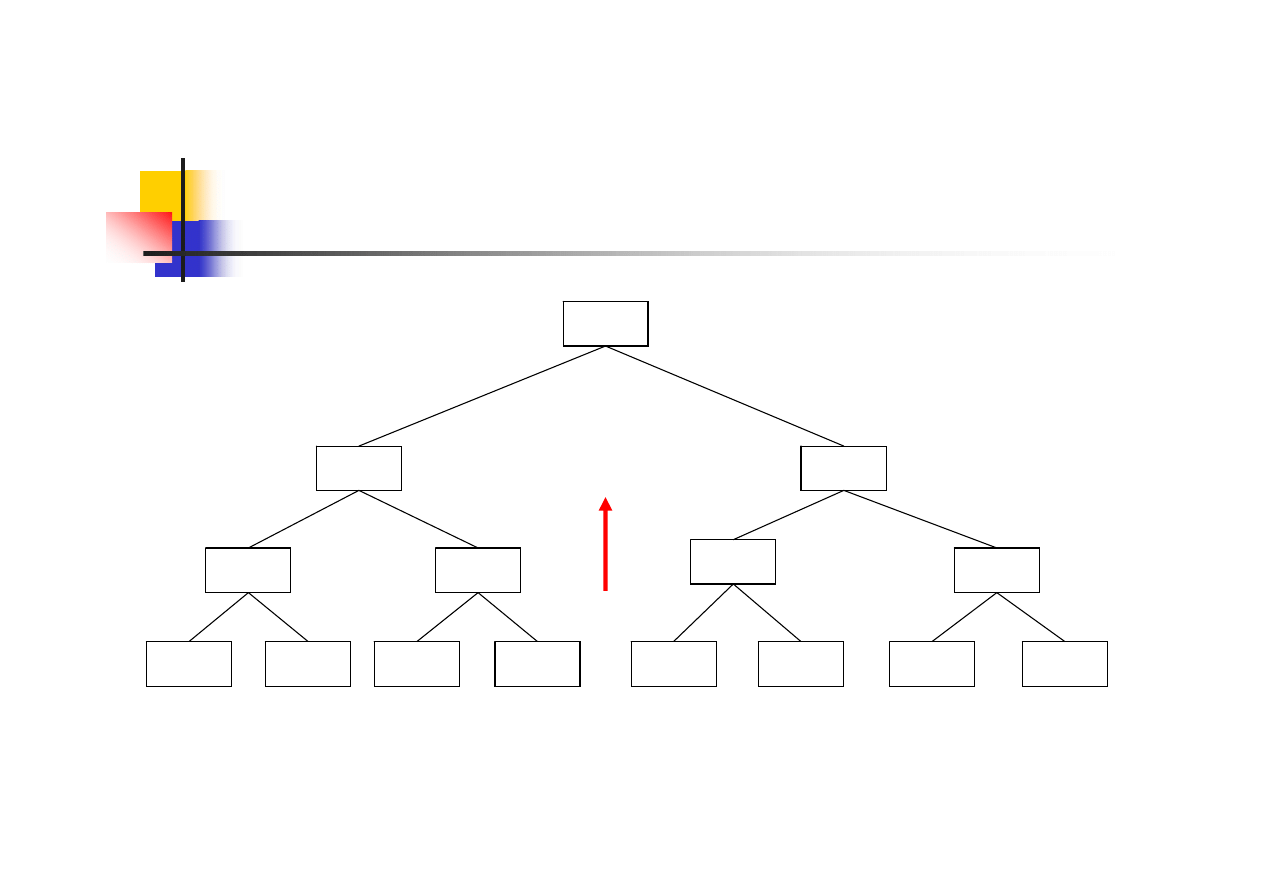
Sortowanie drzewiaste – usunięcie
korzenia- elementu najmniejszego

5

4

8

-

9

10

2

7

2

4

-

9

2

-

-

7/38

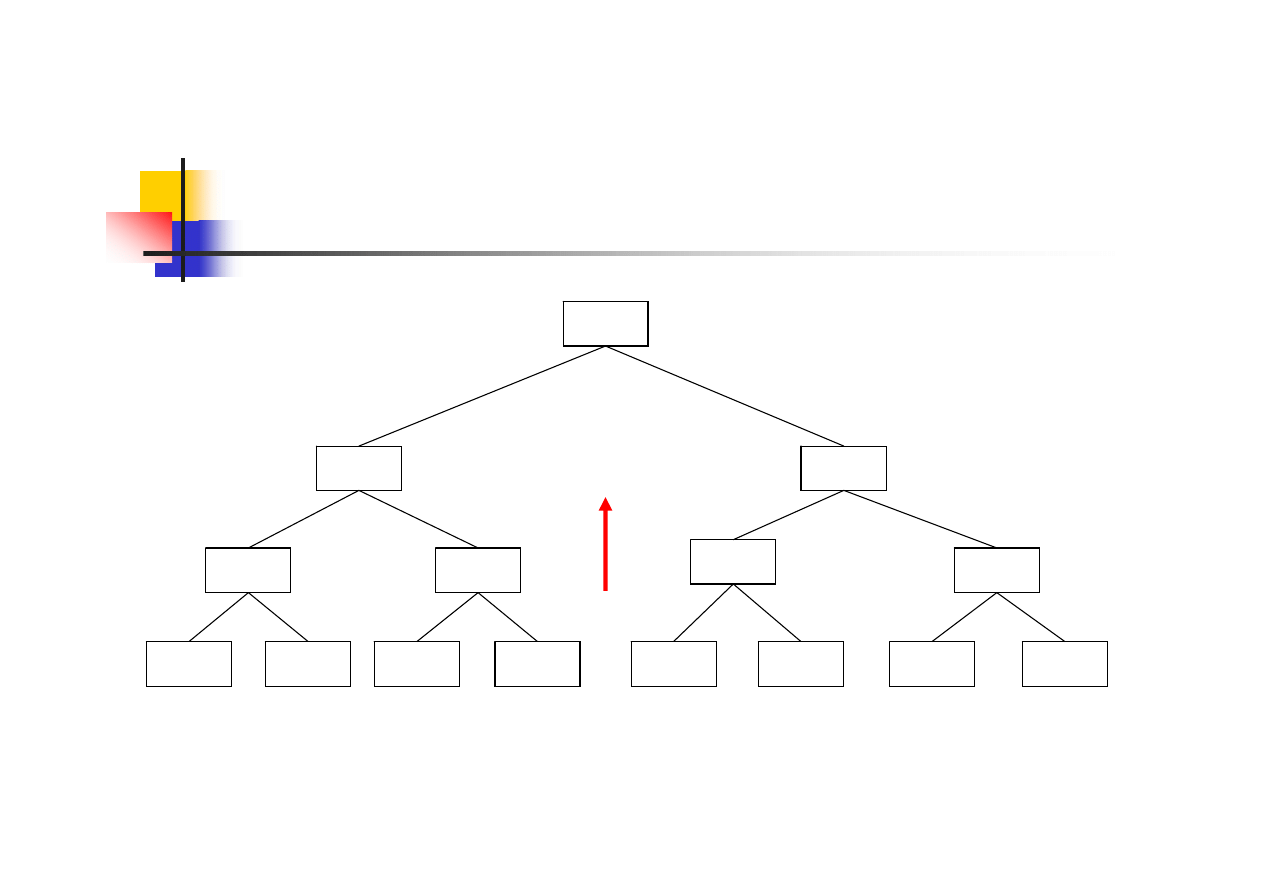
Sortowanie drzewiaste – wybór nowego
korzenia- elementu najmniejszego

5

4

8

-

9

10

2

7

2

4

8

9

2

8

2

8/38

Sortowanie drzewiaste – analiza



po n krokach drzewo jest puste → tablica
posortowana



liczba porównań Pr=log

2

n



cały proces sortowania wymaga n

∙

logn

operacji prostych oraz n operacji
budowania drzewa

9/38

Sortowanie przez kopcowanie

(heap sort)



jest ulepszoną wersją sortowania
drzewiastego



opiera się na pojęciu kopca

10/38

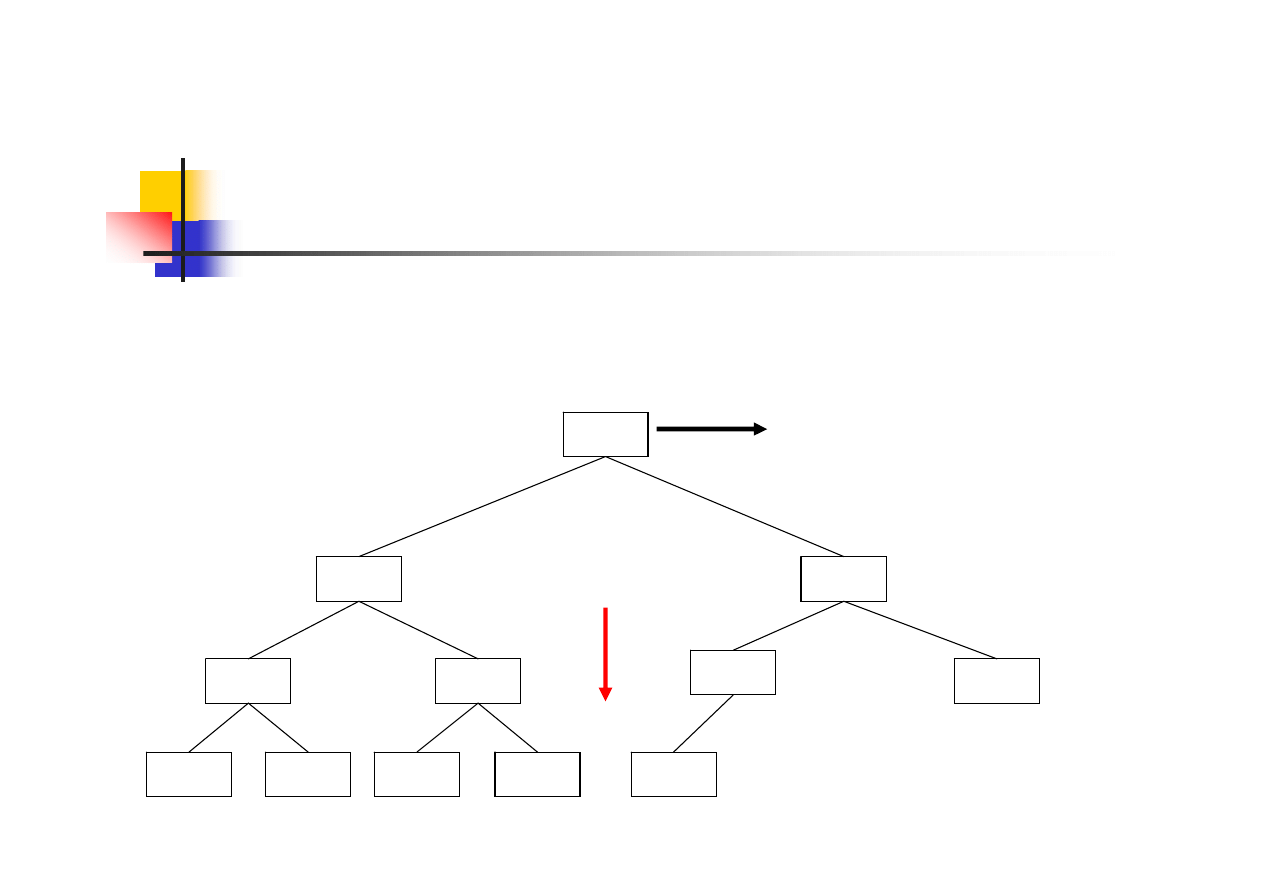
Kopiec (heap) - definicja

ci

ąg elementów h

l

, h

l+1

,…,h

p

spe

łniających zależności:

h

i

≥ h

2i

, h

i

≥

h

2i+1

dla ka

żdego i = l…p/2

h10

h11

h12

h9

h8

h4

h5

h6

h7

h2

h3

h1

h

1

=max(h

l

,…,h

n

)

11/38

Kopiec (heap) - w

łaściwości



tablica reprezentowana jest w postaci kopca (drzewa
binarnego)



kopiec budowany jest od góry



kopiec jest zape

łniony na każdym poziomie, wyjątkiem

jest najni

ższy poziom, zapełniany od lewej strony



ka

żdy węzeł drzewa odpowiada jednemu elementowi

tablicy



dany w

ęzeł dla węzłów poniższych jest ojcem



w

ęzły poniżej ojca (i) → lewy syn (2∙i) i prawy syn

(2∙i+1)



własność kopca: h[ojciec(i)] ≥ h[i] dla każdego węzła
i nie będącego korzeniem

12/38

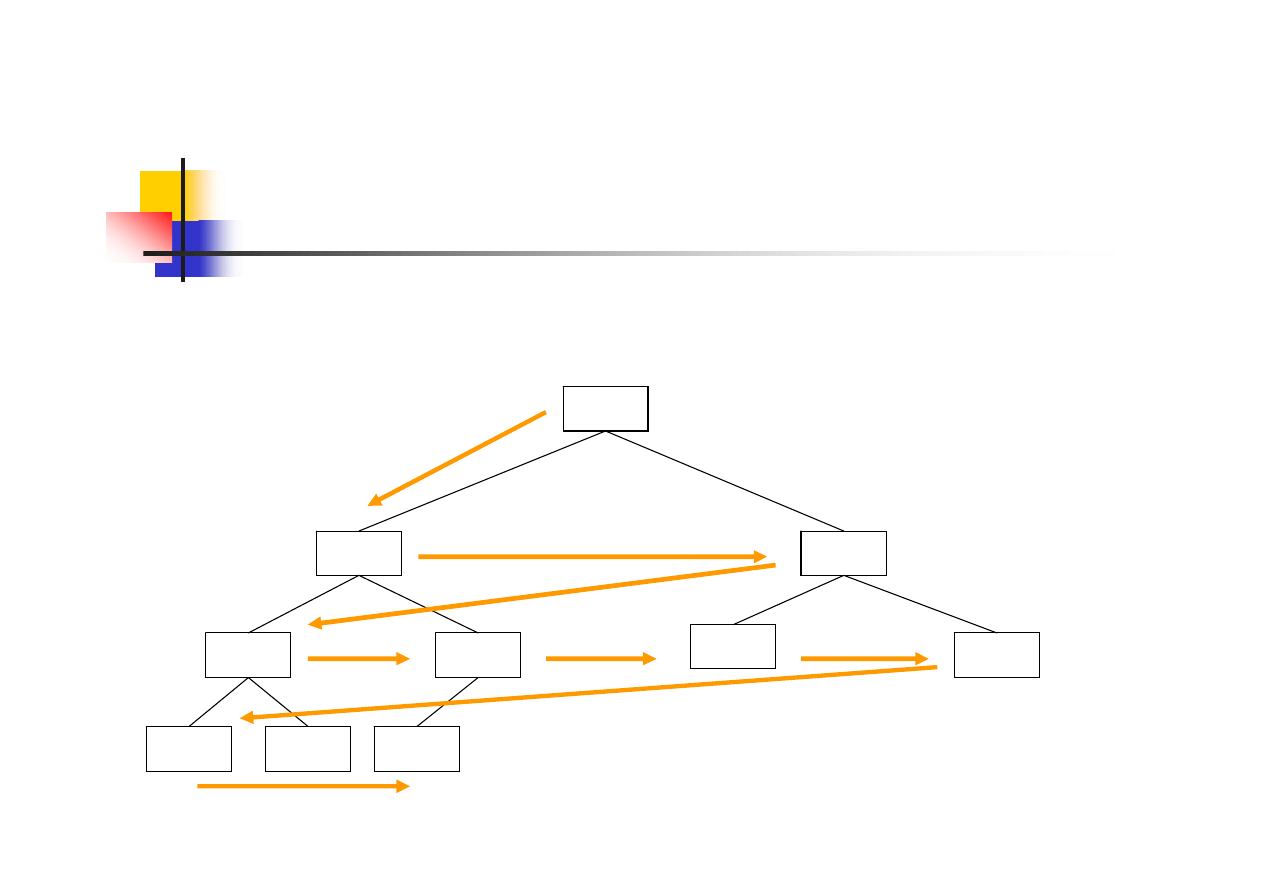
Zamiana listy na kopiec

Elementy listy: 7,2,6,4,8,1,9,10,3,5

5

3

10

4

8

1

9

2

6

7

13/38

Przywracanie własności kopca



procedura wywoływana gdy jeden z elementów
kopca nie spełnia zależności h[ojciec(i)]

≥

h[i]



polega na przesunięciu elementu na niższe poziomy
drzewa (kopca) w ten sposób, aby poddrzewo
zaczepione w danym węźle było kopcem



jeżeli obaj synowie mają większą wartość, to element
sprawdzany zamieniany jest z większym synem



jeżeli tylko jeden syn ma większą wartość, to z nim
następuje zamiana

14/38

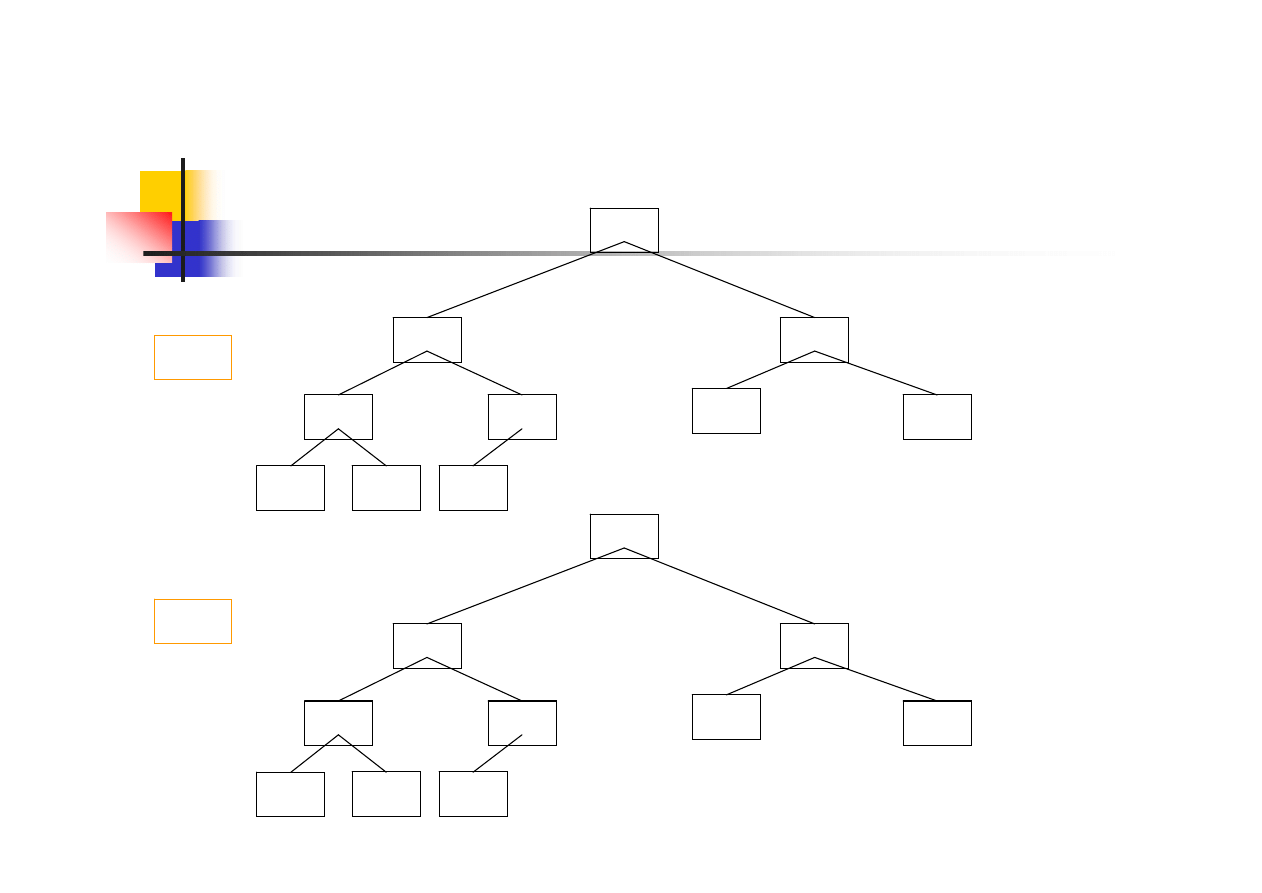
Budowa kopca

5

3

4

10

8

1

9

2

6

7

5

3

4

10

8

1

6

2

9

7

1

2

15/38

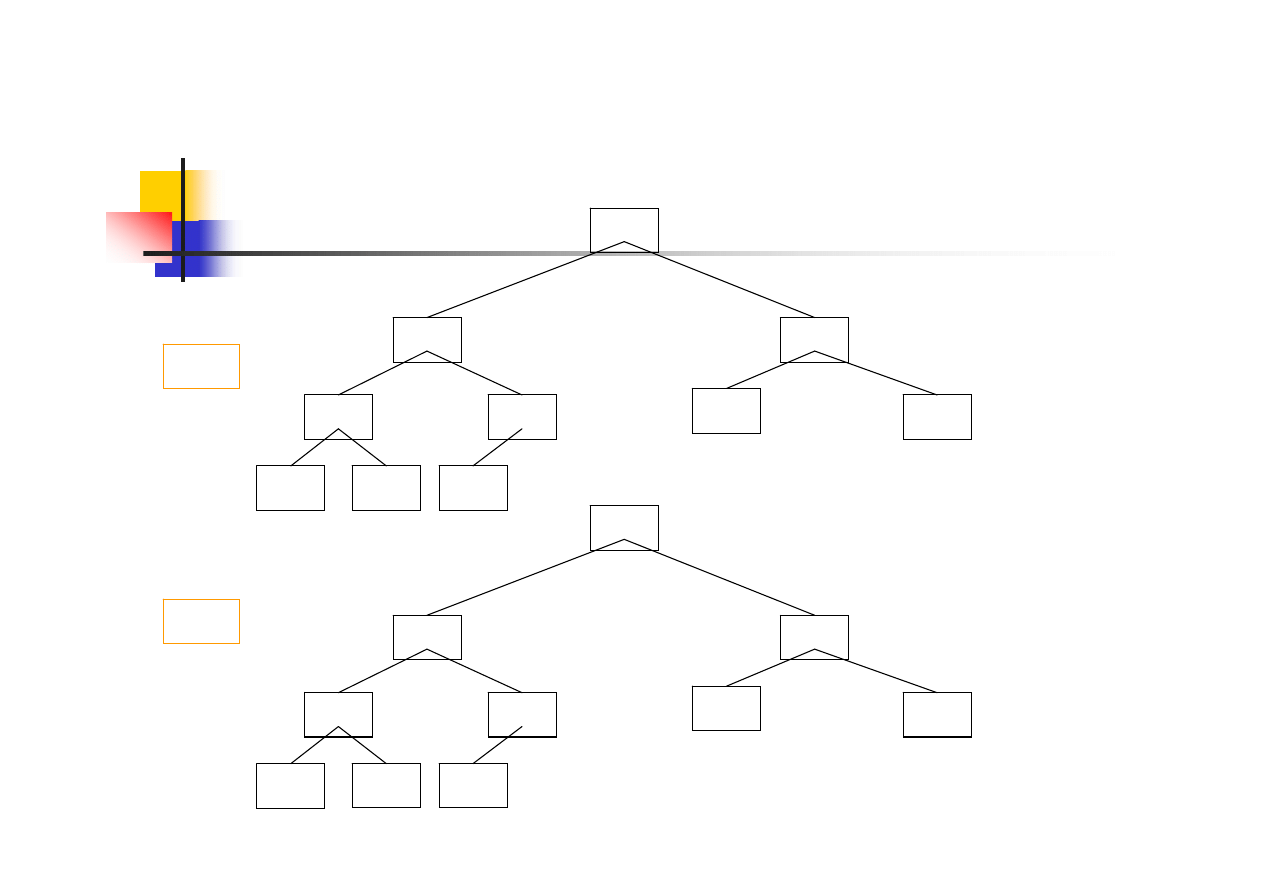
Budowa kopca

5

3

2

4

8

1

6

10

9

7

5

3

2

4

7

1

6

8

9

10

3

4

16/38

Sortowanie danych



sortowaniu podlega tablica T(1..n) reprezentowana przez

zbudowany z jej elementów kopiec o n węzłach



element o największej wartości znajduje się zawsze w

danym kroku sortowania (po przywróceniu właściwości

kopca) w korzeniu (na górze kopca)



element z korzenia h(1) zostaje w danym kroku sortowania

zamieniony w drzewie/kopcu z elementem o największym

indeksie h(n)



węzeł n zostaje usunięty z kopca, dalszemu sortowaniu

podlega tablica T(1..n-1) reprezentowana przez kopiec o

elementach h(1)-h(n-1)



sprawdza się, czy zachowana jest własność kopca i

ewentualnie wykonuje się procedurę jej przywracania

17/38

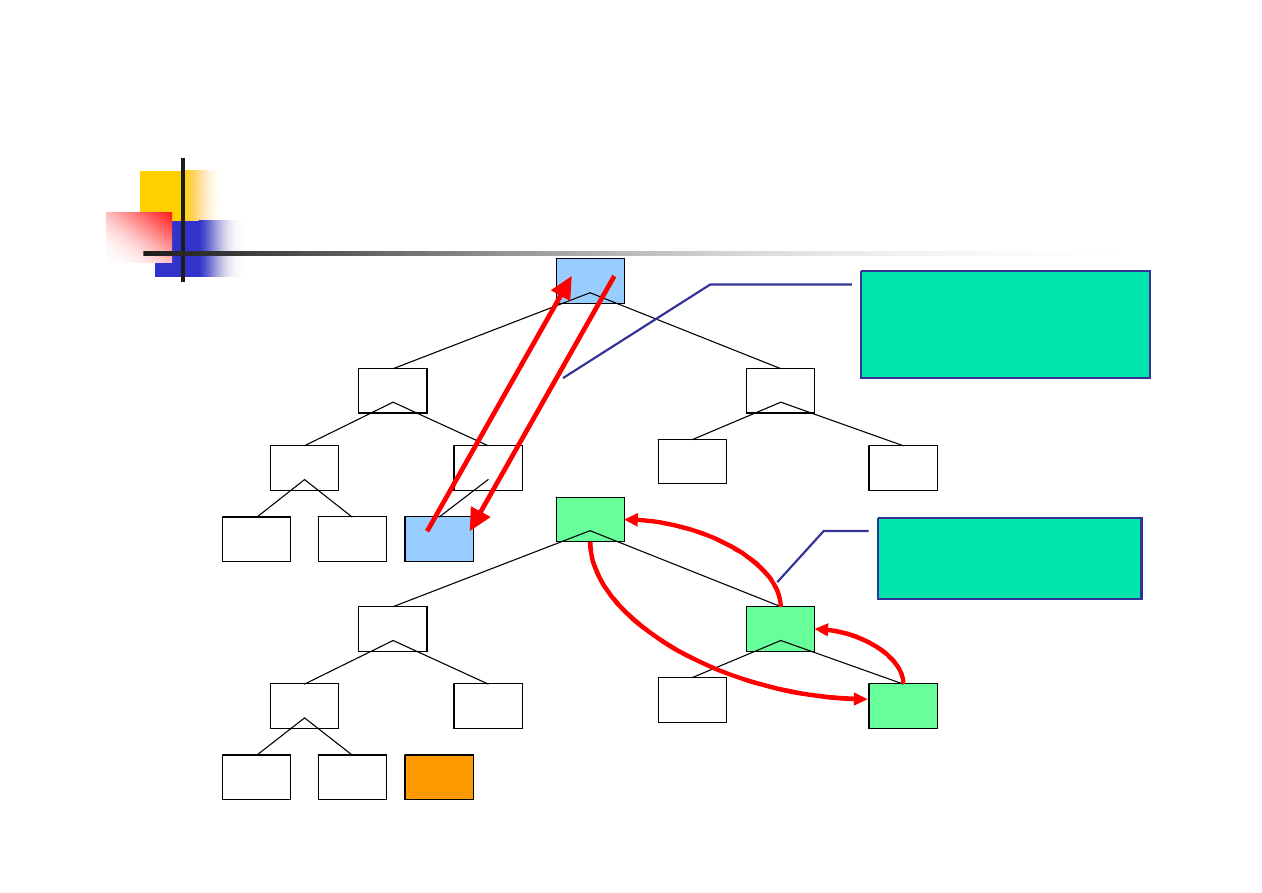
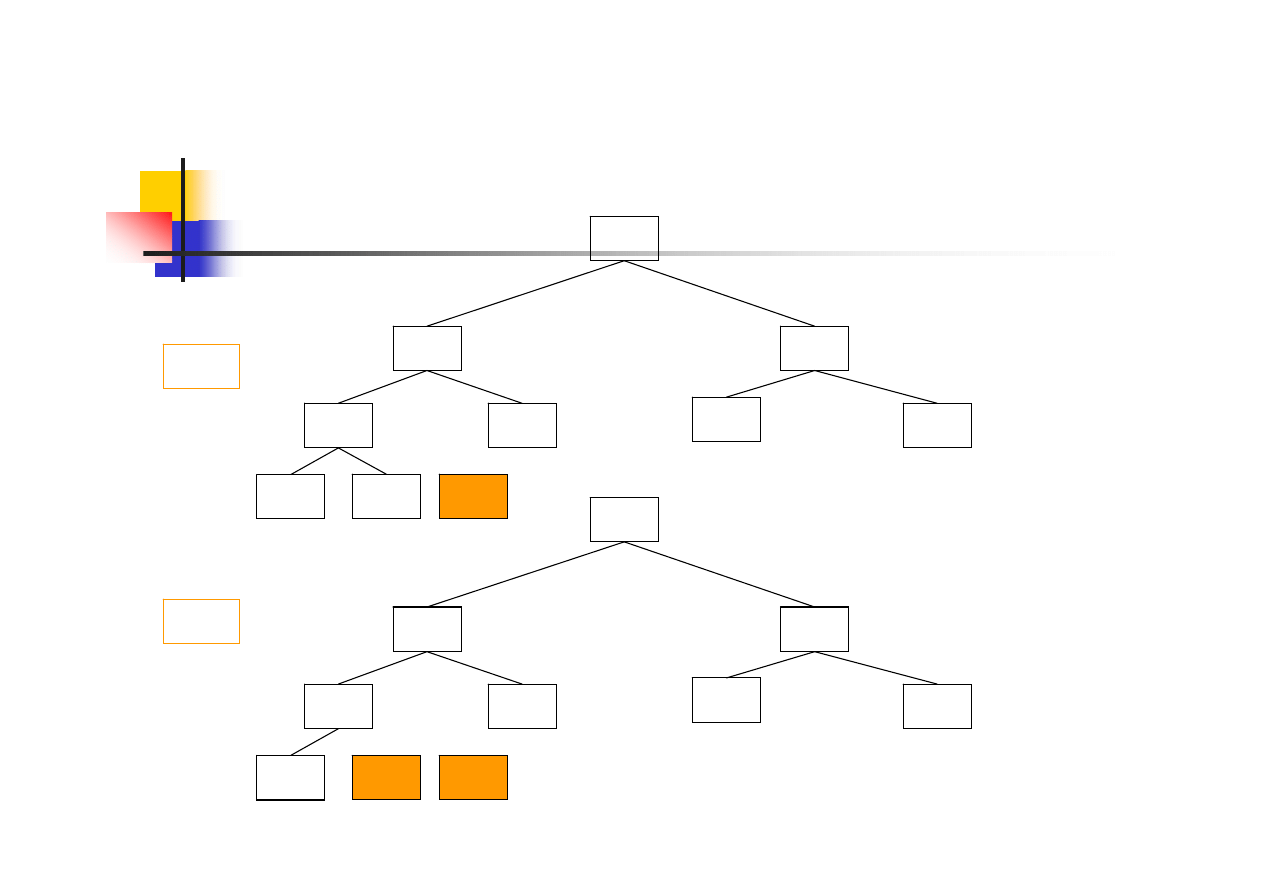
Sortowanie danych – 1. krok

5

3

2

4

7

1

6

8

9

10

10

3

2

4

7

1

6

8

9

5

zamiana elementu

największego i

ostatniego

przywracanie

właściwości kopca

18/38

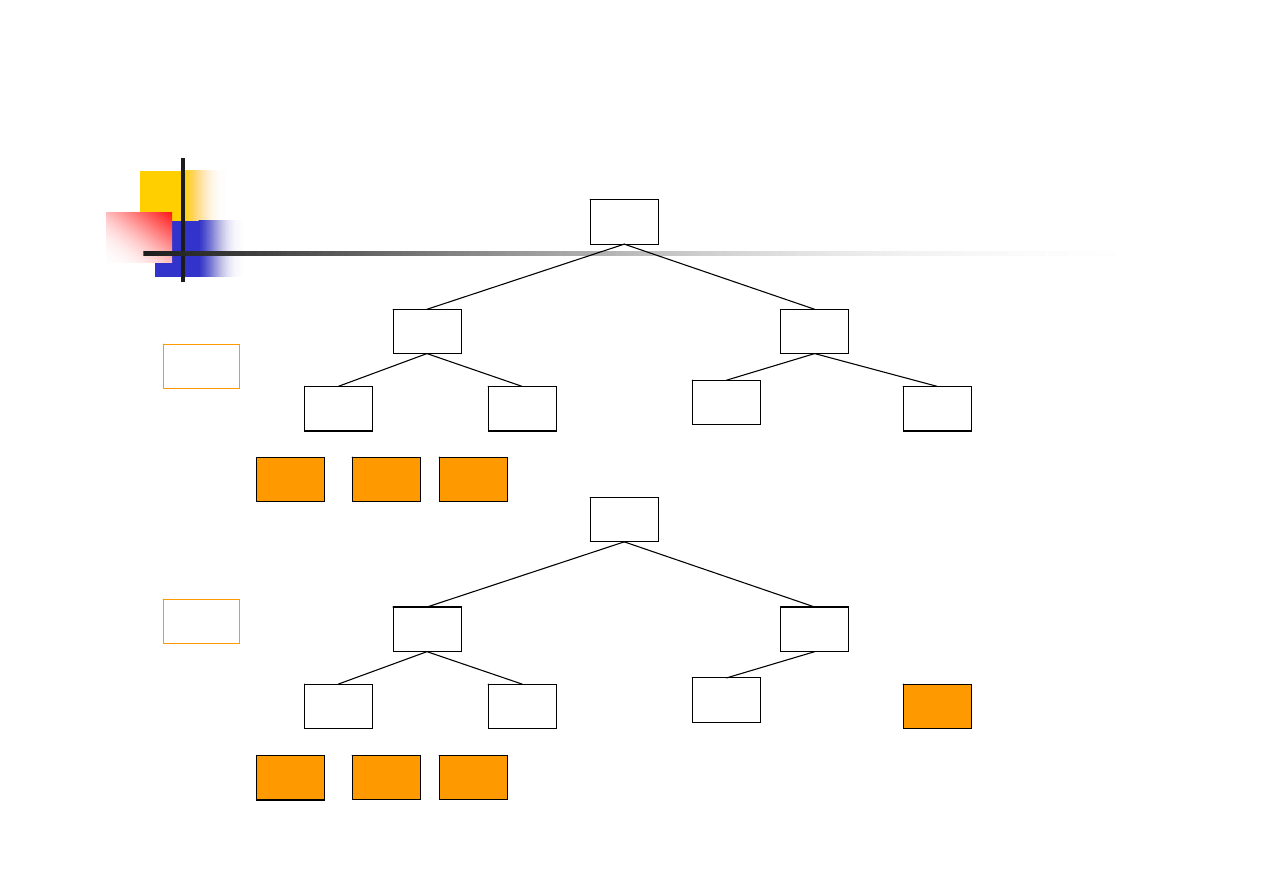
Sortowanie danych – 2. krok

1

2

10

3

2

4

7

1

5

8

6

9

10

9

2

4

3

1

5

7

6

8

19/38

Sortowanie danych 3. i 4. krok

3

4

10

9

8

2

3

1

5

4

6

7

10

9

8

2

3

1

7

4

5

6

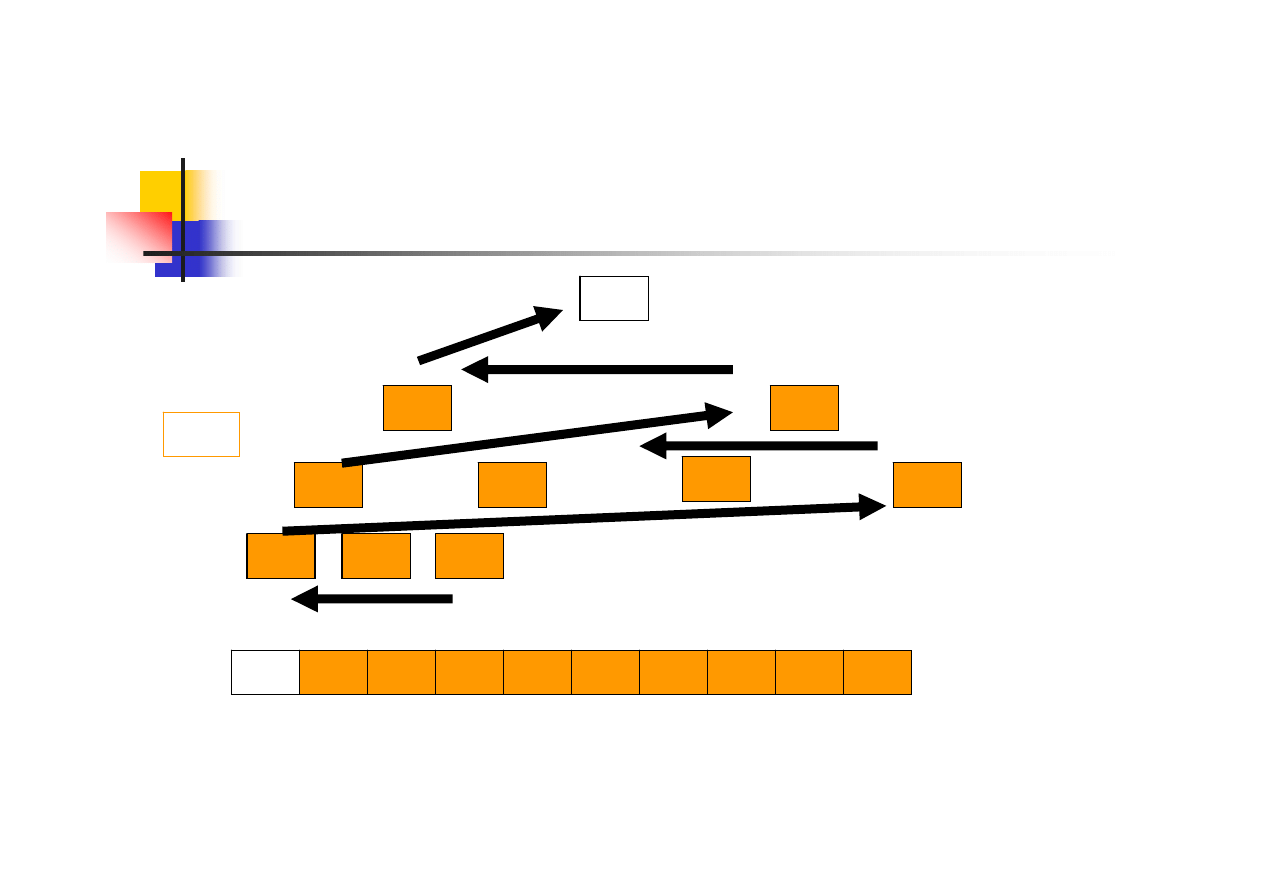
20/38

Sortowanie danych – ostatni krok

9

10

9

8

4

5

6

7

2

3

1

1

2

3

4

5

6

7

8

9

10

21/38

Budowa kopca - procedura

void budowa_kopca(int t[], int r)

{

int wtemp;

for(int k=r/2;k>0;k--)

//indeks ostatniego węzła-ojca

przywracanie_kopca(t,k,r);

do

//rozpoczęcie sortowania poprzez wymiany elementów

{

wtemp=t[0];

t[0]=t[r-1]; t[r-1]=wtemp;

//zamiana największy-ostatni

r--;

// pominięcie (odłączenie) największego elementu

przywracanie_kopca(t,1,r);

//po zamianie najw.-ostatni

} while (r>1);

// r=1 to posortowana cała tablica

}

22/38

Przywracanie własności kopca –
procedura

void przywracanie_kopca(int t[], int k, int r)

{

int j;

int wtemp=t[k-1];

// zapamiętanie sprawdzanego węzła-ojca

while(k<=r/2)

{

j=2*k;

// nr 1. syna dla ojca o nr=k

if(j<r && t[j-1]<t[j]) j++;

//wybranie większego z synów

if(wtemp>=t[j-1]) break;

//ojciec>=syn, więc nie ma zamiany

else

//ojciec<syn, więc jest zamiana

{

t[k-1]=t[j-1];

//zamiana ojca z większym synem

k=j;

//ster. do węzła większego syna aby spr. z jego nowymi synami

}

}

t[k-1]=wtemp;

//ostateczna pozycja ojca

}

23/38

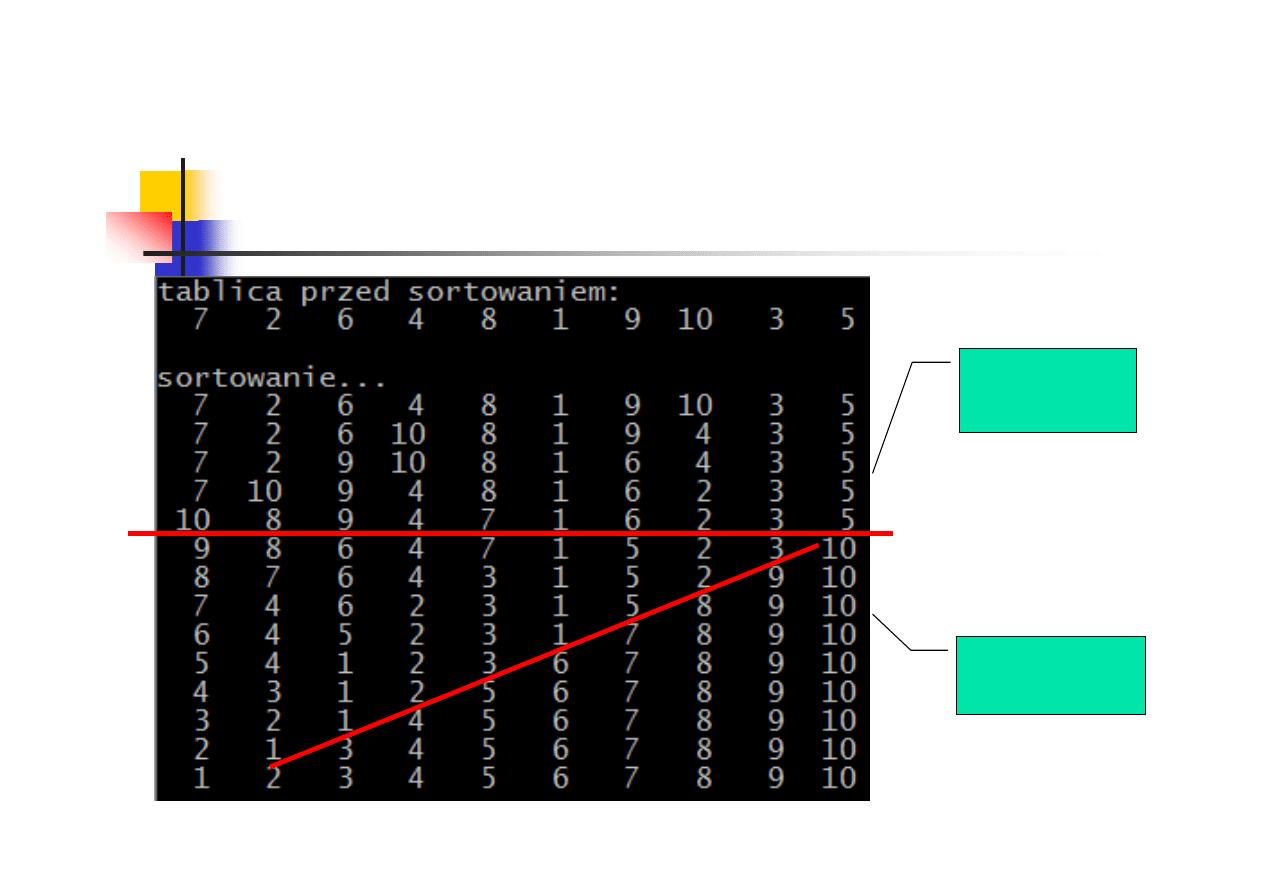
Sortowanie przez kopcowanie - przykład

budowa

kopca

posortowana

część tablicy

24/38

Sortowanie przez kopcowanie -
analiza



zalecane do sortowania dużych tablic



im większa tablica, tym większa efektywność
metody



w najgorszym przypadku wymaga n

∙

logn operacji

podstawowych



średnia liczba przesunięć wynosi 0.5

∙

n

∙

logn



metoda jest wrażliwa na początkowe ułożenie
elementów (zwłaszcza w kolejności odwrotnej)

25/38

Sortowanie przez scalanie



podobna do quicksort



jest metodą rekurencyjną typu „dziel i zwyciężaj”



schemat działania:



podział tablicy n-elementowej na dwie podtablice zawierające
po n1=n/2 oraz n2=n-n1 elementów



sortowanie metodą przez scalanie każdej podtablicy



łączenie posortowanych podtablic w jedną tablicę



tablica dzielona jest aż do pojedynczych elementów
(wówczas p=k)

26/38

Sortowanie przez scalanie

void sort_scalanie(int t[], int p, int k)

{

int m;

if(p<k)

{

m=(p+k)/2;

sort_scalanie(t,p,m);

sort_scalanie(t,m+1,k);

scalanie(t,n,p,m,k);

}

}

podzia

ł na dwie podtablice

wywo

łania rekurencyjne

scalenie podtablic

27/38

Scalanie - opis



wykonywane jest dla podtablic uzyskanych w
procesie dzielenia, w odwrotnej kolejności



scalanie podtablic t1:{x

p

..x

m

} oraz

t2{x

m+1

..x

k

} do tablicy t:{x

p

..x

k

} odbywa się

następująco



i= x

p

..x

m

, j=x

m+1

..x

k



jeżeli t1[i]<=t2[j], wstawianie t1[i] do t; i:=i+1



jeżeli t2[j]<t1[i], wstawianie t2[j] do t; j:=j+1

28/38

Scalanie - procedura

void scalanie( int t[], int r, int p,

int m, int k)

{

int* t2=new int[r];

for(int i=0;i<r;i++) t2[i]=0;

int p1, k1, p2, k2, i;

p1=p; k1=m; p2=m+1; k2=k; i=p1;

while(p1<=k1 && p2<=k2)

{

if(t[p1]<t[p2])

{

t2[i]=t[p1]; p1++;

}

else

{

t2[i]=t[p2]; p2++;

}

i++;

}

while(p1<=k1)

{

t2[i]=t[p1];

p1++; i++;

}

while(p2<=k2)

{

t2[i]=t[p2];

p2++; i++;

}

for(i=p;i<=k;i++)

t[i]=t2[i];

}

po wyczerpaniu p2

po wyczerpaniu p1

kopiowanie z tab.
tymcz. do oryg.

29/38

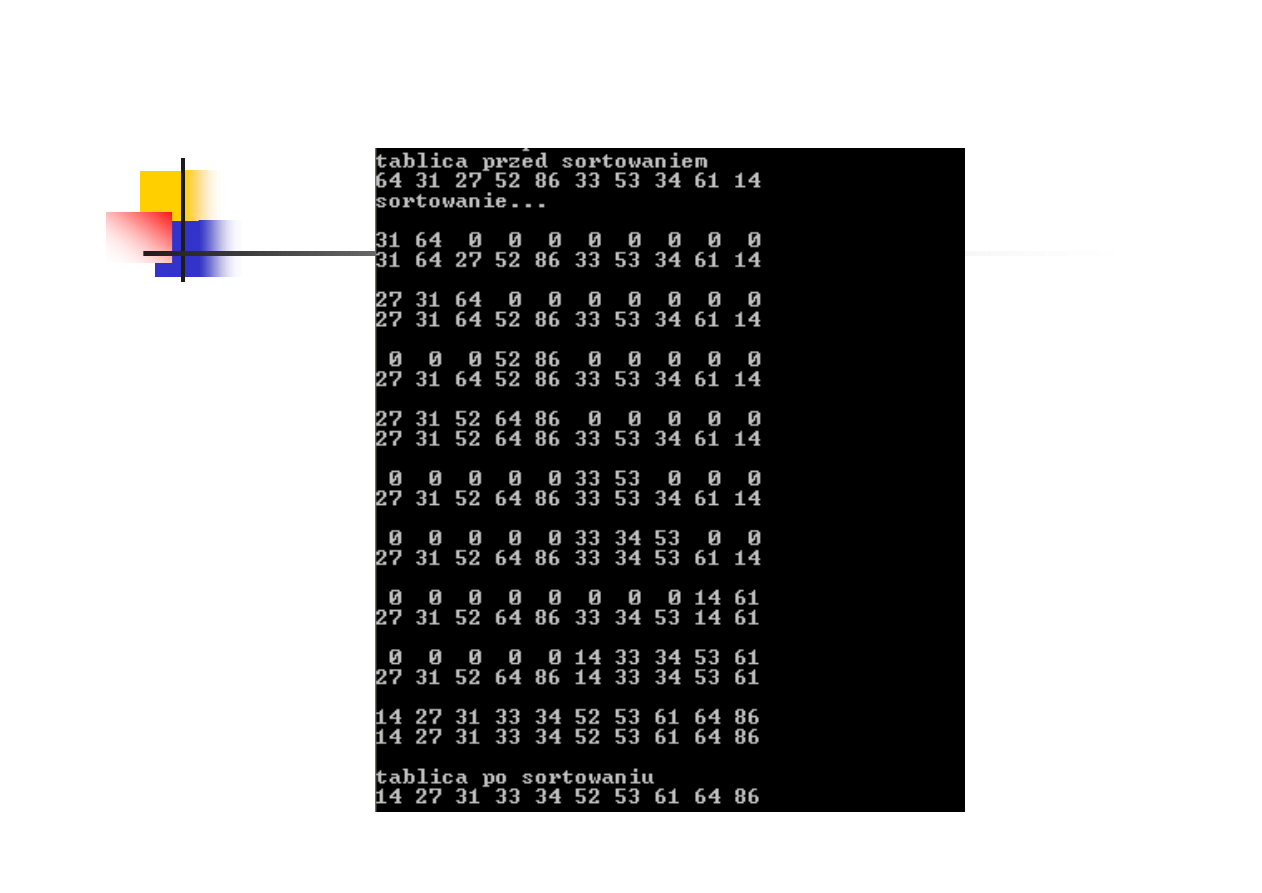
Sortowanie przez scalanie - przykład

30/38

Sortowanie – porównanie
efektywności metod, mały zbiór

187

195

196

scalanie

227

246

264

kopcowanie

75

137

55

szybkie

5757

3071

5

wstrząsanie

5599

3212

610

bąbelkowe

1430

607

76

wybieranie

2150

1129

46

wstawianie

Zbiór odwrotnie

uporz

ą

dkowany

Zbiór losowy

Zbiór

uporz

ą

dkowany

Typ sortowania

źródło: N. Wirth: „Algorytmy + struktury danych = programy”

n=256, czas podany w milisekundach, maszyna: CDC 6400

31/38

Sortowanie – porównanie
efektywności metod, duży zbiór

2,112

1,911

3,293

1,131

bąbelkowe

1,643

2,424

2,504

0,001

wstrząsanie

1,659

2,600

1,176

1,202

wybieranie

0,566

1,125

0,570

0,001

wstawianie

0,031

0,027

0,035

0,033

kopcowanie

0,027

0,024

0,031

0,026

scalanie

0,371

0,471

0,021

0,621

szybkie

Średnia

Zbiór odwrotnie

uporz

ądkowany

Zbiór

losowy

Zbiór

uporz

ądkowany

Typ

sortowania

źródło: własne, n=10000, czas podany w mikrosekundach,

32/38

Wyszukiwanie elementu tablicy o podanym
indeksie w nieuporządkowanym zbiorze



metody:



posortować zbiór i wyznaczyć szukany
element



wyznaczyć szukany element bez
całkowitego sortowania zbioru

33/38

Algorytm Hoare’a



podział tablicy na dwie części z zastosowaniem
wartości podziałowej, podobnie jak w
quicksort, z wartościami l=1, p=n, m=tab[k]
m - punkt podzia

ł

u, k – indeks szukanej wart.



otrzymuje się:



tab[k]

≤

m dla wszystkich k < i



tab[k]

≥

m dla wszystkich k > j



i > j

34/38

Algorytm Hoare’a - trzy przypadki



możliwe trzy przypadki:



wartość dzieląca jest zbyt mała, granica podziału poniżej szukanej
wartości k, proces podziału powtarzany jest dla tab[i]…tab[p]



wartość dzieląca za duża, operacja dzielenia powtarzana dla
przedziału tab[l]…tab[j]



j < k < i → element tab[k] dzieli tablicę na dwa zbiory w
wymaganej proporcji → koniec szukania



proces dzielenia powtarzany jest aż do wystąpienia
ostatniego przypadku

l

m

p

i

j

≤

≥

k

l

k

p

i

j

≤

≥

m

l

p

i

j

≤

≥

k=m

35/38

Algorytm Hoare’a - przykład

void szuk_elem(int t[], int r, int k)

{

int l,p,i,j,m,wtemp;

l=0; p=r-1;

while(l<p)

// dopóki indeksy nie miną się

{

m=t[k]; i=l; j=p;

// m-wartość podziałowa

do

{

while(t[i]<m) i++;

// szukanie 1. niemniejszego od m

while(t[j]>m) j--;

// szukanie 1. niewiększego od m

if(i<=j)

// zamiana wyszukanych powyżej

{ wtemp=t[i]; t[i]=t[j]; t[j]=wtemp; i++; j--; }

} while(i<=j);

// dopóki indeksy i oraz j nie miną się

if(j<k) l=i;

// zawężanie przedziału poszukiwań

if(i>k) p=j;

// zawężanie przedziału poszukiwań

}

}

36/38

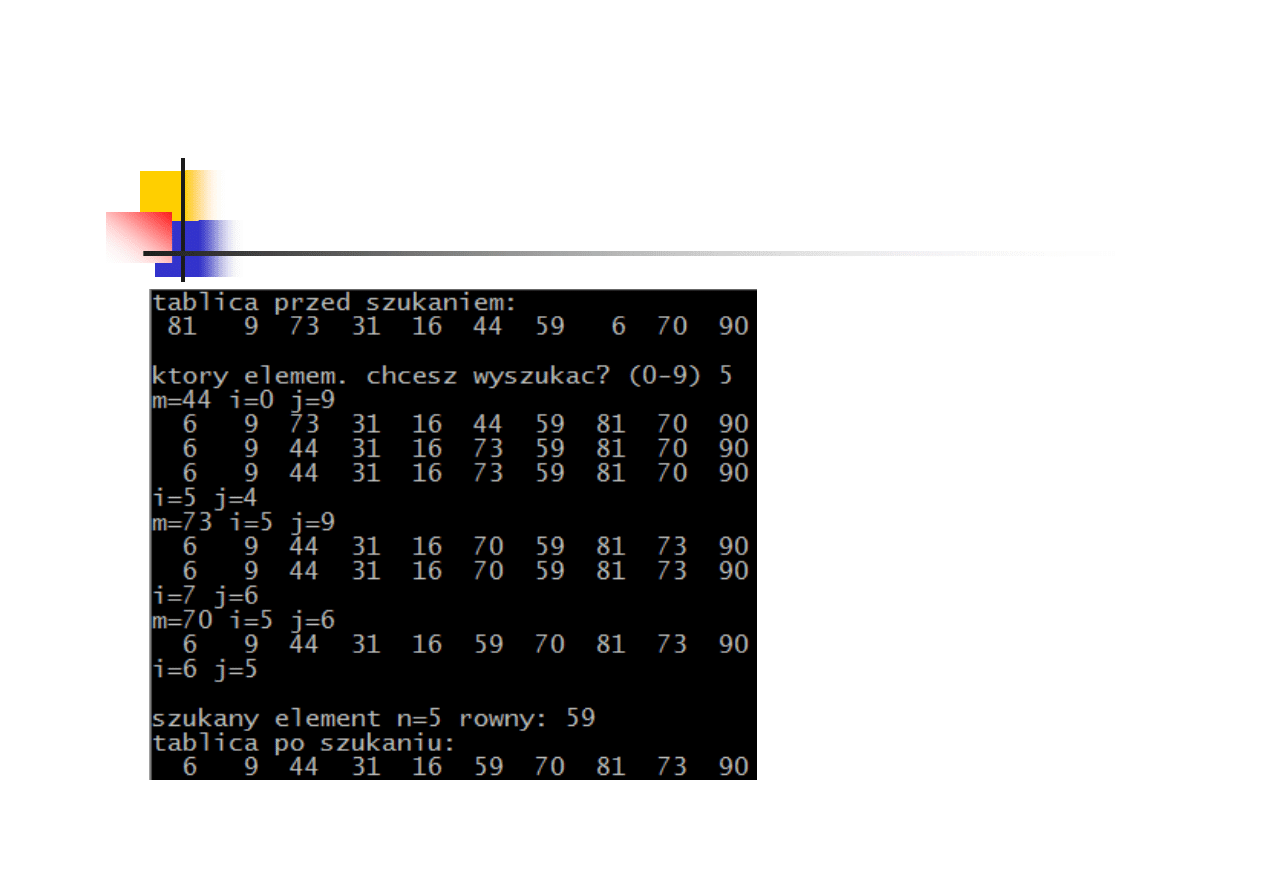
Algorytm Hoare’a - przykład

81 zamieniane z 6, i++, j--

44 zamieniane z 73, i ust. się
na 73, j ust. się na 16

j<k => l=5, i=5, j=9

73 zamieniane z 70, i++, j--
i ust. się na 81, j ust. się na 59
i>k => p=6, i=l=5, j=6

59 zamieniane z 70, i++, j--
i ust. się na 70, j ust. się na 59
i>k => p=j=5, i=l=5,
j=p=5

l nie jest < p => koniec szukania

37/38

Algorytm Hoare’a - podsumowanie



średnia liczba porównań
Pr=n+n/2+n/4+…=2n



duże zbiory → znaczna różnica w stosunku
do metod sortowania (najlepsze klasy
N

∙

logN)



małe zbiory → brak wyraźnej różnicy
między metodą z sortowaniem

38

Dziękuję za uwagę