D
1
1001,3 kN
D
2
1001,3 kN
D
3
849,5 kN
D
4
697,8 kN
D
8
1001,3 kN
D
5
697,8 kN
D
6
849,5 kN
D
7
1001,3 kN
G
2
-
91
6,5
kN
G
1
-1
07
7,9
kN
G
3
- 7
53
,7
kN
G
4
-
59
8,5
kN
G
7
- 9
16,5
kN
G
8
-10
77,9
kN
G
6
- 75
3,7 k
N
G
5
- 59
8,5 k
N
S
1
l
=
1
,5
0
m
0
,0
k
N
S
2
l
=
3
,0
0
m
7
7
,4
k
N
S
3
l
=
4
,5
0
m
1
5
4
,7
k
N
S
4
l
=
6
,0
0
m
4
0
5
,3
k
N
S
5
1
5
4
,7
k
N
S
6
7
7
,4
k
N
S
7
0
,0
k
N
K
1
-16
9,6 k
N
K
2
-
21
6,5
kN
K
3
-
2
77
,4
k
N
K
6
-1
69
,6
kN
K
5
-
2
16
,5
k
N
K
4
-
27
7,
4
kN
l = 3
,35 m
l =
4
,2
4 m
l =
5
,4
1
m
3,3
5 m
6,71
m
6,71
m
13,4
2 m
3,00 m
3,3
5 m
3,3
5 m
3,3
5 m
3,00 m
3,00 m
3,00 m
3,00 m
3,00 m
3,00 m
3,00 m
24,00 m
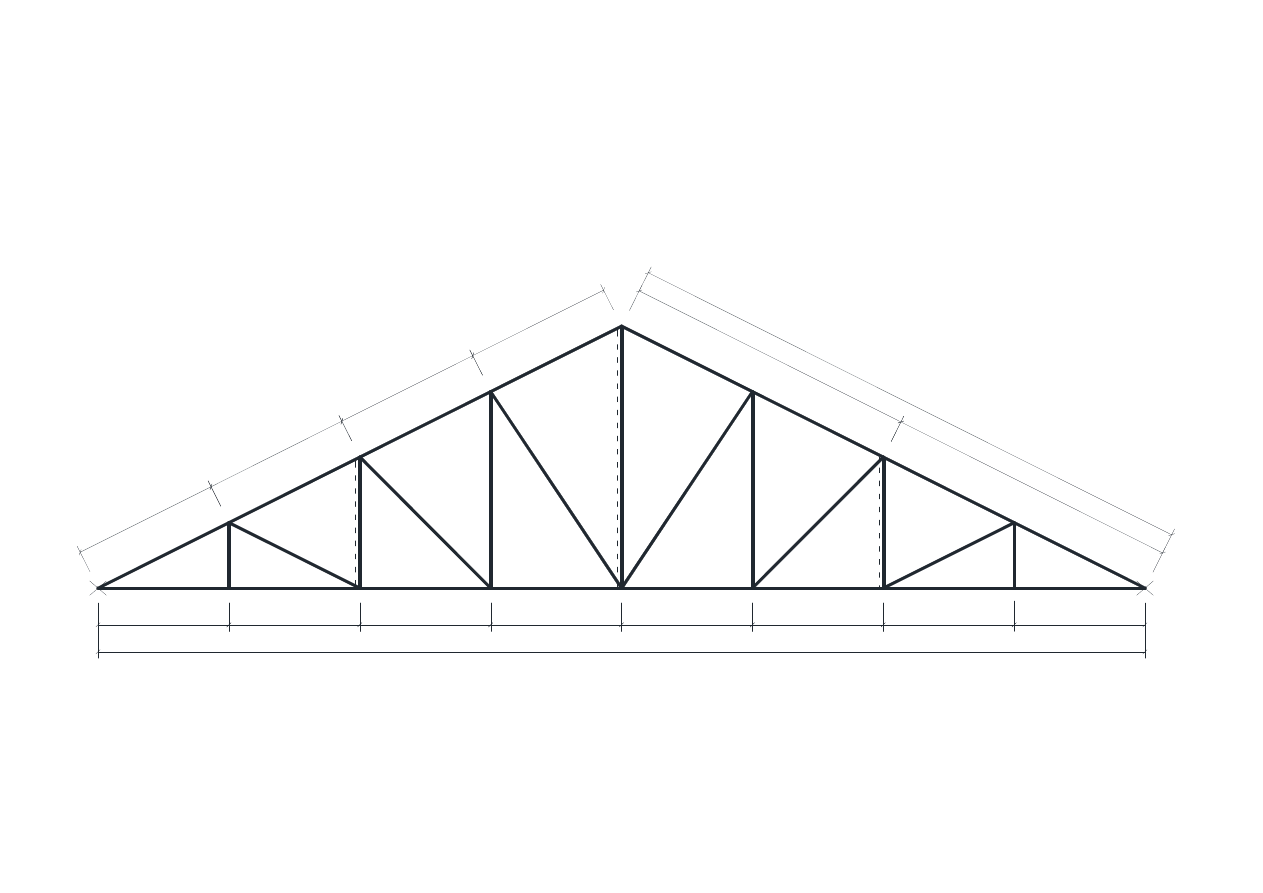
Rys 3a. Maksymalne siły prętach kratownicy
Konstrukcje metalowe 1
Przykład 3
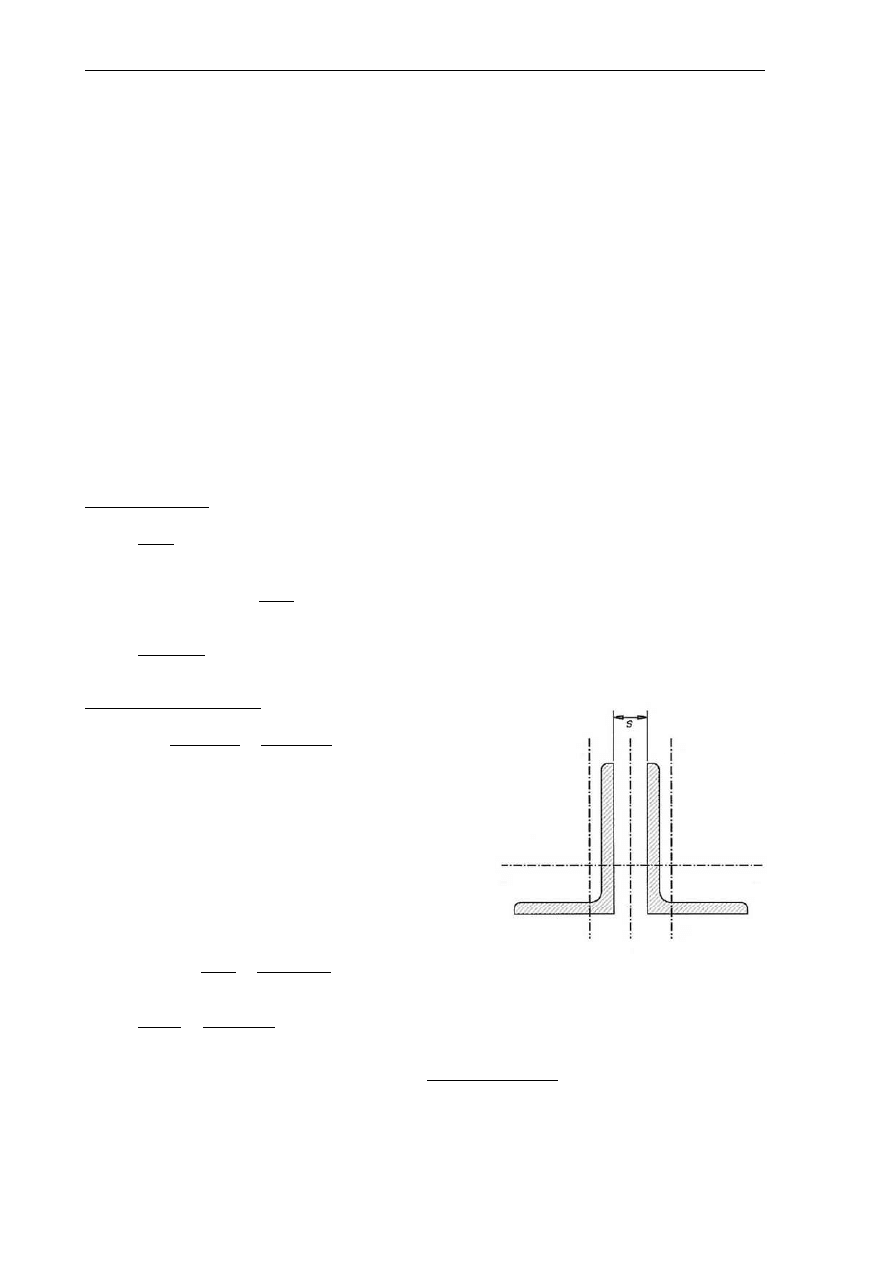
y
y
z
z
KONSTRUKCJE METALOWE 1
Przykład 3
Projektowanie prętów rozciąganych
3. Projektowanie prętów rozciąganych
Siły rozciągające w prętach kratownicy przyjęto z Tablicy 1, Przykładu 2 oraz na rysunku 3a.
3.1 Projektowanie pasa dolnego
Maksymalna siła w pasie dolnym
− D , D , D , D − N = 1001,4kN
•
Dobór przekroju
Warunek nośności
N
N
,
≤ 1,0
N
,
= N
,
=
A · f
γ
N · γ
A · f
≤ 1,0
Wymagane pole przekroju
A ≥
N · γM
f
=
1001,4 · 1
35,5
= 28,2 cm
→ przyjęto kształtownik 2L 135x65x10
A = 38,3 cm ; s = 10 mm
•
Sprawdzenie nośności
N
,
=
A · f
γ
=
38,3 · 35,5
1
= 1359,7 kN
N
N
,
=
1001,4 kN
1359,7 kN = 0,74 < 1,0
→ nośność została zapewniona (74% wykorzystania nośności)
Ponieważ w prętach
/
0
÷ /
2
siły są mniejsze od sił w prętach
D , D , D , D przekrój poprzeczny pasa
dolnego na całej długości przyjęto z kształtowników
2L 135x65x10.
A – pole przekroju;
f − granica plastyczności, (Tablica 3.1 EC 3-1-1)
f = 355 MPa = 35,5 kN/cm ;
γ − współczynnik redukcyjny
(EC 3-1-1 pkt. 6.2.3)
Konstrukcje metalowe 1
Przykład 3
3.2 Projektowanie słupków
Kształty przekrojów będą ustalone po zaprojektowaniu prętów pasa górnego kratownicy.
•
Słupek
S , S ; N = 0,0 kN; l = 1,50 m
•
Słupek
S , S
2
;
N = 77,4 kN; l = 3,00 m
Wymagane pole przekroju:
A ≥
N · γ
f
=
77,4 · 1
35,5 = 2,18 cm
•
Słupek
S
0
,
S
9
;
N = 154,7 kN; l = 4,50 m
Wymagane pole przekroju:
A ≥
N · γ
f
=
154,7 · 1
35,5 = 4,36 cm
•
Słupek
S
:
;
N = 405,3 kN; l = 6,00 m
Wymagane pole przekroju:
A ≥
N · γ
f
=
405,3 · 1
35,5 = 11,36 cm
Konstrukcje metalowe 1
Przykład 3
KONSTRUKCJE METALOWE 1
Przykład 3b
Projektowanie elementów podatnych
(Sz. Pałkowski, Wybrane zagadnienia obliczania i projektowania, pkt 3.8)
1.
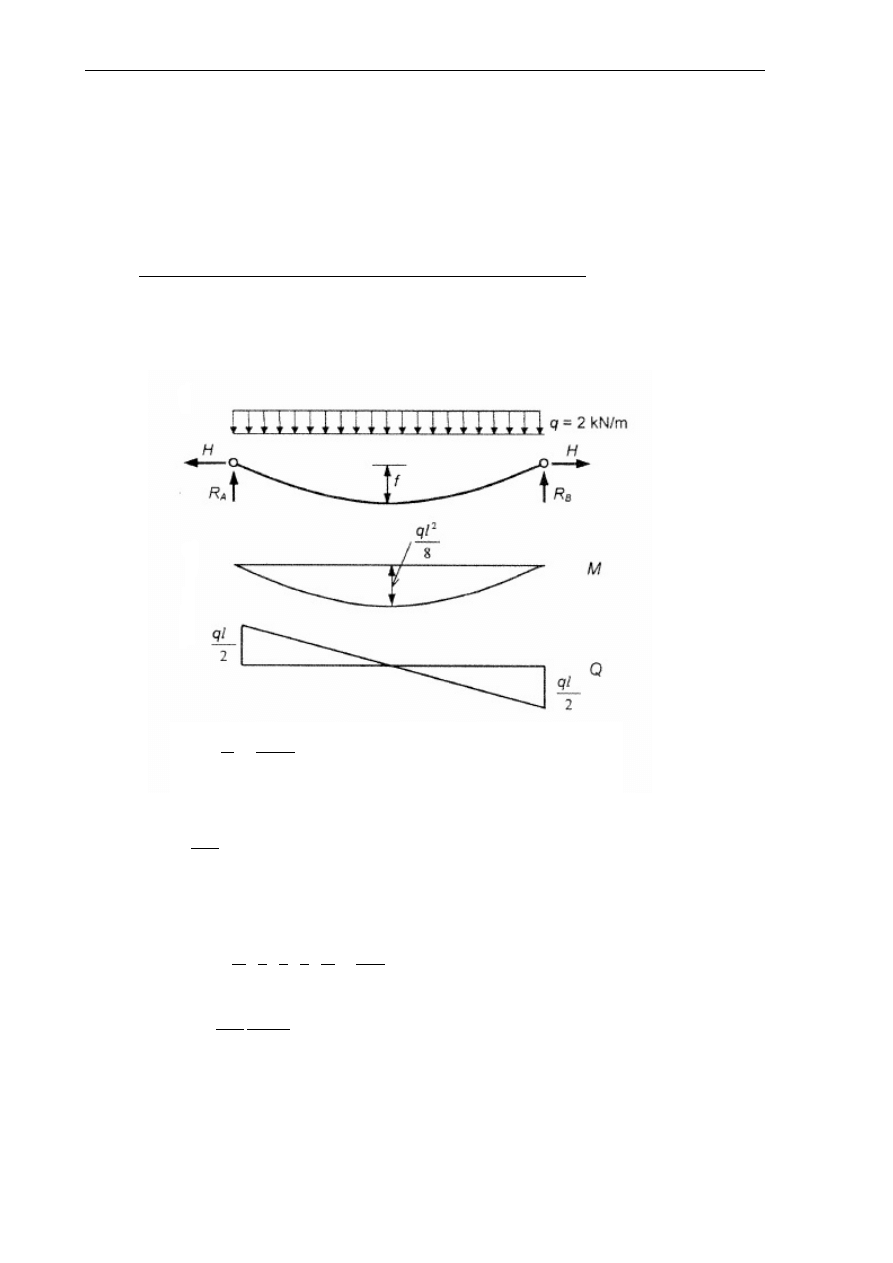
Obliczyć naciąg liny i strzałkę zwisu oraz maksymalną silę w cięgnie.
Dane: - długość
s = 21,0 m
- rozpiętość
l = 20,0 m
Reakcje pionowe
R
<
= R
=
=
ql
2 =
2 · 20
2 = 20 kN
Równanie cięgna
s = l +
1
2H A Q dx
Wyliczenie wyrażenia
D Q dx za pomocą całkowania graficznego:
A Q dx = 2 ·
ql
2 ·
l
2 ·
1
2 ·
2
3 ·
ql
2 =
q l
0
12
21 = 20 +
1
2H
2 20
0
12
Z powyższego wyrażenie wyliczono siłę naciągu
H = 36,5 kN.
Konstrukcje metalowe 1
Przykład 3
A − przekrój cięgna;
E − współczynnik sprężystości cięgna;
α − współczynnik wydłużalności liniowej;
ΔT − przyrost temperatury;
Strzałka zwisu
f =
M
IJK
H =
ql
8H =
2 · 20
8 · 36,5 = 2,74 m
Maksymalna siła w cięgnie
S = LR + H = L20 + 36,5 = 41,6 kN
2.
Obliczyć naciąg dla cięgna z zadania 1 z uwzględnieniem jego wydłużalności.
Dane:
- początkowej długości cięgna
s = 20,1 m
- przekrój cięgna
A = 5,0 cm
- współczynnik sprężystości
E = 150000 kN/cm
Równanie cięgna z uwzględnieniem wydłużeniem sprężystym i wpływu temperatury
s = s + Δl
M
+ Δl
- wprowadzamy zależności
Δl
M
≈ H ·
s
EA
Δl = α ΔTs
l +
1
2H A Q dx = s + H ·
s
EA + α ΔTs
H
0
+ H EA O1 −
1
s Pl − α ΔTs QR =
EA
2s A Q dx
H
0
+ H EA O1 −
1
s Pl − α ΔTs QR =
EA · q l
0
2s · 12
- podstawiamy dane
H
0
+ H 15000 · 5 O1 −
1
20,1 P20 − 0QR =
15000 · 5 · 2 · 20
0
24 · 20,1
H
0
+ 373,1H = 4975124
- naciąg cięgna
H = 102,3 kN
W przypadku gdy rozpiętość cięgna jest równa jego długości
H = S
q · l · EA
24
T
= S
2 · 20 · 75000
24
T
= 171,0 kN