22

INDUKCJA ELEKTROMAGNETYCZNA

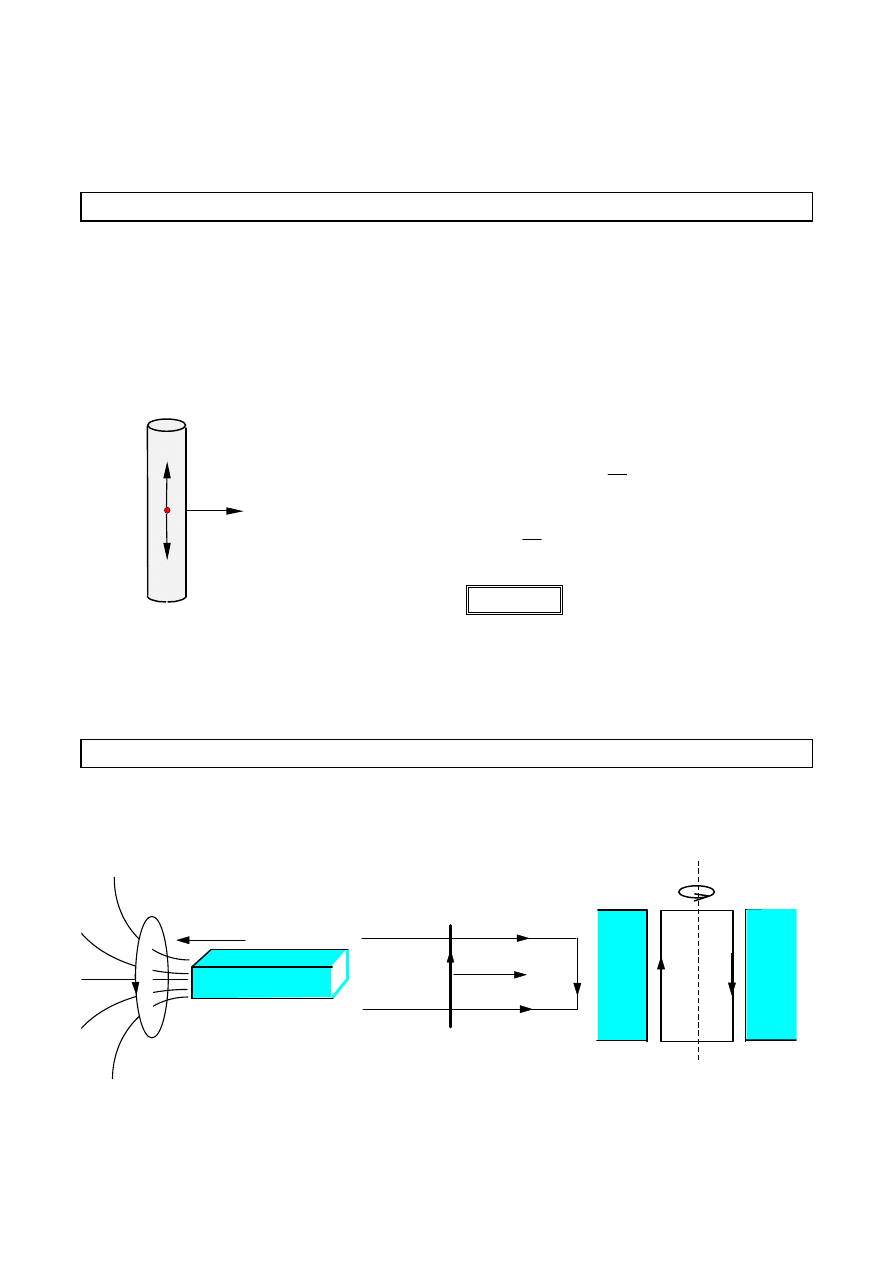
Napięcie na końcach ruchomego przewodnika

Przewodnik o długości l porusza się z prędkością V w jednorodnym polu
magnetycznym o indukcji B. Razem z przewodnikiem poruszają się zawarte w nim
ładunki elektryczne. Na elektrony zawarte w przewodniku działa siła Lorentza, pod
wpływem której przemieszczają się one w kierunku jednego z końców.
Przemieszczanie się elektronów ustaje wtedy gdy siła Lorentza (F

B

) zostaje

zrównoważona przez siłę elektrostatyczną (F

E

).

F

F

BeV

eE

E

U

l

BeV

e

U

l

B

E

====

====

====

====

;

U

BlV

====

Napięcie powstałe na końcach przewodnika poruszającego się w polu magnetycznym
jest zatem efektem oddziaływania pola magnetycznego na ładunki zawarte w tym
przewodniku. Napięcie to może powodować przepływ prądu zwanego indukcyjnym.

Powstawanie prądu indukcyjnego. Reguła Lenza.

Prąd elektryczny może płynąć jedynie w obwodzie zamkniętym. Prąd indukcyjny
płynie w takim obwodzie zamkniętym, gdzie istnieją fragmenty obwodu stanowiące
ź

ródło

napięcia.

Badania

doświadczalne

warunków

powstawania

prądu

indukcyjnego prowadzą do wniosku, że prąd indukcyjny powstaje w takim obwodzie
zamkniętym, przez który przenika zmienny strumień indukcji magnetycznej.

V

r

E

F

r

B

F

r

e

l

+

+

+

+

_

_

_

_

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

⊗

B

r

N

S

∼∼∼∼

B

∼∼∼∼

αααα

∼∼∼∼

S

N

r

V

⊗

⊗

⊗

⊗

r

B

23

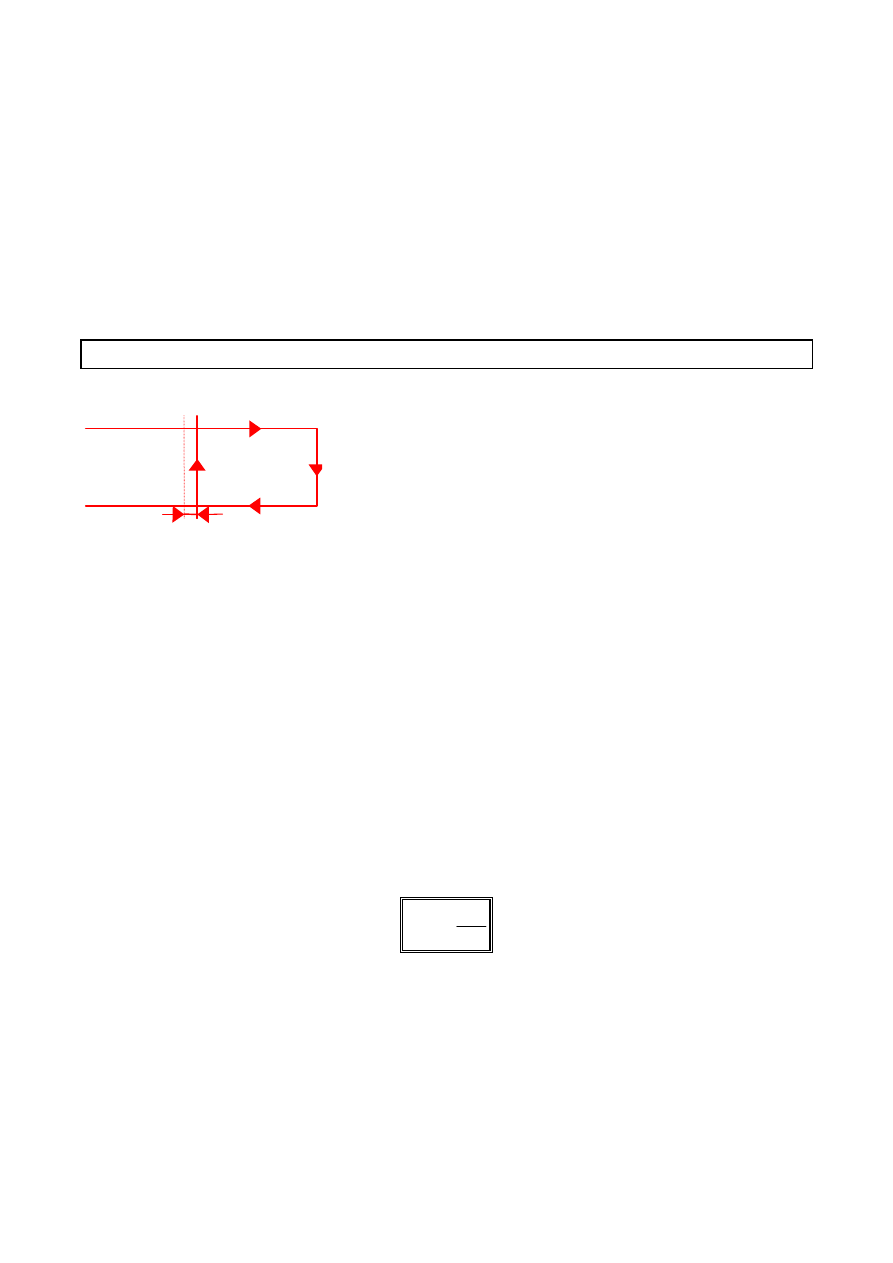
Wiadomo, ze zmiany strumienia zachodzą wtedy, gdy zmienia się indukcja
magnetyczna ( B

∼∼∼∼

), pole powierzchni obwodu (S

∼∼∼∼

), lub kąt jaki tworzą linie sił

pola z powierzchnią obwodu (

αααα

∼∼∼∼

). Kierunek prądu indukcyjnego można ustalić

analizując siły działające na ładunki elektryczne, lub posługując się regułą Lenza:

Kierunek prądu indukcyjnego jest zawsze taki, aby przeciwdziałał tej zmianie
strumienia, która go wywołała.

Reguła ta wynika z zasady zachowania energii.

Siła elektromotoryczna indukcji

Napięcie, które powoduje przepływ prądu indukcyjnego nazywamy siłą

elektromotoryczną

indukcji

(SEM).

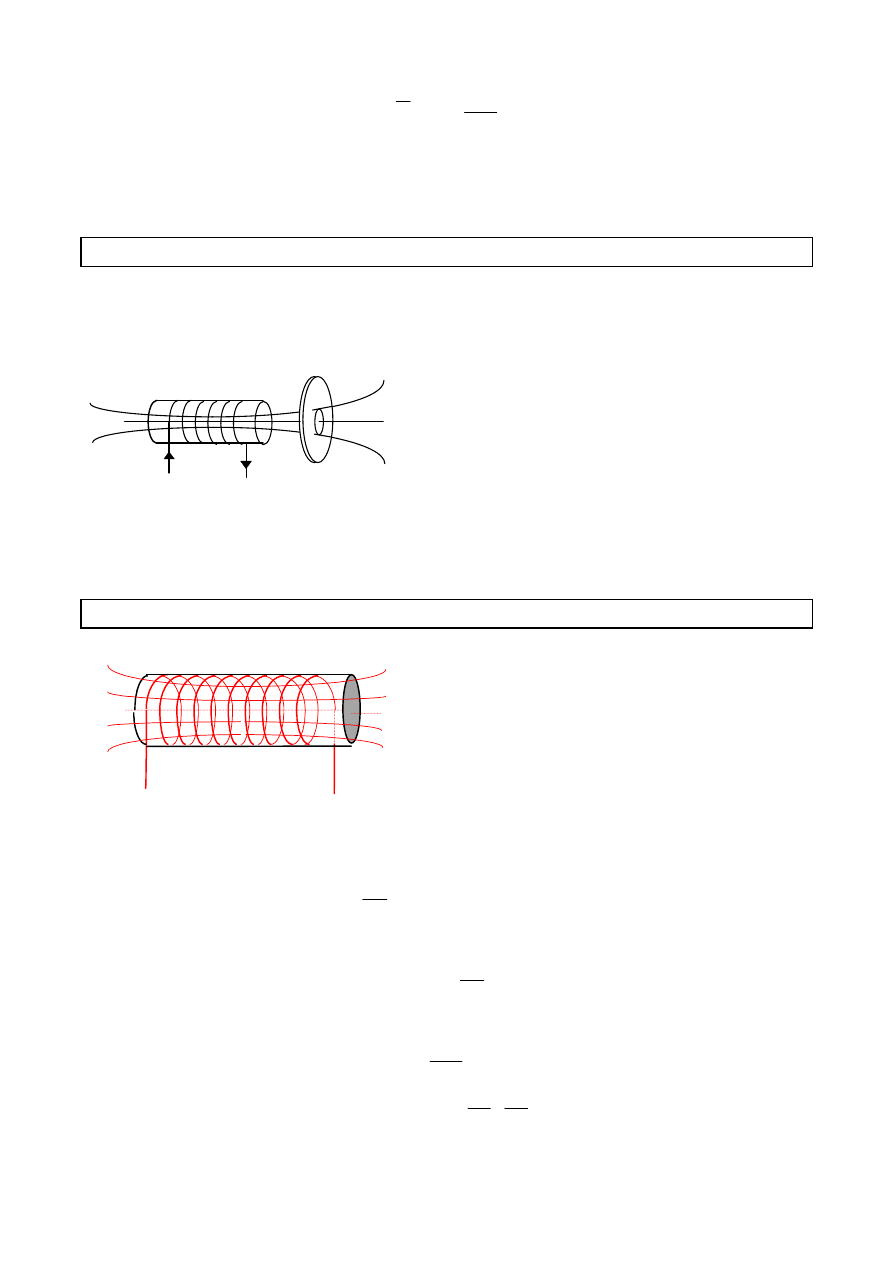
Przesunięcie

poprzeczki na odcinku dx wymaga pracy elementarnej
równej pracy jaką wykona wzbudzony tym ruchem prąd
indukcyjny.

dW

EIdt

====

E - SEM indukcji

Jeśli siła hamująca ruch poprzeczki (siła elektrodynamiczna) wynosi F, to
otrzymujemy:

−−−−

====

Fdx

EIdt

−−−−

====

BIldx

EIdl

l

.

dx

= dS - zmiana powierzchni obwodu

−−−−

====

BdS

Edt

B

.

dS = d

Φ

Φ

Φ

Φ

- zmiana strumienia indukcji magnetycznej przenikającego przez ramkę

−−−−

====

d

E d t

Φ

Φ

Φ

Φ

E

d

dt

==== −−−− Φ

Φ

Φ

Φ

SEM indukcji jest zatem pochodną strumienia indukcji magnetycznej po czasie.
Powyższa zależność przedstawia związek między dwiema funkcjami ( E i

Φ

Φ

Φ

Φ

). Znając

zależność

Φ

Φ

Φ

Φ

(t) można zatem ustalić zależność E(t). Wartość średnia siły

elektromotorycznej wzbudzonej w czasie

∆∆∆∆

t wynosi:

⊗

⊗

⊗

⊗

B

r

I

dx

l

24

(((( ))))

E

t

==== −−−− ∆Φ

∆Φ

∆Φ

∆Φ

∆∆∆∆

Znak (-) informuje, że napięcie E musi być takie, aby przeszkadzało zmianie
strumienia, która go wywołała.

Prądy wirowe

Jeśli zmienne pole magnetyczne przenika przez dowolny materiał przewodzący prąd
elektryczny, to wewnątrz tego materiału powstają prądy indukcyjne, zwane
wirowymi.

Prądy

wirowe

powodują

nagrzewanie

każdego

przewodnika

umieszczonego

w

zmiennym

polu

magnetycznym. Można je wykorzystywać
do topienia metali w tzw. piecach
indukcyjnych. Są one również przyczyną
strat energii w transformatorze, bowiem
powodują

nagrzewanie

się

rdzenia

transformatora. Straty te można zmniejszyć przez wykonanie rdzenia z cienkich
blaszek co utrudnia przepływ prądów wirowych.

Indukcja własna

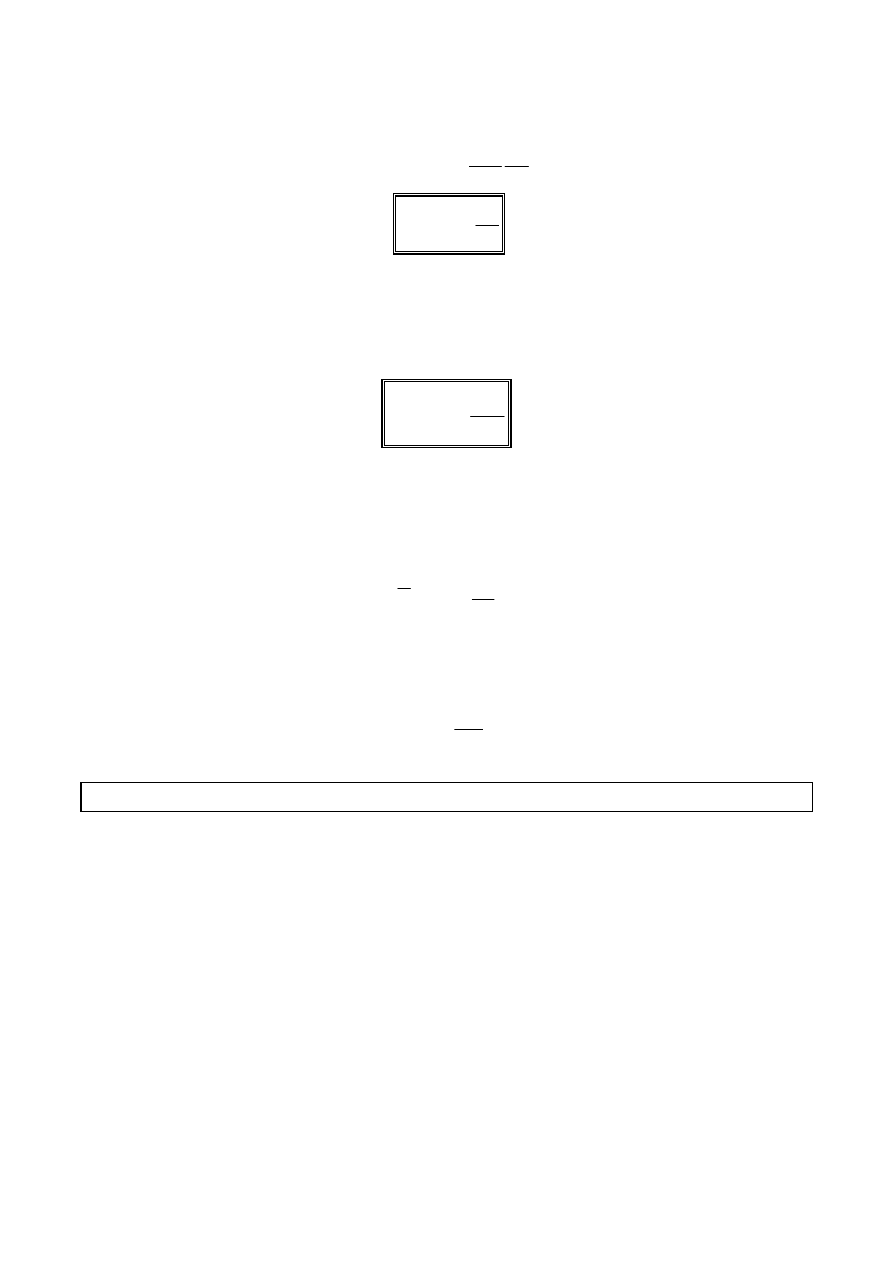
Jeśli przez zwojnicę płynie prąd zmienny, to
wewnątrz zwojnicy powstaje zmienne pole
magnetyczne. Pole to powoduje powstanie na
końcach tej zwojnicy wtórnego napięcia
indukcyjnego. Zjawisko to nazywamy indukcją
własną lub samoindukcją.

W

przypadku długiego solenoidu, w którym

płynie prąd o zmiennym natężeniu I, przez każdy zwój tego solenoidu przenika pole
magnetyczne o indukcji:

B

H

nI

l

o

====

====

µµ

µµ

µµ

µµ

µµ

µµ

µµ

µµ

0

Strumień indukcji magnetycznej

przenikający przez każdy zwój wynosi :

Φ

Φ

Φ

Φ ==== µµ

µµ

µµ

µµ

0

nI

l

s

SEM indukcji powstała w jednym zwoju wynosi:

E

d

dt

E

ns

l

dI

dt

1

1

0

==== −−−−

==== −−−−

⋅⋅⋅⋅

Φ

Φ

Φ

Φ

µµ

µµ

µµ

µµ

B

∼∼∼∼

I

∼∼∼∼

B

∼∼∼∼

I

∼∼∼∼

25

SEM indukcji wzbudzona na końcach solenoidu jest n razy większa i wynosi:

E

n s

l

dI

dt

s

o

==== −−−−µµ

µµ

µµ

µµ

2

E

L

dI

dt

s

==== −−−−

Współczynnik L zależy od cech charakterystycznych obwodu i nazywamy go
współczynnikiem

samoindukcji,

współczynnikiem

indukcji

własnej

lub

indukcyjnością obwodu. Dla długiego solenoidu można wyrazić go wzorem:

L

n s

l

o

==== µµ

µµ

µµ

µµ

2

Siła elektromotoryczna samoindukcji jest zatem proporcjonalna do wartości
pochodnej natężenia prądu po czasie. Korzystając z tej zależności

można

ustalić

E

s

(t)

jeśli znana jest zależność I(t).

Ś

rednia wartość SEM samoindukcji wyrażona jest wzorem:

t

I

L

)

(

E

∆∆∆∆

∆∆∆∆

−−−−

====

Jednostką indukcyjności obwodu jest henr (H). Jest to indukcyjność obwodu, w
którym zmiana natężenia prądu o 1A w czasie 1s powoduje powstanie SEM
samoindukcji 1V.

H

Vs

A

====

Indukcja wzajemna

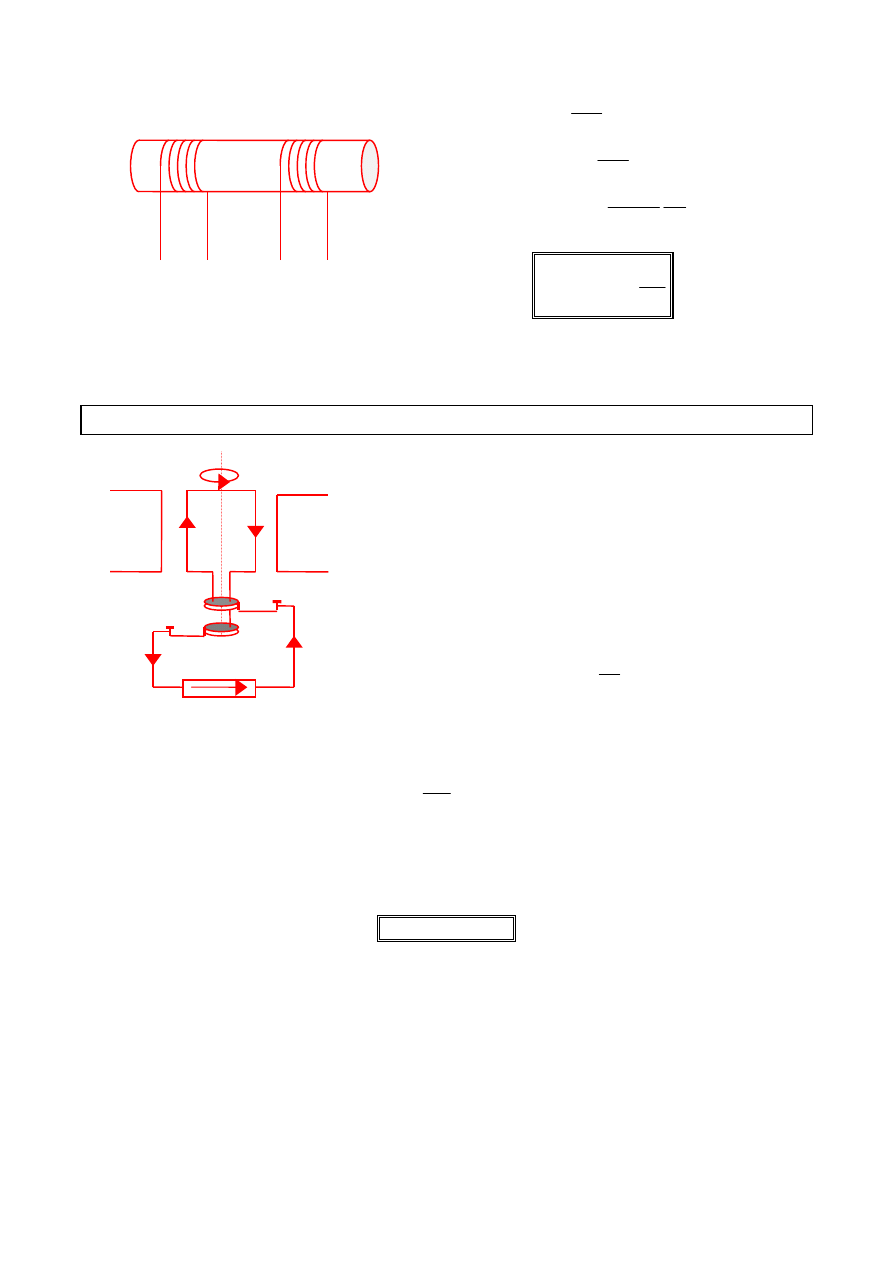
Na wspólnym rdzeniu wykonanym z materiału ferromagnetycznego nawinięte są
dwa uzwojenia liczące n

1

i n

2

zwojów. Przez jedno z nich płynie prąd zmienny

wywołany zmiennym napięciem. Prąd ten wytwarza zmienny strumień indukcji
magnetycznej, który przenika również przez drugie uzwojenie. Na końcach tego
uzwojenia powstaje SEM indukcji E.

26

E

d

dt

n

n I

l

s

E

n n s

l

dI

dt

==== −−−−

====

==== −−−−

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

2

0

1

0

1

2

µµ

µµ

µµ

µµ

µµ

µµ

µµ

µµ

E

L

dI

dt

==== −−−−

1 2

,

L

1,2

- współczynnik indukcji wzajemnej obwodu.

Pr

ą

dnica pr

ą

du zmiennego

Najprostszą prądnicę prądu zmiennego stanowi płaska
ramka o powierzchni

S

wirująca ze stałą prędkością

kątową

ω

ω

ω

ω

w jednorodnym polu magnetycznym o

indukcji

B

. Końce ramki połączone są z pierścieniami,

po których ślizgają się tzw. szczotki. Strumień indukcji
magnetycznej przenikający przez powierzchnię ramki
zmienia się w czasie.

Φ

Φ

Φ

Φ ====

BS cos

αααα

ω

ω

ω

ω

αααα

αααα

ω

ω

ω

ω

====

⇒

⇒

⇒

⇒

====

t

t

Φ

Φ

Φ

Φ ====

BS

t

cos

ω

ω

ω

ω

SEM indukcji wzbudzona w wirującej ramce jest funkcją czasu i wynosi:

t

sin

BS

E

dt

d

E

1

1

ω

ω

ω

ω

ω

ω

ω

ω

====

Φ

Φ

Φ

Φ

−−−−

====

Jeśli ramka liczy n zwojów, to wzbudzona w niej SEM indukcji jest

n

razy większa i

wynosi:

E

nBS

t

====

ω

ω

ω

ω

ω

ω

ω

ω

sin

E = E

o

sin

ω

ω

ω

ω

t ; E

o

= nBS

ω

ω

ω

ω

ΕΕΕΕ

0000

−

maksymalna wartość SEM indukcji (amplituda SEM indukcji).

ω

ω

ω

ω

R

∅

∅

∅

∅

∼∼∼∼

∅

∅

∅

∅

∅

∅

∅

∅

∼∼∼∼

∅

∅

∅

∅

I

∼∼∼∼

n

2

n

1

l

S

Ν

Ν

Ν

Ν

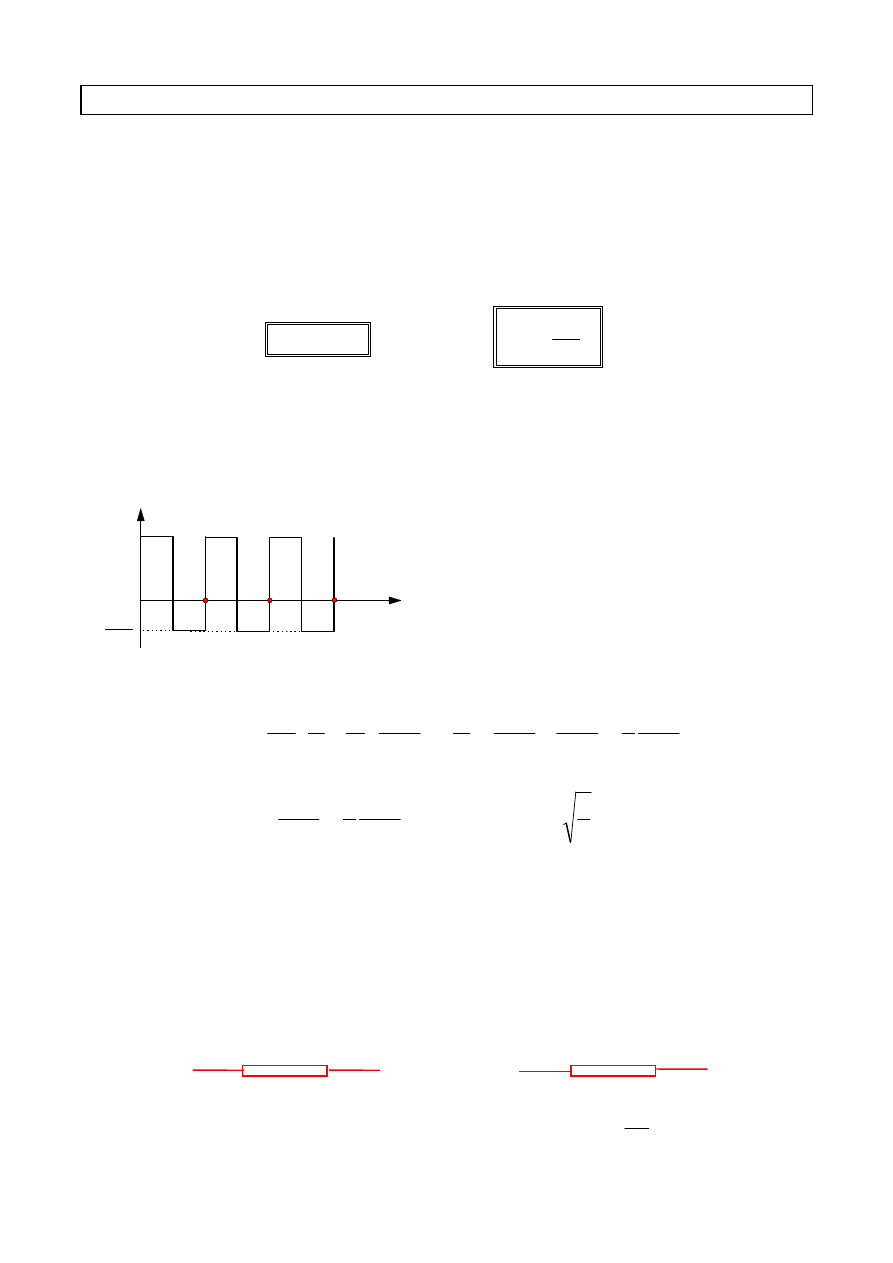
27

Napi

ę

cie skuteczne i nat

ęż

enie skuteczne

Przez dwa identyczne opory R płyną dwa prądy: pewien prąd zmienny i prąd stały o
natężeniu I

s

, wywołany napięciem U

s

. Prąd zmienny w ciągu okresu wykonuje pracę

W

T

.

Jeśli prąd stały płynąc równie długo przez taki sam opór wykonuje taką samą pracę,
to I

s

i U

s

nazywamy odpowiednio natężeniem skutecznym i napięciem skutecznym

danego prądu zmiennego.

W

I RT

T

s

====

2

W

U

R

T

T

s

====

2

Aby określić natężenie i napięcie skuteczne prądu zmiennego trzeba znać pracę
wykonaną przez dany prąd zmienny w ciągu okresu.

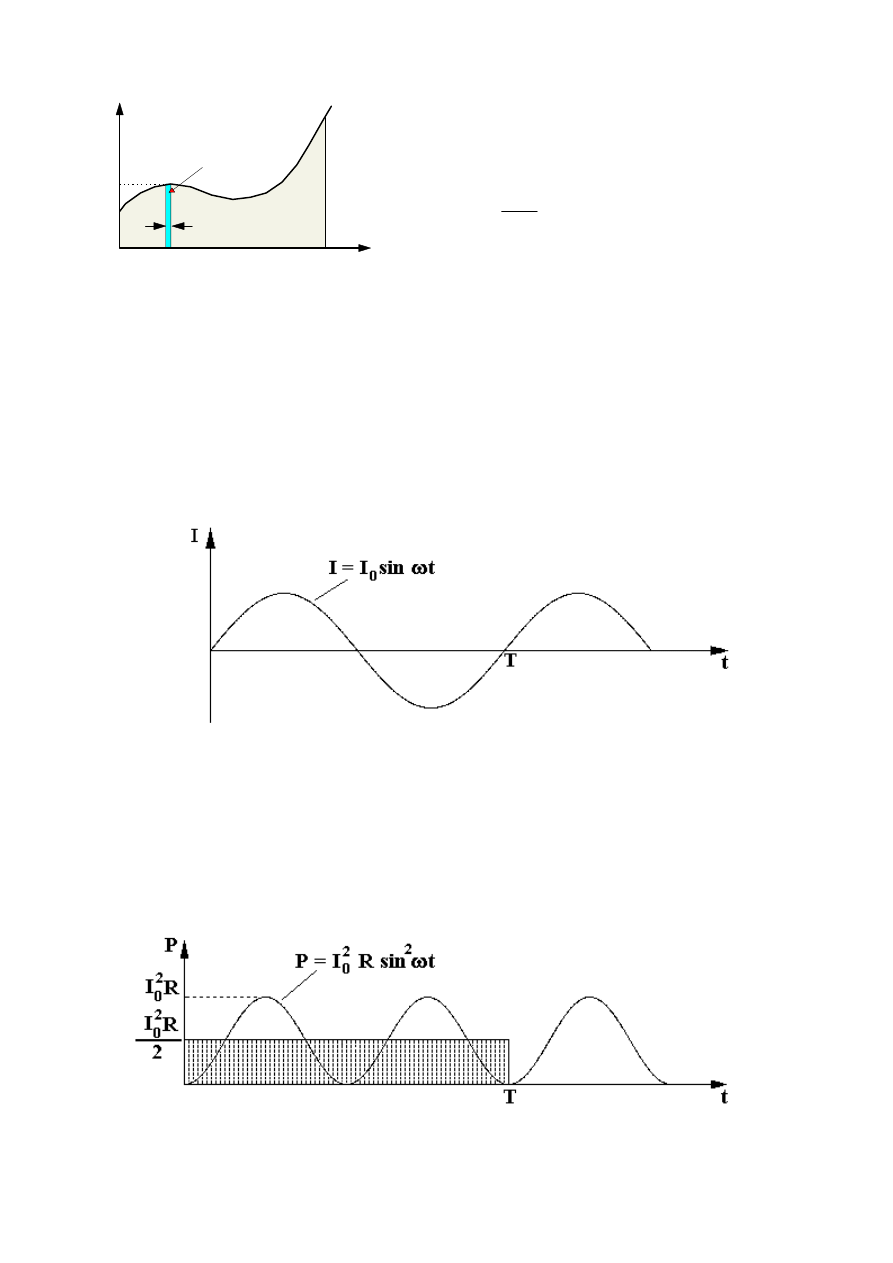
1. Obliczanie napięcia skutecznego w przypadku impulsów prostokątnych.

W

przypadku

prostokątnych

impulsów

napięciowych istnieje możliwość obliczenia
pracy prądu zmiennego w ciągu okresu
sumując prace wykonane przez ten prąd w
poszczególnych

przedziałach

czasowych,

ponieważ płynie on wtedy pod wpływem
stałego napięcia.

W

U

R

T

R

U

T

U T

R

U T

R

U T

R

T

====

⋅⋅⋅⋅ ++++

−−−−











⋅⋅⋅⋅ ====

++++

====

0

2

0

2

0

2

0

2

0

2

2

1

2

2

2

8

5

8

U T

R

U T

R

U

U

s

s

2

0

2

0

5

8

5

8

====

⇒

⇒

⇒

⇒

====

2. Obliczanie napięcia skutecznego, gdy znana jest zależność mocy od czasu

Łatwo można wykazać, że pole figury zawartej pod wykresem mocy w funkcji czasu
jest miarą wykonanej pracy.

R

U

s

I

s

R

W

T

I RT

U

R

T

s

s

2

2

====

−−−−

U

0

2

T

U

0

t

U

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

28

Z definicji mocy wynika, że miarą pracy
elementarnej jest pole wąskiego prostokąta
zawartego pod wykresem mocy w funkcji
czasu:

P

dW

dt

dW

P dt

dS

====

⇒

⇒

⇒

⇒

==== ⋅⋅⋅⋅

−−−−

Praca

wykonana

w

dowolnie

długim

przedziale

czasu

jest

sumą

prac

elementarnych i odpowiada jej pole figury

zawartej pod wykresem mocy w funkcji czasu. Pozwala to na łatwe obliczenie pracy
wykonanej przez prąd zmienny, w przypadku gdy figura pd wykresem mocy jest
figurą regularną.

3. Natężenie skuteczne prądu sinusoidalnego

Przypuśćmy, że przez opór

R

płynie prąd zmienny wywołany o natężeniu:

I = I

0

sin

ω

ω

ω

ω

t

Moc prądu sinusoidalnego jest funkcją czasu i wynosi:

P

I R

I R

t

====

====

2

0

2

2

s i n

ω

ω

ω

ω

Zależność

P(t)

przedstawia poniższy wykres.

dS

dt

t

P

P

29

Praca wykonana przez ten prąd w ciągu okresu stanowi sumę prac elementarnych i
odpowiada jej pole figury pod wykresem. Pole to jest równe polu prostokąta o

podstawie

T

i wysokości

I R

0

2

2

. Praca prądu zmiennego wykonana w ciągu okresu

wynosi zatem:

W

I R

T

T

====

0

2

2

I RT

I R

T

I

I

s

s

2

0

2

0

2

2

====

⇒

⇒

⇒

⇒

====

Analogicznie można wykazać, że napięcie skuteczne takiego prądu wynosi:

U

U

s

====

0

2

Używając wartości skutecznych napięcia i natężenia, pracę prądu zmiennego
płynącego przez opór R można obliczać identycznie jak pracę prądu stałego.
Przyrządy pomiarowe prądu zmiennego mierzą wartości skuteczne napięcia i
natężenia.

Indukcyjność i pojemność w obwodzie prądu zmiennego

Kondensator stanowi przerwę w obwodzie prądu stałego, ale umieszczony w
obwodzie prądu zmiennego musi ustawicznie zmieniać swój ładunek, co umożliwia

przepływ prądu w tym obwodzie. Rozważamy
obwód złożony z połączonych ze sobą szeregowo
trzech elementów: oporu R, kondensatora C i
zwojnicy L. Taki obwód jest nazywany
obwodem RLC. Przyjmijmy, że w tym obwodzie
płynie prąd zmienny, sinusoidalny o natężeniu :

I = I

0

sin

ω

ω

ω

ω

t

, gdzie

ω

ω

ω

ω

t

- faza natężenia.

Prąd taki jest wywołany napięciem zewnętrznym (U), oraz napięciami wtórnymi
powstałymi na końcach zwojnicy (U

L

) i na okładkach kondensatora (U

C

). O

natężeniu prądu płynącego przez opór R decyduje suma tych napięć. Korzystając z
prawa Ohma otrzymujemy:

I

U

U

U

R

L

C

====

++++

++++

U

R

R

U

∅

∅

∅

∅

U

L

L

∅

∅

∅

∅

U

C

C

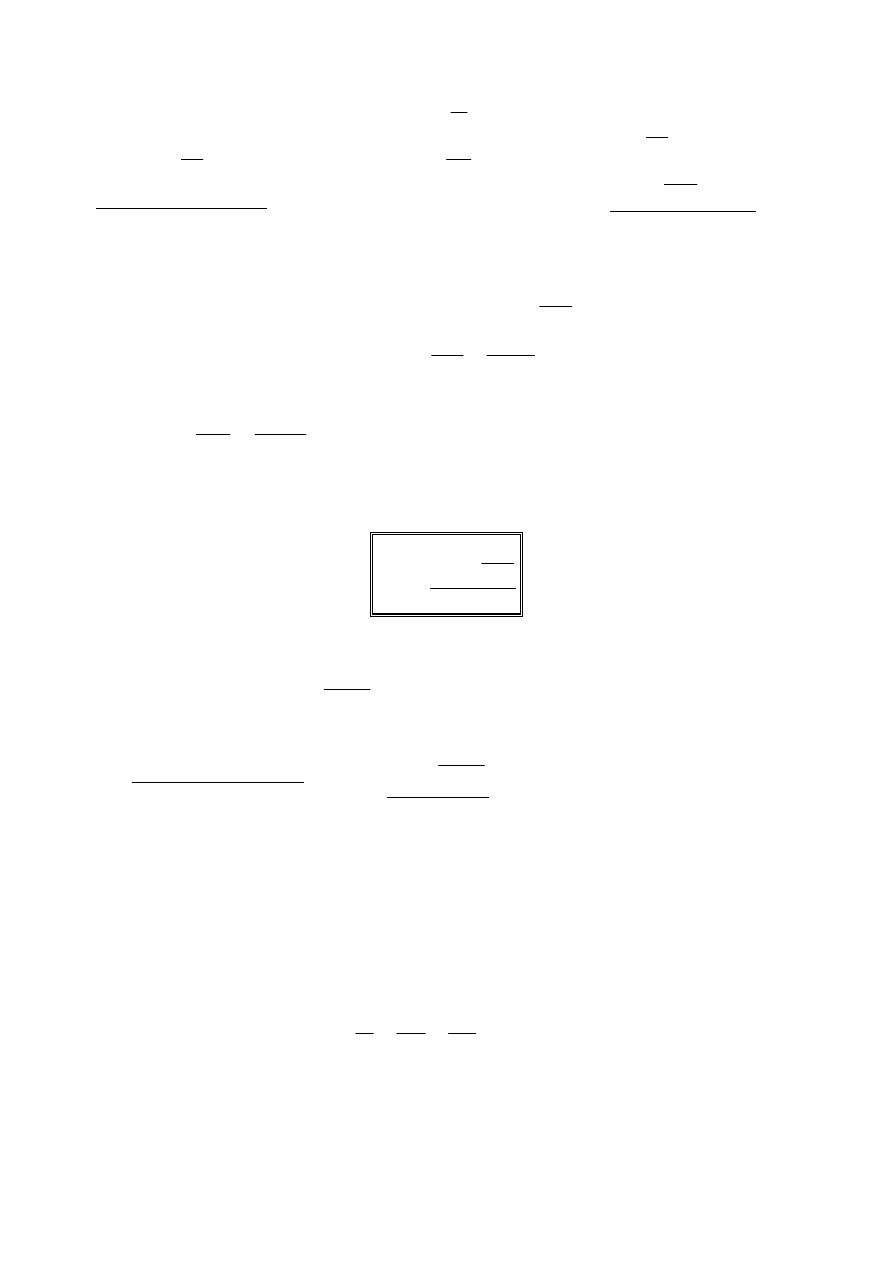
30

I

I

t;

U

L

dI

dt

U

LI

t

L

L

====

==== −−−−
==== −−−−

0

0

sin

sin

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

U

q

C

I

dq

dt

I

I

t

C

====

==== −−−−
====

0

sin

ω

ω

ω

ω

q

I

t

U

I

C

t

C

====

====

0

0

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

cos

cos

IR

U

U

U

L

C

==== ++++

++++

U

I R

t

LI

t

I

C

t

U

I R

t

L

R

RC

t

====

++++

−−−−

====

++++

−−−−























0

0

0

0

1

sin

cos

cos

sin

cos

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

Wyrażenie

L

R

RC

ω

ω

ω

ω

ω

ω

ω

ω

−−−−

1

jest liczbą pozbawioną wymiaru. Każdej liczbie

rzeczywistej można przypisać kąt

ϕϕϕϕ,

o tak dobranej wartości aby było spełnione

równanie:

tg

L

C

R

ϕϕϕϕ

ω

ω

ω

ω

ω

ω

ω

ω

====

−−−−

1

((((

))))

((((

))))

U

I R

t

tg

t

U

I R

t

t

====

++++

====

++++

0

0

sin

cos

cos

sin

cos

sin

cos

ω

ω

ω

ω

ϕϕϕϕ

ω

ω

ω

ω

ϕϕϕϕ

ω

ω

ω

ω

ϕϕϕϕ

ϕϕϕϕ

ω

ω

ω

ω

U

U

t

====

++++

0

sin(

)

ω

ω

ω

ω

ϕϕϕϕ

U

I R

0

0

====

cos

ϕϕϕϕ

ω

ω

ω

ω

t +

ϕϕϕϕ

- faza napięcia

Z powyższych rozważań wynika, że przyczyną prądu o natężeniu I = I

0

sin

ω

ω

ω

ω

t

jest

napięcie U = U

0

sin (

ω

ω

ω

ω

t +

ϕ)

ϕ)

ϕ)

ϕ)

. Napięcie to jest przesunięte w fazie. Kąt

ϕϕϕϕ

nazywamy

przesunięciem fazowym (przesunięcie fazy napięcia względem fazy natężenia).

Jeśli prąd zmienny płynie przez opór R, to stosunek chwilowej wartości napięcia do
chwilowej wartości natężenia jest równy stosunkowi odpowiednich wartości
maksymalnych, jak również stosunkowi odpowiednich wartości skutecznych:

U

I

U

I

U

I

R

s

s

====

====

====

0

0

Jeśli prąd zmienny płynie przez obwód

RLC

, to stosunek wartości maksymalnych

napięcia i natężenia jest większy od oporu omowego i wynosi:

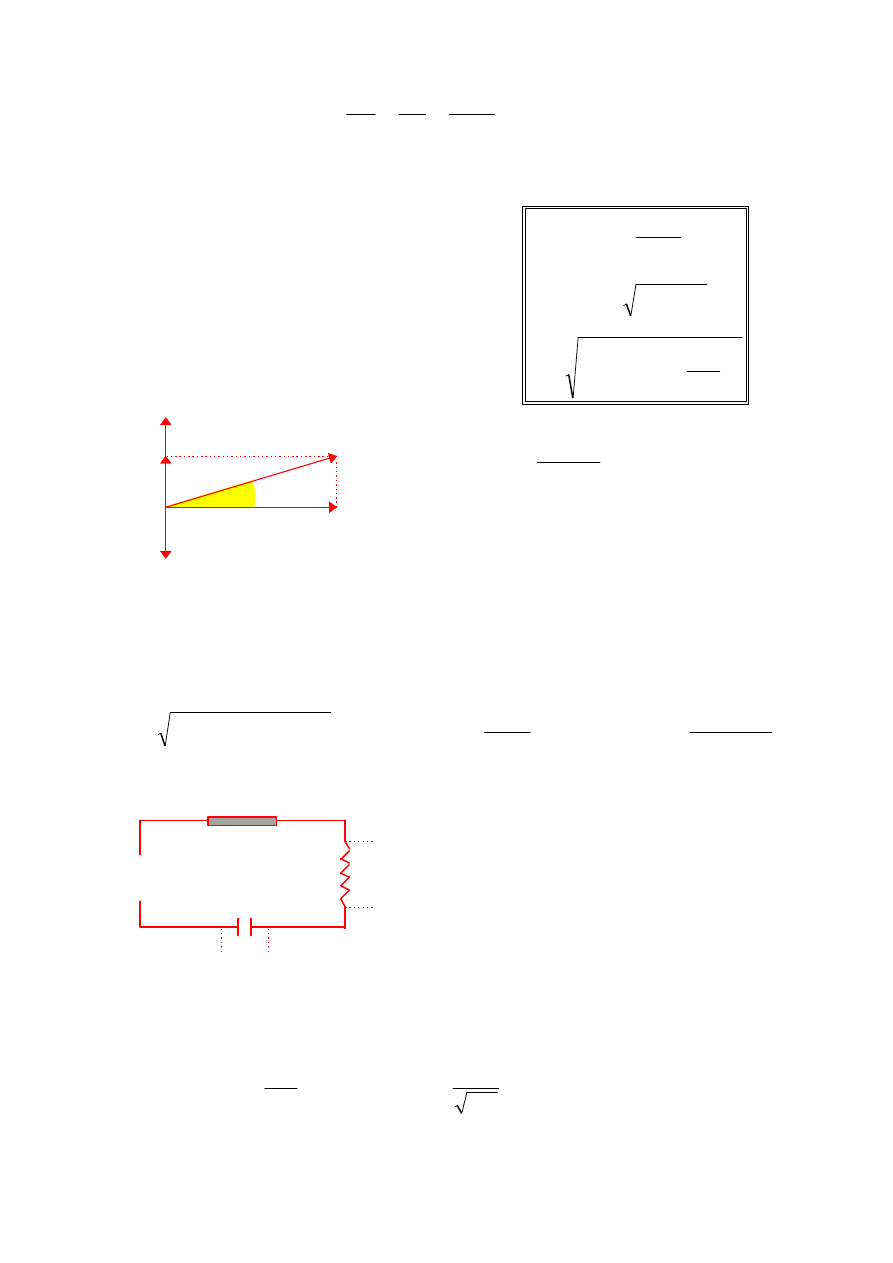
31

U

I

U

I

R

Z

s

s

0

0

====

====

====

cos

ϕϕϕϕ

Stosunek ten nazywamy zawadą obwodu (impedancją obwodu).

Z

R

Z

R

tg

Z

R

L

C

====

====

++++

====

++++

−−−−











cos

ϕϕϕϕ

ϕϕϕϕ

ω

ω

ω

ω

ω

ω

ω

ω

1

1

2

2

2

sin

cos

cos

2

2

2

2

1

1

1

ϕϕϕϕ

ϕϕϕϕ

ϕϕϕϕ

ϕϕϕϕ

++++

====

++++ ====

tg

L

ω =

ω =

ω =

ω =

R

L

- opór indukcyjny (induktancja)

1/C

ω

ω

ω

ω

= R

C

- opór pojemnościowy (kapacytancja)

R

L

- R

C

- opór bierny (reaktancja)

Związki między wielkościami charakteryzującymi obwód RLC, dla elementów
połączonych szeregowo można odtworzyć posługując się tzw. wykresem
wskazowym.

((((

))))

Z

R

R

R

L

C

====

++++

−−−−

2

2

Z

R

====

cos

ϕϕϕϕ

tg

R

R

R

L

C

ϕϕϕϕ ====

−−−−

Pomiędzy napięciami na poszczególnych
elementach obwodu zachodzą następujące
związki:

((((

))))

U

U

U

U

R

L

C

2

2

2

====

++++

−−−−

Istnieje

możliwość

dobrania

takiej

częstotliwości prądu płynącego przez obwód

RLC

, aby w obwodzie nie wystąpiło

przesunięcie fazowe.

ϕϕϕϕ

ω

ω

ω

ω

ω

ω

ω

ω

==== ⇔

⇔

⇔

⇔

====

0

1

L

C

ω

ω

ω

ω ====

1

LC

ω

ω

ω

ω

πν

πν

πν

πν

====

2

R

L

R

L

-R

C

Z

R

ϕϕϕϕ

R

C

U

R

R

U

∅

∅

∅

∅

U

L

L

∅

∅

∅

∅

U

C

C

32

νννν

ππππ

====

1

2

LC

Tak określona częstotliwość prądu jest nazywana częstotliwością rezonansową.

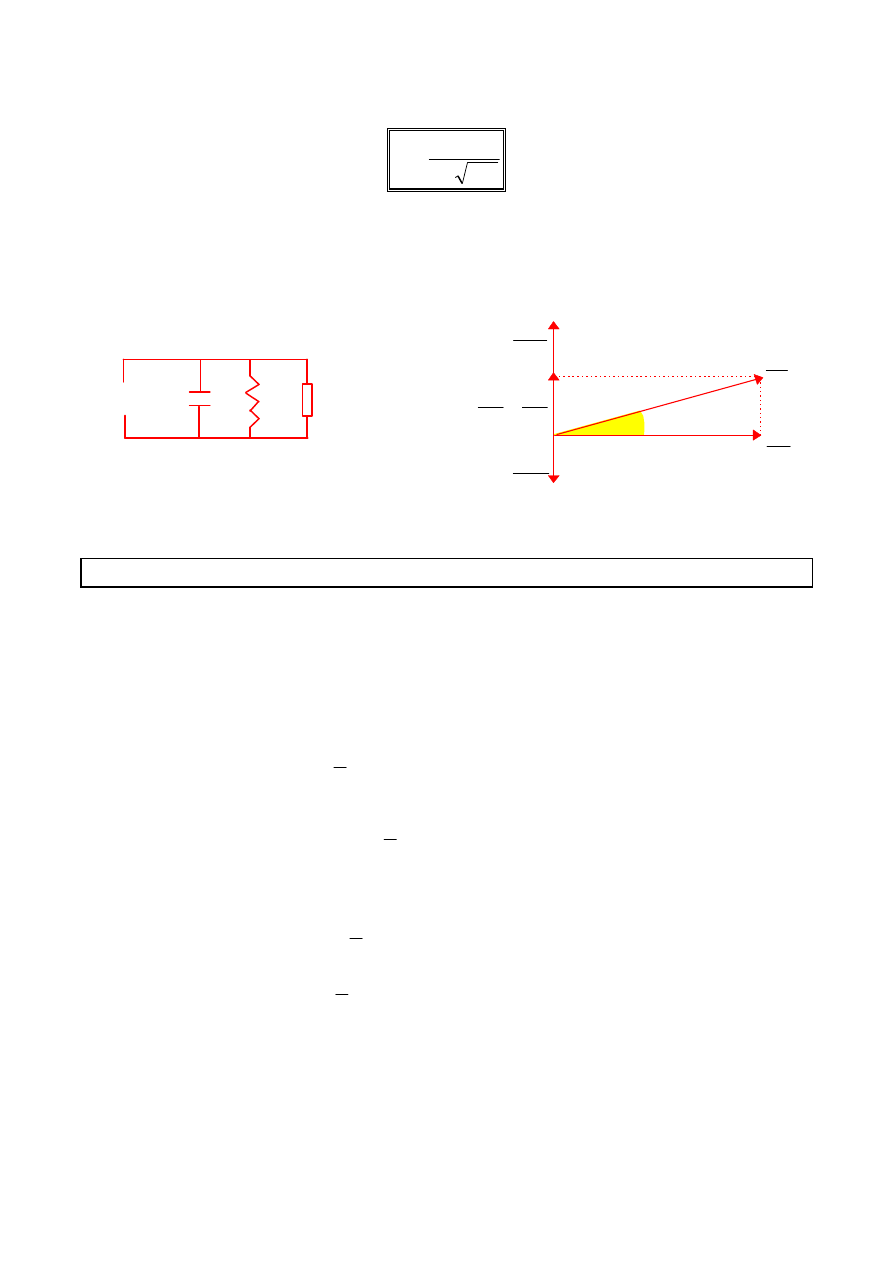
Dla elementów

RLC

połączonych równolegle zachodzą związki, które można

odtworzyć z następującego wykresu wskazowego:

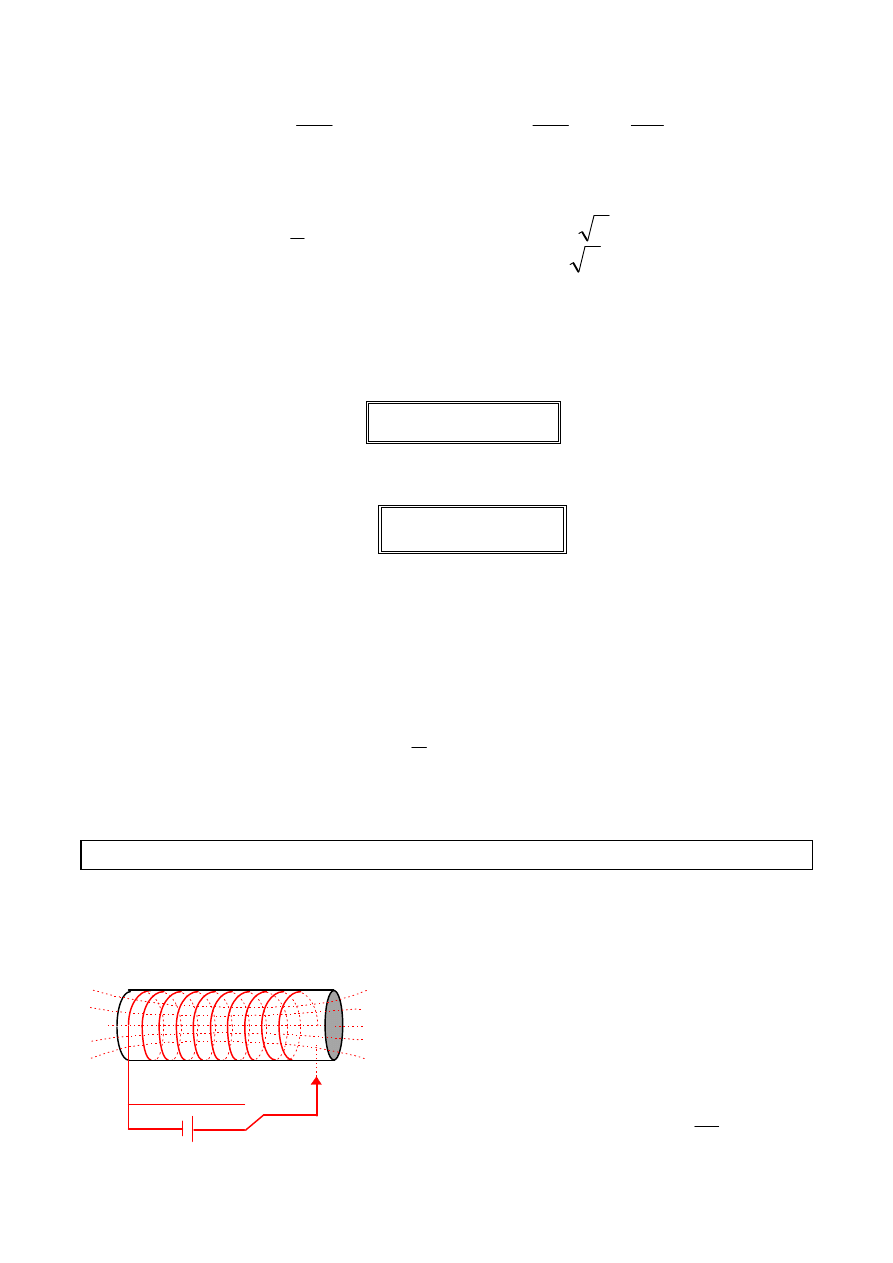
Praca i moc pr

ą

du zmiennego

Przyjmijmy, że w obwodzie płynie prąd zmienny o natężeniu

I = I

0

sin

ω

ω

ω

ω

t

wywołany napięciem

U = U

0

sin (

ω

ω

ω

ω

t+

ϕϕϕϕ).

Praca elementarna wykonana przez taki

prąd wciągu okresu wynosi:

((((

))))

((((

))))

[[[[

]]]]

dW

UIdt

U I

t

t

dt

dW

U I

t

dt

====

====

++++

====

−−−−

++++

0

0

0

0

1

2

2

sin

sin

cos

cos

ω

ω

ω

ω

ω

ω

ω

ω ϕϕϕϕ

ϕϕϕϕ

ω

ω

ω

ω ϕϕϕϕ

((((

))))

((((

))))

[[[[

]]]]

sin

sin

cos

cos

αααα

ββββ

αααα ββββ

αααα ββββ

====

−−−−

−−−−

++++

1

2

Praca wykonana przez taki prąd w ciągu okresu stanowi sumę prac elementarnych i

wynosi:

((((

))))

[[[[

]]]]

((((

))))

W

cos

cos

cos

cos

T

====

−−−−

++++

====

−−−−

++++













∫∫∫∫

∫∫∫∫

∫∫∫∫

1

2

2

1

2

2

0

0

0

0

0

0

0

U I

t

dt

W

U I

dt

t

dt

T

T

ϕϕϕϕ

ω

ω

ω

ω ϕϕϕϕ

ϕϕϕϕ

ω

ω

ω

ω ϕϕϕϕ

cos

cos

cos

ϕϕϕϕ

ϕϕϕϕ

ϕϕϕϕ

dt

dt

T

T

T

0

0

∫∫∫∫

∫∫∫∫

====

====

ϕϕϕϕ

1

R

C

1

1

R

R

L

C

−−−−

1

R

L

1

Z

1

R

U C

L R

∅

∅

∅

∅
∅

∅

∅

∅

33

[[[[

]]]]

cos(

)

sin(

)

sin

sin

2

1

2

2

1

2

4

0

0

0

ω

ω

ω

ω

ϕϕϕϕ

ω

ω

ω

ω

ω

ω

ω

ω ϕϕϕϕ

ω

ω

ω

ω

ππππ

ϕϕϕϕ

ϕϕϕϕ

t

dt

t

T

T

T

T

++++

====

++++

====

++++











−−−−













====

∫∫∫∫

W

U I T

W

U I T

s

s

====
====

1

2

0

0

cos

cos

ϕϕϕϕ

ϕϕϕϕ

U

U

I

I

s

s

0

0

2

2

====

====

Można uważać, że każdy przedział czasu stanowi wielokrotność okresu. Wynika
stąd, że praca prądu zmiennego wykonana w dowolnym czasie t wynosi:

W

U I t

S S

====

cos

ϕϕϕϕ

Moc prądu zmiennego wynosi:

P

U I

S S

====

cos

ϕϕϕϕ

Jeśli w obwodzie nie powstaje przesunięcie fazowe, to wzory na pracę i moc prądu
zmiennego nie różnią się od wzorów na pracę i moc prądu stałego.

W przypadku nieuwzględnienia przesunięcia fazowego otrzymujemy tzw. pracę
pozorną, względnie moc pozorną prądu zmiennego. Dla odróżnienia jej od pracy czy
mocy rzeczywistej, pracę pozorną wyrażamy w woltoamperosekundach, a moc
pozorną - w woltoamperach.

Jeśli przesunięcie fazowe jest bliskie

ππππ

2

to moc takiego prądu jest równa zeru. Prąd

taki nazywamy bezwatowym.

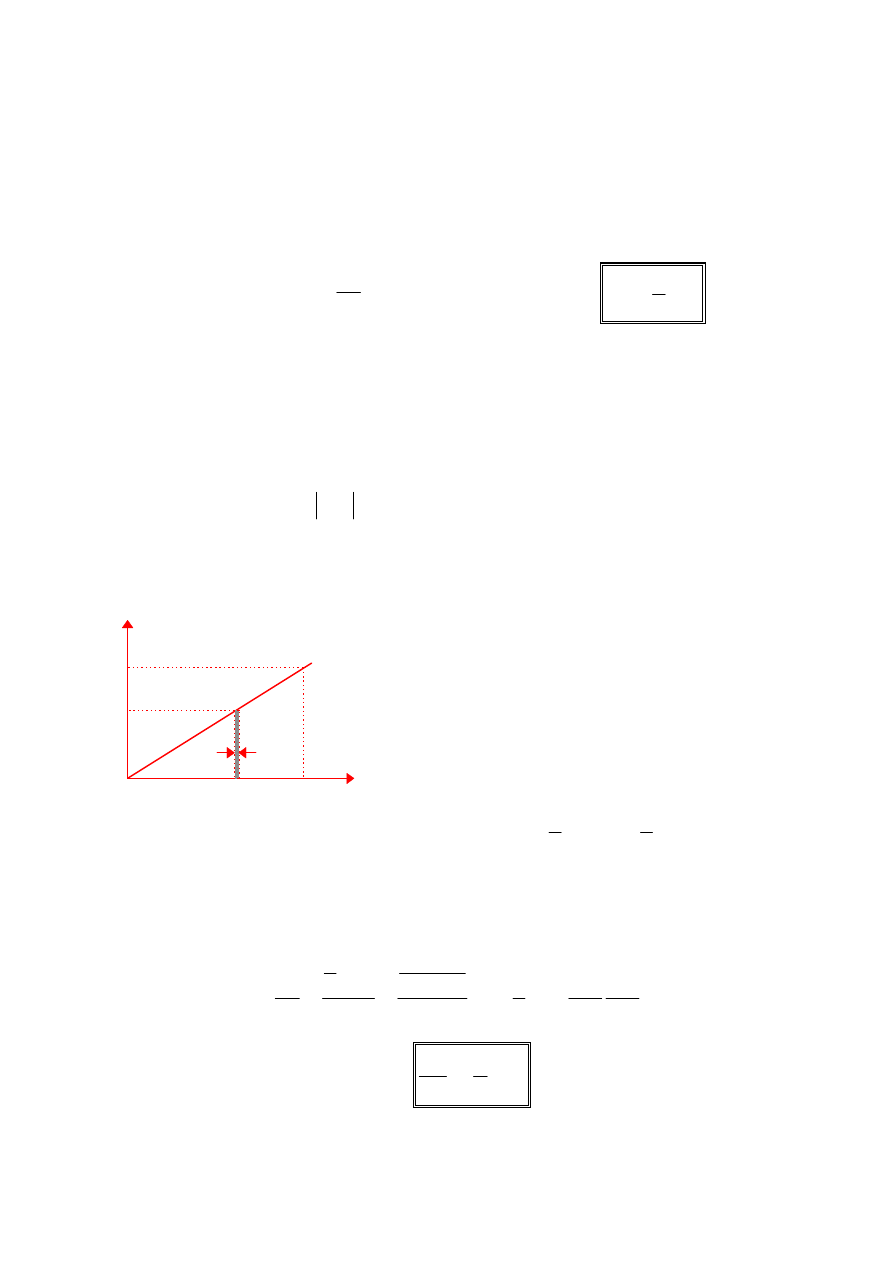
Energia pola magnetycznego

Przez zwojnicę

o indukcyjności L płynie prąd stały o natężeniu I

0

. W wyniku

przerwania obwodu i ponownego połączenia jego końców pole magnetyczne zanika.

W obwodzie płynie prąd indukcyjny, a energia
pola magnetycznego przekształca się w energię
cieplną. Praca elementarna wykonana przez
zanikający prąd indukcyjny wynosi:

dW

EIdt

dW

LIdI

====

==== −−−−

E

L

dI

dt

==== −−−−

I

0

°°°°

°°°°

r

B

34

Praca wykonana przez prąd, którego natężenie maleje do zera stanowi sumę prac
elementarnych i wynosi:

W

dW

LIdI

I

====

==== −−−−

∫∫∫∫

∑

∑

∑

∑

0

0

W

L

I

I

==== −−−−













2

0

2

0

⇒

⇒

⇒

⇒

W

LI

====

1

2

0

2

Sumowanie prac elementarnych można również wykonać metodą całkowania
graficznego. Wartość pracy elementarnej wykonanej przez prąd samoindukcji
wynosi:

YdI

dW

LIdI

dW

====

====

Y

LI

====

Y

jest liniową funkcją natężenia prądu, a zatem

jej wykresem jest linia prosta. Miarą pracy
elementarnej jest pole wąskiego prostokąta
zawartego pod wykresem funkcji Y. Praca
wykonana przy zmianie natężenia prądu o I

0

jest

równa sumie prac elementarnych i odpowiada jej
pole trójkąta zawartego pod wykresem.

W

I LI

LI

====

====

1

2

1

2

0

0

0

2

W przypadku długiego solenoidu, w którym płynie prąd , gęstość energii pola
magnetycznego wynosi:

W

V

LI

lS

n s

l

lS

I

nI

l

nI

l

o

====

====

====

1

2

1

2

0

2

2

0

2

0

0

0

µµ

µµ

µµ

µµ

µµ

µµ

µµ

µµ

Ostatecznie otrzymujemy:

W

V

BH

====

1

2

Y

LI

0

I

0

I

dI

Y

35

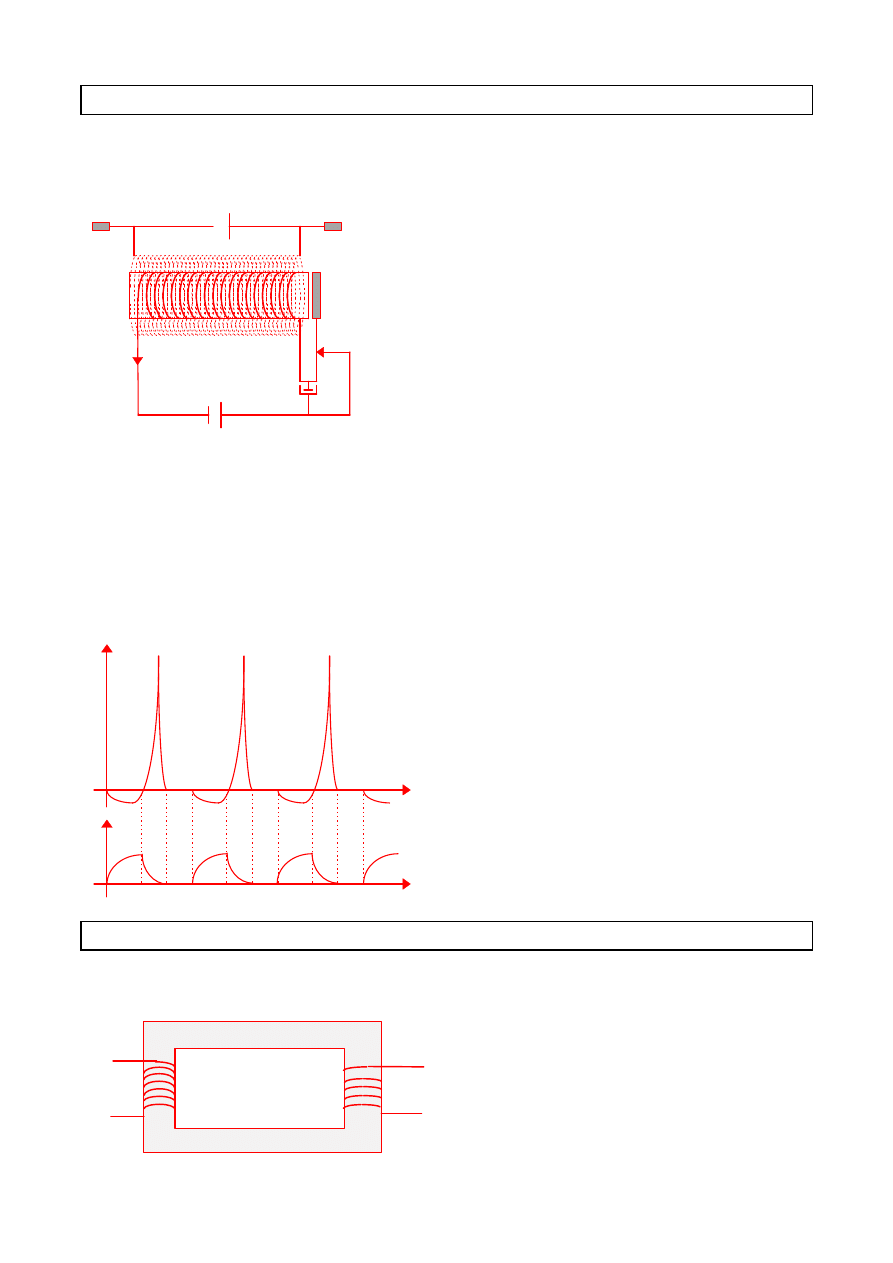
Induktor

Induktor jest urządzeniem, które służy do otrzymywania wysokiego napięcia. Na
rdzeniu wykonanym z miękkiej stali nawinięte jest uzwojenie pierwotne wykonane z
grubego, izolowanego drutu. Uzwojenie to jest zasilane ze źródła prądu stałego o

napięciu kilku woltów. Przepływ prądu powoduje
powstanie pola magnetycznego i namagnesowany
rdzeń przyciąga młoteczek przerywacza. W ten
sposób obwód zostaje przerwany. Rdzeń ulega
rozmagnesowaniu

a

odskakujący

młoteczek

ponownie zamyka obwód. Uzwojenie pierwotne
wytwarza zatem zmienne pole magnetyczne. Pole to
przenika przez uzwojenie wtórne nawinięte na ten
sam rdzeń, liczące wiele tysięcy zwojów cienkiego

drutu. W każdym zwoju powstaje SEM indukcji, w wyniku czego na końcach
uzwojenia wtórnego połączonych z iskiernikiem powstaje wysokie napięcie
umożliwiające np. powstawanie wyładowań iskrowych. Z powodu dużej
indukcyjności uzwojeń, w momentach rozłączenia obwodu powstaje znaczne
napięcie samoindukcji, co prowadzi do iskrzenia na styku przerywacza. Aby nie
dopuścić do zniszczenia styku stosuje się kondensator o dużej pojemności, włączony
równolegle do przerwy iskrowej. Zmiany natężenia prądu w uzwojeniu pierwotnym i
odpowiadające im zmiany napięcia na końcach uzwojenia wtórnego induktora

przedstawiają

zamieszczone

obok

wykresy. Prąd w uzwojeniu wtórnym jest
zmienny, również co do kierunku. Silne
skoki

napięcia

powstają

podczas

przerywania

prądu

w

uzwojeniu

pierwotnym.

Transformator

Transformator służy do uzyskiwania zmian napięcia prądu zmiennego. Na rdzeniu
wykonanym z miękkiej stali są nawinięte dwa uzwojenia liczące różne ilości

zwojów. Do uzwojenia pierwotnego
liczącego n

1

zwojów zostaje włączone

zmienne napięcie o wartości skutecznej
U

1

. Wewnątrz uzwojenia powstaje

zmienne

pole

magnetyczne,

które

I

U

t

t

I

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

∅

n

2

n

1

U

2

U

1

36

przenika do uzwojenia wtórnego liczącego n

2

zwojów. W każdym zwoju powstaje

SEM

indukcji i na końcach uzwojenia wtórnego powstaje zmienne napięcie o

wartości skutecznej U

2

. Jeżeli do uzwojenia pierwotnego zostanie przyłożone

napięcie sinusoidalne U’ = U

0

sin

ω

ω

ω

ω

t

, to z powodu znacznej indukcyjności tego

uzwojenia popłynie w nim prąd, którego natężenie jest przesunięte

w fazie praktycznie o

ππππ

2

I

I

t

I

t

'

sin

cos

====

−−−−











==== −−−−

0

0

2

ω

ω

ω

ω

ππππ

ω

ω

ω

ω

Strumień indukcji magnetycznej wytworzony w uzwojeniu pierwotnym jest wprost
proporcjonalny do natężenia płynącego prądu i wynosi:

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

==== −−−−

0

cos

ω

ω

ω

ω

t

Chwilowe natężenie prądu płynącego przez uzwojenie pierwotne można określić z
prawa Ohma:

I

U

d

dt

n

R

'

'

====

−−−− Φ

Φ

Φ

Φ

1

1

dt

d

n

'

U

R

'

I

1

1

Φ

Φ

Φ

Φ

−−−−

====

⇒

⇒

⇒

⇒

R

U

n

d

dt

1

1

0

≈≈≈≈

⇒

⇒

⇒

⇒

====

'

Φ

Φ

Φ

Φ

d

dt

t

Φ

Φ

Φ

Φ ΦΦΦΦ

====

0

ω

ω

ω

ω

ω

ω

ω

ω

sin

U

n

t

'

sin

==== Φ

Φ

Φ

Φ

0

1

ω

ω

ω

ω

ω

ω

ω

ω

Przez uzwojenie wtórne przenika ten sam strumień indukcji magnetycznej.
Powoduje to powstanie na jego końcach napięcia chwilowego:

U

d

dt

n

U

n

t

''

''

sin

==== −−−−

====

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

2

0

2

ω

ω

ω

ω

ω

ω

ω

ω

U

U

U

U

n

n

n

n

1

2

01

02

0

1

0

2

1

2

====

====

====

Φ

Φ

Φ

Φ
Φ

Φ

Φ

Φ

ω

ω

ω

ω
ω

ω

ω

ω

Wynika stąd, że stosunek liczby zwojów w uzwojeniu pierwotnym do liczby
zwojów w uzwojeniu wtórnym jest równy stosunkowi napięć skutecznych na
końcach tych uzwojeń. Stosunek ten nazywamy przekładnią transformatora.

37

U

U

n

n

1

2

1

2

====

n

n

I

I

1

2

2

1

====

W praktyce zachodzi jednak pewne rozpraszanie strumienia indukcji magnetycznej i
stosunek napięć nieco różni się od stosunku liczby zwojów.

Sprawnością transformatora nazywamy stosunek mocy pobieranej z uzwojenia
wtórnego do mocy dostarczonej do uzwojenia pierwotnego:

ηηηη ====

U I

U I

2

2

1 1

Sprawność transformatorów dochodzi do 98%.

Istnieją trzy zasadnicze przyczyny strat energii w obwodzie transformatora:

1. Ciepło Joule’a Lenza.

W każdym przewodniku, w którym płynie prąd wydziela się ciepło Q = I

2

R t

.

Straty spowodowane w ten sposób można zminimalizować przez stosowanie
przewodów wykonanych z bardzo dobrych przewodników (miedź, aluminium), o
odpowiednio dużym przekroju poprzecznym.

2. Prądy wirowe.

Powstają one w rdzeniu transformatora i są wywołane przez zmienne pole
magnetyczne. Aby zmniejszyć straty wywołane przez prądy wirowe rdzenie
transformatorów wykonuje się z cienkich blaszek.

3. Histereza żelaza.

Konieczność ustawicznych zmian stanu namagnesowania rdzenia wiąże się z
nieustannymi obrotami domen magnetycznych. W wyniku tarcia wydziela się ciepło.
Straty spowodowane histerezą żelaza można zmniejszyć wykonując rdzeń
transformatora ze szczególnie miękkich materiałów ferromagnetycznych.

Prawa Maxwella

Wokół przewodnika z prądem istnieje pole magnetyczne. Zgodnie z prawem
Ampere’a zachodzi związek:

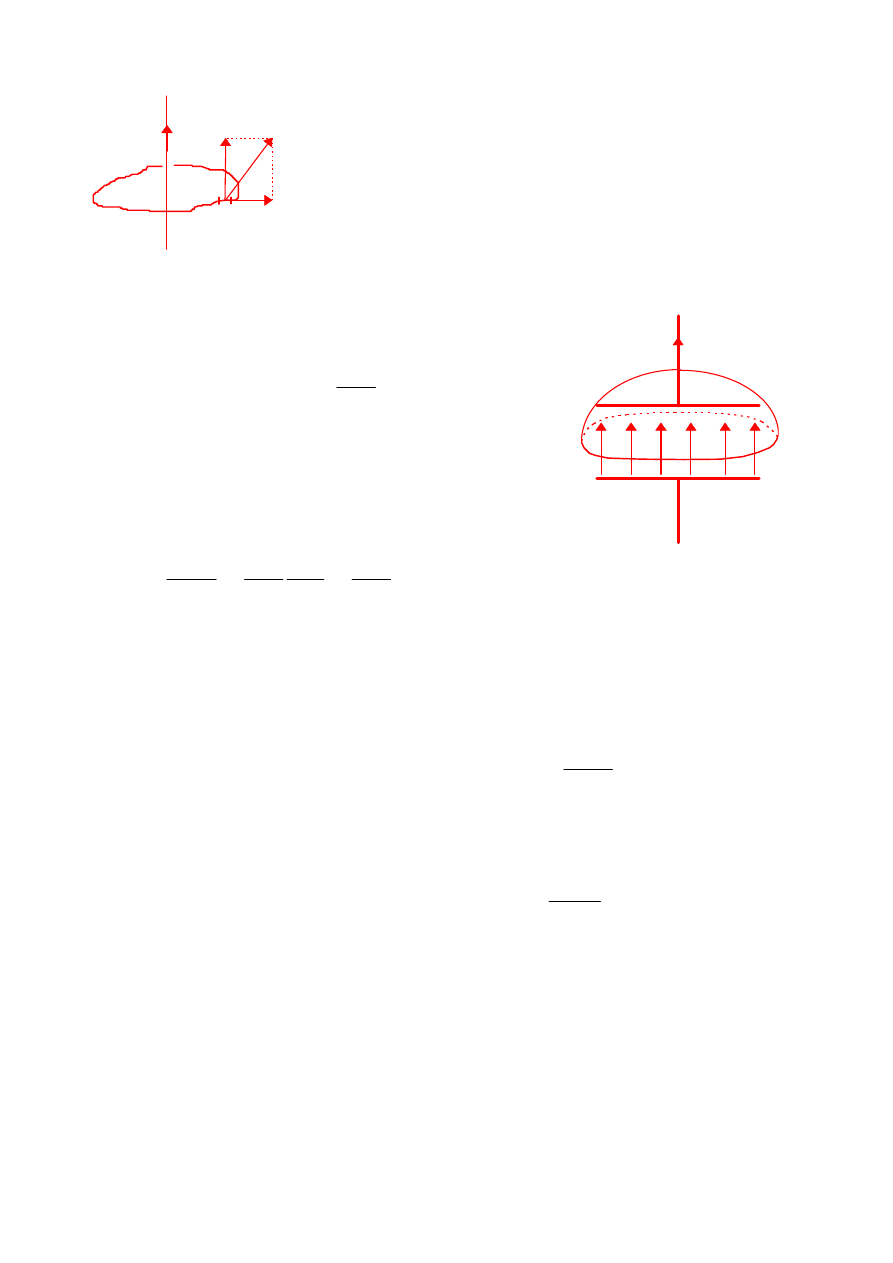
38

H dl

I

||

∑

∑

∑

∑

====

Krążenie

H

r

po konturze zamkniętym jest równe natężeniu

prądu przepływającego przez ten kontur.

Jeśli w obwodzie prądu zmiennego znajduje się
kondensator, to pomiędzy okładkami tego kondensatora
istnieje zmienne pole elektryczne. Przez powierzchnię

zamykającą jedną z okładek przenika zmienny strumień natężenia pola
elektrycznego. Zgodnie z prawem Gaussa zachodzi
równość:

Ψ

Ψ

Ψ

Ψ

E

Q

====

εε

εε

εε

εε

0

Ψ

Ψ

Ψ

Ψ

E

- strumień całkowity natężenia pola przenikający

powierzchnię, która zamyka ładunek Q.
Pochodna strumienia natężenia pola po czasie wynosi:

d

dt

dQ

dt

I

E

p

Ψ

Ψ

Ψ

Ψ ====

====

1

1

0

0

εε

εε

εε

εε

εε

εε

εε

εε

Zmiana strumienia jest zatem równoważna przepływowi prądu. Wynika stąd, że
chociaż między okładkami kondensatora nie płynie prąd elektryczny, to wokół linii
sił zmiennego pola elektrycznego musi istnieć pole magnetyczne. Zgodnie z prawem
Ampere’a otrzymujemy:

H dl

I

d

dt

p

E

||

∑

∑

∑

∑

====

==== εε

εε

εε

εε

0

Ψ

Ψ

Ψ

Ψ

Jeśli przez pewien kontur zamknięty przepływa prąd elektryczny i przenika zmienne
pole elektryczne, to dla tego konturu zachodzi związek:

H dl

I

d

dt

E

||

∑

∑

∑

∑

==== ++++ εε

εε

εε

εε

0

Ψ

Ψ

Ψ

Ψ

Powyższa zależność jest określona jako pierwsze prawo Maxwella. Jego istotą jest
związek między polem elektrycznym jako przyczyną i polem magnetycznym jako
skutkiem. Przyczyną pola magnetycznego jest nie tyle prąd płynący w przewodniku
co pole elektryczne, które ten prąd wywołało. Zmienne pole elektryczne jest
przyczyną zmiennego, wirowego pola magnetycznego.

B

r

H

r

H

||

+ + + + + + + + + + + +

+

- - - - - - - - - - - -

39

Jeśli przez obwód zamknięty przenika zmienne
pole magnetyczne, to w tym obwodzie powstaje
prąd indukcyjny. Zgodnie z prawem indukcji
Faradaya, SEM indukcji wyraża się wzorem:

SEM

d

dt

==== −−−− Φ

Φ

Φ

Φ

Napięcie, które jest przyczyną prądu indukcyjnego jest sumą różnic potencjałów
liczonych wzdłuż obwodu.

SEM

dV

====

∑

∑

∑

∑

Różnica potencjałów na odcinku dl obwodu wiąże się z natężeniem pola
elektrycznego skierowanym wzdłuż dl:

E

dV

dl

dV

E dl

SEM

E dl

||

||

||

====

⇒

⇒

⇒

⇒

====

====

∑

∑

∑

∑

Prawo indukcji Faradaya można zatem zapisać w postaci:

E dl

d

dt

||

∑

∑

∑

∑

==== −−−− Φ

Φ

Φ

Φ

Sumę po lewej stronie równania nazywamy krążeniem wektora E po konturze
zamkniętym. Powyższą zależność nazywamy drugim prawem Maxwella.

Prawo to stanowi uogólnienie prawa indukcji Faraday’a. Jego istotą jest związek
między polem magnetycznym jako przyczyną i polem elektrycznym jako skutkiem.
Zmienne pole magnetyczne wytwarza zmienne, wirowe pole elektryczne. Prąd
elektryczny jest skutkiem istnienia pola elektrycznego.

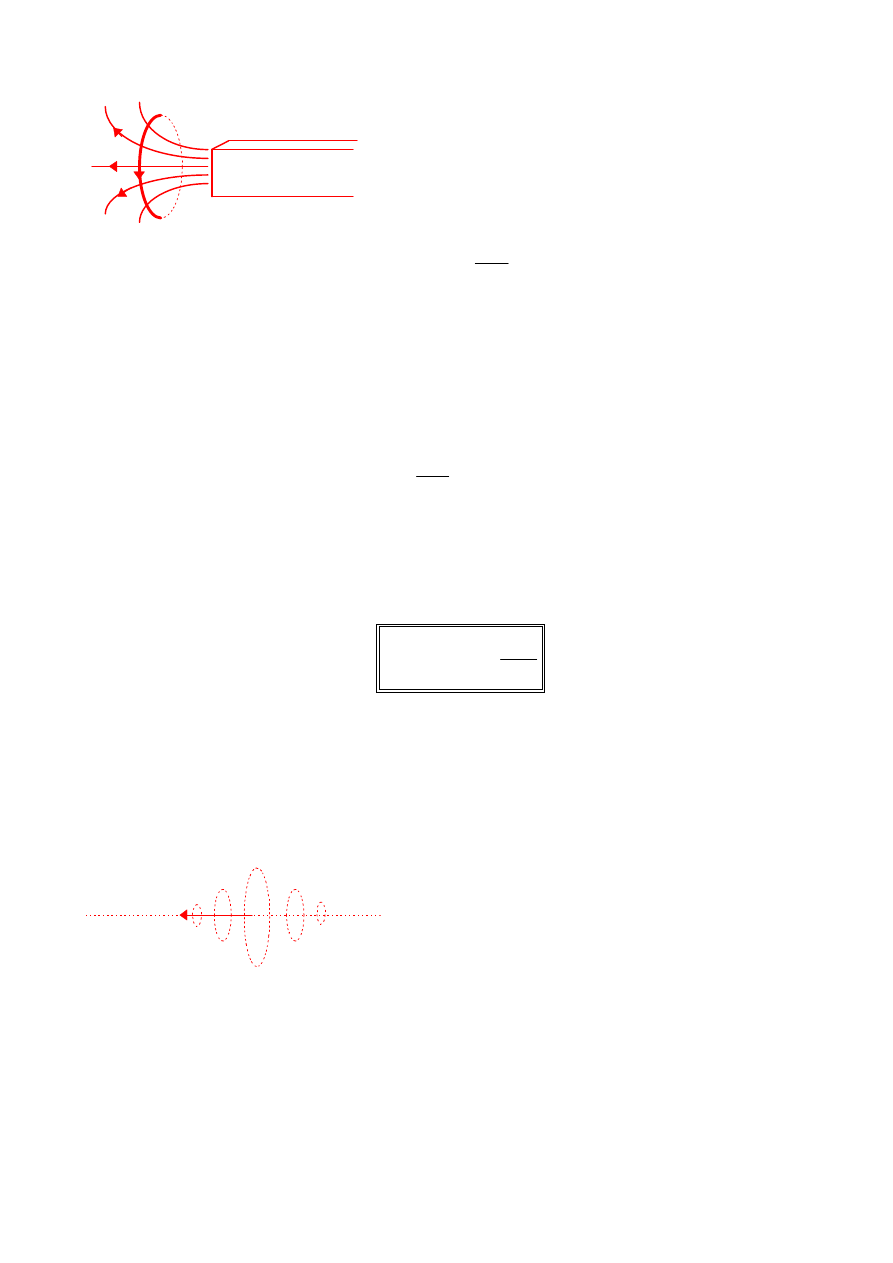
Ruchomy

ładunek

elektryczny

wytwarza

zmienne pole magnetyczne. Zmienne pole
magnetyczne jest z kolei przyczyną zmiennego,
wirowego pola elektrycznego. Oznacza to, że

ruchomy ładunek jest przyczyną powstania ciągu pól: magnetycznego i
elektrycznego. Taki ciąg pól nazywamy falą elektromagnetyczną. Źródłem fali jest
każde zmienne pole elektryczne lub magnetyczne.

N

•