Fizyka - Zadania - Indukcja elektromagnetyczna

Poniżej znajdują się treści zadań związanych z wybranym tematem. Kliknij na odnośnik "więcej..." aby zobaczyć rozwiązanie zadania.
Uwaga! kolorem czerwonym zaznaczono zadania, których rozwiązania są dostępne dopiero po wykupieniu abonamentu. Jeśli nie masz w pełni aktywnego konta, kliknij tutaj.

01.	Dwa przewodniki kołowe o promieniach r i 2r umieszczone są w jednorodnym polu magnetycznym B prostopadłym do płaszczyzn przewodników (rys.). Ile wynosi strumień indukcji magnetycznej przenikający przez powierzchnię między przewodnikami? więcej...
02.	Ramka kwadratowa o boku a=10cm jest umieszczona prostopadle do linii sił jednorodnego pola magnetycznego o indukcji B1=0.5T. Ile była równa siła elektromotoryczna indukcji, jeżeli indukcja pola magnetycznego zmalała jednostajnie w czasie t=0.04s do wartości B2=0.1T? więcej...
03.	Wartość indukcji jednorodnego pola magnetycznego wynosi B=2T. W polu tym porusza się przewodnik o długości l=0.4m z prędkością v=50m/s. Wektory prędkości i indukcji pola magnetycznego B są do siebie prostopadłe, a wektor prędkości jest prostopadły do przewodnika. Oblicz wartość SEM powstałej na końcach przewodnika. więcej...

Zadanie 1

Treść: Dwa przewodniki kołowe o promieniach r i 2r umieszczone są w jednorodnym polu magnetycznym B prostopadłym do płaszczyzn przewodników (rys.). Ile wynosi strumień indukcji magnetycznej przenikający przez powierzchnię między przewodnikami?

Dane: r 2r B

Szukane: Φ = ?

Wzory: Strumień pola magnetycznego

Rozwiązanie:
Strumień pola magnetycznego Φ o indukcji B przez powierzchnię o polu ΔS definiujemy jako:

gdzie α oznacza kąt, jaki tworzy wektor indukcji pola magnetycznego z prostą prostopadłą do powierzchni ΔS.
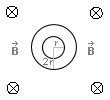
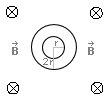
Nasza powierzchnia ΔS to powierzchnia pierścienia. Otrzymamy ją poprzez odjęcie pola koła S₂ o promieniu r od pola powierzchni koła S₁ o promieniu 2r.

gdzie:

W zadaniu jest napisane, że przewodniki są umieszczone w polu magnetycznym prostopadle do wektora B. Oznacza to, że prosta prostopadła do powierzchni ΔS, jaką tworzą te dwa przewodniki, jest nachylona do wektora indukcji B pod kątem prostym, czyli α=90⁰. Dzięki temu:

Podstawiając po kolei wyszystko co wyżej zostało napisane do pierwotnego wzoru, otrzymujemy:

Strumień indukcji magnetycznej przenikającej przez powierzchnię między przewodnikami (czyli pierścienia) wynosi 3Bπr².

Zadanie 2

Treść: Ramka kwadratowa o boku a=10cm jest umieszczona prostopadle do linii sił jednorodnego pola magnetycznego o indukcji B1=0.5T. Ile była równa siła elektromotoryczna indukcji, jeżeli indukcja pola magnetycznego zmalała jednostajnie w czasie t=0.04s do wartości B2=0.1T?

Dane: a = 10 cm = 0.1 m B1 = 0.5 T B2 = 0.1 T t = 0.04 s

Szukane: ε = ?

Wzory: 1. Siła elektromotoryczna (prawo Faradaya) 2. Strumień pola magnetycznego

Rozwiązanie:
Prawo Faradaya mówi nam, że siła elektromotoryczna SEM zależy od zmiany strumienia w czasie. Potrzebujemy zatem wyznaczyć zmianę strumienia w naszym znanym czasie t.
Strumień pola magnetycznego Φ o indukcji B przez powierzchnię o polu ΔS definiujemy jako:

gdzie α oznacza kąt, jaki tworzy wektor indukcji pola magnetycznego z prostą prostopadłą do powierzchni ΔS.
Zatem prawo Faradaya (czyli wzór na szukaną siłę elektromotoryczną) możemy zapisać:

W naszym przypadku powierzchnią ΔS jest powierzchnia, jaką tworzy ramka kwadratowa o boku a:

W zadaniu jest napisane, że ramka jest umieszczona w polu magnetycznym prostopadle do wektora B. Oznacza to, że prosta prostopadła do powierzchni ΔS jest nachylona do wektora indukcji B pod kątem prostym, czyli α=90⁰. Dzięki temu:

Zmiana indukcji pola magnetycznego ΔB jest różnicą pomiędzy wartością końcową pola indukcji B₂ a wartością początkową B₁

Korzystając zatem ze wszystkich powyższych równań otrzymujemy:

Na koniec sprawdzimy poprawność jednostki:

Siła elektromotoryczna indukcji była równa 0,1 V.

Zadanie 3

Treść: Wartość indukcji jednorodnego pola magnetycznego wynosi B=2T. W polu tym porusza się przewodnik o długości l=0.4m z prędkością v=50m/s. Wektory prędkości i indukcji pola magnetycznego B są do siebie prostopadłe, a wektor prędkości jest prostopadły do przewodnika. Oblicz wartość SEM powstałej na końcach przewodnika.

Dane: B = 2 T l = 0.4 m v = 50 m/s

Szukane: ε = ?

Wzory: Prawo Faradaya (siła elektromotoryczna) Droga przebyta ruchem jednostajnym

Rozwiązanie:
Prawo Faradaya mówi nam, że siła elektromotoryczna SEM zależy od zmiany strumienia w czasie.
Strumień pola magnetycznego Φ o indukcji B przez powierzchnię o polu ΔS definiujemy jako:

gdzie α oznacza kąt, jaki tworzy wektor indukcji pola magnetycznego z prostą prostopadłą do powierzchni ΔS.
Zatem prawo Faradaya możemy zapisać:

Rozpatrzmy rysunek opisujący sytuację:

Przewodnik poruszając się z prędkością v przemieszcza się o odległość x, czyli przewodnik zakreśla pole ΔS=xt.
W zadaniu jest napisane, że przewodnik jest umieszczony w polu magnetycznym prostopadle do wektora B. Oznacza to, że prosta prostopadła do powierzchni ΔS jest nachylona do wektora indukcji B pod kątem prostym, czyli α=90⁰. Dzięki temu:

Pole powierzchni, które przebywa przewodnik to prostokąt o bokach l i x. Droga x jest to droga w ruchu jednostajnym, czyli:

Podstawiając wszystko co wiemy do prawa Faradaya, otrzymujemy:

Na koniec sprawdźmy jednostkę:

Na końcach przewodnika powstanie siła elektromotoryczna o wartości 40 V. Znak minus świadczy tylko i wyłącznie o kierunku wektora siły elektromotorycznej.

---