Fizyka - Zadania - Prąd przemienny

Poniżej znajdują się treści zadań związanych z wybranym tematem. Kliknij na odnośnik "więcej..." aby zobaczyć rozwiązanie zadania.
Uwaga! kolorem czerwonym zaznaczono zadania, których rozwiązania są dostępne dopiero po wykupieniu abonamentu. Jeśli nie masz w pełni aktywnego konta, kliknij tutaj.

01.	Rysunek obok przedstawia natężenie prądu w zależności od czasu (przebieg dwóch okresów). Ile wynosi natężenie skuteczne prądu? Ile powinna wynosić amplituda prądu sinusoidalnie zmiennego, aby miał on takie samo natężenie skuteczne, jak prąd na rysunku obok? więcej...
02.	Przez grzejnik o oporze R=50Ω w ciągu t=5min popłynął sinusoidalnie zmienny prąd o wartości maksymalnej I0=2A. Ile wynosi ilość wydzielonego ciepła w tym czasie? więcej...
03.	Obwód prądu zmiennego składający się z połączonych ze sobą opornika R=16Ω oraz cewki o indukcyjności L=12H, zasilany jest sinusoidalnie zmiennym prądem. Amplituda napięcia jest równa U0=50V, a jego częstotliwość wynosi f=1/(2π)Hz. Oblicz: zawadę obwodu, amplitudę płynącego w nim prądu, przesunięcie fazowe napięcia względem prądu oraz wydzielaną moc skuteczną w obwodzie. więcej...

Zadanie 1

Treść: Rysunek obok przedstawia natężenie prądu w zależności od czasu (przebieg dwóch okresów). Ile wynosi natężenie skuteczne prądu? Ile powinna wynosić amplituda prądu sinusoidalnie zmiennego, aby miał on takie samo natężenie skuteczne, jak prąd na rysunku obok?

Dane: wykres

Szukane: IS = ? I0 = ?

Wzory: 1.Praca prądu zmiennego 2.Prawo Ohma 3.Moc średnia 4.Natężenie skuteczne 5.Moc prądu stałego

Rysunek:

Rozwiązanie:
Aby obliczyć natężenie skuteczne tego prądu zmiennego, obliczymy najpierw pracę wykonaną przez prąd. W naszym wypadku:

gdzie:
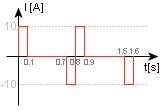
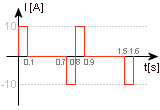
W₁ - praca wykonana przez prąd natężeniu 10 amperów w czasie 0.1 sekundy,
W₂ - praca wykonana przez prąd o natężeniu równym 0 amperów w czasie 0.6 sekundy,
W₃ - praca wykonana przez prąd o natężeniu równym -10 amperów w czasie 0.1 sekundy.
Poszczególne dane zostały odczytane z wykresu.
Okres naszego prądu wynosi 0.8 sekundy (jest to czas, w którym wykres "nie powtarza się"; zauważ, że po 0.8 s wykres wygląda identycznie), więc policzymy czas w zależności od okresu, w jakim wykonywana jest każdy z poszczególnych etapów pracy:

Oczywiście suma tych czasów daje nam cały okres T.

Z prawa Ohma obliczamy napięcie U i wstawiamy je do wzoru na pracę prądu:

Obliczamy teraz pracę wykonaną przez prąd na poszczególnych odcinkach z naszego wykresu:

Całkowita praca zaś wynosi:

Mając całkowitą pracę możemy z łatwością obliczyć moc średnią:

Przyrównując moc średnią z mocą prądu stałego o natężeniu równym I_s (natężenie skuteczne), otrzymamy:

Dlaczego przyrównaliśmy te moce? Ponieważ moc prądu stałego nie zmienia się w czasie, będzie więc ona równa w przybliżeniu średniej mocy prądu zmiennego. Nasz prąd stały jest niczym innym jak odzwierciedleniem wykresu prądu zmiennego w postaci (funkcji) stałej. I dodatkowo znaleźliśmy jeszcze natężenie skuteczne. :)

Skoro mamy już natężenie skuteczne, pozostaje wyliczyć amplitudę dla natężenia prądu sinusoidalnie zmiennego (czyli teraz nasz wykres prądu chcemy przedstawić w postaci sinusoidy; mamy wyliczyć największą wartość wykresu). Wartość tę wyliczymy ze wzoru czwartego:

Zatem natężenie natężenie skuteczne (średnie) wynosi 5A, a amplituda prądu sinusoidalnie zmiennego wynosi 7.07A.

Zadanie 2

Treść: Przez grzejnik o oporze R=50Ω w ciągu t=5min popłynął sinusoidalnie zmienny prąd o wartości maksymalnej I0=2A. Ile wynosi ilość wydzielonego ciepła w tym czasie?

Dane: R = 50 Ω t = 5 min I0 = 2 A

Szukane: Q = ?

Wzory: 1.Zasada zachowania energii 2.Natężenie skuteczne 3.Moc skuteczna 4.Prawo Ohma 5.Praca zmiennego prądu elektrycznego

Rozwiązanie:
Zgodnie z zasadą zachowania energii ciepło pobrane przez układ jest równe wzrostowi jego energii wewnętrznej układu plus pracy wykonanej przez otoczenie nad tym układem.

W naszym przypadku ciepło pobrane przez układ jest równe tylko pracy wykonanej przez prąd:

Praca zmiennego prądu elektrycznego wyraża się wzorem:

Czas przeliczamy na sekundy:

Moc skuteczną prądu określa wzór:

Zgodnie z prawem Ohma możemy zapisać, że:

a w naszym przypadku:

Przekształcamy powyższy wzór do postaci:

i wstawiamy do wzoru na moc skuteczną:

Natężenie skuteczne definiujemy jako iloraz natężenia maksymalnego i pierwiastka z dwóch:

Po tych wszystkich przekształceniach nasz wzór na moc skuteczną wygląda teraz tak:

Podstawiamy ten wzór do wzoru na pracę prądu:

i ostatecznie:

Wstawiamy dane:

Na koniec sprawdzimy poprawność wzoru, wyliczając jednostkę - skoro mamy ciepło, powinien wyjść nam dżul:

Zatem ilość wydzielonego ciepła wynosi 30000 J.

Zadanie 3

Treść: Obwód prądu zmiennego składający się z połączonych ze sobą opornika R=16Ω oraz cewki o indukcyjności L=12H, zasilany jest sinusoidalnie zmiennym prądem. Amplituda napięcia jest równa U0=50V, a jego częstotliwość wynosi f=1/(2π)Hz. Oblicz: zawadę obwodu, amplitudę płynącego w nim prądu, przesunięcie fazowe napięcia względem prądu oraz wydzielaną moc skuteczną w obwodzie.

Dane: R = 16Ω L = 12H U0 = 50V f = 1 /(2π) Hz

Szukane: Z = ? I0 = ? φ = ? PS = ?

Wzory: 1.Impedancja 2.Moc skuteczna 3.Przesunięcie fazowe 4.Natężenie skuteczne 5.Prawo Ohma 6.Częstość kołowa, okres, częstotliwość

Rozwiązanie:
W treści zadania mamy podane, iż nasz obwód elektryczny składa się z opornika i cewki. Taki obwód nazywamy obwodem RL. Policzmy najpierw przesunięcie fazowe. W takim obwodzie napięcie wyprzedza w fazie natężenie prądu o kąt φ, którego tangens wynosi:

gdzie:

zatem:

Żeby obliczyć częstość kołową, skorzystajmy wprost z wzoru 6:

Podstawiając to do wzoru na przesunięcie fazowe otrzymujemy:

Obliczyliśmy już przesunięcie fazowe, a teraz zajmiemy się wyliczeniem impedancji, zwanej inaczej zawadą Z_RL, która z definicji wynosi:

Wartość U_0RL mamy daną, ale niestety nie mamy I₀. Jak to naprawić? Spróbujmy rozpisać nasze natężenie U_0RL:

...aby ostatecznie wyliczyć naszą zawadę:

Na koniec sprawdźmy poprawność jednostki (powinien wyjść om):

Udało się! :)
Teraz czas na amplitudę, czyli maksymalną wartość natężenia. Wyliczymy ją przekształcając poprzedni wzór na zawadę (tym razem nie rozpisujemy już U_0RL):

Ostatnią niewiadomą jaka nam została jest moc skuteczna (wzór 2 przekształcimy korzystając z prawa Ohma):

Aby obliczyć natężenie skuteczne I_S skorzystajmy z zależności między natężeniami: maksymalnym (amplitudą) i skutecznym:

Wstawiamy powyższe do wzoru na moc średnią i wyliczamy ją:

Chyba nie było aż tak źle, jak wyglądało to na początku. :)
Ostatecznie otrzymaliśmy, że impedancja (zawada) wynosi 20 omów, amplituda 2.5 A, przesunięcie fazowe około 36 stopni, a moc skuteczna 50 watów.

---