Fizyka - Zadania - Pole magnetyczne

Poniżej znajdują się treści zadań związanych z wybranym tematem. Kliknij na odnośnik "więcej..." aby zobaczyć rozwiązanie zadania.
Uwaga! kolorem czerwonym zaznaczono zadania, których rozwiązania są dostępne dopiero po wykupieniu abonamentu. Jeśli nie masz w pełni aktywnego konta, kliknij tutaj.

01.	Oblicz natężenie pola magnetycznego w środku kwadratu o boku a, utworzonego przez cztery nieskończenie długie przewodniki z prądem. więcej...
02.	Cząstka α wpada w pole magnetyczne o indukcji B=0.02T prostopadle do kierunku wektora indukcji B i zatacza krąg o promieniu r=0.2m. Oblicz energię cząstki (w J i keV). więcej...
03.

Zadanie 1

Treść: Oblicz natężenie pola magnetycznego w środku kwadratu o boku a, utworzonego przez cztery nieskończenie długie przewodniki z prądem.

Dane: I - prąd płynący przez przewodniki a - długość boku danego kwadratu

Szukane: Hc=?

Wzory: 1. Natężenie pola magnetycznego w odległości r od nieskończenie długiego przewodnika przez który prepływa prąd o natężeniu I

Rysunek:

Rozwiązanie:
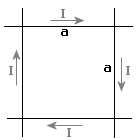
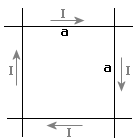
Do obliczenia natężenia pola magnetycznego należy umieścić w przestrzeni wektory H_p pochodzące od poszczególnych przewodników.
Korzystamy przy tym zasady prawej ręki, gdzie kciuk wskazuje kierunek prądu, a zakrzywione palce pokazują kierunek wektorów pola magnetycznego.
Powyższy rysunek przedstwia te wektory i widzimy, że są one zwrócone w jedną stron - za rysunek. Są one idealnie pośrodku kwadratu, lecz dla wyrazistości rysunku są one blisko siebie. Dla przejrzystości zaznaczony jest tylko jeden wektor H_p.
Wiemy oczywiście, że wektory możemy dodawać, więc całkowite natężenie pola będzie sumą poszczególnych wektorów H_p:

Aby obliczyć pojedyncze pole magnetyczne H_p skorzystajmy z podanego na początku wzoru. W naszym przypadku odległością od przewodnika jest

Tak więc otrzymujemy:

Ostatecznym wzorem, a zarazem odpowiedzią na zadanie będzie:

Zadanie 2

Treść: Cząstka α wpada w pole magnetyczne o indukcji B=0.02T prostopadle do kierunku wektora indukcji B i zatacza krąg o promieniu r=0.2m. Oblicz energię cząstki (w J i keV).

Dane: B = 0,02T r = 0,2 m e = 1,6 ^. 10^-19 C qα = 2e mα = 6,644 ^. 10^-27kg 1eV = 1,6 ^. 10^-19J

Szukane: E = ? (w J i keV)

Wzory: Siła dośrodkowa Siła Lorenza Energia kinetyczna Energia kondensatora

Rysunek:

Rozwiązanie:
Skąd się bierze zorza polarna? Pokrótce dlatego, że Ziemia posiada własne pole magnetyczne (niezbędne dla życia), które naładowane cząsteczki pochodzące ze Słońca "ściąga" na bieguny.
Tak samo zachowuje się cząstka α w naszym zadaniu, która wpada w pole magnetyczne o idukcji B. Mając prędkość v zatacza ona krąg o promieniu r.
Siłą zakrzywiającą jest siła Lorenza. Możemy to przedstawić następująco:

czyli:

Skracamy jedno v i wyliczamy prędkość tej cząstki:

Prędkość nie jest tak duża, że trzeba używać wzorów relatywistycznych, dlatego użyjemy zwykłego wzoru na energię:

Podstawiając otrzymaną prędkość dostajemy:

Tak otrzymaliśmy ostateczny wzór na energię tej cząstki. Wiemy, że cząstka α jest po prostu jądrem atomu helu. Tak więc posiada 2 protony i 2 neutrony.
Z tego wnioskujemy, że masa jest równa w przybliżeniu 4 masom protonu (dla dokładności obliczeń masę cząstki odczytujemy z tablic). Jeśli chodzi o ładunek to łatwo się domyślamy, że wyniesie q=+2e.
Teraz już mamy wszystko, aby obliczyć energię. Na początku użyjmy podstawowych jednostek układu SI (czyli ładunek będzie w C):

Sprawdźmy jeszcze jednostkę:

Aby obliczyć energię w eV musimy znaleźć związek między eV oraz J. Skorzystajmy wpierw na wzór podany powyżej na energię przejścia ładunku q przez potencjał U.
Energia ta jest równa 1J, gdy ładunek będzie równy 1C (korzystamy tutaj z energii kondensatora) . A więc przy przejściu tego ładunku przez potencjał 1U więc stwierdzamy, że:

czyli:

Energia wyniesie więc:

Energia cząstki α wynosi E=12,3 ^. 10^-17J (0,77 keV).

Zadanie 3

Treść: W dwóch długich, równoległych i ustawionych do płaszczyzny rysunku przewodnikach płyną prądy w tych samych kierunkach. W jakiej odległości od pierwszego przewodnika indukcja magnetyczna jest równa zero?

Dane: a I1 = I I2 = 2I

Szukane: x - odległość od pierwszego przewodnika, gdzie indukcja się równoważy

Wzory: 1. Indukcja w odległości r od przewodnika, w którym płynie prąd o natężeniu I

Rysunek:

Rozwiązanie:
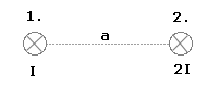
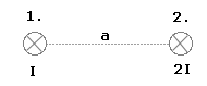
Rozwiązanie polega na znalezieniu miejscu, gdzie indukcja magnetyczna od pierwszego przewodnika równoważy indukcję od drugiego przewodnika.
Rozważamy układ i stwierdzamy, że te miejsce znajduje się na przerywanej linii na rysunku (odległość między dwoma punktami jest zawsze najmniejsza na prostej łączącej te punkty).

Aby określić kierunek i zwrot wektora indukcji pola korzystamy z reguły prawej ręki.
Przez oba przewodniki przepływa prąd skierowany "za kartkę" (czyli monitor :)). Wyobraź sobie ten przewodnik, złap go prawą ręką kciukiem wskazując kierunek prądu (za monitor). Pozostałe palce wskazują teraz kierunek wektora indukcji.

Indukcja B₁ i B₂ mają postać (wykorzystujemy wzór pierwszy, podstawiając odpowiednie dane):

Ponieważ w naszym rozpatrywanym punkcie, indukcja wypadkowa wynosi zero, stwierdzamy więc, że:

Skracamy, co się da i mnożymy "na krzyż":

Ostatecznie:

Szukanym miejscem jest punkt oddalony od pierwszego przewodnika na odległość x = a/3.

---