Fizyka - Zadania - Prąd elektryczny II

Poniżej znajdują się treści zadań związanych z wybranym tematem. Kliknij na odnośnik "więcej..." aby zobaczyć rozwiązanie zadania.
Uwaga! kolorem czerwonym zaznaczono zadania, których rozwiązania są dostępne dopiero po wykupieniu abonamentu. Jeśli nie masz w pełni aktywnego konta, kliknij tutaj.

01.	Ile wynosi natężenie prądu w obwodzie przedstawionym na rysunku? ε1=2V, ε2=9V, R1=2Ω, R2=10Ω, rW=1Ω więcej...
02.	Pięć jednakowych ogniw, każde o SEM ε=6V i oporze wewnętrznym r=3Ω podłączono do oporu R=5Ω, według schematu obok. Ile wynosi natężenie prądu I płynącego przez opór zewnętrzny R? więcej...
03.	Ile wynosi natężenie prądu, płynącego przez opornik R1 (patrz rysunek)? Przyjąć ε1=10V, ε2=5V, r1=1Ω, r2=3Ω, R1=4Ω, R2=3Ω, R3=6Ω, R4=1Ω, R5=2Ω, R6=3Ω, R7=4Ω. więcej...
04.	Ile wynoszą natężenia prądów płynących przez oporniki R2 i R3? Układ jak na rysunku w zadaniu 3, przyjmujemy te same dane. więcej...
05.	Ile wynosi różnica potencjałów między punktem X a punktem Y? Rysunek i dane jak w zadaniu 3. więcej...
06.	Jakie ciepło wydzieli się w całym obwodzie w ciągu czasu t=400s? Rysunek i dane jak w zadaniu 3. więcej...
07.	Do źródła o sile elektromotorycznej ε=28V i oporze wewnętrznym r=0.5Ω dołączono odbiorniki o oporach: R1=3Ω, R2=5Ω R3=8Ω, R4=2.5Ω. Na którym oporniku wydzieli się największa moc? więcej...
08.	Do ogniwa o SEM 6V i oporze wewnętrznym 2Ω podłączono żarówkę o oporze 4Ω. Ile wynosi różnica potencjałów na biegunach tego ogniwa? więcej...
09.	Do ogniwa o sile elektromotorycznej ε=12V i oporze wewnętrznym r podłączono odbiornik o oporze R=5Ω. Woltomierz włączony do obwodu tak, jak na rysunku wskazuje napięcie 10V. Ile wynosi opór wewnętrzny r? więcej...
10.	Ile wynosi napięcie na zaciskach ogniwa, jeżeli opór zewnętrzny obwodu o sile elektromotorycznej ε jest dwa razy większy od oporu wewnętrznego ogniwa? więcej...
11.	Trzy oporniki (R=1Ω) połączono ze źródłem prądu o sile elektromotorycznej ε=12V i oporze wewnętrznym r=2Ω. Jakie natężenie prądu wskaże amperomierz A? Ile wyniosą wskazania woltomierzy? Ile wynosi spadek napięcia na oporze wewnętrznym r? więcej...
12.	Woltomierz V wskazuje 4V. Opór R wynosi 2Ω, siła elektromotoryczna jednego ogniwa 9V, a opór wewnętrzny jednego ogniwa 4Ω. Ile wynosi liczba ogniw połączonych szeregowo? Ile wynosi napięcie na zaciskach baterii? więcej...
13.	W obwodzie SEM ogniw mają wartości ε1=2V, ε2=5V, opory wewnętrzne tych ogniw są równe zeru. Ile wynosi natężenie prądu w obwodzie i w którą stronę jest skierowane? Ile wynoszą potencjały w punktach A, B, C i D? Przyjąć R1=2Ω, R2=1Ω. więcej...
14.	Po zamknięciu klucza K na kondensatorze o pojemności 10mF zgromadził się ładunek 10mC. Oblicz natężenie prądu płynącego w tym obwodzie i siłę elektromotoryczną, jeżeli R=1Ω i r=3Ω? więcej...
15.	n jednakowych ogniw o oporności wewnętrznej r każde, podłączono raz szeregowo, drugi raz równolegle. Ile powinna wynosić oporność zewnętrzna, aby otrzymać w obu przypadkach prąd o tym samym natężeniu? więcej...
16.	Podczas przenoszenia ciała o ciężarze 2200N na wysokość 12m silnik dźwigu elektrycznego przy napięciu 220V pobiera prąd o natężeniu 12A, przy czym podnoszenie trwa 25s. Ile wynosi sprawność silnika? więcej...

Zadanie 1

Treść: Ile wynosi natężenie prądu w obwodzie przedstawionym na rysunku? ε1=2V, ε2=9V, R1=2Ω, R2=10Ω, rW=1Ω

Dane: ε1 = 2 V ε2 = 9 V R1 = 2 Ω R2 = 10 Ω rW = 1 Ω

Szukane: I = ?

Wzory: 1. II prawo Kirchhoffa

Rysunek:

Rozwiązanie:
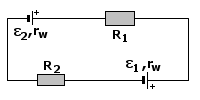
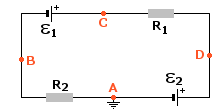
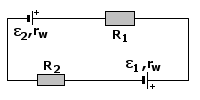
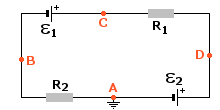
W obwodzie przedstawionym na rysunku siły elektromotoryczne ε₁ i ε₂ są połączone przeciwnie. O kierunku płynięcia prądu I w obwodzie zewnętrznym decyduje więc źródło o większej sile elektromotorycznej. Ponieważ ε₂ > ε₁, więc w obwodzie zewnętrznym prąd płynie od bieguna dodatniego (+) do bieguna ujemnego (-) przez opór R₁, źródło ε₁ i opór R₂.
Aby wyliczyć szukane natężenie prądu, skorzystamy z II prawa Kirchhoffa. Wystartujemy z dowolnego punktu obwodu (np. z A) i przejdziemy cały obwód zgodnie z kierunkiem prądu, aż do chwili, gdy znów znajdziemy się w punkcie wyjścia. Po drodze będziemy notować skoki napięcia na poszczególnych elementach obwodu (oporniki zmniejszają napięcie, podobnie jak siły elektromotoryczne "przeciwnie zwrócone" do kierunku prądu).
Zgodnie z II prawem Kirchhoffa suma tych skoków napięcia jest równa zeru.

Oczywiście dwa powyższe zapisy są równoznaczne, drugi jest bardziej elegancki. ;-)
Z tego wzoru możemy wyliczyć teraz szukane natężenie prądu:

Natężenie prądu wynosi 0.5 A.

Zadanie 2

Treść: Pięć jednakowych ogniw, każde o SEM ε=6V i oporze wewnętrznym r=3Ω podłączono do oporu R=5Ω, według schematu obok. Ile wynosi natężenie prądu I płynącego przez opór zewnętrzny R?

Dane: ε = 6 V r = 3 Ω R = 5 Ω

Szukane: I = ?

Wzory: 1. Natężenie prądu: 2. Szeregowe i równoległe łączenie ogniw.

Rozwiązanie:
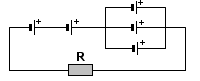
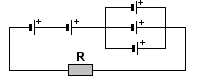
Najpierw rozpatrzymy równoległy układ identycznych ogniw 3 4 5. Zgodnie z zasadami łączenia siła elektromotoryczna wszystkich ogniw równa jest sile elektromotorycznej jednego ogniwa, natomiast całkowity opór wewnętrzny to iloraz oporu wewnętrznego jednego ogniwa przez ilość ogniw:

Teraz rozpatrujemy układ szeregowy ogniw 1 2 345. Wtedy całkowita SEM równa jest sumie poszczególnych SEM, a całkowity opór wewnętrzny równy sumie poszczególnych oporów wewnętrznych, zatem:

Ponieważ mamy tylko jeden opór zewnętrzny R, możemy bez problemu zastosować najprostszy wzór na natężenie prądu I.
Szukane natężenie wynosi:

Natężenie prądu wynosi 1.5 A.

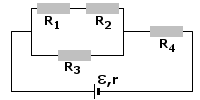
Zadanie 3

Treść: Ile wynosi natężenie prądu, płynącego przez opornik R1 (patrz rysunek)? Przyjąć ε1=10V, ε2=5V, r1=1Ω, r2=3Ω, R1=4Ω, R2=3Ω, R3=6Ω, R4=1Ω, R5=2Ω, R6=3Ω, R7=4Ω.

Dane: ε1 = 10 V ε2 = 5 V r1 = 1 Ω r2 = 3 Ω R1 = 4 Ω R2 = 3 Ω R3 = 6 Ω R4 = 1 Ω R5 = 2 Ω R6 = 3 Ω R7 = 4 Ω

Szukane: I = ?

Wzory: 1. Drugie prawo Kirchhoffa 2. Równoległe łączenie oporników

Rysunek:

Rozwiązanie:
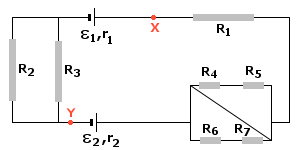
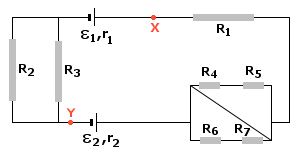
Aby obliczyć prąd całkowity I płynący w obwodzie wykorzystamy II prawo Kirchhoffa.

Należy zaznaczyć, że układ oporów R₄, R₅, R₆, R₇ nie wpływa na wielkość natężenia prądu I. Dzieje się tak dlatego, że połączenie przewodnikiem bezoporowym punktów A i B (patrz rysunek powyżej) spowodowało równość potencjałów elektrycznych na końcach oporników R₄+R₅ i R₆+R₇.
Inaczej mówiąc, nie ma napięcia elektrycznego na tych oporach. Prąd przez nie nie płynie, lecz płynie przez przewód łączący punkty AB.

Ponieważ ε₁ > ε₂, więc kierunek prądu I jest taki jak na rysunku. Zgodnie z II prawem Kirchhoffa suma przyrostów (spadków) potencjałów w całym obwodzie zamkniętym jest równa zeru.
"Obchodząc" obwód należy pamiętać, że poruszając się zgodnie z prądem przesuwamy się w kierunku niższego potencjału (przyrosty potencjału są ujemne), natomiast poruszając się "pod prąd" przesuwamy się w kierunku wyższego potencjału (przyrosty potencjału są dodatnie).

Zaczynając obchodzić obwód w punkcie np. X, zgodnie z kierunkiem prądu mamy:

gdzie

jest oczywiście oporem zastępczym dwóch oporników R₂ i R₃ połączonych równolegle.

Tak więc szukane natężenie prądu wynosi:

Natężenie prądu płynącego przez opornik R₁ wynosi 0.5 A.

Zadanie 4

Treść: Ile wynoszą natężenia prądów płynących przez oporniki R2 i R3? Układ jak na rysunku w zadaniu 3, przyjmujemy te same dane.

Dane: ε1 = 10 V ε2 = 5 V r1 = 1 Ω r2 = 3 Ω R1 = 4 Ω R2 = 3 Ω R3 = 6 Ω R4 = 1 Ω R5 = 2 Ω R6 = 3 Ω R7 = 4 Ω

Szukane: I2 = ? I3 = ?

Wzory: 1. Równoległe łączenie oporników 2. I prawo Kirchhoffa 3. Prawo Ohma:

Rysunek:

Rozwiązanie:
Ponieważ opory R₂ i R₃ połączone są równolegle, to zgodnie z zasadami łączenia oporników napięcia na nich są identyczne:

a co za tym idzie (korzystamy z prawa Ohma):

gdzie I₂ i I₃ oznaczają natężenia prądów płynących przez opory R₂ i R₃.
Zgodnie z pierwszym prawem Kirchhoffa

Przypominam, że natężenie prądu I wyliczyliśmy w poprzednim zadaniu i wynosiło ono:

Teraz już możemy wyliczyć szukane wartości. Z (1) i (2) wyprowadzamy np I₂:

Przyrównujemy te wzory i otrzymujemy wartość I₃:

Wyliczenie I₂ nie powinno sprawić trudności:

Natężenie prądu płynącego przez drugi opornik wynosi 1/3 A, a przez trzeci opornik 1/6 A.

Zadanie 5

Treść: Ile wynosi różnica potencjałów między punktem X a punktem Y? Rysunek i dane jak w zadaniu 3.

Dane: ε1 = 10 V ε2 = 5 V r1 = 1 Ω r2 = 3 Ω R1 = 4 Ω R2 = 3 Ω R3 = 6 Ω R4 = 1 Ω R5 = 2 Ω R6 = 3 Ω R7 = 4 Ω

Szukane: ΔV = VX - VY = ?

Wzory: 1. Równoległe łączenie oporników 2. Prawo Ohma

Rysunek:

Rozwiązanie:
Przed rozpoczęciem rozwiązywania tego zadania warto zapoznać się z zadaniem 3 i zadaniem 4.

I sposób
"Przechodzimy" od punktu Y do punktu X zgodnie z kierunkiem prądu. Pamiętamy o tym, że prąd płynie od potencjału wyższego do potencjału niższego. W punkcie Y jest jakiś potencjał V_Y i notujemy przyrosty potencjałów aż "dojdziemy" do punktu X:

Uwaga!
Ponieważ układ oporników R₂ i R₃ jest równoległy, to zgodnie z zasadami łączenia oporników napięcie jest tam identyczne:

co pociąga za sobą (korzystamy z prawa Ohma):

Tak więc do wyliczenia różnicy potencjałów możemy wykorzystać którąkolwiek część równości. Zatem prawdziwe są wzory:

Wartości I, I₂, I₃ znaleźliśmy w zadaniach 3 i 4.

II sposób
Drugi sposób jest bardzo podobny do pierwszego, jednak z punktu X do punktu Y będziemy przechodzić "pod prąd". Wtedy przyrosty (spadki lub wzrosty) potencjałów będą wynosić:

Różnica potencjałów między punktem X a Y wynosi 8.5 V.

Zadanie 6

Treść: Jakie ciepło wydzieli się w całym obwodzie w ciągu czasu t=400s? Rysunek i dane jak w zadaniu 3.

Dane: ε1 = 10 V ε2 = 5 V r1 = 1 Ω r2 = 3 Ω R1 = 4 Ω R2 = 3 Ω R3 = 6 Ω R4 = 1 Ω R5 = 2 Ω R6 = 3 Ω R7 = 4 Ω t = 400 s

Szukane: W = ?

Wzory: 1. Praca prądu stałego (ciepło Joule'a-Lenza): 2. Szeregowe i równoległe łączenie oporników

Rysunek:

Rozwiązanie:
Przed rozpoczęciem rozwiązywania tego zadania warto zapoznać się z zadaniem 3, w którym znaleźliśmy wartość natężenia prądu I:

Aby znaleźć ciepło W (czasami oznaczane przez Q), musimy znać opór wypadkowy (zastępczy), przez który przepływa prąd I. Oczywiście ważne jest, żeby prąd ten płynął przez wszystkie opory, które w naszym obwodzie odgrywają jakąś rolę (pamiętamy, że przez oporniki 4, 5, 6 i 7 prąd nie płynie - patrz zadanie 3).
Szukamy więc oporu zastępczego R, który wynosi:

Skorzystaliśmy z zasad łączenia szeregowego i równoległego oporników.
Mając opór R, natężenie I oraz czas t, skorzystamy z alternatywnego wzoru na pracę:

Szukane ciepło (wydzielone zgodnie z prawem Joule'a-Lenza) jest równe:

W całym obwodzie w czasie t wydzieli się ciepło w ilości równej 1000 J.

Zadanie 7

Treść: Do źródła o sile elektromotorycznej ε=28V i oporze wewnętrznym r=0.5Ω dołączono odbiorniki o oporach: R1=3Ω, R2=5Ω R3=8Ω, R4=2.5Ω. Na którym oporniku wydzieli się największa moc?

Dane: R1 = 3 Ω R2 = 5 Ω R3 = 8 Ω R4 = 2.5 Ω ε = 28 V r = 0.5 Ω

Szukane: P1 = ? P2 = ? P3 = ? P4 = ?

Wzory: 1. Natężenie prądu: 2. Moc prądu: 3. Prawo Ohma: 4. I prawo Kirchhoffa 5. Szeregowe i równoległe łączenie oporników

Rozwiązanie:
Natężenie prądu w naszym układzie wynosi:

Mamy znaleźć moce wydzielane na poszczególnych opornikach (odbiornikach). Suma tych mocy, da nam tzw. moc użyteczną, którą wyliczamy również ze wzoru:

W obu tych wzorach R oznacza opór zastępczy całego układu. Nie pozostaje nam nic innego, jak go wyliczyć:

Stąd natężenie oraz moc użyteczna wynoszą:

Moc na oporze czwartym jest równa

Aby znaleźć pozostałe moce, musimy rozważyć równoległy układ oporników 12 i 3, czyli znaleźć natężenia prądu I₁₂ oraz I₃ przepływającego przez te oporniki.
W takim układzie mamy stałe napięcie

co pociąga za sobą fakt, że (korzystamy z prawa Ohma):

a z I prawa Kirchhoffa:

Z dwóch powyższych wzorów wyprowadzamy np. I₁₂:

I przyrównując te wzory otrzymamy I₃:

Wyliczenie I₁₂ nie powinno sprawić problemu

Mając natężenie I₃, możemy znaleźć moc na oporniku trzecim:

Zauważmy, że na opornikach 1 i 2 wydzielona moc ma wartość

Czyli widzimy już, że największa moc wydzieli się na oporniku czwartym.
Jeżeli jesteśmy uparci i chcemy wyliczyć wartości P₁ i P₂, to:

Największa moc wydzieli się na oporniku czwartym i wynosi ona 40 watów.

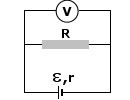
Zadanie 8

Treść: Do ogniwa o SEM 6V i oporze wewnętrznym 2Ω podłączono żarówkę o oporze 4Ω. Ile wynosi różnica potencjałów na biegunach tego ogniwa?

Dane: ε = 6 V r = 2 Ω R = 4 Ω

Szukane: ΔV = ?

Wzory: 1. Natężenie prądu 2. Prawo Ohma

Rysunek:

Rozwiązanie:
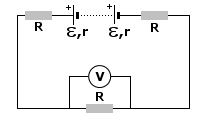
Spójrzmy na dwa powyższe rysunki. One tak naprawdę przedstawiają to samo. Drugi rysunek stosowaliśmy, dopóki nie dowiedzieliśmy się, że jest coś takiego jak siła elektromotoryczna ogniwa (SEM). Czym to się jednak różni?
Siła elektromotoryczna uwzględnia opór wewnętrzny ogniwa lub układu. Jeśli mi nie wierzycie, to przypomnijcie sobie wzór na natężenie prądu

Czyli wychodzi, że napięcie to nic innego jak SEM minus opór wewnętrzny. Dlatego to w pierwszym dziale pomijaliśmy opór wewnętrzny, uznając za źródło prądu napięcie panujące w obwodzie. Ale teraz jesteśmy mądrzejsi. I to wykorzystamy!

Mamy jakiś obwód. Naszym opornikiem zewnętrznym R jest żarówka, dodatkowo mamy opór wewnętrzny r. Szukamy różnicy potencjałów, czyli napięcia na biegunach baterii. To napięcie nazywamy też napięciem użytecznym.
Jak je znaleźć? No właśnie:

Nie mamy natężenia I, więc je znajdujemy:

Tak więc szukane napięcie (czyli różnica potencjałów):

Różnica potencjałów na biegunach ogniwa wynosi 4 V.

Zadanie 9

Treść: Do ogniwa o sile elektromotorycznej ε=12V i oporze wewnętrznym r podłączono odbiornik o oporze R=5Ω. Woltomierz włączony do obwodu tak, jak na rysunku wskazuje napięcie 10V. Ile wynosi opór wewnętrzny r?

Dane: ε = 12 V R = 5 Ω U = 10 V

Szukane: r = ?

Wzory: 1. Natężenie prądu 2. Prawo Ohma 3. Napięcie użyteczne

Rozwiązanie:
To zadanie jest podobne do zadania poprzedniego (ósmego). Mamy baterię o SEM ε i oporze wewnętrznym r (opór wewnętrzny teraz ma bateria, a nie obwód). Mamy też napięcie użyteczne panujące w obwodzie, czyli te, które wykrywa woltomierz podłączony do opornika (odbiornika).
Zatem podobnie jak poprzednio:

Stąd wyliczymy nasz szukany opór wewnętrzny

Potrzebujemy jeszcze znaleźć natężenie prądu I płynącego w obwodzie. W tym celu możemy skorzystać z jednego ze dwóch wzorów:

Pierwszy wzór, to wzór na natężenie z uwzględnieniem SEM, a drugi z uwzględnieniem napięcia użytecznego. Tak naprawdę te wzory przedstawiają nam to samo, my jednak skorzystamy z tego drugiego, bo nie ma w nim niewiadomej r - ułatwi to nam liczenie.
Tak więc:

Opór wewnętrzny ogniwa wynosi 1 Ω.

Zadanie 10

Treść: Ile wynosi napięcie na zaciskach ogniwa, jeżeli opór zewnętrzny obwodu o sile elektromotorycznej ε jest dwa razy większy od oporu wewnętrznego ogniwa?

Dane: R = 2 r ε

Szukane: U = ?

Wzory: 1. Natężenie prądu 2. Napięcie użyteczne

Rozwiązanie:
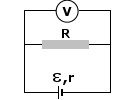
W zadaniu daną mamy siłę elektromotoryczną (SEM) oraz zależność pomiędzy oporem wewnętrznym a oporem zewnętrznym. Zanim poszukamy szukanej wartości napięcia użytecznego, spróbujemy określić wartość siły elektromotorycznej przekształcając wzór

Tak więc

Z poprzednich zadań wiemy, że napięcie użyteczne w obwodzie wynosi

Wykorzystajmy powyższe:

Hm... nie mamy wartości natężenia I. Ale właśnie, korzystając z (1) zauważymy, że

A przecież wartość SEM mamy daną. :)

Napięcie na zaciskach ogniwa wynosi 2/3 ε.

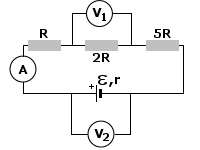
Zadanie 11

Treść: Trzy oporniki (R=1Ω) połączono ze źródłem prądu o sile elektromotorycznej ε=12V i oporze wewnętrznym r=2Ω. Jakie natężenie prądu wskaże amperomierz A? Ile wyniosą wskazania woltomierzy? Ile wynosi spadek napięcia na oporze wewnętrznym r?

Dane: R = 1 Ω r = 2 Ω ε = 12 V

Szukane: I = ? U1 = ? U2 = ? Ir = ?

Wzory: 1. Natężenie prądu 2. Prawo Ohma 3. Szeregowe łączenie oporników 4. Napięcie użyteczne

Rozwiązanie:
Zaczynamy!
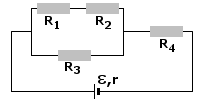
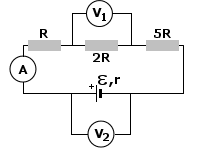
Wyliczenie natężenia prądu I na tym etapie nie powinno już sprawiać trudności, nieprawdaż? Wystarczy tylko podstawić dane do wzoru. Zauważ, że wzór ten mówi o oporze zewnętrznym całkowitym (zastępczym), tak więc najpierw korzystając z zasad szeregowego łączenia oporników wyliczamy opór zastępczy:

Natężenie prądu wynosi

Teraz zajmiemy się woltomierzami. Najpierw tym drugim.
Wskazuje on wartość napięcia użytecznego, ponieważ obejmuje kawałek obwodu, w którym jest bateria (SEM) oraz jej opór wewnętrzny, który powoduje spadek napięcia. Zatem woltomierz drugi wskazuje napięcie

Zauważmy, że wartość I r charakteryzuje nam spadek napięcia na oporze wewnętrznym, a więc:

Pozostaje nam znaleźć wartość napięcia wskazywaną przez woltomierz pierwszy. Nie jest to trudne. Mamy bowiem układ szeregowy oporników, a więc przez każdy z nich przepływa ten sam prąd o natężeniu I. Mając opór 2R tego opornika i korzystając z prawa Ohma możemy wyliczyć szukane napięcie

Amperomierz wskazuje natężenie prądu równe 1.2 A, woltomierz pierwszy wskazuje napięcie 2.4 V, drugi 9.6 V, natomiast spadek napięcia na oporze wewnętrznym wynosi 2.4 V.

Zadanie 12

Treść: Woltomierz V wskazuje 4V. Opór R wynosi 2Ω, siła elektromotoryczna jednego ogniwa 9V, a opór wewnętrzny jednego ogniwa 4Ω. Ile wynosi liczba ogniw połączonych szeregowo? Ile wynosi napięcie na zaciskach baterii?

Dane: U = 4 V R = 2 Ω ε = 9 V r = 4 Ω

Szukane: n = ? UUŻ = ?

Wzory: 1. Szeregowe łączenie ogniw 2. Napięcie użyteczne 3. Natężenie prądu 4. Prawo Ohma 5. Szeregowe łączenie oporników

Rozwiązanie:
W tym dziale nie można zapomnieć o wzorze na natężenie prądu. Spójrzmy na niego:

R to w naszym przypadku opór zastępczy wszystkich oporników zewnętrznych, a ponieważ są one połączone szeregowo, to możemy śmiało stwierdzić, że opór zewnętrzny wynosi 3R. Mamy tu jednak do czynienia jeszcze z układem n ogniw. Gdy zapoznamy się z zasadami łączenia ogniw stwierdzimy, że wzór na natężenie powinien wyglądać w sposób następujący:

Ale mamy dwie niewiadome - szukane n oraz natężenie prądu I. Skąd wziąć tę drugą wartość? Ano zauważmy, że mamy daną przez woltomierz wartość napięcia przy jednym z oporników oraz wartość tego oporu. A korzystając z prawa Ohma, możemy wtedy otrzymać natężenie

Przyrównujemy dwa powyższe wzory i znajdujemy wartość n:

Sprawdzenie jednostki pozostawiam jako proste ćwiczenie. :)

Potrzebujemy jeszcze znaleźć napięcie na zaciskach baterii ogniw. Jest to tzw. napięcie użyteczne, które niejednokrotnie liczyliśmy ze wzoru:

A ponieważ mamy układ n ogniw, to wzór przyjmie postać:

Natężenie prądu I zastępujemy którymś z powyższych wzorów i otrzymujemy:

W układzie jest 12 ogniw połączonych szeregowo, a napięcie na zaciskach układu ogniw wynosi 12 V.

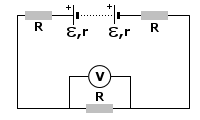
Zadanie 13

Treść: W obwodzie SEM ogniw mają wartości ε1=2V, ε2=5V, opory wewnętrzne tych ogniw są równe zeru. Ile wynosi natężenie prądu w obwodzie i w którą stronę jest skierowane? Ile wynoszą potencjały w punktach A, B, C i D? Przyjąć R1=2Ω, R2=1Ω.

Dane: R1 = 2 Ω R2= 1 Ω ε1 = 2 V ε2 = 5 V

Szukane: I = ? VA = ? VB = ? VC = ? VD = ?

Wzory: 1. II prawo Kirchhoffa

Rozwiązanie:
Na początku określimy, w którą stronę płynie prąd. Zauważmy, że

Tak więc kierunek prądu jest odwrotny do ruchu wskazówek zegara.
I teraz możemy skorzystać z drugiego prawa Kirchhoffa, które mówi, że jak okrążymy cały obwód to suma przyrostów (spadków lub wzrostów) napięć jest równa zeru. Wybieramy sobie dowolny punkt obwodu (ja biorę punkt A) i okrążamy go zgodnie lub niezgodnie z kierunkiem przepływu prądu. Ja tym razem okrążę obwód w kierunku przeciwnym do kierunku prądu, a więc będę szedł od punktu A do punktu A zgodnie z kierunkiem ruchu wskazówek zegara. Wtedy oporniki powodują przyrost napięcia, a więc:

Zauważ, że bateria pierwsza powoduje wzrost napięcia, a druga jego spadek. Liczymy dalej szukane natężenie I:

Teraz będziemy znajdować potencjały w punktach A, B, C i D.
Co oznacza ta "choinka" przy punkcie A? Uziemienie. Obwód w punkcie A jest uziemiony, czyli potencjał w nim wynosi zero. I to trzeba zapamiętać. I właśnie korzystając z wartości potencjału w tym punkcie, będziemy wyliczać potencjał w pozostałych.
W punkcie B mamy potencjał (idziemy przeciwnie do kierunku prądu)

...w punkcie D (zgodnie z kierunkiem prądu)...

...a w punkcie C (zgodnie z kierunkiem prądu, zaczynamy z punktu D):

Natężenie prądu w obwodzie wynosi 1 A, a potencjały w oznaczonych punktach wynoszą:

Zadanie 14

Treść: Po zamknięciu klucza K na kondensatorze o pojemności 10mF zgromadził się ładunek 10mC. Oblicz natężenie prądu płynącego w tym obwodzie i siłę elektromotoryczną, jeżeli R=1Ω i r=3Ω?

Dane: C = 10 mF = 0.01 F Q = 10 mC = 0.01 C R = 1 Ω r = 3 Ω

Szukane: I = ? ε = ?

Wzory: 1. Pojemność elektryczna 2. Natężenie prądu 3. Prawo Ohma 4. Szeregowe łączenie oporników

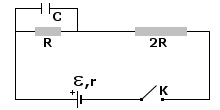
Rozwiązanie:
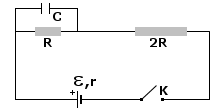
Po zamknięciu klucza K kondensator o pojemności C naładuje się ładunkiem Q. Przekształcając wzór na pojemność elektryczną otrzymamy napięcie panujące na oporniku R:

A teraz mając napięcie U i wartość oporu R, możemy korzystając z prawa Ohma wyliczyć natężenie prądu płynącego przez ten opornik. Pamiętajmy, że przez kondensator prąd nie płynie, więc pozostaje nam szeregowy układ oporników, w którym wszędzie natężenie prądu jest identyczne

Wartość siły elektromotorycznej znajdziemy przekształcając wzór na natężenie. Będzie więc to iloczyn natężenia prądu I przez sumę oporu wewnętrznego i oporu zewnętrznego (całkowitego). Ponieważ jest to układ szeregowy, to opór zastępczy będzie równy:

Obliczamy SEM:

Natężenie prądu płynącego w obwodzie wynosi 1 A, zaś siła elektromotoryczna (SEM) ma wartość 6 V.

Zadanie 15

Treść: n jednakowych ogniw o oporności wewnętrznej r każde, podłączono raz szeregowo, drugi raz równolegle. Ile powinna wynosić oporność zewnętrzna, aby otrzymać w obu przypadkach prąd o tym samym natężeniu?

Dane: n r

Szukane: R = ?

Wzory: 1. Szeregowe i równoległe łączenie ogniw

Rozwiązanie:
Wzór na natężenie prądu ma postać:

Jeżeli połączymy szeregowo n ogniw, to ich opór wewnętrzny oraz siła elektromotoryczna wzrośnie n razy.

Gdy połączymy te ogniwa równolegle, to opór wewnętrzny zmaleje n razy, a siła elektromotoryczna nie zmieni się.

Przyrównujemy oba wzory. Jak widzimy trudność w zadaniu polega tylko na tym, żeby wyprowadzić wzór na R. Ale i to jest łatwe:

Aby natężenie prądu nie zmieniło się, należy wziąć opór zewnętrzny równy oporowi wewnętrznemu.

Zadanie 16

Treść: Podczas przenoszenia ciała o ciężarze 2200N na wysokość 12m silnik dźwigu elektrycznego przy napięciu 220V pobiera prąd o natężeniu 12A, przy czym podnoszenie trwa 25s. Ile wynosi sprawność silnika?

Dane: F = 2200 N h = 12 m U = 220 V I = 12 A t = 25 s

Szukane: η = ?

Wzory: 1. Moc prądu stałego 2. Praca 3. Moc 4. Sprawność

Rozwiązanie:
To jest takie proste zadanie na poznanie tego, czym jest sprawność.
Parametry prądu stałego (napięcie, natężenie) będą nam określać moc maksymalną, jaką może osiągnąć dźwig. Natomiast parametry dynamiczne (wysokość, ciężar, czas) określą nam tzw. moc użytkową, czyli moc, jaką dźwig osiągnął w rzeczywistości. Stosunek mocy użytkowej do mocy maksymalnej określa nam sprawność.

Moc na podstawie prądu stałego:

A jak znaleźć moc używając wartości z dynamiki?

Trzeba więc znaleźć wartość pracy. Zakładamy, że przesunięcie i siła ciężkości mają ten sam kierunek i zwrot. Wtedy kąt α będzie równy zero, a cosinus takiego kąta ma wartość 1. Zatem praca

Znajdujemy teraz wartość mocy użytkowej

Sprawność wynosi więc:

Sprawność silnika dźwigu wynosi 40 %.

---