Z. Kąkol-Notatki do Wykładu z Fizyki

22-1

Wykład 22

22. Pole magnetyczne, indukcja elektromagnetyczna

22.1

Prawo Ampera

Chcemy teraz znaleźć pole magnetyczne wytwarzane przez powszechnie występują-

ce rozkłady prądów, takich jak przewodniki prostoliniowe, cewki itd.

Pole magnetyczne prezentujemy graficznie rysując

tzw.

linie pola magnetycznego

czyli linie wektora indukcji

magnetycznej. Na rysunku pokazane są linie pola magne-
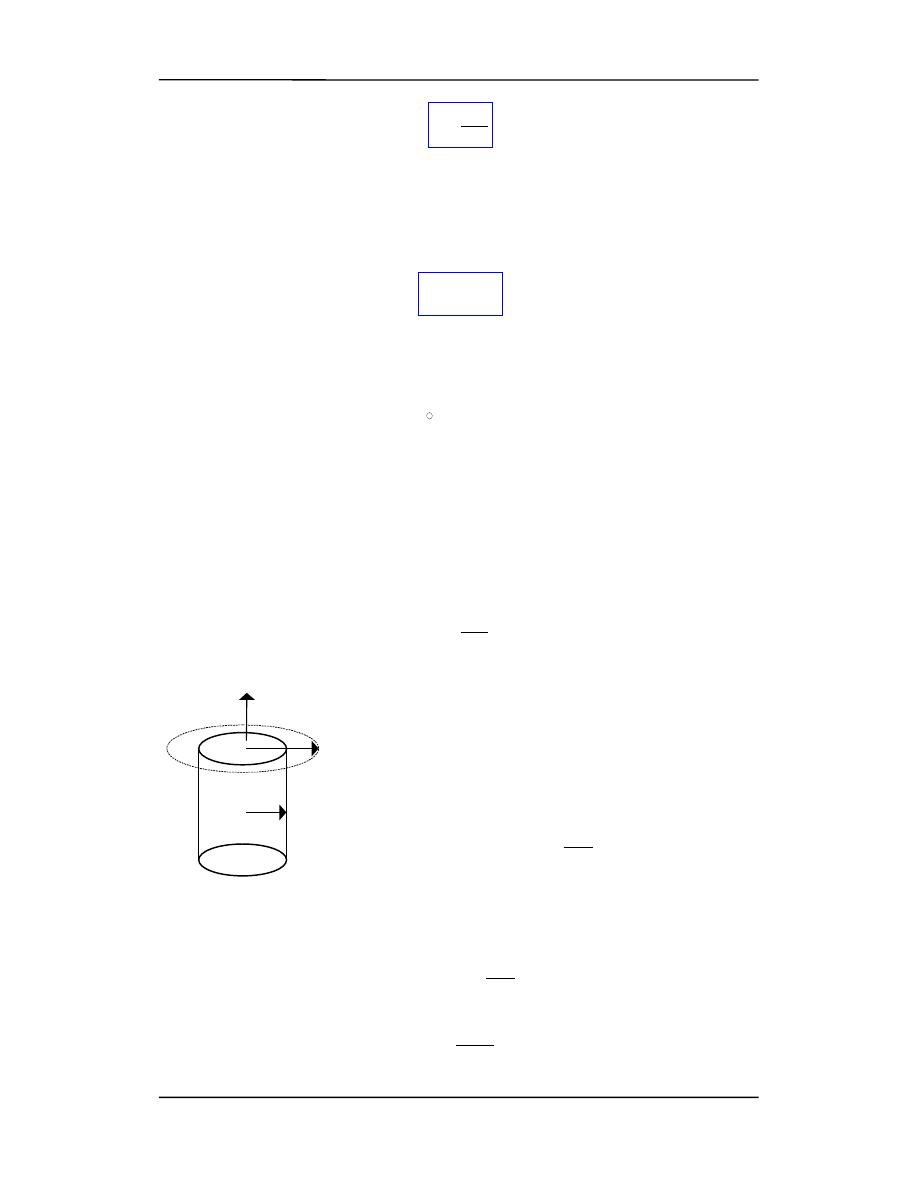
tycznego wokół prostoliniowego przewodnika z prądem.
Wektor B jest styczny do tych linii pola w każdym punk-
cie.

Linie pola B wytwarzanego przez przewodnik są

za-

mkniętymi

współśrodkowymi okręgami w płaszczyźnie

prostopadłej do przewodnika

. To, że linie pola B są za-

mknięte stanowi fundamentalną różnicę między polem
magnetycznym i elektrycznym, którego linie zaczynają się
i kończą na ładunkach.

Zwrot wektora indukcji B wokół przewodnika wyzna-

czamy stosując następującą zasadę: Jeśli kciuk prawej ręki
wskazuje kierunek prądu I, to zgięte palce wskazują kie-

runek B (linie pola B krążą wokół prądu).
Żeby obliczyć pole B potrzeba nam "magnetycznego" odpowiednika prawa Gaussa.
Związek między prądem i polem B jest wyrażony poprzez

prawo Ampera

.

Zamiast sumowania (całki) E po zamkniętej powierzchni, w prawie Ampera sumujemy
(całkujemy) po zamkniętym konturze (całkę krzywoliniową). Taka całka dla pola E
równała się wypadkowemu ładunkowi wewnątrz powierzchni, a w przypadku pola B
jest równa całkowitemu prądowi otoczonemu przez kontur, co zapisujemy

∫

=

I

0

d

µ

l

B

(22.1)

gdzie

µ

0

= 4

π·10

-7

Tm/A, jest

przenikalnością magnetyczną próżni

. Tak jak w przypad-

ku prawa Gaussa wynik był prawdziwy dla dowolnej powierzchni zamkniętej tak dla
prawa Ampera wynik nie zależy od kształtu konturu zamkniętego

Przykład 1

Obliczmy pole wokół nieskończenie długiego prostoliniowego
przewodnika w odległości r od niego. Z prawa Ampera wynika,
że dla konturu kołowego (rysunek obok)

B2

πr = µ

0

I

Stąd

I

r

Z. Kąkol-Notatki do Wykładu z Fizyki

22-2

r

I

B

π

µ
2

0

=

(22.2)

22.2

Strumień magnetyczny

Tak jak liczyliśmy strumień dla pola E (liczbę linii przechodzących przez po-

wierzchnię S) tak też obliczamy strumień pola B

∫

=

S

B

s

B d

φ

(22.3)

Ponieważ linie pola B są zamknięte więc strumień przez zamkniętą powierzchnię musi
być równy zeru

(tyle samo linii wchodzi co wychodzi).

∫

=

S

0

d s

B

22.3

Przykładowe rozkłady prądów

22.3.1 Pręt (przewodnik)

Na zewnątrz pręta (r > R) znamy już pole B.

r

I

B

π

µ
2

0

=

Pole to jest takie jakby cały prąd płynął przez środek pręta
(analogie do rozkładu ładunków).
Jeżeli chcemy obliczyć pole wewnątrz pręta to wybieramy
kontur kołowy o r < R.
Wewnątrz konturu przepływa prąd i będący tylko częścią
całkowitego prądu I

2

2

R

r

I

i

π

π

=

Stąd

B2

πr = µ

0

i

2

2

0

2

R

r

I

r

B

π

π

µ

π

=

Czyli

2

0

2 R

Ir

B

π

µ

=

I

r

R

Z. Kąkol-Notatki do Wykładu z Fizyki

22-3

22.3.2 Cewka (solenoid)

Solenoidem

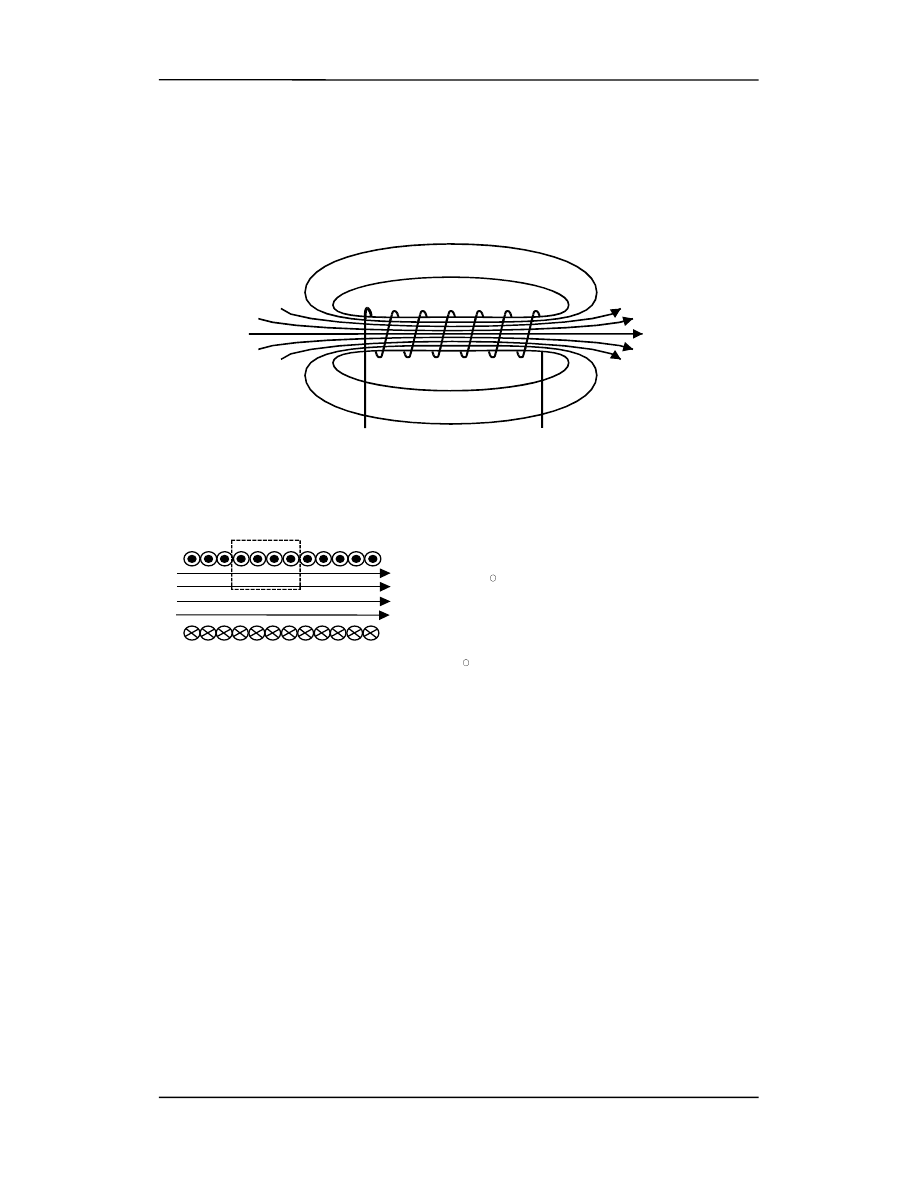
nazywamy cewkę składającą się z dużej liczby zwojów. Linie pola

magnetycznego solenoidu są pokazane schematycznie na rysunku poniżej. Jak widać
pole wewnątrz solenoidu jest jednorodne, a na zewnątrz praktycznie równe zeru.

Jeżeli zwoje solenoidu stykają się ze sobą wówczas możemy rozpatrywać solenoid jako
układ połączonych szeregowo prądów kołowych (rysunek).

Do obliczenia pola wytwarzanego przez sole-
noid zastosujemy prawo Ampera, dla konturu
pokazanego na rysunku obok.

Całkę

∫

l

B d przedstawimy jako sumę czte-

rech całek

∫

∫

∫

∫

∫

+

+

+

=

a

d

d

c

c

b

b

a

l

B

l

B

l

B

l

B

l

B

d

d

d

d

d

Druga i czwarta całka są równe zeru bo B

⊥

l. Trzecia całka jest też równa zero ale to

dlatego, że B = 0 na zewnątrz solenoidu. Tak więc niezerowa jest tylko całka pierwsza
i równa

∫

=

b

a

h

B

l

B d

gdzie h jest długością odcinka ab.
Teraz obliczmy prąd obejmowany przez kontur.
Jeżeli cewka ma n zwojów na jednostkę długości to wewnątrz konturu jest nh zwojów
czyli całkowity prąd przez kontur wynosi:

I = I

0

nh

gdzie I

0

jest prądem przepływającym przez cewkę (przez pojedynczy zwój).

Z prawa Ampera otrzymujemy więc:

a

b

c

d

B

Z. Kąkol-Notatki do Wykładu z Fizyki

22-4

Bh =

µ

0

I

0

nh

czyli

B =

µ

0

I

0

n

(22.4)

22.3.3 Dwa przewodniki równoległe

Dwa przewodniki równoległe umieszczone w odległości d. Płyną w nich prądy I

a

i I

b

odpowiednio.

Przewodnik a wytwarza w swoim otocze-
niu pole

d

I

B

a

a

π

µ

2

0

=

W tym polu znajduje się przewodnik b, w
którym przepływa prąd I

b

. Na odcinek l

tego przewodnika działa siła

d

I

I

l

lB

I

F

b

a

a

b

b

π

µ

2

0

=

=

(22.5)

Zwrot siły widać na rysunku.
To rozumowanie można "odwrócić" za-

czynając od przewodnika b. Wynik jest ten sam.

Fakt oddziaływania przewodników równoległych wykorzystano przy definicji ampe-

ra. Załóżmy, że d = 1m oraz, że I

a

= I

b

= I. Jeżeli dobierzemy tak prąd aby siła przycią-

gania przewodników, na 1 m ich długości, wynosiła 2·10

-7

N to mówimy, że natężenie

prądu jest równe

1 amperowi

.

22.4

Prawo Biota-Savarta

Istnieje inne równanie, zwane

prawem Biota-Savarta

, które pozwala obliczyć B

z rozkładu prądu. Oczywiście to prawo i prawo Ampera muszą być matematycznie rów-
noważne. Prawo Ampera jest jednak "łatwe" w stosowaniu tylko gdy rozkłady prądów
są na tyle symetryczne, że obliczenie odpowiedniej całki nie jest trudne. Gdy rozkład
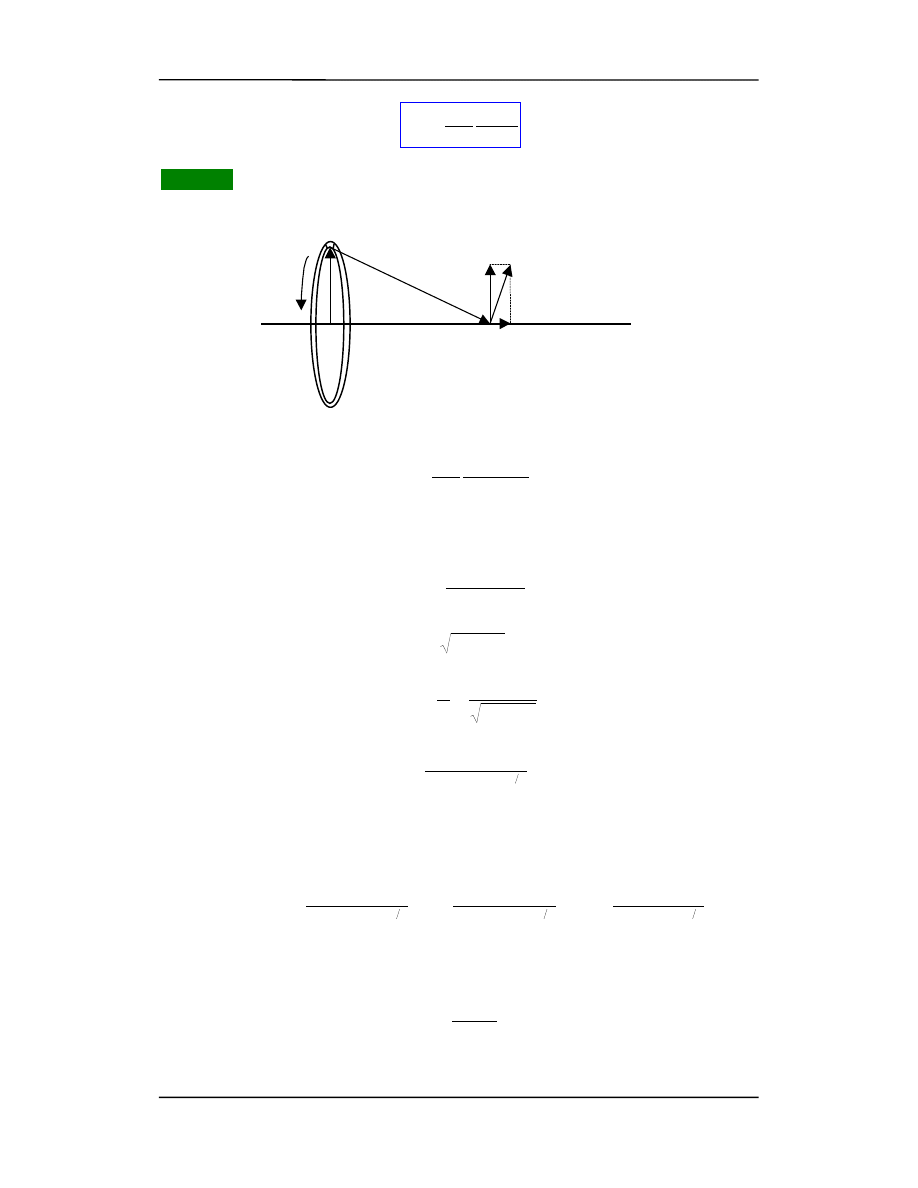
prądów jest skomplikowany (nie znamy jego symetrii) to dzielimy prądy na nieskończe-
nie małe elementy (rysunek) i stosując prawo Biota-Savarta obliczamy pole od takich

elementów, a następnie sumujemy je (całkujemy)
żeby uzyskać wypadkowy wektor B.
Wartość liczbowa dB zgodnie z prawem Biota-
Savarta wynosi

2

0

sin

d

4

d

r

l

I

B

θ

π

µ

=

a zapisane w postaci wektorowej

d

i

a

i

b

F

B

a

l

a

b

r

dl

I

θ

dB

Z. Kąkol-Notatki do Wykładu z Fizyki

22-5

3

0

d

4

d

r

I

r

l

B

×

=

π

µ

(22.6)

Przykład 2

Obliczmy pole B na osi kołowego przewodnika z prądem.

Z prawa B -S otrzymujemy

2

0

90

sin

d

4

d

r

l

I

B

o

π

µ

=

oraz

α

cos

d

d

B

B

II

=

Z tych równań otrzymujemy

2

0

4

d

cos

d

r

l

I

B

II

π

α

µ

=

Ponadto

2

2

x

R

r

+

=

oraz

2

2

cos

x

R

R

r

R

+

=

=

α

Podstawiając otrzymujemy

l

x

R

IR

B

II

d

)

(

4

d

2

3

2

2

0

+

=

π

µ

Zauważmy, że wielkości I, R, x są takie same dla wszystkich elementów prądu.
Całkujemy, żeby obliczyć B (wyłączając stałe czynniki przed znak całki)

2

3

2

2

2

0

2

3

2

2

0

2

3

2

2

0

)

(

2

)

2

(

)

(

4

d

)

(

4

d

x

R

IR

R

x

R

IR

l

x

R

IR

B

B

II

+

=

+

=

+

=

=

∫

∫

µ

π

π

µ

π

µ

Dla x >> R dostajemy

3

2

0

2x

IR

B

µ

=

dB

⊥

dB

II

dB

R

x

r

α

I

Z. Kąkol-Notatki do Wykładu z Fizyki

22-6

22.5

Indukcja elektromagnetyczna

22.5.1 Prawo Faradaya

Zjawisko

indukcji elektromagnetycznej

polega na powstawaniu prądów elektrycz-

nych w zamkniętym obwodzie podczas przemieszczania się względem siebie źródła po-
la magnetycznego i tego zamkniętego obwodu. Mówimy, że w obwodzie jest

indukowa-

na siła elektromotoryczna

(SEM indukcji), która wywołuje przepływ

prądu indukcyjne-

go

.

Prawo indukcji Faradaya stosuje się do trzech różnych sytuacji fizycznych:

•

Nieruchoma pętla, względem której porusza się źródło pola magnetycznego (mamy
tzw. elektryczną SEM).

•

Przewód w kształcie pętli porusza się w obszarze pola magnetycznego (magnetyczna
SEM).

•

Nieruchoma pętla i nieruchome źródło pola magnetycznego lecz zmienia się prąd,
który jest źródłem pola magnetycznego (także elektryczna SEM).

Na podstawie obserwacji Faraday doszedł do wniosku, że czynnikiem decydującym jest

szybkość zmian

strumienia magnetycznego

φ

B

. Ilościowy związek przedstawia prawo

Faradaya

t

B

d

d

φ

ε

−

=

(22.7)

Jeżeli mamy obwód złożony z N zwojów to

t

N

B

d

d

φ

ε

−

=

22.5.2 Reguła Lenza

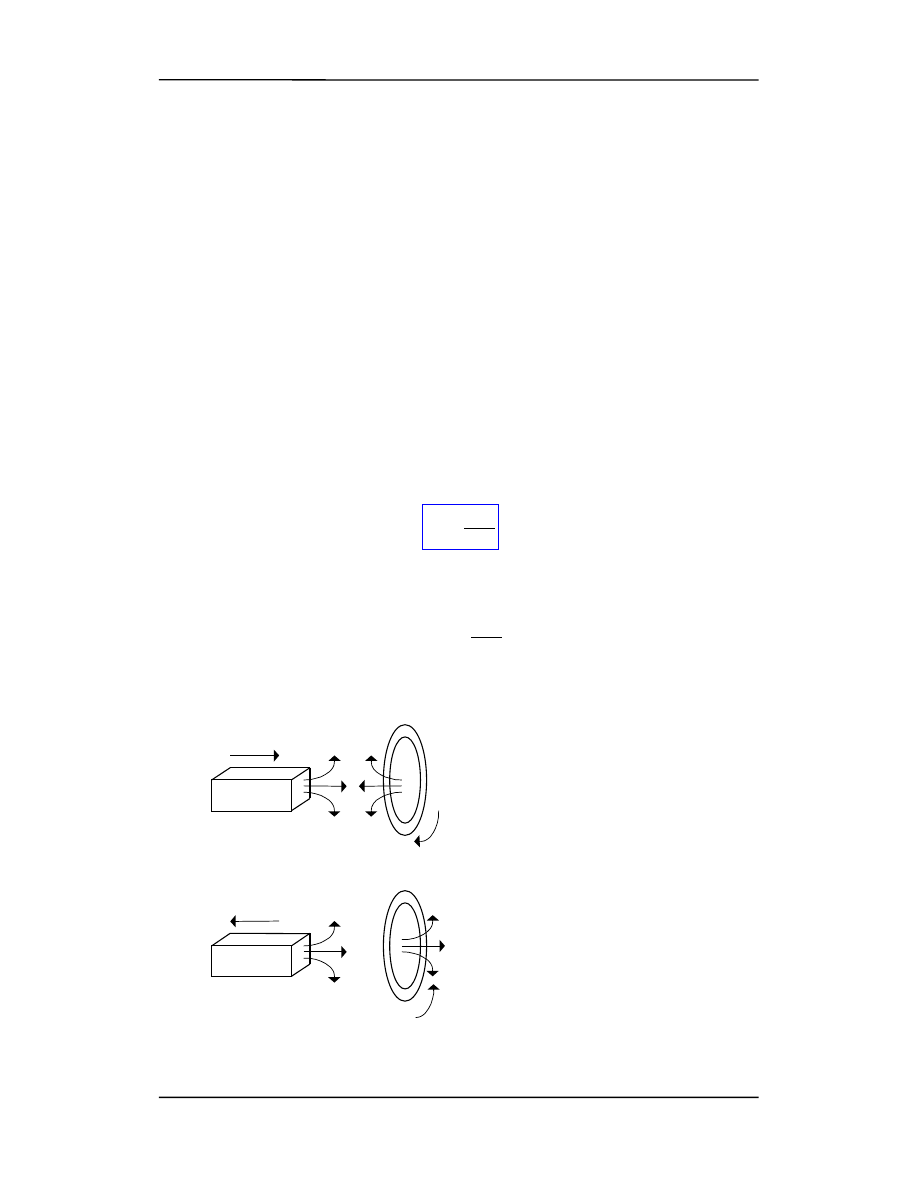
Prąd indukowany ma taki kieru-

nek, że przeciwstawia się zmianie,
która go wywołała. Kierunek prądu
indukowanego w pętli (rysunek
obok) zależy od tego czy strumień
rośnie czy maleje (zbliżamy czy od-
dalamy magnes). Ta reguła dotyczy
prądów indukowanych.

S

N

v

I

S

N

v

I