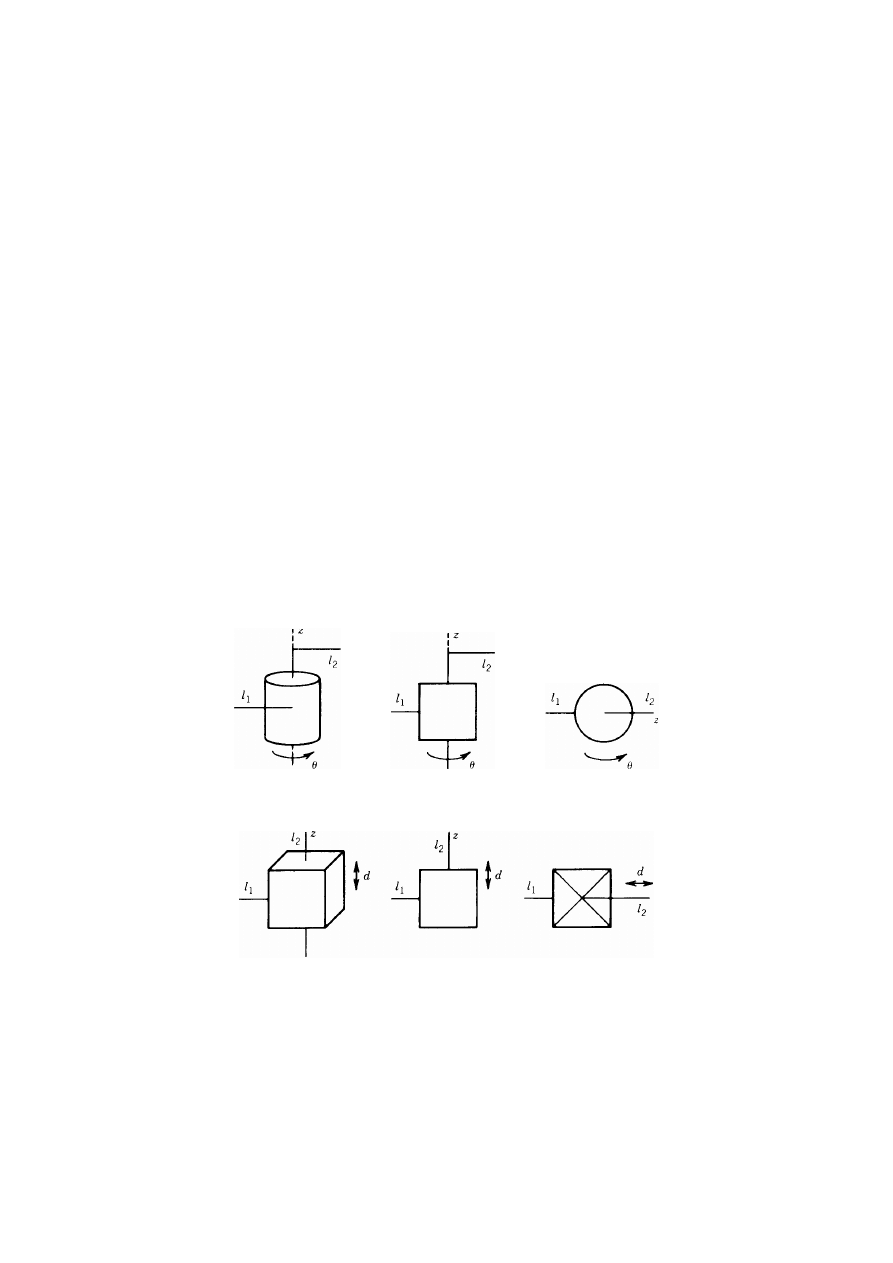
1.

Elementy składowe i struktura robotów

Manipulatory przemysłowe są zbudowane z członów połączonych przegubami w

otwarty łańcuch kinematyczny. Przeguby te są zazwyczaj obrotowe (rotacyjne) lub
pryzmatyczne (liniowe). Przeguby obrotowe są podobne do zawiasów i umożliwiają obrót
jednego członu względem drugiego. Przeguby pryzmatyczne umożliwiają ruch liniowy
jednego członu względem drugiego. Będziemy używać oznaczenia (R) dla przegubu
obrotowego i oznaczenia (P) dla przegubu pryzmatycznego, jak to pokazano na rys. 1. Każdy
przegub reprezentuje wzajemne połączenie dwóch członów, oznaczonych l

1

oraz l

i+1

. Oś

obrotu przegubu obrotowego lub oś, wzdłuż której następuje przemieszczenie w przegubie
pryzmatycznym, oznaczymy przez z

i

, dla przegubu łączącego człony i, i+1. Zmienna

przegubowa, oznaczona jako

θ

1

dla przegubu obrotowego i jako d, dla przegubu

pryzmatycznego, reprezentuje względne przemieszczenie sąsiednich członów.

Przeguby manipulatora mogą być napędzane elektrycznie, hydraulicznie lub

pneumatycznie. Liczba przegubów determinuje liczbę stopni swobody manipulatora. Zwykle
manipulator powinien mieć co najmniej sześć niezależnych stopni swobody: trzy do
pozycjonowania i trzy do orientowania. Przy liczbie stopni swobody mniejszej niż sześć
manipulator nie może osiągnąć każdego punktu w przestrzeni z zadaną orientacją. Niektóre
zadania, takie jak sięganie wokół lub za przeszkodę, wymagają więcej niż sześciu stopni
swobody. Wraz ze wzrostem liczby stopni swobody manipulatora gwałtownie rośnie stopień
trudności jego sterowania. Manipulator mający więcej niż sześć stopni swobody jest
nazywany manipulatorem kinematycznie redundantnym.

Na rys. 1. Przedstawiono sposób symbolicznego przedstawiania obrotowych

przegubów robota, natomiast na rys. 2 – przegubów pryzmatycznych.

Rys. 1. Graficzna reprezentacja przegubów obrotowych robota

Rys. 2. Graficzna reprezentacja przegubów pryzmatycznych robota

Przestrzeń robocza manipulatora jest całkowitym obszarem, do którego sięga jego

końcówka robocza przy pełnych zakresach wszystkich możliwych ruchów manipulatora. Jest
ona ograniczona przez geometrię manipulatora, jak też przez mechaniczne ograniczenia
zakresów ruchów w poszczególnych przegubach. Na przykład zakres ruchu przegubu
obrotowego może być ograniczony do mniej niż 360°. W przestrzeni roboczej często
wyróżnia się przestrzeń roboczą osiągalną i przestrzeń roboczą pełnej sprawności. Przestrzeń
robocza osiągalna jest całkowitym zbiorem punktów osiągalnych przez manipulator, podczas

gdy przestrzeń robocza pełnej sprawności składa się z tych punktów, które manipulator może
osiągnąć z wyznaczoną orientacją końcówki roboczej. Oczywiście przestrzeń robocza pełnej
sprawności jest podzbiorem przestrzeni roboczej osiągalnej.

1.1. Ogólna klasyfikacja kinematyki

Manipulatory przemysłowe są co prawda urządzeniami ogólnego przeznaczenia,

jednak w praktyce zwykle projektuje się je z myślą o pewnej klasie zastosowań, jak np.
spawanie, przenoszenie materiałów lub montaż. Rodzaj zastosowania w dużym stopniu
warunkuje wybór różnych parametrów konstrukcyjnych manipulatora, w tym także jego
strukturę kinematyczną. Przykładowo montaż płytek drukowanych jest zadaniem
odpowiednim dla tzw. manipulatorów typu SCARA, podczas gdy tzw. manipulator sferyczny
może lepiej obsługiwać prasę wykrawającą.

Do klasyfikacji manipulatorów można stosować różne kryteria, takie jak ich

geometria, struktura kinematyczna, rodzaj zastosowania, dla którego manipulator został
zaprojektowany, sposób sterowania itp. W tym rozdziale przedstawimy głównie klasyfikację
manipulatorów na podstawie ich geometrii. Dzisiejsze manipulatory mają przeważnie sześć
lub mniej stopni swobody. Zwykle są one klasyfikowane kinematycznie, biorąc pod uwagę
ramię lub pierwsze trzy stopnie swobody; kiść jest opisywana osobno. Większość
manipulatorów należy do jednej z pięciu grup typów geometrii: stawowy (RRR), sferyczny
(RRP), SCARA (RRP), cylindryczny (RPP) lub kartezjański, (PPP).

1.1.1.

Konfiguracja stawowa (RRR)

Manipulator stawowy jest nazywany również manipulatorem obrotowym lub mani-

pulatorem antropomorficznym. W grupie tej można wyróżnić dwa rozwiązania konstrukcyjne.
Pierwsze z nich to manipulator z łokciem (ang. elbow manipulator), którego przykładem jest
przedstawiony na rys. 3 manipulator PUMA.

Rys. 3. Manipulator UNIMATE PUMA 500

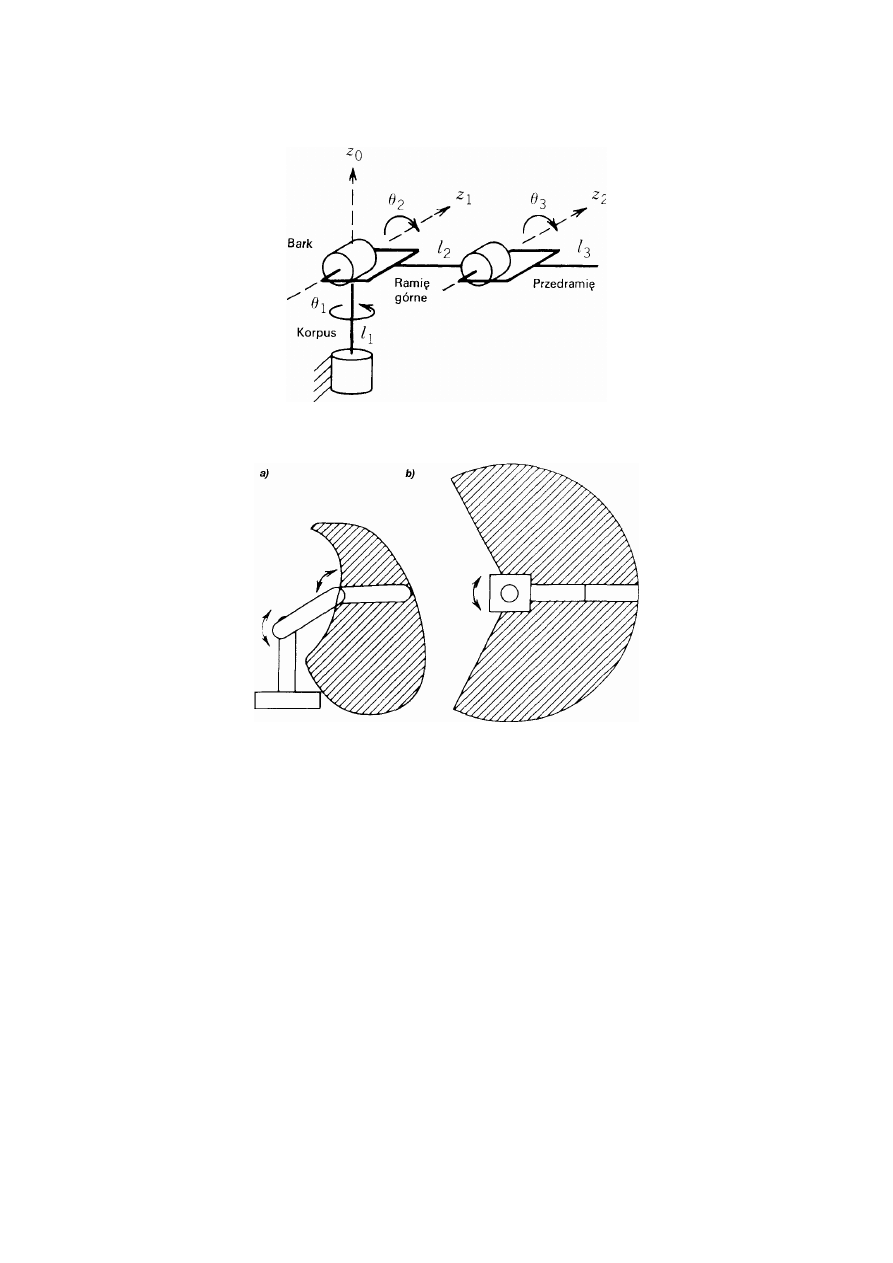
Budowę manipulatora z łokciem oraz związane z nim określenia przedstawiono rys. 4,

a na rys. 5 zilustrowano jego przestrzeń roboczą.

Rys. 4. Struktura manipulatora z łokciem

Rys. 5. Przestrzeń robocza manipulatora z łokciem: a) widok z boku, b) widok z góry

Drugie zaś rozwiązanie konstrukcyjne jest strukturą z równoległobokiem i polega ono

na połączeniu kolejnych stopni swobody, tak jak to ma miejsce w modelu T

3

735 firmy

Cincinnati Milacron, pokazanym na rys. 6. W tej konstrukcji oś z

2

jest równoległa do osi z

1

, a

obie osie z

1

i z

2

są prostopadłe do osi

Z

0

.

Konfiguracja manipulatora z łokciem zapewnia stosunkowo dużo swobody ruchu w

dość zwartej przestrzeni. Natomiast struktura z równoległobokiem, chociaż najczęściej mniej
zwinna niż manipulator z łokciem, ma rónież wiele zalet, które czynią ją atrakcyjną i
popularną. Najważniejszą cechą konfiguracji z równoległobokiem jest to, że silnik trzeciej osi
jest umieszczony na członie l. Ponieważ cały ciężar silnika obciąża człon 1, człony 2 i 3 mogą
być lżejsze, a przez to do ich napędzania mogą być użyte silniki o mniejszej mocy. Również
dynamika manipulatorów równoległobocznych jest prostsza niż manipulatorów z łokciem, co
w efekcie daje prostsze sterowanie.

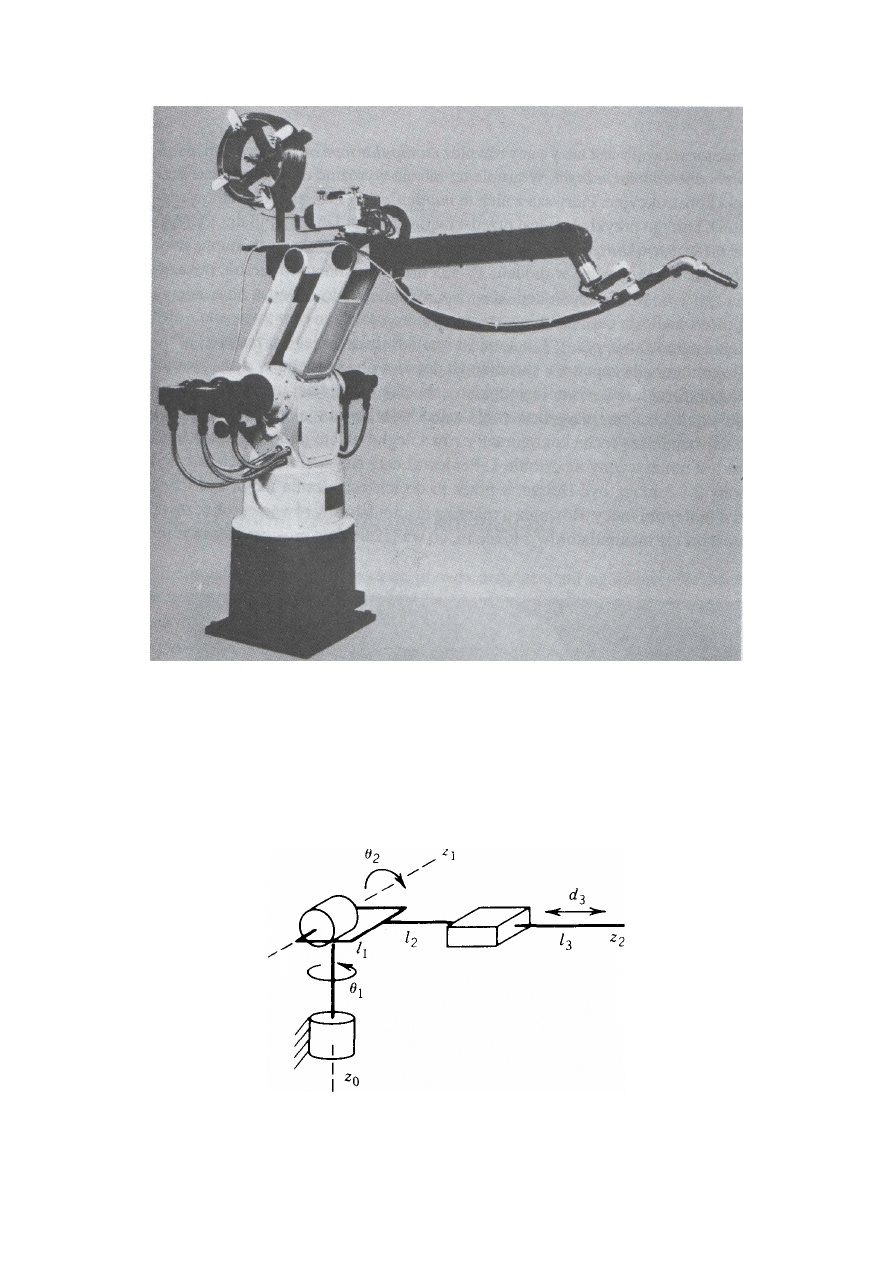
Rys. 6. Manipulator T

3

735 firmy Cincinnati Milacron

1.1.2. Konfiguracja sferyczna (RRP)

Jeśli w manipulatorze o konfiguracji stawowej trzeci przegub zastąpimy przegubem

pryzmatycznym, to otrzymamy konfigurację sferyczną pokazaną na rys. 7, a manipulator o tej
konfiguracji będziemy nazywać manipulatorem sferycznym.

Rys. 7. Konfiguracja manipulatora sferycznego

Nazwa tej konfiguracji wywodzi się stąd, że współrzędne sferyczne, określające

położenie końcówki roboczej względem układu współrzędnych o początku w przecięciu osi z

1

i z

2

, są takie same, jak trzy pierwsze zmienne przegubowe. Przykładem manipulatora o takiej

konfiguracji jest manipulator Stanforda (rys. 8), którego przestrzeń roboczą przedstawiono na
rys. 9.

Rys. 8. Manipulator Stanforda jako przykład manipulatora sferycznego

Rys. 9. Przestrzeń robocza manipulatora sferycznego

1.1.3.

Konfiguracja SCARA (RRP)

Manipulator SCARA (z ang. Selective Compliant Articulated Robot for Assembly czyli

stawowy robot montażowy selektywnie podatny) jest ostatnio coraz bardziej popularny. Jak
sama nazwa wskazuje, robot ten został zaprojektowany z myślą o zadaniach montażowych.
Chociaż konfiguracja SCARA ma strukturę RRP, jednak różni się zdecydowanie od
konfiguracji sferycznej zarówno wyglądem, jak i obszarem zastosowań. W przeciwieństwie
do manipulatora sferycznego Stanforda, forda, który ma osie z

0

, z

1

, z

2

wzajemnie prostopadłe,

manipulator SCARA ma osie z

0

, z

1

, z

2

równoległe. Rysunek 10 przedstawia manipulator tego

typu o nazwie AdeptOne, a rys. 11 jego strukturę schematyczną. Przestrzeń robocza
manipulatora SCARA jest zobrazowana na rys.12.

Rys. 10. Widok robota AdeptOne jako przykład manipulatora typu SCARA

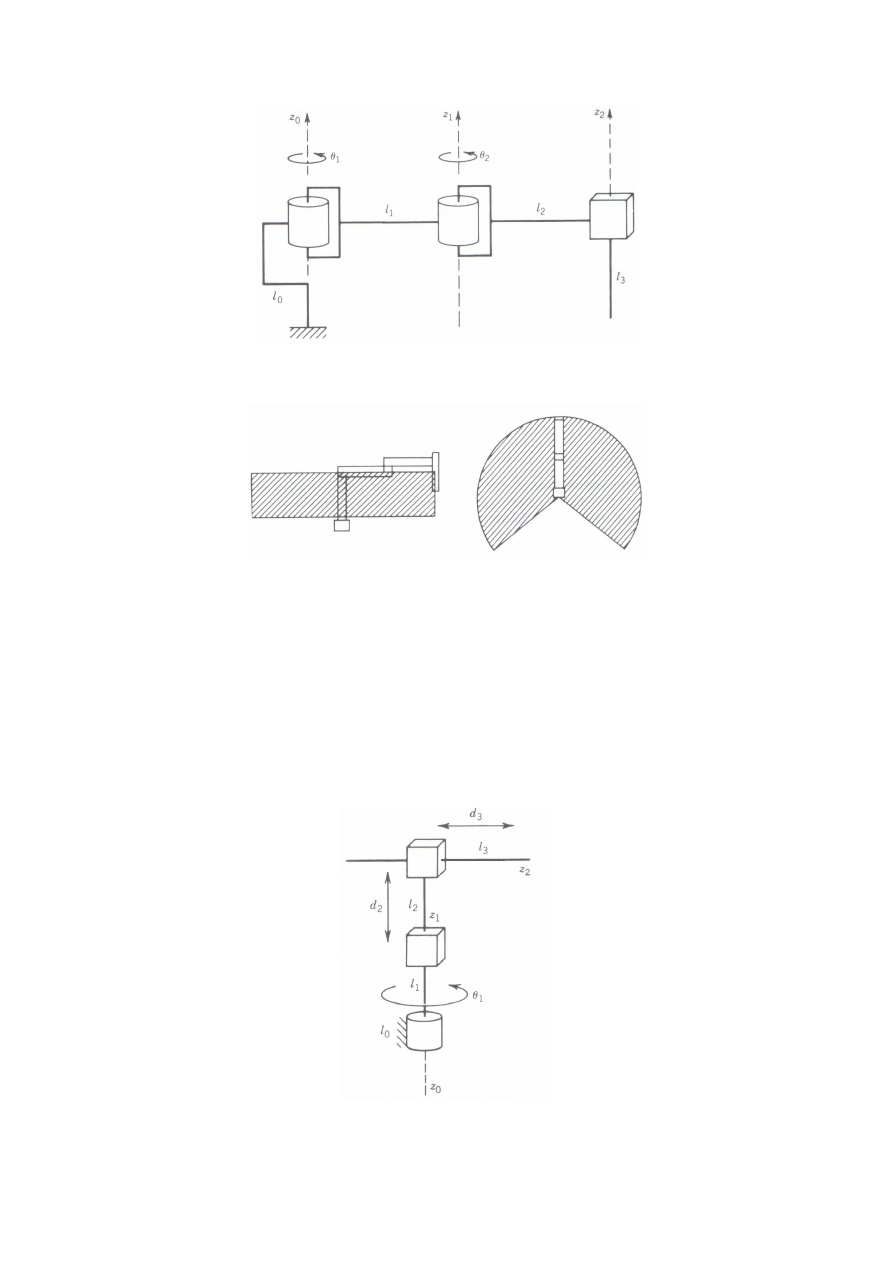
Rys. 11. Konfiguracja manipulatora SCARA

Rys. 12. Przestrzeń robocza manipulatora SCARA

1.1.4.

Konfiguracja cylindryczna (RPP)

Konfiguracja manipulatora cylindrycznego jest przedstawiona na rys 1-5. Pierwszy

przegub jest obrotowy i wykonuje obrót wokół podstawy, podczas gdy przeguby drugi i trzeci
są pryzmatyczne. Jak sugeruje nazwa, zmienne przegubowe są zarazem współrzędnymi
cylindrycznymi końcówki roboczej względem podstawy.

Na rysunku 13 jest pokazana jest struktura schematyczna takiego robota, na rys. 14

przykładowy robot cylindryczny – GMF M-100, a na rys. 15 jego przestrzeń robocza.

Rys. 13. Konfiguracja manipulatora cylindrycznego

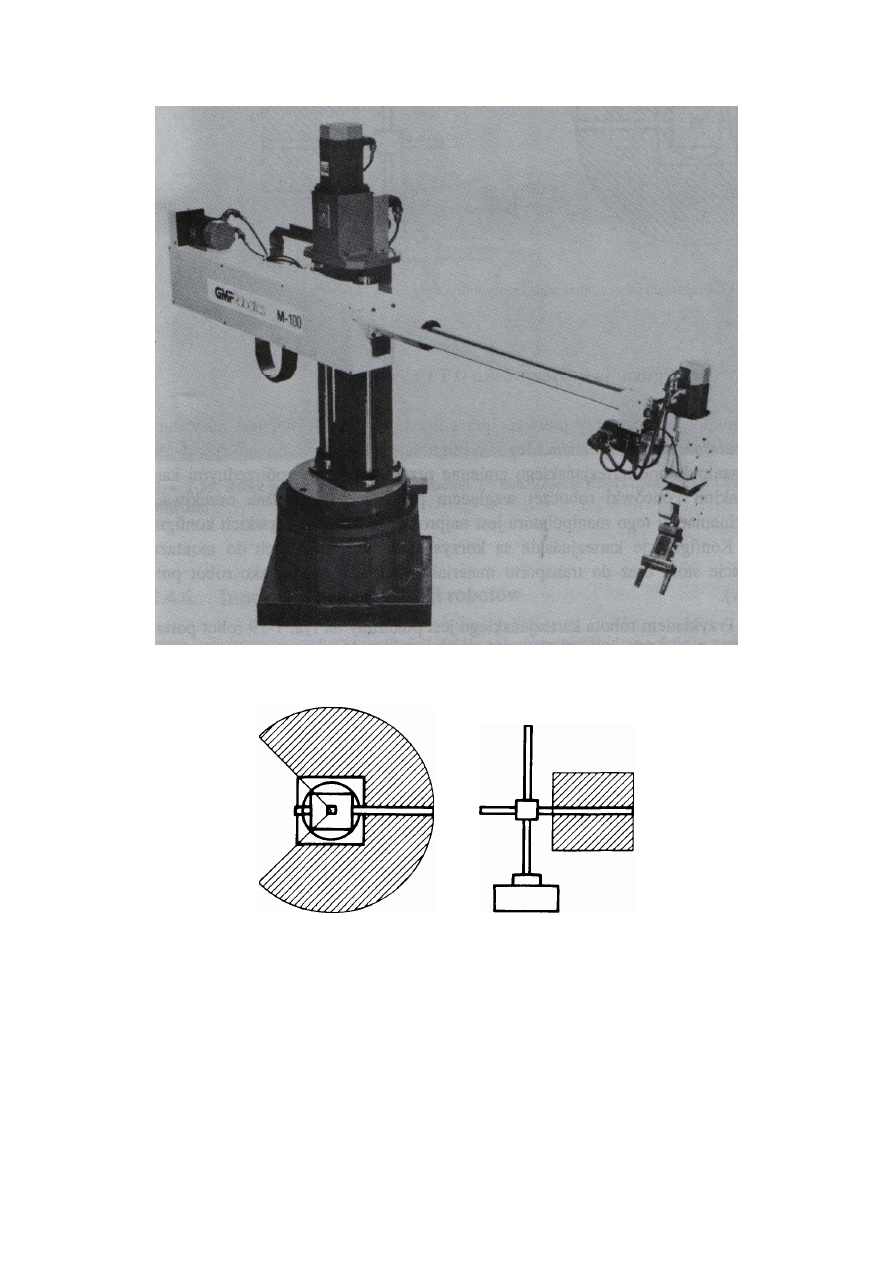
Rys. 14. Robot cylindryczny – GMF M-100

Rys. 15. Przestrzeń robocza manipulatora cylindrycznego

1.1.5.

Konfiguracja kartezjańska (PPP)

Manipulator, którego trzy pierwsze przeguby są pryzmatyczne, jest nazywany

manipulatorem kartezjańskim. Jego konfigurację przedstawiono na rys. 16, a przestrzeń
roboczą na rys. 17. Dla manipulatora kartezjańskiego zmienne przegubowe są współrzędnymi

kartezjańskimi końcówki roboczej względem podstawy. Jak można oczekiwać, opis
kinematyki tego manipulatora jest najprostszy spośród wszystkich konfiguracji. Konfiguracje

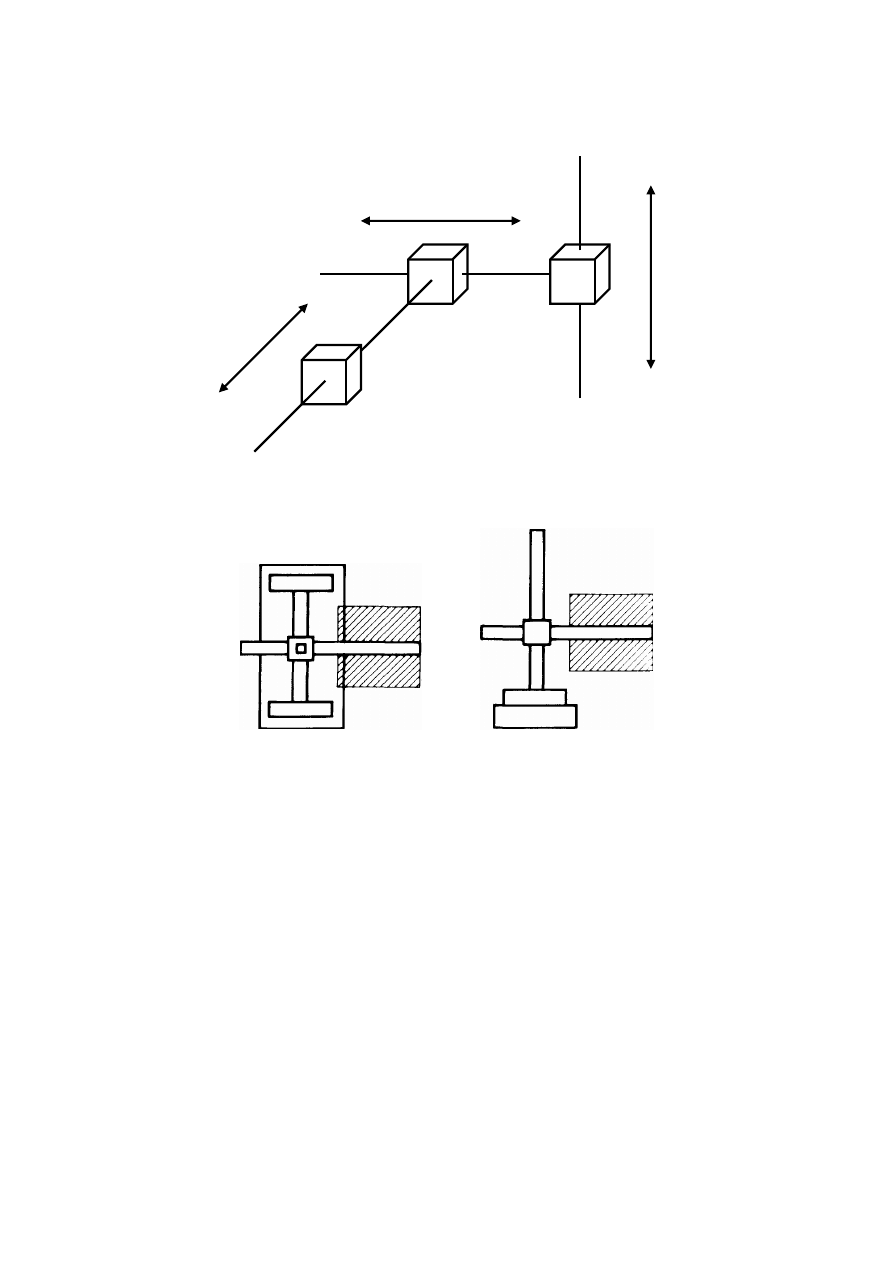
kartezjańskie są korzystne w zastosowaniach do montażu na blacie stołu oraz do transportu

materiałów lub ładunków (jako robot portalowy).

Rys. 16. Konfiguracja manipulatora kartezjańskiego

Rys. 17. Przestrzeń robocza manipulatora kartezjańskiego

1.1.6.

Kiść i końcówka robocza

Pojęcie kiści manipulatora odnosi się do przegubów między ramieniem a dłonią.

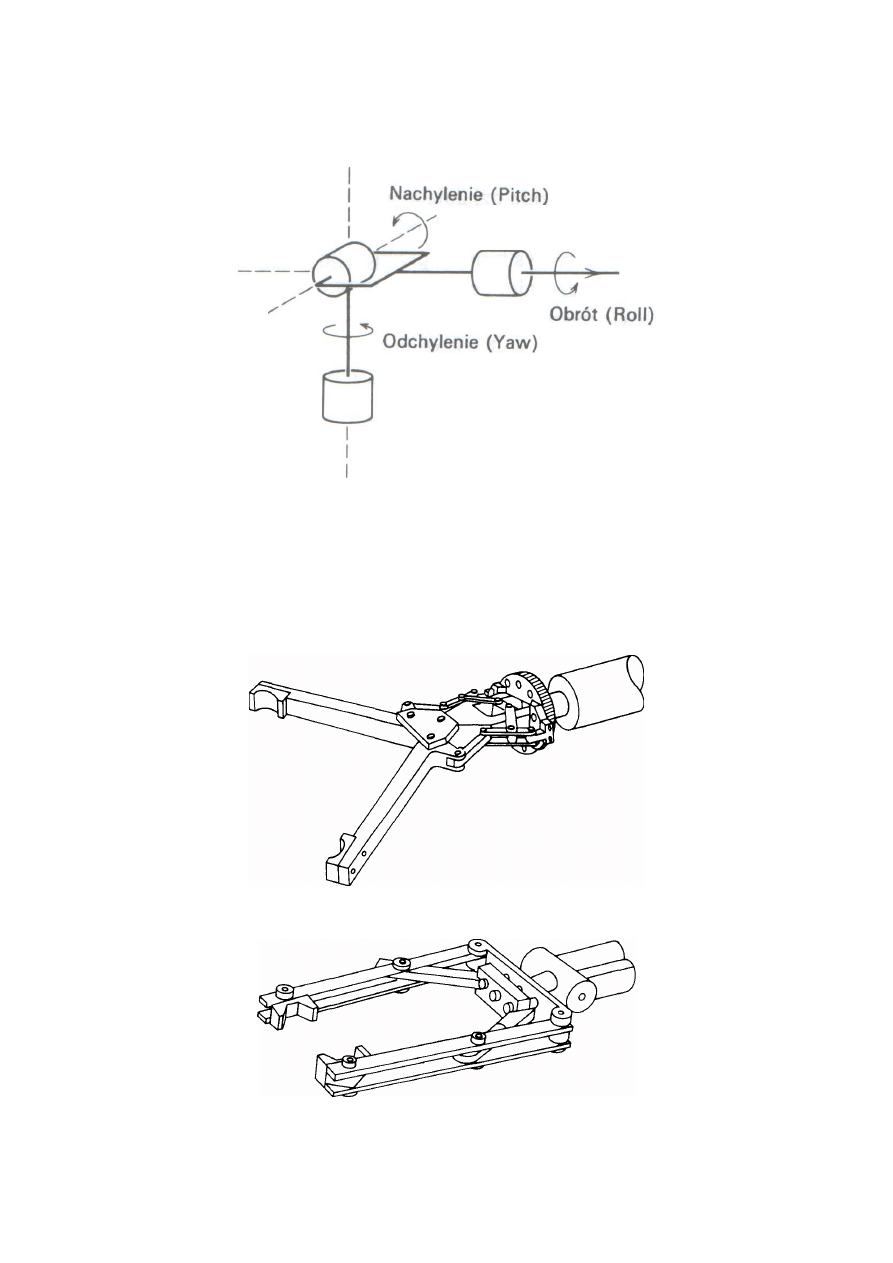
Przeguby kiści są prawie zawsze obrotowe. Coraz więcej manipulatorów projektuje się z
kiścią sferyczna, w której osie przegubów przecinają się w jednym punkcie. Manipulatory
Cincinnati Milacron T

3

(rys 6) oraz stanfordzki (rys. 8) mają kiście sferyczne o trzech

stopniach swobody.

Na rysunku 18 schematycznie przedstawiono kiść sferyczną. Taka konstrukcja kiści

znacznie upraszcza analizę kinematyki manipulatora oraz ułatwia efektywne rozłączenie
pozycjonowania i orientowania obiektu. Zatem typowy manipulator będzie miał trzy stopnie
swobody określające położenie, które są związane z trzema lub więcej przegubami ramienia.
Liczba stopni swobody określających orientację będzie wtedy zależała od stopni swobody
kiści. W zależności od rodzaju zastosowania dobiera się kiść z jednym, dwoma lub trzema

stopniami swobody. Na przykład robot AdeptOne (rys. 10) ma cztery stopnie swobody; jego
kiść ma tylko obrót wokół ostatniej osi z. Manipulator Cincinnati Milacron T

3

735 ma pięć

l

2

z

y

l

1

l

3

x

stopni swobody – kiść ma pochylanie i obrót, ale nie ma ruchu skręcania. Manipulator PUMA

z pełną kiścią o trzech stopniach swobody ma sześć stopni swobody.

Rys. 18. Struktura kiści sferycznej z zaznaczonymi tzw. kątami RPY

Mówi się, że robot jest tak dobry, jak dobra jest jego dłoń lub końcówka robocza.

Ramię i kiść, tworzące robota, są używane przede wszystkim do pozycjonowania końcówki
roboczej i narzędzia, którym robot operuje. Wybór końcówki roboczej lub narzędzia zależy
od aktualnie wykonywanej pracy. Najprostszym typem końcówki roboczej jest chwytak,
którego dwa rodzaje pokazano na rys. 19 i rys. 20.

Rys .19. Chwytak szczękowy równoległy

Rys .20. Chwytak z dwoma palcami

Chwytak taki może wykonywać tylko dwie operacje: otwierania i zamykania.

Wystarczy to do przenoszenia materiałów, operowania częściami lub chwytania prostych
narzędzi, nie nadaje się jednak do realizacji innych zadań, takich jak spawanie, montaż,
gratowanie itp. Dlatego dużo prac badawczych jest poświęconych projektowaniu specjalnych
końcówek roboczych oraz narzędzi, które można szybko zmieniać stosownie do wymagań
wykonywanego zadania. Prowadzi się też wiele badań nad rozwojem sztucznej dłoni
antropomorficznej, a więc podobnej do dłoni człowieka. Takie dłonie są opracowywane

zarówno dla zastosowań w protetyce, jak i do wykorzystania w wytwarzaniu. Ponieważ
skoncentrujemy się na analizie i sterowaniu samego manipulatora, a nie na jego szczególnych
zastosowaniach czy końcówkach roboczych, więc nie będziemy dalej omawiać rozwiązań

budowy tych końcówek ani problemów chwytania i manipulacji.

2. Zagadnienia kinematyki prostej i odwrotnej

2.1. Wprowadzenie

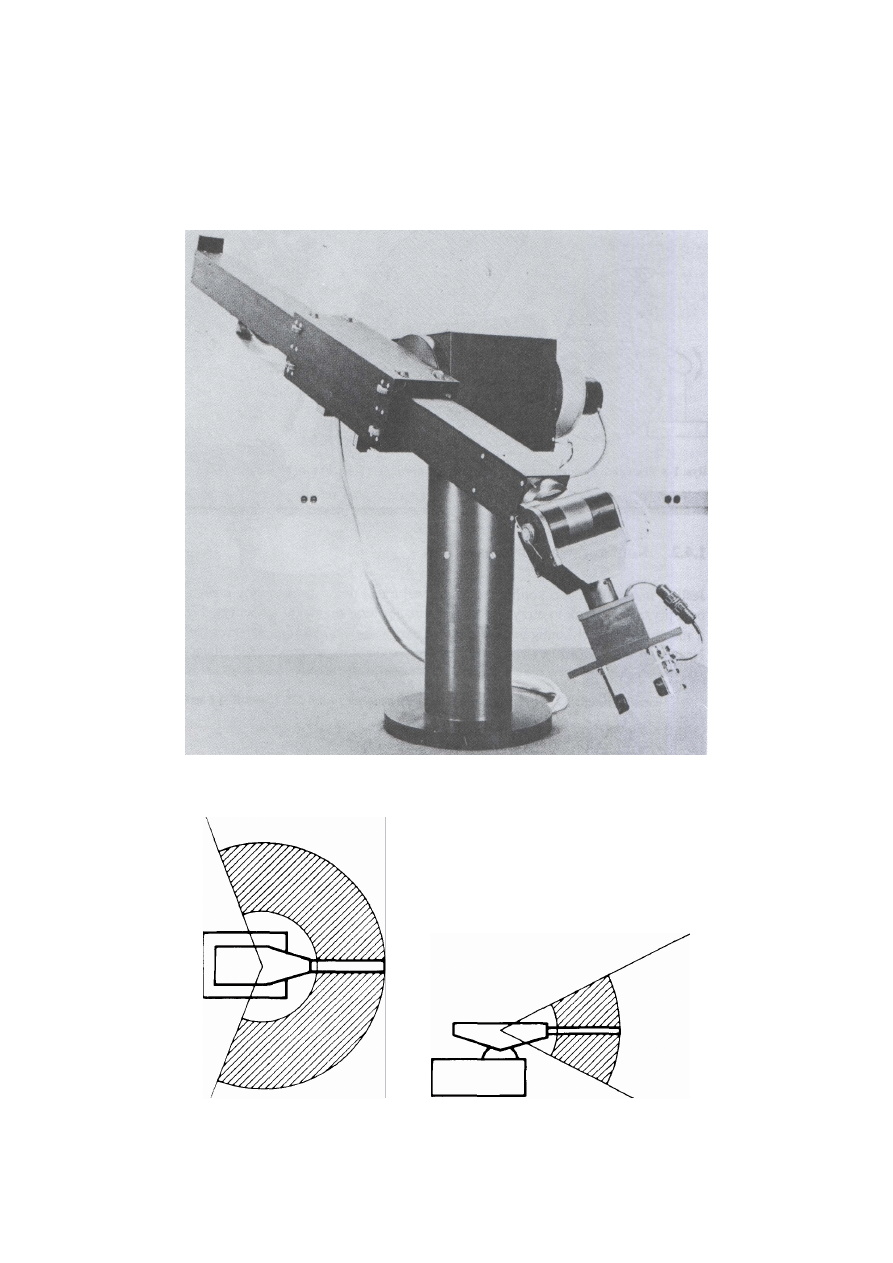
Typowy przykład zastosowania manipulatora przemysłowego jest pokazany na rys.

21.

Rys. 21. Robot o sześciu stopniach swobody z narzędziem szlifierskim

Na powyższym rysunku manipulator o sześciu stopniach swobody przedstawiono z

narzędziem do gratowania, którym robot usuwa określoną warstwę metalu z powierzchni.
Rozważając niniejszy przykład skoncentrujemy się na pytaniu: Jakie są podstawowe
zagadnienia do rozwiązania i co musimy wiedzieć w celu zaprogramowania robota do
wykonania opisanego wyżej zadania ?

Uzyskanie odpowiedzi na to pytanie dla pełnego manipulatora o sześciu stopniach

swobody jest zadaniem wysoce złożonym i niezasadnym do przedstawienia w tym miejscu.
Możemy jednak wykorzystać prosty manipulator płaski o dwóch członach do przedstawienia
głównych zagadnień oraz do wstępnego przeglądu tego tematu.

Rozważmy zatem robota o dwóch członach, przedstawionego na rys. 22. Na końcu

manipulatora jest zamontowane narzędzie w rodzaju tarczy szlifierskiej lub tnącej. Załóżmy,
że chcemy przemieścić manipulator z jego pozycji bazowej A do położenia B, od którego
robot powinien śledzić kontur powierzchni S aż do punktu C, ze stałą prędkością i z
utrzymaniem określonej wartości siły docisku F prostopadłej do powierzchni. Przy takim
postępowaniu robot będzie ciął lub szlifował powierzchnię zgodnie z ustalonym powyżej

opisem.

Rys. 22. Przykład zastosowanie dwuczłonowego robota płaskiego

2.2. Problem 1 – zadanie kinematyki prostej

Pierwszym napotkanym problemem jest opisanie pozycji narzędzia oraz lokalizacji

punktów A i B (a najprawdopodobniej również całej powierzchni S) we wspólnym układzie
współrzędnych. Różne układy współrzędnych oraz związki między nimi przedstawiono w
dalszym cyklu wykładów.

Najczęściej manipulator rozpoznaje swoją pozycję za pomocą czujników

wewnętrznych (tzn. enkoderów pozycji), które są umieszczone na przegubach l i 2 w celu
bezpośredniego pomiaru kątów (zmiennych przegubowych)

θ

1

i

θ

2

. Potrzebujemy zatem

wyrazić pozycje A i B w zależności od tych kątów. Prowadzi to do tzw. zadania kinematyki
prostej, którego istotą jest określenie pozycji i orientacji końcówki roboczej lub narzędzia w
zależności od zmiennych przegubowych.

Przyjęło się ustalać stały układ współrzędnych, nazywany układem odniesienia lub

układem bazowym, względem którego rozpatruje się wszystkie obiekty łącznie z
manipulatorem. W naszym przykładzie przyjmijmy układ bazowy O

0

x

0

z

0

leżący w podstawie

robota, jak to pokazano na rys. 23.

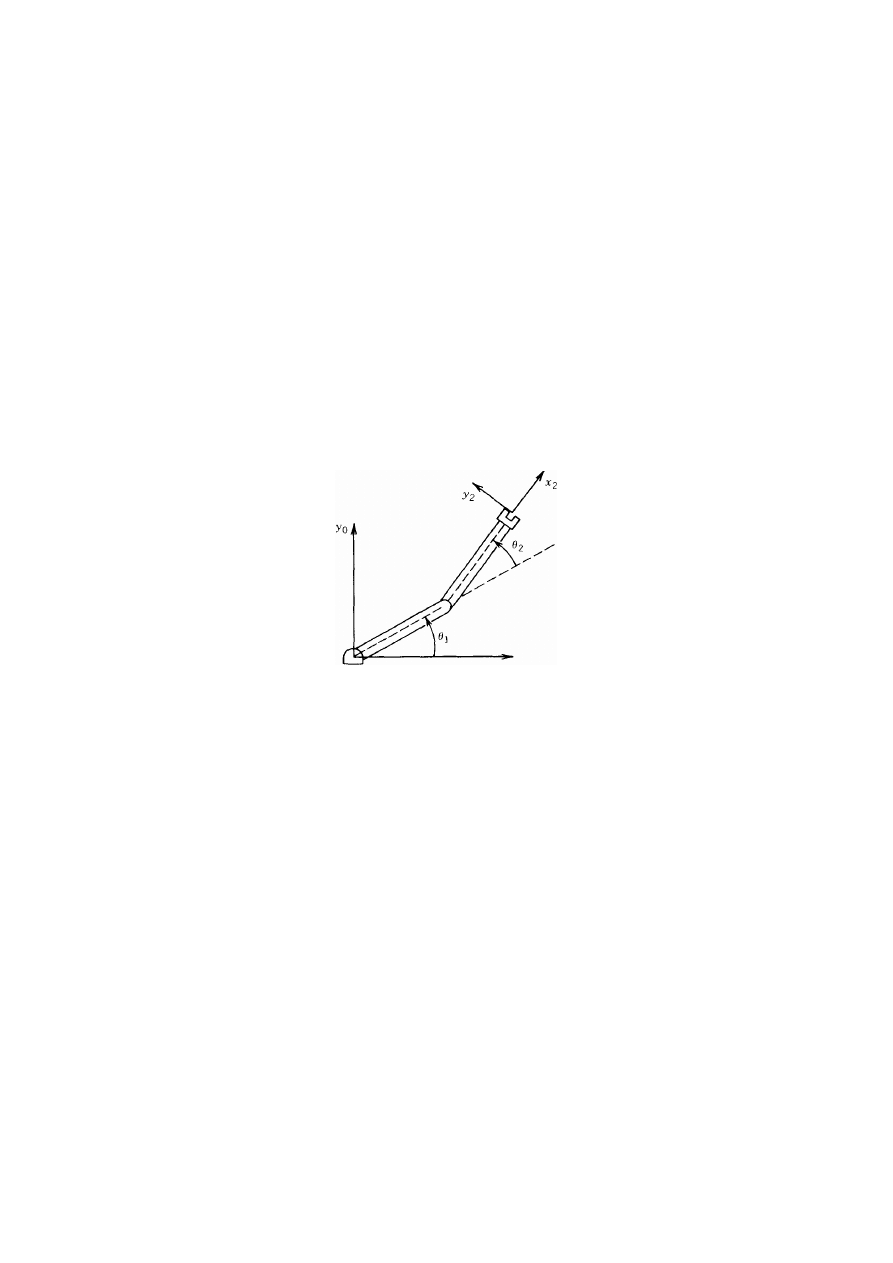
Rys. 23. Układ współrzędnych w dwuczłonowym robocie płaskim

W układzie tym współrzędne (x, y) narzędzia są wyrażone wzorami

x = a1 cos

θ

1

+ a2 cos(

θ

1

+

θ

2

)

(1)

y = a1 sin

θ

1

+ a2 sin(

θ

1

+

θ

2

)

(2)

Z kolei orientacja układu narzędzia względem układu bazowego jest opisana cosinusami
kierunkowymi osi .x

2

i y

2

względem osi x

0

i y

0

, czyli

i

2

• i

0

= 1 · 1 · cos(

θ

1

+

θ

2

) = cos(

θ

1

+

θ

2

)

(3)

i

2

• j

0

= 1 · 1 · cos[90 - (

θ

1

+

θ

2

)] = sin(

θ

1

+

θ

2

)

(4)

j

2

• i

0

= 1 · 1 · cos[90 + (

θ

1

+

θ

2

)] = -sin(

θ

1

+

θ

2

)

(5)

j

2

• j

0

= 1 · 1 · cos(

θ

1

+

θ

2

) = cos(

θ

1

+

θ

2

)

(6)

Zależności te możemy przedstawić w postaci macierzy orientacji













+

+

+

−

+

=













)

cos(

)

sin(

)

sin(

)

cos(

j

j

j

i

i

j

i

i

2

1

2

1

2

1

2

1

0

2

0

2

0

2

0

2

θ

θ

θ

θ

θ

θ

θ

θ

(7)

gdzie

i

0

,

j

0

są standardowymi ortonormalnymi wektorami jednostkowymi w bazowym

układzie współrzędnych,

i

2

,

j

2

są standardowymi ortonormalnymi wektorami jednostkowymi

w układzie współrzędnych narzędzia.

Wzory (1)-(7) są nazywane

równaniami kinematyki prostej. Dla robota o sześciu

stopniach swobody równania te są bardziej skomplikowane i nie da ich się napisać tak łatwo,
jak dla manipulatora dwuczłonowego. Ogólna procedura, którą opiszemy w czasie

późniejszych wykładów, ustala układ współrzędnych w każdym przegubie i umożliwia
przejście między tymi układami współrzędnych, wykorzystując przekształcenia macierzowe.
Jest ona oparta na konwencji Denavita-Hartenberga. W celu uproszczenia przejścia między
układami współrzędnych zastosujemy współrzędne jednorodne i przekształcenia jednorodne.

2.3. Problem 2 – zadanie kinematyki odwrotnej

Teraz, mając dane w przegubach kąty

θ

1

i

θ

2

, możemy określić współrzędne x i y

końcówki roboczej. Jednakże aby nakazać robotowi ruch do pozycji B, potrzebujemy postąpić
odwrotnie, tzn. znaleźć zmienne przegubowe

θ

1

i

θ

2

w zależności od współrzędnych x i y w

pozycji B. Jest to tzw. zadanie kinematyki odwrotnej. Innymi słowy, mając współrzędne x i y
w równaniach (2) i (2) kinematyki prostej, chcemy je rozwiązać dla zmiennych
przegubowych. Ponieważ równania kinematyki prostej są nieliniowe, znalezienie rozwiązania
może nie być łatwe i w ogólności nie będzie to rozwiązanie jednoznaczne. Na przykład w
przypadku dwuczłonowego mechanizmu płaskiego może w ogóle nie być rozwiązania, jeśli
dane współrzędne (x, y) są poza zasięgiem manipulatora. Gdy dane współrzędne (x, y)
mieszczą się w zasięgu manipulatora, mogą istnieć dwa rozwiązania, jak to pokazano na rys.
24. Konfiguracje te są określane „łokieć u góry" lub „łokieć u dołu". Może również istnieć
dokładnie jedno rozwiązanie, jeśli manipulator musi być całkowicie wyciągnięty w celu
osiągnięcia danego punktu. W pewnym przypadku może też być nieskończenie wiele
rozwiązań.

Rys. 24. Rozwiązanie niejednoznaczne kinematyki odwrotnej

Rozważmy schemat przedstawiony na rys. 25. Stosując równania cosinusów postaci

c

2

= a

2

+ b

2

– 2ab cos(

γ

),

(8)

można kąt

θ

2

opisać wzorem

D

a

a

a

a

y

x

=

−

−

+

=

:

2

cos

2

1

2

2

2

1

2

2

2

θ

(9)

Teraz możemy przedstawić

θ

2

w postaci

θ

2

= cos

-1

(D)

(10)

x

0

y

0

A

B

Łokie

ć

u góry

Łokie

ć

u dołu

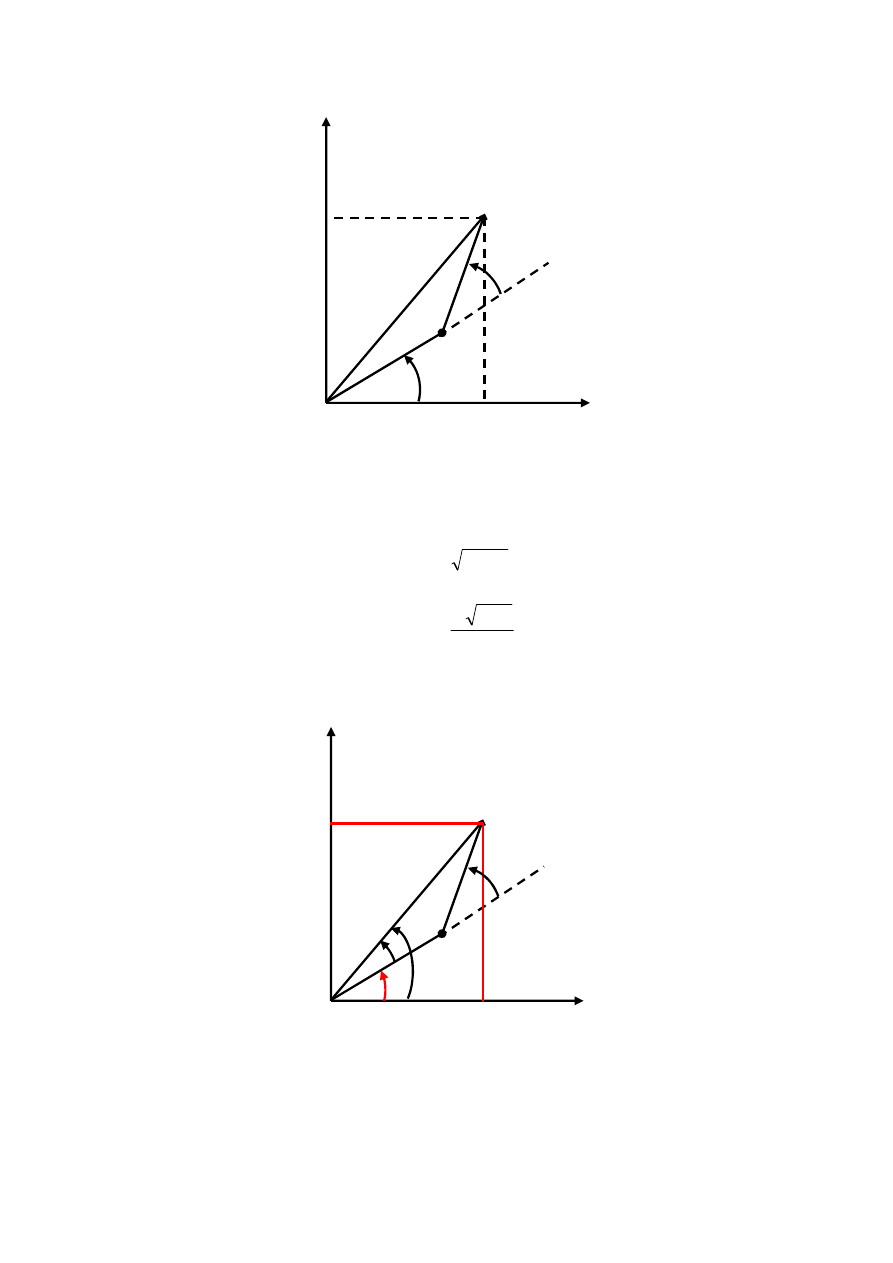
Rys. 25. Wyznaczenie kąta

θ

2

w przegubie drugim dwuczłonowego robota płaskiego

Jednakże lepszym sposobem znalezienia kąta

θ

2

jest zauważenie, że jeśli cos

θ

2

jest

dany wzorem (9), to sin

θ

2

jest dany odpowiednio wzorem

2

2

1

sin

D

−

±

=

θ

(11)

i

stąd można wyznaczyć

D

-D

2

1

2

1

tan

±

=

−

θ

(12)

Zaletą tego drugiego podejścia jest rozróżnienie obu konfiguracji „łokieć u góry" i „łokieć u
dołu" przez wybór odpowiedniego znaku w równaniu (12).

Wyznaczenie kąta

θ

1

zrealizujemy w oparciu o rys. 26.

Rys .26. Wyznaczenie kąta

θ

1

w przegubie pierwszym dwuczłonowego robota płaskiego

Jeśli zauważymy, że

θ

1

=

θ

β

-

θ

α

(13)

oraz

x

x

0

y

0

y

θ

1

θ

2

a

1

a

2

c

x

0

y

0

y

x

θ

1

θ

2

a

1

a

2

c

θ

α

θ

β

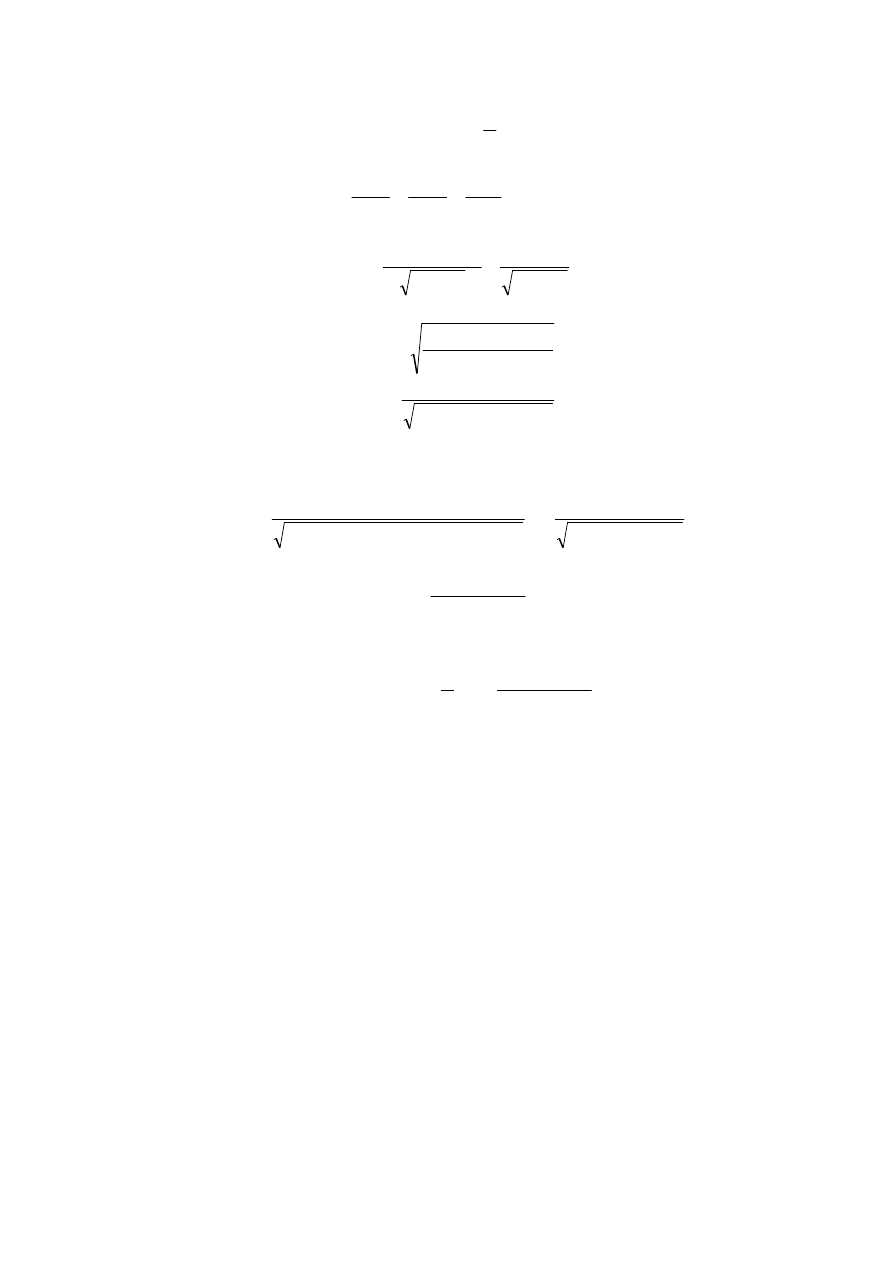
x

y

1

tan

−

=

β

θ

(14)

A następnie skorzystamy z twierdzenia sinusów, postaci

R

c

b

a

2

sin

sin

sin

=

=

=

γ

β

α

(15)

w wyniku czego możemy napisać, że

2

2

2

2

2

2

2

2

sin

)

sin(

sin

y

x

a

y

x

a

+

=

+

−

=

θ

θ

π

θ

α

(16)

Wykonując następnie proste przekształcenia, otrzymujemy następujące zależności

2

2

2

2

2

2

2

sin

cos

y

x

a

y

x

+

−

−

±

=

θ

θ

α

(17)

2

2

2

2

2

2

2

2

sin

sin

tg

θ

θ

θ

α

a

y

x

a

−

+

±

=

(18)

Jeśli teraz poniższą zależność

x

2

+ y

2

= a

1

2

+ a

2

2

+ 2a

1

a

2

cos

θ

2

(19)

podstawimy do wzoru (18), wówczas otrzymamy

2

2

2

1

2

2

2

2

2

2

2

2

1

2

2

2

1

2

2

)

cos

(

sin

sin

cos

2

sin

tg

θ

θ

θ

θ

θ

θ

α

a

a

a

a

a

a

a

a

a

+

±

=

−

+

+

±

=

(20)

a zatem

2

2

1

2

2

1

-

cos

sin

tg

θ

θ

θ

α

a

a

a

+

=

(21)

Podstawiając teraz zależności (14) i (21) do wzoru (13) otrzymamy zależności na wartość
kąta

θ

1

, określoną wzorem

2

2

1

2

2

1

-

1

cos

sin

tg

arctg

θ

θ

θ

θ

θ

α

β

a

a

a

x

y

+

−

=

−

=

(22)

Na zakończenie powyższych rozważań zauważmy jeszcze, że kąt

θ

1

zależy od kąta

θ

2

.

Ma to znaczenie fizyczne, gdyż oczekujemy różnych wartości kąta

θ

1

w zależności od tego,

które rozwiązanie wybierzemy dla kąta

θ

2

.

3. Pozostałe kwestie związane ze sterowaniem manipulatorem

3.1. Kinematyka prędkości

W celu śledzenia konturu ze stałą prędkością lub z określoną daną prędkością musimy

znać zależności między prędkością narzędzia a prędkościami przegubowymi. Po
zróżniczkowaniu równań (1) i (2) otrzymujemy

)

)(

sin(

sin

2

1

2

1

2

1

1

1

θ

θ

θ

θ

θ

θ

&

&

&

&

+

+

−

⋅

−

=

a

a

x

(23)

)

)(

cos(

cos

2

1

2

1

2

1

1

1

θ

θ

θ

θ

θ

θ

&

&

&

&

+

+

−

⋅

=

a

a

y

(24)

Zastosowanie zapisu wektorowego













=

y

x

x

i













=

2

1

θ

θ

θ

pozwala przedstawić

te zależności w

postaci wyrażonej zapisem

θ

J

cos(

)

cos(

cos

)

sin(

)

sin(

sin

x

2

1

2

1

2

2

1

2

1

1

2

1

2

2

1

2

1

1

&

&

&

&

=













⋅













+

+

+

+

−

+

−

−

=

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

a

a

a

a

a

a

(25)

Macierz

J zdefiniowana w równaniu (25) jest nazywana jakobianem manipulatora i

jest podstawowym obiektem określanym dla każdego manipulatora.

Wyznaczenie prędkości przegubowych na podstawie prędkości końcówki roboczej jest

koncepcyjnie proste, ponieważ mamy tu zależność liniową. Zatem prędkości przegubowe
obliczamy z prędkości końcówki roboczej, stosując odwrotność jakobianu

x

J

θ

-1

&

&=

(26)

W celu wyznaczenia macierzy odwrotnej do macierzy Jacobiego skorzystamy ze

wzoru

T

D

)

J

(

J

det

1

J

1

-

=

(27)

Po wykonaniu prostych, otrzymujemy

det

J = a1 a2 sin

θ

2

(28)

oraz













+

−

−

+

+

−

−

+

=

)

sin(

sin

)

sin(

)

cos(

cos

)

cos(

J

2

1

2

1

1

2

1

2

2

1

2

1

1

2

1

2

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

a

a

a

a

a

a

D

(29)

A zatem podstawiając zależność (28) i (29) – po transponowaniu, do wzoru (27) otrzymujemy













⋅













+

−

−

+

−

−

+

+

=













y

x

a

a

a

a

a

a

a

a

&

&

&

&

)

sin(

sin

)

cos(

cos

)

sin(

)

cos(

sin

1

2

1

2

1

1

2

1

2

1

1

2

1

2

2

1

2

2

2

1

2

1

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

(30)

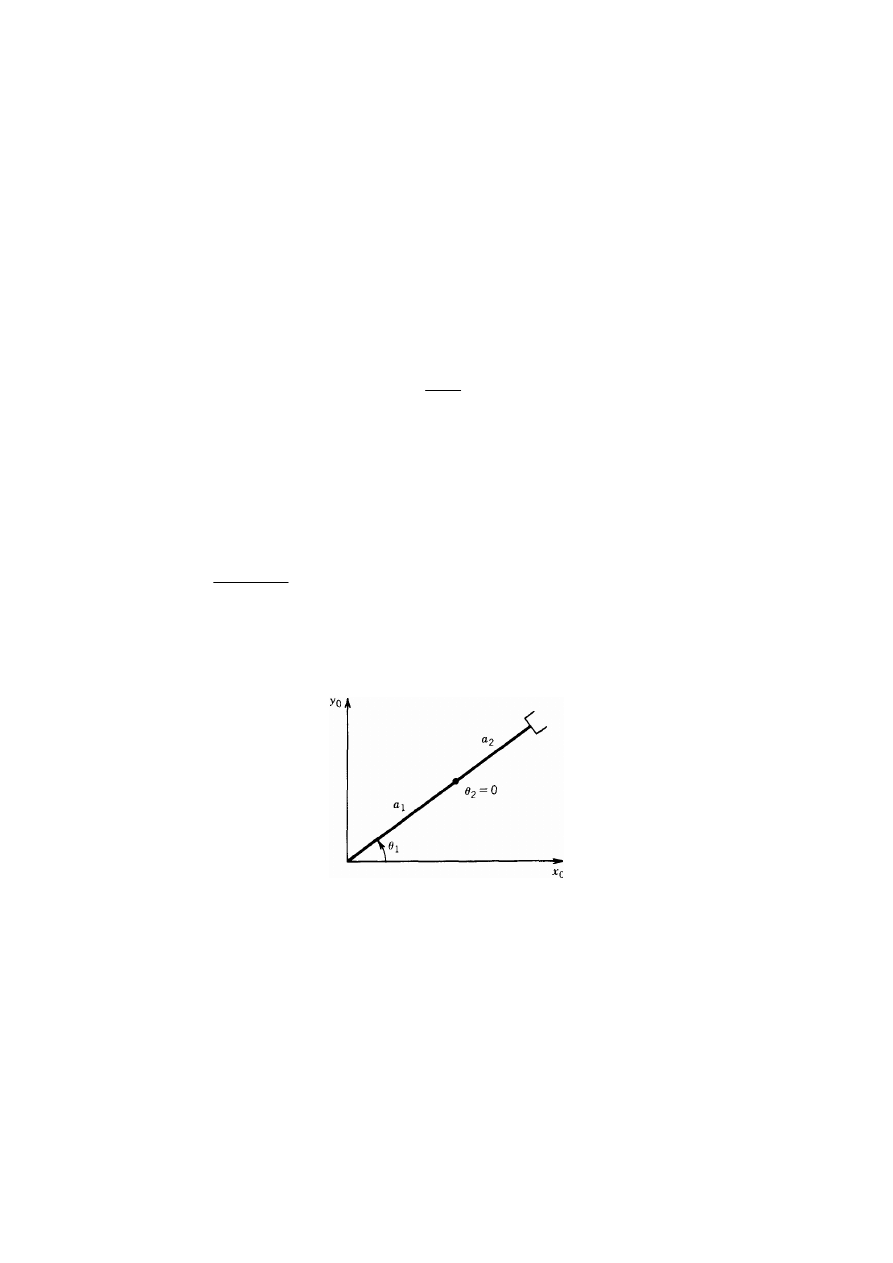
Zauważmy, że jeśli wyznacznik det

J jakobianu z wzoru (25) jest równy a1 a2 sin

θ

2

.

Jakobian nie będzie więc miał odwrotności, gdy

θ

2

= 0 lub

θ

2

=

π

.

W takim przypadku mówi

się, że manipulator ma

konfigurację osobliwą, taką jak pokazano na rys. 27 dla

θ

2

= 0.

Rys. 27. konfiguracja osobliwa manipulatora

Wyznaczenie konfiguracji osobliwych jest ważne z kilku powodów. W konfiguracji

osobliwej mamy do czynienia z pewnymi nieskończenie małymi ruchami, które są

niewykonalne. Oznacza to, że końcówka robocza manipulatora nie może wykonywać ruchów
w pewnych kierunkach. W przedstawionym przykładzie końcówka robocza nie może
poruszać się z konfiguracji osobliwej w kierunku równoległym do

a

1

. Konfiguracje osobliwe

są także związane z niejednoznacznością rozwiązań kinematyki odwrotnej. W omawianym
przykładzie dla danej pozycji końcówki roboczej, mamy w ogólności dwa możliwe
rozwiązania. Zauważmy, że konfiguracja osobliwa oddziela te dwa rozwiązania w takim
sensie, że manipulator nie może przejść z jednej konfiguracji do drugiej bez przejścia przez

osobliwość. Dlatego w wielu zastosowaniach bardzo ważne jest takie zaplanowanie ruchów

manipulatora, które pozwala ominąć konfiguracje osobliwe.

3.2. Problem dynamiki

Manipulator robota jest przede wszystkim urządzeniem pozycjonującym. Jeśli chcemy

sterować pozycją, to musimy znać w

ł

aściwości dynamic

z

ne manipulatora, żeby wiedzieć, jak

dużą siłę należy wywrzeć w celu spowodowania ruchu. Gdy sita ta będzie za mała,
manipulator będzie zbyt wolny. Po przyłożeniu za dużej siły może nastąpić zderzenie z
obiektem lub oscylowanie wokół zadanej pozycji.

Wyprowadzenie dynamicznych równań ruchu dla robota nie jest zadaniem łatwym z

powodu dużej liczby stopni swobody i występujących w układzie nieliniowości. W celu
realizacji tego zagadnienia (wyprowadzenia równań ruchu takiego syst

e

mu) stosuje się tzw.

metodykę wykorzystującą równania dynamiczne Lagrange'a. Dodatkowo dla członów
sztywnych pełny opis dynamiki robota obejmuje dynamikę silników, które są źródłem sił i
momentów, oraz dynamikę zespołów napędowych, które przenoszą moc z silnika do członu
manipulatora. Dlatego też zagadnienia dynamiki silników i zespołów napędowych oraz ich
wpływ na problemy sterowania nie mogą zostać pominięte.

3.3. Zagadnienie sterowania pozycyjnego

Do zaprojektowania algorytmów sterowania w celu wykonania zaprogramowanego

zadania wykorzystuje się niejednokrotnie teorię sterowania. Problem sterowania ruchem
składa się z problemu śledzenia i tłumienia zakłóceń. Polega on na określeniu wejścia
sterującego potrzebnego do śledzenia trajektorii, która została zaplanowana dla manipulatora,
przy równoczesnym tłumieniu zakłóceń, spowodowanych niemożliwymi do modelowania
zjawiskami dynamicznymi, takimi jak tarcie i szum. Standardowe podejścia do sterowania
robota oparte są na metodzie analizy częstotliwościowej. Istotnymi zagadnieniami
dotyczącymi tych kwestii są także pojęcia sterowania wyprzedzającego oraz techniki
obliczanego momentu dynamiki odwrotnej w celu uproszczenia złożonych nieliniowych sił
oddziaływania między członami manipulatora. Ponadto przy użyciu drugiej metody
Lapunowa korzysta się często z tzw. sterowania krzepkiego. inne dodatkowe zaawansowane
metody nieliniowej teorii sterowania, są niejednokrotnie przydatne do sterowania robotów o
dużych możliwościach funkcjonalnych.

3.4. Sterowanie siłą

Gdy manipulator raz osiągnie pozycję B, musi odtwarzać kontur powierzchni S, zapewniając
stałą siłę prostopadłą do powierzchni. Możliwe jest, że znając lokalizację obiektu i kształt
konturu, rozwiążemy to zadanie tylko za pomocą sterowania pozycyjnego. W praktyce trudno
to jednak zrealizować. Ponieważ sam manipulator ma dużą sztywność, każdy błąd pozycji
spowodowany nieznajomością dokładnej lokalizacji powierzchni lub narzędzia może
wywołać na końcówce roboczej wzrost sił do wartości ekstremalnych, które mogą zniszczyć
narzędzie, powierzchnię lub robota. Lepszym rozwiązaniem jest bezpośredni pomiar
działających sił i wykorzystanie schematu sterowania sitowego. W celu realizacji zagadnienia
sterowania siłą powszechnie stosowane są dwa rozwiązania: sterowanie hybrydowe i
sterowanie impedancyjne.

4. Ruchy sztywne i przekształcenie jednorodne

4.1. Wprowadzenie

Znaczna część kinematyki robota jest poświęcona różnym układom współrzędnych,

potrzebnym do przedstawienia położeń i orientacji obiektów sztywnych, oraz
przekształceniom tych układów współrzędnych. Rzeczywiście, geometria przestrzeni
trójwymiarowej i ruchów sztywnych odgrywa główną rolę we wszystkich aspektach
manipulacji robota. W tej części wykładu omówimy obroty (rotacje) i przesunięcia
(translacje) oraz wprowadzimy pojęcie przekształceń jednorodnych. Przekształcenie

jednorodne można traktować jako operację, wyrażającą jednocześnie obroty i przesunięcia za
pomocą jednej macierzy. W dalszej części wykładów zostanie to wykorzystane do
wyprowadzenia tzw. równań kinematyki prostej manipulatorów sztywnych.

4.2. Obroty

Rozpatrzmy zatem następującą sytuację: rys. 28 przedstawia sztywny obiekt S, do

którego przyłożono układ współrzędnych Ox

1

y

1

z

1

.

Rys. 28. Układ współrzędnych związany z ciałem sztywnym

Załóżmy, że chcemy znaleźć zależność pomiędzy współrzędnymi punktu P na

obiekcie S w układzie współrzędnych Ox

1

y

1

z

1

a współrzędnymi tego punktu w stałym (nie

obróconym) układzie odniesienia Ox

0

y

0

z

0

. Niech {i

0

, j

0

, k

0

} oznacza standardową bazę

ortonormalną w układzie Ox

0

y

0

z

0

; wówczas i

0

, j

0

, k

0

są wektorami jednostkowymi

odpowiednio wzdłuż osi x

0

,

y

0

,

z

0

.

Podobnie niech {i

1

, j

1

, k

1

} będzie standardową bazą

ortonormalną w układzie Ox

1

y

1

z

1

. Wektor od wspólnego początku O obu układów do punktu

P na obiekcie może być przedstawiony w układzie Ox

0

y

0

z

0

jako

p

0

= p

0x

i

0

+ p

0y

j

0

+ p

0z

k

0

(31)

albo w układzie Ox

1

y

1

z

1

jako

p

1

= p

1x

i

1

+ p

1y

j

1

+ p

1z

k

1

(32)

Ponieważ p

0

i p

1

są reprezentacjami tego samego wektora p, więc związki między

składowymi wektora p w obu układach współrzędnych można zapisać w postaci

p

0x

= p

0

i

0

= p

1

i

0

= p

1x

i

1

i

0

+ p

1y

j

1

i

0

+ p

1z

k

1

i

0

(33)

p

0y

= p

0

j

0

= p

1

j

0

= p

1x

i

1

j

0

+ p

1y

j

1

j

0

+ p

1z

k

1

j

0

(34)

p

0z

= p

0

k

0

= p

1

k

0

= p

1x

i

1

k

0

+ p

1y

j

1

k

0

+ p

1z

k

1

k

0

(35)

Jeśli przyjąć





















=

z

y

x

p

p

p

0

0

0

0

p

i





















=

z

y

x

p

p

p

1

1

1

1

p

, to równania (33) – (35) możemy zapisać jako równanie

wektorowe

p

0

=

R

0

1

p

1

,

(36)

w którym





















⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

1

0

k

k

k

j

k

i

j

k

j

j

j

i

i

k

i

j

i

i

R

(37)

Macierz 3 x 3 reprezentuje przekształcenie punktu P ze współrzędnych w układzie

Ox

1

y

1

z

1

na współrzędne w układzie Ox

0

y

0

z

0

. Jeżeli punkt w układzie Ox

1

y

1

z

1

jest określony za

pomocą wektora

p

1

, wówczas

R

0

1

p

1

reprezentuje ten sam wektor w układzie współrzędnych

Ox

0

y

0

z

0

.

Podobnie możemy napisać

p

1x

=

p

1

i

1

=

p

0

i

1

= p

0x

i

0

i

1

+ p

0y

j

0

i

1

+ p

0z

k

0

i

1

(38)

p

1y

=

p

1

j

1

=

p

0

j

1

= p

0x

i

0

j

1

+ p

0y

j

0

j

1

+ p

0z

k

0

j

1

(39)

p

1z

=

p

1

k

1

=

p

0

k

1

= p

0x

i

0

k

1

+ p

0y

j

0

k

1

+ p

0z

k

0

k

1

(40)

gdzie





















⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

0

1

k

k

k

j

k

i

j

k

j

j

j

i

i

k

i

j

i

i

R

(41)

Macierz

R

1

0

reprezentuje przekształcenie odwrotne do przekształcenia

R

0

1

.

Ponieważ iloczyn

skalamy jest przemienny, tzn.

i

0

j

0

=

j

0

i

0

itd., więc

T

R

R

R

)

(

)

(

1

0

1

1

0

0

1

=

=

−

(42)

Taka macierz, której odwrotność jest macierzą transponowaną, nazywa się macierzą

ortogonalną. Wektory kolumnowe macierzy

R

0

1

mają długość jednostkową i są wzajemnie

ortogonalne. Można także pokazać, że det

R

0

1

= ±1. Jeżeli ograniczymy się natomiast do

prawoskrętnego układu współrzędnych (rys. 29), wtedy det

R

0

1

= +1.

Macierze ortogonalne o wyznaczniku +1 są nazywane macierzami obrotów lub

rotacji. Zbiór wszystkich macierzy obrotów o wymiarze 3x3 określa się symbolem SO(3).

Rys. 29. Prawoskrętny układ współrzędnych

Przykład 1.

Załóżmy, że układ Ox

1

y

1

z

1

obrócono o kąt

θ

wokół osi z

0

(rys. 30). Chcemy znaleźć

macierz R

0

1

tego przekształcenia. Zwróćmy uwagę, że (zgodnie z konwencją) dodatni

kierunek kąta

θ

jest określony regułą prawej ręki, tzn. dodatni obrót o kąt

θ

wokół osi z dałby

przesunięcie śruby prawoskrętnej wzdłuż dodatniego kierunku osi z.

Rys. 30. Obrót wokół osi z

0

Z rys. 30 widać, że

i

0

i

1

= cos

θ

(43)

j

1

i

0

= -sin

θ

(44)

j

0

j

1

= cos

θ

(45)

i

1

j

0

= sin

θ

(46)

k

0

k

1

= 1

(47)

a wszystkie pozostałe iloczyny są równe 0. Wówczas to przekształcenie R

0

1

jest postaci

x

y

z

θ





















=

1

0

0

0

cos

sin

0

sin

-

cos

R

1

0

θ

θ

θ

θ

(48)

Macierz (48) jest nazywana

podstawową macierzą obrotu lub rotacji (wokół osi z). W

takim przypadku bardziej przydatny jest opisowy zapis

R

z,

θ

zamiast R

0

1

do oznaczenia tej

macierzy. Łatwo sprawdzić, że podstawowa macierz obrotu

R

z,

θ

ma następujące własności

R

z,0

=

I

(49)

R

z,

θ

R

z,

φ

= R

z,

θ

+

φ

(50)

z czego wynika kolejna własność

R

z,

θ

-1

= R

z,-

θ

(51)

Podobnie podstawowe macierze obrotów reprezentujące obroty wokół osi

x i y są równe





















=

=

θ

θ

θ

θ

θ

cos

sin

0

sin

-

cos

0

0

0

1

R

R

,

1

0

x

(52)





















=

=

θ

θ

θ

θ

θ

cos

0

sin

-

0

1

0

sin

0

cos

R

R

,

1

0

y

(53)

i spełniają własności analogiczne do wyrażonych wzorami (49) – (51).

Możemy także interpretować daną macierz obrotu jako macierz wyznaczającą

orientację układu współrzędnych

Ox

1

y

1

z

1

względem układu

Ox

0

y

0

z

0

. Rzeczywiście, kolumny

macierzy

R

0

1

są cosinusami kierunkowymi osi układu

Ox

1

y

1

z

1

w stosunku do osi układu

Ox

0

y

0

z

0

. Na przykład pierwsza kolumna (i

1

i

0

,

i

1

j

0

,

i

1

k

0

)

T

macierzy

R

0

1

opisuje kierunek osi

x

1

względem układu

Ox

0

y

0

z

0

.

Przykład 2.

Rozważmy układy

Ox

0

y

0

z

0

i

Ox

1

y

1

z

1

pokazane na rys. 31.

Rys. 31. określenie wzajemnej orientacji dwóch układów współrzędnych

Rzutowanie wektorów jednostkowych

i

1

,

j

1

,

k

1

na

i

0

,

j

0

,

k

0

daje współrzędne wektorów

i

1

,

j

1

,

k

1

w układzie

Ox

0

y

0

z

0

. Widzimy, że współrzędne wektora i

1

są równe (l/

2

, 0, l/

2

)

T

,

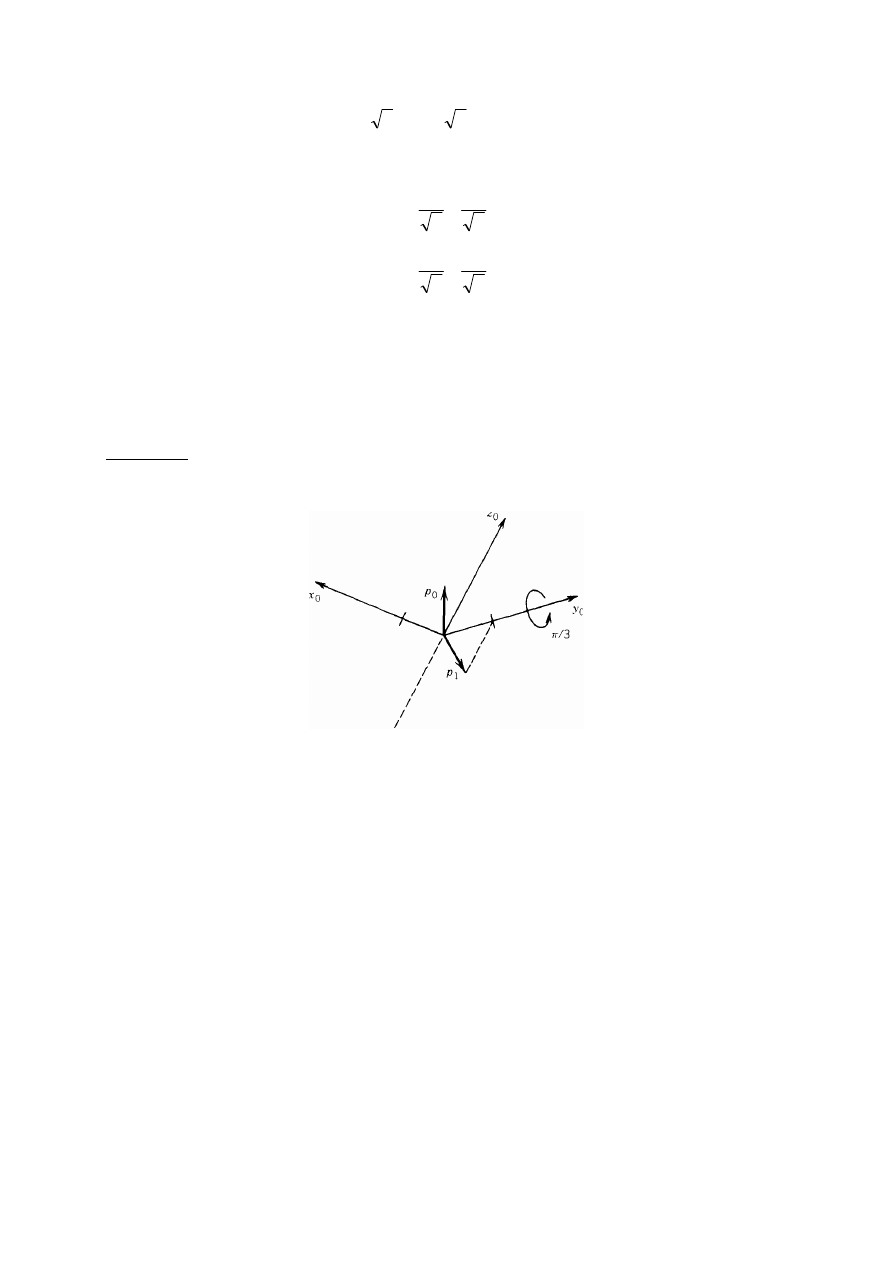
współrzędne wektora j

1

są równe (l/

2

, 0, -l/

2

)

T

i współrzędne wektora k

1

są równe (0, 1,

0)

T

. Macierz obrotu R

0

1

określająca orientację układu Ox

1

y

1

z

1

względem układu Ox

0

y

0

z

0

zawiera te współrzędne jako kolumny, tzn.





























−

=

0

2

1

2

1

1

0

0

0

2

1

2

1

R

1

0

(54)

W trzeciej interpretacji macierz obrotu R

∈

SO(3) jest operatorem działającym na

wektory w ustalonym układzie współrzędnych

Ox

0

y

0

z

0

. Inaczej mówiąc, zamiast odnoszenia

współrzędnych ustalonego wektora do dwóch różnych układów współrzędnych, wyrażenie
(41) może reprezentować współrzędne punktu

P

1

w układzie

Ox

0

y

0

z

0

otrzymanego z punktu

P

0

przez dany obrót.

Przykład 3.

Obracamy wektor p

0

= (l, l, 0)

T

wokół osi

y

0

o kąt

π

/2, jak pokazano na rys. 32.

Rys. 32. Obrót wektora wokół osi

Otrzymany wektor

p

1

jest dany wzorem





















−

=





















⋅





















=

⋅

=

1

1

0

0

1

1

0

0

1

-

0

1

0

1

0

0

p

R

p

0

2

/

,

1

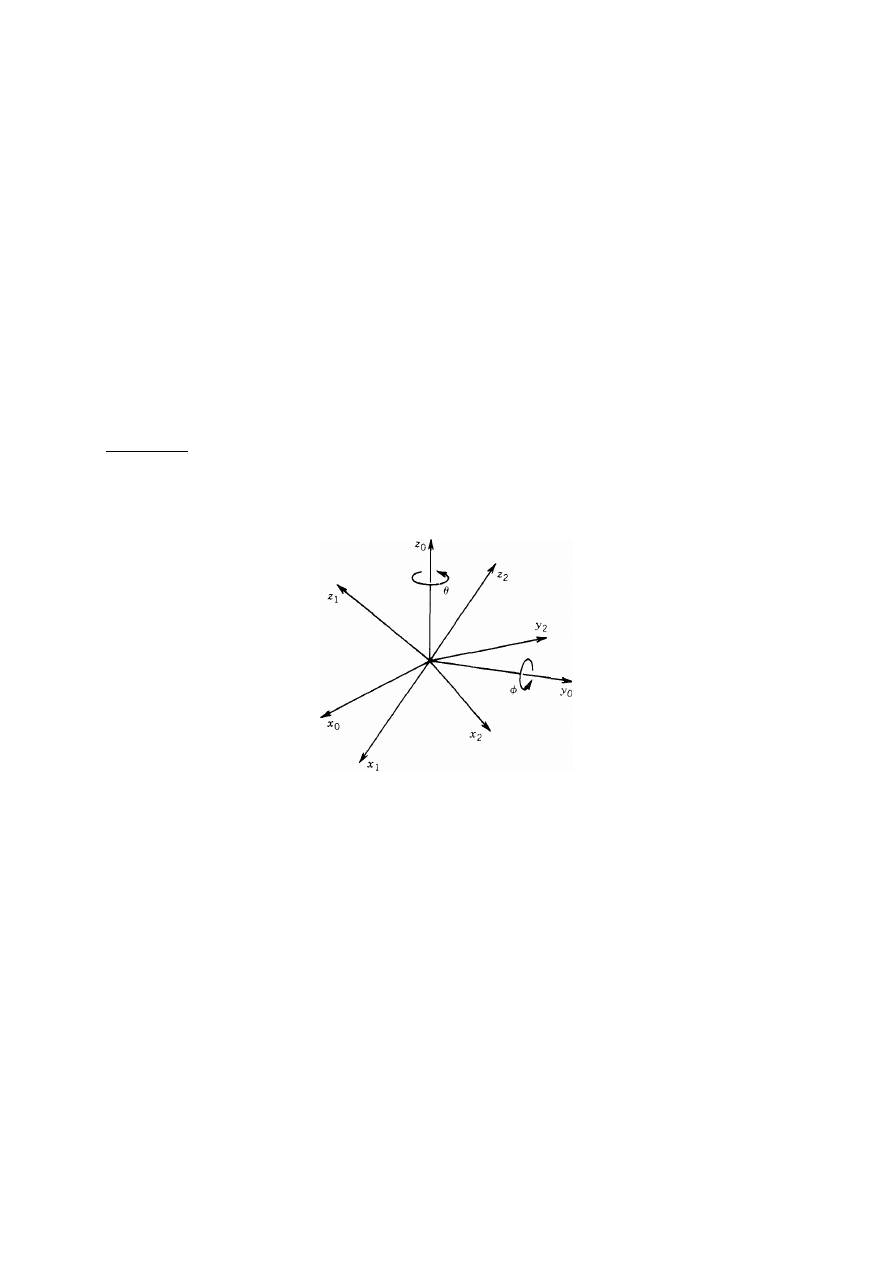
π

y

(55)

Podsumowanie:

W tym dziale zobaczyliśmy, że macierz obrotu

R

∈

SO(3) może być interpretowana na

trzy różne sposoby:

1) reprezentuje przekształcenie współrzędnych punktu

P w dwóch różnych układach,

2) wyznacza orientację przekształconego układu współrzędnych w odniesieniu do ustalonego
układu współrzędnych,

3) jest operatorem przekształcającym wektor p przez obrót w nowy wektor

Rp w tym samym

układzie współrzędnych.

Konkretna interpretacja danej macierzy obrotu

R zastosowanej w problemie musi być

sprecyzowana w kontekście tego problemu.

4.3. Składanie obrotów

W tym rozdziale omówimy składanie obrotów. Dla zrozumienia treści następnych

wykładów ważne jest, aby Czytelnik dobrze przyswoił sobie materiał z tej części, przed
przejściem dalej. Przypomnijmy, że macierz R

0

1

w równaniu (36) reprezentuje obrót między

układami współrzędnych Ox

0

y

0

z

0

i Ox

1

y

1

z

1

. Załóżmy, że dokładamy trzeci układ

współrzędnych Ox

2

y

2

z

2

powiązany z układami Ox

0

y

0

z

0

i Ox

1

y

1

z

1

przez obroty. Dany punkt P

może być wtedy reprezentowany na trzy sposoby przez wektory: p

0

, p

1

, p

2

w trzech układach

współrzędnych. Związki między tymi trzema reprezentacjami punktu P są następujące

p

0

= R

0

1

p

1

(56)

p

1

= R

0

2

p

2

(57)

p

1

= R

1

2

p

2

(58)

gdzie każda macierz R

i

j

jest macierzą obrotu. Zauważmy, że macierze R

0

1

i R

0

2

reprezentują

obroty względem osi układu Ox

0

y

0

z

0

, podczas gdy R

1

2

reprezentuje obrót względem układu

Ox

1

y

1

z

1

. Jeśli podstawimy wzór (58) do równości (56), to otrzymamy

p

0

= R

0

1

R

1

2

p

2

(59)

a po porównaniu zależności (57) i (59) dostajemy równość

R

0

2

= R

0

1

R

1

2

(60)

Równanie (60) jest prawem składania dla obrotów. Oznacza, że aby przekształcić

współrzędne punktu P z jego reprezentacji p

2

w układzie Ox

2

y

2

z

2

na reprezentację p

0

w

układzie Ox

0

y

0

z

0

, możemy ją najpierw przekształcić na jego reprezentację p

1

, w układzie

Ox

1

y

1

z

1

, używając macierzy R

1

2

, a potem przekształcić p

1

na p

0

używając macierzy R

0

1

.

Natomiast równanie (59) możemy interpretować następująco. Załóżmy początkowo,

że wszystkie trzy układy pokrywają się. Najpierw obracamy układ Ox

1

y

1

z

1

względem układu

Ox

0

y

0

z

0

zgodnie z przekształceniem R

0

1

.

Potem, przy pokrywających się układach Ox

1

y

1

z

1

i

Ox

2

y

2

z

2

obracamy układ Ox

2

y

2

z

2

względem Ox

1

y

1

z

1

zgodnie z przekształceniem R

1

2

. W

każdym przypadku układ, względem którego odbywa się obrót, nazywamy układem
bieżącym.

Uwaga! Odtąd dla wygody będziemy stosować skrócone zapisy funkcji

trygonometrycznych: c

θ

= cos

θ

,

S

θ

= sin

θ

.

Przykład 4.

Załóżmy, że macierz R reprezentuje obrót o kąt

φ

wokół bieżącej osi y z następnym

obrotem o kąt

θ

wokół bieżącej osi z. Wówczas macierz R jest określona wzorem





















⋅

⋅

⋅

−

⋅

=





















⋅





















−

=

⋅

=

φ

θ

φ

θ

φ

θ

θ

φ

θ

φ

θ

φ

θ

θ

θ

θ

φ

φ

φ

φ

θ

φ

c

s

s

c

s

-

0

c

s

s

s

c

c

c

1

0

0

0

c

s

0

s

-

c

c

0

s

0

1

0

s

0

c

R

R

R

,

,

z

y

(61)

Należy pamiętać, że kolejność wykonywania obrotów, a co za tym idzie kolejność

mnożenia macierzy obrotów, jest decydująca. Obrót, w przeciwieństwie do położenia, nie jest
wielkością wektorową i nie podlega prawu dodawania wektorów, wobec tego składanie

obrotów na ogół nie jest przemienne.

Przykład 5.

Załóżmy, że poprzednio opisane obroty są wykonywane w odwrotnej kolejności, tzn.

najpierw obrót wokół bieżącej osi

z, potem obrót wokół bieżącej osi y.

Wówczas macierz obrotu jest określona wzorem





















⋅

⋅

⋅

−

⋅

=





















−

⋅





















=

⋅

=

φ

φ

φ

θ

θ

φ

θ

θ

φ

θ

θ

φ

φ

φ

φ

φ

θ

θ

θ

θ

φ

θ

c

0

s

-

s

s

c

c

s

c

s

s

c

c

c

0

s

0

1

0

s

0

c

1

0

0

0

c

s

0

s

-

c

R

R

R

,

,

'

y

z

(62)

Po porównaniu wzorów (61) i (62) wyraźnie widać, że

R ≠ R'.

Często jest pożądane wykonanie raczej ciągu obrotów, każdego wokół danego

ustalonego układu współrzędnych, niż wokół kolejnych bieżących układów. Przykładowo
możemy chcieć dokonać obrotu wokół osi

X

0

,

a następnie obrotu wokół osi

y

0

(nie zaś

y

1

).

Wtedy układ

Ox

0

y

0

z

0

jest tzw.

układem ustalonym. W tym przypadku wcześniej określone

prawo składania nie jest prawdziwe, natomiast właściwym prawem składania jest po prostu
mnożenie kolejnych macierzy obrotów w kolejności odwrotnej do podanej wzorem (60).
Zauważmy, że same obroty nie są wykonywane w odwrotnej kolejności. Raczej są one
wykonywane wokół układu ustalonego niż wokół bieżącego.

Przykład 6.

Załóżmy, że macierz obrotu

R reprezentuje obrót o kąt

φ

wokół osi

y

0

, a następnie

obrót o kąt

θ

wokół ustalonej osi

Z

0

.

Odnieśmy to do rys. 33. Niech

p

0

,

p

1

i

p

2

będą

reprezentacjami wektora

p.

Rys. 33. Składanie obrotów

Początkowo osie ustalone i bieżące są te same, mianowicie

Ox

0

y

0

z

0

, i dlatego możemy

napisać jak poprzednio

p

0

=

R

y,

φ

p

1

(63)

gdzie

R

y,

φ

jest podstawową macierzą obrotu wokół osi

y. Teraz, ponieważ drugi obrót odbywa

się wokół ustalonego układu

Ox

0

y

0

z

0

, a nie bieżącego układu

Ox

1

y

1

z

1

, nie możemy stwierdzić,

czy

p

1

=

R

z,

θ

p

2

(64)

ponieważ to wymagałoby interpretacji

R

z,

θ

jako obrotu wokół osi

z

1

. Aby móc użyć naszego

wcześniejszego prawa składania, musimy mieć układy: ustalony i bieżący. W tym przypadku
osie

z

0

i

z

1

nałożone na siebie. Dlatego trzeba najpierw „cofnąć" poprzedni obrót, następnie

wykonać obrót wokół osi

z

0

i na koniec przywrócić wyjściowe przekształcenie, czyli

p

1

=

R

y,-

φ

R

z,

θ

R

y,

φ

p

2

(65)

To jest właściwe wyrażenie, a nie zależność (64). Teraz podstawiając je do wzoru (63),
otrzymujemy

P

0

=

R

y,

φ

p

1

=

R

y,

φ

R

y,-

φ

R

z,

θ

R

y,

φ

p

2

(66)

Nie musimy pamiętać powyższego wyprowadzenia; wystarczy zauważyć przez

porównanie wzorów (61) i (66), że otrzymujemy te same podstawowe macierze obrotów w
odwrotnej kolejności.

Prawo składania obrotów możemy podsumować następującą obserwacją. Dla danego

układu ustalonego Ox

0

y

0

z

0

, układu bieżącego Ox

1

y

1

z

1

i macierzy obrotu R

0

1

wiążącej te

układy, jeżeli trzeci układ Ox

2

y

2

z

2

jest otrzymany przez obrót R

1

2

wykonany względem

układu bieżącego, to aby otrzymać obrót R

0

2

mnożymy prawostronnie macierz R

0

1

przez R

1

2

,

czyli

R

0

2

= R

0

1

R

1

2

(67)

Jeżeli drugi obrót ma być wykonany względem układu ustalonego, to mnożymy

lewostronnie macierz R

0

1

przez R

1

2

, i otrzymujemy

R

0

2

= R

1

2

R

0

1

(68)

W każdym przypadku macierz R

0

2

reprezentuje przekształcenie między układami Ox

0

y

0

z

0

i

Ox

2

y

2

z

2

. Jednakże układ, który powstaje z zależności (67), będzie inny od powstałego z

zależności (68).

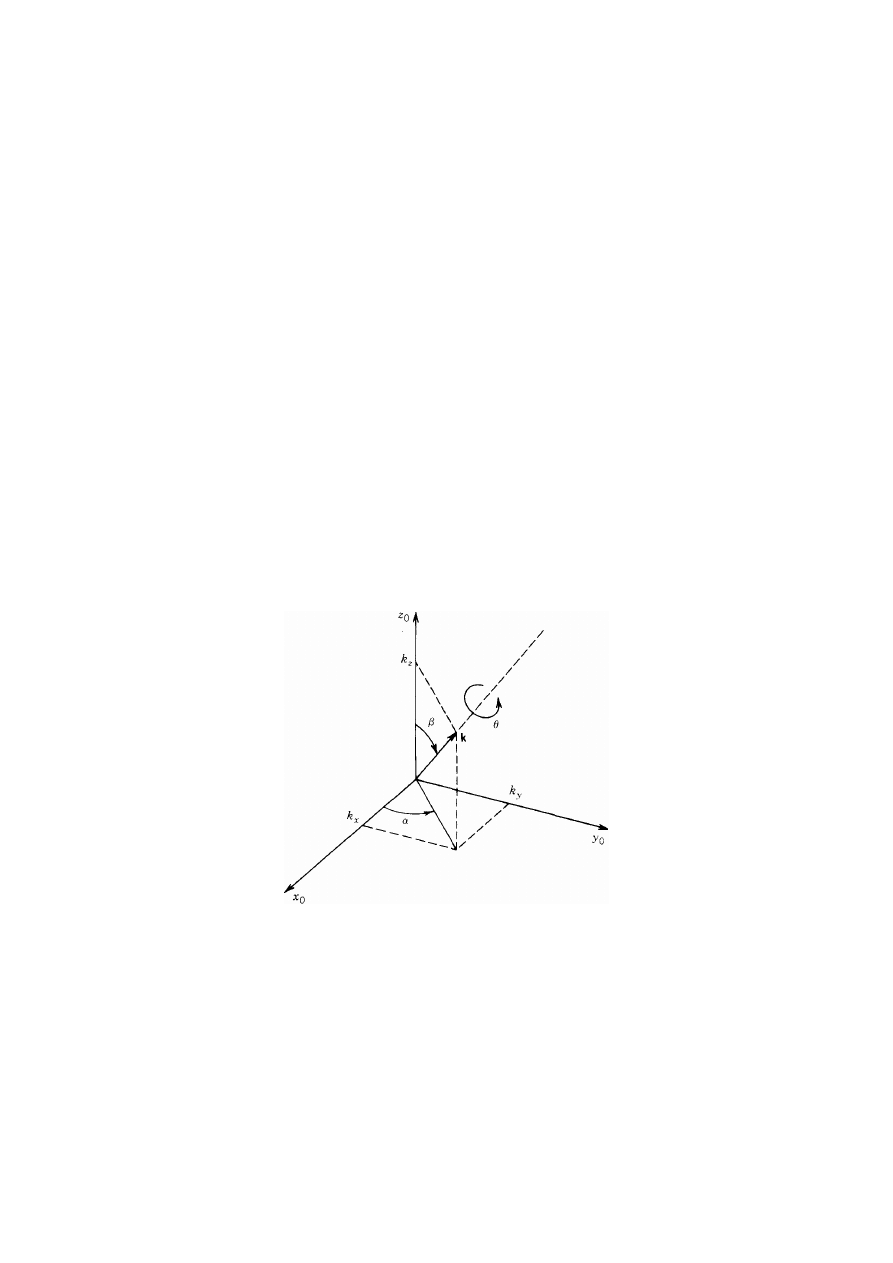
4.4. Obrót wokół dowolnej osi

Obroty nie zawsze są wykonywane wokół osi układu współrzędnych. Często jesteśmy

zainteresowani obrotem wokół dowolnej osi w przestrzeni. Niech k = (k

x

, k

y

, k

z

)

T

będzie

wyrażonym w układzie Ox

0

y

0

z

0

wektorem jednostkowym, definiującym pewną oś. Chcemy

wyprowadzić macierz obrotu R

k,

θ

reprezentującą obrót o kąt

θ

wokół tej osi (rys. 34).

Rys. 34. Obrót wokół dowolnej osi

Istnieje kilka sposobów otrzymania macierzy R

k,

θ

. Najłatwiejszym jest obrócenie

wektora k na jedną z osi układu, np. z

0

, potem obrócenie wokół osi z

0

o kąt

θ

i wreszcie

obrócenie wektora k z powrotem do jego wyjściowego położenia. Na rys. 34 pokazano, że

możemy obrócić wektor k na oś z

0

,

obracając najpierw wokół osi z

0

o kąt -

α

, potem zaś

obracając wokół osi y

0

o kąt -

β

. Ponieważ wszystkie obroty są wykonywane względem

ustalonego układu Ox

0

y

0

z

0,

więc macierz R

k,

θ

otrzymamy jako złożenie

R

k,

θ

= R

z,

α

R

y,

β

R

z,

θ

R

y,-

β

R

z,-

α

(69)

Na podstawie rys. 34 widzimy, że jeśli k jest wektorem jednostkowym, to

2

2

sin

y

x

y

k

k

k

+

=

α

(70)

2

2

cos

y

x

x

k

k

k

+

=

α

(71)

2

2

sin

y

x

k

k

+

=

β

(72)

cos

β

= k

z

(73)

Po podstawieniu równań (70)-(73) do zależności (69) i dość długich lecz niezbyt

złożonych obliczeniach otrzymujemy





















+

−

−

−

+

+

+

−

+

=

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

cos

sin

sin

sin

cos

sin

sin

sin

cos

R

2

2

2

v

k

k

v

k

k

k

v

k

k

k

v

k

k

v

k

k

v

k

k

k

v

k

k

k

v

k

k

v

k

z

x

z

y

y

z

x

x

z

y

y

z

y

x

y

z

x

z

y

x

x

k,

(74)

Gdzie v

θ

= 1 – cos

θ

.

4.4. Dalsze własności obrotów

Dziewięć elementów r

ij

dowolnej macierzy obrotów

R jak we wzorze (37) nie jest

wielkościami niezależnymi. Rzeczywiście, ciało sztywne ma co najwyżej trzy obrotowe
stopnie swobody i dlatego co najwyżej trzy wielkości są potrzebne do wyznaczenia jego
orientacji. W tej części wykładu omówimy trzy sposoby reprezentacji dowolnego obrotu przy
użyciu tylko trzech niezależnych wielkości. Pierwszym jest tzw. reprezentacja „os-kąt” Drugi

to reprezentacja za pomocą kątów Eulera, a trzeci – reprezentacja „obrót-nachylenie-
odchylenie".

Reprezentacja „oś-kąt”

Macierz obrotu

R

∈

SO(3) można zawsze przedstawić w postaci pojedynczego obrotu

wokół odpowiedniej osi o odpowiedni kąt jako

R = R

k,

θ

(75)

gdzie

k jest wektorem jednostkowym definiującym oś obrotu, a

θ

jest kątem obrotu wokół tej

osi. Równanie (75) jest nazywane reprezentacją „oś-kąt” macierzy

R. Jeśli zatem mamy

dowolną macierz obrotu

R o elementach (r

ij

), to kąt

θ

i oś wektora

k odpowiadające tej

macierzy są dane wyrażeniami













−

+

+

=













−

=

−

−

2

1

cos

2

1

)

R

(

cos

33

22

11

1

1

r

r

r

Tr

θ

(76)

Gdzie Tr(

R) oznacza ślad macierzy R oraz





















−

−

−

=

12

21

31

13

23

32

2sin

1

k

r

r

r

r

r

r

θ

(77)

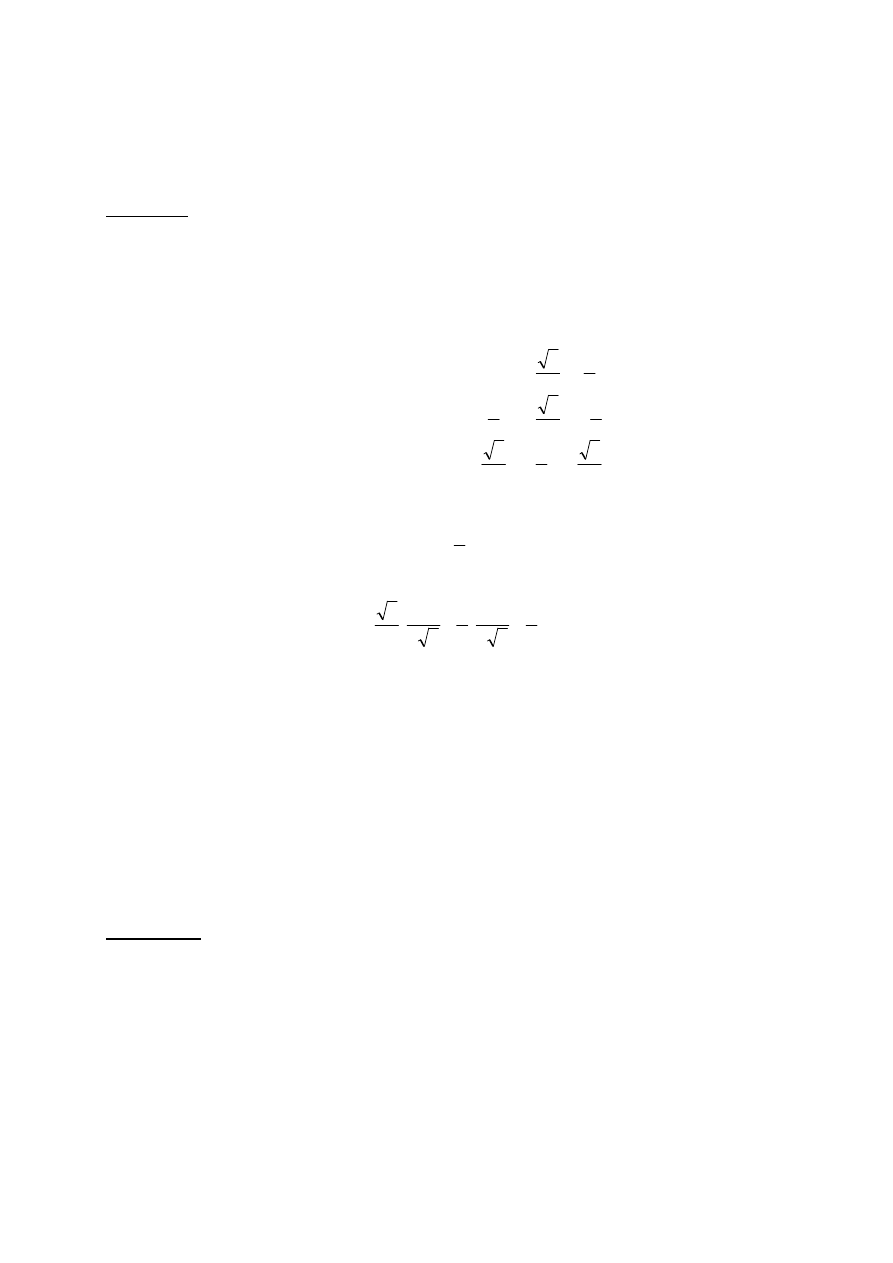
Reprezentacja „oś-kąt" nie jest jednoznaczna, ponieważ obrót o kąt -

θ

wokół osi wektora – k

jest taki sam, jak obrót o kąt

θ

wokół osi wektora k, tzn.

R

k,

θ

= R

-k,-

θ

(78)

Jeżeli

θ

=

0, to R jest macierzą jednostkową, a oś obrotu nie jest określona.

Przykład 7.

Załóżmy, że macierz R została utworzona przez obrót o 90° wokół osi z

0

,

następnie

przez obrót o 30° wokół osi y

0

, a w końcu przez obrót o 60° wokół osi x

0

. Wówczas





































−

−

−

=





















°

°

°

−

°

⋅

⋅





















°

°

−

°

°

⋅





















°

°

°

−

°

=

=

4

3

4

1

2

3

4

3

4

3

2

1

2

1

2

3

0

1

0

0

0

90

cos

90

sin

0

90

sin

90

cos

30

cos

0

30

sin

0

1

0

30

sin

0

30

cos

60

cos

60

sin

0

60

sin

60

cos

0

0

0

1

R

R

R

R

90

,

30

,

60

,

z

y

x

(79)

Widzimy, że Tr(

R) = 0 i stąd odpowiedni kąt ze wzoru (76) jest równy

°

=

−

=

−

120

)

2

1

(

cos

1

θ

(80)

Natomiast z wzoru (77) oś jest określona przez wektor

T













+

−

=

2

1

3

2

1

,

2

1

3

2

1

,

3

3

k

(81)

Powyższa reprezentacja „

oś-kąt" charakteryzuje dany obrót za pomocą czterech

wielkości, a mianowicie trzech składowych osi wektora

k oraz kąta

θ

. Jednak, ponieważ oś

wektora

k jest wyznaczona przez wektor jednostkowy, tylko dwie z jej składowych są

niezależne. Trzecia jest narzucona przez warunek, że wektor

k ma długość jednostkową.

Dlatego tylko trzy niezależne wielkości są wymagane w tej reprezentacji obrotu

R. Możemy

przedstawić reprezentację „

kąt-oś" za pomocą pojedynczego wektora r postaci

T

z

y

x

T

z

y

x

k

k

k

r

r

r

r

)

,

,

(

)

,

,

(

⋅

⋅

⋅

=

=

θ

θ

θ

(82)

Zauważmy, że ponieważ

k jest wektorem jednostkowym, więc długość wektora r jest równa

mierze kąta

θ

, a kierunek jest ten sam co osi k.

Kąty Eulera

Bardziej ogólną metodą wyznaczania macierzy obrotu w zależności od trzech

niezależnych wielkości jest użycie tzw.

kątów Eulera. Rozważmy ponownie ustalony układ

współrzędnych

Ox

0

y

0

z

0

i układ obrócony

Ox

1

y

1

z

1

pokazane na rys. 35. Możemy wówczas

określić orientację układu

Ox

1

y

1

z

1

względem układu

Ox

0

y

0

z

0

za pomocą trzech kątów (

θ

,

φ

,

ψ

)

znanych jako

kąty Eulera, a otrzymanych przez trzy kolejne, następujące obroty: najpierw

obrót wokół osi

z o kąt

φ

, następnie obrót wokół bieżącej osi

y o kąt

θ

, na końcu zaś obrót

wokół bieżącej osi

z o kąt

ψ

.

Rys. 35. Reprezentacja kątów Eulera

W terminologii podstawowych macierzy obrotów wynikowy obrót R

0

1

może być

otrzymany jako iloczyn





















−

+

−

+

−

−

−

=

=





















−

⋅





















−

⋅





















−

=

⋅

⋅

=

θ

ψ

θ

ψ

θ

θ

φ

ψ

φ

ψ

θ

φ

ψ

φ

ψ

θ

φ

θ

φ

ψ

φ

ψ

θ

φ

ψ

φ

ψ

θ

φ

ψ

ψ

ψ

ψ

θ

θ

θ

θ

φ

φ

φ

φ

ψ

θ

φ

cos

sin

sin

cos

sin

sin

sin

cos

cos

sin

cos

sin

sin

cos

cos

cos

sin

sin

cos

cos

sin

sin

cos

cos

sin

sin

cos

cos

cos

1

0

0

0

cos

sin

0

sin

cos

cos

0

sin

0

1

0

sin

0

cos

1

0

0

0

cos

sin

0

sin

cos

R

R

R

R

z,

y,

z,

1

0

(83)

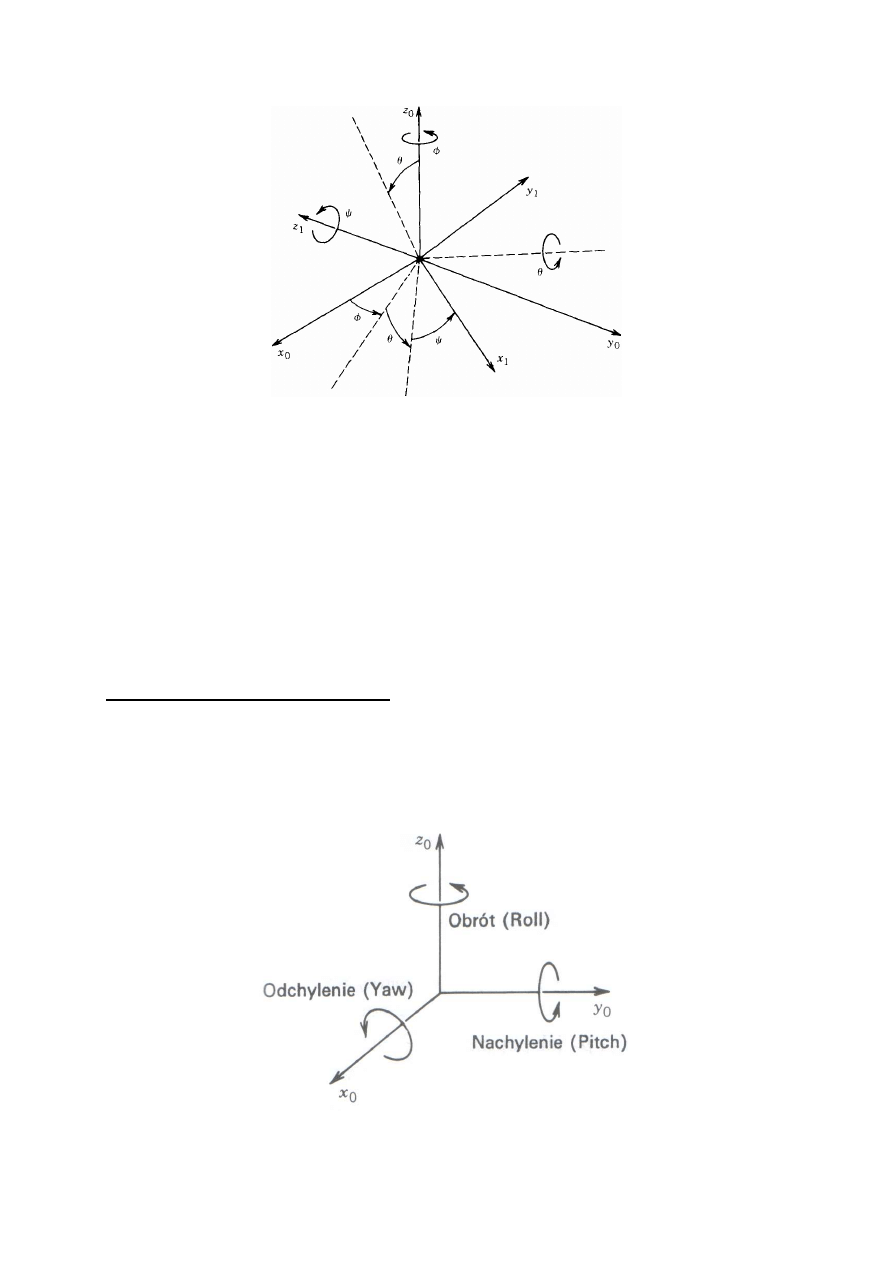
Kąty obrotu, nachylenia i odchylenia

Macierz obrotu

R może także być określona jako iloczyn kolejnych obrotów wokół osi

układu współrzędnych

x

0,

y

0,

z

0

wziętych w określonej kolejności. Obroty te określają tzw.

kąty

obrotu, nachylenia i odchylenia

,

które możemy także zapisać jako

φ

,

θ

,

ψ

. Zilustrowano je na

rys. 36.

Rys. 36. Kąty obrotu, nachylenia, odchylenia (RPY – Roll, Pitch, Yaw)

Określamy kolejność obrotów jako x-y-z, innymi słowy najpierw odchylenie wokół osi

x

0

o kąt

ψ

, potem nachylenie wokół osi y

0

o kąt

θ

i ostatecznie obrót wokół osi

Z

0

kąt

φ

.

Ponieważ kolejne obroty są odnoszone do układu ustalonego, wynikowa macierz
przekształcenia jest dana przez iloczyn





















−

+

−

+

+

+

−

=

=





















−

⋅





















−

⋅





















−

=

⋅

⋅

=

ψ

θ

ψ

θ

θ

ψ

θ

φ

ψ

φ

ψ

θ

φ

ψ

φ

θ

φ

ψ

θ

φ

ψ

φ

ψ

θ

φ

ψ

φ

θ

φ

ψ

ψ

ψ

ψ

θ

θ

θ

θ

φ

φ

φ

φ

ψ

θ

φ

cos

cos

sin

cos

sin

cos

sin

sin

sin

cos

sin

sin

sin

sin

cos

cos

sin

cos

sin

cos

sin

sin

sin

sin

cos

cos

sin

cos

cos

cos

sin

0

sin

cos

0

0

0

1

cos

0

sin

0

1

0

sin

0

cos

1

0

0

0

cos

sin

0

sin

cos

R

R

R

R

x,

y,

z,

1

0

(84)

Oczywiście zamiast odchylenia-nachylenia-obrotu względem układów ustalonych

możemy także interpretować powyższe przekształcenie jako obrót-nachylenie-odchylenie, w
tej kolejności, rozpatrując każde w stosunku do układu bieżącego. Końcowym rezultatem jest
ta sama macierz (84).