Małgorzata Bielewicz
204829

Projekt reduktora dwustopniowego

Dane wejściowe

Moment na wale wyjściowym

Prędkośc na wale wyjściowym Całkowite przełożenie

Mwy

273



Nm

nwy

94



uc

31



obr

min

DOBÓR SILNIKA

1. Moc na wale wyjściowym

Pwy Mwy

nwy

9550



2.687





kW

2. Współczynnik sprawności napędu

ηwpz

0.97



sprawność walcowej przekładni zębatej

Kurmaz - Tabela 2.1., str 12

ηłt

0.993



sprawność łożysk tocznych

ηs

0.98



sprawność sprzęgła

η0

ηwpz ηłt



ηs



ηwpz



ηłt



0.909





3. Moc obliczeniowa silnika

Pso

Pwy

η0

2.955





kW

4. Obliczeniowa częstotliwość obracania wału wyjściowego dla zadanego
przełożenia

nwy

94



obr

min

5. Dobór silnika z katalogu

Sg 100L-2

Ps

3



kW

ns

2905



obr

min

6. Rzeczywiste przełożenie całkowite układu napędowego

u0

ns

nwy

31





7. Przełożenie na poszczególnych stopniach reduktora

u1

6



u2

uc
u1

5.167





8. Moc poszczególnych wałów napędowych

Ps

3



kW

P1 Ps



P2 P1 ηwpz ηłt









2.89





kW

P3 P2 ηwpz ηłt









2.783





kW

9. Prędkość obracania się poszczególnych wałów

ns

2905



obr

min

n1 ns

2905





obr

min

n2

n1
u1

484





obr

min

n3

n2
u2

94





obr

min

10. Moment obrotowy

Ms

9550

Ps

ns



10





Nm

M1

9550

P1

n1



10





Nm

M2

9550

P2

n2



57





Nm

M3

9550

P3

n3



284





Nm

11. Obliczenie średnicy wałów

ks

25



MPa

Kurmaz , str. 11

dw1

3

10

3

M1



0.2

ks



12.54





mm

przyjmuję

dw1

15



mm

dw2

3

10

3

M2



0.2

ks



22.506





mm

dw2

25



mm

dw3

40



mm

dw3

3

10

3

M3



0.2

ks



38.42





mm

OBLICZENIA PRZEKŁADNI ZĘBATYCH

O ZĘBACH PROSTYCH

STOPIEŃ I

Dobieram materiał z tabeli

Mazanek, Tabela 4.10, str 241

Stal konstrukcyjna do ulepszenia cieplnego 34CrNiMo6

wytrzymałość zmęczeniowa kontaktowa

σH_lim

770



MPa

wytrzymałość zmęczeniowej podstawy zęba

σF_lim

320



MPa

1. Naprężenia dopuszczalne

σHP

0.8

σH_lim



616





Czas pracy przekładni

τ

10000



h

Liczba cykli pracy przekładni

nt

60

ns



τ



1.743

10

9







Dobieram współczyniki trwałości

YNT

1



ZNT

1



Dobieram współczyniki zastosowania

KA

1.5



KH

1.5



Mazanek, Tabela 4.3, str 228

2. Średnica podziałowa zębnika

κ

1



współczynnik szerokości wieńca

Przyjmuję

dp1

16.2 10

3



3

Ps KH



κ σHP

2



ns



u1

1



u1





27.256





mm

dp1

30



mm

3. Odległość między środkami kół (określenie długości osi kół)

a

dp1

2

1

u1









105





mm

z tabeli dobieram

aw

125



mm

4. Ponowne obliczenie średnicy podziałowej

dp1

2

a



1

u1



30





mm

5. Liczba zębów zębnika

zp1

17



6. Obliczenie modułu

m

dp1
zp1

1.8





m

2



7. Obliczenie liczby zębów koła

zp2 zp1 u1



102





8. Nominalna odległość osi

a

zp1 zp2



2

m



119





mm

aw

125



mm

9. Obliczenie średnicy podziałowej zębnika i koła zębatego

dp1 m zp1



34





mm

dp2 m zp2



204





mm

10. Ustalenie współczynników przesunięcia zarysu

Br

aw a



a

0.05





Bp Br

1

7

Br







0.059





Σx

0.5

Bp



zp1 zp2









3.489





k

0.5

Bp Br









zp1 zp2









0.489





Podział sumy współczynników przesunięcia zarysu dokonujemy odwrotnie
proporcjonalnie do liczby zębów

x1 Σx

zp2

zp1 zp2





2.991





x2 Σx x1



0.498





11. Szerokość wieńca

bzp

30



mm

12. Średnica głów zębów

dg1 m zp1

2









38





mm

dg2 m zp2

2









208





13. Średnica stóp zębów

d1s m zp1

2.5









29





mm

d2s m zp2

2.5









199





mm

14. Toczny kąt przyporu

α

20

°



a

119



mm

cosαw

a

aw

cosα



=

aw

125



mm

αw

26.54

°



15. Wysokość głów zębów

y

1



ha1

m y

x1









7.982





mm

mm

ha2

m y

x2









2.997





Obliczenia wskaźnika zazębienia przekładni

16. Obliczenie czołowego wskaźnika zazębienia

εα

zp1

2

π



1

2

ha1



dp1











2

1

0.94

2



1





zp2

2

π



1

2

ha2



dp2











2

1

0.94

2



1







aw

0.342



π m



0.94





3.259





εα 

1.4

=

zgodne z założeniem

współczynniki:

Z

ε

4

εα



3

0.497





Y

ε

0.25

0.75

εα



0.48





17. Obciążenie zębów

Moment obrotowy

M1p

9550

Ps

n1



10





Nm

M2p

M1p m



20





Nm

Nominalna siła obwodowa

P

2000

M1p

dp1



580





N

Wartości prędkości rezonansowej

β

0

°



bo zęby proste

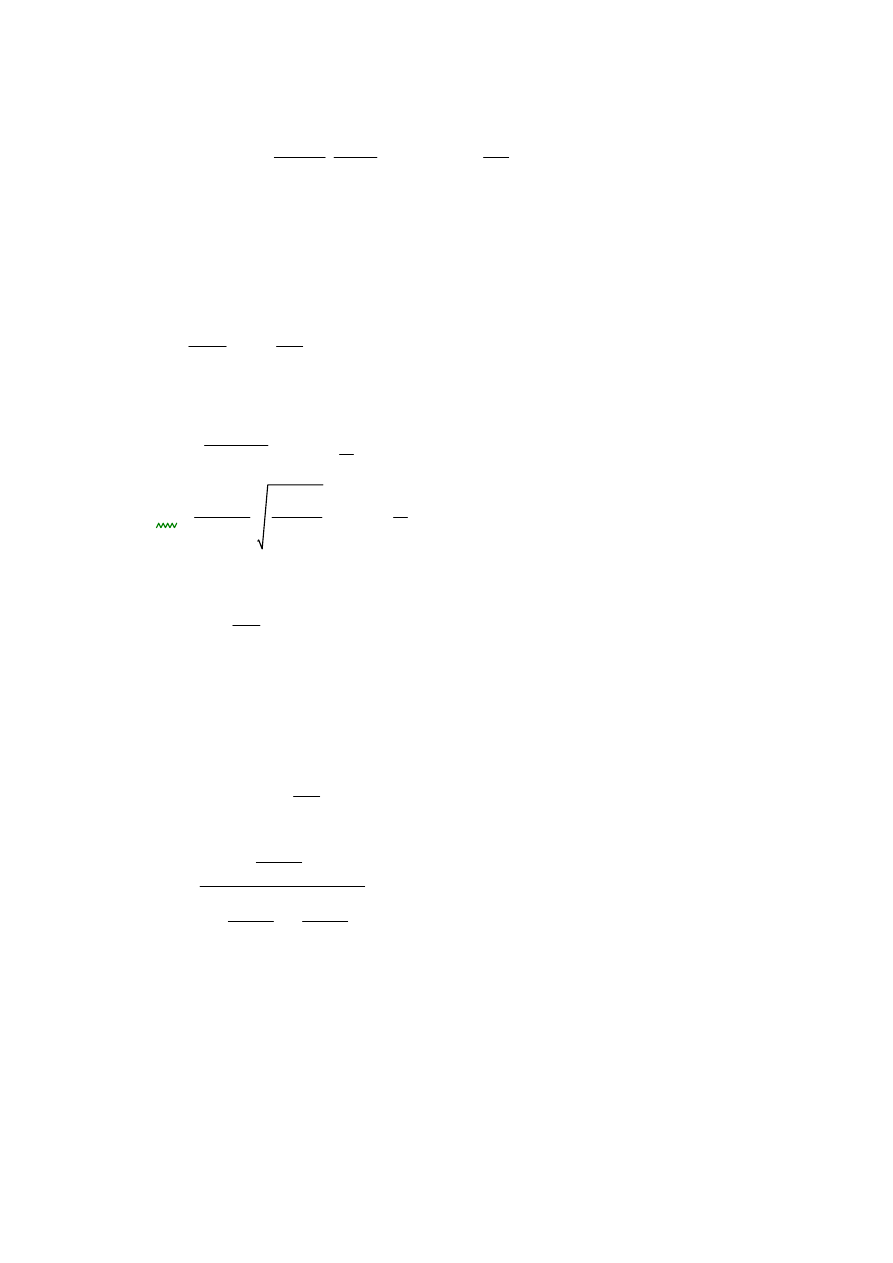
nE1zp

2.1 10

7



cos β

( )

zp1

2

m





u1

1



u1



42387.543





obr

min

Przekładnia pracuję w zakresie podrezonansowym bo

n1

0



7

nE1zp



Wskaźnik obciażenia jednostkowego

q

KA P



bzp

29





N

mm

Wskaźnik prędkości przekładni

νzp

π dp1



n1



60 1000



5.172





m

s

W

zp1 νzp



100

u1

2

u1

2

1





0.867





m

s

Obliczam współczynnik dynamiczny

K

ν

1

14.9

q

0.0193











W





1.46





Przyjmuję

KHα

1



KFα

1



Współczynnik

KHβ

1.05

0.31

bzp
dp1









2





3.8 10

3





bzp





1.405





NT

bzp

2.25

m















2

1

bzp

2.25

m





bzp

2.25

m















2



0.853





KFβ KHβ

NT

1.34





18. Sprawdzenie współczynnika bezpieczeństwa na nacisk stykowy

dla stali

Współczynnik dla zębów prostych

ZE

189.8



Z

β

1



ZH

2

sin αw

 

cos αw

 



2.237





Mazanek, Tabela 4.7 str. 235

Zx

1



Zw

1



SH

σH_lim

ZH ZE



Z

ε



Z

β



P

bzp dp1



u1

1



u1





ZNT

1

 Zw



Zx



KA Kν



KHβ



KHα





2.551





Otrzymana wartość jest poprawna

SH

1.25



czyli maksymalna niezawodność

19. Nominalna wartość sił działająca na wał

Przp1 P tan αw

 



290





N

Pnzp1

P

cos αw

 

648





N

STOPIEŃ II

Obliczenie przekładni zębatych o zębach prostych dla drugiego stopnia

Dobieram materiał z tabeli

Mazanek, Tabela 4.10 str.241

Stal konstrukcyjna do ulepszenia cieplnego 34CrNiMo6

wytrzymałość zmęczeniowa kontaktowa

σH_lim

770



wytrzymałość zmęczeniowej podstawy zęba

σF_lim

320



1. Naprężenia dopuszczalne

σHP

0.8

σH_lim



616





Czas pracy przekładni

τ

10000



h

Liczba cykli pracy przekładni

nt

60

ns



τ



1.743

10

9







Dobieram współczyniki trwałości

YNT

1



ZNT

1



Dobieram współczyniki zastosowania

KA

1.5



KH

1.5



Mazanek, Tabela 4.3 str.228

2. Średnica podziałowa zębnika

κ

1



współczynnik szerokości wieńca

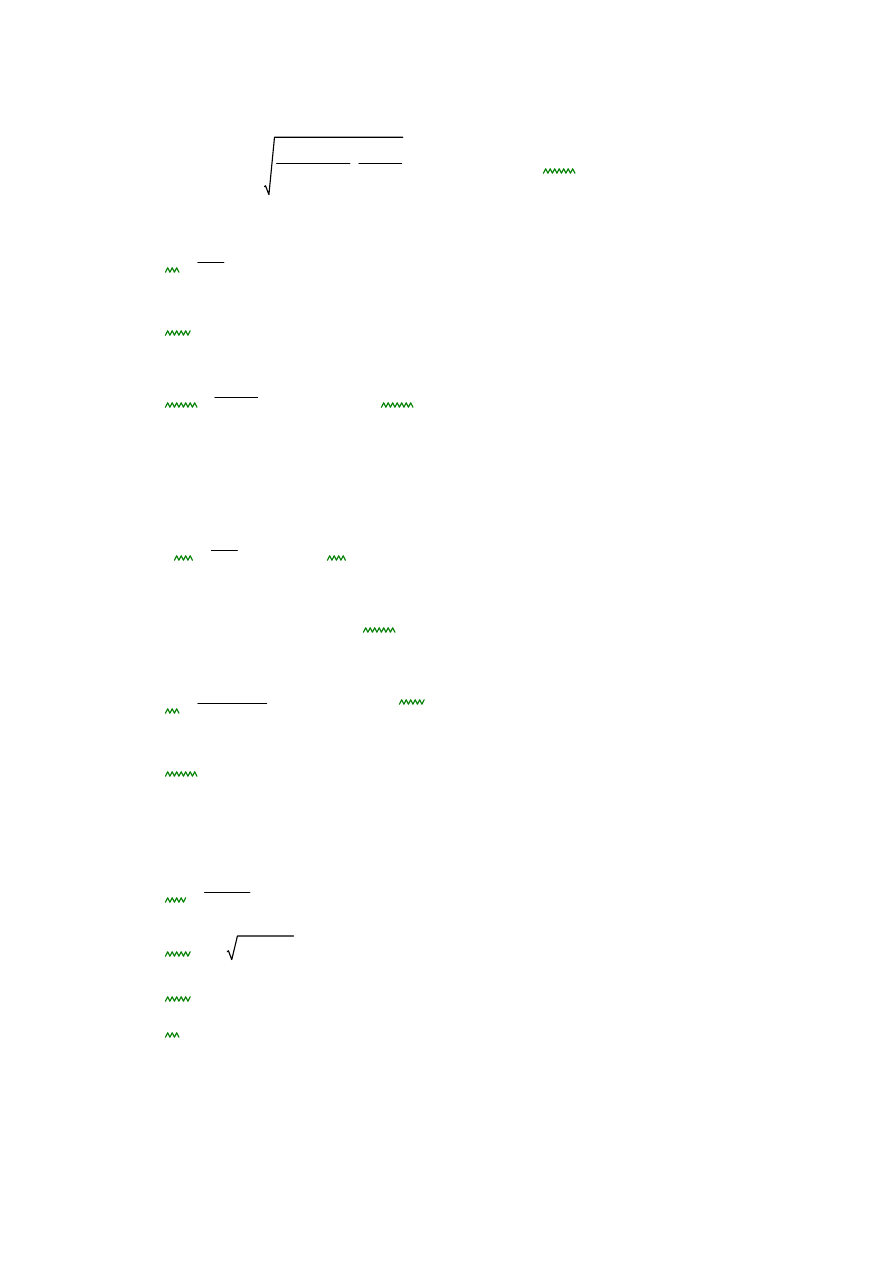
dp3

16.2 10

3



3

Ps KH



κ σHP

2



n2



u2

1



u2





49.905





mm

dp1

50



mm

3. Odległość między środkami kół (określenie długości osi kół)

a

dp3

2

1

u2









153.875





mm

z tabeli dobieram

aw

160



mm

4. Ponowne obliczenie średnicy podziałowej

dp3

2

a



1

u2



49.905





mm

dp3

50



mm

5. Liczba zębów zębnika

zp3

17



6. Obliczenie modułu

m

dp1
zp1

2.9





m

3



7. Obliczenie liczby zębów koła

zp4

zp3 u2



87.833





zp4

88



8. Nominalna odległość osi

aw

160



mm

a

zp3 zp4



2

m



157.5





mm

9. Obliczenie średnicy podziałowej zębnika i koła zębatego

dp3

m zp3



51





mm

dp4

m zp4



264





mm

10. Ustalenie współczynników przesunięcia zarysu

Br

aw a



a

0.016





mm

Bp Br

1

7

Br







0.017





mm

Σx

0.5

Bp



zp3 zp4









0.878





k

0.5

Bp Br









zp3 zp4









0.045





Podział sumy współczynników przesunięcia zarysu dokonujemy odwrotnie
proporcjonalnie do liczby zębów

x3 Σx

zp4

zp3 zp4





0.736





x4 Σx x3



0.142





11. Szerokość wieńca

bzp

50



mm

12. Średnica głów zębów

dg3

m zp3

2









57





mm

dg4

m zp4

2









270





mm

13. Średnica stóp zębów

d3s m zp3

2.5









43.5





mm

d4s m zp4

2.5









256.5





mm

14. Toczny kąt przyporu

α

20

°



a

157.5



mm

cosαw

a

aw

cosα



=

aw

160



mm

αw

22.33

°



15. Wysokość głów zębów

Wysokość głów zębów

y

1



ha3

m y

x3









5.209





mm

mm

ha4

m y

x4









3.427





Obliczenia wskaźnika zazębienia przekładni

16. Obliczenie czołowego wskaźnika zazębienia

εα

zp3

2

π



1

2

ha3



dp3











2

1

0.94

2



1





zp4

2

π



1

2

ha4



dp4











2

1

0.94

2



1







aw

0.342



π m



0.94





2.115





εα 

1.4

=

zgodne z założeniem

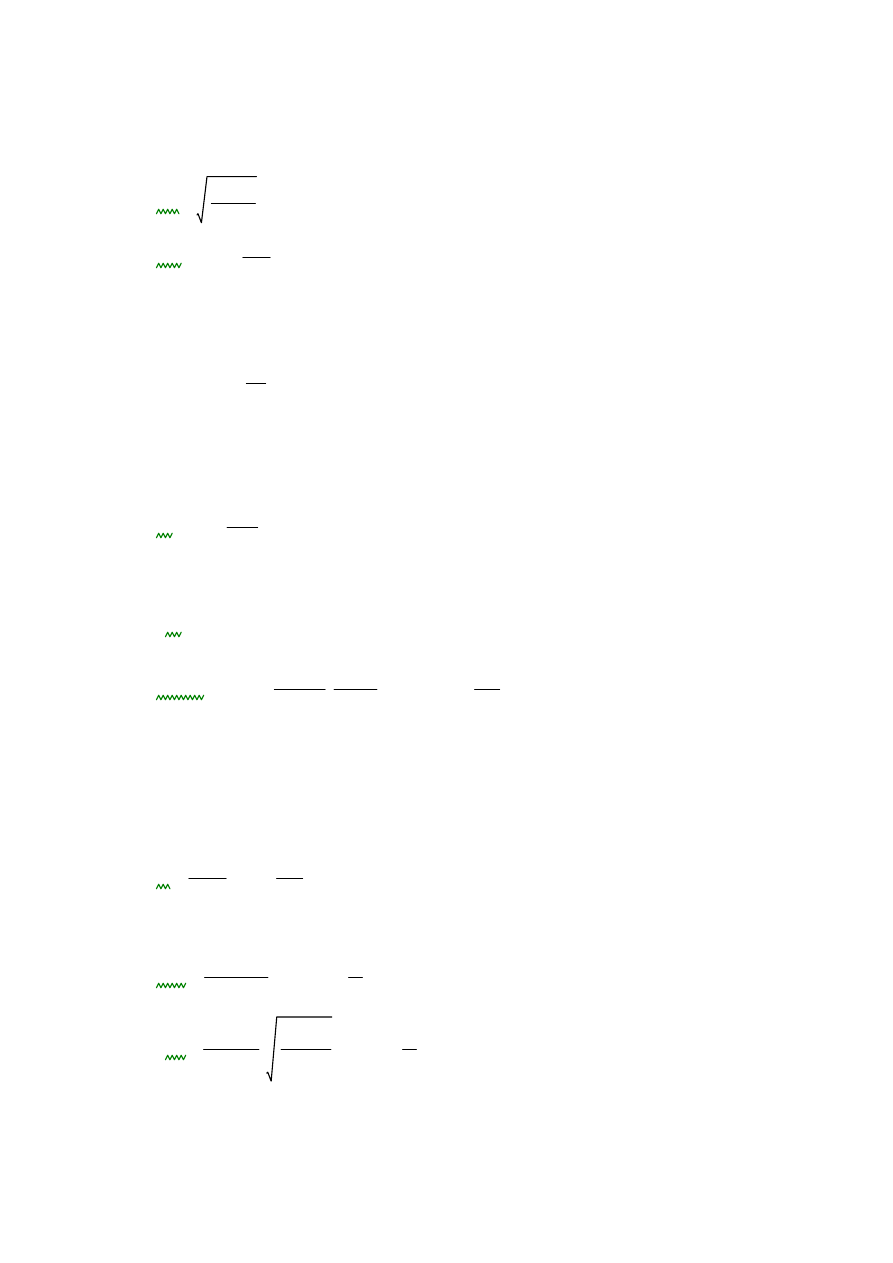
współczynniki

Z

ε

4

εα



3

0.793





Y

ε

0.25

0.75

εα



0.605





17. Obciążenie zębów

Moment obrotowy

M3p

9550

P2

n2



57





Nm

M4p

M3p m



171





Nm

Nominalna siła obwodowa

P

2000

M3p

dp3



2235





N

Wartości prędkości rezonansowej

β

0

°



bo zęby proste

nE1zp

2.1 10

7



cos β

( )

zp2

2

m





u2

1



u2



803.041





obr

min

Przekładnia pracuję w zakresie podrezonansowym bo

n1

0



7

nE1zp



Wskaźnik obciażenia jednostkowego

q

KA P



bzp

67





N

mm

Wskaźnik prędkości przekładni

νzp

π dp3



n2



60 1000



1.293





m

s

W

zp3 νzp



100

u2

2

u2

2

1





0.216





m

s

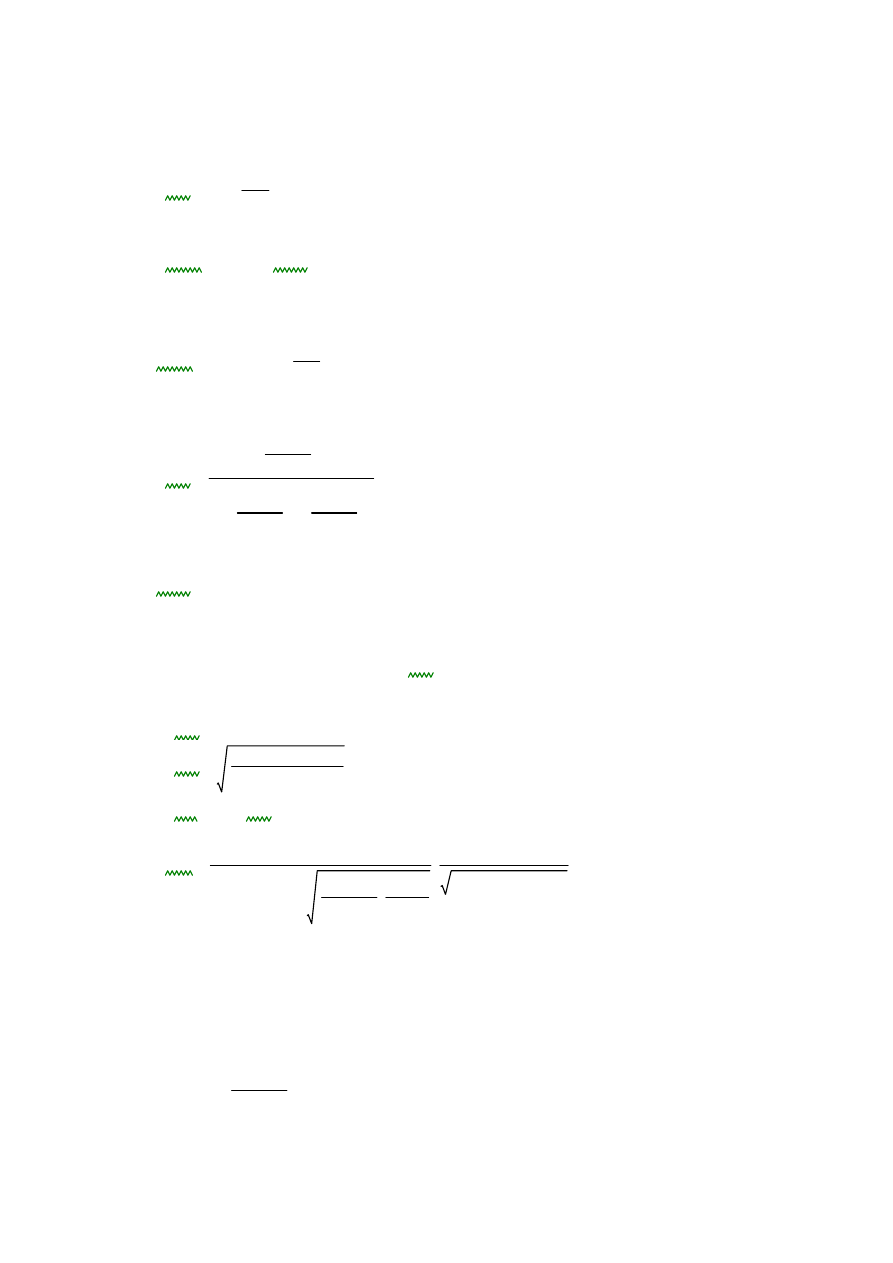
Obliczam współczynnik dynamiczny

K

ν

1

14.9

q

0.0193











W





1.05





Przyjmuję

KHα

1



KFα

1



Współczynnik

KHβ

1.05

0.31

bzp
dp3









2





3.8 10

3





bzp





1.538





NT

bzp

2.25

m















2

1

bzp

2.25

m





bzp

2.25

m















2



0.867





KFβ KHβ

NT

1.45





18. Sprawdzenie współczynnika bezpieczeństwa na nacisk stykowy

Współczynnik dla zębów prostych

Z

β

1



dla stali

ZE

189.8



ZH

2

sin αw

 

cos αw

 



2.386





u1

6



Zx

1



Zw

1



SH

σH_lim

ZH ZE



Z

ε



Z

β



P

bzp dp3



u2

1



u2





ZNT

1

 Zw



Zx



KA Kν



KHβ



KHα





1.346





Otrzymana wartość jest poprawna

SH

1.25



czyli maksymalna niezawodność

19. Nominalna wartość sił działająca na wał

Przp2 P tan αw

 



918





N

Pnzp2

P

cos αw

 

2416





N

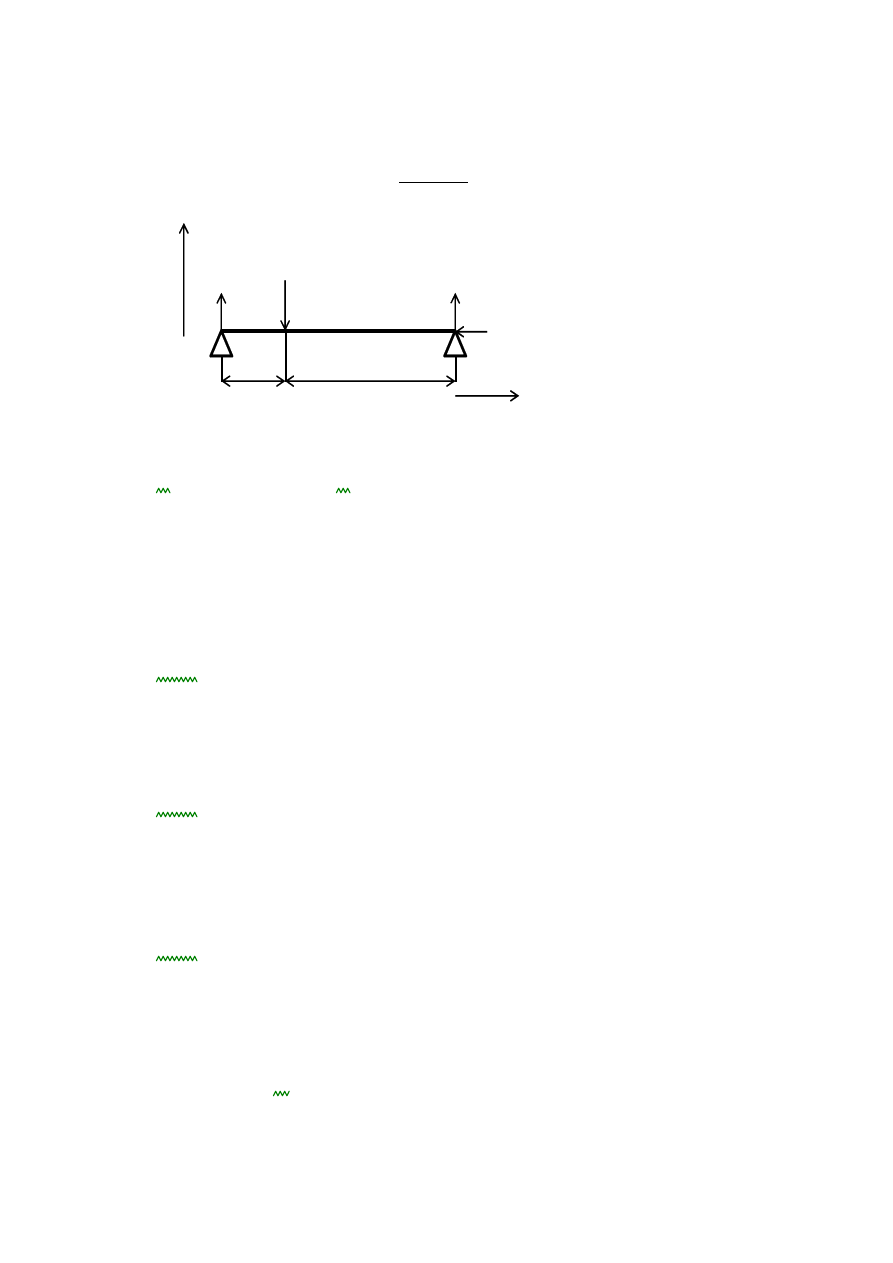
OBLICZENIA WAŁÓW

WAŁ NR 1

 

y

R

ay

P

n

R

by

x

R

bx

a

b

Z rozplanowania reduktora

a

0.036



b

0.090



c

a

b





Pn Pnzp1

648





N

Obliczanie reakcji

Rby1

500



Given

Pn a



Rby1 c





0

=

Rby1 Find Rby1





185





N

Ray1

500



Given

0

Ray1 Pn



Rby1



=

Ray1 Find Ray1





463





N

Rbx1

1



Given

0

Rbx1



=

Rbx1 Find Rbx1





0





N

Momenty gnące

L do P

0

x1



a



N x1

 

N

0



N

T x1

 

T

Ray1

463





N

Mg1 x1

 

Ray1 x1





Mg1

0

( )

0



Mg1 a

( )

17



Nm

P do L

0

x2



b



N x2

 

N

0



N

T x2

 

T

Rby1

185





N

Mg2 x2

 

Rby1 x2





Mg2

0

( )

0



Mg2 b

( )

17



Nm

Maksymalny moment gnący

Mg max Mg1

0

( ) Mg1 a

( )



Mg2 b

( )







17





Nm

Naprężenia gnące i skręcające

Dobieram materiał C55

Dane materiałowe Pa

σg

Mg
Wg

kg



=

kg

260 10

6





ks

145 10

6





τs

Ms
W0

ks



=

kgo

85 10

6





kjs

102 10

6





Zgo

340 10

6





Zso

205 10

6





Obliczenie średnicy wału z naprężeń zastępczych

Mz1

Mg

2

kgo

kjs

2

M1















2



17





Nm

dw1

3

32

Mz1



π kgo



0.013





m

Obliczenie średnicy teoretycznej z wytrzymałości zmęczeniowej

Mgz1

Mz1

2

Zgo

2

Zso



M1











2



19





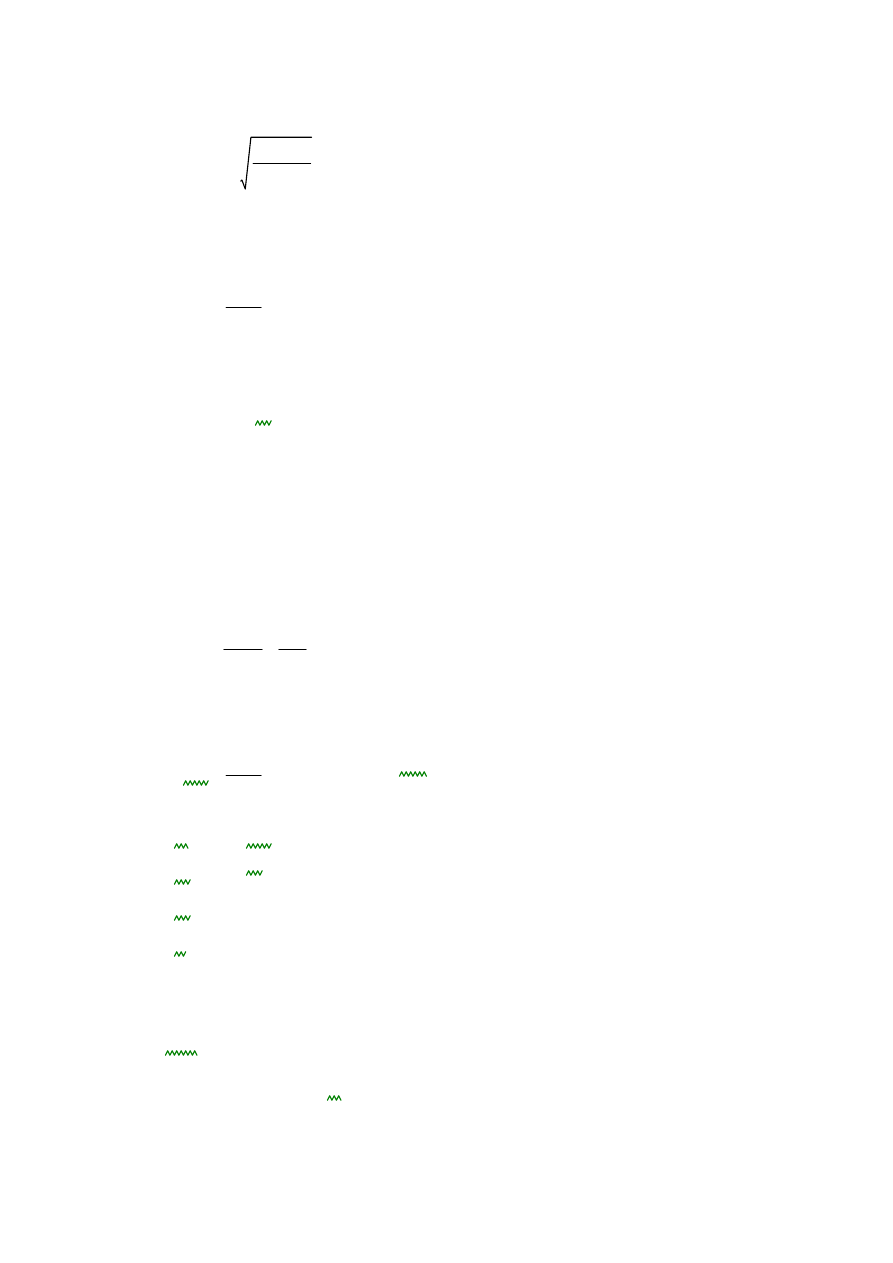
dteor1

3

Mgz1

32



π kgo



0.013





m

Dobór łożysk: Łożysko toczne kulkowe

siła poprzeczna promieniowa

Pp

Ray1

1000

0.46





Pw

0



Dane łożyska:

Co – nośność spoczynkowa,
C – nośność ruchowa,
PW – obciążenie osiowe [kN],
PP – obciążenie promieniowe
[kN]

d

17



Co

13.5



C

6.55



B

14



D

47



r

1



Obciążenia zastępcze

Pz1 Pp

0.46





Trwałość łożyska

p

3



Lh

16660

n1

C

Pz1













p



16217





h

Dobór drugiego łożyska: Łożysko toczne kulkowe

siła poprzeczna promieniowa

Pw

0



Pp

Rby1

1000

0.19





Dane łożyska:

d

15



Co

5.6



Co – nośność spoczynkowa,
C – nośność ruchowa,
PW – obciążenie osiowe [kN],
PP – obciążenie promieniowe
[kN]

C

2.83



B

8



D

32



r

0.3



Obciążenia zastępcze

Pz1 Pp

0.19





Trwałość łożyska

p

3



Lh

16660

n1

C

Pz1













p



20437





h

WPUSTY

Stal C55 z ulepszeniem cieplnym

Wpust pod sprzęgło

N

m2

Re

550 10

6





Siła działająca na wpust:

dpk

0.013



m

E

210 10

9





kd

0.5

Re



2.75

10

8







Fsp

2

M1







dpk

1517.3





N

wysokość

h

0.005



m

szerokość

B

0.005



m

długość wpustu w granicy 10-56

mm

Długość wpustu

l0p

2

Fsp

kd h





0.0022





m

przymuję wpust:

l0p

10



mm

Wpust pod pierwsze koło zębate

Stal C55 z ulepszeniem cieplnym

Siła działająca na wpust:

N

m2

dpk

0.020



m

Re

550 10

6





E

210 10

9





Fsp

2

M1







dpk

986.2





N

kd

0.5

Re



2.75

10

8







wysokość

h

0.006



m

szerokość

B

0.0056



m

Długość wpustu

długość wpustu w granicy 14-70

mm

l0p

2

Fsp

kd h





0.0012





m

przymuję wpust:

l0p

12



mm

SZTYWNOŚĆ WAŁU

Sprawność sztywności wału oblicza się poprzez obliczenie strzałki ugięcia

w miejscu zębnika zębnikiem

Mazanek

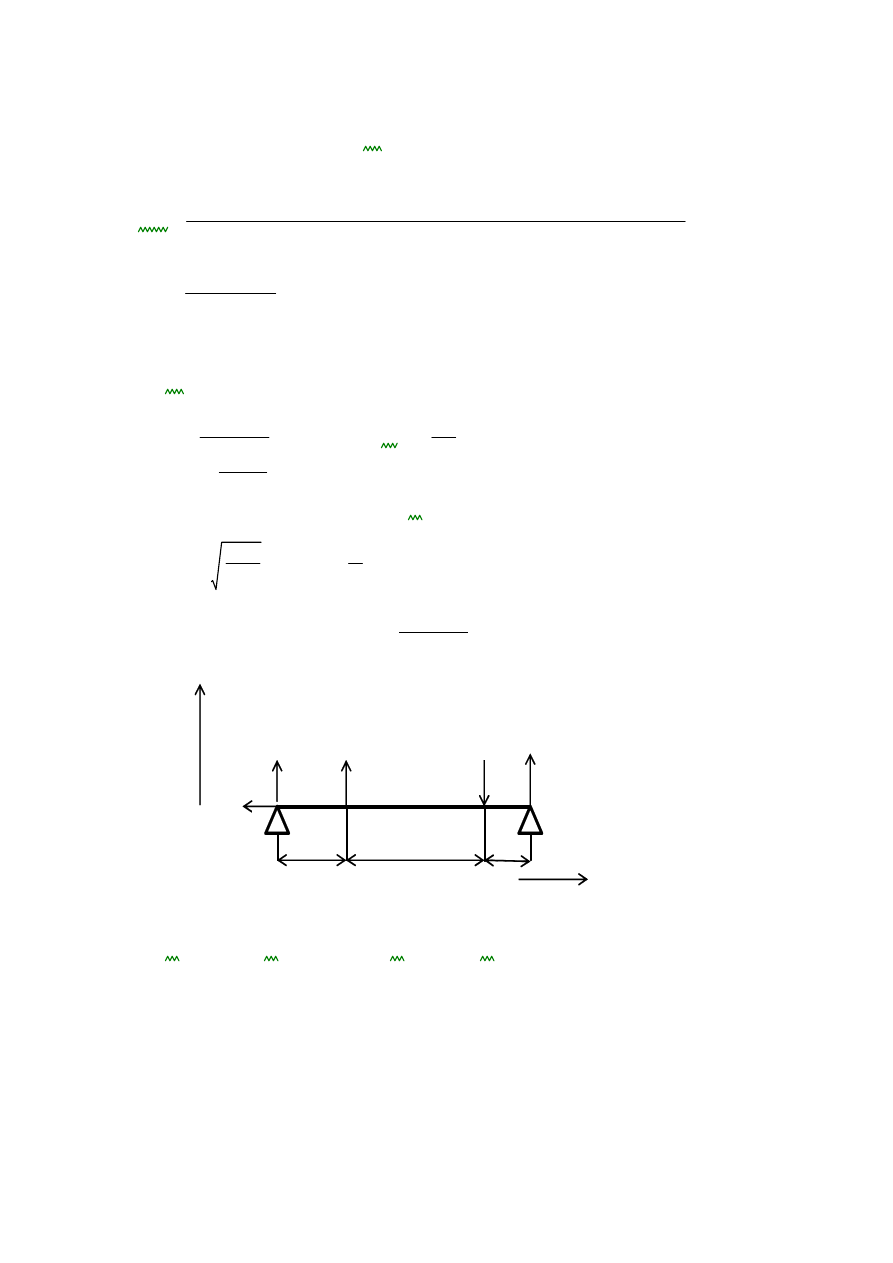
m

2



fdop

0.003

m



0.006





dpk

0.007 0.017



0.044 0.02





0.01 0.024





0.03 0.02





0.031 0.018





0.004 0.015





0.007

0.044



0.01



0.03



0.031



0.004



0.02





f

Pn

64



a

2



b

2



3

π

 E

 dpk

4



c



0.000012083





Kąt skręcający

G

80 10

9





φ

M1 c



G

π dpk

4



32



0.001





rad

φ

φ

180

π



0.063





Prędkość krytyczna

fmax f



g

9.81



ωkr

g

fmax

901.061





m

s

WAŁ NR 2

 

y

R

ay

P

n

R

by

x

R

ax

a

d

P

n2

b

Z rozplanowania reduktora

a

0.036



b

0.046



d

0.044



c

a

b



d





Pn2

Pnzp2

2416





N

Reakcje :

Rby2

500



Given

Pn



a



Pn2 a d



(

)





Rby2 c





0

=

Rby2 Find Rby2





1349





N

Ray2

500



Given

0

Ray2 Pn



Pn2



Rby2



=

Ray2 Find Ray2





419





N

Rax2

1



Given

0

Rax2



=

Rax2 Find Rax2





0





N

Momenty gnące

L do P

0

x1



a



N x1

 

N

Rax2

0





N

T x1

 

T

Ray2

419





N

Mg1 x1

 

Ray2 x1





Mg1

0

( )

0



Mg1 a

( )

15



Nm

L do P

a

x2



a

d





N x2

 

N

Rax2

0





N

T x2

 

T

Ray2 Pn



1067





N

Mg2 a d



(

)

15



Nm

Mg2 x2

 

Ray2 x2



Pn x2 a













Mg2 a

( )

15



P do L

0

x3



b



N x3

 

N

0



N

T x3

 

T

Rby2

1349





N

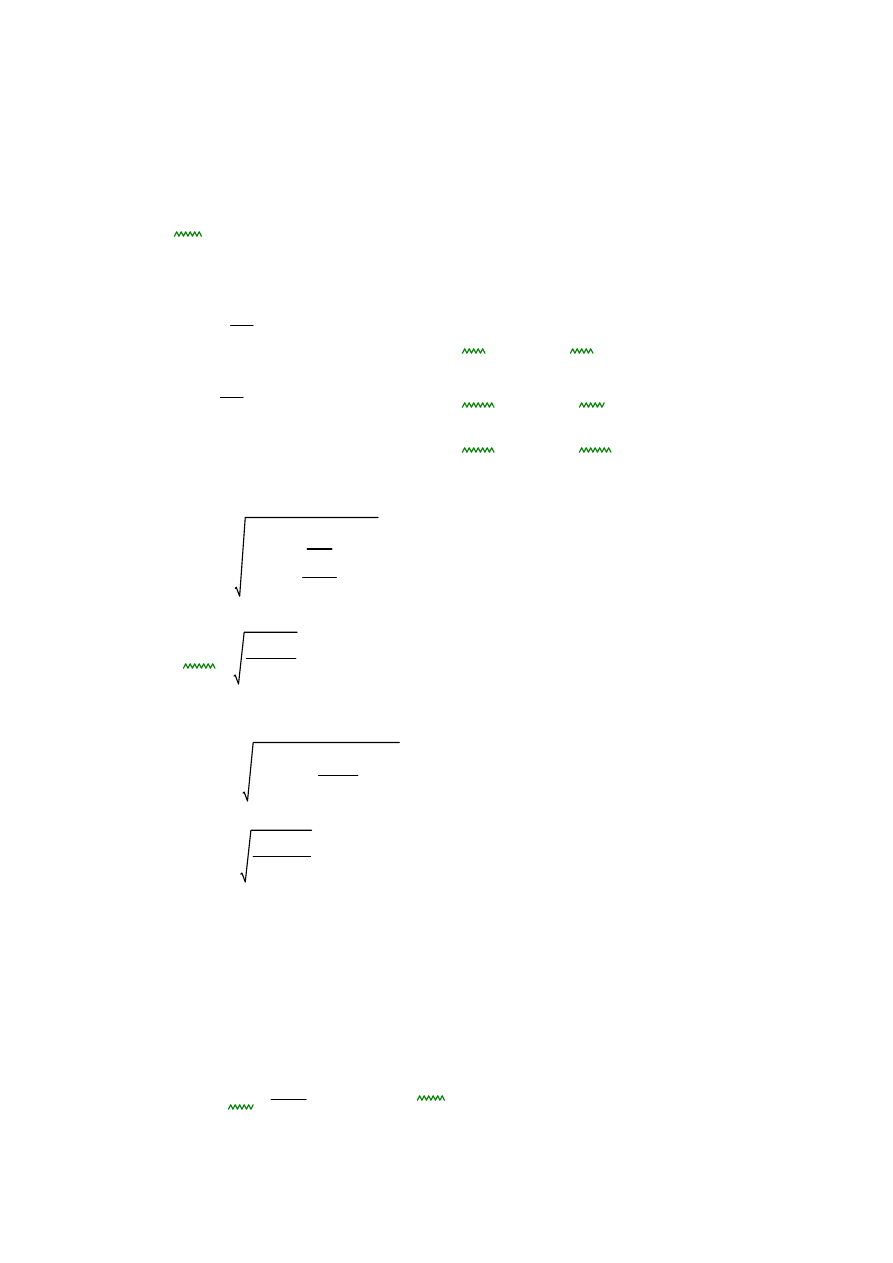
Mg3 x3

 

Rby2 x3





Mg3

0

( )

0



Mg3 b

( )

62



Nm

Maksymalny moment gnący

Mg max Mg1

0

( ) Mg1 a

( )



Mg3 b

( )



Mg2 a d



(

)



Mg2 a

( )







62





Nm

Naprężenia gnące i skręcające

Dane materiałowe Pa

σg

Mg
Wg

kg



=

kg

260 10

6





ks

145 10

6





τs

Ms
W0

ks



=

kgo

85 10

6





kjs

102 10

6





Zgo

340 10

6





Zso

205 10

6





Obliczenie średnicy wału z naprężeń zastępczych

Mz2

Mg

2

kgo

kjs

2

M2















2



66





Nm

dw2

3

32

Mz2



π kgo



0.02





m

Obliczenie średnicy teoretycznej z wytrzymałości zmęczeniowej

Mgz2

Mz2

2

Zgo

2

Zso



M2











2



82





dteor

3

Mgz2

32



π kgo



0.021





m

Dobór łóżysk: Łożysko toczne kulkowe

siła poprzeczna promieniowa

Pw

0



Pp

Ray2

1000

0.42





Dane łożyska:

Co – nośność spoczynkowa,
C – nośność ruchowa,
PW – obciążenie osiowe [kN],
PP – obciążenie promieniowe
[kN]

d

25



Co

4.3



C

2.95



B

9



D

37



r

0.3



Obciążenia zastępcze

Pz1 Pp

0.42





Trwałość łożyska

Lh

16660

n2

C

Pz1













p



12011





h

p

3



Dobór drugiego łożyska: Łożysko toczne kulkowe

siła poprzeczna promieniowa

Pw

0



Pp

Rby2

1000

1.35





Dane łożyska:

Co – nośność spoczynkowa,
C – nośność ruchowa,
PW – obciążenie osiowe [kN],
PP – obciążenie promieniowe
[kN]

d

22



Co

18.4



C

9.25



B

16



D

56



r

1.1



Obciążenia zastępcze

Pz1 Pp

1.35





Trwałość łożyska

p

3



Lh

16660

n2

C

Pz1













p



11095





h

WPUSTY

Stal C55 z ulepszeniem cieplnym

Wpust pod pierwsze koło zębate

N

m2

Re

550 10

6





Siła działająca na wpust:

dpk

0.030



m

E

210 10

9





kd

0.5

Re



2.75

10

8







Fsp

2

M2







dpk

3799.8





N

wysokość

h

0.007



m

szerokość

B

0.008



m

długość wpustu w granicy 18-90

mm

Długość wpustu

l0p

2

Fsp

kd h





0.0039





m

przymuję wpust:

l0p

18



mm

Wpust pod drugi zębnik

Stal C55 z ulepszeniem cieplnym

Siła działająca na wpust:

N

m2

dpk

0.030



m

Re

550 10

6





E

210 10

9





Fsp

2

M2







dpk

3799.8





N

kd

0.5

Re



2.75

10

8







wysokość

h

0.007



m

szerokość

B

0.008



m

Długość wpustu

długość wpustu w granicy 18-90

mm

l0p

2

Fsp

kd h





0.0039





m

przymuję wpust:

l0p

18



mm

SZTYWNOŚĆ WAŁU

Sprawność sztywności wału oblicza się poprzez obliczenie strzałki ugięcia

w miejscu zębnika zębnikiem

m

2



z mazanka 1

fdop

0.003

m



0.006





dpk

0.0045 0.025



0.0455 0.03





0.005 0.036





0.05 0.03





0.013 0.026





0.008 0.022





0.0045

0.0455



0.005



0.05



0.013



0.008



0.029





a

0.036



b

0.046



d

0.044



Pn2 Pnzp2

2416





N

C

Pn2

b

3

6



Ray2

c

3

6





Pn

b

d



(

)

3

6





c

1.423







f1

64

E π

 dpk

4



C a



Ray2

a

3

6



















0.0000065







w miejscu zębnika zębnikiem

m

3



fdop

0.002

m



0.006





f2

64

E π

 dpk

4



C a

d



(

)



Ray2

a

d



(

)

3

6





Pn

d

3

6



















0.000009267







Kąt skręcający

G

80 10

9





φ

M2 c



G

π dpk

4



32



0.0013





rad

φ

φ

180

π



0.073





Prędkość krytyczna

fmax

max f1 f2









g

9.81



ωkr

g

fmax

1232.882





m

s

Współczynnik bezpieczeństwa zmęczeniowy

Kurmaz, Tabela 8.6.1, str 106

Zso

205 10

6





Współczynnik wielkości przedmiotu

ε

0.8



Kurmaz, Rysunek 8.6.2, str 106

Dla wpustów

Amplituda cyklu naprężeń gnących

σg

Mg

1000



π

dpk

1000







3

32



B

5



1000



B

1000



5



(

)

2



2

dpk



1000





25.611





MPa

βkσ

2



współczynnik działania karbu dla zginania, Kurmaz, Tabela 8.6.2, str. 107

βpσ

1.1



współczynnik stanu powierzchni dla stalowych części zginanych, Kurmaz,
Rysunek 8.6.4, str. 107

βσ

βkσ βpσ



1



2.1





współczynnik uwzględniający działanie karbu i stan
powierzchni dla stalowych części zginanych

rzeczywisty współczynnik bezpieczeństwa wg naprężeń
normalnych (od zginania)

δg

Zgo ε



σg βσ



5.057

10

6







Amplituda cyklu naprężeń stycznych

τs

M3

1000



π dpk

1000







3



16

B

5



1000



B

1000



5



(

)

2



2

dpk



1000





58.464





βpτ

1.05



współczynnik stanu powierzchni dla stalowych części skręcanych, Kurmaz,
Rysunek 8.6.4, str. 107

βkτ

1.9



współczynnik działania karbu dla skręcania, Kurmaz, Tabela 8.6.2, str. 107

βτ

βpτ βkτ



1



1.95





współczynnik uwzględniający działanie karbu i stan
powierzchni dla stalowych części skręcanych

rzeczywisty współczynnik bezpieczeństwa wg naprężeń
stycznych (od skręcania)

δτ

Zso ε



τs βτ



1.439

10

6







δ

δg δτ



δg

2

δτ

2



1.384

10

6







δ

1



5



rzeczywisty współczynnik bezpieczeństwa
dla obciążeń złożonych

Dla zmiany średnicy

σg

Mg

1000



π

dpk

1000







3

32



25.546





βkσ

3.5



βpσ

1.2



βσ

βkσ βpσ



1



3.7





δg

Zgo ε



σg βσ



2.878

10

6







τs

M3

1000



π dpk

1000







3



16

58.389





βpτ

1.1



βkτ

2.1



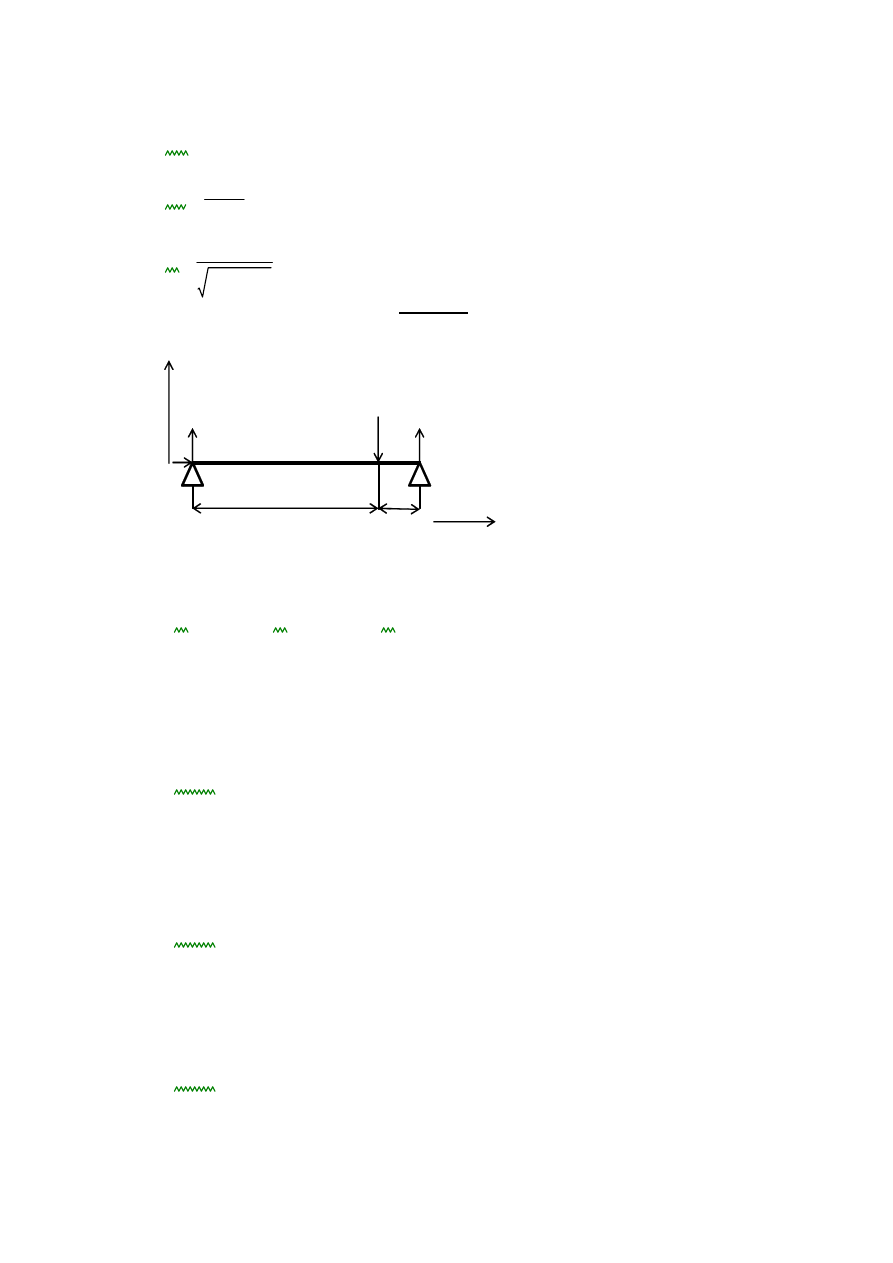
βτ

βpτ βkτ



1



2.2





δτ

Zso ε



τs βτ



1.277

10

6







δ

δg δτ



δg

2

δτ

2



1.167

10

6







δ

1



5



WAŁ NR 3

 

R

ay

R

by

x

a

P

z

b

y

R

ax

Z rozplanowania reduktora

a

0.080



b

0.46



c

a

b





Pn2

2416



N

Rby3

500



Reakcje

Given

Pn2 a



Rby3 c





0

=

Rby3 Find Rby3





358





N

Ray3

500



Given

0

Ray3 Pn2



Rby3



=

Ray3 Find Ray3





2058





N

Rax3

1



Given

0

Rax3 Pn2



=

Rax3 Find Rax3





2416





N

Momenty gnące

L do P

0

x1



a



N x1

 

N

Rax3

2416





N

T x1

 

T

Ray3

2058





N

Mg1 x1

 

Ray3 x1





Mg1

0

( )

0



Mg1 a

( )

165



Nm

P do L

0

x2



b



N x2

 

N

0



N

T x2

 

T

Rby3

358





N

Mg2 x2

 

Rby3 x2





Mg2

0

( )

0



Mg2 b

( )

165



Nm

Maksymalny moment gnący

Mg max Mg1

0

( ) Mg1 a

( )



Mg2 b

( )







165





Nm

Naprężenia gnące i skręcające

Dane materiałowe Pa

σg

Mg
Wg

kg



=

kg

260 10

6





ks

145 10

6





τs

Ms
W0

ks



=

kgo

85 10

6





kjs

102 10

6





Zgo

340 10

6





Zso

205 10

6





Obliczenie średnicy wału z naprężeń zastępczych

Mz3

Mg

2

kgo

kjs

2

M3















2



203





Nm

dw3

3

32

Mz3



π kgo



0.029





m

Obliczenie średnicy teoretycznej z wytrzymałości zmęczeniowej

Mgz3

Mz3

2

Zgo

2

Zso



M3











2



311





dteor

3

Mgz3

32



π kgo



0.033





m

Łożysko toczne kulkowe

siła poprzeczna promieniowa

Pw

0



Pp

Ray3

1000

2.06





Dane łożyska

d

45



Co

21



Co – nośność spoczynkowa,
C – nośność ruchowa,
PW – obciążenie osiowe [kN],
PP – obciążenie promieniowe
[kN]

C

15.10



B

16



D

75



r

1



Obciążenia zastępcze

Pz1 Pp

2.06





p

3



Trwałość łożyska

Lh

16660

n3

C

Pz1













p



70184





h

Dobór drugiego łożyska: Łożysko toczne kulkowe

siła poprzeczna promieniowa

Pw

0



Pp

Rby3

1000

0.36





Dane łożyska:

Co – nośność spoczynkowa,
C – nośność ruchowa,
PW – obciążenie osiowe [kN],
PP – obciążenie promieniowe
[kN]

d

35



Co

4.9



C

4.05



B

7



D

47



r

0.3



Obciążenia zastępcze

Pz1 Pp

0.36





Trwałość łożyska

p

3



Lh

16660

n3

C

Pz1













p



257440





h

WPUSTY

Wpust pod drugie koło zębate

Stal C55 z ulepszeniem cieplnym

Siła działająca na wpust

dpk

0.040



m

N

m2

Re

550 10

6





E

210 10

9





Fsp

2

M3







dpk

14182.5





N

kd

0.5

Re



2.75

10

8







wysokość

h

0.008



m

szerokość

B

0.012



m

długość wpustu w granicy 28-140 mm

Długość wpustu

przymuję wpusty:

l0p

2

Fsp

kd h





0.0129





m

l0p

28



mm

Wpust pod drugie sprzęgło

Stal C55 z ulepszeniem cieplnym

Siła działająca na wpust

N

m2

Re

550 10

6





dpk

0.036



m

E

210 10

9





Fsp

2

M3







dpk

15758.3





N

kd

0.5

Re



2.75

10

8







wysokość

h

0.010



m

szerokość

B

0.008



m

długośc wpustu w granicy 22-110 mm

przymuję wpusty:

l0p

2

Fsp

kd h





0.0115





m

l0p

22



mm

Sztywność wału

Sprawność sztywności wału dokonuję przez obliczenie strzałki ugięcia:

w miejscu zębnika zębnikiem

m

3



Mazanek

fdop

0.003

m



0.009





dpk

0.008 0.045



0.035 0.054





0.013 0.048





0.0665 0.040





0.0035 0.035





0.008

0.035



0.013



0.0665



0.0035



0.045





f

Pn2

64



a

2



b

2



3

π

 E

 dpk

4



c



0.000048244





Kąt skręcający

G

80 10

9





φ

φ

180

π



4.164





φ

M3 c



G

π dpk

4



32



0.005





rad

Prędkość krytyczna

fmax f



g

9.81



ωkr

g

fmax

450.932





m

s