DANE DO PROJEKTU:
informacje o wytrzymałości:
-Beton C20

*wytrzymałość charakterystyczna na

ściskanie

fck 20 MPa



:=

γc 1.4

:=

*wytrzymałość obliczeniowa betonu

na ściskanie

fcd

fck

γc

14.3 MPa



=

:=

*średnia gwarantowana

wytrzymałość na rozciąganie

fctm 0.3 fck

2
3



:=

fctm 0.3 20

2
3



MPa



2.21 MPa



=

:=

*wytrzymałość charakterystyczna

na rozciąganie

fctk 0.7 fctm



:=

fctk 0.7 2.21



MPa



1.55 MPa



=

:=

*wytrzymałość obliczeniowa

na rozciąganie

fctd

fctk

γc

:=

fctd

1.55 MPa



1.4

1.11 MPa



=

:=

-Zbrojenie główne

*wytrzymałość charakterystyczna stali

zbrojeniowej

fyk 450 MPa



:=

*współczynnik materiałowy dla

stali zbrojeniowej

γs 1.15

:=

*wytrzymałość obliczeniowa stali

zbrojeniowej

fyd

fyk

γs

:=

fyd

450 MPa



1.15

391.3 MPa



=

:=

-Strzemiona

f.yk 400 MPa



:=

*wytrzymałość charakterystyczna stali

zbrojeniowej

f.yd

f.yk

γs

:=

f.yd

400 MPa



1.15

:=

f.yd 347.8 MPa



=

*wytrzymałość obliczeniowa stali

zbrojeniowej

-Rozpiętość w świetle (obliczneniowa)

ln 6.40 m



:=

-Całkowite obciążenie obliczeniowe

g0 q0

+

80 kN

m



=

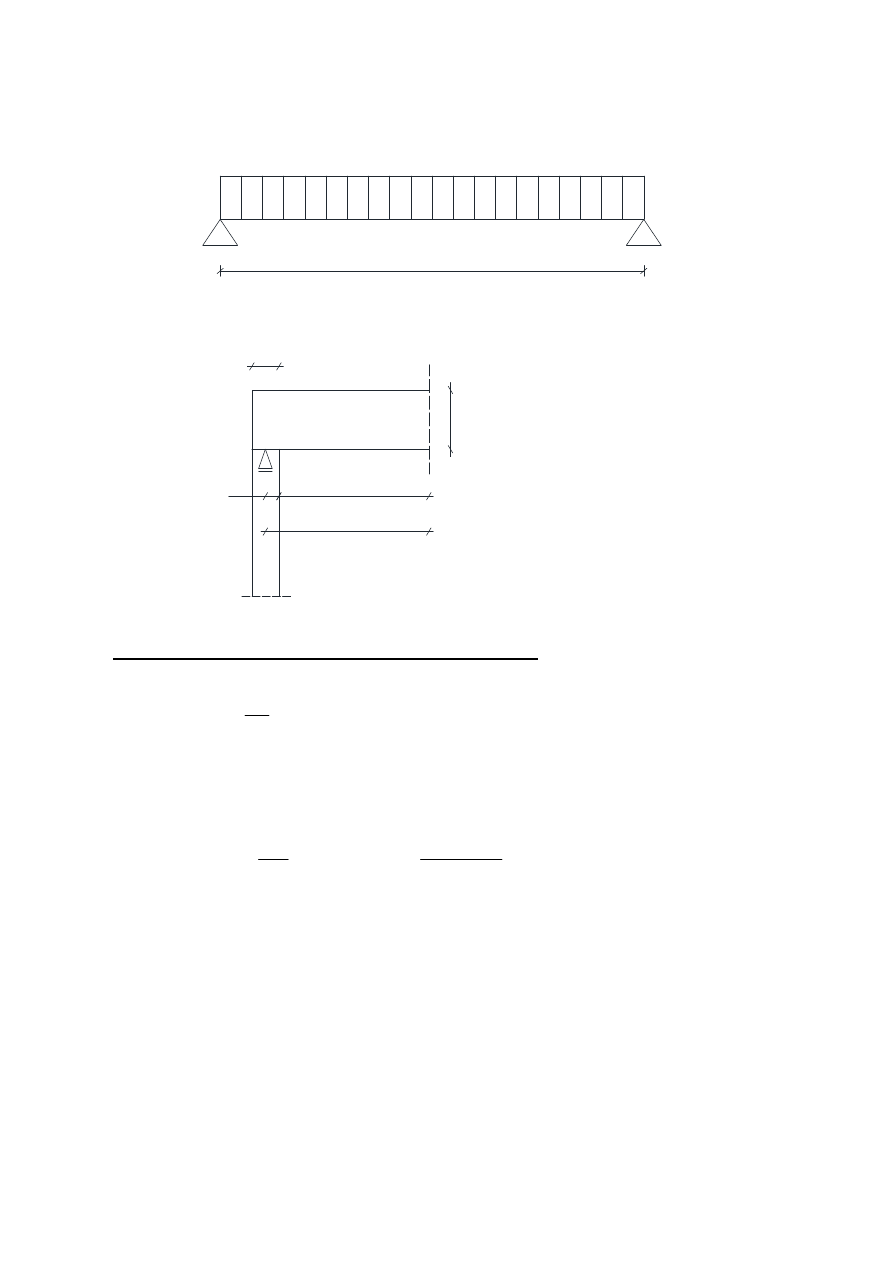
Schemat statyczny belki:

L.eft

g.0+q.0

t

h

a.n l.n

L.eft

t

30 cm



:=

an 0.5 t

:=

an 0.5 30

 cm



15 cm



=

:=

Left ln 2 an



+

:=

Left 6.40 m



2 15

 cm



+

6.7m

=

:=

1. Wyznaczenie wymiarów przekroju betonowego:

Med 0.125 80



kN

m



Left

( )

2



44890 kN cm





=

:=

ρeft 0.8 %



:=

założono :

wskaźnik :

β

r

f.yd

fcd

:=

β

r

347.8 MPa

14.3 MPa

24.32

=

:=

ξeft ρeft βr



:=

ξeft 0.008 24.32



0.195

=

:=

z tablic odczytano

r0 2.385

:=

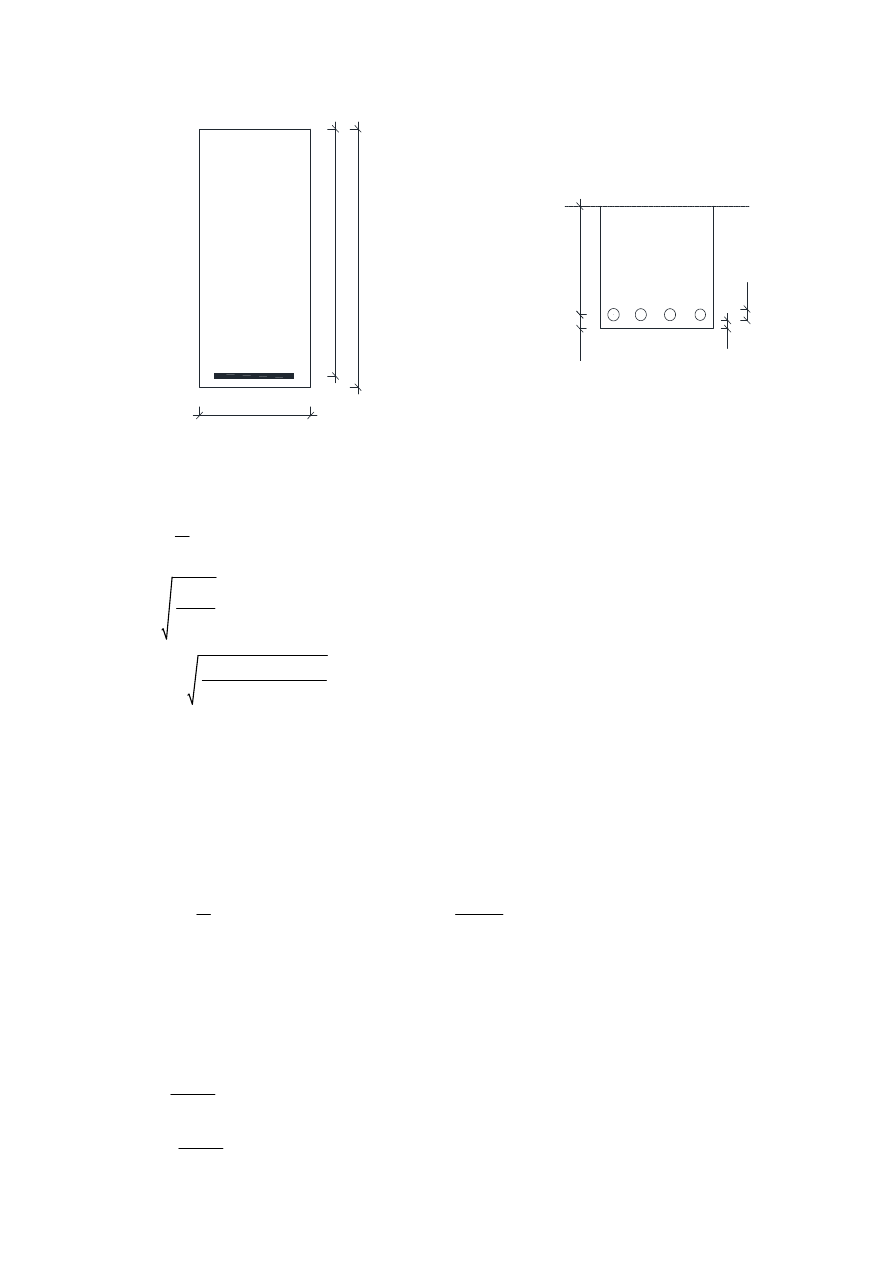
Założono :

b

35 cm



:=

b

h

d

As1

d

d1

O

c

d1 c

ϕ

2

+

Δc

+

=

c

2.5 cm



:=

Δc 0.5 cm



:=

d

r0

Med

b fcd





:=

d

2.385

44890 kN cm



35 cm



14.3



MPa



:=

d 71.4 cm



=

przyjęto zbrojenie główne

średnica strzemiona

ϕ

20 mm



:=

ϕs 6 mm



:=

obliczenie wysokości belki

d1 c

ϕ

2

+

Δc

+

:=

d1 2.5 cm



20mm

2

+

0.5 cm



+

4 cm



=

:=

h

d d1

+

0.754m

=

:=

hzaok 75 cm



:=

przyjęto

przyjęto przekrój 350x750 mm

1.5

hzaok

b



2.5



1

=

warunek spełniony

hzaok

b

2.143

=

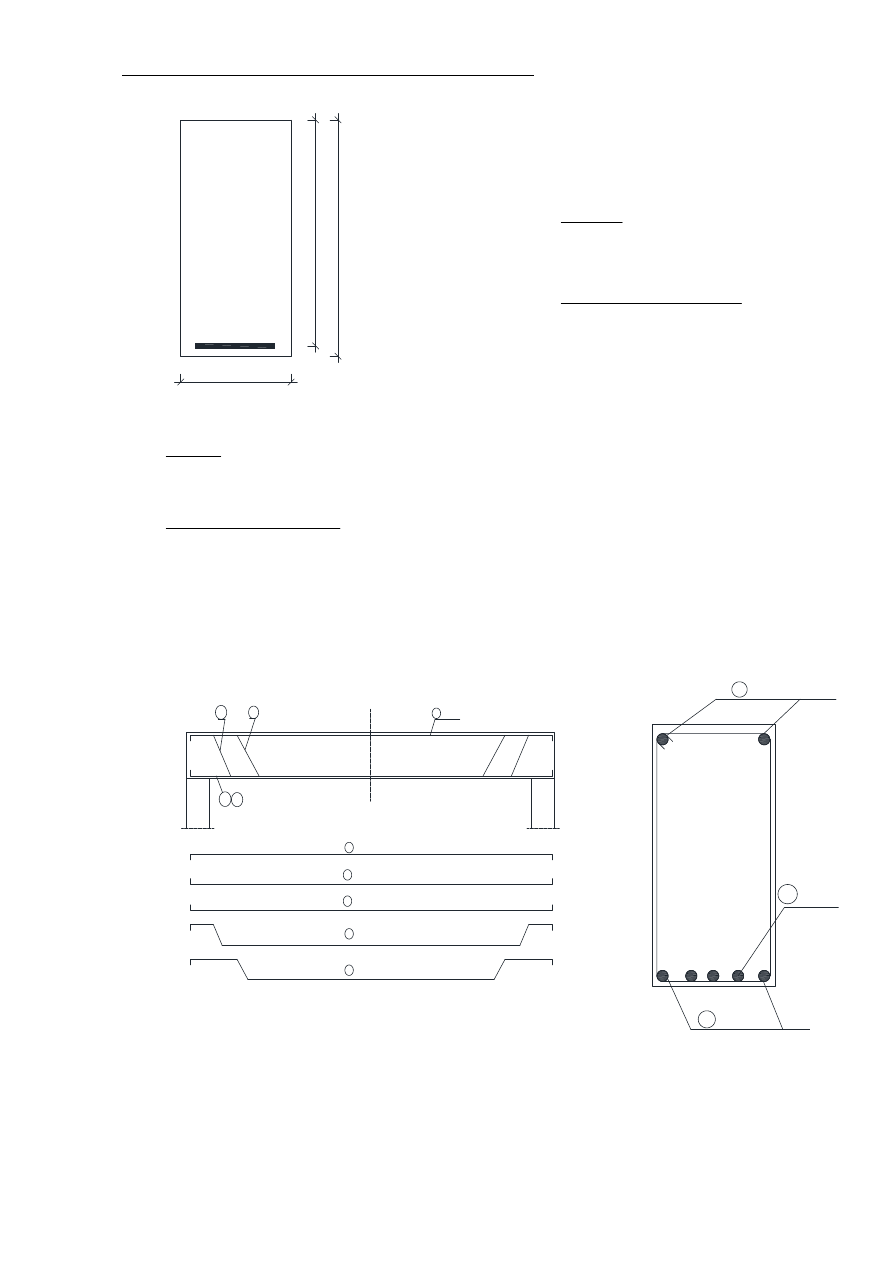
2. Przekrój zbrojenia ze względu na moment zginający

350

75

0

d

As1

d

hzaok 4 cm



-

:=

d

75 cm



4cm

-

71 cm



=

:=

ηSE

Med

fcd b d

2



:=

ηSE

44890 kN



cm



14.3MPa 35

 cm 71cm

(

)

2



:=

ηSE 0.178

=

z tablic odczytano

ξ

0.901

:=

AS1

Med

ξ

d

 fyd



:=

AS1

44890 kN



cm



0.901 71

 cm 391.3



MPa

17.93 cm

2



=

:=

przyjęto pręty zbrojeniowe : 5ϕ20 + 1ϕ18

AS 15.71 cm

2



2.54 cm

2



+

18.25 cm

2



=

:=

A-A

1 2O8

2 3O20

3 1O18

A

A

1 2O8

5

4

2 3

1 2O8

2 3O20

3 1O18

4 1O20

5 1O20

3. Przekrój zbrojenia ze względu na siłę poprzeczną

Przyjęto , że zbrojeniem na ścinanie są pręty odgięte i strzemiona prostopadłe do osi podłużnej belki.
Obliczeniowa siła poprzeczna na krawędzi podpory.

VEd 0.5 g0 q0

+

(

)



ln



:=

VEd 0.5 80

 kN

m

6.4

 m

:=

VEd 256 kN



=

obliczeniowa nośność na ścinanie w strzemionach bez zbrojenia poprzecznego

VRd.c 0.128 k 100 qL

 fck



(

)

1
3



b

 d



=

k

1

200mm

d

+

:=

k

1

200mm
710mm

+

1.531

=

:=

k 2.0



1

=

warunek spełniony

qL

AS
b d



:=

qL

9.43cm

2

2.54cm

2

+

35cm 71

 cm

:=

qL 0.004817

=

qL 0.02



1

=

warunek spełniony

VRd.c 0.128 k 100 qL

 fck



(

)

1
3



b

 d



:=

VRd.c 0.128 1.53



100 0.00481



20



(

)

1
3

MPa



350



mm 710



mm

:=

VRd.c 103.503 kN



=

VRd.c VEd

<

1

=

warunek spełniony

103.503 kN 256 kN

<

1

=

Lt

VEd VRd.c

-

q0 g0

+

:=

Lt

256 kN 103.503 kN

-

80 kN

m

1.91m

=

:=

S

b

- średnia odległość między płaszczyznami odgięć mierzona wzdłuż osi podłużnej belki

Przyjęto:

cotΘ

2

:=

α0 45deg

:=

sin α0

( )

0.707

=

cot α0

( )

1

=

Sbmax 0.6 d 1 cot α0

( )

+

(

)



85.2 cm



=

:=

Sb Sbmax 85.2 cm



=

:=

Asw0 3.14cm

2

:=

przekrój prętów odgiętych w jednej płaszczyźnie odgięcia

z

0.9 d



63.9 cm



=

:=

Siła poprzeczna przenoszona przez strzemiona:

VRds0

Asw0

Sb

z

 fyd



cotΘ cot α0

( )

+

(

)



sin α0

( )



195.48 kN



=

:=

Siła poprzeczna przenoszona przez pręt odgięty

VRdsy VEd VRds0

-

60.52 kN



=

:=

Strzemiona projektuje się na siłę poprzeczną conajmniej 0,5*V

Ed

, a więc:

VRdsy 0.5 VEd



128 kN



=

:=

Dobrano średnicę strzemion ϕ6mm.

as 0.28cm

2

:=

Asw 2 as



0.56 cm

2



=

:=

przekrój pionowy gałęzi strzemion

Sy

Asw fyd



VRdsy

z

 cotΘ



21.9 cm



=

:=

odległość między strzemionami na odcinsku ścinania l

t

Wybieramy S

ymax

z dwóch poniższych warunków:

αs 90deg

:=

Sy 750mm

:=

Sy 0.7 d 1 cot αs

( )

+

(

)



50 cm



=

:=

min Sy

( )

50 cm



=

Przyjęto:

Symax min Sy

( )

50 cm



=

:=

4. Sprawdzenia warunku:

VEd VRdmax



αcw 1

:=

dla konstrukcji betonowych i żelbetowych niesprężonych

ν1 0.6

:=

tanΘ

0.5

:=

VRdmax

αcw b z ν1

 fcd



cotΘ tanΘ

+

766.8 kN



=

:=

siła poprzeczna powodująca zmiażdzenie betonu

VEd VRdmax



1

=

waunek spełniony

VEd2 VEd 2 Sbmax



g0 q0

+

(

)



-

119.68 kN



=

:=

Sy2

Asw fyd



VEd2

z

 cotΘ



23.4 cm



=

:=

g0 40

kN

m



:=

q0 40

kN

m



:=