Adam Bodnar: Wytrzymałość Materiałów. Równania fizyczne.

60

7. RÓWNANIA FIZYCZNE
7.1. Związki między stanem odkształcenia i naprężenia. I i II postać równań Hooke’a

Zależność deformacji bryły od obciążeń zewnętrznych narzuca istnienie zależności między
odkształceniami i naprężeniami. Będziemy się starali ustalić te zależności dla przestrzennych
stanów odkształcenia i naprężenia. Jest rzeczą powszechnie znaną, że konstrukcje o tej samej
geometrii, obciążeniach i więzach, wykonane z różnych materiałów, doznają różnych
deformacji więc jest oczywiste, że poszukiwane zależności muszą być oparte na
doświadczeniach.

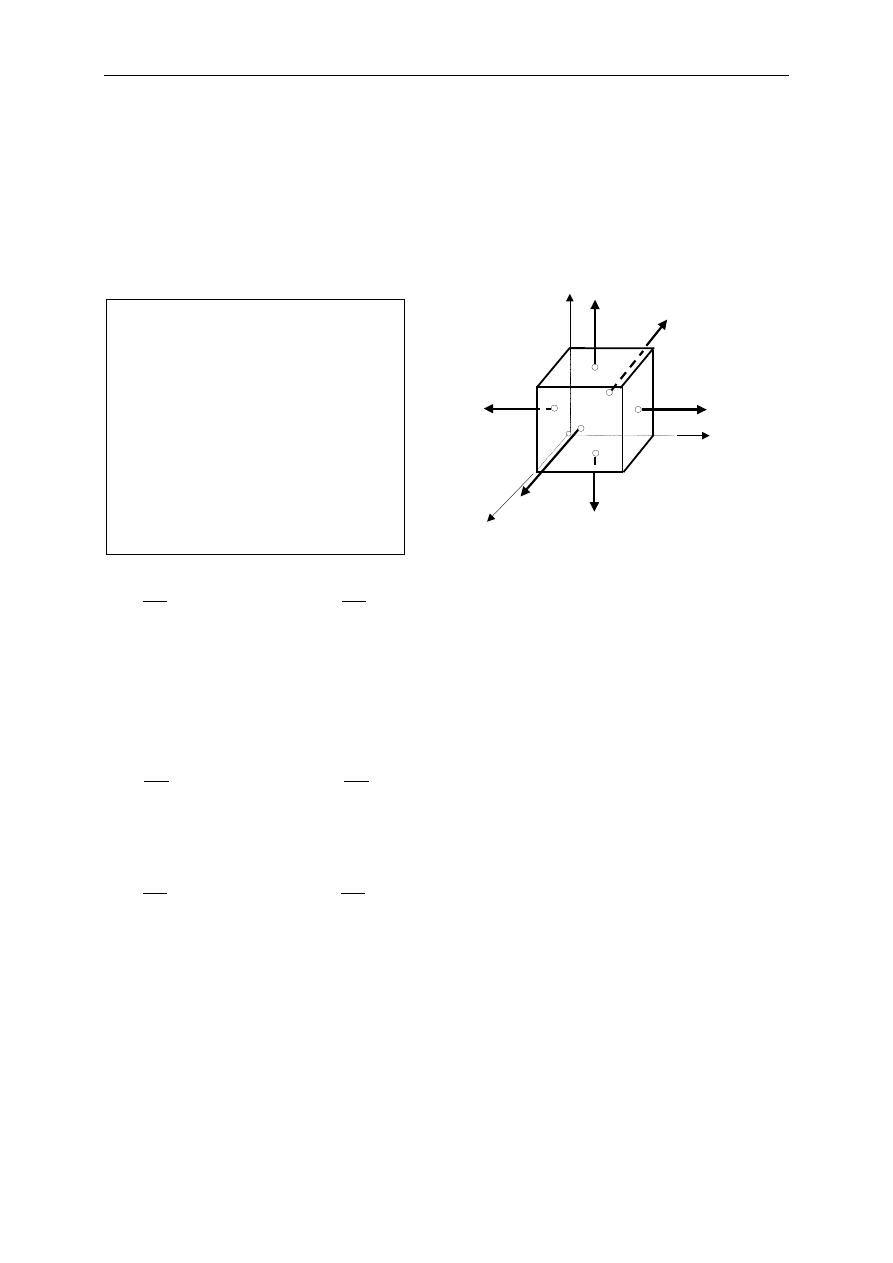
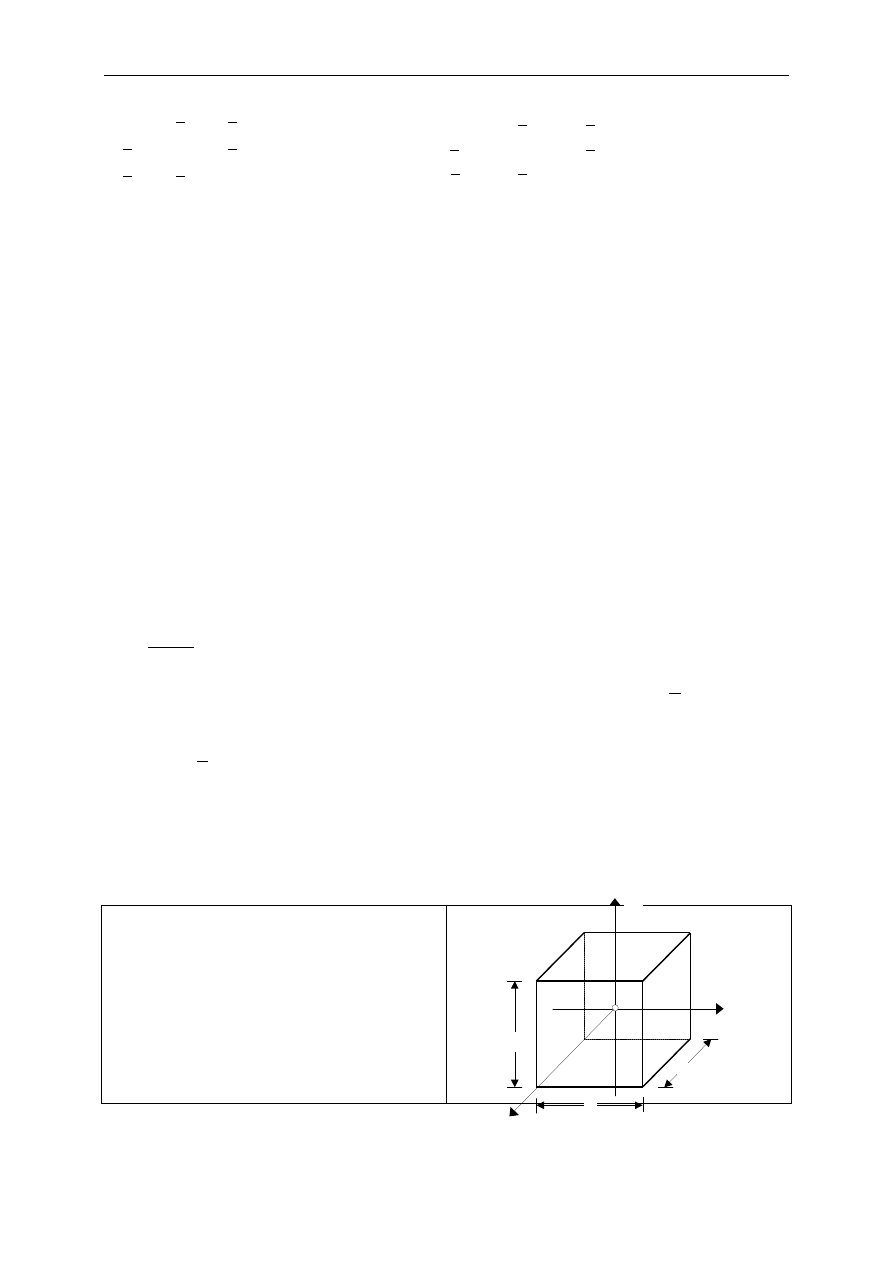
Wyobraźmy sobie dowolnie mały
sześcian o ściankach równoległych do
płaszczyzn układu współrzędnych i
poddajmy go działaniu naprężenia
normalnego

x

σ

,

równomiernie

rozłożonego na dwóch przeciwległych
ś

ciankach. Doświadczenia pokazują, że

w przypadku materiału sprężystego i
izotropowego

naprężenia

te

nie

wywołają

ż

adnych

odkształceń

kątowych sześcianu, a odkształcenia
liniowe będą miały wartości:

E

E

x

x

z

y

x

x

σ

ν

ε

ν

ε

ε

σ

ε

−

=

−

=

=

=

,

gdzie: E oraz

ν stałe materiałowe noszące odpowiednio nazwy moduł sprężystości (moduł

Younga) i liczba Poissona.
Jeżeli nasz sześcian poddamy działaniu jedynie naprężenia normalnego

y

σ

, równomiernie

rozłożonego na dwóch przeciwległych ściankach to wywoła ono jedynie odkształcenia
liniowe:

E

E

y

y

z

x

y

y

σ

ν

ε

ν

ε

ε

σ

ε

−

=

−

=

=

=

,

.

I analogicznie, przy działaniu równomiernie rozłożonego naprężenia normalnego

z

σ

,

otrzymamy:

E

E

z

z

y

x

z

z

σ

ν

ε

ν

ε

ε

σ

ε

−

=

−

=

=

=

,

.

Nasuwa się teraz pytanie, czy w przypadku jednoczesnego działania tych trzech naprężeń
liniowe odkształcenia w danym kierunku będzie można przedstawić jako sumę algebraiczną
odkształceń przy oddzielnym działaniu tych naprężeń (tzn. jako dodanie do siebie efektów
trzech jednoosiowych stanów naprężenia). Odpowiedź na to pytanie jest pozytywna,
potwierdzają ją doświadczenia i formułuje zasada superpozycji:
skutek w określonym kierunku, wywołany przez zespół przyczyn działających
równocześnie jest równy algebraicznej sumie skutków wywołanych w tym kierunku
przez każdą z przyczyn działających oddzielnie.
Należy w tym miejscu podkreślić, że stosowalność zasady superpozycji ograniczona jest
dwoma warunkami:

z

σ

x

σ

x

σ

X

Z

Y

y

σ

y

σ

z

σ

Rys. 7.1

Adam Bodnar: Wytrzymałość Materiałów. Równania fizyczne.

61

• warunkiem proporcjonalności – wymagającym, aby poszczególne skutki były liniowo

zależne od przyczyn, które je wywołały,

• warunkiem niezależności działania – wymagającym, aby żaden ze skutków nie wpływał

na sposób działania pozostałych przyczyn.

Przyjęte przez nas założenia odnośnie materiału oraz małości przemieszczeń i odkształceń
prowadzą do spełnienia tych warunków.
Tak więc, wykorzystując zasadę superpozycji możemy zapisać:

(

)

[

]

(

)

[

]

(

)

[

]

y

x

z

z

z

x

y

y

z

y

x

x

E

E

E

σ

σ

ν

σ

ε

σ

σ

ν

σ

ε

σ

σ

ν

σ

ε

+

−

=

+

−

=

+

−

=

1

1

1

(7.1)

Powyższe równania pokazują, że związki między odkształceniami liniowymi i naprężeniami
normalnymi określone są poprzez dwie stałe materiałowe E i

ν

.

Do określenia związków

między odkształceniami kątowymi i naprężeniami stycznymi mogą również służyć te same
stałe. Aby tego dowieść rozważmy stan naprężenia określony macierzą :





















−

=

σ

σ

σ

0

0

0

0

0

0

0

T

.

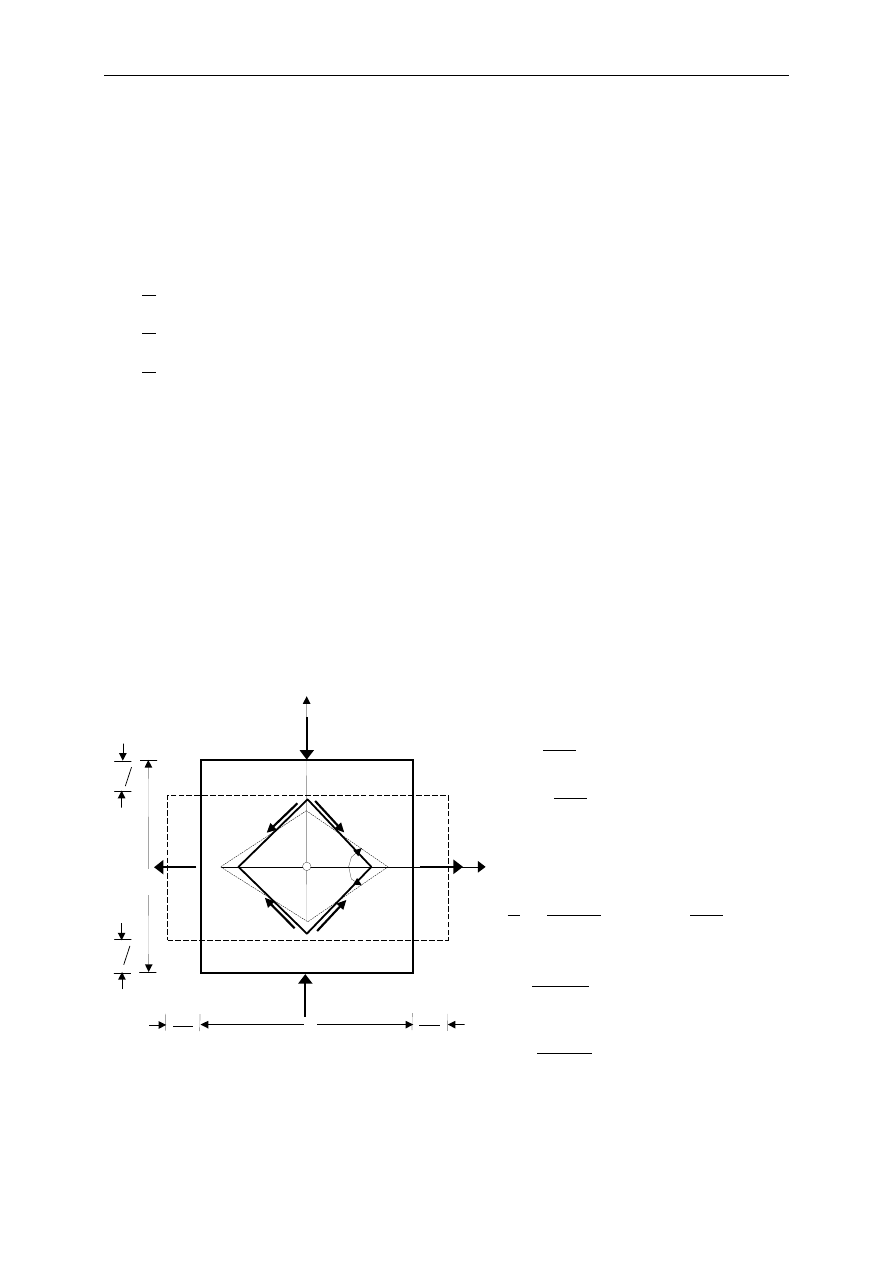
Jest to płaski stan napr

ęż

enia w płaszczy

ź

nie (Y, Z) i - jak pokazano na rys. 7.2 - na

płaszczyznach nachylonych pod k

ą

tem 45 do osi (Y, Z) wyst

ę

puj

ą

jedynie napr

ęż

enia styczne

σ

τ

=

(por. przykład 5.4.2).

Odkształcenia liniowe w kierunkach
osi układu wynosz

ą

:

σ

ν

ε

σ

ν

ε

E

E

z

y

+

−

=

+

=

1

1

,

a k

ą

towe jest rowne zeru.

Odkształcenie

k

ą

towe

γ

osi

obróconych o k

ą

t 45

° wynosz

ą

:

(

)

σ

ν

ε

ε

γ

E

z

y

+

=

−

−

−

=

1

90

sin

2

2

o

,

ale

σ

τ

=

st

ą

d:

(

)

τ

ν

γ

E

+

=

1

2

.

Oznaczaj

ą

c przez

(

)

ν

+

=

1

2

E

G

, ostatecznie mo

ż

emy

zapisa

ć

zwi

ą

zek mi

ę

dzy odkształceniem k

ą

towym i napr

ęż

eniem stycznym w formie:

σ

Y

2

z

ε

2

z

ε

γγγγ

−

o

90

σ

τ

=

σ

Y

Y

Z

1

2

y

ε

2

y

ε

1

Rys. 7.2

σ

Y

σ

Y

Adam Bodnar: Wytrzymało

ść

Materiałów. Równania fizyczne.

62

G

τ

γ

=

,

(7.2)

gdzie stała materiałowa G nazywana jest modułem

ś

cinania lub Kirchhoffa albo modułem

spr

ęż

ysto

ść

i poprzecznej.

Powracaj

ą

c

do

rozwa

ż

anego

na

pocz

ą

tku

sze

ś

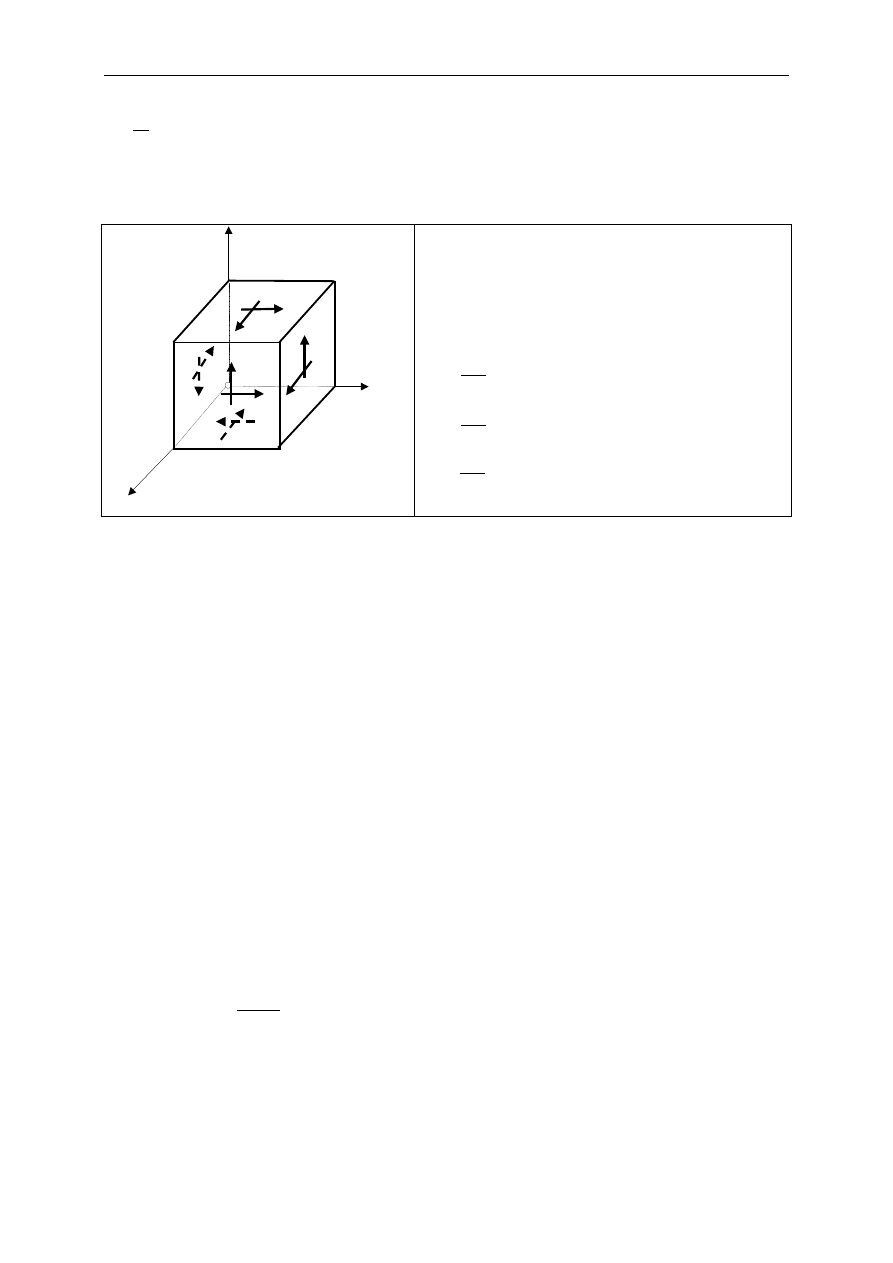
cianu poddajmy go teraz kolejno działaniu

równomiernie rozło

ż

onych napr

ęż

e

ń

stycznych

pokazanych na rys. 7.3. W przypadku spr

ęż

ystego

ciała izotropowego nie wywołaj

ą

one odkształce

ń

liniowych a k

ą

towe b

ę

d

ą

równe:

G

xy

xy

τ

γ

=

,

G

yz

yz

τ

γ

=

, (7.3)

G

xz

xz

τ

γ

=

.

Równania (7.1) i (7.3) okre

ś

laj

ą

ce zwi

ą

zki mi

ę

dzy odkształceniami i napr

ęż

eniami nazywaj

ą

si

ę

równaniami Hooke’a lub zwi

ą

zkami konstytutywnymi lub fizycznymi. T

ę

posta

ć

równa

ń

fizycznych w których odkszałcenia s

ą

funkcjami napr

ęż

e

ń

nazwiemy I postaci

ą

równa

ń

Hooke’a.
Poniewa

ż

rozwa

ż

amy materiały z załozenia izotropowe to wyst

ę

puj

ą

w nich tylko dwie stałe

materiałowe które nale

ż

y wyznaczy

ć

do

ś

wiadczalnie. Sposób ich wyznaczenia podany

zostanie w toku dalszych wykładów.
Udowodnimy teraz wa

ż

ne twierdzenie: w ciele spr

ęż

ystym i izotropowym kierunki napr

ęż

e

ń

głównych pokrywaj

ą

si

ę

z kierunkami odkształce

ń

głównych.

Dowód: niech osie X, Y i Z to osie głównych napr

ęż

e

ń

. Je

ś

li tak to napr

ęż

enia styczne

0

=

=

=

zx

yz

xy

τ

τ

τ

a dalej z (7.3)

0

=

=

=

zx

yz

xy

γ

γ

γ

co dowodzi,

ż

e te osie s

ą

osiami

odkształce

ń

głównych.

Aby wyprowadzi

ć

zwi

ą

zki mi

ę

dzy napr

ęż

eniami i odkształceniami nale

ż

y odwróci

ć

równania

(7.1) i (7.3). Odwrócenie tych drugich jest spraw

ą

bardzo prost

ą

. Pierwsze odwrócimy

kolejno wykonuj

ą

c:

(

)

z

y

x

x

E

σ

σ

ν

σ

ε

+

−

=

,

(

)

z

x

y

y

E

σ

σ

ν

σ

ε

+

−

=

,

(

)

y

x

z

z

E

σ

σ

ν

σ

ε

+

−

=

.

Dodanie stronami tych trzech równa

ń

daje zale

ż

no

ść

:

(

)

(

)

z

y

x

z

y

x

E

ε

ε

ε

ν

σ

σ

σ

+

+

−

=

+

+

2

1

.

(7.4)

Przekształcamy pierwsze równanie dodaj

ą

c i odejmuj

ą

c po prawej stronie:

(

)

(

)

(

)

z

y

x

x

x

x

x

z

y

x

x

E

E

σ

σ

σ

ν

σ

ν

ε

σ

ν

σ

ν

σ

σ

ν

σ

ε

+

+

−

+

=

→

+

−

+

−

=

1

Wstawienie (7.4) daje:

yx

τ

xz

τ

xy

τ

yz

τ

zy

τ

zx

τ

X

Z

Y

Rys. 7.3

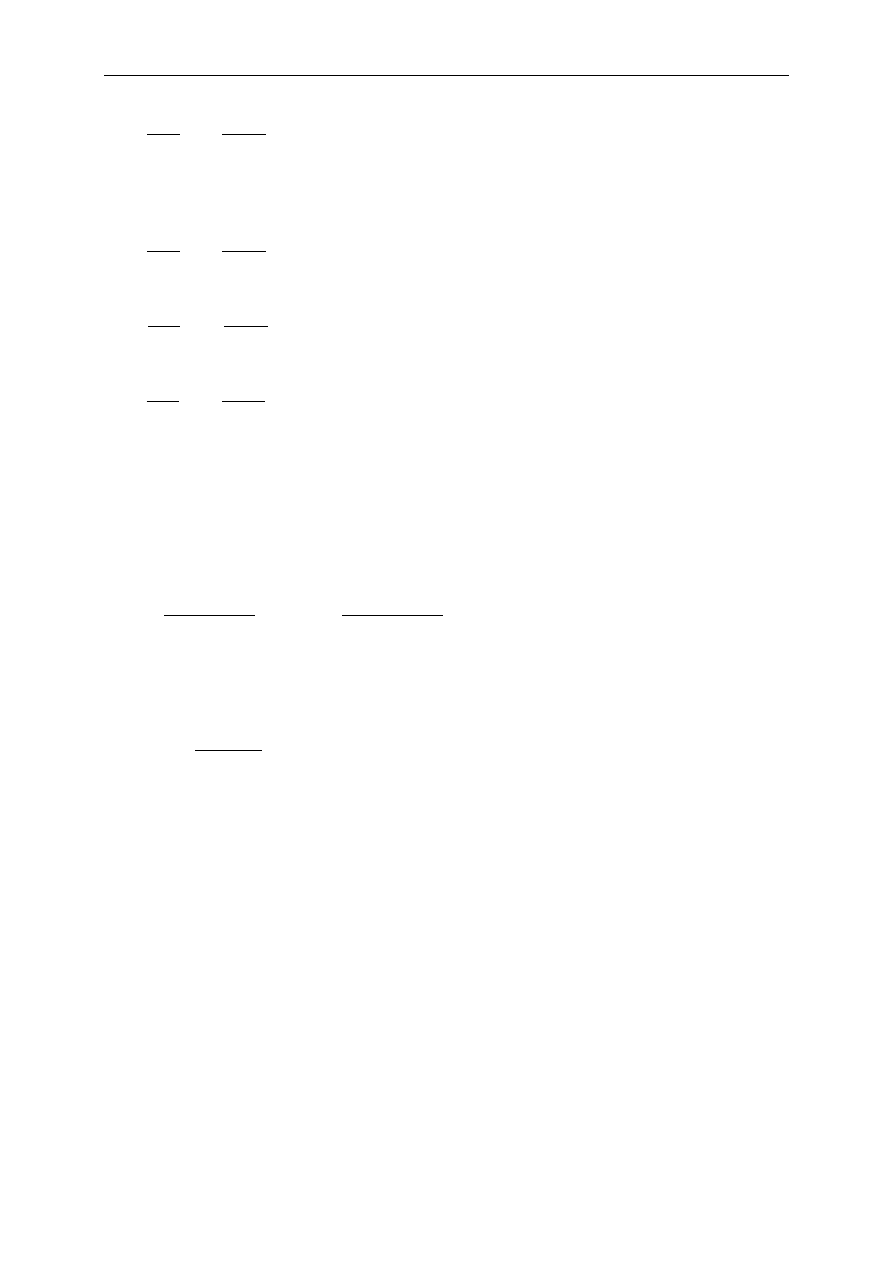
Adam Bodnar: Wytrzymało

ść

Materiałów. Równania fizyczne.

63

(

)













+

+

−

+

+

=

z

y

x

x

x

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

i post

ę

puj

ą

c analogicznie z nast

ę

pnymi napr

ęż

eniami

normalnymi dostajemy równania wi

ążą

ce je z odkształceniami liniowymi.

II posta

ć

równa

ń

fizycznych Hooke’a :

(

)













+

+

−

+

+

=

z

y

x

x

x

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

(

)













+

+

−

+

+

=

z

y

x

y

y

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

(7.5)

(

)













+

+

−

+

+

=

z

y

x

z

z

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

zx

zx

yz

yz

xy

xy

G

G

G

γ

τ

γ

τ

γ

τ

=

=

=

,

,

7.2. III postać równań Hooke’a - prawo zmiany objętości i prawo zmiany postaci

Przyjmijmy na mocy definicji:

3

z

y

x

m

def

ε

ε

ε

ε

+

+

=

,

3

z

y

x

m

def

σ

σ

σ

σ

+

+

=

(7.6)

jako odkształcenie

ś

rednie i napr

ęż

enie

ś

rednie. Przy tych oznaczeniach wzór (7.4) mo

ż

emy

zapisa

ć

w formie:

m

m

K

ε

σ

3

=

(7.7)

gdzie:

(

)

ν

2

1

3

−

=

E

K

jest stał

ą

materiałow

ą

i nazywana jest modułem obj

ę

to

ś

ciowej

ś

ci

ś

liwo

ś

ci spr

ęż

ystej lub modułem Helmholtza.

Dokonajmy rozkładu macierzy napr

ęż

e

ń

na dwie cz

ęś

ci

σ

σ

σ

Α

Τ

D

+

=





















z

zy

zx

yz

y

yx

xz

xy

x

σ

τ

τ

τ

σ

τ

τ

τ

σ





















=

m

m

m

σ

σ

σ

0

0

0

0

0

0





















−

−

−

+

m

z

zy

zx

yz

m

y

yx

xz

xy

m

x

σ

σ

τ

τ

τ

σ

σ

τ

τ

τ

σ

σ

gdzie:

σ

Α

- aksjator napr

ęż

e

ń

,

σ

D

- dewiator napr

ęż

e

ń

;

i analogicznie macierzy odkształce

ń

:

ε

ε

ε

Α

Τ

D

+

=

Adam Bodnar: Wytrzymało

ść

Materiałów. Równania fizyczne.

64





















z

zy

zx

yz

y

yx

xz

xy

x

ε

γ

γ

γ

ε

γ

γ

γ

ε

2

1

2

1

2

1

2

1

2

1

2

1





















=

m

m

m

ε

ε

ε

0

0

0

0

0

0





















−

−

−

+

m

z

zy

zx

yz

m

y

yx

xz

xy

m

x

ε

ε

γ

γ

γ

ε

ε

γ

γ

γ

ε

ε

2

1

2

1

2

1

2

1

2

1

2

1

gdzie:

ε

Α

- aksjator odkształce

ń

,

ε

D

- dewiator odkształce

ń

.

Łatwo sprawdzi

ć

,

ż

e zachodz

ą

poni

ż

sze zwi

ą

zki mi

ę

dzy aksjatorami i dewiatorami napr

ęż

e

ń

i

odkształce

ń

:

ε

σ

Α

Α

K

3

=

,

(7.8)

ε

σ

D

G

D

2

=

,

(7.9)

które stanowi

ą

III posta

ć

równa

ń

Hooke’a i nosz

ą

nazwy prawa zmiany obj

ę

to

ś

ci i prawa

zmiany postaci.
Uzasadnienie tych nazw nie jest trudne. Działanie aksjatora napr

ęż

e

ń

wywołuje jedynie

zmian

ę

obj

ę

to

ś

ci, a odkształcenia postaciowe s

ą

równe zeru. Natomiast pod działaniem

dewiatora napr

ęż

e

ń

powstaj

ą

odkształcenia postaciowe, a suma odkształce

ń

liniowych na

przek

ą

tnej dewiatora odkształce

ń

jest równa zeru, co dowodzi,

ż

e nie ma zmiany obj

ę

to

ś

ci.

Wró

ć

my jeszcze do równania (7.7). Wykorzystuj

ą

c,

ż

e zmiana obj

ę

to

ś

ci jest równa:

m

z

y

x

D

ε

ε

ε

ε

3

=

+

+

=

,

mo

ż

emy zapisa

ć

:

m

E

D

σ

ν

2

1

3

−

=

.

Je

ś

li

0

>

m

σ

, to oczywi

ś

cie D>0, a wi

ę

c musi zachodzi

ć

: 1-2

ν

> 0,

czyli

2

1

≤

ν

νν

ν

.

Maksymalna zmiana obj

ę

to

ś

ci b

ę

dzie zachodzi

ć

dla materiału którego

0

=

ν

νν

ν

, materiał

którego

2

1

=

ν

jest nie

ś

ci

ś

liwy. Guma ma liczb

ę

Poissona blisk

ą

0.5, a korek blisk

ą

0.

7.3. Przykłady
Przykład 7.3.1.

Jakie obci

ąż

enie sze

ś

cianu o boku a wykonanego z materiału spełniaj

ą

cego

równania Hooke’a, powoduje przemieszczenia dowolnego jego punktu okre

ś

lone funkcjami:

,

,

,

z

C

w

y

C

v

x

C

u

−

=

−

=

−

=

je

ś

li stałe materiałowe s

ą

równe E i

ν.

a

X

a

a

Z

Y

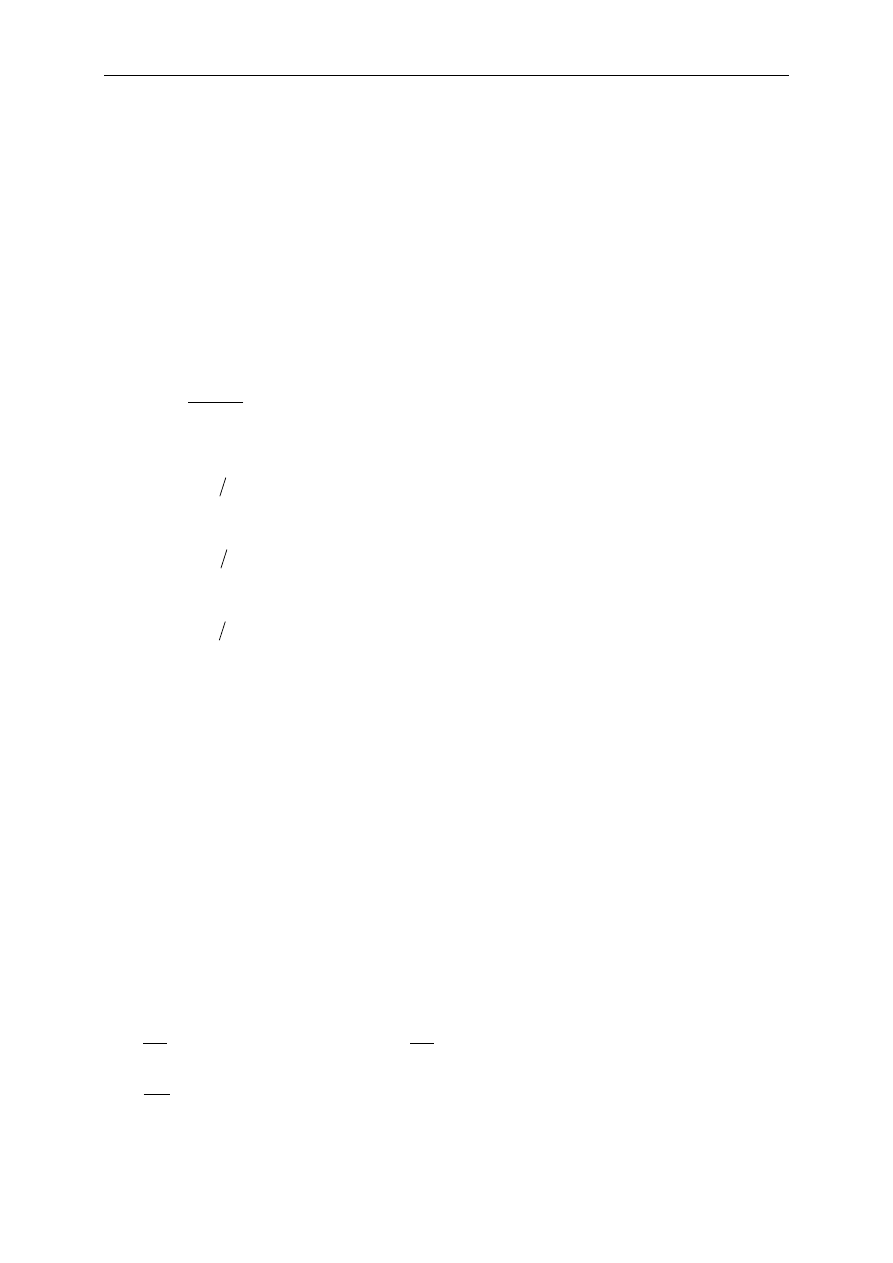
Adam Bodnar: Wytrzymało

ść

Materiałów. Równania fizyczne.

65

Rozwiązanie

Z równa

ń

Cauchy’ego łatwo wyznaczy

ć

,

ż

e odkształcenia liniowe s

ą

równe

C

z

y

x

−

=

=

=

ε

ε

ε

a odkształcenia k

ą

towe równaj

ą

si

ę

zeru

0

=

=

=

zy

xz

xy

γ

γ

γ

Odpowiadaj

ą

ce im współrz

ę

dne tensora napr

ęż

e

ń

s

ą

równe

0

=

=

=

−

=

=

=

zy

xz

xy

z

y

x

BC

τ

τ

τ

σ

σ

σ

gdzie :

(

)

ν

2

1

−

=

E

B

.

Obci

ąż

enie

ś

cianek sze

ś

cianu wyznaczymy ze statycznych warunków brzegowych.

Ś

cianki

2

a

x

±

=

, współrz

ę

dne wersora normalnego zewn

ę

trznego

0

,

1

=

=

±

=

n

m

l

.

0

,

=

=

=

vz

vy

vx

q

q

BC

q

m

.

Ś

cianki

2

a

y

±

=

, współrz

ę

dne wersora normalnego zewn

ę

trznego

0

,

1

=

=

±

=

n

l

m

.

0

,

=

=

=

vz

vx

vy

q

q

BC

q

m

.

Ś

cianki

2

a

z

±

=

, współrz

ę

dne wersora normalnego zewn

ę

trznego

0

,

1

=

=

±

=

m

l

n

.

0

,

=

=

=

vy

vx

vz

q

q

BC

q

m

.

Tak wi

ę

c

ś

cianki sze

ś

cianu obci

ąż

one s

ą

równomiernie rozło

ż

onym obci

ąż

eniem

ś

ciskaj

ą

cym

o intensywno

ś

ci BC.

Przykład 7.3.2.

Dane s

ą

funkcje przemieszcze

ń

w konstrukcji wykonanej z materiału

liniowo spr

ęż

ystego:

(

)

4

10

*

1

.

0

5

−

+

=

xy

u

m,

(

)

4

10

*

1

.

0

−

−

=

xy

y

v

m,

(

)

4

2

2

10

*

−

−

=

z

x

w

m,

wyznaczy

ć

macierz odkształce

ń

i napr

ęż

e

ń

w punkcie

(

)

1

,

2

,

1

−

A

m, je

ś

li moduł Younga

E =

205 GPa i liczba Poissona

ν = 0.3.

Rozwiązanie

Z równa

ń

geometrycznych Cauchy’ego wyznaczymy funkcje odksztace

ń

a po wstawieniu do

nich wspólrz

ę

dnych punktu A otrzymamy warto

ś

ci wyst

ę

puj

ą

cych w nim odkształce

ń

:

4

4

10

*

2

.

0

10

*

1

.

0

−

−

=

=

∂

∂

=

y

x

u

x

ε

,

(

)

4

4

10

*

1

.

1

10

*

1

.

0

0

.

1

−

−

=

−

=

∂

∂

=

x

y

v

y

ε

,

4

4

10

*

0

.

2

10

*

2

−

−

−

=

−

=

∂

∂

=

z

z

w

z

ε

,

Adam Bodnar: Wytrzymało

ść

Materiałów. Równania fizyczne.

66

(

)

4

4

10

*

3

.

0

10

*

1

.

0

1

.

0

−

−

−

=

−

=

∂

∂

+

∂

∂

=

y

x

x

v

y

u

xy

γ

,

4

4

10

*

0

.

2

10

*

2

−

−

−

=

=

∂

∂

+

∂

∂

=

x

x

w

w

u

xz

γ

,

0

=

∂

∂

+

∂

∂

=

y

w

z

v

yz

γ

.

Macierz odkształce

ń

ma posta

ć

:

4

2

1

2

1

2

1

2

1

2

1

2

1

10

*

0

.

2

0

0

.

1

0

1

.

1

15

.

0

0

.

1

15

.

0

2

.

0

−





















−

−

−

−

−

=





















=

z

zy

zx

yz

y

yx

xz

xy

x

T

ε

γ

γ

γ

ε

γ

γ

γ

ε

ε

.

Napr

ęż

enia wyznaczymy korzystaj

ą

c z II postaci równa

ń

Hooke’a:

(

)

=













+

+

−

+

+

=

z

y

x

x

x

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

(

)

125

.

5

10

*

0

.

2

1

.

1

2

.

0

3

.

0

*

2

1

3

.

0

2

.

0

3

.

0

1

10

*

205

4

9

−

=













−

+

−

+

+

=

−

MPa,

(

)

=













+

+

−

+

+

=

z

y

x

y

y

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

(

)

067

.

9

10

*

0

.

2

1

.

1

2

.

0

3

.

0

*

2

1

3

.

0

1

.

1

3

.

0

1

10

*

205

4

9

=













−

+

−

+

+

=

−

MPa,

(

)

=













+

+

−

+

+

=

z

y

x

x

z

E

ε

ε

ε

ν

ν

ε

ν

σ

2

1

1

(

)

817

.

39

10

*

0

.

2

1

.

1

2

.

0

3

.

0

*

2

1

3

.

0

0

.

2

3

.

0

1

10

*

205

4

9

−

=













−

+

−

+

−

+

=

−

MPa,

(

)

(

)

365

.

2

10

*

3

.

0

3

.

0

1

2

10

*

205

4

9

−

=

−

+

=

=

−

xy

xy

G

γ

τ

MPa,

(

)

(

)

769

.

15

10

*

0

.

2

3

.

0

1

2

10

*

205

4

9

−

=

−

+

=

=

−

xz

xz

G

γ

τ

MPa,

0

=

=

yz

yz

G

γ

τ

.

Macierz napr

ęż

e

ń

przedstawia si

ę

wi

ę

c nast

ę

puj

ą

co:





















−

−

−

−

−

−

=





















=

817

.

39

0

769

.

15

0

067

.

9

365

.

2

769

.

15

365

.

2

125

.

5

z

zy

zx

yz

y

yx

xz

xy

x

T

σ

τ

τ

τ

σ

τ

τ

τ

σ

σ

MPa.