Ćwiczenie nr 2
ŁĄCZENIE OBWODÓW ELEKTRYCZNYCH

Samodzielne wykonanie połączeń prostych obwodów elektrycznych stanowi główną

część samodzielnej pracy podczas tego ćwiczenia. Konieczne będzie także wykonanie
prostych pomiarów wielkości elektrycznych. Uczestnicy zaznajomią się z zasadami
dotyczącymi opracowania wyników pomiarów i przygotowania sprawozdania z ćwiczenia.

Wstęp teoretyczny

1. Prawo Ohma

Napięcie elektryczne, U, mierzone na końcach przewodnika o rezystancji R (oporze

elektrycznym) podczas przepływu prądu o natężeniu I jest równe iloczynowi rezystancji i
prądu:

U = R I

jednostka rezystancji

Jeden om jest rezystancją między dwoma punktami przewodu prostoliniowego, gdy

różnica potencjałów równa jednemu woltowi, działająca między tymi dwoma punktami,
wywołuje, w tym przewodzie przepływ prądu o natężeniu jednego ampera.


2. Pomiary podstawowych wielkości obwodu elektrycznego

Pomiary natężenia prądu

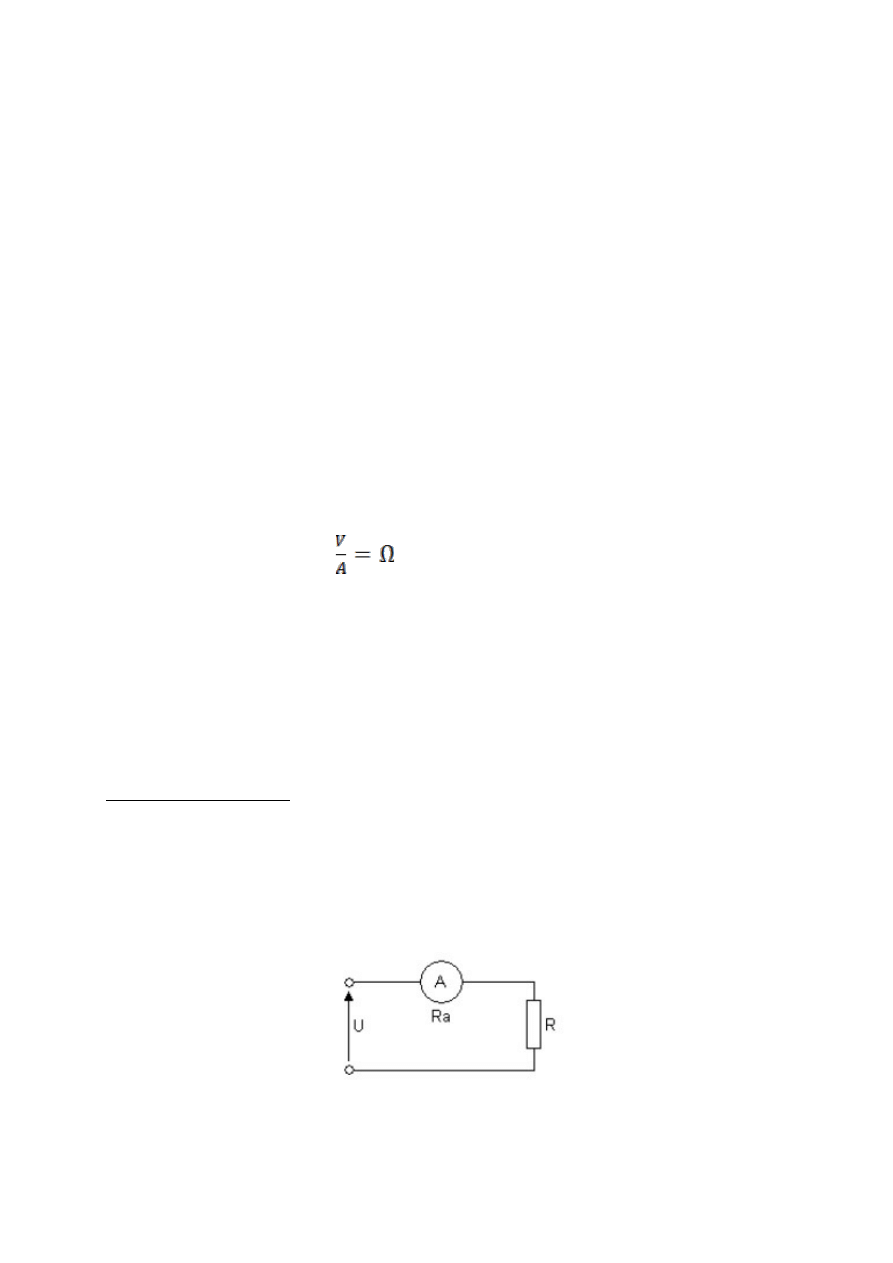
Do pomiaru prądu służy amperomierz. Aby przez organ pomiarowy miernika i

odbiornik przepływał ten sam prąd, amperomierz powinien być połączony szeregowo z
odbiornikiem (rys. 1). W celu uniknięcia zmiany prądu w obwodzie, wynikającej z włączenia
amperomierza, jego oporność wewnętrzna powinna być bardzo mała.

Rys. 1. Sposób włączania amperomierza w obwód elektryczny.

Pomiary napięcia elektrycznego

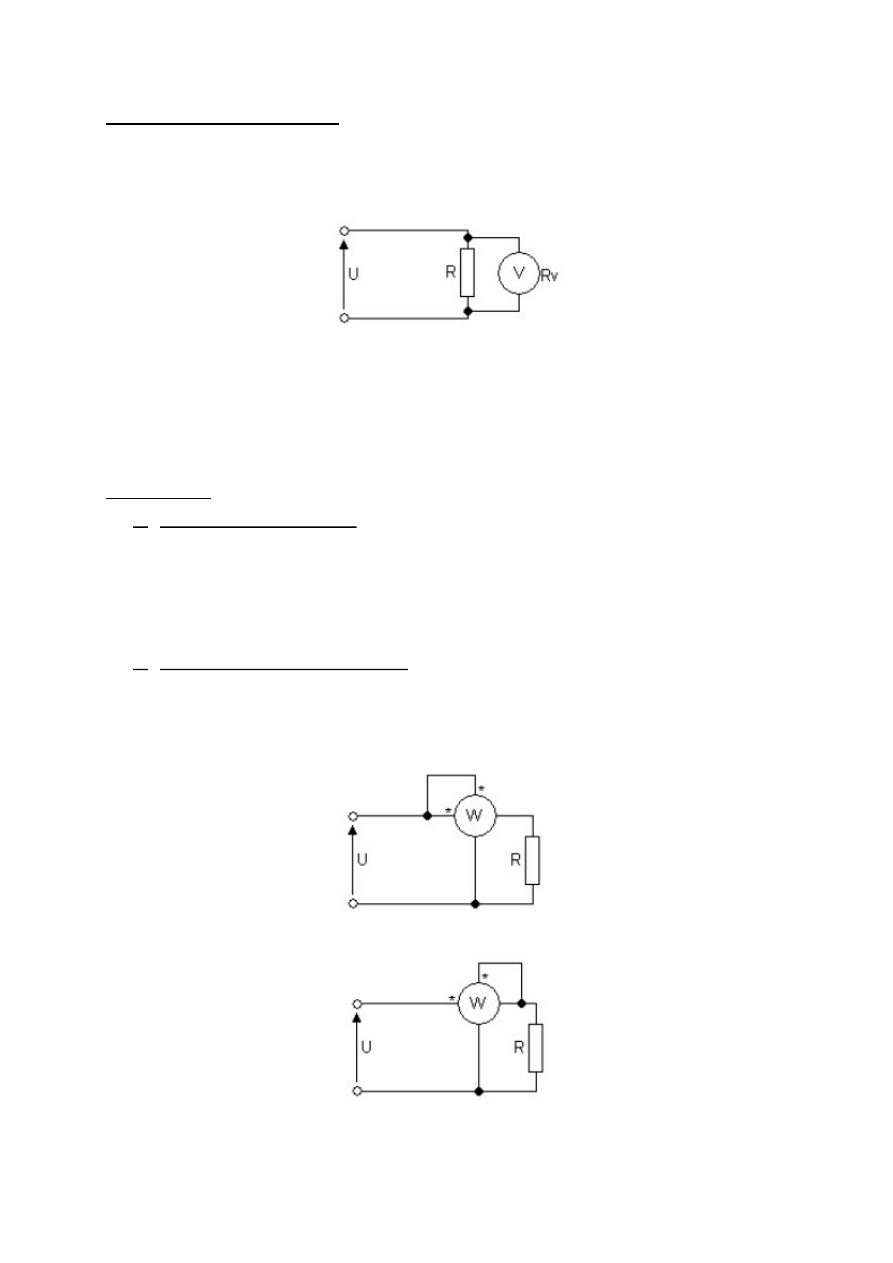
Woltomierz dołącza się do zacisków, między którymi ma być pomierzone napięcie, a

więc równolegle do rozpatrywanego elementu obwodu (rys. 2).

Rys. 2. Sposób włączania woltomierza w obwód elektryczny.

Aby prąd płynący przez miernik był jak najmniejszy, woltomierz posiada dużą

oporność wewnętrzną R

v

.

Pomiary mocy

a) w obwodach prądu stałego

W obwodach prądu stałego wyznaczenie mocy pobieranej przez odbiorniki opiera się
na pomiarze napięcia U przyłożonego do odbiornika lub ich grupy oraz natężenia
prądu I, przepływającego przez te odbiorniki. Obliczenie opiera się na wzorze

P = U ∙ I

b) w obwodach prądu przemiennego

Pomiaru mocy czynnej odbiornika w obwodzie jednofazowym dokonuje się

watomierzem. Układ do pomiaru mocy czynnej przedstawiono na rys. 3.

Rys. 3a. Układ z poprawnie mierzonym prądem.

Rys. 3b. Układ z poprawnie mierzonym napięciem.

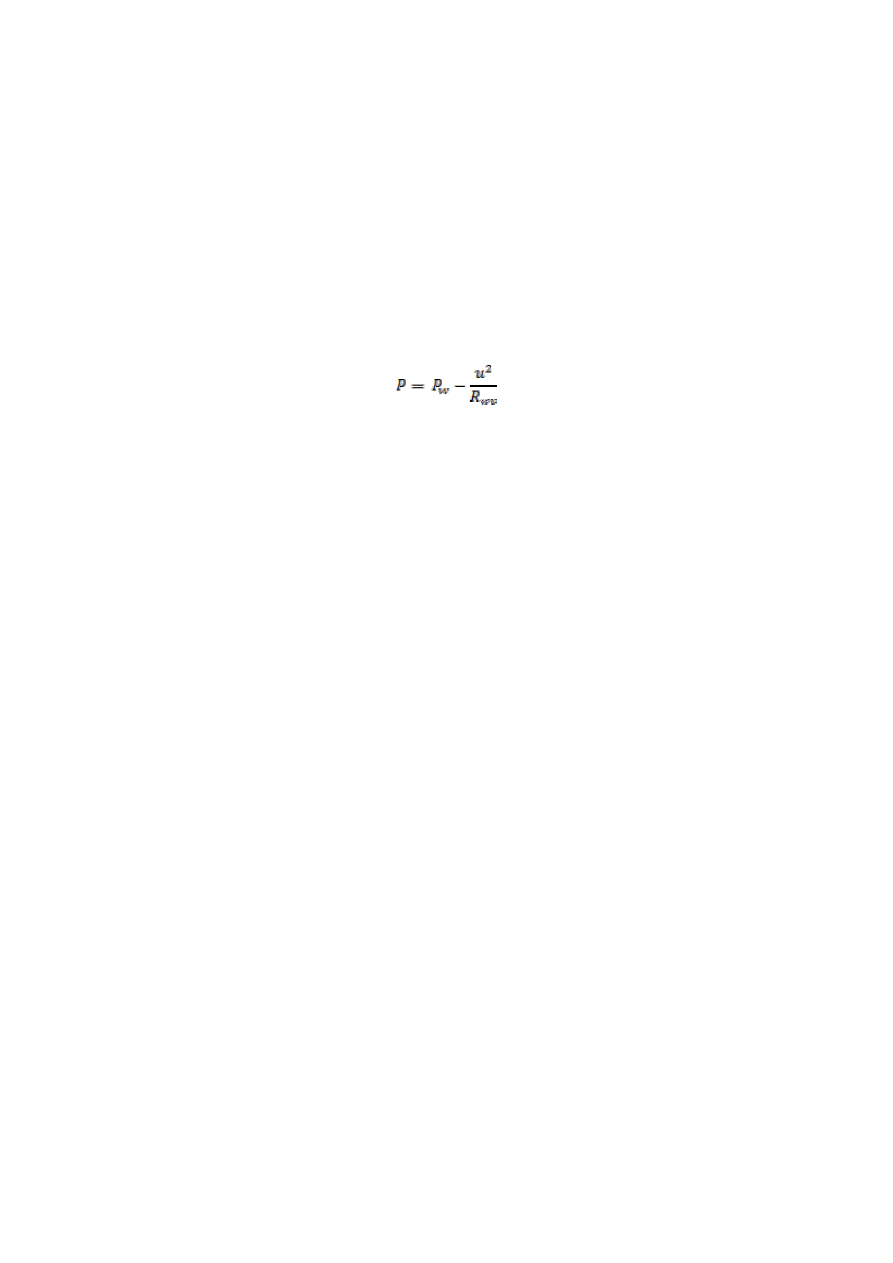
Moc P

w

wskazywana przez watomierz jest w obydwóch układach większa od mocy

czynnej odbiornika o stratę mocy w mierniku. W przypadku układu z poprawnie mierzonym
prądem (rys. 3a.) dokładnie obliczona moc czynna odbiornika wynosi:

P = P

w

– I

2

R

wa

gdzie R

wa

– rezystancja cewki prądowej watomierza.

Dokładnie obliczona moc czynna odbiornika na podstawie pomiarów w układzie z

poprawnie mierzonym napięciem (rys. 3b.) wynosi:

gdzie R

wv

– rezystancja cewki napięciowej watomierza.

Nie uwzględniając poboru mocy przez watomierz, popełnia się błąd, którego wartość

jest tym mniejsza im większa jest moc odbiornika oraz im mniejsza jest moc tracona w
mierniku.

W obwodach prądu przemiennego dla dużej grupy odbiorników występuje

przesunięcie fazowe  pomiędzy przebiegiem czasowym napięcia zasilającego oraz
przebiegiem czasowym natężenia prądu w obwodzie. Takie odbiorniki nie wykorzystują
całkowitej mocy źródła zasilania, tylko jej część. Stopień wykorzystania mocy źródła
charakteryzuje tzw. współczynnik mocy określany jako cos . Z tego powodu w obwodach
prądu przemiennego wyróżnia się trzy wielkości mocy: czynną, bierną oraz pozorną.
Wykorzystanie w takich obwodach do obliczenia mocy wyłącznie pomiaru napięcia zasilania
oraz natężenia prądu, prowadzi do obliczenia wartości mocy pozornej, ustalanej na
podstawie wzoru:

S = U ∙ I

Jednak znacznie ważniejsza jest znajomość tzw. mocy czynnej, czyli mocy rzeczywiście
przetwarzanej przez obwód elektryczny na pracę użyteczną. Wartość mocy czynnej określa
się na podstawie znajomości współczynnika mocy danego odbiornika i wyznacza ze wzoru:

P = U ∙ I ∙ cos 

Watomierze są konstruowane w taki sposób, że wskazują wartość mocy czynnej.

Zatem dokonując jednocześnie pomiaru mocy czynnej, napięcia oraz natężenia prądu w
obwodzie możliwe jest wyznaczenie współczynnika mocy cos .

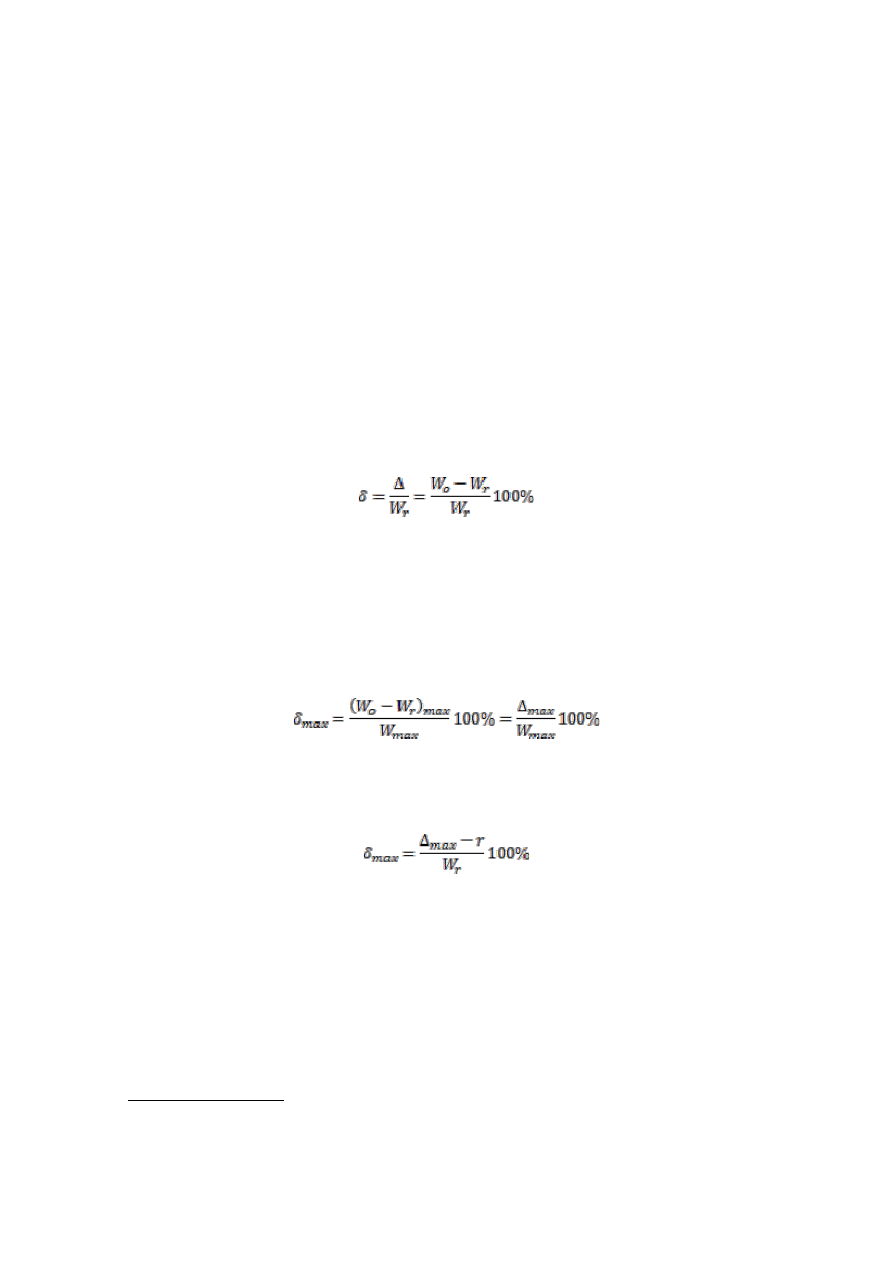
3. Analiza błędów

Pomiar jest doświadczeniem fizycznym. Ograniczona dokładność narzędzi

pomiarowych, zmienność warunków, w których odbywa się doświadczenie, niedostateczna
znajomość wszystkich okoliczności związanych z badanym zjawiskiem wywołują
zniekształcenia wyników. Wartość otrzymana z wyniku pomiaru różni się od wartości
rzeczywistej wielkości mierzonej. Różnica między tymi wartościami, zwana błędem lub
uchybem pomiaru, jest miarą niedokładności pomiaru. Różnicę między wartością W

o

otrzymaną z pomiaru, a wartością rzeczywistą, W

r

, mierzonej wielkości nazywa się błędem

bezwzględnym pomiaru (Δ = W

o

– W

r

).

Dla oceny jakości pomiaru bardziej odpowiednie jest pojęcie błędu względnego

pomiaru – jest to wyrażony w procentach stosunek błędu bezwzględnego do wartości
rzeczywistej:

Dokładność przyrządu pomiarowego określa się za pomocą błędu

charakterystycznego miernika analogowego (klasa dokładności), który jest wyrażony w
procentach stosunkiem największego błędu bezwzględnego, jaki stwierdzono podczas
skalowania miernika, do końcowej wartości W

max

zakresu pomiarowego przyrządu:

W przypadku mierników cyfrowych klasa dokładności wyrażona jest wzorem:

r – rozdzielczość (najmniejsza możliwa do odczytania wartość na wykorzystywanym zakresie
pomiarowym).

Z powyższego rozważania wynika wniosek, że wykonując pomiary należy tak

dobierać zakresy przyrządów, aby mierzyły one wartości zbliżone do ich zakresu
pomiarowego, gdyż w takich warunkach pomiar obarczony jest najmniejszym błędem.

Błędy występujące w pomiarach wielkości fizycznych dzielimy ze względu na ich

istotę:
a) błędy systematyczne – są to takie błędy, których pochodzenie jest znane mierzącemu.
Błędy te mogą mieć wartość stałą lub też zmieniającą się wg skreślonego prawa. Obecność

błędów systematycznych może być wykryta doświadczalnie. Wpływ błędów systematycznych
na wynik pomiaru daje się wyeliminować przez specjalne podejście do pomiaru lub też przez
określenie wartości błędów za pomocą doświadczenia i uwzględnienia tych wartości w
trakcie matematycznego opracowywania wyników.
b) błędy przypadkowe – są to błędy, których pochodzenie i wartość nie są znane
mierzącemu. Obecność błędów przypadkowych dostrzega się otrzymując przy wielokrotnym
powtórzeniu pomiaru odczytu różniące się między sobą ostatnimi znaczącymi wartościami,
nie mogą być wyeliminowane na drodze doświadczalnej. Posługując się teorią
prawdopodobieństwa i metodami statystyki matematycznej można określić wpływ tych
błędów na wynik pomiaru.
c) błędy grube – czyli omyłki są to bardzo duże błędy, zniekształcające w sposób rażący
wynik pomiaru. Omyłki spowodowane są zwykle przez nieuwagę obserwatora. Przy
matematycznym opracowywaniu wyników pomiaru należy odrzucać odczyty obarczone
błędami grubymi.


Statystyczna analiza wyników pomiarów

Statystyczną analizę wyników pomiarów można przeprowadzić dysponując wynikami

pomiarów (x

1

, x

2

, …, x

n

) n-krotnie powtarzając ten sam pomiar w jednakowych warunkach.

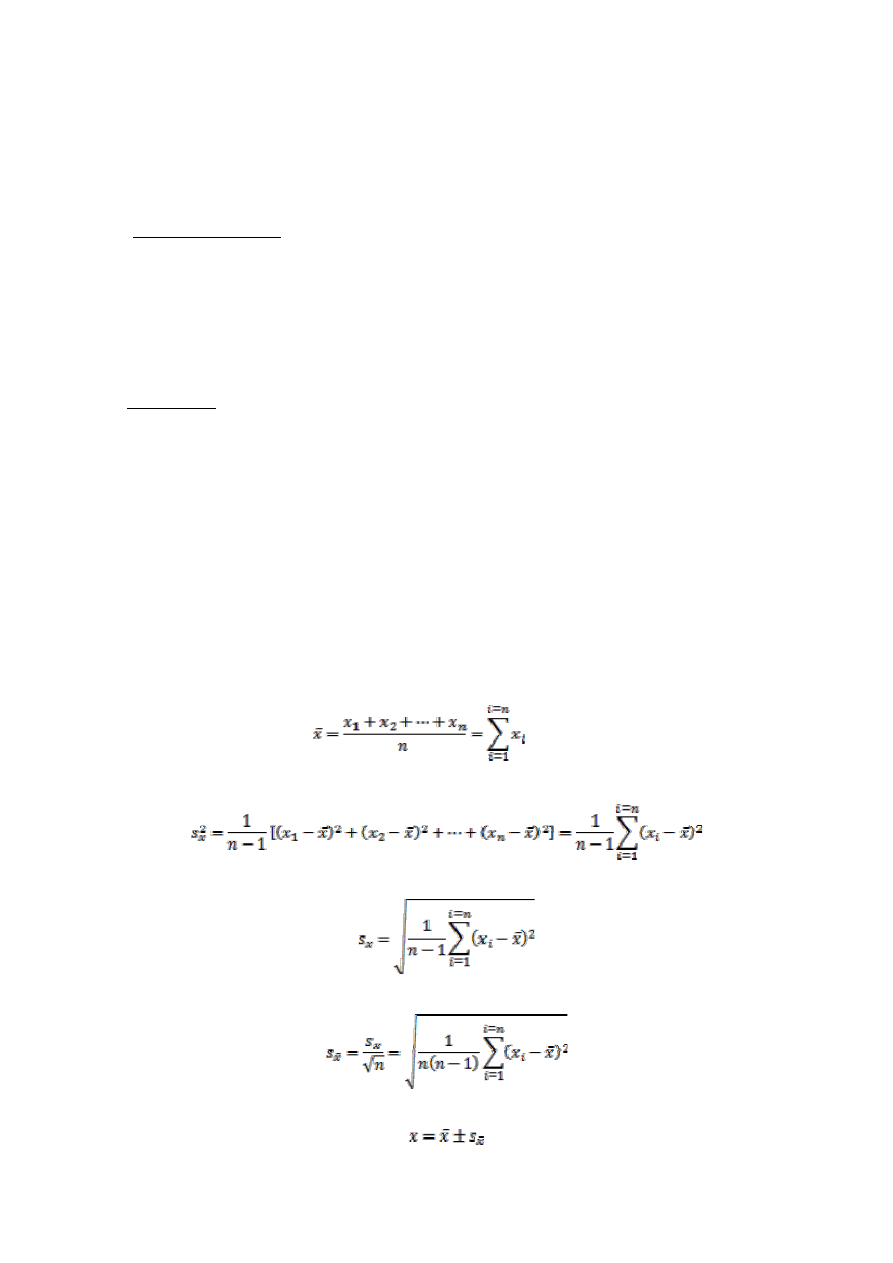
Można dzięki temu wyznaczyć średnią arytmetyczną wartość wyników pomiarów:

razy 1/n

Następnie należy obliczyć wariancję jako miarę niepewności pomiaru:

Wówczas odchylenie standardowe pojedynczego pomiaru można jest równe:

a odchylenie standardowe średniej arytmetycznej wyniesie:

Ostatecznie wynik pomiaru przedstawia się w postaci:

W trakcie opracowywania pomiarów będziemy stosowali następujące zasady:

A. Błąd zaokrąglamy do jednej cyfry znaczącej.
B. Błąd zaokrąglamy „do góry”.
C. Wartość wyznaczanej wielkości zaokrąglamy do rzędu wielkości błędu.

Zaokrąglanie rozpoczynamy od zaokrąglenia wartości błędu bezwzględnego. Należy

pamiętać, że cyfra znacząca błędu nie musi znajdować się po przecinku. Jeżeli obliczona
wartość błędu jest równa np. 0,0234, to po zaokrągleniu będzie to 0,03 (zasada B!). Jeżeli
jednak wartość ta będzie równa np. 123,764, to po zaokrągleniu dostaniemy 200. Wartość
wyznaczonej wielkości zaokrąglamy, nie tak jak w przypadku błędu „do góry”, a wg ogólnie
przyjętych zasad. W pierwszym z powyższych przykładów rząd wielkości błędu, to części
setne wiec nasz wynik zaokrąglimy również do części setnych. W drugim przykładzie rząd
wielkości błędu, to pełne setki, wynik zaokrąglamy wiec do pełnych setek. Np. jeżeli
obliczona wielkość ma wartość x = 537,314, a błąd bezwzględny jest równy 0,03, to wynik
powinniśmy zapisać jako x = 537,31 ± 0,03. Gdyby zmierzona wielkość miała wartość
27543,567, a błąd był równy 200, to zapis mierzonej wielkości powinien wyglądać
następująco x = 27500 ± 200. Podane przykłady dotyczą wielkości niemianowanych. W
wypadku wielkości mianowanych należy pamiętać, aby zawsze podawać jednostkę.
Prawidłowo zapisany wynik pomiaru napięcia może mieć postać U = 120 ± 10 V.

Wykonanie ćwiczenia:

UWAGA!!

PRZED WŁĄCZENIEM ZASILANIA NALEŻY BEZWZGLĘDNIE POPROSIĆ

PROWADZĄCEGO O ZGODĘ!!

1.

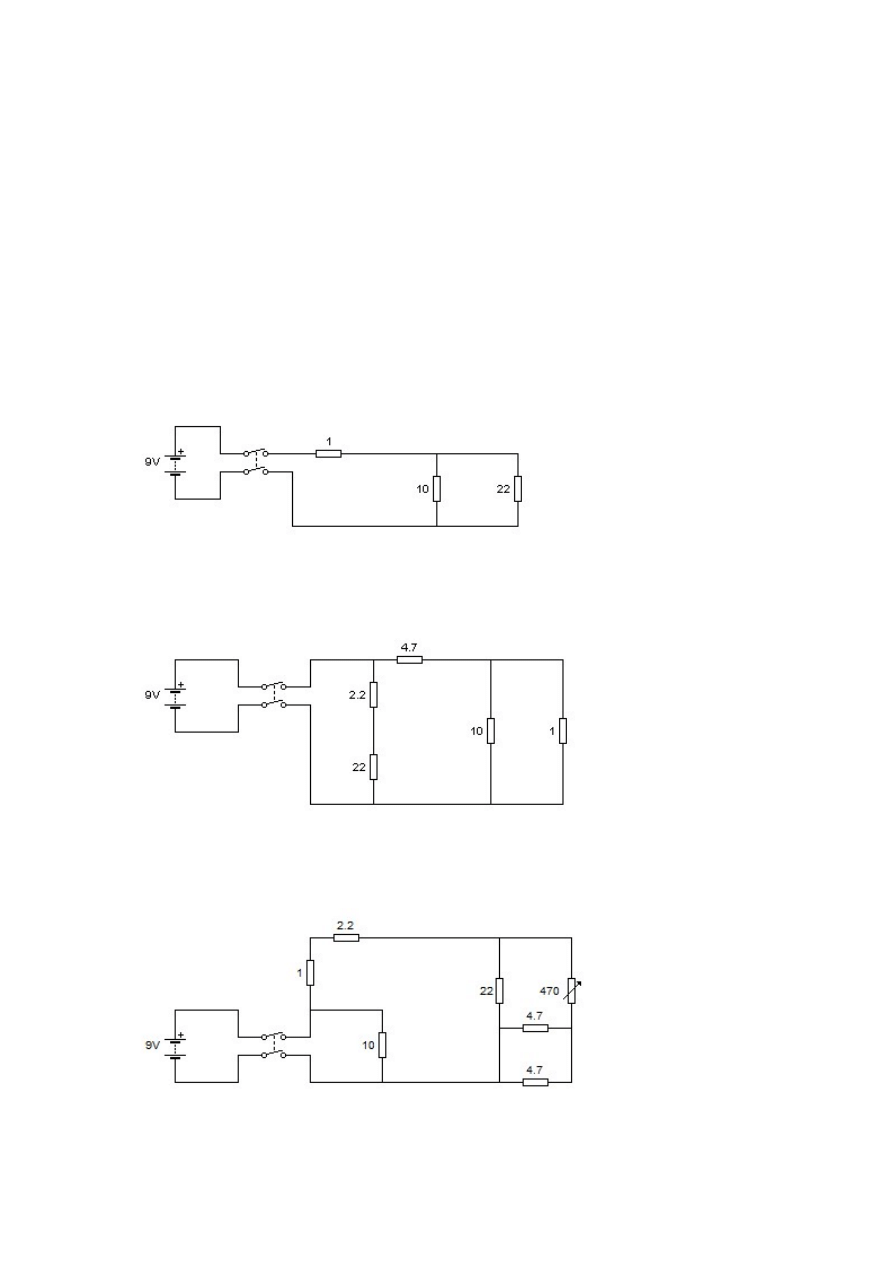
Z dostępnych elementów złożyć obwody elektryczne przedstawione na poniższych

schematach:
a)

b)

c)

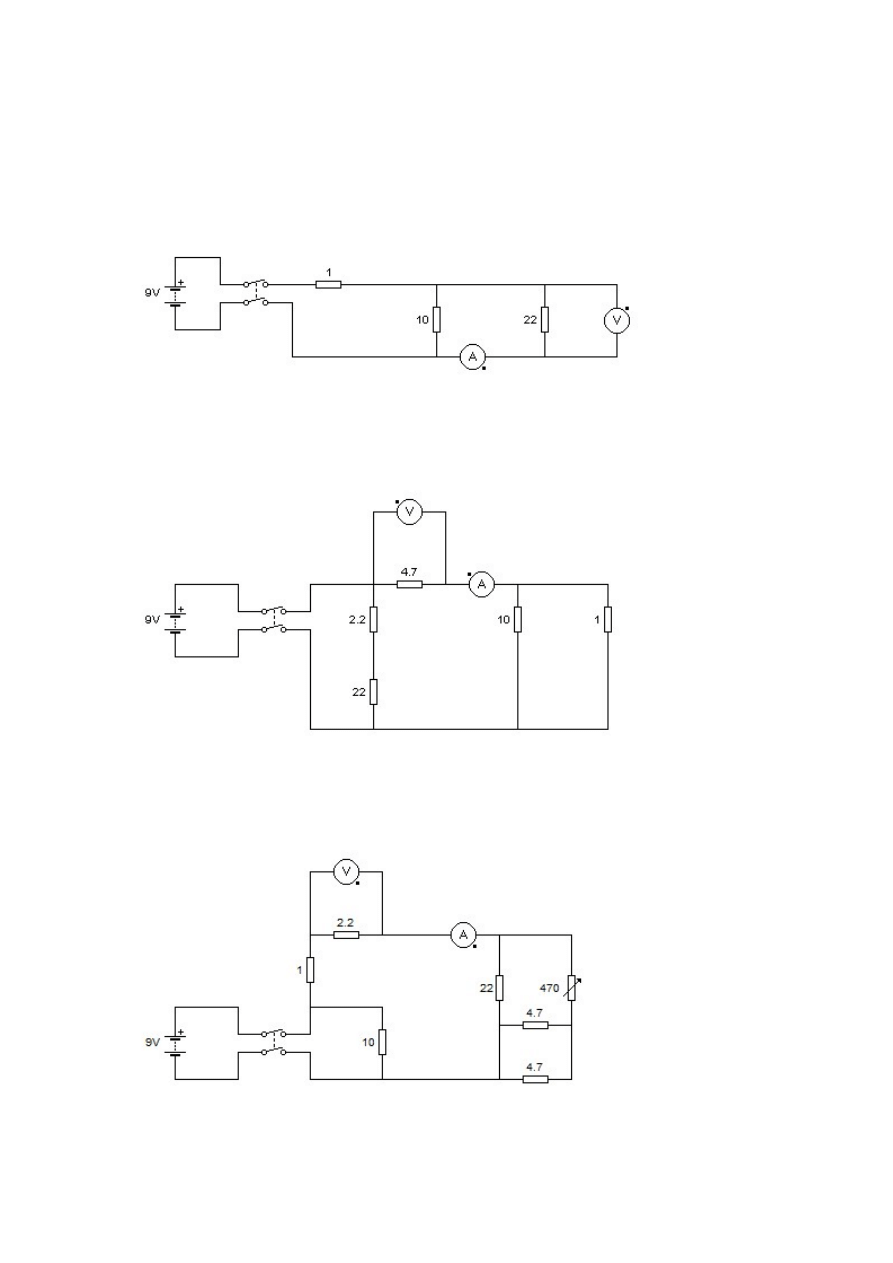
2.

Dokonać pomiarów podstawowych napięcia oraz natężenia prądu w poniższych

obwodach elektrycznych. Dla każdej mierzonej wielkości każda osoba uczestnicząca w
ćwiczeniu powinna dokonać jednego odczytu wartości wskazywanych przez mierniki.
a)

b)

c)

Uzyskane wartości zestawić w poniższej tabeli i obliczyć wartości rezystancji odpowiednich
oporników. Porównać otrzymane wartości z wartościami deklarowanymi przez producenta.

Układ nr …
L. p.

Napięcie [V]

Natężenie [A]

Rezystancja []

1.

2.

3.

4.

3.

Na podstawie wyników przeprowadzonych pomiarów dokonać analizy błędów.
Wyniki obliczeń przedstawić w postaci X = X

śr.

 X.

4.

Przedstawić samodzielne wnioski i uwagi dotyczące przeprowadzonego
ćwiczenia.