sieci jednowarstwowe

w MATLABie

LABORKA © Piotr Ciskowski

•

trzy funkcje do obsługi sieci jednowarstwowej…:

–

init1.m

- tworzy sieć, inicjuje wagi

(losowo)

–

dzialaj1.m

– symuluje działanie sieci

(na pojedynczym przykładzie)

–

ucz1.m

- uczy sieć na zadanym ciągu uczącym

•

…i jeden skrypt:

–

test1.m

- sieć 5-3, przykład: rozpoznawanie zwierząt

•

init1.m

- tworzy sieć, czyli jej macierz wag

i wypełnia ją wartościami losowymi z zakresu -0.1 ÷ 0.1

- w sieciach jednowarstwowych

rezygnujemy z wejścia zerowego – biasu

function [ W ] = init1 ( S , K )

% funkcja tworzy sieć jednowarstwową
% i wypełnia jej macierz wag wartościami losowymi
% z zakresu od -0.1 do 0.1
% parametry: S – liczba wejsć do sieci
% K – liczba neuronów w warstwie
% wynik: W – macierz wag sieci

W = ...

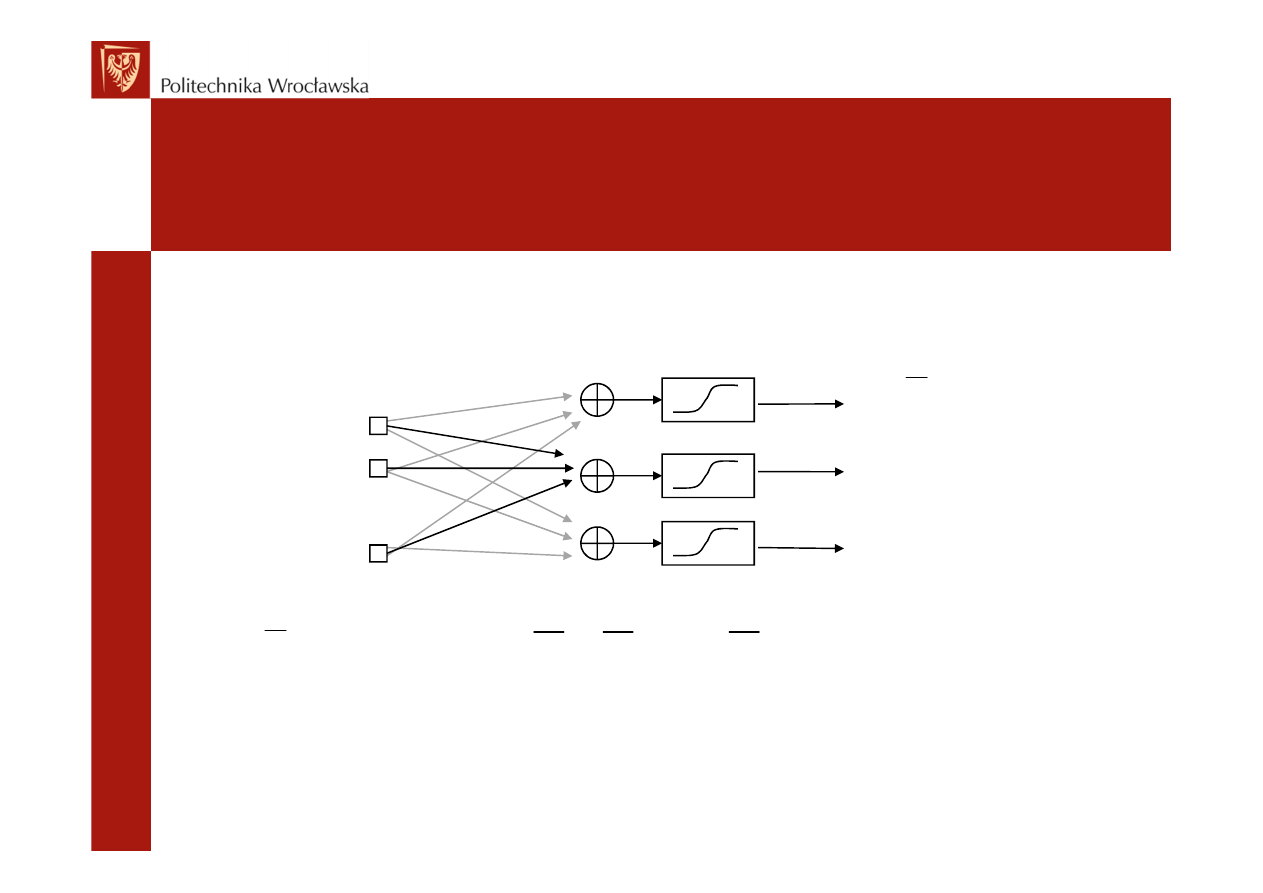
function [ W ] = init1 ( S , K )

1

x

2

x

S

x

M

M

,1

k

w

,2

k

w

,

k S

w

k

y

1

y

M

M

K

y

1

2

1

S

S

x

x

x

×

= 























X

M

1

2

1,1

2,1

,1

1,2

2,2

,2

1,

2,

,

K

K

K

S

S

K S

S K

w

w

w

w

w

w

w

w

w

×





=

= 



























W

W

W

W

L

L

L

M

M

O

M

L

1

2

1

K

K

y

y

y

×

= 























Y

M

1

u

k

u

K

u

•

dzialaj1.m

- dla sieci o danej macierzy wag W

dla podanego na wejście wektora X
oblicza wektor wyjść Y

- neurony warstwy mają sigmoidalną funkcję aktywacji

function [ Y ] = dzialaj1 ( W , X )

% funkcja symuluje działanie sieci jednowarstwowej
% parametry: W – macierz wag sieci
% X – wektor wejść do sieci
% sygnał podany na wejście
% wynik: Y – wektor wyjść sieci
% sygnał na wyjściu sieci

beta = 5 ;

U = ...

Y = ...

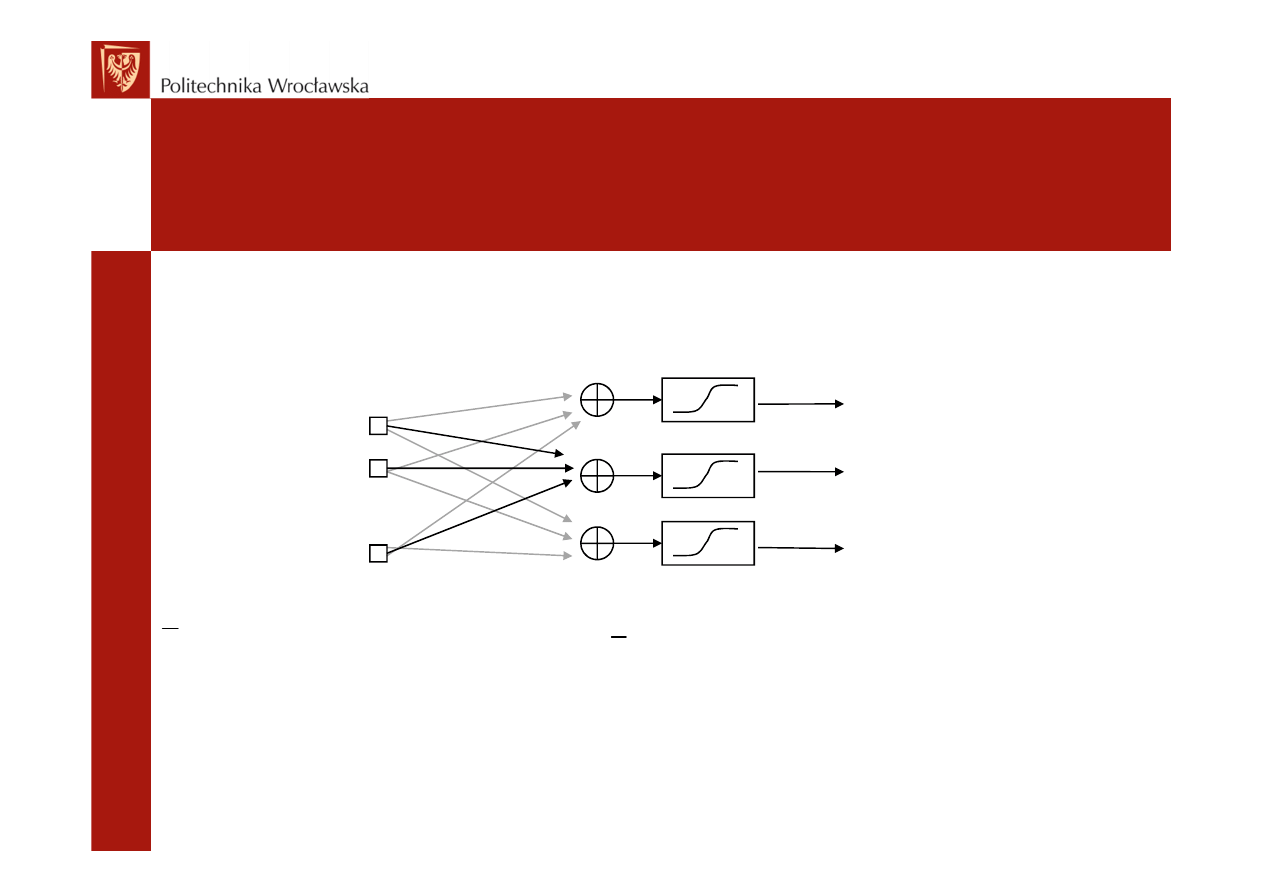
function [ Y ] = dzialaj1 ( W , X )

1

x

2

x

S

x

M

M

,1

k

w

,2

k

w

,

k S

w

k

y

1

y

M

M

K

y

1

2

1

S

S

x

x

x

×

= 























X

M

1,1

2,1

,1

1,2

2,2

,2

1,

2,

,

K

K

S

S

K S

S K

w

w

w

w

w

w

w

w

w

×

= 























W

L

L

M

M

O

M

L

1

u

k

u

K

u

1

1,1 1

1,2

2

1,

2

2,1 1

2,2

2

2,

,1 1

,2

2

,

1

?

S

S

S

S

K

K

K

K S

S

K

u

w x

w x

w x

u

w x

w x

w x

u

w

x

w

x

w

x

×

=

=

+

+

=

















+

+

























+

+









U

L

L

M

M

L

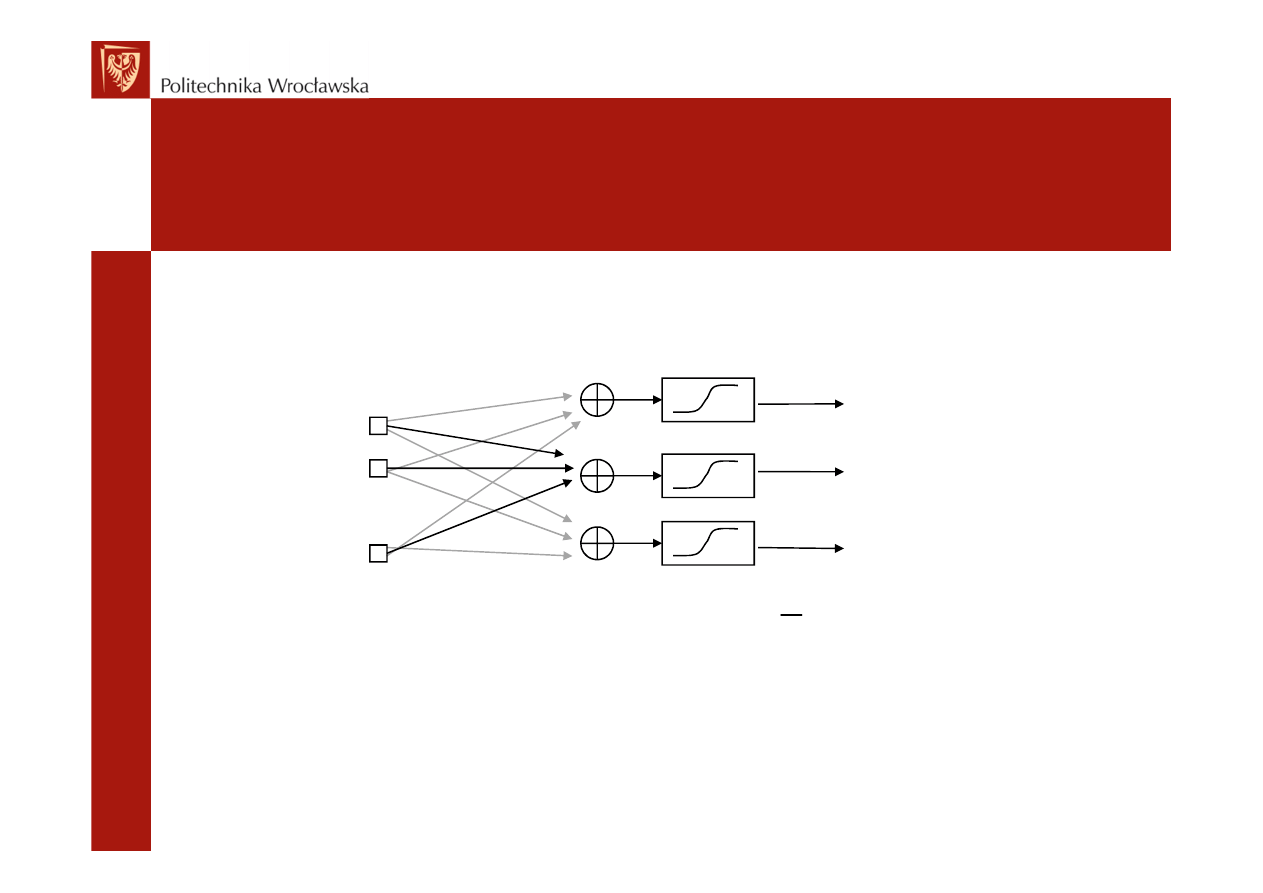
function [ Y ] = dzialaj1 ( W , X )

1

x

2

x

S

x

M

M

,1

k

w

,2

k

w

,

k S

w

k

y

1

y

M

M

K

y

( )

( )

( )

1

1

2

2

1

K

K

K

y

f u

y

f u

y

f u

×

=

= 



















































Y

M

M

1

u

k

u

K

u

»

beta = 1 ;

»

U = od -5 do 5 co 0.01;

»

Y = ...

»

plot ( U , Y )

»

hold on

»

beta = 2 , Y = ... , plot ...

»

beta = 5 , Y = ... , plot ...

»

beta = 10 , Y = ... , plot ...

( )

1

1

u

y

f u

e

β

−

=

=

+

( )

1

gdy

0

0

gdy

0

u

y

f u

u

≥



=

=



<



( )

(

)

'

...

1

f

u

y

y

=

= ⋅

−

-10

-8

-6

-4

-2

0

2

4

6

8

10

-0.5

0

0.5

1

1.5

•

przykład - rozpoznawanie zwierząt - w pliku

test1.m

przykład 1

przykład 2 przykład 3

% wejścia sieci:

P = [ 4 2 -1 ;

% we 1 - ile ma nóg

0.01 -1 3.5 ;

% we 2 - czy żyje w wodzie

0.01 2 0.01 ;

% we 3 - czy umie latać

-1 2.5 -2 ;

% we 4 - czy ma pióra

-1.5 2 1.5 ]

% we 5 - czy jest jajorodny

przykład 1

przykład 2 przykład 3

% żądane wyjścia sieci:

T = [ 1 0 0

;

% ssak

0 1 0 ;

% ptak

0 0

1 ]

% ryba

Wprzed = init1 ( 5 , 3 )

Yprzed = dzialaj1 ( Wprzed , P )

% Wpo

= ucz1

( Wprzed , P , T , 100 )

% Ypo

= dzialaj1 ( Wpo

, P )

•

ucz1.m

- dla sieci o danej macierzy wag W

uczy siec przez zadaną liczbę epok
na podanym ciągu uczącym – macierze P i T

function [ Wpo ] = ucz1 ( Wprzed , P , T , n )

% funkcja uczy sieć jednowarstwową
% na podanym ciągu uczącym (P,T)
% przez zadaną liczbę epok (n)
% parametry: Wprzed – macierz wag sieci przed uczeniem
% P – ciąg uczący – przykłady - wejścia
% T - ciąg uczący – żądane wyjścia
% dla poszczególnych przykładów
% n - liczba epok
% wynik: Wpo

– macierz wag sieci po uczeniu

•

ucz1.m

- dla sieci o danej macierzy wag W

uczy siec przez zadaną liczbę epok
na podanym ciągu uczącym – macierze P i T

function [ Wpo ] = ucz1 ( Wprzed , P , T , n )

% schemat funkcji:

% losuj numer przykładu
% podaj przykład na wejścia i oblicz wyjścia
% oblicz błędy na wyjściach
% oblicz poprawki wag
% dodaj poprawki do wag

% i to wszystko n razy

function [ Wpo ] = ucz1 ( Wprzed , P , T , n )

liczbaPrzykladow = size ( P , 2 ) ;

W = Wprzed ;

for i = 1 : n ,

% losuj numer przykładu

nrPrzykladu =

% podaj przykład na wejścia i oblicz wyjścia

X =

P ( : , nrPrzykladu ) ;

Y =

dzialaj1 ( W , X ) ;

% oblicz błędy na wyjściach

D =

T ( : , nrPrzykladu ) – Y ;

% oblicz poprawki wag

dW = ...

% dodaj poprawki do wag

W =

W + dW ;

end

% i to wszystko n razy

Wpo = W ;

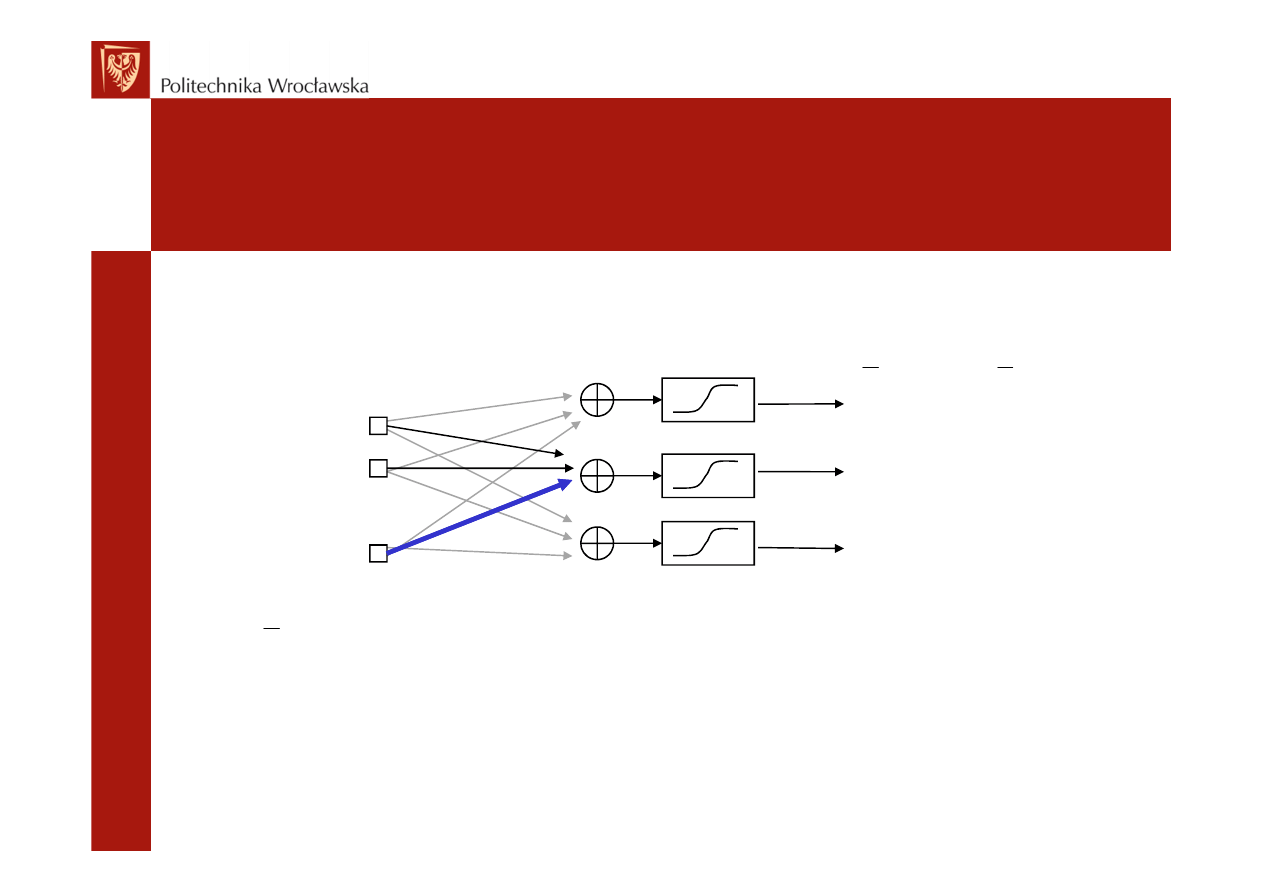
function [ Wpo ] = ucz1 ( Wprzed , P , T , n )

1

x

2

x

5

x

M

M

,1

k

w

,2

k

w

2,5

w

2

y

1

y

M

M

K

y

1

1

2

S

S

x

x

x

×

= 























X

M

1,1

2,1

,1

1,2

2,2

,

2,

2

1,

,

5

K

K

S

K S

S K

d

dw

dw

dw

dw

dw

dw

dw

w

w

d

×

= 























dW

L

L

M

M

O

M

L

1

1

2

K

K

y

y

y

×

= 























Y

M

1

u

2

u

K

u

1

1

2

K

K

t

t

t

×

 

 

 

 

 

 

M

1

1

2

K

K

d

d

d

×

= 























D

M

2,5

?

dw

=

•

przykład - rozpoznawanie zwierząt - w pliku

test1.m

przykład 1

przykład 2 przykład 3

% wejścia sieci:

P = [ 4 2 -1 ;

% we 1 - ile ma nóg

0.01 -1 3.5 ;

% we 2 - czy żyje w wodzie

0.01 2 0.01 ;

% we 3 - czy umie latać

-1 2.5 -2 ;

% we 4 - czy ma pióra

-1.5 2 1.5 ]

% we 5 - czy jest jajorodny

przykład 1

przykład 2 przykład 3

% żądane wyjścia sieci:

T = [ 1 0 0

;

% ssak

0 1 0 ;

% ptak

0 0

1 ]

% ryba

Wprzed = init1 ( 5 , 3 )

Yprzed = dzialaj1 ( Wprzed , P )

Wpo

= ucz1

( Wprzed , P , T , 100 )

Ypo

= dzialaj1 ( Wpo

, P )

•

sprawdzenie:

% wejścia sieci:

czlowiek = [ 2 ;

% we 1 - ile ma nóg

0.2 ;

% we 2 - czy żyje w wodzie - Otylia

0.2 ;

% we 3 - czy umie latać - Adam

0.1 ;

% we 4 - czy ma pióra - Winnetou

0 ]

% we 5 - czy jest jajorodny

odp = dzialaj1 ( Wpo , czlowiek )

% ???

•

sprawdzenie:

% wejścia sieci:

nietoperz = [ ? ;

% we 1 - ile ma nóg

? ;

% we 2 - czy żyje w wodzie - Otylia

? ;

% we 3 - czy umie latać - Adam

? ;

% we 4 - czy ma pióra - Winnetou

? ]

% we 5 - czy jest jajorodny

strus = ...

waz = ...

odp = dzialaj1 ( Wpo , ... )

•

do funkcji ucz1 dodaj parametry:

–

m - maksymalna liczba epok uczenia

–

e

- błąd, który sieć ma osiągnąć
- sieć będzie się uczyć do osiągnięcia zadanego błędu,

ale nie dłużej niż przez maksymalną liczbę epok

–

k

- liczba pokazów w epoce
- liczba przykładów pokazywanych w jednej epoce uczenia

do zrobienia

•

opracowany na zajęciach zestaw init1-dzialaj1-ucz1-test1
nazwij init1-dzialaj1-ucz1a-test1a

•

opracuj kolejne:

–

init1-dzialaj1-ucz1b-test1b

–

funkcja ucz1b rysuje wykres błędu średniokwadratowego podczas uczenia

(w kolejnych epokach)

do zrobienia

•

opracowany na zajęciach zestaw init1-dzialaj1-ucz1-test1
nazwij init1-dzialaj1-ucz1a-test1a

•

opracuj kolejne:

–

init1-dzialaj1-ucz1c-test1c

–

funkcja ucz1c rysuje wykres błędu średniokwadratowego

oraz wykres liczby błędnych klasyfikacji podczas uczenia

do zrobienia

•

opracowany na zajęciach zestaw init1-dzialaj1-ucz1-test1
nazwij init1-dzialaj1-ucz1a-test1a

•

opracuj kolejne:

–

init1-dzialaj1-ucz1d-test1d

–

funkcja ucz1d rysuje wykres błędu średniokwadratowego

oraz wykres liczby błędnych klasyfikacji podczas uczenia

i wykres wszystkich wag sieci

do zrobienia

•

opracowany na zajęciach zestaw init1-dzialaj1-ucz1-test1
nazwij init1-dzialaj1-ucz1a-test1a

•

opracuj kolejne:

–

init1-dzialaj1-ucz1dd-test1dd

–

funkcja ucz1dd rysuje wykres błędu średniokwadratowego

oraz wykres liczby błędnych klasyfikacji podczas uczenia

i wykresy wag poszczególnych neuronów

do zrobienia

•

opracowany na zajęciach zestaw init1-dzialaj1-ucz1-test1
nazwij init1-dzialaj1-ucz1a-test1a

•

opracuj kolejne:

–

init1-dzialaj1-ucz1e-test1e

–

funkcja ucz1e rysuje wykres błędu średniokwadratowego

oraz wykres liczby błędnych klasyfikacji podczas uczenia

i wykresy wag poszczególnych neuronów
i granice decyzyjne poszczególnych neuronów

do zrobienia

•

…

do zrobienia